Transient scrutiny of $M^X/G(a, b)/1$ queueing system with feedback, balking and two phase of service subject to server failure under Bernoulli vacation

1.   Introduction

In the analysis of real-world sustainability data, it is common to utilize continuous random distributions like the Burr-Hatke exponential (BHE) distribution. However, there are instances where the measurement of lifetimes is discrete, such as recording survival time in months or weeks. In such cases, employing a discrete random variable is more suitable. Additionally, practical problems in engineering and applied sciences often involve count phenomena, like the number of earthquakes in a year, accidents at a location, doctor visits, or insurance claims. Despite the availability of various established discrete models, there is a continued need for more flexible distributions that can effectively capture the diverse characteristics of sustainability datasets. This includes factors like asymmetry, under or over-dispersion, and variations in the failure rate function. Recognizing the significance of discrete probability models in our previous survey, we have developed and extensively explored a discrete probability distribution. This new model serves as the discrete counterpart to the BHE distribution. The BHE distribution has gained widespread utility in reliability analysis, survival modeling, and risk assessment due to its versatility in capturing diverse data patterns. Known for its flexibility in modeling right-skewed and heavy-tailed data, the BHE model is well-suited for characterizing a broad spectrum of real-world phenomena. Its adaptability extends to applications in survival analysis, providing a valuable tool for researchers to effectively model complex datasets and gain a deeper understanding of the underlying mechanisms governing observed events. For additional information and in-depth details about the BHE distribution, please refer to the citation labeled as ^[1]. If the expression for the survival function (SF) and probability density function (PDF) of a random variable $X$ conforms to the following, it is recognized as adhering to the BHE distribution

and

respectively, where $\lambda > 0$ is a scale parameter. In accordance with survival discretization techniques, one can derive a discrete BHE (DBHE) distribution. Survival discretization techniques are a set of statistical methods used to transform continuous probability distributions, such as the BHE distribution, into discrete versions suitable for practical applications. These techniques are particularly valuable when dealing with real-world data, which is often recorded in discrete units or intervals. By means of this process, the probability mass function can be obtained as

Several discrete distributions have been suggested and examined, utilizing the discrete survival function and other techniques as a foundation, including: Discrete Burr-Hatke ^[2], discrete linear exponential ^[3], discrete Pareto ^[4], discrete inverse Rayleigh ^[5], discrete inverse Weibull ^[6], discrete Lindley ^[7], new discrete extended Weibull ^[8], discrete generalized geometric ^[9], discrete Gompertz ^[10], discrete generalized exponential type II ^[11], an overview of discrete models for fitting COVID-19 datasets ^[12], discrete Ramos-Louzada ^[13], discrete generalized Rayleigh ^[14], and discrete Marshall-Olkinin ^[15], as well as the references cited within.

The structure of this article is as follows: In Section 2, we introduce the DBHE distribution, developed through the survival discretization approach. Section 3 explores a range of statistical properties. Section 4 delves into the estimation of distribution parameters using various methods. In Section 5, we present a comprehensive simulation study based on ranking techniques. Section 6 demonstrates the versatility of the DBHE distribution by analyzing different datasets. Finally, Section 7 offers concluding remarks summarizing the findings presented in this paper.

2.   The structural characteristics of the DBHE distribution

Using Eqs (1.1) and (1.3), the SF for the DBHE distribution is expressed as

where $0 < \beta = e^{-\lambda} < 1$ and $\mathbb{N} _{0} = 0, 1, 2, 3, ...$. The behavior of the SF is described by

The associated cumulative distribution function (CDF) and probability mass function (PMF) for (2.1) can be formulated as follows:

and

respectively, where $\beta$ controls the shape of the distribution. The behavior of the PMF is given by

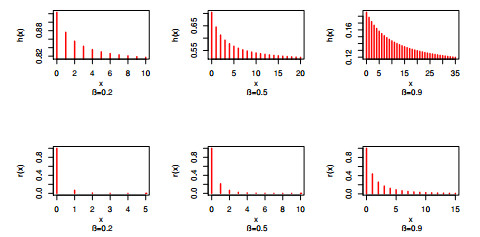
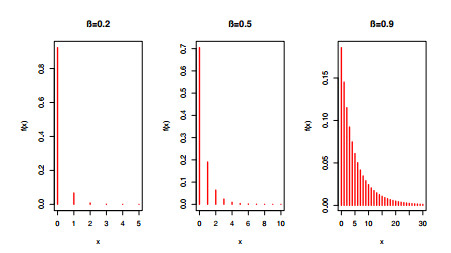
Figure 1 displays the PMF plots for different values of the parameter $\beta$.

It is worth noting that the PMF is highly effective for modeling unimodal-shaped data. Furthermore, it can also be applied to analyze asymmetric "positively-skewed" data, showcasing its versatility in capturing various data patterns. The hazard rate function (HRF) can be formulated as

The reversed hazard rate function (RHRF) is expressed as follows:

The hazard rate is a measure of an item's death rate at a specific age $x$ and is a component of the broader hazard function equation. This equation evaluates the probability that an item, having survived up to a certain time $t$, will continue to endure beyond that point. In essence, it quantifies the likelihood that an item surviving one moment will persist to the next one. The hazard rate is particularly relevant to non-repairable items and is sometimes referred to as the failure rate. Its significance extends to the design of secure systems in various domains such as commerce, engineering, finance, insurance, and regulatory industries. It can be expressed as a ratio of probability density to its corresponding survival function. Conversely, the reversed hazard rate of a random life is defined as the ratio between the life probability density and its distribution function. This concept holds significance in the analysis of censored data and finds applications in fields such as forensic sciences. Figure 2 illustrates the HRF and RHRF plots for varying values of the parameter $\beta$.

The observation of decreasing HRF and RHRF carries significant implications across multiple disciplines. This includes reliability engineering, where it signifies a decrease in system failure rates over time, healthcare, where it indicates improving survival probabilities, finance, where it suggests decreasing default probabilities, environmental sciences, where it hints at slowed environmental degradation, manufacturing, where it implies improved product quality, and public policy, where it informs safety measures and disaster preparedness, highlighting the importance of statistical analysis and hazard rate modeling for informed decision-making and process optimization in risk assessment and reliability domains.

3.   Some statistical features

3.1.   Statistical moments and associated notions

The moment generating function (MGF) and cumulant generating function (CGF) are essential tools in probability theory and statistics, offering valuable insights and advantages in various aspects of statistical analysis and probability modeling. Consider $X$ as a random variable conforming to the DBHE distribution. The MGF, denoted as $\Pi_{X}\left(t\right)$, and the CGF, denoted as $K_{X}\left(t\right)$, can be represented in terms of generalized hypergeometric functions as follows:

and

where $\lambda_{1} = \frac{-1}{\ln\beta}$, $\lambda_{2} = \frac{(\beta-2)\ln \beta+1-\beta}{(-1+\beta)\ln\beta}, \lambda_{3} = \frac{-1+2\ln\beta}{\ln\beta}$, and $\lambda_{4} = \frac{1-\ln\beta-\beta}{(-1+\beta)\ln\beta}$. The equation represented by (3.1) can be derived using the Maple software, utilizing the $hypergeom(.)$ function, which is a generalized hypergeometric function. This mathematical function finds applications across diverse fields such as complex analysis, differential equations, and statistical mechanics. Renowned for its role as a solution to the hypergeometric differential equation, it is extensively employed in expressing solutions to problems characterized by symmetry, particularly those featuring spherical or cylindrical symmetry. The initial four moments of the DBHE distribution can be formulated as follows:

and

where $A = \frac{\beta\left[ \left(-2+\beta\right) \ln\beta+1-\beta\right] }{1+2(\ln\beta)^{2}-3\ln\beta}$, $B = \frac{-1+\ln\beta}{\ln\beta}$, $C = \frac{(-3+2\beta)\ln\beta+1-\beta}{(-1+\beta)\ln\beta}$, $D = \frac {-1+3\ln\beta}{\ln\beta}$, $E = \frac{(-2+\beta)\ln\beta+1-\beta}{(-1+\beta)\ln\beta}$. Let $n = [n_{1}, n_{2}, ...]$, $p = nops(n)$, $d = [d_{1}, d_{2}, ...]$, and $q = nops(d)$. The $hypergeom(n, d, z)$ calling sequence is the generalized hypergeometric function $F(n, d, z)$. This function is frequently denoted by $pFq(n, d, z)$. For the variable $z$, the $pFq(n, d, z)$ can be formulated as

where

The Pochhammer symbol can be listed as

For additional information, please refer to the Maple software's library. Using Eqs 3.3–3.6, the variance, skewness and kurtosis can be derived as

and

Table 1 provides a compilation of numerical descriptive measures that serve as valuable tools for gaining insights into the attributes of the DBHE distribution. These measures aid researchers and analysts in comprehending aspects like central tendency, variability, shape, and other critical properties. The choice of which measures to emphasize may vary depending on the specific analysis and application.

Based on the information in Table 1, it's evident that as $\beta$ approaches 1, the mean and variance of the DBHE distribution exhibit an increase, whereas the skewness and kurtosis experience a decrease. Moreover, the presented model demonstrates its capability to effectively model distributions that are positively skewed and leptokurtic in nature. Leptokurtic is a statistical term used to describe a distribution that has heavier tails and a sharper peak (higher kurtosis) compared to a normal distribution. This indicates that the distribution has more extreme values or outliers than a normal distribution, leading to a higher concentration of data points in the center and in the tails. In simple terms, a leptokurtic distribution has a more peaked and less spread-out shape than a normal distribution.

3.2.   Dispersion index and variation coefficient

The index of dispersion (IOD) quantifies the absolute spread of data, while the coefficient of variation (COV) gauges the relative spread. Both metrics are valuable across diverse fields like epidemiology, finance, and quality control, where understanding data variability is crucial for decision-making. An IOD below 1 suggests underdispersion, indicating data points cluster closely around the mean. In contrast, values exceeding 1 signal overdispersion, revealing greater variability than expected by the assumed model. An IOD of 1 suggests a random distribution where spread is proportional to the mean. When interpreting the COV, a low COV indicates minor relative variability compared to the mean, while a high COV suggests significant relative variability. These measures offer essential insights for effective analysis and decision-making in various domains. Consider $X$ as a random variable conforming to the DBHE distribution, then the IOD and the COV can be formulated as

and

The statistics for the DBHE distribution, including the IOD and COV can be reported in Table 2.

Based on the information in Table 2, it's evident that as $\beta$ approaches 1, the IOD increases while the COV decreases. Additionally, the proposed model is best suited for modeling data with overdispersion characteristics.

3.3.   Order statistics and L-moment statistics

Consider a scenario where we have a set of $n$ random variables, denoted as $X_{1}, X_{2, }$...$, X_{n}$, which are arranged in nondecreasing order and expressed as $X_{1:n}\leq X_{2:n}\leq \;...\leq X_{n:n}$. In the context of order statistics, it's important to note that there are no constraints placed on whether these $X_{i}^{, }$s are independent or identically distributed. However, many well-established results pertaining to order statistics are derived under the classical assumption that the $X_{i}^{, }$s are independent and identically distributed (iid). The CDF of the $i$th order statistic is expressed as follows:

where $\Phi_{m}^{(n, k)} = \left(-1\right) ^{j}\binom{n}{k}\binom{n-k}{j}$. Moreover, the associated PMF of the $i$th order statistic is given by

Thus, the $r$th moments of $X_{i:n}$ can be expressed as

L-moments are statistical summary measures for probability distributions, introduced by ^[11]. They share similarities with ordinary moments but are calculated using linear functions applied to the ordered data values. The L-moment of a random variable $X$ is expressed as follows:

Using (3.15), several statistical measures based on L-moment statistics can be computed, including: mean = $\lambda_{1},$ coefficient of skewness = $\frac{\lambda_{3} }{\lambda_{2}}$, and coefficient of kurtosis. = $\frac{\lambda_{4}}{\lambda_{2}}$. In summary, order statistics help organize and analyze data by arranging it in a specific order, while L-moment statistics provide robust and efficient tools for estimating distribution parameters and understanding the shape and characteristics of a distribution. Higher-order L-moments provide information about the shape and tail characteristics of the distribution. Both concepts play important roles in various statistical applications, particularly when dealing with nonparametric or nonstandard distributions.

4.   Various estimation approaches

4.1.   Maximum product of spacings estimator (MPSE)

In this section, we delve into the estimation of DBHE parameter through the MPSE method, utilizing a complete sample. Consider a random sample $X_{1}$, $X_{2} , \ldots, X_{n}$ drawn from the DBHE distribution. For $j = 1, 2, \ldots, m+1$, let

be the uniform spacings of a random sample from the DBHE model, where $F\left(x_{(0)}|\beta\right) = 0$, $F\left(x_{(m+1)}|\beta\right) = 1$ and $\sum_{j = 1}^{m+1}W_{j}(\beta) = 1$. The MPSE of $\beta$, say $\widehat{\beta }_{MPS}$, can be derived by maximizing the geometric mean of the spacings

with respect to the parameter $\beta$.

4.2.   Anderson-Darling and right-tail Anderson-Darling estimators

Assume a random sample $X_{1}$, $X_{2} , \ldots, X_{n}$ drawn from the DBHE model. The Anderson-Darling estimator (ADE) is another type of minimum distance estimator. The ADE of the DBHE parameter, say $\widehat{\beta}_{AD}$, is derived by minimizing

Concerning the parameter $\beta$, the model is subject to optimization, while the right-tail Anderson-Darling estimator (RADE) of the model parameter is achieved through minimization

with respect to the parameter $\beta$.

4.3.   Maximum likelihood estimation (MLE)

Consider a random sample $X_{1}$, $X_{2} , \ldots, X_{n}$ drawn from the DBHE model. The log-likelihood function ($L$) for the DBHE distribution can be represented as follows:

Taking the derivative of the log-likelihood with respect to $\beta$ and equating it to zero, we obtain

Finding an analytical solution for this equation is not possible. Therefore, it requires the application of a numerical iterative method, like the Newton-Raphson method, within the R software, or other optimization techniques.

4.4.   Weighted (least-squares) estimators

Consider a random sample from the DBHE model, with order statistics $X_{(1)}, X_{(2)}, \cdots, X_{(m)}$. The least-squares estimator (LSE) of the DBHE parameter, denoted as $\widehat{\beta}_{LS}$, can be obtained by solving the nonlinear equation defined as follows:

with respect to the parameter $\beta$, where

Note that the solution of $\Delta_{\beta}\left(x_{(j)}|\beta\right)$ can be obtained numerically. The weighted LSE (WLSE), say $\widehat{\beta}_{WLS}$, can be derived by solving the nonlinear equation defined by

with respect to the parameter $\beta$.

4.5.   Cramer-Von-Mises estimator (CVME)

The CVME arises as the disparity between the estimated CDF and the empirical CDF. Estimating the CVME of the DBHE parameter involves solving the non-linear equation defined as follows:

with respect to the parameter $\beta$, where $\Delta_{\beta}\left(x_{(j)}|\alpha, \beta\right)$ is defined in Eq (4.7).

4.6.   Percentile estimator (PCE)

Consider $z_{j} = j/\left(m+1\right)$ to be an unbiased estimator of $F\left(x_{(j)}|\beta\right)$. Hence, the PCE of the parameter $\beta$, denoted by $\widehat{\beta}_{PC}$, can be reported by minimizing

with respect to the parameter $\beta$ where $D\left(z_{j}\right) = F^{-1}\left(x_{(j)}|\beta\right)$ is the quantile function of the DBHE model.

5.   Simulation ranking techniques: different estimators

In this segment, we assess the effectiveness of MPSE, ADE, MLE, LSE, RADE, PCE, CVME, and WLSE concerning the sample size '$n$', and utilizing the R software with DEHB parameters. The process of generating a random variable $X$ from the DEHB distribution begins by generating the value $Y$ from the continuous distribution. Subsequently, the obtained $Y$ value undergoes discretization to produce $X$, where $X$ is defined as the greatest integer less than or equal to $Y$. To replicate this, we perform Markov Chain Monte Carlo (MCMC) simulations using various schemes. The assessment is carried out through a simulation study:

(1) Generate $N = 10000$ samples of various sizes "$n_{i}; i = 1, 2, 3, 4, 5$" from the DBHE model as follows:

● Scheme I: $\beta = 0.2 \; | \; n_{1} = 50, \ n_{2} = 150, \ n_{3} = 300, \ n_{4} = 700, \ n_{5} = 1000.$

● Scheme II: $\beta = 0.4 \; | \; n_{1} = 50, \ n_{2} = 150, \ n_{3} = 300, \ n_{4} = 700, \ n_{5} = 1000.$

● Scheme III: $\beta = 0.7 \; | \; n_{1} = 50, \ n_{2} = 150, \ n_{3} = 300, \ n_{4} = 700, \ n_{5} = 1000.$

● Scheme III: $\beta = 0.9 \; | \; n_{1} = 50, \ n_{2} = 150, \ n_{3} = 300, \ n_{4} = 700, \ n_{5} = 1000.$

(2) Compute the MPSE, ADE, MLE, LSE, RADE, PCE, CVME, and WLSE for the $10000$ samples, say $\widehat{\beta}_{k}$ for $k = 1, 2, ..., 10000.$

(3) Caculate the bias, mean squared errors (MSE), and mean relative errors (MRE) for $N = 10000$ samples as

The MSE measures the average squared difference between predicted and actual values, with a lower MSE indicating closer predictions to actual values. On the other hand, MRE expresses the average relative difference as a percentage, offering insights into accuracy and normalization across varying data magnitudes. MSE emphasizes precision by squaring errors, while MRE considers the relative magnitude of errors. MSE can be sensitive to outliers, while MRE, in percentage terms, may be less influenced. Despite MSE being less interpretable due to squared units, MRE, as a percentage, provides a standardized measure of error. The choice between MSE and MRE depends on data characteristics and the desired focus on precision or accuracy in predictions.

(4) The empirical results of simulation are reported in the Tables 3–7.

From Tables 3 to 7, it is evident that as the sample size '$n$' increases, the bias of the parameter $\beta$ tends to decrease toward zero. Similarly, both the MSE and MRE of the DBHE parameter also decrease toward zero with increasing sample size '$n$'. These findings indicate the consistent performance of the derived estimators. Furthermore, all estimation methods demonstrate good performance across different sample sizes, with Table 7 highlighting that the ADE method performs the best.

6.   Sustainability data analysis: goodness-of-fit

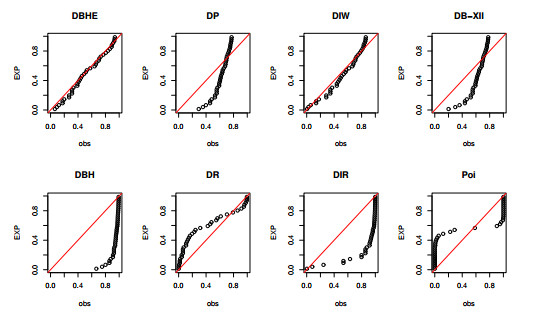
In this section, we will delve into the significance of the proposed distribution by analyzing various datasets from different domains. We will evaluate how well the DBHE distribution fits these datasets in comparison to several other competing distributions, including the discrete Pareto (DP), discrete Rayleigh (DR), discrete inverse Rayleigh (DIR), discrete Burr-Hatke (DBH), Poisson (Poi), and discrete Burr-XII (DB-XII) distributions. To assess the goodness-of-fit (GOF), we will employ various criteria, which encompass the negative log-likelihood ($-L$), Akaike information criterion (AIC), Bayesian information criterion (BIC), corrected Akaike information criterion (CAIC), Hannan-Quinn information criterion (HQIC), and the Kolmogorov-Smirnov (KS) test, along with its associated P-value. In the interpretation of AIC, CAIC, BIC, and HQIC, lower values indicate a better balance between model fit and simplicity. Consequently, the model with the lowest AIC, CAIC, BIC, and HQIC is considered the most suitable among the available options. BIC imposes a stricter penalty on complex models in comparison to AIC and CAIC, displaying a more conservative preference for selecting simpler models, especially in scenarios with smaller sample sizes. On the other hand, since there is a limited number of frequencies for each observation in datasets I, II, and IV the Pearson's Chi-square statistic cannot be employed for an inference test. Therefore, the KS measure is adequate in this case.

6.1.   Dataset I: Failure times

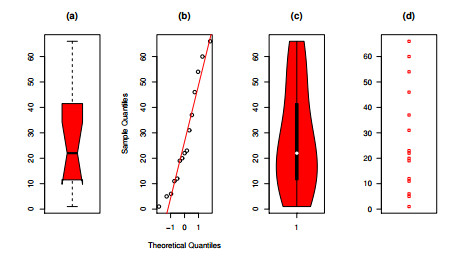
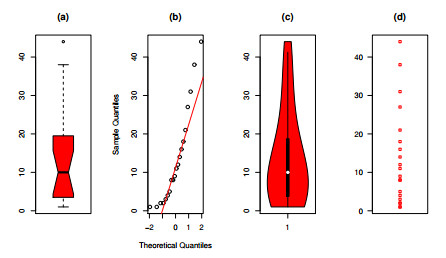
The first dataset pertains to the time until failure of 15 electron components during an accelerated life test (refer to ^[16]). To explore the characteristics of dataset I, we have created nonparametric plots, which include box plots, normal quantile-quantile (Q-Q) plots, violin plots, and strip plots. For additional details and visual representations, please refer to Figure 3.

The MLEs along with their respective SE, C.I for the parameter(s), and GOF test results for this dataset can be found in Tables 8 and 9. Notably, the values of $-L$, AIC, BIC, CAIC, HQIC, and KS are all lower, and the P-value is higher for the DBHE distribution in comparison to the values obtained for the other models. As a result, based on this analysis of the real dataset, it appears that the proposed distribution is a highly competitive model.

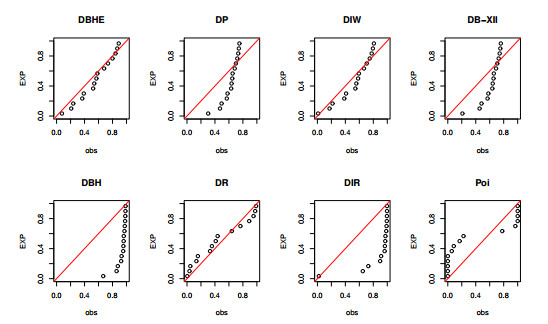
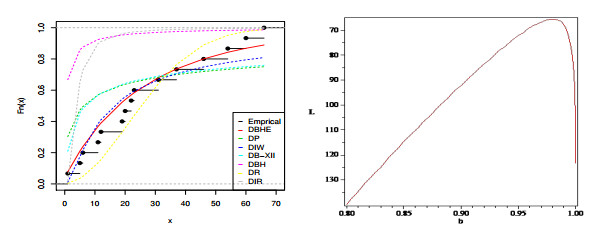
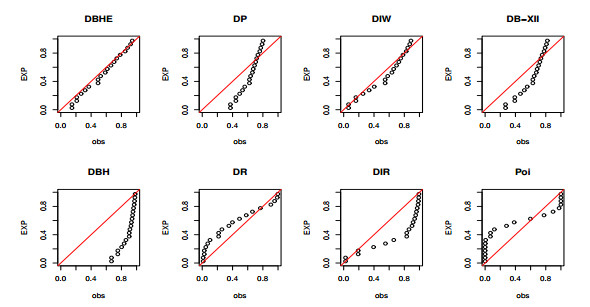
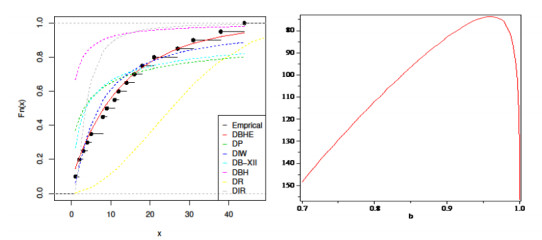
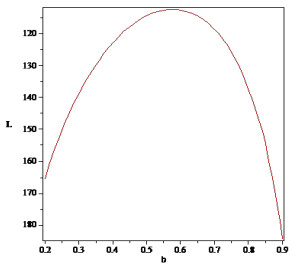
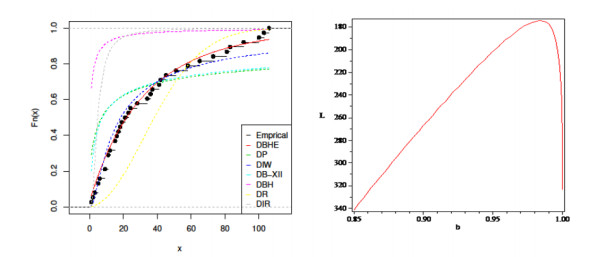
Figure 4 depicts the probability-probability (P-P) plot for dataset I, while Figure 5 showcases the estimated CDFs and the profile of the $L$ for the parameter $\beta$ in dataset I. Figure 5 reinforces our empirical findings, supporting the conclusion that the DBHE distribution is a more suitable fit for analyzing this data. Additionally, it highlights that the estimator for $\beta$ is indeed unique.

Table 10 provides a compilation of various estimation methods applied to dataset I within the framework of the proposed model.

The analysis revealed that all estimation methods perform satisfactorily for data fitting, with the WLSE approach emerging as the most effective among them.

6.2.   Dataset II: Leukemia remission times

This dataset pertains to leukemia remission times, measured in weeks, for a total of 20 patients, as described in ^[17], utilizing the concept of discretization. In order to delve into the characteristics of dataset II, we have generated nonparametric plots, including box plots, normal Q-Q plots, violin plots, and strip plots. For more comprehensive information and visual representations, please consult Figure 6.

The MLEs along with their corresponding SE, C.I for the parameter(s), and the results of the GOF tests for this dataset are provided in Tables 11 and 12. Importantly, it's noteworthy that the values of $-L$, AIC, BIC, CAIC, HQIC, and KS all exhibit lower values, while the P-value is higher when considering the DBHE distribution in comparison to the values obtained for the other models. Consequently, based on this comprehensive analysis of the real dataset, it is evident that the proposed distribution stands out as a highly competitive model.

Figure 7 illustrates the P-P plot for dataset II, while Figure 8 presents the estimated CDFs and the profile of the $L$ for the parameter $\beta$ in dataset II. Figure 8 reaffirms our empirical observations, providing further support for the suitability of the DBHE distribution in analyzing this dataset. Furthermore, it underscores the uniqueness of the estimator for $\beta$.

Table 13 presents an overview of diverse estimation techniques applied to dataset II under the proposed model framework.

The examination indicated that all estimation methods demonstrate satisfactory performance in terms of fitting the data, with the ADE approach emerging as the most effective among the available methods.

6.3.   Dataset III: Carious teeth

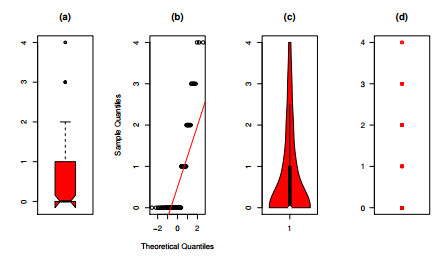
The third dataset pertains to the count of carious teeth among the four deciduous molars. Detailed information regarding this dataset can be referenced in the work of Krishna and Pundir, as cited in ^[4]. In order to investigate the attributes of dataset III, we have generated nonparametric plots, which encompass box plots, normal Q-Q plots, violin plots, and strip plots. For more comprehensive information and visual representations, see consult Figure 9.

The MLEs along with their corresponding SE, C.I for the parameter(s), and the results of the GOF tests for this dataset are available in Tables 14–16. Remarkably, it is evident that the DBHE distribution shows lower values for the chi-squared ($\chi^{2}$) statistic while yielding higher p-values in comparison to the values obtained for the other models. As a result, this comprehensive analysis of the real dataset strongly suggests that the proposed distribution is a highly competitive model.

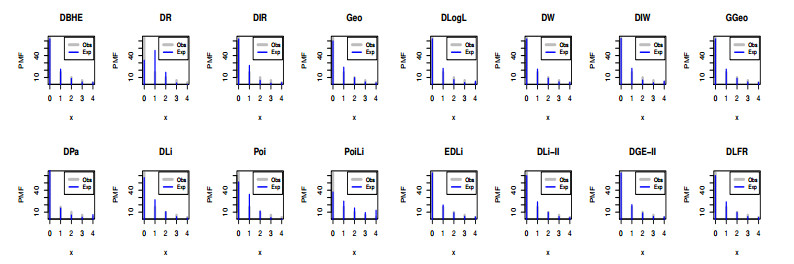
Figure 10 illustrates the observed and expected PMFs for dataset III. Figure 11 displays the $L$ profile of the DBHE model parameters for dataset III, and it's noteworthy that the estimators are distinct and singular.

Table 17 offers a consolidated overview of diverse estimation techniques employed for dataset III within the context of the proposed model.

The analysis has shown that all the estimation methods perform well in terms of fitting the data, with the MPSE approach being the most effective among them.

6.4.   Dataset IV: COVID-19 pandemic

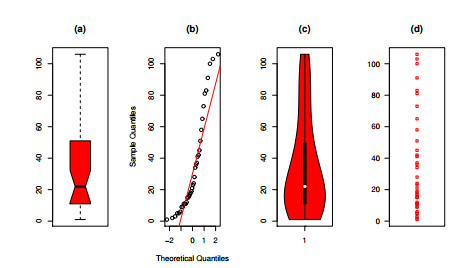
The forth dataset comprises the number of deaths attributed to coronavirus in the Punjab region during the period from March 24, 2020, to April 30, 2020. The dataset is as follows: 1, 2, 3, 5, 5, 6, 9, 9, 11, 11, 11, 12, 15, 15, 16, 17, 18, 19, 21, 23, 24, 28, 34, 36, 37, 41, 42, 45, 51, 58, 65, 73, 81, 83, 91,100,103,106. To examine the attributes of dataset IV, we have generated non-parametric plots, encompassing box plots, normal Q-Q plots, violin plots, and strip plots. For more in-depth information and visual representations, please consult Figure 12.

The MLEs along with their corresponding SE, C.I for the parameter(s), and the results of the GOF tests for this dataset can be located in Tables 18 and 19. Significantly, it is evident that for the DBHE distribution, the values of $-L$, AIC, BIC, CAIC, HQIC, and KS all show lower values, while the P-value is higher when compared to the values obtained for the other models. Consequently, based on this comprehensive analysis of the real dataset, it is clear that the proposed distribution emerges as a highly competitive model.

Figure 13 presents the P-P plot for dataset IV, whereas Figure 14 exhibits the estimated CDFs and the profile of the $L$ for the parameter $\beta$ in dataset IV. Figure 14 further reinforces our empirical observations, providing additional support for the appropriateness of the DBHE distribution in analyzing this dataset. Additionally, it emphasizes the uniqueness of the estimator for $\beta$.

Table 20 offers a comprehensive compilation of various estimation techniques applied to dataset IV within the context of the proposed model framework.

The examination indicated that all estimation techniques adequately achieve data fitting, with the WLSE method standing out as the most efficient among them.

7.   Concluding remarks and future work

This article centers on a discrete distribution with one parameter, developed using the survival discretization approach, referred to as the DBHE distribution. The statistical properties of the DBHE model have been derived and expressed in terms of generalized hypergeometric functions. It has been established that the DBHE model is particularly suitable for modeling right-skewed datasets characterized by leptokurtic shapes. The presented discrete distribution can serve as a valuable statistical tool for modeling a decreasing HRF in the presence of outlier observations. The DBHE parameter has been estimated using various approaches, including MPSE, ADE, MLE, LSE, RADE, PCE, CVME, and WLSE. Simulation studies conducted across different sample sizes, revealed that all these techniques are effective in estimating the DBHE parameter, with the ADE approach performing best. Furthermore, the study includes the analysis of four real datasets to demonstrate the effectiveness of the DBHE distribution. It was observed that the DBHE distribution outperforms all other competing distributions across all aspects of the analysis. Looking ahead, the article hints at future directions, including the proposal and detailed discussion of bivariate extensions of the DBHE models, as well as the exploration of regression models and the integer-valued autoregressive of order one process along with their applications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2023/01/27231).

Conflict of interest

The authors declare no conflicts of interest.