Reversible codes and applications to DNA codes over $F_{4^{2t}}[u]/(u^2-1)$

1.   Introduction

Lattices and rough sets serve as potent mathematical tools extensively applied in efficiently resolving numerous significant problems. Lattices find their utility in computer science and approximation spaces ^[36], while the genesis of rough sets can be traced back to Pawlak's introduction in the early 1982s via the approximation space ^[55,56]. Pawlak notably investigated a rough membership function ^[57].

However, the stringent requirement of an equivalence relation imposes certain limitations on the applications of conventional rough set theory. In response, various generalizations of the theory have surfaced, employing either arbitrary or specific relations. In the paapers ^[70,71], Yao pioneered this avenue of research. Here, specific relations were considered to establish distinct types of generalized rough sets, encompassing tolerance ^[42,43], and a general relation (see for instance ^{[5,7,24,25,26,46,47,54,58]}). Topological structures were used in rough set generalizations (for examples the papers ^[4,8,10,11]), fuzzy set applications (see ^[1,3,50]), and covering ^[2].

The abstract consideration of topological structures involves analyzing the universal set $\mathfrak{U}$ using its family of open sets. Each space within this framework can be viewed as a lattice, denoted $\mathfrak{LA}(\mathfrak{U})$, associated with every subset of $\mathfrak{U}$. The study of these lattices is contingent upon the elements of $\mathfrak{LA}(\mathfrak{U})$, not the points in $\mathfrak{U}$. Initial explorations into topological extensions were conducted for Kolmogorov spaces ^{[13,15,30,45]}. Diverse extension methodologies include employing ideals ^{[28,29,53,68]}, algebraic concepts ^[5,32,51], matroids ^[49,62,65], graphs ^[5,21,22], and preordered topological structures ^{[9,20,28,29,31,33,34,35,60,69]}. In the realm of topology, many researchers regard open sets as points in the topology lattice, with Pawlak's traditional approximation structure resembling a quasi-discrete topology where each subset is open ^[48,61,63]. This concept introduces rough sets that may not necessarily be open. Thus, within a quasi-discrete topology, two distinct types of sets exist: Pawlak's upper and lower approximations manifest as open sets. In the topological lattice, these open sets correspond to the interior and closure of sets within a quasi-discrete topology. Furthermore, the lower (or upper) approximation in the topological lattice signifies the largest (or smallest) open set containing (or contained within) a given set, termed as the greatest lower bound (or least upper bound) in the lattice. Zhou and Hu ^[76] explored rough sets on a complete completely distributive lattice.

In fact, Zhou and Hu focused on the crisp power set of a universe, represented as an atomic Boolean lattice. Pawlak's rough sets were introduced, where equivalence classes were identified as elements of this power set lattice. The study then delved into lower and upper approximations based on the lattice order relation, leading to the exploration of natural ideals within a lattice. To extend this line of inquiry, they introduced a novel perspective by investigating rough sets from the standpoint of lattice theory. They took the lattice itself as the universe and explored the definition of lower and upper approximations within this lattice context. Building upon Järvinen's framework, Mordeson's approximation operators, and the work of Qi and Liu ^[59] on rough sets and generalized rough sets, their contribution lies in defining rough sets on a complete completely distributive (CCD) lattice using an arbitrary binary relation. Unlike existing approaches that primarily focus on covers or partitions, they proposed a unified framework for the study of rough sets by employing a binary relation on a CCD lattice. This framework encompasses rough sets based on ordinary binary relations, rough fuzzy sets, and interval-valued rough fuzzy sets. The adoption of a binary relation introduces a new level of generality, allowing them to establish a connection between relations and partitions on CCD lattices. Furthermore, their paper established a pair of lower and upper approximation operators on CCD lattices based on this binary relation, offering a broader generalization of rough sets. They emphasized that their approach is not only applicable to CCD lattices but also extends the understanding of rough sets on Boolean lattices and power lattices. By demonstrating that the rough sets defined in ^[17] are special cases within their framework, they underscored the uniqueness and irreplaceability of their proposed rough sets.

In summary, their manuscript contributes significantly to the field by introducing a comprehensive study of rough sets on lattices, specifically CCD lattices, through the innovative use of binary relations. We believe that this approach brings a fresh perspective to rough set theory, paving the way for new horizons in the understanding and application of rough sets, while others investigated them on general lattices (for example, see the references ^{[12,16,17,27,52,66,67]}).

The applications of rough sets in many fields, such as information fusion ^[74], feature selection ^[37,75], fuzzy covering based rough sets ^[38,39], multi-level granularity entropies for fuzzy coverings ^[39], fuzzy-$\beta$-covering-based multigranulation rough sets ^[40,41], and three-way decision ^[77].

Our research introduces lower and upper extension approximations within an extension lattice framework, exhibiting promise for integration into practical applications. These extension approximations demonstrate versatility, enabling their integration with specific applications in diverse domains. In data science and artificial intelligence, their capability to discern detailed relationships among elements could enhance pattern recognition and data analysis methodologies, contributing to more refined decision-making processes. Moreover, their finer granularity in defining rough and exact sets holds the potential for modeling and handling uncertain or imprecise data in practical applications, such as risk management systems or predictive modeling in financial markets. The advantages of our introduced extension approximations lie in their ability to capture more detailed relationships among elements, potentially leading to enhanced pattern recognition, data analysis, and decision-making processes. The finer granularity they provide in defining rough and exact sets facilitates more accurate and sophisticated modeling of uncertain or imprecise data, offering improved insights and solutions in real-world applications. Despite these advantages, it is essential to consider the limitations and disadvantages of existing methods that our proposed approach seeks to address. Some methods may lack the precision and detailed relationships offered by our extension approximations, making them less suitable for certain applications. Empirical validations and targeted studies are crucial steps toward demonstrating the efficacy and practical utility of our approach within specific domains.

In addition to our contribution, the paper explores the extension of topological structures through lattices, employing an equivalence relation to obtain an extension topological lattice. The comparison between the topological lattice and its extension is scrutinized, and various types of rough-bounded distributive lattices and their properties are investigated. The isomorphism between topology and its extension holds significant implications, particularly in practical applications involving data analysis, decision-making, and information retrieval systems. Understanding this isomorphism facilitates a more comprehensive characterization of relationships and structures within complex datasets. One practical significance lies in the realm of data representation and modeling. The isomorphism provides a bridge between the original topology and its extended form, enabling a seamless translation of concepts and relationships. This translation facilitates more accurate and efficient representations of complex data structures, which is invaluable in fields like pattern recognition, where precise data representations are critical.

Furthermore, in decision-making processes, the isomorphism allows for a clearer understanding of relationships between different elements or features within datasets. This clarity aids in more informed decision-making by revealing underlying connections or similarities that might otherwise remain obscured without the isomorphic mapping. Moreover, the isomorphism between topology and its extension has implications in the realm of computational efficiency. It can streamline algorithms and computations by leveraging the correspondences between the original topology and its extended version. This streamlined approach could enhance the efficiency of various computational processes, such as data retrieval or analysis. In essence, the isomorphism between topology and its extension offers practical applications in data representation, decision-making, and computational efficiency. Its ability to bridge the gap between different topological structures enriches our understanding of complex datasets and enhances the efficacy of algorithms and processes utilized in various real-world applications. Furthermore, the paper acknowledges the importance of fuzzy lattices in the context of rough set theory. While our current discussion primarily centers on the representation of topological structures using lattices and rough sets, we recognize the need to explore fuzzy lattices to address the complexities inherent in data with fuzzy relationships. This acknowledgment opens avenues for future research endeavors, aiming to provide a more comprehensive understanding of how rough set theory can accommodate and address the nuances of real-world data.

2.   Basic concepts and properties

Some basic concepts and results on lattices are introduced and studied in the papers ^{[14,18,19,34,64]}. The collection of topologies on fixed set $X$ is a partially ordered. $\tau_{1}$ $\leq$ $\tau_{2}$ if $\tau_{1}$ $\subseteq$ $\tau_{2}$. In other words, if every open set of $\tau_{1}$ is an open set of $\tau{2}$, then $\tau_{1}$ is weaker than $\tau_{2}$. We recall the following definitions which are useful in the sequel.

2.1.   Lattices

Definition 2.1. ^[14] A lattice $\mathfrak{LA}$ = $(\mathfrak{U}, \leq)$ is distributive if either $x\wedge (y\vee z) =$ $(x\wedge y)\vee (x\wedge z)$ or $x\vee (y\wedge z) =$ $(x\vee y)\wedge (x\vee z)$ is satisfied, $\forall$ $x, y, z\in \mathfrak{U}$. It is bounded if it has zero as a smallest element and unit as a greatest element of $\mathfrak{LA}$.

Definition 2.2. ^[14] An element $x'$ $\in \mathfrak{U}$ is the complement of $x$ $\in \mathfrak{U}$ if $x \vee x' = 1$ and $x\wedge x' = 0$. A bounded, complemented, and distributive lattice is called a Boolean lattice.

Definition 2.3. ^[14] An equivalence relation $\Omega$ on $\mathfrak{LA}$ is called congruence if $\forall$ $a, b, c, d$ $\in \mathfrak{U}$ such that (s.t.) $a$ $\Omega$ $b$ and $c$ $\Omega$ $d$. Moreover,

(i) If $(a\vee c)$ $\Omega$ $(b\vee d)$, then $\Omega$ is called a congruence on the join semilattice $(\mathfrak{LA}, \vee)$.

(ii) If $(a\wedge c)$ $\Omega$ $(b\wedge d)$, then $\Omega$ is called a congruence on meet semilattice $(\mathfrak{LA}, \wedge)$.

(iii) If $(a\vee c)$ $\Omega$ $(b\vee d)$ and $(a\wedge c)$ $\Omega$ $(b\wedge d)$, then $\Omega$ is called a congruence on the lattice $\mathfrak{LA}$.

Definition 2.4. ^[20] Let $\mathfrak{LA}$ be a lattice. Then,

(i) A nonempty subset $\mathcal{J}$ of $\mathfrak{LA}$ is called an ideal if

(a) $a, b\in \mathcal{J}$ implies $a\vee b\in \mathcal{J}$.

(b) $a\in \mathfrak{LA},$ $b\in \mathcal{J}$, and $a\le b$ imply $a\in \mathcal{J}$.

Thus, the ideal is a nonempty down set closed under join.

(ii) A nonempty subset $\mathcal{G}$ of $\mathfrak{LA}$ is called a filter if

(a) $a, b\in \mathcal{G}$ implies $a\wedge b\in \mathcal{G}$.

(b) $a\in \mathfrak{LA},$ $b\in \mathcal{G}$, and $a\ge b$ implies $a\in \mathcal{G}$.

Then, a filter is nonempty subsets closed under meet.

Definition 2.5. ^[53] The atom of a lattice $\mathfrak{LA}$ to be an element $x\in \mathfrak{U}$ s.t. $x$ covers $0$ (i.e., $x > 0$) and there is no element $a$ s.t. $x > a > 0$. If every element in $\mathfrak{LA}- \{0\}$ is the join atoms, then $\mathfrak{LA}$ is an atomic lattice. Furthermore, if $\mathfrak{LA}$ is finite, then it is a finite atomic lattice.

Definition 2.6. ^[44] Let $C \mathfrak{LA} =$ $(B, \subseteq)$ be a complete atomic lattice, $\mathcal{A}(B)$ be a lattice of $B$, and $\varphi:$ $\mathcal{A}(B)$ $\rightarrow$ $B$ be any function, for any element $x\in B$. The lower and upper approximation of $x$ with respect to $\varphi$ are

$\underline{\Omega}(x) =$ $\vee\{a\in \mathcal{A}(B):$ $\varphi(x)\le x\}$, and

$\overline{\Omega}(x) =$ $\vee\{a\in \mathcal{A}(B):$ $\varphi(a)\wedge x \neq \phi\}$, respectively.

Definition 2.7. ^[66] Let $\phi\neq \mathfrak{LA}\subseteq \mathcal{P}(\mathfrak{U})$ on $\mathfrak{U}$. If $\bigcap\limits_{i\in I} \mathcal{X}_{i}\in \mathfrak{LA}$ for a class $\{ \mathcal{X}_{i}:$ $i\in I\}$ $\subseteq$ $\mathfrak{LA}$, where $I$ is an index set, then $\mathfrak{LA}$ is called a closure system.

2.2.   Rough sets

Definition 2.8. ^[55] Let $(\mathfrak{U}, \Omega)$ be an approximation structure, where $\Omega$ be an equivalence relation on $\mathfrak{U}$ and $\mathfrak{U}/\Omega =$ $\{[x]_\Omega:$ $x\in \mathfrak{U}\}$ are equivalence classes of $\Omega$. Then, for any $\mathcal{X}\subseteq \mathfrak{U}$, lower and upper approximation of $\mathcal{X}$ are defined by

$\underline{\Omega}(\mathcal{X}) =$ $\{x\in \mathfrak{U}:$ $[x]_\Omega \subseteq \mathcal{X}\}$, and

$\overline{\Omega}(\mathcal{X}) =$ $\{x \in \mathfrak{U}:$ $[x]_\Omega \cap \mathcal{X} \neq \phi\}$, respectively.

$\mathcal{X}$ is called rough, using Pawlak's definition, if $\underline{\Omega}(\mathcal{X})\neq \overline{\Omega}(\mathcal{X})$.

Proposition 2.9. ^[73] Let $\Omega$ be a relation on $\mathfrak{U}$. The following hold:

(L1) $\underline{\Omega}(\mathcal{X})\subseteq \mathcal{X} .\;\;\;(U1) \mathcal{X} \subseteq \overline{\Omega}(X)$.

(L2) $\underline{\Omega}(\phi) = \phi .\;\;\; (U2) \overline{\Omega}(\phi) = \phi$.

(L3) $\underline{\Omega}(\mathfrak{U}) = \mathfrak{U} . \;\;\; (U3) \overline{\Omega}(\mathfrak{U}) = \mathfrak{U}$.

(L4) $\underline{\Omega} (\mathcal{X}\cap \mathcal{Y}) =$ $\underline{\Omega}(\mathcal{X})\cap$ $\underline{\Omega}(\mathcal{Y}) . \;\;\; (U4) \overline{\Omega} (\mathcal{X}\cup \mathcal{Y}) = \overline{\Omega}(\mathcal{X})\cup$ $\overline{\Omega}(\mathcal{Y})$.

(L5) If $\mathcal{X}\subseteq \mathcal{Y}$, then $\underline{\Omega}(\mathcal{X})\subseteq$ $\underline{\Omega}(\mathcal{Y}) . \;\;\; (U5) If \mathcal{X}\subseteq \mathcal{Y}$, then $\overline{\Omega}(\mathcal{X})\subseteq$ $\overline{\Omega}(\mathcal{Y})$.

(L6) $\underline{R}(X)\cup$ $\underline{R}(Y)$ $\subseteq$ $\underline{R} (X\cup Y) .\;\;\; (U6) \overline{\Omega}(\mathcal{X})\cap$ $\overline{\Omega}(\mathcal{Y})$ $\supseteq$ $\overline{\Omega} (\mathcal{X}\cap \mathcal{Y})$.

(L7) $\underline{\Omega}(\mathcal{X}^c) = (\overline{\Omega}(\mathcal{X}))^c . \;\;\; (U7) \overline{\Omega}(\mathcal{X}^c) = (\underline{\Omega}(\mathcal{X}))^c$.

(L8) $\underline{\Omega}(\underline{\Omega}(\mathcal{X})) =$ $\underline{\Omega}(\mathcal{X}) . \;\;\; (U8) \overline{\Omega}(\overline{\Omega}(\mathcal{X})) =$ $\overline{\Omega}(\mathcal{X})$.

(L9) $\underline{\Omega}((\underline{\Omega}(\mathcal{X}))^c) =$ $(\underline{\Omega}(\mathcal{X}))^c .\;\;\; (U9) \overline{\Omega}((\overline{\Omega}(\mathcal{X}))^c) =$ $(\overline{\Omega}(\mathcal{X}))^c$.

Where $\mathcal{X}^c$ the complement of $\mathcal{X}$ in $\mathfrak{U}$.

Definition 2.10. ^[72] The boundary region for $\mathcal{X}$ is given by $BN_g (\mathcal{X}) =$ $\overline{\Omega}(\mathcal{X})- \underline{\Omega}(\mathcal{X})$. In other words, $BN_g (\mathcal{X}) =$ $\bigcup \{[x]_\Omega \in \mathfrak{U}/\Omega:$ $[x]_\Omega\cap \mathcal{X}\neq \phi$ $\wedge$ $[x]_\Omega \nsubseteq \mathcal{X}\}$.

3.   Methods

In this section, the lattice through an equivalence relation is introduced. This relation forms an exact lattice on its equivalence classes. In this case, the relation between exact lattices and rough lattices is discussed. $\mathfrak{U}/\Omega_{1}$ $\leq$ $\mathfrak{U}/\Omega_{2}$ if $\mathfrak{U}/\Omega_{1}$ is a subclass of $\mathfrak{U}/\Omega_{2}$. A subset $A$ of $\mathfrak{U}$ is definable in $(\mathfrak{U}, \Omega)$ if it is a union of $\Omega$-classes. Otherwise, it is called undefinable.

Definition 3.1. Let $(\mathfrak{U}, \tau_\Omega)$ be a quasi discrete topological structure. Its lattice is called an exact lattice and is denoted by $(\mathfrak{ELA}(\mathfrak{U}),$ $\subseteq_\Omega)$ (briefly, $\mathfrak{ELA}_\Omega(\mathfrak{U}$). A zero element is $\emptyset$ and a unit element is $\mathfrak{U}$.

Definition 3.2. Let $(\mathfrak{U}, \Omega_{1})$ and $(\mathfrak{U}, \Omega_{2})$ be approximation structures on exact lattices $(\mathfrak{ELA}(\mathfrak{U}),$ $\subseteq_{\Omega_{1}})$ and $(\mathfrak{ELA}(\mathfrak{U}),$ $\subseteq_{\Omega_{2}})$, respectively. If $\mathfrak{U}/\Omega_{1}$ $\leq$ $\mathfrak{U}/\Omega_{2}$, then $(\mathfrak{ELA}(\mathfrak{U}),$ $\subseteq_{\Omega_{1}})$ is finer than $(\mathfrak{ELA}(\mathfrak{U}),$ $\subseteq_{\Omega_{2}})$.

Definition 3.3. Let $(\mathfrak{U}, \tau_{\Omega})$ be a topological structure on $(\mathfrak{U}, \Omega)$ with a basis $\mathcal{B} = \mathfrak{U}/\Omega$. A topology $\tau_{\Omega}$ can be extended using a rough set $A$ by $\mathcal{B}^{*} =$ $\mathfrak{U}/\Omega_S =$ $\mathcal{B}$ $\cup$ $\{B \cap A: B\in \mathcal{B}\}$.

Proposition 3.4. $\mathcal{B}^{*}$ is a basis for a topological structure $(\mathfrak{U}, \tau_{\Omega_S})$.

Proof. Using Definition 3.3, it is necessary to prove that $\tau_{\Omega_S}$ is a topology on $\mathfrak{U}$. Clearly, $\mathfrak{U}, \phi$ $\in$ $\tau_{\Omega_S}$, since $\phi =$ $\bigcup \{B:$ $B \in \emptyset$ $\subseteq$ $\mathcal{B}\}$. Now, let $\{G_i:$ $i\in I\}$ be a class of members of $\tau_{\Omega_S}$. Then, each $G_i =$ $\bigcup\limits_{x \in \mathfrak{U}}$ $x\Omega_S$, $x\in G_i$ for each $i$. So, each $G_i$ is the union of elements of $\mathcal{B}$ and so $\bigcup\limits_{i\in I} G_i$ is a union of elements of $\mathcal{B}^{*}$. Similarly, $G_1\cap G_2$ is a union of members of $\mathcal{B}^{*}$, for each $G_1, G_2$ $\in \tau_{\Omega_S}$. □

$(\mathfrak{U}, \tau_{\Omega_S})$ is called an extension topological structure. Now, we give an equivalent concept of topological homeomorphic in a viewpoint of lattices.

Proposition 3.5. Two topologies $\tau_{\Omega}(\mathcal{X})$ and $\tau^{*}_{\Omega}(\mathcal{Y})$ are homeomorphic if their topological extension lattices are homeomorphic.

Proof. Let $\tau_{\Omega}(\mathcal{X})$ and $\tau^{*}_{\Omega}(\mathcal{Y})$ be homeomorphic s.t $\mathcal{X}, \mathcal{Y}$ $\subseteq \mathfrak{U}$ is homeomorphic. To prove that $(\mathfrak{ELA}(\mathcal{X}),$ $\subseteq_{\Omega})$ and $(\mathfrak{ELA}(\mathcal{Y}),$ $\subseteq_{\Omega})$, it is necessary to prove that there is a homeomorphism function $f$ from $\mathfrak{ELA}_\Omega(\mathcal{X})\}$ onto $\mathfrak{ELA}_\Omega(\mathcal{Y})\}$. For any $G, H\subseteq$ $\mathfrak{ELA}_\Omega(\mathcal{X})\}$, $f(A\cap B) =$ $f(A)\wedge f(B)$ and $f(A), f(B)\in$ $\mathfrak{ELA}_{\Omega}(\mathcal{Y})$. Also, for any $\{F_{i}:$ $F_{i}\in \tau_{\Omega}(\mathcal{X})\}$, we get, by assumption, $f(\bigcup \{F_{i}:$ $F_{i}\in \tau^{*}_{\Omega}(\mathcal{Y})\}) =$ $\bigvee \{f(F_{i}):$ $f(F_{i})\in \mathfrak{ELA}_{\Omega}(\mathcal{Y})\}$. Hence, open subsets of $\mathfrak{ELA}_{\Omega}(\mathcal{X})$ and $\mathfrak{ELA}_{\Omega}(\mathcal{Y})$ are in one-to-one correspondence due to a bijective function. Therefore, $f$ is a homeomorphism of $\mathfrak{ELA}_\Omega(\mathcal{X})\}$ onto $\mathfrak{ELA}_\Omega(\mathcal{Y})\}$. □

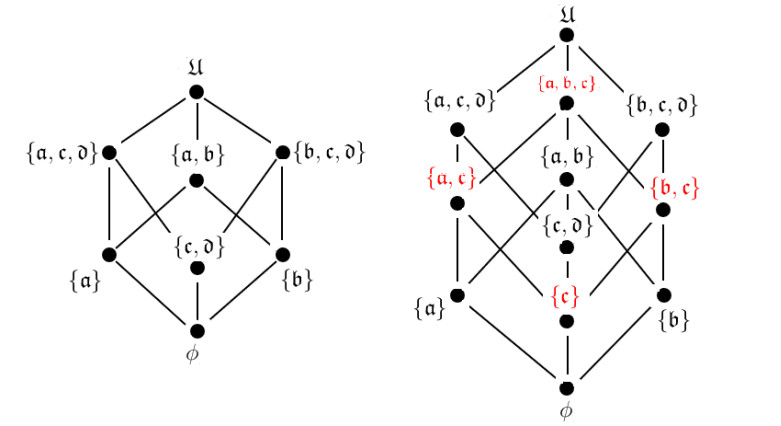
Example 3.6. Let $(\mathfrak{U}, \Omega)$ be approximation structure with $\mathfrak{U} =$ $\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}, \mathfrak{d}\}$. The basis is $\mathcal{B} =$ $\{\{\mathfrak{a}\}, \{\mathfrak{b}\},$ $\{\mathfrak{c}, \mathfrak{d}\}\}$ and so its quasi discrete topology is $\tau_{\Omega} =$$\{ \mathfrak{U}$, $\phi$, $\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{a}, \mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{b}, \mathfrak{c}, \mathfrak{d}\}\}$. Set $A =$ $\{\mathfrak{a}, \mathfrak{c}\}$. Then, the extended basis is $\mathcal{B}^{*} =$ $\{\{\mathfrak{a}\},$ $\{\mathfrak{b}\},$ $\{\mathfrak{c}\},$ $\{\mathfrak{c},$ $\mathfrak{d}\}\}$. Then, the extension of quasi discrete topology is $\tau_{\Omega_S} =$ $\{ \mathfrak{U}$, $\phi$, $\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{c}\}$, $\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{a}, \mathfrak{c}\}$, $\{\mathfrak{b}, \mathfrak{c}\}$, $\{\mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}$, $\{\mathfrak{a}, \mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{b}, \mathfrak{c}, \mathfrak{d}\}\}$. The lattices for each topology are shown in Figure 1.

The extension topology of quasi discrete topology (maybe for any topology) is established using rough sets. Moreover, for each $G, H$ $\in$ $\tau_\Omega$ s.t. $G \leq H$, any element in $\tau_{\Omega_S}$ has the form $P = G \cup (H\cap P)$. So, if $\tau_{\Omega} =$ $\{ \mathfrak{U}$, $\phi$, $\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{a}$, $\mathfrak{b}\}$, $\{\mathfrak{c}$, $\mathfrak{d}\}$, $\{\mathfrak{a}$, $\mathfrak{c}$, $\mathfrak{d}\}$, $\{\mathfrak{b}, \mathfrak{c}, \mathfrak{d}\}\}$. For instance, if $\{\mathfrak{a}, \mathfrak{d}\}$ is a rough set, then $\tau_{\Omega_S} =$ $\{ \mathfrak{U}$, $\phi$, $\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{d}\}$, $\{\mathfrak{a}$, $\mathfrak{b}\}$, $\{\mathfrak{a}$, $\mathfrak{d}\}$, $\{\mathfrak{b}$, $\mathfrak{d}\}$, $\{\mathfrak{c}$, $\mathfrak{d}\}$, $\{\mathfrak{a}$, $\mathfrak{b}$, $\mathfrak{d}\}$, $\{\mathfrak{a}$, $\mathfrak{c}$, $\mathfrak{d}\}$, $\{\mathfrak{b}$, $\mathfrak{c}$, $\mathfrak{d}\}\}$ is shown in Figure 2. It is noted that there is a homeomorphic between topologies of lattices which are extended by rough sets $\{\mathfrak{a}, \mathfrak{c}\}$ and $\{\mathfrak{a}, \mathfrak{d}\}$.

Definition 3.7. Let $(\mathfrak{U}, \Omega)$ be an approximation structure. A minimal equivalence class for each $a \in \mathfrak{U}$ is given by $\mathcal{N}(a) =$ $\bigcap \{ \mathcal{Y}\in \mathfrak{U}/\Omega:$ $\forall a \in \mathcal{Y}\}$.

Definition 3.8. Let $(\mathfrak{U}, \Omega)$ be a approximation structure with $| \mathfrak{U}| = n$ s.t $n$ be finite and $| \mathfrak{U}|$ be the cardinality of $\mathfrak{U}$. A minimal basis of $(\mathfrak{U}, \Omega)$ is defined by $\mathcal{B}_{ \mathcal{N}} =$ $\{ \mathcal{N}(a_i):$ $a_i\in \mathfrak{U}\}$.

Example 3.9. Consider $\mathfrak{U} =$ $\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}$. The equivalence classes on $\mathfrak{U}$ are given by bases $\mathcal{B}_{\{\mathfrak{a}\mathfrak{b}, \mathfrak{c}\}} =$ $\{\{\mathfrak{a}$, $\mathfrak{b}\},$ $\{\mathfrak{c}\}$, $\phi\}$, $\mathcal{B}_{\{\mathfrak{a}\mathfrak{c}, \mathfrak{b}\}} =$ $\{\{\mathfrak{a}, \mathfrak{c}\}$, $\{\mathfrak{b}\}$, $\phi\}$, and $\mathcal{B}_{\{\mathfrak{b}\mathfrak{c}, \mathfrak{a}\}} =$ $\{\{\mathfrak{b}, \mathfrak{c}\}$, $\{\mathfrak{a}\}$, $\phi\}$. In addition, a unit element is $\mathcal{B}_{\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}} =$ $\{\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{c}\}$, $\phi\}$, and a zero element is $\mathcal{B}_{\{\mathfrak{a}\mathfrak{b}\mathfrak{c}\}} =$ $\{\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}$, $\phi\}$. It is noted that the intersection of every two lattices is a unit element, that is, $\mathcal{B}_{\{\mathfrak{a}\mathfrak{b}, \mathfrak{c}\}}$ $\bigcap$ $\mathcal{B}_{\{\mathfrak{a}\mathfrak{c}, \mathfrak{b}\}} =$ $\{\{\mathfrak{a}\}, \{\mathfrak{b}\}$, $\{\mathfrak{c}\}$, $\phi\} =$ $\mathcal{B}_{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}}$. Also, the union is a zero element, that is, $\mathcal{B}_{\{\mathfrak{a}\mathfrak{b}, \mathfrak{c}\}}$ $\bigcup$ $\mathcal{B}_{\{\mathfrak{a}\mathfrak{c}, \mathfrak{b}\}} =$ $\{\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}$, $\phi\} =$ $\mathcal{B}_{\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}\}}$.

Remark 3.10. In the framework of $(\mathfrak{U}, \Omega)$, a subset is precisely categorized as an exact (or definable) set or a rough (or undefinable) set based on two distinct exact sets: The lower and upper approximation. While a rough set is defined approximately within $(\mathfrak{U}, \Omega)$, the exact set aligns with openness in Pawlak's approximation structure, forming a point within a lattice generated by an extension topology. Consequently, an open set is denoted as an exact point within a topological lattice, whereas any other set is termed a rough point. Essentially, any rough point can be defined by two exact points. For instance, if $a, b \in \mathfrak{LA}(\mathfrak{U})$ such that $(a \leq b)$, five cases exemplify their relation in the extension lattice:

(i) Any rough point $c \notin \mathfrak{LA}(\mathfrak{U})$ such that $a \leq c \leq b$. This establishes $a \leq c$ and $c \leq b$. $(\mathfrak{U}, \Omega).$

(ii) If $a \leq b$, then $a \vee b = b$ and $a \wedge b = a$ in both lattices and their extensions.

(iii) For $a \leq c \leq b$, $a \vee c = c$, $a \wedge c = a$, $c \vee b = b$, and $c \wedge b = c$. This configuration is termed a rough point approximation.

(iv) If $a \vee b = a \vee (c \vee b) = (a \vee c) \vee b = c \vee b = b$, it denotes an upper rough point approximation.

(v) When $a \wedge b = (a \wedge c) \wedge b = a \wedge (c \wedge b) = a \wedge c = a$, it signifies a lower rough point approximation.

Thus, $a \leq b$ in the extending lattice, and the rough pair of any rough point lies within $(a, b)$ such that $a \leq c \leq b$.

Proposition 3.11. Let $\mathfrak{ELA}_{\Omega}(\mathfrak{U})$ be a topology of an exact lattice and $(\mathfrak{U}, \tau_{\Omega_S})$ be an extension topological structure of $(\mathfrak{U}, \tau_\Omega)$. Then, $\mathfrak{ELA}_\Omega(\mathfrak{U})$ and $(\mathfrak{U}, \tau_{\Omega_S})$ are equivalent.

Proof. Using Definitions 3.2 and 3.3, each of $\mathfrak{ELA}_\Omega(\mathfrak{U})$ and $(\mathfrak{U}, \tau_{\Omega_S})$ is a topology. It is necessary to prove that for each $A\in \mathfrak{ELA}_\Omega(\mathfrak{U})$, using Proposition 3.5, there is a unique point $B\in (\mathfrak{U}, \tau_{\Omega_S})$ s.t. $\mathcal{N}(a, \mathfrak{ELA}_\Omega(\mathfrak{U})) =$ $\mathcal{M}(b, (\mathfrak{U}, \tau_{\Omega_S}))$ for $a\in A$ and $b\in B$, respectively. Define a function $f:$ $\mathfrak{ELA}_{\Omega}(\mathfrak{U})$ $\rightarrow$ $(\mathfrak{U}, \tau_{\Omega_S})$ by $f(a) =$ $b$. Thus, $f$ is a bijective function from $\mathfrak{ELA}_\Omega(\mathfrak{U})$ onto $(\mathfrak{U}, \tau_{\Omega_S})$, and for each $a\in A$, $\mathcal{N}(a, \mathfrak{ELA}_\Omega(\mathfrak{U})) =$ $\mathcal{N}(f(a), (\mathfrak{U}, \tau_{\Omega_S}))$. In particular, $\forall$ $x\in \mathfrak{U}$, $\mathcal{N}(\beta(x)$, $\mathfrak{ELA}_\Omega(\mathfrak{U})) =$ $\mathcal{N}(f(\beta(x))$, $(\mathfrak{U}, \tau_{\Omega_S}))$, where $\beta(x)$ is a basis element containing $x$. Finally, it is sufficient to find a homeomorphism $f$ from $\mathfrak{ELA}_\Omega(\mathfrak{U})$ onto $(\mathfrak{U}, \tau_{\Omega_S})$. For any $G, H\subseteq$ $\tau_{\Omega_S}$ with $f(A\cap B) =$ $f(A) \wedge f(B)$ and $f(A), f(B)\in \mathfrak{ELA}_{\Omega}(\mathfrak{U})$. Also, for any $\{F_{i}:$ $F_{i}\in \tau_{\Omega_S}\}$, $f(\bigcup \{F_{i}:$ $F_{i}\in \tau_{\Omega_S}\}) =$ $\bigvee \{f(F_{i}):$ $f(F_{i})\in \mathfrak{ELA}_{\Omega}(\mathfrak{U})\}$. Therefore, open sets in both of $\mathfrak{ELA}_{\Omega}(\mathfrak{U})$ and $(\mathfrak{U}, \tau_{\Omega_S})$ in terms of a bijective function $f$ are in a one-to-one correspondence. Hence, $f$ is homeomorphism. □

Definition 3.12. Let $(\mathfrak{U}, \tau_{\Omega_S})$ be an extension of $(\mathfrak{U}, \Omega)$. A lower and upper extension approximation for a rough set $\mathcal{X}$ are

$\underline{app}_{S}(\mathcal{X}) =$ $\bigcup \{ \mathcal{Y} \in \mathfrak{U}/\Omega_S:$ $\mathcal{Y} \subseteq \mathcal{X}\}$.

$\overline{app}_{S}(\mathcal{X}) =$ $\bigcap \{ \mathcal{Y} \in \mathfrak{U}/\Omega_S:$ $\mathcal{X} \subseteq \mathcal{Y}\}$, respectively.

The product of approximations of $\mathfrak{ELA}_\Omega(\mathfrak{U})$ has the form $\mathfrak{ELA}_{\Omega}(\mathfrak{U})$ $\times \mathfrak{ELA}_{\Omega}(\mathfrak{U}) =$ $\{(\underline{app}(\mathcal{X}), \overline{app}(\mathcal{X})):$ $\mathcal{X}\subseteq \mathfrak{U}\}$. The location of each subset $A$ in $(\mathfrak{U}, \Omega)$ is assigned with a function $\mathscr{P}:$ $\mathcal{P}(\mathfrak{U})$ $\rightarrow$ $\mathbb{Z}^{+}$ and is calculated by $\mathscr{P}(A) =$ $\frac{1}{| \mathfrak{U}|}(\frac{|\underline{app}(A)|+ |\overline{app}(A)|}{2})$. Similarly, the location of each subset $A$ in $(\mathfrak{U}, \Omega_S)$ is assigned with a function $\mathscr{P}_S:$ $\mathcal{P}(\mathfrak{U})$ $\rightarrow$ $\mathbb{Z}^{+}$ and is calculated by $\mathscr{P}_S(A) =$ $\frac{1}{| \mathfrak{U}|}(\frac{|\underline{app_S}(A)|+ |\overline{app_S}(A)|}{2})$.

Note that: The introduced lower and upper extension approximations differ from the classical Pawlak approximation operators in the context of their construction within an extension lattice. The classical Pawlak approximation structure relies on exact sets (lower and upper approximations) to delineate between definable (exact) and undefinable (rough) sets within $(\mathfrak{U}, \Omega)$. However, the extension lattice enriches this paradigm by incorporating an equivalence relation-based extension of the Pawlak structure. Here, the lower and upper extension approximations transcend the classical approach by utilizing a generalized binary relation. This extension allows for a more nuanced depiction of relationships between elements, offering a refined characterization of rough and exact sets within a topological lattice.

Lemma 3.13. Let $(\mathfrak{ELA}(\mathfrak{U})\times \mathfrak{ELA}(\mathfrak{U}), \subseteq)$ be an approximation lattice of $(\mathfrak{U}, \Omega)$. Then, $\phi$ and $\mathfrak{U}$ are zero and unit elements in their lattice's location. Otherwise, $0 \leq \mathscr{P}(\mathcal{X}) \leq 1$.

Proof. The locations of $\phi$ and $\mathfrak{U}$ are $\frac{1}{| \mathfrak{U}|}(\frac{0+0}{2}) =$ $0$ and $\frac{1}{| \mathfrak{U}|}(\frac{| \mathfrak{U}|+| \mathfrak{U}|}{2}) = 1$, respectively. Moreover, for any $\phi \subseteq \mathcal{X} \subseteq \mathfrak{U}$, $\mathscr{P}(\mathcal{\phi})\leq \mathscr{P}(\mathcal{X})$ $\leq$ $\mathscr{P}(\mathfrak{U})$. Therefore, $0 \leq$ $\mathscr{P}(\mathcal{X})$ $\leq 1$. □

Lemma 3.14. Let $(\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U}),$ $\subseteq)$ be an approximation lattice of $(\mathfrak{U}, \Omega)$. Then, $\mathscr{P}_S(\mathcal{X}) =$ $\mathscr{P}(\mathcal{X})$, $\forall$ $\mathcal{X} \subseteq \mathfrak{U}$.

Proof. For any $\mathcal{X} \in \mathfrak{U}/\Omega$, $\underline{app}(\mathcal{X}) =$ $\overline{app}(\mathcal{X})$. Then, $\mathscr{P}(\mathcal{X}) =$ $\frac{1}{| \mathfrak{U}|}(\frac{2|\underline{app}(\mathcal{X})|}{2}) =$ $\frac{|\underline{app}(X)|}{| \mathfrak{U}|}$. Also, if $\mathcal{X} \in \mathfrak{U}/\Omega_S$, then $\underline{app}_S(\mathcal{X}) =$ $\overline{app}_S(\mathcal{X})$, and so $\mathscr{P}_S(\mathcal{X}) =$ $\frac{1}{| \mathfrak{U}|}(\frac{2|\underline{app}_S(\mathcal{X})|}{2}) =$ $\frac{|\underline{app}_S(\mathcal{X})|}{| \mathfrak{U}|}$. Since $\underline{app}(\mathcal{X}) =$ $\underline{app}_S(X)$ and $\overline{app}(\mathcal{X}) =$ $\overline{app}_S(\mathcal{X})$, then $\mathscr{P}_S(\mathcal{X}) =$ $\frac{1}{| \mathfrak{U}|}$ $(\frac{|\underline{app}_S(\mathcal{X})| +|\overline{app}_S(\mathcal{X})|}{2}) =$ $\frac{1}{| \mathfrak{U}|}$ $(\frac{|\underline{app}(\mathcal{X})|+ |\overline{app}(\mathcal{X})|}{2}) =$ $\mathscr{P}(\mathcal{X})$. □

Example 3.15. Let $\mathfrak{U} =$ $\{\mathfrak{a}, \mathfrak{b} \mathfrak{c}\}$ with $\mathfrak{U}/\Omega =$ $\{\{\mathfrak{a}\}$, $\{\mathfrak{b}, \mathfrak{c}\}\}$. Lower approximation, upper approximation, and the location $\mathscr{P}$ for every $A\subseteq \mathfrak{U}$ are given and computed in Table 1 and Figure 3. If $\mathcal{X} =$ $\{\mathfrak{a}, \mathfrak{b}\}$ is a rough set, then the extension of the approximation structure is $\tau_{\Omega_S} =$ $\{ \mathfrak{U}$, $\phi$, $\{\mathfrak{a}\}$, $\{\mathfrak{b}\}$, $\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{b}, \mathfrak{c}\}\}$. In addition, the extension lower approximation and extension upper approximation are obtained and the location $\mathscr{P}_S$ for every $A\subseteq \mathfrak{U}$ is determined in Table 2 and Figure 4.

Definition 3.16. A function $\psi:$ $(\mathfrak{U}, \tau_{\Omega})$ $\rightarrow$ $(\mathfrak{U}, \tau_{\Omega_S})$ is called an order isomorphism if $\forall$ $a, b \in \mathfrak{U}$ s.t. $a \leq b$, then $\psi(a)\leq \psi(b)$.

Proposition 3.17. Let $(\mathfrak{U}, \tau_\Omega)$ be topological structure and $(\mathfrak{U}, \tau_{\Omega_S})$ be its extension. Then, a bijective function $\psi:$ $(\mathfrak{U}, \tau_\Omega)$ $\rightarrow$ $(\mathfrak{U}, \tau_{\Omega_S})$ is an order isomorphism.

Proof. Let $a, b$ be open sets in $\tau_\Omega$ with $\underline{app}(a)$ and $\overline{app}(b)$, respectively. It is needed to prove that $(\mathfrak{U}, \tau_\Omega)$ and $(\mathfrak{U}, \tau_{\Omega_S})$ have same locations. There are two cases:

Case 1. If $G$ and $H$ are exact points, then they have same approximations and so has a determined location. Since $G \leq H$ in $\tau_\Omega$ are exacts points, then $\underline{app}(H)$ $\leq$ $\underline{app}(H)$ and $\overline{app}(G)$ $\leq$ $\overline{app}(H)$ in the topological lattice and its extension, since upper and lower approximation are the same. Therefore, both lattices have the same location.

Case 2. If $a$ and $b$ are rough points, then their location are not the same and so they have a tide boundary region. Then, if $a, b$ $\in$ $\tau_{\Omega_S}$ are rough s.t. $a \leq b$, then lower and upper approximations are different. Since $\underline{app}(a) \leq \underline{app}(b)$ and $\overline{app}(a) \leq \overline{app}(b)$, then $\underline{app}(a) \leq \overline{app}(b)$ and $\underline{app}(a)\leq \overline{app}(b)$. Thus, $\forall$ $a, b$ $\in$ $\tau_\Omega$ s.t. $\underline{app}(a)\leq \underline{app}(b)$ and $\overline{app}(a) \leq \overline{app}(b)$ in $\tau_\Omega$. Therefore, $\underline{app}_S(a)\leq \underline{app}_S(b)$ and $\overline{app}_S(a) \leq \overline{app}_S(b)$ in $\tau_{\Omega_S}$. □

4.   Results and discussions

From Example 3.15, we note the following:

The set $\mathfrak{ELA}(\mathfrak{U})$, encompassing all definable subsets of $\mathfrak{U}$, constitutes a complete atomic Boolean algebra, functioning as a sub-algebra within the Boolean algebra of $\mathfrak{U}$'s subsets. Given $\mathcal{X} \subseteq \mathfrak{U}$, $\underline{app}(\mathcal{X}) = \sup \{ \mathcal{Y} \in \mathfrak{ELA}(\mathfrak{U})\}$ represents the greatest element in $\mathfrak{ELA}(\mathfrak{U})$ for $\mathcal{Y} \subseteq \mathcal{X}$, while $\underline{app}(\mathcal{X}) = \inf \{ \mathcal{Y} \in \mathfrak{ELA}(\mathfrak{U})\}$ signifies the smallest element in $\mathfrak{ELA}(\mathfrak{U})$ for $\mathcal{X} \subseteq \mathcal{Y}$. Now, a rough set $\mathcal{X}$ in $(\mathfrak{U}, \Omega)$ is elucidated as a pair $(\underline{app}(\mathcal{X}), \overline{app}(\mathcal{X}))$ in $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$ satisfying $\underline{app} \subseteq \overline{app}$. When $\underline{app}(\mathcal{X}) = \overline{app}(\mathcal{X}) = \mathcal{X}$, the scenario emerges where $\sup \{ \mathcal{Y} \in \mathfrak{ELA}(\mathfrak{U})\} = \inf \{ \mathcal{Y} \in \mathfrak{ELA}(\mathfrak{U})\}$, designating the rough set as exact. It's notable that the smallest rough set is $(\phi, \phi)$, representing the empty set, while the greatest rough set is $(\mathfrak{U}, \mathfrak{U})$, signifying the entire universe $\mathfrak{U}$.

Example 3.15 presents a concrete scenario where the extension lattice reveals a more detailed characterization of relationships among elements compared to the original lattice. The tables (Tables 1 and 2) with figures provide a visual representation of the sets and their approximations in both the original and extension lattices, highlighting the finer granularity achieved by our proposed approach. This example and comparisons substantiate the claim regarding the finer granularity of the extension lattice compared to the original lattice.

The assertion that the extension lattice offers increased granularity stems from its ability to capture more detailed relationships among elements than the original lattice. For instance, in the context of rough set approximations, the extension lattice, constructed through equivalence relations and generalized binary relations, allows for a more nuanced depiction of relationships between elements compared to the classical Pawlak approximation operators.

Consider the scenario where the extension lattice incorporates an equivalence relation-based extension. This extension introduces a more extensive set of equivalence classes, resulting in a refined delineation of relationships among elements. Similarly, utilizing a generalized binary relation in defining lower and upper extension approximations enables a more detailed characterization of rough and exact sets within the lattice. While specific examples or comparisons illustrating the finer granularity of the extension lattice compared to the original lattice would enhance clarity, it is essential to emphasize that the increased detail and precision in representing relationships among elements are foundational to the claim of its finer nature.

Further empirical studies and targeted comparisons between the extension and original lattices in specific applications would provide concrete instances demonstrating the enhanced granularity of the extension lattice. These comparative analyses would substantiate the claim and elucidate the practical implications of employing the extension lattice for more detailed data representations. We will strive to incorporate specific examples or comparative analyses in our work to bolster the claim regarding the finer nature of the extension lattice compared to the original lattice, thereby enhancing the comprehensibility and credibility of our findings.

Proposition 4.1. Let $(\mathfrak{U}, \Omega)$ be an approximation structure. The structure $(\mathfrak{ELA}(\mathfrak{U})$, $\cap$, $\cup$, $0$, $1)$ is a bounded distributive lattice s.t. the lattice $(\mathfrak{ELA}(\mathfrak{U}),$ $\cap, \cup)$ is distributive with a minimal element $0$ corresponding to $\phi$ and maximal $1$ corresponding to $\mathfrak{U}$.

Proof. First, for $\mathcal{X} =$ $(\underline{app}(\mathcal{X}), \overline{app}(\mathcal{X}))$ and $\mathcal{Y} =$ $(\underline{app}(\mathcal{Y}), \overline{app}(\mathcal{Y}))$, the sum $\oplus$ law is defined join or union by $\mathcal{X} \oplus \mathcal{Y} =$ $\mathcal{X} \vee \mathcal{Y} =$ $\mathcal{X} \cup \mathcal{Y} =$ $(\underline{app}(\mathcal{X}), \overline{app}(\mathcal{X}))$ $\cup$ $(\underline{app}(\mathcal{Y}), \overline{app}(\mathcal{Y})) =$ $(\underline{app}(\mathcal{X})$ $\cup$ $\underline{app}(\mathcal{Y}), \overline{app}(\mathcal{X})$ $\cup$ $\overline{app}(\mathcal{Y}))$. Second, the dot $\odot$ law is defined meet or intersection by as $\mathcal{X} \odot \mathcal{Y} =$ $\mathcal{X} \wedge \mathcal{Y} =$ $\mathcal{X} \cap \mathcal{Y} =$ $(\underline{app}(\mathcal{X}), \overline{app}(\mathcal{X}))$ $\cap$ $(\underline{app}(\mathcal{Y}), \overline{app}(\mathcal{Y})) =$ $(\underline{app}(\mathcal{X})$ $\cap$ $\underline{app}(\mathcal{Y}), \overline{app}(\mathcal{X})$ $\cap \overline{app}(\mathcal{Y}))$, where $\underline{app}(\mathcal{X})$, $\underline{app}(\mathcal{Y})$, $\overline{app}(\mathcal{X})$, and $\overline{app}(\mathcal{Y})$ $\in$ $\mathfrak{ELA}(\mathfrak{U})$. Then, $\underline{app}(\mathcal{X})$ $\cap$ $\underline{app}(\mathcal{Y}) \in$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$, or $\underline{app}(\mathcal{X})$ $\cup$ $\underline{app}(\mathcal{Y}) \in$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$. $\overline{app}(\mathcal{X})$ $\cap$ $\overline{app}(\mathcal{Y}) \in$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$, or $\overline{app}(\mathcal{X})$ $\cup$ $\overline{app}(\mathcal{Y}) \in$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$. Therefore, $(\mathfrak{ELA}(\mathfrak{U}),$ $\cap,$ $\cup)$ is distributive lattice and the union of all equivalence classes which gives the universal set. Then, $(\mathfrak{U}, \mathfrak{U})$ belongs to the $\mathfrak{ELA}(\mathfrak{U})$ and the $\phi$ belongs to any nonempty set. So, $(\mathfrak{ELA}(\mathfrak{U})$, $\cap$, $\cup$, $0, 1)$ is bounded distributive. □

Recall that a function $\mathfrak{F}: \mathcal{P}(\mathfrak{U})$ $\rightarrow$ $\mathcal{P}(\mathfrak{U})$ is increasing if for any $A$, $B$ $\in \mathcal{P}(\mathfrak{U})$ with $A \subseteq B$, implies $\mathfrak{F}(A)$ $\subseteq$ $\mathfrak{F}(B)$. It is called a fixed point function if $\mathfrak{F}(A) =$ $\mathfrak{F}(B)$. A subset $A$ is called fixed point set if $\mathfrak{F}(A) =$ $A$.

Definition 4.2. Let $(\mathfrak{U}, \Omega)$ be an approximation structure. For $\mathcal{X} \subseteq \mathfrak{U}$, a rough function $\mathfrak{F}_{\Omega}:$ $\mathcal{P}(\mathfrak{U})\times \mathcal{P}(\mathfrak{U})$ $\rightarrow$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$ is defined by $\mathfrak{F}_{\Omega}(\mathcal{X}) =$ $(\mathfrak{F}_{\underline{app}(\mathcal{X})}, \mathfrak{F}_{\overline{app}(\mathcal{X})})$ s.t. $\mathfrak{F}_{\underline{app}(\mathcal{X})} =$ $\bigcup\{[x] \subseteq \mathcal{X}:$ $[x]\in \mathfrak{U}/\Omega\}$, $\mathfrak{F}_{\overline{app}(\mathcal{X})} =$ $\bigcup\{[x] \subseteq \mathcal{X}:$ $[x]\cap \mathfrak{U}/\Omega$ $\neq \phi\}$.

Lemma 4.3. A rough function is an increasing (resp. fixed point) function if for any $A, B \in \mathcal{P}(\mathfrak{U}) \times \mathcal{P}(\mathfrak{U})$ s.t. $A \subseteq B$, then $\mathfrak{F}(A)\subseteq \mathfrak{F}(B)$ (resp. $\mathfrak{F}(A) = \mathfrak{F}(B)$), where $\mathfrak{F} =$ $(\mathfrak{F}_{\underline{app}}, \mathfrak{F}_{\overline{app}})$.

Proof. First, define the rough lower approximation and rough upper approximation function by $\mathfrak{F}_{\underline{app}}:$ $\mathcal{P}(\mathfrak{U})$ $\rightarrow \mathfrak{ELA}$ $(\mathfrak{U})$, $\mathfrak{F}_{\overline{app}}:$ $\mathcal{P}(\mathfrak{U})$ $\rightarrow \mathfrak{ELA}$ $(\mathfrak{U})$. From rough inclusion properties, since $A \subseteq B$, then $\underline{app}(A)$ $\subseteq$ $\underline{app}(B)$ and $\overline{app}(A)$ $\subseteq$ $\overline{app}(B)$. So, for any $A, B \in$ $\mathcal{P}(\mathfrak{U}) \times \mathcal{P}(\mathfrak{U})$ s.t. $A \subseteq B$, we get $(\mathfrak{F}_{\underline{app}(A)}, \mathfrak{F}_{\overline{app}(A)})$ $\subseteq$ $(\mathfrak{F}_{\underline{app}(B)}, \mathfrak{F}_{\overline{app}(B)})$. Then, $\mathfrak{F}$ is increasing. Second, for any $A \in \mathfrak{ELA}(\mathfrak{U})$, $\underline{app}(A) = A = \overline{app}(A)$ is known. Then, $\mathfrak{F}_{\underline{app}}(A) =$ $\mathfrak{F}_{\overline{app}}(A)$, for any $A$ $\in$ $\mathcal{P}(\mathfrak{U})$. Therefore, $\mathfrak{F}$ is a fix point function, for any $\mathfrak{F}(A)$ $\in$ $\mathfrak{ELA}(\mathfrak{U})\times \mathfrak{ELA}(\mathfrak{U})$. □

Proposition 4.4. Let $(\mathcal{P}(\mathfrak{U}), \subseteq)$ be a complete lattice and $\mathfrak{F}:$ $\mathcal{P}(\mathfrak{U}) \times \mathcal{P}(\mathfrak{U})$ $\rightarrow$ $\mathfrak{ELA}(\mathfrak{U}) \times \mathfrak{ELA}(\mathfrak{U})$ be an increasing function. Then, $\mathfrak{ELA}(\mathfrak{U})\neq \phi$ and $(\mathfrak{ELA}(\mathfrak{U}), \subseteq)$ is also a complete lattice.

Proof. To begin, it is necessary to prove that $\mathfrak{ELA}(\mathfrak{U})$ is lattice using meet and join on $\mathfrak{ELA}(\mathfrak{U})$ through union and intersection. Consider

Clearly, $\bigvee \mathfrak{ELA}(\mathfrak{U}) \in \mathfrak{ELA}(\mathfrak{U})$ $\times$ $\mathfrak{ELA}(\mathfrak{U})$. Now, it is sufficient to prove that $\bigvee \mathfrak{ELA}(\mathfrak{U})$ is the supremum of all fixed point of $(\mathfrak{U}, \Omega)$. Consider $H =$ $(H_{\underline{app}}, H_{\overline{app}}) =$ $(\bigcup\limits_{ \mathcal{X}}\{ \mathfrak{F}_{\underline{app}}(X):$ $\mathfrak{F}_{\underline{app}}(\mathcal{X})$ $\subseteq X\}$, $\bigcup\limits_{ \mathcal{X}}$ $\{ \mathfrak{F}_{\overline{app}}(\mathcal{X}):$ $\mathcal{X} \subseteq$ $\mathfrak{F}_{\overline{app}}(\mathcal{X}))$. Take $H_{\overline{app}} =$ $\bigcup\limits_{ \mathcal{X}} \{ \mathfrak{F}_{\overline{app}}(\mathcal{X}):$ $\mathcal{X} \subseteq$ $\mathfrak{F}_{\overline{app}}(\mathcal{X})\}$. Since $\mathcal{X} \subseteq$ $H_{\overline{app}}$, for every $\mathcal{X} \in \mathfrak{U}/\Omega$, then $\mathcal{X} \subset$ $\mathfrak{F}_{\overline{app}}(\mathcal{X})$. By assumption, $\mathfrak{F}$ is an increasing function, we get $\mathfrak{F}(X) \subseteq \mathfrak{F}(H_{\overline{app}})$ and $\mathfrak{F}_{\overline{app}}(\mathcal{X})$ $\subseteq$ $\mathfrak{F}_{\overline{app}}(H_{\overline{app}})$. Since $\mathcal{X}$ is a fixed point, that is, $\mathfrak{F}_{\overline{app}}(\mathcal{X}) =$ $\mathcal{X}$, then $\mathcal{X} \subseteq$ $\mathfrak{F}_{\overline{app}}(H_{\overline{app}})$ and so $\mathfrak{U}_U =$ $\bigcup\limits_{ \mathcal{X}} \{ \mathfrak{F}_{\overline{app}}(H_{\overline{app}}):$ $\mathcal{X} \subseteq$ $\mathfrak{F}_{\overline{app}}(H_{\overline{app}})\}$. So, $\mathfrak{F}_{\overline{app}}(H_{\overline{app}})$ $\subseteq$ $H_{\overline{app}}$. Since $H_{\overline{app}}$ $\subseteq$ $\mathfrak{F}_{\overline{app}}(H_{\overline{app}})$, then $\mathfrak{F}_{\overline{app}}(H_{\overline{app}}) =$ $H_{\overline{app}}$. This means that $H_{\overline{app}}$ is a fixed point. Similarly, $H_{\underline{app}}$ is also fixed point. By the same manner, consider

Clearly, $\bigwedge \mathfrak{ELA}(\mathfrak{U}) \in \mathfrak{ELA}(\mathfrak{U})$ and it is the greatest lower bound of fixed points. Now, let $\mathcal{G} \subseteq \mathfrak{U}$, then $(\mathcal{P}(\mathcal{G}), \subseteq)$ be a complete lattice. Let $\mathcal{B} =$ $(\{ \mathfrak{ELA}(\mathcal{G}), \subseteq\})$ is a complete lattice of fixed points on $\mathfrak{ELA}(\mathcal{G})$. For $\mathcal{X} \in \mathfrak{ELA}(\mathcal{G})$, we get $\mathcal{X} \subseteq$ $\bigvee \mathfrak{ELA}(\mathcal{G})$, $\mathcal{X} =$ $\mathfrak{F}_{\Omega}(\mathcal{X})$ $\subseteq$ $\mathfrak{F}(\bigvee \mathfrak{ELA}(\mathcal{G}))$. If $\mathfrak{F}(\bigvee \mathfrak{ELA}(\mathcal{G})) \subseteq W$, then $\mathfrak{F}(\bigvee \mathfrak{ELA}(\mathcal{G}))$ $\subseteq \mathfrak{F}_{\Omega}(W)$. □

In Proposition 4.4, the existence of a fixed point for every increasing function is a necessary condition for a complete lattice. This can be shown in Example 4.5.

Example 4.5. Let $\mathfrak{U} =$ $\{\mathfrak{a}, \mathfrak{b}, \mathfrak{c}, \mathfrak{d}\}$ with an equivalence relation $\Omega =$ $\{(\mathfrak{a}, \mathfrak{a}), (\mathfrak{b}, \mathfrak{b})$, $(\mathfrak{c}, \mathfrak{c}), (\mathfrak{d}, \mathfrak{d})$, $(\mathfrak{a}, \mathfrak{b}), (\mathfrak{b}, \mathfrak{a})$, $(\mathfrak{c}, \mathfrak{d}), (\mathfrak{d}, \mathfrak{c})\}$ and so $\mathfrak{U}/\Omega =$ $\{\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{c}, \mathfrak{d}\}\}$. Then,

(i) If $A =$ $\{\mathfrak{a}\}$, then $\mathfrak{F}_{\Omega}(\{\mathfrak{a}\}) =$ $(\mathfrak{F}_{\underline{app}}(\{\mathfrak{a}\})$, $\mathfrak{F}_{\overline{app}}(\{\mathfrak{a}\})) =$ $(\phi,$ $\{\mathfrak{a}, \mathfrak{b}\})$ which is rough.

(ii) If $A =$ $\{\mathfrak{c}, \mathfrak{d}\}$, then $\mathfrak{F}_{\Omega}(\{\mathfrak{c}, \mathfrak{d}\}) =$ $(\mathfrak{F}_{\underline{app}}(\{\mathfrak{c}, \mathfrak{d}\}), \mathfrak{F}_{\overline{app}}(\{\mathfrak{c}, \mathfrak{d}\})) =$ $(\{\mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{c}, \mathfrak{d}\})$. Then, $A$ is exact and a fixed point.

(iii) The set of all fixed points is $\mathfrak{ELA}(\mathfrak{U}) =$ $\{ \mathfrak{U},$ $\phi,$ $\{\mathfrak{a}, \mathfrak{b}\},$ $\{\mathfrak{c}, \mathfrak{d}\}$ which is a distributive compete lattice. The accuracy measure is $\eta(\mathfrak{ELA}$ $(\mathfrak{U})) =$ $\frac{0+2+2+4}{0+2+2+4} =$ $1$.

(iv) If $Z =$ $\{\mathfrak{a}\}$ $\notin$ $\mathcal{P}(\mathfrak{U})$, then $\mathfrak{F}_{\Omega}(\{\mathfrak{a}\}) =$ $(\phi,$ $\{\mathfrak{a}, \mathfrak{b}\})$ and the rough extension lattice of fixed points is given by $\Omega(Z) =$ $\{(\phi, \phi)$, $(\phi, \{\mathfrak{a}, \mathfrak{b}\})$, $(\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{a}, \mathfrak{b}\})$, $(\{\mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{c}, \mathfrak{d}\})$, $(\{\mathfrak{c}, \mathfrak{d}\}$, $\mathfrak{U}),$ $(\mathfrak{U}, \mathfrak{U})\}$ is a distributive rough lattice. The accuracy measure is $\eta(\Omega(Z)) =$ $\frac{0+0+2+2+2+4}{0+2+2+2+4+4} =$ $\frac{10}{14} =$ $0.71$.

(v) If $Z =$ $\{\mathfrak{a}, \mathfrak{c}\}$, then $\mathfrak{F}_{\Omega}(Z) =$ $\{\phi, \mathfrak{U}\}$ is a totally undefinable rough set. The lattice is $(\Omega(Z), \subseteq) =$ $\{(\phi,$ $\phi)$, $(\phi$, $\{\mathfrak{a}, \mathfrak{b}\})$, $(\phi,$ $\{\mathfrak{c}, \mathfrak{d}\}),$ $(\{\mathfrak{a}, \mathfrak{b}\}$, $\{\mathfrak{a}, \mathfrak{b}\}),$ $(\{\mathfrak{c}, \mathfrak{d}\}$, $\{\mathfrak{c}, \mathfrak{d}\}),$ $(\{\mathfrak{a}, \mathfrak{b}\}$, $\mathfrak{U})$, $(\{\mathfrak{c}, \mathfrak{d}\}, \mathfrak{U})$, $(\mathfrak{U}, \mathfrak{U})\}$. The accuracy measure is $\eta(\Omega(Z)) =$ $\frac{0+0+0+0+2+2+2+2+4}{0+2+2+2+2+4+4+4+4} =$ $\frac{12}{24} =$ $0.50$. The rough extension lattice is shown in Figure 5.

5.   Conclusions

In this research, we explored the rich mathematical landscape of lattices and rough sets, essential tools in addressing various significant problems. Lattices, applied extensively in computer science and approximation spaces, and rough sets, originating from Pawlak's early work, have seen diverse generalizations utilizing different binary relations. Our focus extended to the abstract consideration of topological structures, where the universal set $\mathfrak{U}$ was analyzed through its family of open sets, forming lattices denoted as $\mathfrak{LA}(\mathfrak{U})$. Topological extensions were explored for Kolmogorov spaces, employing methodologies such as ideals, algebraic concepts, matroids, graphs, and preordered topological structures. Zhou and Hu's exploration of rough sets on a complete completely distributive lattice provided a foundational contribution. Their innovative approach considered the lattice itself as the universe, defining rough sets on a CCD lattice using an arbitrary binary relation. Unlike previous methods focusing on covers or partitions, they proposed a unified framework, demonstrating the generality of their approach for ordinary binary relations, rough fuzzy sets, and interval-valued rough fuzzy sets. The significance of our manuscript lies in introducing a comprehensive study of rough sets on lattices, through the novel use of binary relations. We believe this approach offers a fresh perspective to rough set theory, opening new avenues for understanding and applying rough sets. Moreover, our research introduces lower and upper extension approximations within an extension lattice framework, showcasing promise for practical applications. These extension approximations exhibit versatility, offering integration potential in diverse domains such as data science and artificial intelligence. The finer granularity in defining rough and exact sets could enhance pattern recognition, data analysis methodologies, and decision-making processes, particularly in handling uncertain or imprecise data. While our approach presents several advantages, empirical validations and targeted studies are crucial steps to demonstrate its efficacy within specific domains. Future research endeavors could explore fuzzy lattices to address the complexities of data with fuzzy relationships, providing a more comprehensive understanding of how rough set theory adapts to real-world data nuances. Additionally, our investigation into the extension of topological structures through lattices and equivalence relations has practical implications. The isomorphism between topology and its extension facilitates more accurate data representation, decision-making processes, and computational efficiency. This bridging of different topological structures enriches our understanding of complex datasets and enhances the efficacy of algorithms and processes in real-world applications.

In conclusion, our study contributes both theoretically and practically to the field of rough set theory, lattice theory, and topological structures. We believe that the insights gained from this research will stimulate further exploration, leading to advancements in various applications and domains.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Firstly, the authors express their gratitude to Zarqa University-Jordan, as this research is fully funded by them. The authors also extend their thanks to the Editor-in-Chief, Area Editor, and referees for their valuable comments and suggestions, which significantly enhanced the quality of this work. Heartfelt appreciation is further extended to all colleagues at the Tanta Topological Seminar, under the leadership of Prof. Dr. A. M. Kozae, for their interest, ongoing encouragement, and lively discussions. Additionally, the authors dedicate this work to the memory of Prof. Dr. M. E. Abd El-Monsef and Prof. Dr. A. Kandil "May God's mercy be upon them".

Conflict of interest

The authors of this manuscript affirm that they do not have any conflicts of interest regarding its publication.

Funding

This research is fully funded by Zarqa university-Jordan.