Let G be a graph of order n and size m. A vertex magic total labeling of G is a one-to-one function f: V(G)∪E(G)→{1,2,⋯,n+m} with the property that for each vertex u of G, the sum of the label of u and the labels of all edges incident to u is the same constant, referred to as the magic constant. Such a labeling is even if f[V(G)]={2,4,6,⋯,2n}. A graph G is called an even vertex magic if there is an even vertex magic total labeling of G. The primary goal of this paper is to study wheel related graphs with the size greater than the order, which have an even vertex magic total labeling. For every integer n≥3 and t≥1, the t-fold wheel Wn,t is a wheel related graph derived from a wheel Wn by duplicating the t hubs, each adjacent to all rim vertices, and not adjacent to each other. The t-fold wheel Wn,t has a size nt+n that exceeds its order n+t. In this paper, we determine the magic constant of the t-fold wheel Wn,t, the bound of an integer t for the even vertex magic total labeling of the t-fold wheel Wn,t and the conditions for even vertex magic Wn,t, focusing on integers n and t are established. Additionally, we investigate the necessary conditions for the even vertex magic total labeling of the n-fold wheel Wn,n when n is odd and the n-fold wheel Wn,n−2 when n is even. Furthermore, our study explores the characterization of an even vertex magic Wn,t for integer 3≤n≤9.
Citation: Supaporn Saduakdee, Varanoot Khemmani. The even vertex magic total labelings of t-fold wheels[J]. AIMS Mathematics, 2023, 8(11): 27513-27527. doi: 10.3934/math.20231407
| [1] | Shahbaz Ali, Muhammad Khalid Mahmmod, Raúl M. Falcón . A paradigmatic approach to investigate restricted hyper totient graphs. AIMS Mathematics, 2021, 6(4): 3761-3771. doi: 10.3934/math.2021223 |
| [2] | Syed Ahtsham Ul Haq Bokhary, Zill-e-Shams, Abdul Ghaffar, Kottakkaran Sooppy Nisar . On the metric basis in wheels with consecutive missing spokes. AIMS Mathematics, 2020, 5(6): 6221-6232. doi: 10.3934/math.2020400 |
| [3] | Jing Su, Qiyue Zhang, Bing Yao . The connection between the magical coloring of trees. AIMS Mathematics, 2024, 9(10): 27896-27907. doi: 10.3934/math.20241354 |
| [4] | Gohar Ali, Martin Bača, Marcela Lascsáková, Andrea Semaničová-Feňovčíková, Ahmad ALoqaily, Nabil Mlaiki . Modular total vertex irregularity strength of graphs. AIMS Mathematics, 2023, 8(4): 7662-7671. doi: 10.3934/math.2023384 |
| [5] | Saeed Kosari, Yongsheng Rao, Zehui Shao, Jafar Amjadi, Rana Khoeilar . Complexity of signed total $k$-Roman domination problem in graphs. AIMS Mathematics, 2021, 6(1): 952-961. doi: 10.3934/math.2021057 |
| [6] | Kotte Amaranadha Reddy, S Sharief Basha . New classes of reverse super edge magic graphs. AIMS Mathematics, 2022, 7(3): 3590-3602. doi: 10.3934/math.2022198 |
| [7] | T. Deepa, Raúl M. Falcón, M. Venkatachalam . On the r-dynamic coloring of the direct product of a path with either a complete graph or a wheel graph. AIMS Mathematics, 2021, 6(2): 1470-1496. doi: 10.3934/math.2021090 |
| [8] | Linyu Li, Jun Yue, Xia Zhang . Double total domination number of Cartesian product of paths. AIMS Mathematics, 2023, 8(4): 9506-9519. doi: 10.3934/math.2023479 |
| [9] | Muhammad Amir Asif, Rashad Ismail, Ayesha Razaq, Esmail Hassan Abdullatif Al-Sabri, Muhammad Haris Mateen, Shahbaz Ali . An application on edge irregular reflexive labeling for $ m^t $-graph of cycle graph. AIMS Mathematics, 2025, 10(1): 1300-1321. doi: 10.3934/math.2025060 |
| [10] | Baolin Ma, Chao Yang . Distinguishing colorings of graphs and their subgraphs. AIMS Mathematics, 2023, 8(11): 26561-26573. doi: 10.3934/math.20231357 |
Let G be a graph of order n and size m. A vertex magic total labeling of G is a one-to-one function f: V(G)∪E(G)→{1,2,⋯,n+m} with the property that for each vertex u of G, the sum of the label of u and the labels of all edges incident to u is the same constant, referred to as the magic constant. Such a labeling is even if f[V(G)]={2,4,6,⋯,2n}. A graph G is called an even vertex magic if there is an even vertex magic total labeling of G. The primary goal of this paper is to study wheel related graphs with the size greater than the order, which have an even vertex magic total labeling. For every integer n≥3 and t≥1, the t-fold wheel Wn,t is a wheel related graph derived from a wheel Wn by duplicating the t hubs, each adjacent to all rim vertices, and not adjacent to each other. The t-fold wheel Wn,t has a size nt+n that exceeds its order n+t. In this paper, we determine the magic constant of the t-fold wheel Wn,t, the bound of an integer t for the even vertex magic total labeling of the t-fold wheel Wn,t and the conditions for even vertex magic Wn,t, focusing on integers n and t are established. Additionally, we investigate the necessary conditions for the even vertex magic total labeling of the n-fold wheel Wn,n when n is odd and the n-fold wheel Wn,n−2 when n is even. Furthermore, our study explores the characterization of an even vertex magic Wn,t for integer 3≤n≤9.
A graph labeling is an assignment of integers to the vertices or edges, or both, subject to certain conditions. Gallian [3] has written a dynamic survey of graph labeling. MacDougall et al. [5] introduced the notion of a vertex magic total labeling of graphs. Let G be a graph of order n and size m. A vertex magic total labeling of G is defined as a one-to-one function
| f:V(G)∪E(G)→{1,2,⋯,n+m} |
with the property that for each vertex u of G,
| f(u)+∑v∈N(u)f(uv)=k |
for some constant k where N(u) is the neighborhood of u. The constant k is called the magic constant for f. The vertex-magic total labelings of wheels and related graphs were studied in [6], and later in [11]. The properties of the general graphs such as cycles, paths, complete graphs, wheels, bipartite graphs and trees, which satisfy the vertex magic total labelings, were studied in [10]. MacDougall et al. [4] introduced the concept of a super vertex magic total labeling. They defined a vertex magic total labeling to be super if
| f[V(G)]={1,2,⋯,n}. |
In 2017, Nagaraj et al. [7] introduced the concept of an even vertex magic total labeling. They called a vertex magic total labeling as even if
| f[V(G)]={2,4,⋯,2n}. |
A graph G is called an even vertex magic if there exists an even vertex magic total labeling of G. We note that if G is an even vertex magic, then n≤m. The following results, which appeared in [7], are useful to us.
Theorem 1.1. [7] Let G be a nontrivial graph of order n and size m. If G is an even vertex magic, then magic constant k is given by the following:
| k=m2+2mn+mn. |
A wheel Wn, n≥3, is a graph of order n+1 that contains a cycle Cn, for which every vertex in the cycle Cn is connected to one other vertex known as the hub. The edges of the wheel which are incident to the hub are called spokes. The vertices and edges of the cycle Cn in Wn are called rim vertices and rim edges, respectively. It was shown in [7] that a wheel Wn has no even vertex magic total labeling, as we state next.
Theorem 1.2. [7] A wheel Wn is not even vertex magic.
In this paper, the labeling problem is related to the work in [1]. In addition to the aforementioned vertex labeling by even numbers 2,4,⋯,2n, they studied vertex labelings by using three consecutive numbers 0,1,2 with some specific properties. These labelings were referred to as a weak Roman dominating function and a perfect Roman dominating function.
From the studies in [8,9,12], there exist graphs with the same order and size that are even vertex magics. Moreover, the wheel related graphs, namely fans, cycles and suns, having the even vertex magic total labelings were established in [7]. However, since these graphs have the same order and size, it is interesting and challenging to study wheel related graphs when the size is greater than the order, which have an even vertex magic total labeling.
The t-fold wheel Wn,t, n≥3, t≥1, is a wheel related graph derived from a wheel Wn by duplicating the t hubs, each adjacent to all rim vertices, and not adjacent to each other. It is observed that the t-fold wheel Wn,t has a size nt+n that exceeds its order n+t. The goal of this paper is to study conditions for an even vertex magic Wn,t in terms of n and t. Furthermore, we also determine an even vertex magic total labeling of some t-fold wheel Wn,t.
Since the 1-fold wheel Wn,1 is isomorphic to the wheel Wn and by Theorem 1.1, Wn is not an even vertex magic. In this section, we consider the t-fold wheel Wn,t, where n and t are integers with n≥3 and t≥2.
In order to present the conditions for an even vertex magic Wn,t, we initially explore the magic constant of the t-fold wheel Wn,t of order n+t and size nt+n by employing Theorem 1.1.
Proposition 2.1. Let n and t be integers with n≥3 and t≥2. If the t-fold wheel Wn,t is an even vertex magic, then the magic constant is defined as follows:
| k=2nt+3n+n2t2+2n2t+nn+t. |
We are able to show the bound of an integer t for the t-fold wheel having an even vertex magic total labeling as follows.
Proposition 2.2. Let n and t be integers with n≥3 and t≥2. If the t-fold wheel Wn,t is an even vertex magic, then 2≤t≤n.
Proof. Suppose that the t-fold wheel Wn,t is an even vertex magic with magic constant k. By Proposition 2.1, we obtain the following:
| k=2nt+3n+n2t2+2n2t+nn+t. |
On the contrary, assume that t>n. Let t=n+r, for some r≥1. Then,
| n2t2+2n2t+n=n4+2n3r+n2r2+2n3+2n2r+n |
and
| n+t=n+(n+r)=2n+r. |
Let
| P(n)=n4+2n3r+n2r2+2n3+2n2r+n. |
By using the remainder theorem, the remainder when P(n) is divided by 2n+r is as follows:
| P(−r2)=r4+4r3−8r16. |
If
| P(−r2)=0, |
then r=−2, which is a contradiction. Thus,
| P(−r2)≠0. |
Specifically, n2t2+2n2t+n is not divisible by n+t. Thus, k is not an integer, which is a contradiction. Therefore, 2≤t≤n.
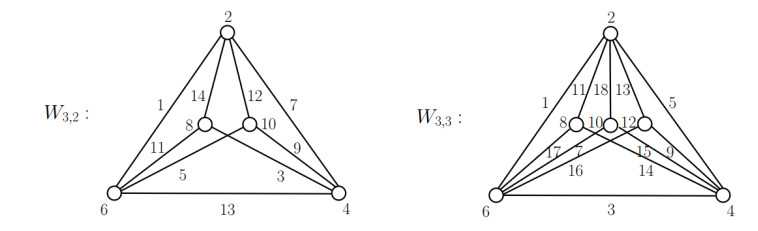
According to Proposition 2.2, the t-fold wheel W3,t is not an even vertex magic, where t≥4. Figure 1 shows the even vertex magics W3,2 and W3,3 with magic constants k=36 and k=50, respectively, where their vertices and edges are labeled by the even vertex magic total labelings. We present an even vertex magic total labeling of the t-fold wheel Wn,t by considering only the integer n as the following results.
Proposition 2.3. For every integer n≥3, if the n-fold wheel Wn,n is an even vertex magic, then n is odd.
Proof. Let n be an integer with n≥3. Suppose that the n-fold wheel Wn,n is an even vertex magic with a magic constant k. On the contrary, assume that n is even. There exists an integer q such that n=2q. By Proposition 2.1,
| k=2n2+3n+n3+2n2+12. |
Since
| n3+2n2+1=8q3+8q2+1 |
is odd, n3+2n2+1 is not divisible by 2. Thus, k is not an integer, which is a contradiction. Therefore, n is odd.
As we have seen in Figure 1, the 3-fold wheel W3,3 is an even vertex magic, as indicated by Proposition 2.3. By an argument similar to the one used in the proof of Proposition 2.3, we obtain the condition for an even vertex magic Wn,n−2, as we now show.
Proposition 2.4. For every integer n≥4, if the (n−2)-fold wheel Wn,n−2 is an even vertex magic, then n is even.
The even vertex magic total labeling of the 2-fold wheel W4,2 with a magic constant k=50 is shown in Figure 2.
In order to deduce an even vertex magic total labeling of the t-fold wheel for achieving the main result, we need some additional notation for the t-fold wheel Wn,t. For every pair of integers n≥3 and t≥2, let
| V(Wn,t)={u1,u2,…,un,v1,v2,…,vt} |
and
| E(Wn,t)={uiui+1|1≤i≤n−1}∪{unu1}∪{uivj|1≤i≤n,1≤j≤t}. |
Suppose the t-fold wheel Wn,t is an even vertex magic. Then, for any even vertex magic total labeling f of Wn,t, let
| Srv=n∑i=1f(ui), Sre=n−1∑i=1f(uiui+1)+f(unu1) |
and
| Sh=t∑j=1f(vj), Ss=t∑j=1n∑i=1f(uivj). |
Next, we present the following lemma to show the necessary condition for an even vertex magic Wn,t with the following magic constant:
| k=2nt+3n+n2t2+2n2t+nn+t. |
Note that
| Srv+2Sre−Sh=(n−t)k. |
Lemma 2.5. Let n and t be integers where n≥3 and t≥2. If the t-fold wheel Wn,t is an even vertex magic, then
| Srv+2Sre−Sh=(t2+4t+3)n2+(−2t3−6t2−3t+1)n+(t3+2t2−1)(2nt)n+t. |
With the aid of Lemma 2.5 and Proposition 2.2, the necessary condition for an even vertex magic total labeling of the t-fold wheel Wn,t can also be given in terms of n and t.
Proposition 2.6. Let n and t be integers where n≥3 and t≥2. If the t-fold wheel Wn,t is an even vertex magic, then
| (−t2−2t+1)n2+(2t3+6t2+7t+1)n−(t2+t)−(t3+2t2−1)(2nt)n+t≥0. |
Proof. Suppose that the t-fold wheel Wn,t is an even vertex magic. By Lemma 2.5,
| Srv+2Sre−Sh=(t2+4t+3)n2+(−2t3−6t2−3t+1)n+(t3+2t2−1)(2nt)n+t. |
Next, we consider the maximum of (Srv+2Sre−Sh).
By Proposition 2.2, 2≤t≤n, and then 2n+2t<nt+n+t+1. The maximum of
| (Srv+2Sre−Sh)=∑2t+2≤i≤2n+2tiis eveni+2nt+2n+t∑i=nt+n+t+1i−∑2≤i≤2tiis eveni=(∑2≤i≤2n+2tiis eveni−∑2≤i≤2tiis eveni)+2(nt+2n+t∑i=1i−nt+n+t∑i=1i)−∑2≤i≤2tiis eveni=((2n+2t)(2n+2t+2)4−(2t)(2t+2)4)+2((nt+2n+t)(nt+2n+t+1)2−(nt+n+t)(nt+n+t+1)2)−(2t)(2t+2)4=2n2t+4n2+4nt−t2+2n−t. |
Since Srv+2Sre−Sh does not exceed the maximum of (Srv+2Sre−Sh), the maximum of
| (Srv+2Sre−Sh)−(Srv+2Sre−Sh)≥0. |
Therefore,
| (−t2−2t+1)n2+(2t3+6t2+7t+1)n−(t2+t)−(t3+2t2−1)(2nt)n+t≥0. |
Now, we investigate the sufficient condition for a labeling f that can be an even vertex magic total labeling of Wn,n when n is odd.
Theorem 2.7. Let n be an odd integer where n≥3. For every n-fold wheel Wn,n, let
| f:V(Wn,n)∪E(Wn,n)→{1,2,…,n2+3n} |
be defined by the following:
| f(ui) = 2i, if 1≤i≤n,f(vj) = 2n+2j, if 1≤j≤n,f(uiui+1) = 2n+1−2i, if 1≤i≤n−1,f(unu1) = 1, f(un+1−jvj) = n2+3n+1−2j, if 1≤j≤n,f[EH]−f[{un+1−jvj|1≤j≤n}] = {2n+1,2n+3,…,n2+n−1} ∪{4n+2,4n+4,…,n2+3n}, if EH={uivj|1≤i,j≤n}. |
If
| n−1∑j=1f(u1vj)=n3+4n2−52, |
then f can be an even vertex magic total labeling of Wn,n.
Proof. Assume that
| n−1∑j=1f(u1vj)=n3+4n2−52. |
We have that
| Ss−n∑j=1f(un+1−jvj)=∑2n+1≤i≤n2+n−1iis oddi+∑4n+2≤i≤n2+3niis eveni=(∑1≤i≤n2+n−1iis oddi−∑1≤i≤2n−1iis oddi)+(∑2≤i≤n2+3niis eveni−∑2≤i≤4niis eveni)=((n2+n)24−(2n)24)+((n2+3n)(n2+3n+2)4−4n(4n+2)4)=n4+4n3−4n2−n2, |
and then,
| (Ss−n∑j=1f(un+1−jvj))−n−1∑j=1f(u1vj)=n4+3n3−8n2−n+52. |
Next, we consider the sum of the label of each vertex and the labels of all edges incident to this vertex. By the assumption, for 1≤j≤n,
| f(vj)+n∑i=1f(uivj)=f(vj)+f(un+1−jvj)+∑1≤i≤ni≠n+1−jf(uivj)=f(vj)+f(un+1−jvj)+Ss−n∑j=1f(un+1−jvj)n=(2n+2j)+(n2+3n+1−2j)+n3+4n2−4n−12=n3+6n2+6n+12, |
| f(u1)+f(u1u2)+f(unu1)+n∑j=1f(u1vj)=f(u1)+f(u1u2)+f(unu1)+f(u1vn)+n−1∑j=1f(u1vj)=2+(2n+1−2)+1+(n2+n−1+2)+n3+4n2−52=n3+6n2+6n+12. |
For 2≤i≤n,
| f(ui)+f(uiui+1)+f(ui−1ui)+n∑j=1f(uivj)=f(ui)+f(uiui+1)+f(ui−1ui)+f(uivn+1−i)+∑1≤j≤nj≠n+1−if(uivj)=f(ui)+f(uiui+1)+f(ui−1ui)+f(uivn+1−i)+(Ss−n∑j=1f(un+1−jvj))−n−1∑j=1f(u1vj)n−1=2i+(2n+1−2i)+(2n+1−2i+2)+(n2+n−1+2i)+n3+4n2−4n−52=n3+6n2+6n+12. |
Therefore, f can be an even vertex magic total labeling of Wn,n with a magic constant
| k=n3+6n2+6n+12. |
Now, we investigate the sufficient condition for a labeling f that can be an even vertex magic total labeling of Wn,n−2 when n is even.
Theorem 2.8. Let n be an even integer with n≥4. For every (n−2)-fold wheel Wn,n−2, let
| f:V(Wn,n−2)∪E(Wn,n−2)→{1,2,…,n2+n−2} |
be defined by the following:
| f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n−2,f[EC]={a1,a2,⋯,an},if EC={uiui+1,unu1|1≤i≤n−1},f[EH]={1,2,⋯,n2+n−2}−{2,4,⋯,2n+4,a1,a2,⋯,an},if EH={uivj|1≤i≤n,1≤j≤n−2}. |
If
| Ss=n4+n3−15n2+20n−42, |
then f can be an even vertex magic total labeling of Wn,n−2.
Proof. Assume that
| Ss=n4+n3−15n2+20n−42. |
It suffices to show that for each vertex u of Wn,n−2,
| f(u)+∑v∈N(u)f(uv)=k, |
where
| k=n3+3n2−3n2. |
To do this, we consider the relevant sums, as follows.
Since the sum of the labels of all rim edges is equal to the sum of the labels of all vertices and the labels of all edges subtracted by the sum of the labels of all vertices and the labels of all spokes, it follows that
| Sre=n2+n−2∑i=1i−∑2≤i≤4n−4iis eveni−Ss=(n2+n−2)(n2+n−1)2−(4n−4)(4n−2)4−n4+n3−15n2+20n−42=n3+5n2−11n+22. |
Since the sum of the labels of all hubs is equal to the sum of even integers from 2n+2 to 4n−4,
| Sh+Ss=∑2n+2≤i≤4n−4iis eveni+Ss=(∑2≤i≤4n−4iis eveni−∑2≤i≤2niis eveni)+Ss=(4n−4)(4n−2)4−(2n)(2n+2)4+n4+n3−15n2+20n−42=n4+n3−9n2+6n2. |
Since the sum of the labels of all rim vertices is equal to the sum of even integers from 2 to 2n,
| Srv+2Sre+Ss=∑2≤i≤2niis eveni+2Sre+Ss=(2n)(2n+2)4+2(n3+5n2−11n+22)+n4+n3−15n2+20n−42=n4+3n3−3n22. |
Next, we consider the sum of the label of each vertex and the labels of all edges incident to this vertex. We have the sum of the label of each hub and the labels of all edges incident to this hub as follows.
For 1≤j≤n−2,
| f(vj)+n∑i=1f(uivj)=Sh+Ssn−2=n3+3n2−3n2. |
We obtain the sum of the label of each rim vertex and the labels of all edges incident to this rim vertex as follows.
For 2≤i≤n−1,
| f(ui)+f(uiui+1)+f(ui−1ui)+n−2∑j=1f(uivj)=Srv+2Sre+Ssn=n3+3n2−3n2. |
Similarly,
| f(un)+f(unu1)+f(un−1un)+n−2∑j=1f(unvj)=n3+3n2−3n2 |
and
| f(u1)+f(u1u2)+f(unu1)+n−2∑j=1f(u1vj)=n3+3n2−3n2. |
Therefore, f can be an even vertex magic total labeling of Wn,n−2 with the following magic constant:
| k=n3+3n2−3n2. |
In this section, we establish a characterization of an even vertex magic Wn,t for an integer 3≤n≤9. First, we present an n-fold wheel Wn,n which has an even vertex magic total labeling for every odd integer 3≤n≤9 as follows.
Theorem 3.1. For every odd integer 3≤n≤9, the n-fold wheel Wn,n is an even vertex magic.
Proof. Let n be an odd integer where 3≤n≤9. We define
| f:V(Wn,n)∪E(Wn,n)→{1,2,⋯,n2+3n}, |
as the sufficient condition of Theorem 2.7, by
| f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n,f(uiui+1)=2n+1−2i,if 1≤i≤n−1,f(unu1)=1, |
and for 1≤i,j≤n, f(uivj) are shown in Tables 1–4,
| f(uivj) | v1 | v2 | v3 |
| u1 | 11 | 18 | 13 |
| u2 | 14 | 15 | 9 |
| u3 | 17 | 7 | 16 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 |
| u1 | 15 | 21 | 36 | 38 | 31 |
| u2 | 13 | 30 | 29 | 33 | 28 |
| u3 | 40 | 24 | 35 | 19 | 17 |
| u4 | 34 | 37 | 11 | 23 | 32 |
| u5 | 39 | 27 | 26 | 22 | 25 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 |
| u1 | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| u2 | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| u3 | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| u4 | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| u5 | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| u6 | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| u7 | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 |
| u1 | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| u2 | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| u3 | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| u4 | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| u5 | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| u6 | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| u7 | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| u8 | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| u9 | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
For every odd integer 3≤n≤9, the labeling f, as defined above, is an even vertex magic total labeling of the n-fold wheel Wn,n with magic constants k=50,153,340 and 635, respectively. Therefore, Wn,n is an even vertex magic.
As a consequence of an even vertex magic W3,2, Proposition 2.2 and Theorem 3.1, in any t-fold wheel W3,t, we are able to show that both W3,t and W3,t are only even vertex magics.
Theorem 3.2. For every integer t≥2, the t-fold wheel W3,t is an even vertex magic if and only if t=2,3.
The following result gives the necessary and sufficient condition for the t-fold wheel Wn,t to be an even vertex magic for every odd integer 5≤n≤9.
Theorem 3.3. For every odd integer 5≤n≤9 and an integer t≥2, the t-fold wheel Wn,t is an even vertex magic if and only if t=n.
Proof. Let n be an odd integer where 5≤n≤9 and t is an integer where t≥2. Assume that the t-fold wheel Wn,t is an even vertex magic. By Proposition 2.2, 2≤t≤n.
Case 1. n=5,7. If 2≤t≤n−1, then n2t2+2n2t+n is not divisible by n+t, and hence k is not an integer, which is a contradiction. Therefore, t=n.
Case 2. n=9. If either t=2 or 4≤t≤n−1, then n2t2+2n2t+n is not divisible by n+t, and hence k is not an integer, which is a contradiction. If t=3, then,
| 2nt3−n2t2−2n2t+6nt2+7nt+n2−t2+n−t−2nt4+4nt3−2ntn+t=−174<0, |
which is a contradiction with Proposition 2.6. Therefore, t=n.
Conversely, assume t=n. By Theorem 3.1, Wn,t is an even vertex magic.
We show an even vertex magic total labeling of Wn,n−2 for every even integer 4≤n≤8 as follows.
Theorem 3.4. For every even integer 4≤n≤8, the (n−2)-fold wheel Wn,n−2 is an even vertex magic.
Proof. Let n be an even integer with 4≤n≤8. We define
| f:V(Wn,n−2)∪E(Wn,n−2)→{1,2,…,n2+n−2} |
as the sufficient condition of Theorem 2.8, by
| f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n−2, |
for 1≤i≤n−1, f(uiui+1) and f(unu1) are shown in Tables 5–7.
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u1) |
| 18 | 9 | 11 | 13 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u1) |
| 40 | 39 | 38 | 13 | 17 | 19 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u7) | f(u7u8) | f(u8u1) |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
And for 1≤i≤n and 1≤j≤n−2, f(uivj) are shown in Tables 8–10.
| f(uivj) | v1 | v2 |
| u1 | 16 | 1 |
| u2 | 14 | 5 |
| u3 | 7 | 17 |
| u4 | 3 | 15 |
| f(uivj) | v1 | v2 | v3 | v4 |
| u1 | 36 | 24 | 3 | 29 |
| u2 | 11 | 25 | 33 | 1 |
| u3 | 26 | 9 | 5 | 30 |
| u4 | 22 | 23 | 34 | 15 |
| u5 | 37 | 21 | 28 | 27 |
| u6 | 7 | 35 | 32 | 31 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 |
| u1 | 69 | 3 | 40 | 56 | 39 | 50 |
| u2 | 1 | 67 | 5 | 59 | 31 | 35 |
| u3 | 21 | 17 | 65 | 7 | 44 | 46 |
| u4 | 42 | 38 | 23 | 33 | 9 | 57 |
| u5 | 61 | 27 | 37 | 34 | 30 | 15 |
| u6 | 41 | 53 | 49 | 32 | 47 | 25 |
| u7 | 29 | 60 | 54 | 52 | 63 | 36 |
| u8 | 58 | 55 | 45 | 43 | 51 | 48 |
For every even integer 4≤n≤8, the labeling f, as defined above, is an even vertex magic total labeling of the (n−2)-fold wheel Wn,n−2 with magic constants k=50,153 and 340, respectively. Therefore, Wn,n−2 is an even vertex magic.
There is a similar methodology of the proof of Theorem 3.4, which is also used in the study of graph operations (see [2]). Next, we determine a characterization of the t-fold wheel Wn,t to be an even vertex magic for every even integer 4≤n≤8. In order to we need to present the following lemma involving a 3-fold wheel W8,3.
Lemma 3.5. The 3-fold wheel W8,3 is not an even vertex magic.
Proof. On the contrary, assume that the 3-fold wheel W8,3 is an even vertex magic with a magic constant k. Since W8,3 has an order 11 and a size 32 and by Proposition 2.1, k=160. We have that
| Srv=132, 2Sre=1,628−2Ss |
and
| Srv+2Sre+Ss=8k=1,280. |
Thus, Ss=480. However, Sh+Ss=3k=480. This is a contradiction because Sh>0. Therefore, W8,3 is not an even vertex magic.
We are able to show that the necessary and sufficient condition for the t-fold wheel Wn,t is an even vertex magic for every even integer 4≤n≤8.
Theorem 3.6. For every even integer 4≤n≤8 and integer t≥2, the t-fold wheel Wn,t is an even vertex magic if and only if t=n−2.
Proof. Let n be an even integer where 4≤n≤8 and t is an integer where t≥2. Assume that the t-fold wheel Wn,t is an even vertex magic. By Proposition 2.2, 2≤t≤n.
Case 1. n=4,6. If either 2≤t≤n−3 or n−1≤t≤n, then n2t2+2n2t+n is not divisible by n+t, and hence k is not an integer, which is a contradiction. Therefore, t=n−2.
Case 2. n=8. If either 4≤t≤n−3 or n−1≤t≤n, then n2t2+2n2t+n is not divisible by n+t, and hence k is not an integer, which is a contradiction. If t=3, then, by Lemma 3.5, Wn,t is not an even vertex magic, which is a contradiction. If t=2, then,
| 2nt3−n2t2−2n2t+6nt2+7nt+n2−t2+n−t−2nt4+4nt3−2ntn+t=−62<0, |
which is a contradiction with Proposition 2.6. Therefore, t=n−2.
Conversely, assume t=n−2. By Theorem 3.4, Wn,t is an even vertex magic.
In this paper, we have not only established the bound of an integer t for the even vertex magic total labeling of the t-fold wheel, but have also presented the necessary condition for such labeling in terms of n and t. Furthermore, we have conducted an investigation into the sufficient conditions for labelings that can serve as even vertex magic total labelings for Wn,n when n is odd, and Wn,n−2 when n is even.
Our research has led us to the following significant conclusions:
● For every integer t≥2, the t-fold wheel W3,t is an even vertex magic total labeling if and only if t=2,3.
● For every odd integer 5≤n≤9 and an integer t≥2, the t-fold wheel Wn,t is an even vertex magic total labeling if and only if t=n.
● For every even integer 4≤n≤8 and an integer t≥2, the t-fold wheel Wn,t is an even vertex magic total labeling if and only if t=n−2.
In essence, our work has discussed the characterizations of t-fold wheel Wn,t to possess an even vertex magic total labeling for an integer 3≤n≤9. It would be interesting to apply the results of this paper to further study under what conditions for Wn,t will be an even vertex magic, especially for a larger n.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare that they have no conflicts of interest.
| [1] |
A. Alhevaz, M. Darkooti, H. Rahbani, Y. Shang, Strong equality of perfect Roman and weak Roman domination in trees, Mathematics, 7 (2019), 997. http://doi.org/10.3390/math7100997 doi: 10.3390/math7100997

|
| [2] |
A. Alhevaz, M. Baghipur, H. A. Ganie, Y. Shang, The generalized distance spectrum of the join of graphs, Symmetry, 12 (2020), 169. http://doi.org/10.3390/sym12010169 doi: 10.3390/sym12010169

|
| [3] | J. A. Gallian, A dynamic survey of graph labeling, Electron. J. Comb., 2009. |
| [4] | J. A. MacDougall, M. Miller, K. A. Sugeng, Super vertex-magic total labeling of graphs, Proceedings of the 15th Australasian Workshop on Combinatorial Algorithms, 2004. |
| [5] | J. A. MacDougall, M. Miller, Slamin, W. D. Wallis, Vertex-magic total labeling of graphs, Utilitas Math., 61 (2002), 3–21. |
| [6] | J. A. MacDougall, M. Miller, W. D. Wallis, Vertex-magic total labelings of wheels and related graphs, Utilitas Math., 62 (2002), 175–183. |
| [7] | C. T. Nagaraj, C. Y. Ponnappan, G. Prabakaran, Even vertex magic total labeling, Int. J. Pure Appl. Math., 115 (2017), 363–374. |
| [8] | C. T. Nagaraj, C. Y. Ponnappan, G. Prabakaran, Even vertex magic total labeling of isomorphic and non isomorphic suns, Int. J. Math. Trends Technol., 52 (2017), 458–467. |
| [9] | C. T. Nagaraj, C. Y. Ponnappan, G. Prabakaran, Even vertex magic total labeling of some 2-regular graphs, Int. J. Math. Trends Technol., 54 (2018), 52–59. |
| [10] | V. A. Nageswari, V. Maheswari, Vertex magic total labeling of some general graphs and its properties, Int. J. Pure Appl. Math., 118 (2018), 4637–4643. |
| [11] | M. T. Rahim, I. Tomescu, Slamin, On vertex-magic total labeling of some wheel related graphs, Utilitas Math., 73 (2007), 97–104. |
| [12] |
M. Sindhu, S. C. Kumar, Even vertex in-magic total labeling of some 2-regular digraphs, J. Electron. Comput. Networking Appl. Math., 1 (2021), 1–11. http://doi.org/10.55529/jecnam.12.1.11 doi: 10.55529/jecnam.12.1.11

|
| f(uivj) | v1 | v2 | v3 |
| u1 | 11 | 18 | 13 |
| u2 | 14 | 15 | 9 |
| u3 | 17 | 7 | 16 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 |
| u1 | 15 | 21 | 36 | 38 | 31 |
| u2 | 13 | 30 | 29 | 33 | 28 |
| u3 | 40 | 24 | 35 | 19 | 17 |
| u4 | 34 | 37 | 11 | 23 | 32 |
| u5 | 39 | 27 | 26 | 22 | 25 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 |
| u1 | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| u2 | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| u3 | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| u4 | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| u5 | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| u6 | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| u7 | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 |
| u1 | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| u2 | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| u3 | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| u4 | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| u5 | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| u6 | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| u7 | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| u8 | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| u9 | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u1) |
| 18 | 9 | 11 | 13 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u1) |
| 40 | 39 | 38 | 13 | 17 | 19 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u7) | f(u7u8) | f(u8u1) |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
| f(uivj) | v1 | v2 |
| u1 | 16 | 1 |
| u2 | 14 | 5 |
| u3 | 7 | 17 |
| u4 | 3 | 15 |
| f(uivj) | v1 | v2 | v3 | v4 |
| u1 | 36 | 24 | 3 | 29 |
| u2 | 11 | 25 | 33 | 1 |
| u3 | 26 | 9 | 5 | 30 |
| u4 | 22 | 23 | 34 | 15 |
| u5 | 37 | 21 | 28 | 27 |
| u6 | 7 | 35 | 32 | 31 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 |
| u1 | 69 | 3 | 40 | 56 | 39 | 50 |
| u2 | 1 | 67 | 5 | 59 | 31 | 35 |
| u3 | 21 | 17 | 65 | 7 | 44 | 46 |
| u4 | 42 | 38 | 23 | 33 | 9 | 57 |
| u5 | 61 | 27 | 37 | 34 | 30 | 15 |
| u6 | 41 | 53 | 49 | 32 | 47 | 25 |
| u7 | 29 | 60 | 54 | 52 | 63 | 36 |
| u8 | 58 | 55 | 45 | 43 | 51 | 48 |
| f(uivj) | v1 | v2 | v3 |
| u1 | 11 | 18 | 13 |
| u2 | 14 | 15 | 9 |
| u3 | 17 | 7 | 16 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 |
| u1 | 15 | 21 | 36 | 38 | 31 |
| u2 | 13 | 30 | 29 | 33 | 28 |
| u3 | 40 | 24 | 35 | 19 | 17 |
| u4 | 34 | 37 | 11 | 23 | 32 |
| u5 | 39 | 27 | 26 | 22 | 25 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 |
| u1 | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| u2 | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| u3 | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| u4 | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| u5 | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| u6 | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| u7 | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 |
| u1 | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| u2 | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| u3 | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| u4 | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| u5 | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| u6 | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| u7 | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| u8 | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| u9 | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u1) |
| 18 | 9 | 11 | 13 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u1) |
| 40 | 39 | 38 | 13 | 17 | 19 |
| f(u1u2) | f(u2u3) | f(u3u4) | f(u4u5) | f(u5u6) | f(u6u7) | f(u7u8) | f(u8u1) |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
| f(uivj) | v1 | v2 |
| u1 | 16 | 1 |
| u2 | 14 | 5 |
| u3 | 7 | 17 |
| u4 | 3 | 15 |
| f(uivj) | v1 | v2 | v3 | v4 |
| u1 | 36 | 24 | 3 | 29 |
| u2 | 11 | 25 | 33 | 1 |
| u3 | 26 | 9 | 5 | 30 |
| u4 | 22 | 23 | 34 | 15 |
| u5 | 37 | 21 | 28 | 27 |
| u6 | 7 | 35 | 32 | 31 |
| f(uivj) | v1 | v2 | v3 | v4 | v5 | v6 |
| u1 | 69 | 3 | 40 | 56 | 39 | 50 |
| u2 | 1 | 67 | 5 | 59 | 31 | 35 |
| u3 | 21 | 17 | 65 | 7 | 44 | 46 |
| u4 | 42 | 38 | 23 | 33 | 9 | 57 |
| u5 | 61 | 27 | 37 | 34 | 30 | 15 |
| u6 | 41 | 53 | 49 | 32 | 47 | 25 |
| u7 | 29 | 60 | 54 | 52 | 63 | 36 |
| u8 | 58 | 55 | 45 | 43 | 51 | 48 |