Asymptotic synchronization analysis of fractional-order octonion-valued neural networks with impulsive effects

1.   Introduction

It is well-known that the chemical compounds can be represented by graphs (or chemical graphs) in which vertices correspond to the atoms while edges represent the covalent bonds between atoms. Predicting physicochemical properties of chemical compounds is considered to be a fascinating issue in theoretical chemistry. Many predictive methods have been and are being developed for correlating molecular structures with their physicochemical properties. One of the simplest such methods is topological indices. In chemical graph theory, graph invariants are usually referred as topological indices. Nowadays the most active problem in the theory of topological indices is finding the extremal structures under certain constraints, that maximize or minimize the given topological index.

Suppose that $G$ is a connected graph with vertex set $V(G)$ and edge set $E(G)$. The degree of vertex $u$ is denoted by $d(u)$. A vertex $u$ in $G$ is called pendant if $d(u) = 1$. The distance from $u$ to $v$, denoted by $d(u, v)$, is defined as the smallest length of all $u-v$ paths in $G$. The eccentricity of $v$, denoted as $ecc(v)$, is the maximum distance between $v$ and other vertices in $G$. For other notation and terminology not defined here, the readers are referred to the book by West ^[24].

A topological index is a numerical descriptor of the molecular structure derived from the corresponding molecular graph. The first Zagreb index (the second Zagreb index as well) was first introduced by Gutman and Trinajstić ^[13] and has been closely related to many chemical properties ^[13,22]. The first Zagreb index of a graph $G$ is defined by:

Some mathematical properties of the first Zagreb index can be found in ^{[15,16,17,21,23]} and the comprehensive surveys ^[5,12,20].

Roman dominating function $RDF$ of $G$ is a function $f:V(G)\rightarrow \{0, 1, 2\}$ satisfying the condition that every vertex with label 0 is adjacent to a vertex with label 2. The weight of an $RDF$ $f$ is $w(f) = \sum_{v\in V(G)} f(v)$. The Roman domination number of $G$, denoted by $\gamma_R (G)$, is the minimum weight among all RDF in $G$. The concept of Roman domination number of graphs was introduced by Cockayne et al. ^[8], and further studied in ^{[1,2,3,9,11,14,19]} and references therein.

Relationship between various topological indices and domination number of graphs is in the focus of interest of the researchers for quite many years, and this direction is continuously vital, see ^[4,6,10,18], the surveys ^[5,20] and references therein. In this paper, we determine the trees with the maximum first Zagreb index when Roman domination number is fixed.

Let $G-v$ be the graph obtained from $T$ by deleting the vertex $v$ and its incident edges, for $v \in V(G)$. Let $\mathbb{T} (n, \gamma_{R})$ be the set of trees whose order is $n$ and Roman domination number is $\gamma_{R}$, where $n \ge \max\left\{ \lceil \frac{3 \gamma_{R} - 5}{2} \rceil, \gamma_{R} + 3 \right\}$.

2.   Main results

In this section, we will determine the trees with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$ step by step.

2.1.   Some properties about the Roman domination number of trees

Let us introduce some properties about the Roman domination number of trees which will be used later.

The first lemma reveals the effect on the Roman domination number of trees after deleting a pendant vertex (there are two possibilities for the effect).

Lemma 2.1. Let $T$ be a tree with a pendant vertex $v$. Then

Proof. First, we prove the left inequality $\gamma_{R} (T- v) \le \gamma_{R} (T)$. If $v$ is labeled as $0$ in an RDF (Roman dominating function) of $T$ with weight $\gamma_{R} (T)$, then delete such label $0$ of $v$, it leads to an RDF of $T - v$ still with weight $\gamma_{R} (T)$, so $\gamma_{R} (T- v) \le \gamma_{R} (T)$. If $v$ is labeled as $1$ in an RDF of $T$ with weight $\gamma_{R} (T)$, then similarly we have $\gamma_{R} (T- v) \le \gamma_{R} (T) - 1 < \gamma_{R} (T)$. Assume that $v$ is labeled as $2$ in an RDF of $T$ with weight $\gamma_{R} (T)$, and denote by $u$ the unique neighbor of $v$ in $T$. Obverse that $u$ must be labeled as $0$, otherwise we may obtain another RDF of $T$ with a smaller weight than $\gamma_{R} (T)$, by decreasing the label $2$ of $v$. At this time, we may change the labels of $u$ and $v$ both into $1$, and keep the labels of other vertices unchanged. Clearly, the weight under this new RDF of $T$ is still $\gamma_{R} (T)$. But now $v$ is labeled as $1$, so by the above comments, we obtain $\gamma_{R} (T- v) < \gamma_{R} (T)$ again.

The second inequality $\gamma_{R} (T) \le \gamma_{R} (T- v) + 1$ is straightforward. Starting from the tree $T-v$, when we add a new vertex $v$, we may always label it as $1$. So there is an RDF of $T$ with weight $\gamma_{R} (T- v) + 1$, which results in $\gamma_{R} (T) \le \gamma_{R} (T- v) + 1$.

From the above lemma, after deleting a pendant vertex $v$ from a tree $T$, either $\gamma_{R} (T- v) = \gamma_{R} (T)$ or $\gamma_{R} (T- v) = \gamma_{R} (T) - 1$. In the following lemma, we present a condition in which $\gamma_{R} (T- v) = \gamma_{R} (T)$ holds.

Lemma 2.2. Let $T$ be a tree. Assume that there are (at least) three pendant vertices sharing the same neighbor in $T$. In particular, one of the three pendant vertices is denoted by $v$. Then $\gamma_{R} (T) = \gamma_{R} (T- v)$.

Proof. From Lemma 2.1, we already have $\gamma_{R} (T- v) \le \gamma_{R} (T)$. So we are left to show the reversed counterpart that $\gamma_{R} (T) \le \gamma_{R} (T-v)$. Assume that $v, u, w$ are the three pendant vertices sharing the same neighbor $z$. If there is an RDF of $T-v$ with weight $\gamma_{R} (T- v)$ such that $z$ is labeled as $2$, then in addition to such RDF of $T-v$, assign the label $0$ to the new added vertex $v$, an RDF of $T$ with weight $\gamma_{R} (T- v)$ follows, which leads to $\gamma_{R} (T) \le \gamma_{R} (T-v)$ immediately.

Next let us analyze if we can always have such ideal RDF of $T-v$ (with weight $\gamma_{R} (T- v)$ such that $z$ is labeled as $2$). If $u$ or $w$ is labeled as $0$, then $z$ must be labeled as $2$, from the definition of Roman domination number. Otherwise, the labels of $u$ and $w$ are both at least $1$, means that the sum of labels of $u$ and $w$ is at least $2$, then we modify such RDF of $T-v$, such that $u$ and $w$ are both labeled as $0$, $z$ is labeled as $2$, keep the labels of other vertices unchanged, clearly it is just our desired RDF of $T-v$ (such revised RDF of $T - v$ would not increase the weight).

The proof is completed now by noting that $\gamma_{R} (T) \le \gamma_{R} (T-v)$ always holds.

The maximum degree of trees in $\mathbb{T} (n, \gamma_{R})$ plays an important role in our subsequent deduction, which is at most $n-\gamma_{R}+1$ established as following.

Lemma 2.3. ^[7] If $G$ is an $n$-vertex graph with maximum degree $\Delta (G)$, then $\gamma_{R}(G) \leq n - \Delta(G)+1$.

Based on this lemma, subsequently we partition our consideration into two parts: Trees with maximum degree exactly $n-\gamma_{R}+1$ and trees with maximum degree less than $n-\gamma_{R}+1$.

2.2.   Trees with maximum degree $n-\gamma_{R}+1$

Actually the trees with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$ are of maximum degree $n-\gamma_{R}+1$. We focus on such trees (with maximum degree $n-\gamma_{R}+1$) in the following several lemmas, which is crucial for our final results.

First, we observe that such trees have a small eccentricity.

Lemma 2.4. Let $T \in \mathbb{T} (n, \gamma_{R})$.Assume that $v$ is a vertex in $T$ with degree $n-\gamma_{R}+1$. Then $ecc (v) \le 3$.

Proof. First, we introduce a realizable RDF of $T$ with weight $\gamma_{R}$. Let us label $v$ as $2$, label all the neighbors of $v$ (there are $n-\gamma_{R}+1$ such neighbors) as $0$, and label the remaining vertices (there are $\gamma_{R} - 2$ vertices) as $1$. Such RDF of $T$ gives the weight $\gamma_{R}$. It is worth mentioning that there is no RDF of $T$ with a smaller weight than $\gamma_{R}$, from the definition of Roman domination number (since $\gamma_R (T) = \gamma_{R}$).

Assume that $x, y, z \in V(T)$ such that $xy$ and $yz$ are edges of $T$. We claim that at least one of $x, y, z$ is adjacent to $v$. Suppose that it is not true (none of $x, y, z$ is adjacent to $v$). Under the above-mentioned RDF of $T$, each of $x, y, z$ should be labeled as $1$. But if we change the labels of $x, y, z$ such that the vertex $y$ is labeled as $2$, vertices $x, z$ are both labeled as $0$, and the labels of other vertices keep unchanged, it leads to a new weight $\gamma_{R} - 1$ (less than $\gamma_{R}$), which is a contradiction to the definition of Roman domination number.

Finally, $ecc (v) \le 3$ follows from the above claim immediately (otherwise we can find the vertices $x, y, z$ satisfying the above condition).

Lemma 2.5. Let $G$ be a tree of order $n$ with maximum degree $\Delta(G)$. If $\Delta(G) = n - \gamma_R + 1$, then for every vertex $v$ of maximum degree have to labeled by 2.

Proof. Let $G$ be a graph with $\Delta(G) = n - \gamma_R + 1$ and let $v$ a vertex of maximum degree. Consider an RDF $f$ that assigns the value 2 to $v$, 0 to every neighbor of $v$ and 1 to the remaining vertices. Clearly $w(f) = n - \gamma_R + 1$ and thus $f$ is a $\gamma_R$-function. Now suppose to the contrary that $v$ has a neighbor $w$ having at least three neighbors in $N(w)$. Then reassigning $w$ a 2 instead of 0 and each vertex of $N(w)$ a 0 instead of 1 produces an RDF with smaller weight than $\gamma_R$, a contradiction.

We present the definition of branches of a tree, which helps us describe the local structures of trees with the maximum first Zagreb index.

Definition 2.1. Let $T$ be a tree with $v \in V(T)$. Let $u$ be some neighbor of $v$ in $T$. Based on $T$, delete all the neighbors of $v$ except $u$, the component of the resulting forest containing $v$ is said to be a branch of $T$ at $v$.

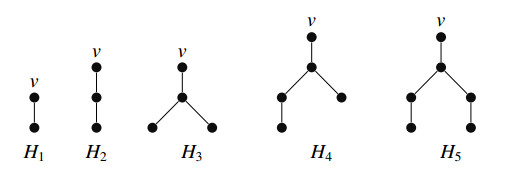
For a tree with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R}$), there are exactly five possibilities for the branches at a vertex of maximum degree $n-\gamma_{R}+1$.

Lemma 2.6. Let $T$ be a tree with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$.Assume that $v$ is a vertex in $T$ with degree $n-\gamma_{R}+1$, and $H$ is a branch of $T$ at $v$. Then $H \cong H_i$, for $1 \le i \le 5$ (all the $H_i$ are depicted in Figure 1).

Proof. Let $H$ be a branch of $T$ at $v$, and set $s = \max \{ d (v, x) : x \in V(H) \}$. From Lemma 2.4, $s = 1, 2, 3$. In particular, the cases $s = 1, 2$ corresponding to $H_1, \; H_2, \; H_3$ are clear. Assume that $s = 3$ in the following.

Just like the proof of Lemma 2.4, we deduce that there are no two pendant vertices, at distances $3$ from $v$, sharing a common neighbor in $H$ (otherwise we have a weight less than $\gamma_{R}$ after modifying the labels of the two pendant vertices and their common neighbor, just like the proof of Lemma 2.4), which implies the existence of a pendant path of length $2$ or $3$ in $H$.

If $H$ is the pendant path of length $3$ (at $v$), then reformulate $H$ as $H_3$, keep other parts unchanged, the weight of $T$ keeps the same, but the first Zagreb index becomes larger, which is a contradiction to our choosing of $T$ (with the maximum first Zagreb index).

Suppose that there is a pendant path of length $2$ in $H$. Denote by $u$ the root vertex of such pendant path ($u$ is adjacent to $v$). If $u$ is of degree at least $4$, then $u$ has (at least) three neighbors (each one is labeled as $1$) besides $v$, modify the labels of $u$ and its neighbors such that $u$ is labeled as $2$, all the neighbors of $u$ except $v$ are labeled $0$, keep the labels of other vertices except $v$ unchanged, such a new RDF of $T$ would have a smaller weight than $\gamma_{R}$, a contradiction. Thus, $u$ is of degree $3$, $H \cong H_4$ or $H_5$ follows easily.

At the next stage, let us go ahead under the same hypothesis as Lemma 2.6. Let $T$ be a tree with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$. Assume that $v$ is a vertex in $T$ with degree $n-\gamma_{R}+1$. Lemma 2.6 has revealed that each branch of $T$ at $v$ can only be $H_i$, for $1 \le i \le 5$. Furthermore, we determine the possible occurrence numbers for each $H_i$ in $T$, $1 \le i \le 5$.

Denote by $n_i$ the number of branches of $T$ at $v$ with the form $H_i$, for $1 \le i \le 5$. Then

and

The former equation follows from the degree $n-\gamma_{R}+1$ of $v$, and the latter equation comes from the Roman domination number $\gamma_{R}$ of $T$, where the uncounted vertex $v$ is labeled as $2$.

For convenience, we use $T = (n_1, n_2, n_3, n_4, n_5)$ to represent a tree $T \in \mathbb{T} (n, \gamma_{R})$ having $n_i$ branches $H_i$ of $T$ at $v$, for $1 \le i \le 5$. When $T = (n_1, n_2, n_3, n_4, n_5)$, it is trivial to get that

Lemma 2.7. Let $T = (n_1, n_2, n_3, n_4, n_5)$ be a tree with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$. Then none of the following conditions would occur:

(i) $n_1 \ge 1$ and $n_5 \ge 1$;

(ii) $n_2 \ge 2$;

(iii) $n_2 \ge 1$ and $n_4 \ge 1$;

(iv) $n_1 \ge 1$ and $n_4 \ge 2$;

(v) $n_2 \ge 1$ and $n_5 \ge 1$.

Proof. Define

In each case, it is easy to see that $T'$ has the same number of vertices and Roman domination number as $T$ from Eqs (2.1) and (2.2), but

from Eq (2.3). It means that under each of such conditions, we may always construct another tree on the same number of vertices and Roman domination number but having a larger $M_1$ value, which contradicts with our choosing for $T$ (with the maximum first Zagreb index).

In virtue of Lemma 2.7, the number of candidates (with the maximum first Zagreb index) is depleted.

Remark 2.1. Roman domination number is unchanged after using transformations in the proof of Lemmas 2.6 and 2.7.

Lemma 2.8. Let $T \in \mathbb{T} (n, \gamma_{R})$, where $n \ge \max\left\{ \lceil \frac{3 \gamma_{R} - 5}{2} \rceil, \gamma_{R} + 3 \right\}$. Assume that the maximum degree of $T$ is $n-\gamma_{R}+1$.Then

In particular:

● When $\gamma_{R}$ is even, the equality holds if and only if $T = \left(\frac{2n - 3 \gamma_{R} + 4}{2}, 0, \frac{\gamma_{R} - 2}{2}, 0, 0 \right)$.

● When $\gamma_{R}$ is odd, the equality holds if and only if $T = \left(\frac{2n - 3 \gamma_{R} + 3}{2}, 1, \frac{\gamma_{R} - 3}{2}, 0, 0 \right)$ or $T = \left(\frac{2n - 3 \gamma_{R} + 5}{2}, 0, \frac{\gamma_{R}- 5}{2}, 1, 0 \right)$.

Proof. Assume that $T = (n_1, n_2, n_3, n_4, n_5)$ is a tree with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$. We partition the proof into two parts: $n_1 \ge 1$ and $n_1 = 0$.

Case $1$. $n_1 \ge 1$.

From Lemma 2.7 (ⅰ), (ⅱ) and (ⅳ), $n_2 = 0$ or $1$, $n_4 = 0$ or $1$, $n_5 = 0$. So there are actually three candidates ($n_2 = n_4 = 1$ is impossible from Lemma 2.7 (ⅲ)):

$({\rm{i}})$ $n_1 = \frac{2n - 3 \gamma_{R} + 4}{2}$, $n_2 = 0$, $n_3 = \frac{\gamma_{R} - 2}{2}$, $n_4 = 0$, $n_5 = 0$;

$({\rm{ii}})$ $n_1 = \frac{2n - 3 \gamma_{R} + 3}{2}$, $n_2 = 1$, $n_3 = \frac{\gamma_{R} - 3}{2}$, $n_4 = 0$, $n_5 = 0$;

$({\rm{iii}})$ $n_1 = \frac{2n - 3 \gamma_{R}+ 5}{2}$, $n_2 = 0$, $n_3 = \frac{\gamma_{R} - 5}{2}$, $n_4 = 1$, $n_5 = 0$.

Under the condition (ⅰ), we have that $\gamma_{R}$ is even, and

As to the conditions (ⅱ) and (ⅲ), in either case, $\gamma_{R}$ is odd, and

Case $2$. $n_1 = 0$.

Notice that $n_2 = 0$ or $1$, from Lemma 2.7 (ⅱ).

First suppose that $n_2 = 1$. Then $n_4 = n_5 = 0$ from Lemma 2.7 (ⅲ) and (ⅴ). Furthermore, $n_3 = n - \gamma_{R}$ (from Eq (2.1)) and $2 n = 3 \gamma_{R} - 3$ (from Eq (2.2)), implying that $\gamma_{R}$ is odd, which coincides with condition (ⅱ) mentioned in Case $1$.

Next suppose that $n_2 = 0$. Then by Eqs (2.1) and (2.2),

Clearly,

equivalently $\gamma_{R} - 2 \ge 2(n - \gamma_{R} + 1)$, i.e., $3 \gamma_{R} - 4 \ge 2n$. Recall that $2n \ge 3 \gamma_{R} - 5$, from the hypothesis about the lower bound of $n$. So either $2n = 3 \gamma_{R} - 4$ or $2n = 3 \gamma_{R} - 5$. The former is actually the above condition (ⅰ) occurring in Case $1$, while the latter is identical to condition (ⅲ) in Case $1$.

The proof is completed now.

Remark 2.2. In order to provide a visual representation for the three trees attaining the equality cases, we draw such three trees in Figure 2.

All the trees in $\mathbb{T} (n, \gamma_{R})$ with maximum degree $n-\gamma_{R}+1$ have been done now. In fact, the trees attaining the equality cases obtained above are also the ones with the maximum first Zagreb index in $\mathbb{T} (n, \gamma_{R})$, which will be proved subsequently.

3.   Results

In the next theorem, we obtain the upper bound for the first Zagreb index of trees with given Roman domination number, and the trees attaining the upper bound are also characterized (they coincide exactly with the ones occurred in Lemma 2.8).

Theorem 3.1. Let $T \in \mathbb{T} (n, \gamma_{R})$, where $n \ge \max\left\{ \lceil \frac{3 \gamma_{R} - 5}{2} \rceil, \gamma_{R} + 3 \right\}$.Then

In particular:

● When $\gamma_{R}$ is even, the equality holds if and only if $T = \left(\frac{2n - 3 \gamma_{R} + 4}{2}, 0, \frac{\gamma_{R}- 2}{2}, 0, 0 \right)$.

● When $\gamma_{R}$ is odd, the equality holds if and only if $T = \left(\frac{2n - 3 \gamma_{R} + 3}{2}, 1, \frac{\gamma_{R} - 3}{2}, 0, 0 \right)$ or $T = \left(\frac{2n - 3 \gamma_{R} + 5}{2}, 0, \frac{\gamma_{R} - 5}{2}, 1, 0 \right)$.

Proof. For convenience, set

That is to say, we would like to show that $M_1 (T) \le f(n, \gamma_{R})$, and characterize the equality cases.

Recall that the maximum degree of $T$ is at most $n-\gamma_{R}+1$, from Lemma 2.3. In Lemma 2.8, we have considered the upper bound of the first Zagreb index when the maximum degree of $T$ is exactly $n-\gamma_{R}+1$. So we are left to show that $M_1 (T) < f(n, \gamma_{R})$ when the maximum degree of $T$ is less than $n-\gamma_{R}+1$. We will realize it by using induction on $\gamma_{R}$.

When $\gamma_{R} = 2, 3$, there is no tree whose maximum degree is less than $n-\gamma_{R}+1$. When $\gamma_{R} = 4$, the trees under consideration should be double stars, the result can be checked easily. Now assume that the result holds for any tree with order less than $n$ and Roman domination number less than $\gamma_{R}$, and $T$ is a tree on $n$ vertices with Roman domination number $\gamma_{R}$.

Recall an obvious observation about a tree $T$: There is some vertex, say $u$, having $d(u) - 1$ pendant neighbors, where $d(u) \ge 2$. Let $v$ be a pendant neighbor of $u$ in $T$.

When $d(u) \ge 4$ ($u$ has at least three pendant neighbors), from Lemma 2.2, we get $\gamma_R(T) = \gamma_R(T-v) = \gamma_{R}$. Observe that

and $d(u) < n - \gamma_{R} + 1$ (since the maximum degree of $T$ is less than $n-\gamma_{R}+1$). Therefore, together with induction, it follows that

i.e., $M_1 (T) < f(n, \gamma_{R})$.

We may assume that $d(u) = 2$ or $3$ in the following. Furthermore, we may assume that $\gamma_R(T - v) = \gamma_R(T) - 1 = \gamma_{R} - 1$, otherwise $\gamma_R (T - v) = \gamma_R (T) = \gamma_{R}$ from Lemma 2.1, which can be settled by the method used for the case $d(u) \ge 4$ again.

For $\gamma_R(T - v) = \gamma_R(T) - 1 = \gamma_{R} - 1$, it is easy to see that

Thus, when $d(u) = 2$, by induction, we have

In particular, if $M_{1}(T) = f (n, \gamma_R (T))$, then $T- v$ is a tree with maximum degree $(n - 1) - \gamma_{R} (T - v) + 1 = n - \gamma_{R} + 1$, which contradicts with the hypothesis that the maximum degree of $T$ is less than $n - \gamma_{R} + 1$. So $M_1 (T) < f (n, \gamma_R (T)) = f(n, \gamma_{R})$.

When $d(u) = 3$, assume that $v$ and $w$ are the two pendant neighbors of $u$ in $T$. Then

Notice that either $\gamma_R (T-v-w) = \gamma_R (T) - 1 = \gamma_{R} - 1$, or $\gamma_R (T-v-w) = \gamma_R (T) - 2 = \gamma_{R} - 2$. If $\gamma_R (T-v-w) = \gamma_{R} - 1$, then

and thus,

since $n - \gamma_{R} +1 > 3$ (considering the hypothesis about the maximum degree of $T$). If $\gamma_R (T-v-w) = \gamma_{R} - 2$, then

and thus,

In particular, if $M_1 (T) = f (n, \gamma_R (T))$, then $T- v-w$ is a tree with maximum degree $(n-2) - \gamma_R (T-v-w) + 1 = n - \gamma_{R} + 1$, which contradicts with the hypothesis that the maximum degree of $T$ is less than $n - \gamma_{R} + 1$. So $M_1 (T) < f(n, \gamma_R(T)) = f(n, \gamma_{R})$.

The proof is completed.

4.   Conclusions

This paper is devoted to the investigation of relationship between the first Zagreb index and Roman domination number of trees. More precisely, we establish an upper bound of the first Zagreb index of trees in terms of Roman domination number, and all the tree(s) attaining the equality case are characterized.

As a possible sequel in the future, it is interesting to investigate the relationship between the first Zagreb index (or other well-known topological indices, e.g., Randić index, Wiener index) and other types of domination number of graphs.

To end this paper, we pose the following problem:

Problem 1. Study the extremal topological indices in the class of all connected graphs with a given Roman domination number.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11701505) and the Research Intensified Grant Scheme (RIGS), Phase 1/2019, Universiti Malaysia Terengganu, Malaysia with Grant Vot. 55192/6.

Conflict of interest

The authors declare no conflicts of interest.