An inverse volatility problem in a degenerate parabolic equation in a bounded domain

1.   Introduction

An option is a contract that gives an option holder the right to buy (call option) or sell (put option) an underlying asset with the strike price at a certain date or at any time before that date. Some contracts, known as the "American option", allow the holder to exercise at any time before an expiration date, whereas options that can only be exercised on the maturity date are called "European options". In this paper, we focus on the European call option.

In the last 20 years, the parameter inversion problem in the option pricing field has been extensively studied by many scholars, and the results of these studies have all relied on the famous Black-Scholes model. An important parameter in the Black-Scholes model is the volatility of the underlying asset associated with the option, which has a significant impact on the market value of the options, and as such, many scholars and practitioners in the financial industry have focused intensively on the volatility of an underlying asset in option pricing. In the real market, the volatility of the underlying asset price cannot be directly observed, and it is certainly unpredictable. However, the market price of an option is directly observable and provides information about volatility.

The derivation of the Black-Scholes partial differential equations builds on the basic components of derivatives theory, such as delta hedging and no arbitrage. One of the erroneous assumptions of the Black-Scholes model is that the volatility of the underlying asset is a constant. Empirical research on implied volatility shows that implied volatility depends on strike prices. The value of a call option is obviously a function of various parameters in the contract, such as the strike price $K$ and the remaining time to maturity $T-t$, where $T$ is the expiration time and $t$ is the current time. For our inverse problem, we will just use $u(s, t; K, T)$ for the option value.

Problem P1: Considering the option on the stock without paying the dividend, it is well known that $u(s, t; K, T)$ for a call option satisfies the following Black-Sholes equation ^[1]

Here, $s$ is the price of the underlying stock, $K$ is the strike price, $T$ is the time of expiry and $\mu$ and $r$ are, respectively, the risk-neutral drift and the risk-free interest rate, which are assumed to be constants. The parameter $\sigma(s)$ is the volatility coefficient to be identified. We assume that

where $g(s)$ is a small perturbation of the constant $\sigma_{0}$. Given the following additional condition:

where $s^{*}$ is the market price of the stock at time $t^{*} = 0$ and $u^{*}(K, T)$ indicates the market price of the option with the strike $K$ at a given expiry time $T$. The inverse problem is to determine the functions $u$ and $\sigma$ satisfying (1.1) and (1.2), respectively.

The inverse volatility problem for the Black-Scholes equation has been discussed intensively in the literature. The inverse problem was first considered by Dupire in ^[1]. He applied the symmetric property of the transition probability density function to replace the option pricing inverse problem with an equation containing the parameters $K$ and $T,$ which have duality, and proposed Dupire's formula for calculating implied volatility. Although this formula is seriously ill-posed, Dupire's solution lays an important foundation for later scholars to study this problem. In ^[2], the authors reduce the identification of volatility to an inverse parabolic problem with terminal observation and establish uniqueness and stability results by using Carleman estimates. This approach produces a nonlinear Fredholm integral equation in which the approximated solution is obtained by solving the integral equation iteratively. In ^[3], a time-dependent and a space-dependent volatility have been studied, respectively. A class of non-Gaussian stochastic processes has been generated in the study of spatially correlated volatility. The problem is transformed into a known inverse coefficient problem with final observations and uniqueness and stability theorems are established by using the dual equations. In ^[4], Jiang and Tao used an optimal control framework to determine the implied volatility and carried out a rigorous mathematical analysis of the inverse problem, proving that the approximate optimal solution converges to an appropriate solution to the original problem. Similar results are derived in ^[5]. In ^[6,7], the inverse problem of identifying the principal coefficient is investigated when the solution is known, and a well-posed approximation algorithm to identify the coefficient is proposed. The existence, uniqueness and stability of such solutions are proved. The Tikhonov regularization method has always been an important tool for solving ill-posed problems. In ^[7], a new two-dimensional numerical differentiation method is proposed through Tikhonov regularization. Convergence analysis and numerical examples are given. The authors of ^[8] studied the stable identification problem of the local volatility surface $\sigma(S, t)$ in the Black-Scholes/Dupire equation from the market price of European options. The stability and convergence of the approximation obtained by Tikhonov regularization. In the case of a known term-structure of volatility, based on the assumption that the volatility is constant for time $\sigma(S, t) = \sigma(S)$, the convergence rate under simple smoothness and decay conditions on the true volatility is proved. In recent years, linearization techniques have been applied to the inverse problem of option pricing. In ^[9,10,11,12], linearization techniques are applied to transform the problem into an inverse source problem from which unknown volatility can be recovered. A stable numerical solution to the inverse problem is obtained by using the integral equation method and the Landweber iteration method. Both the theoretical analysis and the numerical examples demonstrate the effectiveness of the proposed method.

The inverse Problem P1 was first considered in ^[10], where the non-linear problem is linearized to the following Problem P2:

Problem P2: Consider the following parabolic equation ^[10]:

where $\sigma_{0}$ is a positive constant, $\alpha_{0}(y, \tau)$ is a known function and

is the unknown coefficient. Assume that an additional condition is given as follows:

where $V(y) = u^{*} (s^{*}e^{y}, T)-V_{0} (y, T)$ is a known function and $V_{0}$ is the final data for the unperturbed problem (i.e., with volatility $\sigma_{0}^{2}$). More detail is given in Section 2. Then, we shall identify the functions $u$ and $g$ from the above condition.

It is worth mentioning that the aforementioned scholars and their research have made outstanding contributions to the inverse volatility problem in option pricing. However, there are some deficiencies in these studies that need to be improved. One of the significant deficiencies is to consider that the original Problem P2 is in the unbounded region, so many scholars conduct numerical simulations by artificial truncation. There is a potential trouble with this approach, that is, if we truncate the interval too large, it will increase the amount of calculation, and if the truncation interval is too small, it will increase the error. In practical applications, this approach will fail to precisely control the volatility risk. In order to solve this deficiency, our main objective in this paper is to use some variable substitution that transforms Problem P2 into the following degenerate Problem P:

Taking

Problem P: Consider the following degenerate parabolic equation:

with the additional condition

in which

and $g(x)$ is an unknown source term in (1.5). We shall determine the functions $W$ and $g$ satisfying (1.5) and (1.6).

One can find that with substitutions our Problem P becomes determining the source term in the degenerate parabolic equation with terminal data. Unlike the classical parabolic equation, the mathematical model in our paper may allow degeneration at some part of the boundary, which may lead to missing corresponding boundary conditions (see, e.g., ^[13,14,15]). A lot of work has been done on the identification of the coefficients in degenerate parabolic equations. In ^[16], an inverse problem of simultaneously reconstructing the initial value and source coefficient is investigated for the following degenerate parabolic equation:

The uniqueness and conditional stability of the solution for the original problem are proved by a Carleman estimate, and the iteration algorithm of the Landweber type is designed to obtain the numerical solution. In ^[17], an inverse problem for the restoration of source temperature from the information of the final observation is studied. The uniqueness is obtained by taking an integral transform and using Liouville's theorem (complex analysis). With the implication of integral identity, a Lipschitz stability for the inverse problem is constructed. In ^[18], the authors study the inverse problem of the reconstruction of the degenerate diffusion coefficient in the following parabolic equation

the uniqueness and Lipschitz stability for identification of a constant coefficient $a(x)$ and power $\alpha$ by the interior data at some time are proved by the energy method. Based on the global Carleman estimates for hyperbolic problems and an inversion of the integral transform, the uniqueness results for identification of a general coefficient $a(x)$ and power $\alpha$ from boundary data on one side of the space interval are obtained. In ^[19], based on the optimal control framework, an inverse problem of determining the radiative coefficient in the degenerate parabolic equation from the final data is transformed into an optimization problem. The existence, necessary conditions, uniqueness and stability of the minimizer are proved. The convergence of the minimizer for noisy input data is obtained by minor modification to the cost functional and some a priori regularity conditions imposed on the forward operator. Not attempting to review all we mention the most recent paper ^[20] on the basis of the study of the unique solvability of the direct problem, in which authors prove the existence and uniqueness theorems for inverse problems of determination of lower order coefficient in the Black-Scholes type equation with the additional condition of integral observation. For other topics about the degenerate parabolic equations, e.g., the null controllability, we may refer the readers to ^{[21,22,23,24,25,26,27]} and the reference therein.

The contribution of this paper is two-fold. Theoretically speaking, we first apply the linearization method and variable substitutions to transform the Problem P2 into an inverse source Problem P with a degenerate parabolic equation in a bounded area, from which an unknown volatility can be recovered. Based on the optimal control framework, we transform the Problem P into an optimization problem and establish the existence, necessary conditions, uniqueness and stability of the minimizer. Furthermore, in the numerical part, we design an iteration algorithm of the Landweber type to solve the inverse problem. To the best of our knowledge, that is the first paper which is concerned with determining the space-dependent volatility in option pricing by using the theory of degenerate parabolic equations.

The remainder of this paper is organized as follows. In Section 2, the linearization method and variable substitutions are applied to transform the original problem into a degenerate parabolic equation and the well-posedness of the degenerate parabolic equation is proved. On the basis of the optimal control framework, the existence of the minimizer is proved in Section 3. In Section 4, the necessary conditions of the optimization problem are deduced. The uniqueness and stability of the minimizer are established in Section 5. In Section 6, a Landweber iterative method is designed to obtain a stable numerical solution to the inverse problem. Some numerical experiments are presented to show the validity of the inversion method in Section 7.

2.   Linearization and variable substitutions

We shall assume that the option price premium $u(\cdot, \cdot; K, T)$ satisfies the equation dual to the Black-Scholes equation (1.1) with respect to the strike price $K$ and expiry time $T$:

Equation (2.1) was found by Dupire in ^[4].

In the lognormal variables,

The inverse Problem P1 transforms into

with the additional market data

where

The goal is to recover the unknown space-dependent volatility coefficient $a(y)$ from the market data $U(y)$.

If

we have

where $V_{0}$ is the solution of (2.3) when $a = \sigma_{0}$ and $v$ is quadratically small with respect function $g$. The principal linear term $V$ satisfies

with the additional final data

in which

are known.

The recovery of $g$ in (2.6) and (2.7) is a linear inverse source problem. However, because this is a matter of unbounded areas, we make use of some variable substitutions here so that the above problem is transformed into a linear inverse source degenerate parabolic problem in bounded areas.

Take

Problem P: Consider the following parabolic equation:

with the additional final data

in which

For the sake of analysis, we take

where $a(x), b(x), c, \varphi(x)$ and $\alpha(x, \tau)$ are given smooth unctions on $(-\frac{\pi}{2}, \frac{\pi}{2})$ which satisfy

and $g(x)$ is an unknown source term in (2.9). We shall determine the functions $W$ and $g$ satisfying (2.9) and (2.10).

Equation (2.9) belongs to the degenerate parabolic equations. Being different from the classical parabolic equations, the degenerate one may get rid of the restriction of boundary conditions on some degenerate part. By the well-known Fichera's theory (see ^[15]), whether or not boundary conditions should be given is determined by the sign of the Fichera function. Specifically, if the sign of the Fichera function is non-negative, then boundary conditions should not be given; otherwise, the reverse is exactly the case. For general one-dimensional degenerate parabolic equations

where $k(x, t)$ satisfies

the Fichera function can be defined as follows:

where $n_{i}$ are taken as 1 and -1 as $x = 0$ and $x = l$, respectively. For (2.9), it can be easily seen that $B(x, t)|_{x = -\frac{\pi}{2}, \frac{\pi}{2}} = 0$. Therefore, the boundary conditions on $x = -\frac{\pi}{2}$ and $x = \frac{\pi}{2}$ should not be given either.

3.   Optimal control problem

In general, uniqueness is vital for the inverse problems, because it indicates if the extra condition is sufficient to identify the unknown information. Many tools, including the energy estimate, integral equation, maximum principle and Carleman estimate, can be used to derive the uniqueness and Lipschitz stability for inverse problems. It should be mentioned that the Carleman estimate is an effective tool to derive the uniqueness and Lipschitz stability for inverse problems. But, unfortunately, it fails in treating the terminal control problems such as the inverse Problem P. Before we consider the regularization of Problem P, we discuss the forward problem and give some basic definitions, lemmas and estimations.

Definition 3.1. Define $\mathcal{B}$ to be the closure of $C_{0}^{\infty}(Q)$ under the following norm:

Definition 3.2.A function $W(x, \tau)$ is called the weak solution of (2.9) if $W\in C\left([0, T]; L^{2}\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\bigcap \mathcal{B}\right)$ and, for any $\psi\in L^{\infty}\left((0, T); L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})\bigcap \mathcal{B}\right), \frac{\partial\psi}{\partial\tau}\in L^{2}(Q), \psi(\cdot, T) = 0$, the following integration identity holds:

Theorem 3.1. For any given $f\in L^{\infty}(Q), \; \varphi\in L^{\infty}(-\frac{\pi}{2}, \frac{\pi}{2})$, there exists a unique weak solution to (2.9) that satisfies the following estimate:

Proof. First, we prove the existence. For any given $0 < \varepsilon < 1$, we consider the following regularized problem

where

From the well-known theory for degenerate parabolic equations, there exists a unique weak solution $W_{\varepsilon}(x, \tau)$ to (2.9).

Then, we will give some a priori estimates for $W_{\varepsilon}(x, \tau)$. Without loss of generality, we assume that $W_{\varepsilon}(x, \tau)$ is the classical solution of (3.2). Otherwise, one can smooth the coefficients of (3.2) and then consider the solution of the approximation problem.

Multiplying both sides of (3.2) by $W_{\varepsilon}$ and integrating on $Q_{\tau} = [-\frac{\pi}{2}, \frac{\pi}{2}]\times(0, \tau),$ we have

Applying integration by parts, we get

Notice that

hence,

Integrating the second term from the left side of the inequality by parts, we get

where we take $M$ as the supremum of $-\frac{1}{2}(a'_{\varepsilon}+b)_{x}$. From the Gronwall inequality, letting $\varepsilon\rightarrow 0$, one can immediately obtain

which implies the existence of weak solutions.

Next, we prove the uniqueness of weak solutions. Suppose that $W_{1}$, $W_{2}$ are two solutions of (2.9) and let

It can be easily seen that $U\in C\left([0, T]; L^{2}\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\right)\bigcap \mathcal{B},$ and for any $\psi\in L^{\infty}\left((0, T); L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})\right)\bigcap \mathcal{B}, \; \frac{\partial\psi}{\partial\tau}\in L^{2}(Q), \; \psi(\cdot, T) = 0$, the following integration identity holds:

For any given $w\in C_{0}^{\infty}(Q)$, by the existence obtained above, we know that there exists a weak solution $v\in C\left([0, T]; L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})\right)\bigcap \mathcal{B},$ and $\frac{\partial v}{\partial\tau}\in L^{2}(Q)$ for the following equation:

Letting $\psi = v$ in (3.5), we obtain

Noting the arbitrariness of $w$, we have

i.e.,

This completes the proof of Theorem 3.1.

Remark 3.1. The weak solution defined above is on the whole domain $Q$. If we only consider the spatial case, we can modify Definition 3.1 as follows:

Definition 3.1.' Define $H_{a}^{1}(-\frac{\pi}{2}, \frac{\pi}{2})$ to be the closure of $C_{0}^{\infty}(-\frac{\pi}{2}, \frac{\pi}{2})$ under the following norm:

Definition 3.2 can also be rewritten as follows:

Definition 3.2.' A function $W\in H^{1}\left([0, T]; L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})\right)\bigcap L^{2}\left((0, T); H_{a}^{1}(-\frac{\pi}{2}, \frac{\pi}{2})\right)$ is called the weak solution of (2.9) if $W$ satisfies

and the integration identity

holds for a.e. $\tau \in (0, T]$. Then, by analogous arguments, one can establish the existence, uniqueness and regularity of weak solutions, which are similar to those of Theorem 3.1.

Since the inverse Problem P is ill-posed, i.e., its solution depends unstably on the data, we turn to consider the following optimal control Problem P3:

Problem P3. Find $\overline g(x)\in \mathcal{A}$ such that

where

$W(x, \tau; g)$ is the solution of (2.9) for a given source term $g(x)\in \mathcal{A}$, $N$ is the regularization parameter and $\alpha, \; \beta$ are two given positive constants.

For the extra condition (2.10), we shall assume that

From (3.11) and Theorem 3.1, it can be easily seen that the control function (3.9) is well-defined for any $g\in \mathcal{A}$.

We are now going to show the existence of minimizers for the problem (3.8). First, we assert that the functional $J(g)$ is of some continuous property in $\mathcal{A}$ in the following sense.

Lemma 3.1. For any sequence $\{g_{n}\}$ in $\mathcal{A}$ which converges to some $\{g\}\in \mathcal{A}$ in $L^{1}(-\frac{\pi}{2}, \frac{\pi}{2})$ as $n\rightarrow \infty$, we have

Proof. Step 1: By taking $g = g_{n}$ and choosing the test function as $W(g_{n})(\cdot, \tau)$ in (3.7) and then integrating with respect to $\tau$, we derive that

for any $\tau\in(0, T]$.

From (3.13), we know that the sequence $\{W(g_{n})\}$ is uniformly bounded in the space $L^{2}\left((0, T); H_{a}^{1}(-\frac{\pi}{2}, \frac{\pi}{2})\right)$. So, we may extract a subsequence, still denoted by $\{W(g_{n})\}$, such that

Step 2: $W^{*}(x, \tau) = W(g)(x, \tau).$ By taking $g = g_{n}$ in (3.7) and multiplying both sides by a function $\eta (\tau)\in C^{1}[0, T],$ with $\eta(T) = 0$, we have

Then, integrating with respect to $\tau$, letting $n\rightarrow \infty$ in (3.15) and using (3.14), we get

By noticing that (3.16) is valid for any $\eta (\tau)\in C^{1}[0, T]$ with $\eta(T) = 0,$ we have

and $W^{*}(x, 0) = \varphi(x)$.

Therefore, $W^{*} = W(g)$ by the definition of $W(g)$.

Step 3: Prove $\left\|W(g_{n})(\cdot, T)-w\right\|_{L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})}\rightarrow \left\|W(g)(\cdot, T)-w\right\|_{L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})}$ as $n\rightarrow \infty$.

We rewrite (3.8) for $g = g_{n}$ in the following form

Taking $\psi = W(g_{n})-w$ in (3.18), we have

Similar relations hold for $W(g)$, namely,

Subtracting (3.20) from (3.19), we obtain

Taking $\psi = W(g_{n})-W(g),$ in (3.7), we have

Similarly, for $\left(W(g_{n})-W(g)\right)_{\tau}\left(W(g)-w\right)$, we have

Substituting (3.22) and (3.23) into (3.21), and after some manipulations, we derive

where

Integrating over the interval $(0, \tau)$ for any $\tau\leq T$, we get

By the convergence of $\{g_{n}\}$ and weak convergence of $\{W(g_{n})\}$, one can easily get

Combining (3.25) and (3.26), we have

On the other hand, we have the following from the H$\ddot{o}$lder inequality:

From (3.11), (3.13), (3.27) and (3.28), we obtain

This completes the proof of Lemma 3.1.

Theorem 3.2. There exists a minimizer $\overline{g}\in \mathcal{ A}$ of $J(g)$, i.e.,

Proof. It is obvious that $J(g)$ is non-negative and thus $J(g)$ has the greatest lower bound $\inf_{g\in \mathcal{A}}J(g)$. Let $\{g_{n}\}$ be a minimizing sequence, i.e.,

By noticing that $J(g_{n})\leq C,$ we deduce

where $C$ is independent of $n$. Noticing the boundedness of $\{g_{n}\}$ and (3.29), we also have

So, we can extract a subsequence, still denoted by $\{g_{n}\}$, such that

By the Sobolev imbedding theorem (see ^[2]), we obtain

It can be easily seen that $\{g_{n}(x)\}\in \mathcal{A}$. So, we get, as $n\rightarrow \infty$, that

in $L^{1}(-\frac{\pi}{2}, \frac{\pi}{2})$.

Moreover, from (3.31) we have

From Lemma 3.1 and the convergence of $\{g_{n}\}$, we know that there exists a subsequence of $\{g_{n}\}$, still denoted by $\{g_{n}\}$, such that

From (3.33)–(3.35), we get

Hence,

This completes the proof of Theorem 3.2.

4.   Necessary condition

Theorem 4.1. Let $g$ be the solution of the optimal control problem (3.8). Then, there exists a triplicate of functions $(W, \xi; g)$ satisfying the following system:

and

for any $h\in \mathcal{A}$.

Proof. For any $h\in \mathcal{A}, 0\leq\delta\leq1$, we have

Then,

Let $W_{\delta}$ be the solution of (2.9) given $g = g_{\delta}$. Since $g$ is an optimal solution, we have

Let $\widetilde{W}_{\delta}\equiv \frac{\partial W_{\delta}}{\partial\delta}$; direct calculations lead to the following equation:

Let $\xi = \widetilde{W}_{\delta}|_{\delta = 0}$; then, $\xi$ satisfies

From (4.5), we have

This completes the proof of Theorem 4.1.

5.   Uniqueness and stability

The optimal control Problem P3 is non-convex. That means, in general, one may not expect a unique solution. In fact, it is well known that the optimization technique is a classic tool for obtaining general solution, not unique solution for inverse problems. However, we find that, if the terminal time $T$ is relatively small, the minimizer of the cost functional can be proved to be locally unique and stable.

Throughout this paper, if there is no specific illustration, $C$ will denote the different constants.

Theorem 5.1. Let $g_{1}(x), g_{2}(x)$ be the minimizers of the optimal control problem P3 corresponding to $w_{1}(x), w_{2}(x),$ respectively. If there exists a point $x_{0}\in(-\frac{\pi}{2}, \frac{\pi}{2})$ such that

then, for a relatively small $T$, we have

where the constant $C$ is dependent of $\pi$ and $N$.

Proof. By taking $h = g_{2}$ when $g = g_{1}$ and taking $h = g_{1}$ when $g = g_{2}$ in (4.3), we have

where $\{W_{i}, \xi_{i}\}(i = 1, 2)$ are solutions of the system (4.1)/(4.2) with $g = g_{i}(i = 1, 2)$, respectively.

Assuming that

$\Xi$ and $\Upsilon$ satisfy the following equations:

According to the weak maximum principle, it is known that (5.4) has only zero solutions. So,

and $\xi_{1}$ satisfies the following equations:

Noticing (5.3) and (5.6), we have

From (5.1), (5.2), (5.5) and (5.7), we obtain

For $-\frac{\pi}{2} < x < \frac{\pi}{2}$, from the assumption of Theorem 5.1 and the H$\ddot{o}$lder inequality, we have

Thus we derive

Combining (5.8) and (5.10), we have

This completes the proof of the Theorem 5.1.

Remark 5.1. It should be mentioned that the regularization parameter plays a major role in the numerical simulation of ill-posed problems. From Theorem 5.1, we can obtain that, if there exists a constant $\delta$ such that

then the reconstructed optimal solution is unique and stable, which is consistent with the existing result. Since the parameter $N$ is often taken to be very small, particularly in numerical computations, Theorem 5.1 is indeed the local well-posedness of the optimal solution. Generally speaking, for ill-posed problems, the regularization parameter appropriately depends on when the data error approaches zero, and the convergence result can be obtained. In addition, under some additional assumptions, the convergence rate can also be derived.

6.   Landweber iterations

Based on the optimal control method, we have obtained the result of Problem P from the perspective of theoretical analysis. However, it is difficult for us to use this method to obtain the corresponding numerical results. In fact, the optimal control method used in this article is actually the Tikhonov regularization method based on the $L^{2}$ gradient norm. We consider the following linear system:

where $X$ and $Y$ are Hilbert spaces and $T:X\rightarrow Y$ is a bounded linear operator. Then, the Tikhonov functional can be written as follows:

Obviously, the minimal element of the functional described above is equivalent to the solution of the following equation:

which is

However, this method is not suitable for solving the problem of this article. There are two main difficulties. First, we do not know the specific form of $(\alpha I+T^{*}T)^{-1}$. In fact, we can write the specific form of $(\alpha I+T^{*}T)^{-1}$ only for individual operators, for example, $T$ is a matrix. Second, the control functional (3.9) established in the previous chapter has a penalty term of an $H^{1}$ norm. Correspondingly, a second derivative term of the unknown function appears in the form of Euler's equation, which makes the numerical simulation process very complicated.

Therefore, we use the iterative method to solve the inverse problem P3. In this article, we particularly use the Landweber iteration method to get the numerical results.

Define the linear operator as shown below:

where $W$ is the solution of (2.9) under the following initial value condition:

Notice that (6.2) can also be written in the following form:

for $\alpha > 0$; $K^{*}$ is the adjoint operator of $K$, so the following iterative format can be used to solve (6.4):

It is easy to verify that (6.5) is the fastest descent method to solve the following equation, where $\alpha$ is the step size.

Besides, there is the following lemma for the conjugate adjoint $K^{*}.$

Lemma 6.1. For any given $h(x)\in H^{1}_{a}(-\frac{\pi}{2}, \frac{\pi}{2}),$ let $\omega(x, 0) = K^{*}h,$ which is

then, $\omega$ satisfies the following parabolic equation:

The proof of Lemma 6.1 is similar to the references (see ^[5]).

Remark 6.1 In our case, $\varphi(x) = 0, x\in (-\frac{\pi}{2}, \frac{\pi}{2})$. For the non-general situation, that is, $\varphi(x)\neq0$, we can define $p$ as the following mapping:

where $W_{1}$ satisfies the following equation:

And, $W_{2}$ satisfies the following equation:

We have already known that $K$ is a linear mapping, so problem (2.9)–(2.10) can be transformed into the first type of operator equation:

Notice that (6.9) can be rewritten in the following form:

So, the following iterative format can be used to solve (6.10):

Equation (6.11) is the fastest descent method to solve the following equation, where $\alpha$ is the step size.

From the definition of $H$ and (6.11), we have

where $W_{m-1}$ is the solution of (2.9)–(2.10) when $g = g_{m-1}$. From (6.13) and the defined $K^{*}$, the following adjoint equation is introduced:

Assume that the true solution $w(x)$ is available, that is, there is a $g(x)\in L^{2}(-\frac{\pi}{2}, \frac{\pi}{2})$ such that

and the noise of the observation data has an upper bound $\delta$, that is,

In summary, the calculation steps of the iteration format can be stated as follows:

Step one: Choose an initial iterative function $g = g(x)$. The initial function can be selected arbitrarily for the convenience of calculation. We generally choose $g(x) = 0, \; x\in(-\frac{\pi}{2}, \frac{\pi}{2})$;

Step two: $W_{0}(x, \tau)$ is obtained by solving the initial boundary value problem (2.9), where $g = g(x)$;

Step three: Solve (6.14) to get $\omega_{0}(x, \tau)$, where $W(x, T) = W_{0}(x, T)$;

Step four: Let $g_{1}(x) = g(x)-\alpha \omega_{0}(x, T)$, where $\alpha\geq0$, and let $W_{1}(x, \tau)$ be the solution of (2.9) when $g = g_{1}(x)$;

Step five: Choose an arbitrarily small normal number $\varepsilon$ as the error limit, calculate $\|W_{1}(x, T)-w(x)\|$ and compare the size with $\varepsilon$; if

then terminate the iteration and take $g = g_{1}(x)$ at this time. Otherwise, continue to execute Step two, let $g_{1}(x)$ be the new initial value of the iteration and continue to execute the inductive criterion until the iteration meets the termination condition.

Normally, if the input data are accurate, the more iterations of the Landweber iterative method, the higher the accuracy of the output data. However, in the case of noise, there will be errors in the initial iteration process. This calculation error will initially decrease as the number of iterations increases, but when a certain threshold is reached, it will increase rapidly as the number of iterations increases. Therefore, the iteration must be terminated at the appropriate time. In other words, in order to balance accuracy and stability, a compromise solution must be found, that is, a suitable parameter must be selected so that the iteration format is both accurate and stable.

If $x\in(K^{*}K)^{r}(X), \; r\in N$, then the following error estimation formula can be obtained:

where $M$ is the boundary of $(K^{*}K)^{r}x$. Therefore, in this case, it is different from Tikhonov's regularization method.

7.   Numerical experiments

We would like to give some numerical examples to test the validity of the proposed methods in Section 2. The simulated data are generated by using the standard finite difference method to solve the direct problems (2.9) and (2.10) under some appropriate artificial boundary conditions. We use $T = 1$; for numerical convenience, the $x$ interval $(-\frac{\pi}{2}, \frac{\pi}{2})$ is divided into 100 equal intervals, and on $x$ axis, we show the number of an interval. It is same for the case of $\tau$.

Assume that $Q = [-\frac{\pi}{2}, \frac{\pi}{2}]\times[0, T]$ is divided into a $J\times N$ mesh with the spatial step size $h = \frac{\pi}{J}$ in the $x$ direction and the time step size $t = \frac{T}{N}$.

Grid points $(x_{j}, \tau_{n})$ are defined by

where $J$ and $N$ are two integers. The notation $W_{j}^{n}$ is used for the finite-difference approximation of $W(jh, nt)$.

Using the finite-volume method (see ^[14]), one can derive the following implicit difference scheme of (2.9):

for $1\leq j\leq J-1$ and $0\leq n\leq N-1$, where $a_{j} = a(x_{j})$ and $b_{j} = b(x_{j})$.

In this section, we assume that $a(x)$ at least belongs to $C^{2}[-\frac{\pi}{2}, \frac{\pi}{2}].$ Note that, on the lateral boundary $x = -\frac{\pi}{2}$ and $x = \frac{\pi}{2},$ (2.9) degenerates into the first-order equation:

Therefore, the boundary conditions of (2.9) depend on the value of $b(x)$. Because $b\left(-\frac{\pi}{2}\right) = b\left(\frac{\pi}{2}\right) = 0$, the boundary conditions can be derived from (7.2) and (2.9):

It can be easily seen that the different quotients used to approximate derivatives are one-sided; thus, the truncations of schemes given by (7.3) and (7.4) are denoted as $O(t+h^{2})$.

To check the effectiveness of the difference scheme for the forward problem, we consider the following equation:

where

The above equation has the analytic solution $W(x, \tau) = \tau \cos x$. The numerical solution is shown in Figure 1, while the error surface between the exact solution and numerical one is shown in Figure 2.

It can be seen from Figure 2 that the maximal error between the exact solution and numerical one is less than $9\times10^{-3}$, which is consistent with the accuracy of the computational scheme.

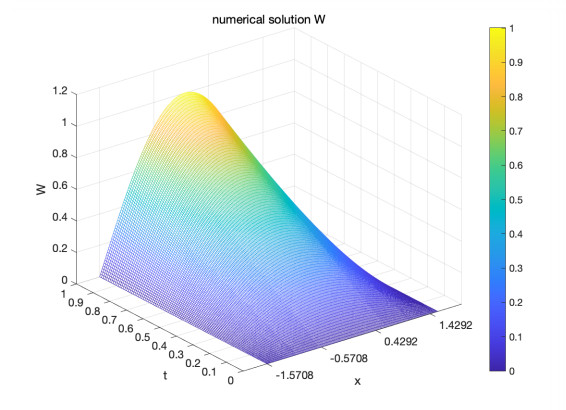
Example 1. Take

and

the numerical results are shown in Figure 3, where the iteration number $k = 1000$. It can be seen from this figure that the main shape of unknown functions is recovered well.

We also consider the case of noisy input data to test the stability of our algorithm. The noisy data are generated in the following form:

with $\delta = 0.001, 0.01, 0.08$.

The reconstruction result is displayed in Figure 4, where a satisfactory approximation is obtained under the case of noisy data as well. For $\delta = 0.001, 0.01$ and $0.08$, the corresponding iteration numbers are $k = 1500, 1200$ and $k = 1000$, respectively. Since the observation data contain errors, to obtain stable numerical results, we shall cease the iteration at some suitable time. Generally speaking, it is not easy to reconstruct the information of an unknown function near the boundary of parabolic equations due to the selection of initial values and the absence of data for the model at the boundary.

Example 2. In the second numerical experiment, we take

the numerical results are shown in Figure 5, where the iteration number $k = 800$.

From this figure, we can see the main error which appears near the boundary is very small. Analogously, we also consider the noisy case, where the noisy levels are the same as those in Example 1, i.e., $\delta = 0.001, 0.01, 0.08.$ The corresponding numerical result is displayed in Figure 6. One can see that, for the noisy case, our algorithm is still stable and the unknown function is reconstructed very well. For $\delta = 0.001, 0.01,$ and $0.08,$ the corresponding iteration numbers are $k = 980,820$ and 500, respectively.

A final point worth mentioning is that, despite the first example going through iterations 1000 times, it is not much in practical application, because it only takes 6.28 seconds to complete the iteration. The same truth holds for the second example, which takes only 2.57 seconds to complete the iteration. Compared with ^[28,29], they only discussed the exact case without the noisy case. Consequently, the proposed algorithm in this article is fast and effective, even under the noisy conditions. Unlike the exact case, we cannot iterate endlessly for noisy situations. Usually, we need to stop the iteration at the right time; otherwise, the data will overflow. This is the reason why the iteration number for the noisy case is much less than that of the exact case.

8.   Conclusions

The inverse problem of identifying the space-dependent volatility in Black-Scholes/Dupire equations from extra market data is very important in financial mathematics and risk management. Identification of the volatility in classic parabolic models has been discussed and developed extensively, while documents that deal with identifying the volatility in degenerate parabolic models are scarce.

In this paper, we solved the inverse problem P of recovering the source function $g(x)$ in the following degenerate parabolic equation:

in an optimal control framework; being different from other works (see, e.g., ^[9,10,11,12]), which also treat with inverse volatility problems, the mathematical model discussed in this paper contains degeneracy at the lateral boundaries. On the basis of the optimal control framework, existence, necessary conditions, uniqueness and stability of the minimizer for the cost functional have been established.

This paper focuses on the theoretical analysis and numerical simulation of the 1-D inverse problem. For the multi-dimensional case (two-asset space-dependent volatility Black-Scholes equation), i.e.,

and $\Omega\subset R^{2}$ is an unbounded domain. We can use the same techniques to transform the problem into the inverse source problem for degenerate parabolic equations.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Nos. 61663018, 11461039, 11961042), Foundation of A Hundred Youth Talents Training Program of Lanzhou Jiaotong University (2011028) and NSF of Gansu Province of China (No. 18JR3RA122).

Conflict of interest

The authors declare that they have no competing interests.