1.
Introduction
The problem that arises in daily life tends to concentrate on making appropriate, intelligent decisions in a variety of circumstances and environments. To address this problem, Zadeh [1] introduced fuzzy sets (FSs) theory. As a decision-making process, the FS plays a major role in dealing with uncertain and vague information and represents the characteristics of human nature. Fuzzy sets map each object in the universe to a value in the interval [0, 1]. Applications on FS were introduced by Maiers and Sherif's [2]. A combination between the FS and possibility theory was studied by Klir [3]. Later, Mendel [4] introduced fuzzy relations (FRs) and Cartesian products of FS. Zho et al. [5] used fuzzy relation analysis (FRS) to investigate the application of a hybrid method. Recently, several scholars applied and generalized FS to different fields [6,7,8,9,10,11].
In the beginning, Zadeh [1] offered two thresholds, α and β, to split a universe into three disjoint regions. He divided the membership degrees into three regions: (a) Complete belonging when degrees are equal to or greater than α; (b) complete exclusion when degrees are equal to or less than β; and (c) uncertainty when degrees are between β and α. Besides, the three disjoint regions (a), (b), and (c) in FS are analogous to those of the three-way decision theory, called the positive, negative, and boundary regions, respectively [12,13,14,15]. Hirota [16] found that most membership values are associated with grades around 0.5. In contrast, assigning values close to "1" or "0" is more confident in human mentality. On the other hand, the membership values that lie around 0.5 always lead to some hesitation and some difficulties to be substituted on a simple numeric scale. This finding helps Pedrycz [12] develop the notion of a shadowed set (SHS). Shadowed sets specify an impact of vagueness allocation instead of the whole space as in FS. The SHS approximates the FS to a set with some marked vagueness zones or named shadows, and SHS is considered an example of three-way or three-valued approximations of FSs. The structure of approximating the memberships maps the universe set U to 1, 0, or [0, 1]. The elements with membership degrees close to 1 are elevated to 1, the elements with membership degrees close to 0 are reduced to 0, and the elements with membership degrees around 0.5 are assigned to [0, 1]. Recently, several methods of uncertainty sets have been widely used based on the Pedrycz approach. In 2020, Zhang et al. [17] defined the notion of interval-shadowed sets based on the interval fuzzy entropy. In 2021, Yang and Yao [18] constructed SHS from Atanassove intuitionistic FSs by introducing two methods. In 2023, Jin and Hu [19] introduced three-way decisions based on hesitant sets.
The FS is unable to convey complex information combining two variables, notably uncertainty and periodicity data, at the same time. Ramot et al. [20] solved this difficulty by introducing complex fuzzy set (CFS). CFS maps any object in the universe to a value located inside the unit disk in the complex plane. As a result, a complex membership function contains two components: amplitude and phase terms. Furthermore, Ramot et al. [21] studied the complex fuzzy relations (CFRs) and Cartesian products of CFSs. Some operations of CFS were proposed and examined by Zhang et al. [22]. In 2011, Ma et al. [23] employed CFS to solve multiple periodic factor prediction problems. Additionally, many scholars utilized and expanded the notion of broadening the range of membership degrees from the interval [0, 1] to a unit disk inside the complex plane across a variety of fields and uncertainty sets. Al-Qudah and Hassan [24,25] proposed and studied the notion of complex multi-fuzzy sets and soft sets with their operations and properties. Yazdanbakhsh and Dick [26] made a review of CFS and logic. Li and Tu [27] applied CFS to the neural fuzzy system and gave an application to multi-class prediction by using CFS. The notions of bipolar δ-equal complex fuzzy concept lattice and complex fuzzy concept lattice were introduced by Singh [28,29]. Alkouri and Salleh [30] introduced complex intuitionistic FSs by adding phase terms to both membership and nonmembership functions with some constraints. Also, Alkouri and Salleh [31] defined the notion of complex fuzzy soft multisets. Talafha et al. [32] presented the complex hesitant FSs with an application in decision-making.
The limitation of the ability to solve two-dimensional phenomena was solved by using CFS. Therefore, complex fuzzy information needs two variables to be represented and illustrated. This representation costs the decision-makers a lot of time and calculations during the complex fuzzy decision process. Hence, a new trend in CFS is motivated by the approximations of CFS with a smaller number of complex membership values. This can be constructed by combining CFS and SHS to reduce the decision partition cost and calculation amount of the uncertain object in the CF decision process.
The sheer number of research and the practical uses of CFS, coupled with the problem of efficiently representing multivariable information, have been the key motivation behind the development of complex shadowed sets (CSHS). CSHS introduced pioneering research in the framework of integrating the ideas of CFS and SHS. This notion can be founded by extending the shadowed set codomain from {0,[0,1],1} to {0eiθ,[0,1]eiθ,1eiθ}. Our methodology can be highlighted by dividing the unit disk into three disjoint regions. In other words, the disjoint regions can be conveyed as a disk and two rings in the unit disk of a complex plane. Choosing two suitable thresholds, α and β, 0≤β<α≤1, and θ is any real value belonging to [0, 2π], to split a universe into a disk and two rings in the unit disk of a complex plane.
We divide the complex membership degrees into regions: (a′) is the accepted region (acceptance/ core zone) that elevates values which are close to 1eiθ to exactly 1eiθ, when the modulus of complex degrees are equal to or greater than α, (b′) is the rejected region (rejection/ dropped zone) that decreases values which are close to 0eiθ to exactly 0eiθ, when the modulus of complex degrees are equal to or less than β, and (c′) is the complex shadowed region (complex shadowed zone) that contains the values which retained inside the closed interval [0,1]eiθor aeiθ, where a∈[0,1] and θ∈[0,2π], when the modulus of complex degrees are between β and α. As well, the three disjoint regions (a′), (b′), and (c′) in CFS are analogous to SHS. Therefore, CSHS offers an example of a three-way approximation that can handle complex information with multivariable.
This research aims to enhance the SHS model by dividing the complex fuzzy membership grades into three disjoint regions. So, a formal definition of CSHS is constructed and illustrated. After that, some basic mathematical operations are proposed with arithmetical examples. Definitively, an application to decision-making is clarified to verify the effectiveness and advantages of the proposed CSHS method.
2.
Preliminaries
Definition 2.1. [1] A is called a FS if there is a function μA defined over the universal set U, μA:U→[0,1] and called the membership function ofA.
Definition 2.2. [12] The SHS approximates the FS by approximating the memberships as follows: The set A:U→{0,[0,1],1} is said to be a SHS on the universe U and
where αr and βr are optimal pairs of thresholds chosen to satisfy the following equation:
and we have 0≤βr<αr≤1. These three areas are defined on the shadow set A where the elevated area is the region where the membership is defined to be 1, the reduced area is the region where the membership is defined to be 0 and the shadowed area is the region where the membership is defined to be [0, 1].
Some properties of SHSs
1) Complement: Let A be a shadow set, A:U→{0,[0,1],1}, then the complement of A is ˉA and defined from A by
It is important to note from definition of the complement for SHSs that the property x∈A⟺x∉ˉA does not satisfy since the element [0, 1] belongs to both sets at the same time, but we notice that the property is satisfied only for ={0,1}.
2) Union: Let A and B be SHSs. Then, the union of A and B is A∪B and assigns as follows:
3) Intersection: Let A and B be SHSs. Then, the intersection of A and B is A∩B and assigns as follows:
Definition 2.3. [20] A CFS S, defined on a universe of discourse U, is characterized by a membership function μs(x) that assigns any element x∈U a complex-valued grade of membership in S. By definition, the values μs(x) may all lie within the unit circle in the complex plane, and are thus of the form rs(x).eiws(x), where (i=√−1), rs(x), and ws(x) are both real-valued, and rs(x)∈[0,1], ws(x)∈[0,2π]. The CFS S may be represented as the set of ordered pairs:
Some basic properties of CFSs are presented:
If A and B are CFSs on Uwith memberships μA(x)=rA(x)eiωA(x), μB(x)=rB(x)eiωB(x), respectively.
1) The complex union of A and B, A∪B is defined as
2) The complex intersection of A and B, A∩B is defined as
3) The complement of A, ˉA is defined as
Proposition 2.1. [20] If A, B, and C are CFSs on U, then the following properties are satisfied:
a. A∩(B∪C)=(A∩B)∪(A∩C),
b. A∪(B∩C)=(A∪B)∩(A∪C),
c. A∩(A∪B)=A,
d. A∪(A∩B)=A,
e. ˉˉA=A,
f. ¯A∩B=ˉA∪ˉB and ¯A∪B=ˉA∩ˉB.
3.
Complex shadowed sets
In this section, we define the concept CSHS, which is a combination of the SHSs and the CFSS. Some definitions and properties are given.
Definition 3.1. Let U be a universal set. The set ACSHS is said to be a CSHS of the universe U if it is a function mapping as follows:
where the codomain of ACSHS is denoted as polar form in the complex plane by ACSHS(x)=rACSHS(x)eiωACSHS(x). We may denote the phase term ωACSHS(x) by using the property of periodic in complex number as ωACSHS(x)=ωACSHS(x)+2kπ,k=0,±1,±2,…. Based on proper values of threshold αandβ, the codomain function of CSHS divides the codomain of CFSs into three disjoint regions; the disk and two rings in the unit disk in the complex plane are as follows:
where x∈U, r(x)∈[0,1], and ω(x) has any value in the interval [0, 2π].
All CFSs values lie in the unit disk of the complex plane. The aim of presenting CSHS in Definition 3.1 is dividing CFS values in the unit disk to three disjoint regions. These regions represent the accepted region (acceptance/ core zone) that elevates values which are close to 1eiω(x) to exactly 1eiω(x), the rejected region (rejection/ dropped zone) that decreases values which are close to 0eiω(x) to exactly 0eiω(x), and the complex shadowed region (complex shadowed/ vagueness zone) that contains the values which are retained inside the closed interval [0,1]eiω(x) or aeiω(x) where a∈[0,1] and θ∈[0,2π].
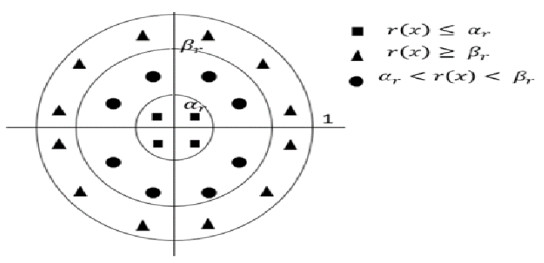
We keep the phase values that have appeared in the structure of CSHS. That is to keep the advantage of periodicity within the unit disk. This allows us to assign each approximation value a phase and can represent the full meaning of the approximation of CF information. For example, to study climate change in a region, we must measure the temperature on a daily basis during different seasons or years to determine the change that is occurring. Take note that some temperatures can be repeated numerous times per year. For example, a 25-degree Celsius temperature is expressed the same way in FSs throughout the year, as does the amplitude term in CFS. This temperature can be given full meaning in CFS by including the phase term, which represents the season. As a result, 25 degrees Celsius in the summer indicates cold or cool weather, but the same amount (25 degrees Celsius) in the winter indicates warm weather. So the phase term lies in the interval [0, 2π] in CSHS to keep the ability to approximate complex fuzzy information to the form of CFS without losing the full meaning of the information that occurs from adding the phase term. On the other hand, the value of phase term lies in [0, 2π] and is used to confine the performance of the phases within the unit disk and can be graphed to three regions in polar form as in Figure 1.
For more illustration, Figure 1 illustrates three disjoint regions. These disjoint regions are divided to a disk and two rings. It's clear that the union of these three regions represents the unit disk that contains all values of CFS. Therefore, the region of disk indicated all values/objects of CFS "r(x)eiω(x)" with amplitude terms less than the level value "αr". Meanwhile, the first ring indicated all values/objects of CFSS "r(x)eiω(x)" with amplitude terms lying between level values "α" and "β". Lastly the second ring indicated all values/objects of CFS "r(x)eiω(x)" with amplitude terms greater than the level value "β" and less than or equal to "1", where "ω(x)" moving from "0" to "2π" as a real value for all three regions.
Note 3.1. The CSHS may reduce to a classical shadowed set if all objects in U mapping to the values 0eiωA(x),1ei0,or[0,1]ei0. The value 0eiωA(x) represents the number 0 in the classical SHS (Rejection zone), where rA(x)=0 and ωA(x) has any value in the interval [0,2π]. Meanwhile, the value 1ei0 represents the number 1 in the classical SHS (Core zone), where rA(x)=1 and ωA(x)=0. Finally, the value [0,1]ei0 represents the number a=[0,1] in the classical SHS (Shadow zone), where rA(x)=1 and ωA(x)=0.
Note 3.2. The following example (Example 3.1) illustrates the type of information represented by CFS as demonstrated in [29].
Example 3.1. Let U={u1,u2,u3,u4,u5} be the universal set of five undergraduate students. Suppose a lecturer wants to measure the academic achievement of his students in each year {y1: first year, y2: second year, y3: third year, y4: fourth year}. It is accepted that the achievement of students fluctuates several times during an academic year. In this situation, CFS is the suitable tool to precisely convey this kind of dataset. The amplitude term could reflect the rate of improvement in academic performance, while the phase terms reflect the time consumed to improve student performance during the year. Therefore, if the value of the amplitude term is near 1 or near 0, this means that the student is having a maximal or minimal improvement in their academic performance, respectively. After that, if the value of the phase term is near zero or near 2π, it means improvement happens in the academic performance of students for a short or long time, respectively. We may represent the presented type of information (CFS A) for five students' academic achievement regarding the four years as follows:
Let the values of threshold αr=0.3 and βr=0.7.Then, the complex shadowed set ACSHScan be defined as follows:
here, a=[0,1].
Definition 3.2. Let U be universe of discourse and ACSHS is the complex shadow set defined as ACSHS:U→{0ei[0,2π],[0,1]ei[0,2π],1ei[0,2π]}. The complement of ACSHS is defined as follows: ¯ACSHS={(x,μˉA(x)):x∈U}, where
and then Table 1 represents the complement CSHSs.
Note that [0,1]ei[0,2π] belongs to both sets at the same time which implies that x∈ACSHS⇎x∉¯ACSHS for any CSHSs ACSHS.
Definition 3.3. Let ACSHS and BCSHS be two CSHSs defined with memberships ACSHS(x) and BCSHS(x) as subsets of the set {0ei[0,2π],[0,1]ei[0,2π],1ei[0,2π]}. The union of ACSHS and BCSHS is denoted as ACSHS∪BCSHS and is defined as follows:
and Table 2 represents the union of two CSHSs.
Definition 3.4. Let ACSHS and BCSHS be two CSHSs defined with memberships ACSHS(x) and BCSHS(x) as subsets of the set {0ei[0,2π],[0,1]ei[0,2π],1ei[0,2π]}. The intersection of ACSHS and BCSHS is denoted as ACSHS∩BCSHSand the membership defined as follows:
and then Table 3 represents the union of two complex shadowed sets.
Proposition 3.1. Let ACSHS be a CSHS defined as ACSHS:U→{0ei[0,2π],[0,1]ei[0,2π],1ei[0,2π]}. Then, the following property holds ¯¯ACSHS=ACSHS.
Proof. Table 4 shows how we prove ¯¯ACSHS=ACSHS by using Definition 3.2.
Clearly, the third row is equal to the first row in Table 4 that proved the property ¯¯ACSHS=ACSHS.
Proposition 3.2. Let ACSHS, BCSHS, and CCSHS be three CSHSs defined as ACSHS,BCSHSandCCSHS:U→{0,[0,1]ei[0,2π],1}. Then, the following property holds
a. ACSHS∪BCSHS=BCSHS∪ACSHS.
b. ACSHS∩BCSHS=BCSHS∩ACSHS.
c. ACSHS∪(BCSHS∩CCSHS)=(ACSHS∪BCSHS)∩(ACSHS∪CCSHS).
d. ACSHS∩(BCSHS∪CCSHS)=(ACSHS∩BCSHS)∪(ACSHS∩CCSHS).
Proof. For part (a), we prove it by using Definition 3.3 as follows (Table 5):
Clearly, the third column is equal to the fourth column in Table 5 containing all cases of CSH values that proved the property ACSHS∪BCSHS=BCSHS∪ACSHS.
For part (b), the proof is similarly to part (a) using Definition 3.4 instead of Definition 3.3.
For parts (c) and (d), the proof is straightforward by using Definition 3.3 and Definition 3.4.
Proposition 3.3. Let ACSHSand BCSHS be two complex fuzzy shadow sets defined as ACSHS,BCSHS:U→{0ei[0,2π],[0,1]ei[0,2π],1ei[0,2π]}. Then the following Demorgan's lows properties hold:
a. ¯ACSHS∪BCSHS=¯BCSHS∩¯ACSHS,
b. overlineACSHS∩BCSHS=¯ACSHS∪¯BCSHS.
Proof. For part (a), the Tables 6 and 7 containing all cases of values cover the proof of property ¯ACSHS∪BCSHS=¯BCSHS∩¯ACSHS.
Clearly, the third column in Table 6 is equal to the third column in Table 7 containing all cases of CSH values that proved the property ¯A∪B=ˉA∩ˉB,where the phase term contains
4.
Application
The data in the following example is recalled from reference [29]. Also, Example 3.1. used the same data, where the significance of the phase term in CFS is clear and illustrated.
The significance of the phase term in CFS is clear and illustrated in Example 3.1. In this section, we employ complex fuzzy data (CFD) in Example 3.1. to represent the rate of improvement in academic performance and consume time on the improvement of some students's performance during the year simultaneously. Then we apply CSHS to approximate their CFD to minimize the calculation and process to obtain the most eminent student(s) to be funded to continue their graduate studies.
Example 4.1. Suppose a university or academic center wants to award scholarships to some undergraduate students to continue their graduate studies. After a long analysis of the academic performance during the final year of an undergraduate program, we consider five possible candidate students listed as x1:Mohammed, x2:Mona, x3:Tariq, x4: Azeez, and x5: Aless. Analogously, they supposed six courses (attributes) denoted by y1: Public culture, y2: Mathematics, y3:Advanced English, y4:Chemistry, y5:Management, and y6:Physics, to evaluate the rate of improvement in academic performance of these students among these courses during the final year of an undergraduate program. Now, we may get the decision matrix with CFS as follows in Table 8.
Now, by letting the threshold values αr=0.4andβr=0.7, we may get the decision matrix with CSHS as follows in Table 9.
The ranking values getting by score xj, j=1,2,3,4, and 5.
According to the illustration in Example 3.1, the amplitude term could reflect the rate of improvement in academic performance while the phase terms reflect the consumed time on the improvement of student performance during the year. Therefore, if the value of amplitude term is near to 1 or near to 0, this means that the student has a maximal or minimal improvement in academic performance, respectively. After that, if the value of phase term is near to zero or near to 2π, this means improvement happens in academic performance of students at a short or long time, respectively.
Now, we find the score of each student of xj,j=1,2,3,4,and 5 as in Table 10, where S0 is the number of repetitions of (0) in the amplitude terms, S1 is the number of repetitions of (1) in the amplitude terms, and S[0, 1] is the number of repetitions of ([0, 1]) in the amplitude terms. So, according to Table 10, student x1 and x2 have the highest rejection scores, whereas the student x5 has the highest waiting scores and x3 and x4 have the highest acceptance score.
Additionally, the student x3 and x4 have the highest acceptance scores. The average phase values of S1 for the student x3 is equal to 1.5π, which is less than the average phase values of S0 for the student x4 which is equal 1.66π. Since the average phase term of S1 for the student x3 "which is equal 1.5π" is near to 0π, this means improvement happens in academic performance of the student who needed a shorter time. Therefore, the most accepted student will be student x3: Tariq.
Also, the student x1 and x2 have the highest rejection scores. The average phase values of S0 for the student x1is equal to 0.46π, which is less than the average phase values of S0 for the student x2 which is equal 0.82π. Since the average phase term of S0 for the student x2 "which is equal 0.82π" is near to 2π, which means improvement happens in academic performance of the student who needed a longer time. Therefore, the most rejected student will be student x2:Mona.
5.
Conclusions
This research recognized the notion of CSHSs as an exceptional type of threshold approximation example to deal with dataset clustering performance employing CFS. CSHS faced the difficulty of keeping the full meaning of complex information during the decision making process by presenting a phase term into the codomain of membership. The classical SHS codomain extended to {0ei2πθ,[0,1]eiθ,1eiθ}, which offered three disjoint regions for CSHS. Furthermore, the basic mathematical operations of CSHS, such as complement, union, and intersection, were introduced. Also, the relation between classical SHS and CSHS was highlighted when we substituted the phase value ωA(x)by "0" in the structure of CSHS, and then CSHs were reduced to the classical SHS. In addition, an application of CSHS in DM processes has been demonstrated, and we highlighted its potential to improve the representation of meaningful information from complicated datasets.
Author contributions
Doaa Alsharo and Eman Abuteen: Validated the research outputs and wrote the original draft of this research; Abd Ulazeez M. J. S. Alkouri: Scrutinized the formal analysis, methodology, ideas and formulated the overarching research goals and aims; Mutasem Alkhasawneh: Played the role of project administration and investigation in this research; Fadi M. A. Al-Zubi: Prepared and created the published work by those from the original research group and helped to create the final form of this research after revision stages.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare there are no conflicts of interest.









 DownLoad:
DownLoad:





