1.
Introduction
Conventional continuum mechanics is based upon Noll's postulated axiom of local action, Truesdell et al [1]. That axiom restricts the dependence of the stresses on the point of interest and especially upon the local derivative of various functions, like energies, stresses, displacements, etc. However, that axiom presupposes the existence of derivatives of various functions and also the existence of geometry. Likewise, Mandelbrot [2] introduced fractal geometries without smooth derivatives of continuous bodies. The power of that theory is considered quite strong since fractal geometry has been introduced in applications in almost every scientific area of physics, mechanics, biology, economy, etc. [3,4,5,6].
Fractional calculus was introduced by Leibnitz in 1695, suggesting derivatives with non-local influence [7], contrary to the established local derivatives and the differential analysis. That analysis helped in discussing problems with fractal geometries and not only. Fractional calculus introduced non-local analysis in various fields of physics, engineering, economics, etc. Eringen [9] introduced non-local mechanics, discussing micro and nanomechanics. Also, that theory is recalled for fractal and fracture analysis. In addition, fatigue and composite material problems may be analyzed through that theory.
Many well-known mathematicians and scientists have worked on fractional calculus, and foreseen the importance of such a theory. Liouville [8], Riemann, and also Poincare has highly contributed to the development of that field. Nevertheless, the introduced non-local fractional derivatives exhibit a major defect. They are not derivatives equipped with the prerequisites of differential topology. Indeed, fractional derivatives fulfill the linearity property, although the rules of the derivative of the product of functions and the Leibnitz rule are not valid. Hence the fractional derivatives do not correspond to differentials and fractional differential geometry is not feasible, although fractional calculus is used in discussing problems in physics, mechanics, biology, economics, etc. Details concerning fractional calculus may be found in [10,11,12,13].
Lazopoulos [14] introduces the Λ-fractional derivative with the Λ-fractional space, where derivation in that space is conventional (local). The Λ-fractional analysis introduces derivatives conforming to the prerequisites of differential topology. Hence Λ-fractional differential geometry is feasible and its use in physics, mechanics, and other applied sciences is justified. The Λ-fractional analysis has already been introduced in developing the Λ-fractional geometry of curves [15], of surfaces [16]. Further, the Λ-fractional continuum mechanics has been proposed, [17], followed by the Λ-fractional linear elasticity theory [18]. Similar beam bending problems have also been presented [19].
Silling [20,21] has already presented a non-local theory, the peridynamic theory, for dealing with specific problems in solid mechanics, where singularities like cracks, fatigue, and other non-smooth phenomena may be discussed in realistic conditions. The term horizon was introduced in that theory, just to specify the non-local region that participated in the discussed problem. Since Λ-fractional analysis and peridynamic theory have similar goals, they may be combined. Lazopoulos [22] has already suggested applications with the Λ-fractional analysis and mechanics with the horizon, concerning the Cantor bar. In the present work, the Λ-fractional peridynamic mechanics of a bar will be discussed, evaluating the peridynamic stresses and displacements of a Cantor bar. Further references closely connected to the present non-local analysis with applications in various fields may be found in Refs [25,26,27,28,29,30].
2.
Materials and method
2.1. Outline of fractional calculus
Fractional Calculus is considered an important branch of applied mathematics with considerable applications in physics, biology, economy, etc. Many books, [10,11,12,13], describe various aspects of the theory and its applications considered more realistic. A summary is presented.
The left and right fractional integrals for a fractional dimension 0 < γ ≤ 1 is defined by Eqs 1,2:
where Γ(γ) Euler's Gamma function and γ is the order of fractional integrals. There exists a plethora of fractional derivatives. They all have a common characteristic. Although they are called derivatives, they are only functions, since they fail to satisfy the prerequisites of differential topology for being derivatives. Nevertheless, fractional derivatives are considered derivatives, in the fractional calculus society, able to generate fractional geometry and formulate variational procedures. Further, sometimes formulation of the fractional differential equations is shown up, without the existence and uniqueness of solutions.
One of the first of them is Riemann-Liouville fractional derivative (RL). Further, the left RL derivative is defined by Eq 3:
Likewise, the right Riemann-Liouville's fractional derivative (RL) is defined by Eq 4:
The relation between fractional integrals and derivatives is expressed by Eq 5,
The right fractional derivative and the right fractional integrals are connected by similar relations.
It is well known that the fractional derivatives fail to satisfy the prerequisites for corresponding to differentials. Therefore, fractional calculus is not able to generate fractional differential geometry, demanded in applications in physics and not only. Hence, various mathematical procedures, such as variational problems, the existence, and uniqueness of solutions of the various fractional equations, fractional field theorems, etc, do not have the demanded mathematical accuracy.
According to the prerequisites of differential topology, the derivatives should satisfy, Chillingworth Eqs 6–8 [23],
The Λ-fractional analysis, Lazopoulos [14], is composed of the Λ-fractional derivative and the Λ-fractional space, where the non-local fractional derivative, in the initial space, becomes local in the Λ-fractional space, generating differential geometry, since it corresponds to differentials. Indeed, the Λ-fractional derivatives satisfy both the prerequisites of Differential Topology addition to the fractional postulates the well-known fractional derivatives.
The Λ-fractional derivative (Λ-FD) is defined as Eq 9:
According to Riemann Liouville's fractional derivative definition, Eq 3, the Λ-FD is given by Eq 10,
Further, the Λ-fractional space is formed by (X, F(X)) coordinates, with Eq 11,
Therefore, the Λ-FD is transformed into a local derivative, in the Λ-fractional space (X, F(X)). Hence, all the mathematical analysis concerning differential calculus is valid in that space. Thus, fractional differential geometry may be developed, along with variational procedures and field theories, that are necessary for studying physics problems. Nevertheless, results may be transferred to the initial space, following the relation Eq 12,
3.
Results
3.1. The Λ-Fractional deformation of a bar
Let us consider a bar of initial length l, fixed at the one end, while an axial force p is applied at the other. Following the principles of the Λ-fractional analysis, the material point defined by the x coordinate in the initial space is transformed into the X, in the Λ-space, with Eq 13,
In addition, the axial load p in the initial space corresponds to the load P in the Λ-space Eq 14,
In addition, the axial length L in the Λ-space of the bar corresponds to the axial length l in the initial space with Eq 15,
Moreover, the constant elastic modulus E and the constant cross-section area in the initial space are transferred in the Λ-fractional space, as non-constant functions EΛ and AΛ along the x-axis. Indeed,
and,
The axial stress Σ(Χ) in the Λ-space is defined by Eq 18:
since the conventional rules of mechanics are valid in the Λ-space.
Transferring the axial stress in the initial space Eq 19,
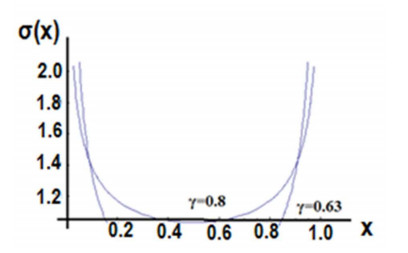
Recalling the influence of the right fractional derivatives with the corresponding right Λ-fractional space, the diagram of the stress σ(x) is shown in Figure 1.
Let us point out that the strain of the bar in the Λ-fractional space is local and defined by Eq 20,
Recalling, further, X=x2−γΓ(3−γ), the Λ-fractional strain is defined by Eq 21:
Hence, the Λ-fractional displacement is defined by Eq 22:
Transferring the displacement field from the Λ-space to the initial one, the displacement field in the initial space is defined by Eq 23,
Considering the left and right fractional deformation, the non-dimensional displacement of the fractional unit bar for the fractional-order γ = 0.63 is shown in Figure 2. Further information may be found in Lazopoulos [22].
3.2. The Λ-Fractional peridynamic deformation of a bar
Peridynamic theory formulates elastic problems, not in the form of differential equations, but in the form of Integral equations [20,21]. Peridynamic theory does not conform to Noll's axiom of local action [1], but the particles interact a finite distance apart. Based on that theory, fracture or damaged problems may be worked out without the requirement of smoothness of the functions.
Trying to formulate the peridynamic problem of the axial extension of a bar, horizon H is considered around the discussed point, where the points in the interior of that neighborhood interact with the point. No interaction exists outside that neighborhood. The various functions, like stresses, displacements, etc., depend upon the neighborhood H in the Λ-space. Therefore, for a function y(x) in the initial space, the function Y(X) corresponds in the Λ-space. However, for functions with horizon H in the Λ-space, it is postulated that Eq 24:
where H is the horizon in the Λ-space. Moreover, the constant horizon H is defined in the initial space by the function h(x) with Eq 25,
3.2.1. The stresses
The stress Σ(Χ) in the Λ-space is defined by Eqs 26, 27,
With,
Let us remind that the Λ-space is defined by the functions (X, F(X)), see Eq 10.
Considering Eq 25, the left peridynamic stress Σ(x) yields Eqs 28, 29:
For the deformation of the Cantor rod with γ = 0.63,
Figure 3 shows the variation of the stress Σ in the Λ-fractional space for various values of the horizon H.
Further, the real stress in the initial space is defined by Eq 30,
Figure 4, shows the stress distribution in the initial space for various values of the horizon H.
In addition, for the symmetric right Λ-fractional peridynamic problem of the Cantor rod, the distribution of the real stress in the initial space is defined by Eq 31 and Figure 5,
3.2.2. The displacements
Proceeding to the definition of the Λ-fractional strain in the Λ-space Eq 32,
Therefore, considering Eqs 26–27, Eq 32 yields,
Further, the displacement Y(X) in the Λ-space is defined by the integration,
Recalling Eq 12,
Figure 6 shows the displacement in the Λ-fractional space expressed in the x variable of the initial space, with the parameter b having the value of the classical strain ε.
Equation 35 defines the displacement in the Λ-fractional space expressed with the x variable of the initial space. Finally, the displacement yl(x) in the initial space is defined through the transformation Eq 36,
Combining the left and the right fractional peridynamic displacements in the initial space Eq 37,
The final Λ-fractional peridynamic displacement of the Cantor rod in the initial plane is shown in Figure 7. The parameter ε is the classical strain of the bar. It is pointed out that strain may not be discussed in the initial space, since derivatives do not exist in the initial space.
3.3. Composites with variable distribution of particulates
Composite materials are two or more materials macroscopically combined forming a useful material shows in Figure 8. Different materials may be microscopically combined so that they form a macroscopically homogeneous material with extremely different qualities from the ones of their constituents.
The composite materials are classified as fibrous, laminated, and particulate composites. The present analysis concerns the particulate composites consisting of one or more materials, suspended in a matrix of another material.
Considering the material of the particulates distributed in spherical surfaces, a composite homogeneous material may be formulated (Figure 9).
The following assumptions are imposed:
1. The fillers and the matrix are homogeneous, elastic, and isotropic.
2. Fillers are spherical.
3. Fillers are uniformly distributed and large in number. Hence the composite may be regarded as homogeneous and isotropic material.
4. The interaction between the fillers is neglected.
5. Small deformations are adopted because linear stress-strain relations are considered.
Proceeding to the formulation of the composite particulate materials show in Figure 10, a spherical particulate, and a spherical composite material are considered.
Following Spathis et al [24] the homogenized Young's modulus Ec and Poisson's ratio νc depend upon the various characteristics of the materials. In fact, as Eqs 38, 39:
where, Ef, νf, Em, νm, are the moduli of the fillers and the matrix, λ = P0/P1 and vf and vm are the volume percentages of the fillers and the matrix. Details concerning the present theory of composite materials and experimental results may be found in the Appendix.
Let us consider purely radial displacements U in the Λ-fractional space. The strain components in that space are expressed by Eq 40,
The stress components are defined by Eq 41,
The equilibrium equation, under general radial body force B is defined by Eq 42,
with the λ, μ the Lame parameters, depending upon the Ec and νc moduli.
In the case of zero body force B, the radial displacement vector U is defined through,
3.3.1. The left fractional problem
As it has already been pointed out, the stresses ΣΓΔ and the displacements U may be transferred from the Λ-space to the initial one, since they are functions. Nevertheless, the strains ΕΓΔ cannot be transferred, since they are derivatives not acceptable in the fractional initial space.
Transferring the various functions into the left initial space, the radius r in the initial space should be transferred into the radius R in the Λ-space as a function of the initial coordinate r, through the transformation,
Nevertheless, when the sphere is not compact in the Λ-space but is defined through the region, A < R < B corresponding to the initial radii a and b, through Eq 44, the displacement vector U is expressed through Eq 43, where, A1, A2 depends upon the external and internal pressures, P1, P0, and the radii, R1 and R0, corresponding to b and a radii respectively. Further, P1 and P2 correspond to Eq 45,
Further, the displacement vector u(r) into the initial space, may be transferred into the Λ-fractional space through the function U(R), where U is the displacement and R the radius in the Λ-fractional space. In that case, A1 and A2 depend upon the external and internal pressures P1 and P0 and the corresponding radii, R1 and R0. Hence, expressing the displacement vector U in the Λ-space in terms of the corresponding radius r in the initial space, see Eq 44 it appears the displacement in the Λ-fractional space as a function of the radius r in the initial space and the fractional order γ:
Further, the parameters A1 and A2 are evaluated by the pressures P1 and P0 applied at the surfaces with R = R1 and R = R0. Eq 47 yields the pressure P = −(ΣRR) at any R by Eqs 47–50,
With,
And,
Hence,
Then the displacement in the initial space u(r) is expressed by Eq 51,
Recalling the expression R and substituting its value into the stress equation, the expression of the stress ΣRR is revealed, for variables connected with the initial space. Indeed Eq 52,
Recalling the same rule for evaluating the stresses in the initial space we get Eq 53:
The same procedure may be followed for defining the other stresses, σφφ, σθθ.
3.3.2. The right fractional problem
For the analysis of the right fractional influence, the right Λ-fractional space may be considered.
As it has already been pointed out, the stresses ΣΓΔ and the displacements U in the right Λ-fractional space may be transferred from the right Λ-space to the initial one, since they are functions. Nevertheless, the strains ΕΓΔ cannot be transferred, since they are derivatives not acceptable in the fractional initial space.
Transferring the various functions into the left initial space, the radius r in the initial space should be transferred into the radius R in the right Λ-space as function of the initial coordinate r, through the transformation,
Nevertheless, when the sphere is not compact in the Λ-space but is defined through the region, A < R < B corresponding to the initial radii a and b, through Eq 54, the displacement vector U is expressed through Eq 43, where, A1, A2 depends upon the external and internal pressures, P1, P0, and the radii, R1 and R0, corresponding to b and a radii respectively. Further, P1 and P2 correspond to Eq 55,
and P1 = p1.
Further, the displacement vector u(r) into the initial space, may be transferred into the Λ-fractional space through the function U(R), where U is the displacement and R the radius in the Λ-fractional space. In that case, A1 and A2 depend upon the external and internal pressures P1 and P0 and the corresponding radii, R1 and R0. Hence, expressing the displacement vector U in the Λ-space in terms of the corresponding radius r in the initial space, see Eq 54 it appears the displacement in the Λ-fractional space as a function of the radius r in the initial space and the fractional order γ:
where, R(r) is defined by Eq 54.
Further, the parameters A1 and A2 are evaluated by the pressures P1 and P0 applied at the surfaces with R = R1 and R = R0. Eq 41 yields the pressure P = −(ΣRR) at any R by Eqs 57–60:
With,
And,
Hence,
Then the displacement in the initial space u(r) is expressed by Eq 61,
Recalling the expression R and substituting its value into the stress equation, the expression of the stress ΣRR is revealed, for variables connected with the initial space. Indeed Eq 62,
Recalling the same rule for evaluating the stresses in the initial space we get Eq 63:
The same procedure may be followed for defining the other stresses, σφφ, σθθ.
3.4. The Λ-fractional peridynamics of composite materials
3.4.1. The left peridynamic problem
For the left peridynamic problem of the composite materials, horizon H is considered in the Λ-fractional space. Hence, the radial stress ΣRR is defined by Eq 64,
Transferring the various functions into the initial space, the radius R should be transferred into a function of the initial coordinate r, through the transformation Eq 54. Yet,
Recalling the same rule for evaluating the stresses into the initial space we get for the left Λ-fractional peridynamic composite materials Eq 66:
Further, the Λ-fractional peridynamic displacement field is defined in the Λ-fractional space by Eq 67,
Substituting R from Eq 64, the displacement U in the Λ-space is defined as a function of the radius r in the initial space Eq 68,
Finally, the displacement in the initial space for the left Λ-fractional peridynamic problem is expressed by Eq 69,
3.4.2. The right peridynamic problem
For the left peridynamic problem of the composite materials, horizon H is considered in the Λ-fractional space. Hence, the radial stress ΣRR is defined by Eq 70,
Transferring the various functions into the initial space, the radius R should be transferred into a function of the initial coordinate r, through the transformation defined by Eq 54.
Yet,
Recalling the same rule for evaluating the stresses into the initial space we get for the left Λ-fractional peridynamic composite materials:
Further, the Λ-fractional peridynamic displacement field is defined in the Λ-fractional space by Eq 73,
Substituting R from Eq 54, the displacement U in the Λ-space is defined as a function of the radius r in the initial space,
Finally, the displacement in the initial space for the left Λ-fractional peridynamic problem is expressed by Eq 69.
The medium value of the left and right stresses, Eqs 66, 72 in the initial place yields the final stress of the Λ- fractional peridynamic problem. The same is valid for the displacements u(r) in the initial space.
The peridynamic problem of the composite materials has now been completed.
4.
Applications
Applying the peridynamic composite materials theory, just mentioned, non-dimensionalized figures have been drawn for the radially symmetric stresses and displacements in the initial space, with the help of the Mathematika pack. Indeed, the stresses and the displacements in the initial space have been computed for the values of p0 = 0.50, p1 = 1.50, ro = 0.05, r1 = 1.0, γ = 0.6, and for the horizon value H = 0.03. The distribution of the stress σrr in the initial space is presented in Figure 11.
The corresponding Λ-fractional peridynamic displacement u(r) in the initial space is shown in Figure 12.
5.
Conclusion
The Λ-fractional peridynamic mechanics is introduced. The Λ-fractional analysis is considered as an ideal mathematical tool for peridynamic problems, especially with non-homogeneous materials and also in micro and nanomechanics. Fractional calculus is a non-local mathematical procedure. With the additional consideration of the horizon H, the theory of the Λ-fractional peridynamic composite materials is established. The peridynamic description of a tensioned Cantor rod has been described. Further, the peridynamic description of the composite materials has been presented. The homogeneous distribution of the fillers in the Λ-fractional space is destroyed in the initial space, through the transferring from the Λ-fractional space to the initial space. Theory and experimental evidence concerning the proposed methodology, for discussing composite materials, are presented in the appendix.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:
















