Assessing the mechanical properties of molecular materials from atomic simulation

1.   Introduction

For crystalline materials, the prediction of elastic properties became a routine task that usually relies on energy minimization to get equilibrium structures, followed by (numerical) assessment of the second derivatives of energy upon simulation cell deformation ^[1,2,3]. While this approach leads to elastic moduli of quite reasonable accuracy when characterizing metals and ionic crystals, molecular materials—in particular if they are not crystalline—show strong, and often non-linear, temperature-dependence of mechanical properties ^[4,5]. This opposes to the zero Kelvin approximation inherent to structures derived from energy minimization. Instead, Monte-Carlo or molecular dynamics simulation methods are required to account for temperature effects to atomistic models ^[6,7].

A very intuitive molecular dynamics simulation approach for the assessment of mechanical properties is to essentially mimic the corresponding experiment by inducing a deformation of the simulation model and sampling the restoring forces. On this basis, each mode of deformation (tensile loading, shear, bulk compression) can be probed, and the elastic moduli attributed to the curvature of the respective stress-strain diagram. On the other hand, a very elegant route was originally suggested more than 50 years ago—by attributing the spontaneous fluctuations of a sample volume to a linear response model ^[8,9]. This allows for simultaneous sampling of all elastic moduli from constant-temperature, constant-pressure molecular dynamics or Monte-Carlo simulations.

Both of these approaches call for careful implementation when applied to complex molecular materials. In what follows, we will review the fundamental simulation protocols and outline strategies for error control. To demonstrate the assessment of temperature-dependent elastic moduli, we selectively picked a recent molecular dynamics simulation model that mimics an epoxy polymer ^[10]. This not only reflects a particularly prominent class of molecular materials, but also a rather rigorous benchmark for system complexity. Indeed, freshly cured epoxy resins are non-crystalline (and desired to remain so within most technical applications), like most polymer materials, and show little ordering beyond the range of 1–2 nm. On the other hand, there is significant local ordering at the < 1 nm scale stemming from the well-defined chemistry of binding the monomeric units into polymer strands. These strands may occur as in principle stand-alone fibers which are however twisted and entangled with each other ^[11]. More robust polymer materials, such as epoxy resins, are however comprised of covalently bonded networks ^[12,13]. As a consequence, the entire sample of the material may be considered as a single molecule. The mechanical properties dramatically depend on the degree of cross-linking which, in state-of-the-art industrial application, reaches almost 100% of the available binding sites ^[14]. In our benchmark model, we achieved 98% crosslinking of the base monomer (bisphenol F diglycidyl ether, BFDGE) and the linker species (4, 6-diethyl-2-methylbenzene-1, 3-diamine, DETDA) ^[10,15]. This could be achieved from systematically exploring the curing process from combined quantum/molecular mechanical treatment of linking reactions and extended analyses of overall network relaxation upon increasing degree of cross-linking ^[10,15].

Despite this high level of crosslinking, epoxy resins are best described as molecular networks with a clear distinction between strands and nodes ^[12,13]. The nodes that (covalently) connect 2-4 strands are separated by 1–2 nm, whereas the strands comprise of molecular moieties which atoms are bonded at ~0.15 nm distance. This structural diversity has important implications on the mechanical properties. While damaging and fracture is related to the cleavage of crosslinks or, much less frequently, rupture of strands, even the network of intact nodes gives rise to non-linear stress-strain characteristics ^[10]. The 1–2 nm sized strands are comparably flexible and may rotate, bend, or twist in response to mechanical load—but also by thermal fluctuations. For this reason, we find strong changes of the mechanical properties as functions of temperature. For the same reason, we however also find strong dependence of the stress-strain diagrams as functions of the strain rates used to deform the material ^[4,5].

2.   Elastic moduli from energy minimization

The most frequently used approach to computing elastic moduli from atomic simulations is based on non-dynamic calculations ^[16,17]. Starting points are relaxed structures resulting from energy minimization. These are then subjected to small deformations $\bar{\varepsilon }$ (e.g. by linearly shifting atom positions according to ±1% uniaxial deformation ${ϵ}_{11}, {ϵ}_{22}\; \text{and}\; {ϵ}_{33}$ or ±1° shear in ${ϵ}_{23}, {ϵ}_{13}\; \text{and}\; {ϵ}_{12}$, respectively) and the corresponding stress $\bar{\sigma }$ is related to (using Voigt notation) ^[18]:

Despite the inherent zero Kelvin approximation, this is the method of choice for crystalline materials, provided that the melting point is far above the technically relevant temperature (usually 300 K) for which the prediction of elastic properties shall apply.

For such systems, typical calculations focus on units cells subjected to periodic boundary conditions—which implies only few explicit atoms and hence allows for high-accuracy quantum mechanical description. Using this single crystal approximation, symmetry-equivalent elastic moduli ${c}_{ij}$ may be ruled out and the independent deformation modes may be either probed individually or concerted fitting of $\overline{\overline c}$ according to Eq 1 is performed ^[19]. Along this line, tensile deformations and shear are typically implemented as < 5% deformation and < 10° shear of the unit cell vectors, whereas the explicit atoms therein are allowed to relax according to energy minimization as a function of $\bar{\varepsilon }$.

For simple crystals like pure metals, structure relaxation typically leads to linear atomic displacements according to $\bar{\varepsilon }$, however for more complex systems such as intermetallic phases, ionic and molecular crystals the atomic displacements significantly depend on the interplay of overall unit cell deformation and the heterogeneity of local interactions. This is particularly evident for molecular crystals which feature strong covalent bonds within the molecules and much weaker interactions (H-bonds, π-stacking, van-der-Waals) between the molecules.

3.   Temperature-dependent stress-strain profiles

Inhomogeneous atomic displacements upon crystal deformation are also crucial for rationalizing the temperature-dependence of the elastic properties. The reorganization of local atomic moieties may involve significant displacements normal to the overall mode of deformation $\bar{\varepsilon }$ applied to the crystal. Examples are zig-zag shifts leading to the puckering of layers or rotation/slipping of molecular fragments such as polymer strands ^[5]. Subject to the strength of local interactions, these displacements may occur spontaneously during deformation—or involve the crossing of energy barriers $\Delta E$ before locking into a favorable configuration. While the former situation is well-described by energy minimization approaches, barrier crossing calls for explicit account of temperature T and thus requires Monte-Carlo or molecular dynamics (MD) simulations. Among these two techniques, MD simulations are widely preferred for rationalizing complex materials because of its direct insights into reorganization dynamics.

In MD simulations of material deformation, the likeliness of reorganization events triggered by the crossing an energy barrier $\Delta E$ is related to $p = {p}_{0}{e}^{-\frac{\Delta E}{{k}_{B}T}}$ with ${k}_{B}$ being the Boltzmann constant and ${p}_{0}$ being a kinetic pre-factor which depends on the strain rate applied to induce deformation. Atomic displacements confined by only small barriers, say $\Delta E < {k}_{B}T$, typically occur on time scales that are much lower than the time scales at which deformation experiments are performed. Such small-barrier reorganization hence appear as elastic modes unless the deformation rate reaches the speed of sound. On the other hand, local reorganization events that require the crossing of large barriers happen only rarely. As a consequence, the material will undergo only a fraction of all possible relaxation moves. Each reorganization event lowers the stress and the overall restoring force response to a given deformation will thus depend on the available relaxation time.

As a simplified picture, such pseudo-elastic behavior may be considered as a first order kinetics assuming at least two types of local deformations, (a) linearly strained regions with comparably large potential energy and (b) domains in which atomic displacements normal to the applied deformation mode helped to lower energy. The overall stress σ will then result from a combination of type (a) and type (b) contributions, subject to the corresponding occurrences ${h}_{a}$ and ${h}_{b} = 1-{h}_{a}$, respectively:

where the characteristic relaxation time scale ${\tau }_{relaxation}$ is the inverse of the a→b transition rate ${r}_{a\to b}\left(T\right)$—which is a function of temperature as given by the Arrhenius law ^[20].

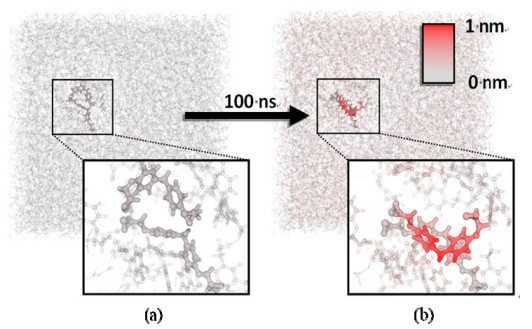
To illustrate the importance of local reorganization events, in Figure 1 we depicted snapshots from an epoxy polymer model taken from ^[10]. In this 100 ns MD simulation run we did not apply external loading to the model system, but only used an (anisotropic) barostat-thermostat algorithm to inspect thermal fluctuations at 1 atm and 300 K, respectively. Comparing the two snapshots, we find (i) a quite homogeneous distribution of atomic displacements in the ball-park of 0.1–0.2 nm and (ii) a strongly inhomogeneous pattern of atomic displacements up to 1 nm. Here, (i) reflects typical vibrations of atoms with respect to their lattice site. In contrast to this, the much rarer, but larger displacements of type (ii) illustrate local reorganization of polymer strands. For the latter, the system must overcome energy barriers stemming from the dissociation of strand-strand contacts and the sliding of adjacent molecular moieties ^[5].

Figure 1.  (a): Snapshot from a 98%-cured epoxy polymer model as adopted from ^[10]. (b): same system after 100 ns MD simulation at 1 atm and 300 K. The scale bar indicates 1 nm. The extend of atomic displacements is highlighted by a color code to discriminate (i) 0.1–0.2 nm scale fluctuations (grey) that are homogeneously distributed in the polymer model—and actually occur on much faster time scales < 10 ns. On the other hand, (ii) we identified 0.5–1 nm scale atomic displacements that stem from local rearrangement of polymer strands with respect to each other. The close-ups highlight the flipping of a polymer strand (red) with a maximum atomic displacement of about 1 nm. This kind of reorganization events (ii) involves the crossing of energy barriers and thus occurs on much slower time scales as compared to the 0.1–0.2 nm vibrations (i). Note that the extent of chain flexibility strongly depends on the type of polymer and increases with decreasing degree of cross-linking.

DownLoad: Full-Size Img PowerPoint

In absence of external loading, such local rearrangement events occur without orientation preference and thus lead to fluctuations of the simulation cell (which we will inspect more closely in the next section). However, in a model system which experiences deformation, the rotation of polymer strands within the twisted network gets biased in favor of stress reduction. This leads to an exponential decay of $\sigma \left(t\right)$ as predicted by Eq 1—and monitored within MD simulations at constant strain as illustrated in Figure 2.

Figure 2.  (a): tensile stress relaxation as a function of time as observed in deform-and-hold MD simulations. Using the same starting point, relaxation at constant elongation of the simulation model is explored at different temperatures and subjected to exponential fits. On this basis, the cascade of relaxation moves is approximated by first-order kinetics triggered by an average reorganization barrier $\Delta E$. (b): the Arrhenius plot of the relaxation rate according to Eq 3 leads to $\Delta E = 2.5\left(\pm 0.7\right){k}_{B}\cdot 300\mathrm{K}$. Note that the simulation model uses a reactive force-field that diminishes barriers from bond formation/cleavage. The relaxation kinetics reported here hence refer to the sliding and twisting of polymer strands, exclusively (see also Figure 1).

DownLoad: Full-Size Img PowerPoint

The most widely spread approach to assessing elastic moduli at non-zero temperature is to perform MD simulations combined with induced deformation of the simulation cell. In analogy to the experiment, tensile testing or shearing within MD runs may be implemented by application of external stress with is ramped up linearly as a function of time. The fundamental difference here is however the large gap between experimental time scales and the ns to μs time scales available to MD simulation using force-fields of atomic resolution. This is even worse for ab-initio MD with offer electronic resolution, but barely reach the ns time scale. To get meaningful stress-strain diagrams from molecular simulation, the common route is to apply strain to the simulation cell and sample the resulting stress.

Along this line, the shape of the simulation cell is controlled externally, typically whilst maintain the overall volume of the system. In ref. ^[10], we used an unbiased approach for this purpose, namely via implementation of axial deformation at constant rate using ${ϵ}_{11} = 1+\dot{ϵ}\cdot \left(t-{t}_{0}\right)$ and fixing the length of the corresponding cell vector $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over a}$ to $a = {ϵ}_{11}\cdot a\left({t}_{0}\right)$, whereas a 2-dimensional barostat algorithm allows relaxation in the perpendicular directions ^[10]. Stress-strain profiles collected in this manner will nevertheless depend on the applied rates and convergence checks from comparing a series of deformation runs of different strain rates are advised. For simple single crystalline systems, this often suffices to obtain reasonable agreement with the experiment. In turn, molecular materials—like the polymer model used as a demonstrator system in Figures 1 and 2—are however quite likely to display very slow relaxation modes ^[5]. Indeed, tensile testing of epoxy polymer shows strain rate dependence even in experiments performed on the time scale of up to 10⁵ s—which exceeds the scope of MD simulations by more than 10 orders of magnitude ^[21].

To model such systems in a more realistic manner, MD simulations need to be redirected to mimic quasi-static conditions. For this, a series of deformed simulation cells may initially be prepared from taking snapshots from constant strain rate runs. Next, the corresponding models are inspected in parallel MD runs at constant strain. This allows investing up to μs of relaxation time to an individual data point of the stress-strain diagram. The underlying relaxation process can be followed by monitoring stress as a function of time—as illustrated in Figure 2. While the overall relaxation might require even longer time scales, already 10 ns scale runs may offer insights into partial relaxation which suffices for exponential fits of the decay in $\sigma \left(t\right)$ as denoted in Eq 2. Using the asymptotic stress $\sigma \left(t\to \infty \right)$ from this procedure for comparison to the experiment, we indeed found quite convincing agreement of the elastic part of the stress-strain diagrams and even the ultimate stress of the epoxy system before fracture ^[10,21].

4.   Stress response from temperature-dependent fluctuations

A very elegant way of assessing elastic properties of materials is to take use of spontaneous fluctuations from the equilibrium geometry ^[8,22]. For a given set of temperature and pressure conditions, we can describe the equilibrium cell of a simulation model by the length of the box edges ${a}_{0}, {b}_{0}, {c}_{0}$ and the angles between the cell vectors ${\alpha }_{0}, {\beta }_{0}, {\gamma }_{0}$, respectively, and expand a Taylor series for describing the energy cost $\Delta E$ of deviations $\Delta a, \Delta \alpha, \Delta b, \Delta \beta, \Delta \mathrm{c}\mathrm{ }\; \mathrm{a}\mathrm{n}\mathrm{d}\; \Delta \mathrm{\gamma }$, respectively. For the example of bulk compression $\Delta V$, we thus get:

whereas full analogous expansions $\Delta E\left(\Delta a\right)$, $\Delta E\left(\Delta \alpha \right)$ etc. are obtained for tensile and shear deformation modes, respectively. Note that all derivatives are taken with respect to the equilibrium geometry which causes the first derivatives in Eq 4 to vanish.

Per definition, elastic deformation implies a linear response of the restoring stress as a function of strain, namely:

with

In absence of external loading, the deviations of simulation cell volume $\Delta V = V\left(t\right)-{V}_{0}$ (and likewise $\Delta a, \Delta \alpha$ etc.) only stem from thermal fluctuations and are hence as small as actually possible at non-zero temperature. As a consequence, the elastic behavior is typically well described by the idealized linear formulation of Eq 5 with $K = {\left.\frac{{\partial }^{2}E}{{\partial V}^{2}}\right|}_{{V}_{0}}$ being a constant. While the implementation of so-called non-linear elastic moduli is straight-forward ^[23], in what follows we focus on the ideal elastic case.

After sufficient relaxation of a material under investigation to ensure thermodynamic equilibrium by means of constant-temperature, constant-pressure MD simulation, the fluctuations of the simulation cell are simultaneously obtained by monitoring the cell vectors as functions of time ^[22]. Taking use of Boltzmann statistics, the occurrence profile h of spontaneously observed deformations related to a given mode can directly be related to the corresponding energy profile. For the example of volume fluctuations$\Delta V = V\left(t\right)-{V}_{0}$ this implies

where the right part of Eq 7 refers to the fitting of a Gaussian distribution to the occurrence statistics of $\Delta V = V\left(t\right)-{\left\langle{V}\right\rangle}_{t}$ with ${V}_{0} = {\left\langle{V}\right\rangle}_{t}$ and ${d}_{V} = {d}_{\Delta V}$ being the standard deviation of $\Delta V\left(t\right)$. Likewise, Gaussian fits may be performed for the occurrence profiles of cell vector dimensions, e.g. $\Delta a\left(t\right)$ or the cell angles, e.g. $\Delta \alpha \left(t\right)$ to provide the corresponding standard deviations ${d}_{a}\; \mathrm{a}\mathrm{n}\mathrm{d}\; {d}_{\alpha }$, respectively. Thus, the analyses of a single MD run at thermodynamic equilibrium offers the entire set of elastic constants:

Despite the elegant simplicity of this approach, practical application to characterizing complex materials is complicated by the overlapping of elastic modes with other processes such as visco-elastic deformation. Indeed, for molecular materials models subjected to direct sampling of occurrence statistics we typically find the elastic moduli from Eq 8 to be underestimated. This is nicely illustrated by our beforehand discussed benchmark system modelling an epoxy polymer ^[10].

To assess the Youngs modulus for deformations along a, we find a superposition of elastic and visco-elastic fluctuations than can formally be written as:

As a consequence, the standard deviation taken from the overall occurrence statistics ${d}_{a}$ is equal or larger than that of the purely elastic deformation models, Figure 3 clearly indicates ${d}_{a} > {d}_{{a^{elastic}}}$ in the epoxy model.

Figure 3.  Dimension of the cell vector a as a function of time as obtained for the epoxy polymer benchmark model. The plot shows a running average over (t, t-3 ns) to help discriminating fast fluctuations from the much slower viscous modes of reorganizing of the model. While the latter reflects rare transitions from one local energy minimum to another, elastic deformation implies fluctuations within a local energy minimum configuration.

DownLoad: Full-Size Img PowerPoint

Ideally, the elastic constants should be derived from an exclusive statistics of ${\Delta a}_{}^{elastic}\left(t\right)$. For this, we however must discriminate elastic from non-elastic deformation which is far from trivial in a complex molecular material. The only guide for such differentiation is given by the different time-scales of elastic deformation (fastest modes) and the usually much slower visco-elastic modes. Indeed, when sampling the occurrence profiles over short (here 5 ns) time intervals we found the standard deviations ${d}_{a}$ in line with experimental values of the Youngs modulus ^[10].

In case of extended sampling over longer periods we therefore suggested to sample ${d}_{a}$ in 5 ns intervals, and then use the overall average $\left\langle{{d}_{a}}\right\rangle$ as input to Eq 8 ^[10,15]. While this lead to excellent agreement of bulk, Youngs and shear moduli in line with the experiment, the obvious downside of this approach is the somewhat arbitrary choice of the time intervals. Moreover, few but still some of these intervals include larger scale deformation stemming from viscous modes of molecular movements. Anyway, we argue that fragmenting the statistics in time intervals converges to $\left\langle{{d}_{a}}\right\rangle\cong \left\langle{{d}_{{a}^{elastic}}}\right\rangle$ for sufficiently short sampling periods, whereas the direct sampling of overall statistics implies $\left\langle{{d}_{a}}\right\rangle = \left\langle{{d}_{{a}^{elastic}}}\right\rangle+\left\langle{{d}_{{a}^{visco}}}\right\rangle$ and thus inadequate inputs to Eq 8. In ref. ^[10], the choice of 5 ns was motivated by choosing the sampling intervals short, whilst still providing smooth occurrence profiles for fitting the Gaussians reliably.

From a materials science perspective, the separation of (ideal) elastic and pseudo/visco-elastic modes reflects the spatial and time-depend fluctuations of elastic constants in polymer materials at the nm (ns) length (and time) scales, respectively ^[5,24]. From a mathematical viewpoint, the separation of scales is routinely performed by means of Fourier filtering. To bring this together, we analyzed the Fourier transforms of the simulation cell shape and dimensions as shown in Figure 4.

Figure 4.  Fourier transforms (FT) of the fluctuations of $a\left(t\right), \alpha \left(t\right)\; \mathrm{a}\mathrm{n}\mathrm{d}\; V\left(t\right)$ being functions of $\nu$ as shown by dashed curves in red, blue and green, respectively (right axis). Estimates of ${a}^{elastic}\left(t\right), {\alpha }^{elastic}\left(t\right)\; \mathrm{a}\mathrm{n}\mathrm{d}\; {V}^{elastic}\left(t\right)$ are obtained from back-transformation using $\nu \ge {\nu }_{cut}$ filtering. On this basis, we obtain the Youngs, shear and bulk moduli (solid curves) at 300 K and 1 atm as functions of ${\nu }_{cut}$, respectively (left axis). To identify the best choice of cut-off delimiters ${\nu }_{cut}$ for separating the time scales of fast, elastic modes and longer termed viscous reorganization, we suggest the first minimum in the corresponding FT-plot. Indeed, this leads to excellent agreement with the experimental data as indicated by (x) along the left axis ^[21,25,26].

DownLoad: Full-Size Img PowerPoint

The intensities of the Fourier transforms of $a\left(t\right), \alpha \left(t\right)\; \mathrm{a}\mathrm{n}\mathrm{d}\; V\left(t\right)$ show a clear peak at low frequencies $\nu < 0.05-0.1\;{\mathrm{n}\mathrm{s}}^{-1}$, subject to the mode of deformation. In turn, a broader spectrum is found for the faster vibrational modes. To separate elastic and visco-elastic type fluctuations, we suggest Fourier-filtering by means of a cut-off frequency delimiter ${\nu }_{cut}$:

with

Likewise, analogous filtering of $\alpha \left(t\right)\; \mathrm{a}\mathrm{n}\mathrm{d}\; V\left(t\right)$ is obtained, however using individual frequency delimiters ${\nu }_{cut}$ to account for the different dynamics of tensile (${\nu }_{cut} = 0.1\;{\mathrm{n}\mathrm{s}}^{-1})$, shear (${\nu }_{cut} = 0.05\;{\mathrm{n}\mathrm{s}}^{-1})$ and bulk volume (${\nu }_{cut} = 0.04\;{\mathrm{n}\mathrm{s}}^{-1})$ deformations.

On the basis of these approximations, we sampled the fluctuations ${d}_{{a}^{elastic}}$ and ${d}_{{a}^{visco}}$ of merely elastic ${a}^{elastic}\left(t\right)$ and viscous ${a}^{visco}\left(t\right)$ deformation modes of the simulation cell as illustrated in Figure 5. This separation of time scales leads to more reliable sampling of the elastic-type fluctuations ${d}_{{a}^{elastic}}$ as compared to the statistics taken from a series of time intervals we discussed earlier. This is also reflected by comparing our modeling results to the experimental assessment of the Youngs, shear and bulk moduli as functions of temperature, respectively.

Figure 5.  (a) Profiles of $a\left(t\right)$, grey curve, and its Fourier-filtered (${\nu }_{cut} =$ 0.1 ns⁻¹) components ${a}^{elastic}\left(t\right)$ and ${a}^{visco}\left(t\right)$ shown in blue and red, respectively. Note that the 10 ns scale shifting of the simulation cell dimension $a\left(t\right)$ is practically exclusively described by ${a}^{visco}\left(t\right)$, whereas the fast, elastic-type vibrations within local energy minima is obtained as ${a}^{elastic}\left(t\right)$. The standard deviations ${d}_{{a}^{elastic}}$ (and likewise ${d}_{{\alpha }^{elastic}}$ and ${d}_{{V}^{elastic}}$) provide reliable estimates of the Youngs, shear and bulk moduli, respectively. (b) Occurrences h of $a\left(t\right), {a}^{elastic}\left(t\right)$ and ${a}^{visco}\left(t\right)$ and corresponding Gaussian fits shown as dots and solid curves, respectively. The color code is analogous for both figures.

DownLoad: Full-Size Img PowerPoint

For such benchmarking, we decided to focus on the study of Littell et al. in which a consistent series based on a constant experimental setup was used (Figure 6) ^[21]. Likewise, we analyzed the elastic properties as a function of temperature using the same atomic configuration as starting point for MD runs at 300,350,400 and 450 K, respectively. While the modeling data obtained at 300 and 350 K nicely agrees with the experimental data available, we find that a clear-cut separation of time scales for elastic/viscous deformation modes may not be achieved for MD runs at 400 K or even larger temperatures. This limitation is in line with the intrinsic difficulty in discriminating elastic and viscous deformations in polymers near their glass transition temperature (~440 K) ^[10].

Figure 6.  Elastic moduli of epoxy polymers cured from bisphenol F diglycidyl ether and 4, 6-diethyl-2-methylbenzene-1, 3-diamine as functions of temperature. The dashed lines show the average results of tensile and compression experiments performed at a strain rate of 10⁻³ s⁻¹ as taken from ref. ^[21]. Youngs, shear and bulk moduli as obtained from MD simulations at 300 and 350 K are marked as (x) using red, blue and green color, respectively.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

Molecular modeling and simulation approaches are continuously catching up with the complexity of modern molecular materials. While early simulation studies of polymer networks mainly coped with the appropriate description of molecular interactions ^[11], current computational resources allow all-atom modeling based on robust empirical interaction potentials such as the OPLS or GAFF force-fields ^[27,28]. Clearly, the length scales inherent to proper modeling of complex polymer networks still oppose a full ab-initio description, in particular when it come to dynamics calculations. However, reactive force-field approaches and combined quantum/classical techniques help to provide near ab-initio accuracy where needed, namely for the cross-links between the polymer precursors ^{[10,15,29,30,31]}.

This not only boosted the quality of assessing the atomic interactions of a given polymer model, but also greatly helped to create the model itself. Indeed, for non-crystalline networks of molecules it is far from trivial to provide realistic starting structures and extensive relaxation of the simulation systems is needed to ensure convergence. With typically dimensions exceeding the 10000 atoms scale and relaxation times beyond the 10 ns scale, the use of smart molecular mechanics models is likely to prevail the state-of-the-art also in the nearer future.

The issue of structural complexity, and the time-dependent diversity of local ordering in molecular materials is also reflected in the analysis and the understanding of mechanical properties. The techniques reviewed in the present work offer a versatile toolbox for this purpose. Among these methods, the computational demand differs quite significantly. Temperature-dependent analyses of molecular dynamics simulation runs are clearly the most expensive option—but allow exciting atomic scale insights into complex network dynamics in parallel to computing macroscopic properties. Thus, for the actual understanding of molecular materials we consider molecular simulations as an important, if not indispensable extension to the experiment.

Acknowledgements

This work was funded by the Graduiertenkolleg GRK 2423, "Frascal" of the Friedrich-Alexander-Universität Erlangen-Nürnberg.

Conflict of interest

The authors declare no conflict of interest.