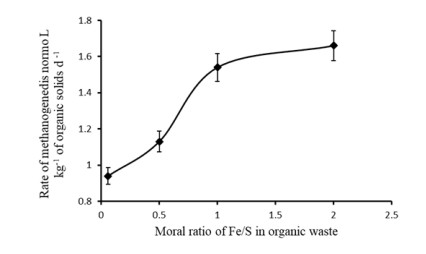
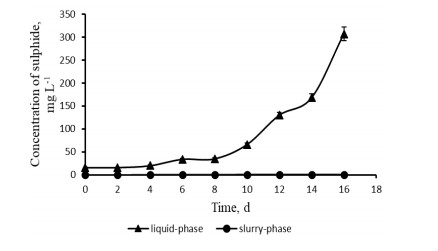
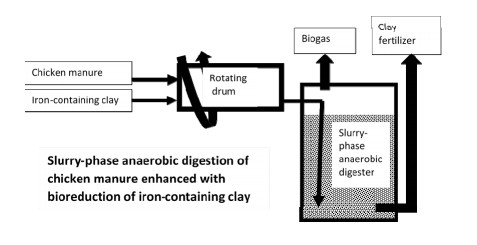
It is shown in this review that addition of clay minerals and hematite iron ore can significantly enhance anaerobic digestion of chicken manure. Liquid-phase anaerobic digestion of chicken manure consumes a lot of fresh water and energy to keep waste as a suspension. Meanwhile, anaerobic digestion of chicken manure in clay slurry without stirring could minimize energy and water consumption because the initial acceptable content of organic solids can be increased. For example, this content can be increased from 5% (w v-1) in suspension of chicken manure for liquidphase anaerobic digestion up to 15% (w v-1) in the slurry of chicken manure for slurry-phase anaerobic digestion than can save up to 13.3 L of water per kilogram of dry organic solids. The slurry-phase anaerobic digestion of nitrogen-, sulphur-, and fat-containing organic wastes can be enhanced using microbial reduction of Fe(Ⅲ) in clay or in hematite iron ore. This is due to adsorption or precipitation of such inhibitors of microbial acidogenesis and methanogenesis as ammonium, sulphide, long-chain fatty acids, humic and fulvic acids with clay or ferrous ions. For example, maximum concentration of ammonium decreased from 11.4 g L-1 during liquid-phase anaerobic digestion to 1.4 g L-1 during slurry-phase process due to adsorption of ammonium ions on clay. Addition of iron-containing clay to slurry-phase anaerobic reactor removed dissolved sulphide totally due to its precipitation with ferrous ions that are produced by bioreduction of Fe(Ⅲ) in clay. Slurry-phase anaerobic digestion enhanced with bioreduction of Fe(Ⅲ) minerals is also more effective process in terms of environmental safety than widely used liquid-phase anaerobic digestion because of an absence of water supply and wastewater effluent.
1.
Introduction
One third-grade emergent bilingual student said of her teacher: "Mrs. Schaeffer always says that we learn more from each other than we learn from her" [1, p. 90]. In her interview, the student was describing a mathematics classroom where communication, participation, and knowledge of emergent bilingual (EB) students were esteemed [1]. But this positioning of EB students, or those students who use, maintain, and develop their home language as they acquire knowledge of English [2], is not uniformly promoted in mathematical communication within U.S. classrooms [3,4]. Some teachers feel unprepared for these students, who now encompass over 1/10 of the country's student population [5], and their unique learning needs [4], as reflected by their assessment results [5] and studies of opportunity-to-learn (OTL) [6]. Disparities between the assessment data of EBs and their English-proficient peers partially framed the need to improve EBs' mathematics instruction [7]. On the fourth-grade National Assessment of Educational Progress mathematics test, 34% and 10% of English-proficient students scored at "proficient" and "advanced, " respectively, while 15% and 1% of EB students scored at "proficient" and "advanced", respectively [5], an inequity that points not to any deficiency in EBs but to the quality of instruction to which they have access. Another disparity used to frame the need for improved mathematics instruction was the differences in OTL between EB and English-proficient students: a study of an urban school's sixth-grade students suggested that simple exposure to assessment material in the classroom may not necessarily yield the same better assessment results for EBs as it did for their English-proficient counterparts [6]. While neither assessment data nor the OTL that may be reflected therein was the focus of this review, EBs' OTL has been linked to language and communication [8]. To explore the mathematics instruction that will encourage EBs in mathematical communication and cast them in the role of knowing and doing mathematics, this review answered the question of what kinds of moves and strategies might facilitate EB participation in mathematics discourse and mathematics discourse communities through interactive and reflexive positioning.
Although previous reviews of research have explored the experience of EBs in K-12 mathematics contexts [9,10,11] and instructional moves that can promote participation in mathematics discourse for all students [12], they have not focused specifically on encouraging EBs through positioning. While validating EBs' informal communication, the current review's findings include positioning EBs as members of the mathematics discourse community by equipping them to face the challenges of comprehending the academic register such as vocabulary and nominalizations, as cataloged by Schleppegrell [11]. The current review also built upon the findings of Walshaw and Anthony [12], who suggested the importance of exploring student ideas by considering how different instructional moves position these students, and Drageset and Ell's [10] consideration of how different moves position students in mathematics communications. Lastly, the review echoes some of De Araujo and colleagues' [9] findings, such as teachers' eliciting and revoicing EBs' ideas, but it also considers how teachers position both themselves and their students in deploying these moves.
2.
Theory and definitions
Teachers' deficit-oriented narratives surrounding EBs and discomfort in giving them space to communicate mathematical thinking [3] make it difficult for teachers to facilitate mathematics discourse. By silencing and limiting their access to discourse, U.S. teachers deny opportunities-to-learn to their EB students, whose participation in discussion and classroom communication is critical to their learning of mathematics [13]. However, teachers who facilitate discourse and create discourse communities within their classrooms can empower their students to learn and overturn the historically marginalized positioning of EBs in mathematics classrooms [13]. By considering how their task selection and classroom talk position their EBs, teachers can use instructional moves that facilitate their EBs' participation in mathematics discourse and consequent OTL [13].
Teachers' positioning EBs in mathematics discourse can either enact an assets-based understanding that these students' ideas, knowledge, and communication are valuable [14] or continue to fortify the traditional marginalization of EBs in U.S. classrooms [13]. In this review, mathematics discourse is defined by communications that make possible and are made possible by mathematics discourse, or the knowledge, beliefs, and ways of doing mathematics that characterize an individual's mathematical understanding [15]. In U.S. classrooms, teachers should give students access to the dominant discourses of schooling, which have historically been most reachable for upper-class English-proficient white students [15]. Instead, teachers have been employing extant discourses to position students' diverse bodies of knowledge and modes of communication as inferior [13]. In the current classroom contexts, the aspects of EB's discourse identities that are manifested through discourses, namely their home lives and out-of-school contexts, are also positioned as incompatible with possessing mathematical knowledge.
Because the definition of discourse used in this article is founded upon systemic functional linguistics (SFL), which holds that language is both defined by and defines its context [16], this review also considers the community, or community of practice, to denote the social and historically established constructs wherein ways of knowing and doing are shared [17]. The mathematics community in U.S. classrooms has been historically exclusive and has valued written discourses with which dominant groups of students are more familiar [15] more than it has valued informal utterances and nonlinguistic communication used by other groups. To maintain the assets-based approach to understanding EBs' extant discourses and how to promote them further [14], this article defined a mathematics discourse community to include shared beliefs, modes of reasoning, and communicational competence in language, visual representations, and gestures [4]. Though Willey [4] noted the necessity of care when applying the definition of mathematics discourse community to classrooms with EBs, whose language traditions and needs have been traditionally and systemically marginalized, this article used mathematics discourse communities to mean idealized spaces where the mathematical communications position the strengths, knowledge, and language of EBs as valid.
The article utilized positioning theory to conceive the different ways that communication may position students (such as EBs) in relation to other students in the classroom or the teacher [18]. Teachers' communication can interactively position their students, thereby casting them in a role within the discourse community, or reflexively position them, allowing teachers to establish their level of authority in the community [18]. For instance, the teacher asking a student a difficult question both interactively positions the student as capable of difficult problem-solving and also reflexively positions the teacher as a director of learning and the "questioner" in the space. Moreover, positioning can be established in the first order or second order. In the first order, a participant initiates a communication, such as when a teacher invites a response, which establishes the high level of expectations the teacher has for students; alternatively, the teacher does not give students opportunities to discuss procedures with one another, fortifying the idea that the teacher holds complete ownership over mathematical knowledge. However, positioning in the second order involves another community participant's response to first-order positioning, either solidifying or changing the positioning that has been established [18]. Second-order positioning may occur when students embrace the high expectations given by their teacher and attempt rigorous problems, showing complicity with their teacher's positioning. In contrast, students may also show resistance to their teacher's positioning by refusing to engage with difficult questions [18].
3.
Methods
The following question guided this synthesis of research: How, if at all, does the literature suggest teachers promote EBs' participation in mathematics discourse and mathematics discourse communities through reflexive and interactive positioning? The search included empirical studies in K-12 settings from the past 25 years to show the growth of the field over time. The exclusive focus of the studies had to be EBs in mathematics contexts in the U.S. because of the changing population and pending need to give all students access to quality mathematics instruction [5]. Upon the advice of a reviewer, one article using vignettes rather than a systematized path of study was included [19]. This article used two cases to conclude the importance of one teacher's instructional moves, especially the introduction of mathematical vocabulary, in shaping students' discourse [19]. The synthesis did not include book chapters or conference proceedings.
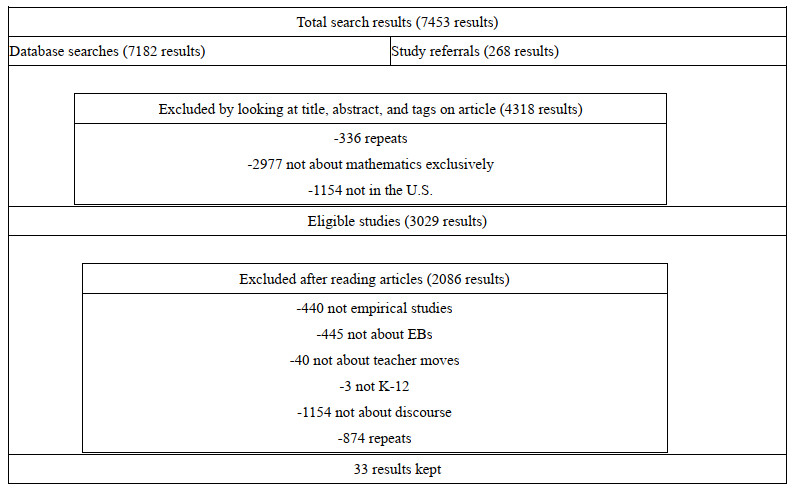
The studies were found first by searching in databases, then using the reference lists of relevant articles, and finally, doing a Web of Science search. In the databases ERIC and Ebscohost, every combination of three different terms was used. The first term of each search was "mathematics" or "math" to indicate the content area on which this synthesis was focused. For the next search term, different terms for "emergent bilingual" were used to denote the population of students whom the instructional moves and strategies are intended to serve. Although the article's use of the term "emergent bilingual learner" was meant to emphasize and positively position the student's growing knowledge of linguistic practices in two languages rather than the student's current lack of English proficiency [2], other terms including "English language learner" were used in the first search as the author realized this was a more common term than the term "emergent bilingual learner". Other terms for EB were found as tags on the articles in the initial search and in the articles themselves. For the third search term, different terms for "discourse" were used, which were also found as tags on relevant articles from the initial search. Then, all bibliographies were analyzed and a Web of Science search was conducted for relevant articles to find other sources. An abridged summary of search results and how many were eliminated based on exclusion criteria is shown below (Figure 1).
The search process revealed 33 relevant studies, whose participants' grade levels are included in Table 1. After reading the studies, the author re-read them to annotate them for the specific moves that they advocated and found 181 initial codes on instructional moves. Then, the author looked for commonalities in the moves suggested amongst the different articles with a deductive approach and compiled the codes under 26 different themes. The first 181 codes included specific information such as "teacher providing problems in English and Spanish", "teacher connecting mathematical vocabulary to native language", and "teacher using gesture to build on student native language use". Then, another round of coding was used to mark whether instructional moves deployed positioning in the first or second order or whether the teacher move achieved reflexive or interactive positioning. For instance, "teacher providing problems in English and Spanish" was also coded as "teacher interactively positioning home language through task selection (first order)", while "teacher using gesture to mirror student usage" was also coded as "teacher using gesture to interactively position students' use of nonlinguistic resources (second order)". Through an inductive process, codes were condensed into themes. The theme "Teacher and/or students validating students' native language/culture" included "teacher positioning home language through task selection (first order)" and 11 other codes. The author also developed a clear definition for each theme and criteria for assigning it. For example, "teacher positioning students with revoicing" was defined as "any repetition or reformulation of students' ideas through verbal utterance, drawing attention to student-created diagrams, or inviting other students to rephrase or build upon student's ideas". After defining all themes and the criteria for assigning each of them, the author checked the themes attached to different articles and then used them to structure the article. The findings are organized by whether a move achieved interactive or reflexive positioning.
4.
Findings
The findings of the review revealed eight positioning moves used by the teachers in the literature to facilitate student discourse. In Table 2, each positioning move is defined and will be further elaborated in the rest of the section.
4.1. Interactive positioning of EB students
The first common finding across six of the studies was that teachers can support EBs' participation in mathematics discourse by being cognizant of the power inequities that exist between English-proficient and other-language-proficient students and interactively positioning EBs as problem-solvers [20,28,29,42,43,44]. In inclusive classrooms that included both native English speakers and EBs, Turner and colleagues [43] noted that EBs, particularly those who did not come from European or Asian backgrounds, were often positioned as marginal members of the classroom discourse community. The authors suggested that interactive positioning, or how teachers position their EB students through different discourse moves, can be highly influential in both the way that other students position EBs and EBs' reflexive positioning and the way they position themselves [43]. As a result, the literature suggested moves that a teacher can make to allow EBs to participate in the mathematics discourse community and understand themselves as active members therein.
4.1.1. First- and second-order positioning through inviting and revoicing
In order to make sure all EBs were able to take on problem-solving roles, teachers in four studies positioned EBs in the first order, or initiating discourse, by calling on them to explain their problem-solving strategies, defend and justify their ideas, build connections amongst different concepts to make claims, and respond to peers' ideas [40,42,43,44]. In the study of one after-school classroom in an urban area, the most common moves were instances where an EB student was invited to either give their own explanation of a strategy or evaluate that of a peer [43]. Employing these strategies in whole-group discussion, the teacher was publicly able to demonstrate that students were capable of mathematical thought and of interacting with the thoughts of their fellow community members. Furthermore, the teacher acted as a language mediator, both posing questions and rephrasing responses in different languages, so that neither linguistic imprecision nor minor errors in problem-solving would prevent EBs' mathematical ideas from being perceived as valid [43]. The moves exhibited EBs' potential as contributors to the discussion in whole-group conversations that English-proficient students traditionally monopolized [28].
In eight of the studies, teachers further demonstrated EBs' potential by using the strategy of revoicing to highlight students' mathematical contributions [28,47], to elaborate, repeat, and reformulate student utterances to emphasize ideas and teach academic vocabulary [19,21], to further understand and correct errors [33,39], and to give students a space to recognize and build on one another's thinking [40,43]. Researchers from a mixed methods study found that one of the most common ways an urban high school teacher used revoicing was to position students as functional parts of giving structure to the task by naming the students and what they had contributed to the rest of the class [28]. The teacher also acted as a language broker by eliciting ideas from the EBs and then elaborating and refining what they had said for the other students in English [28]. However, in this scenario, the students, who were English proficient and mainly identified as African American, did not have their ideas explored and refined with the same frequency [28]. This may not have been indicative of the general practice of that teacher but reflected the possibility of new power imbalances in mathematics discourse communities. Marginalization of any student obstructs the development of the idealized mathematics discourse community that was the basis of this paper.
Whereas the aforementioned two studies featured a language broker in the form of the teacher to play a part in the positioning of EBs as mathematical thinkers, the bilingual teacher resource was not necessary in all the examples of revoicing in the literature [29,43]. The bilingual teacher from the study by Turner and colleagues [43] also asked a student to put a visual representation of the problem solution on the board and then invited other students to interpret this visualization, thereby further broadening the scope for participation in mathematics discourse. Furthermore, it must be noted that revoicing across languages left EBs without access to their ideas after they had been elaborated or reformulated in English [28]. Though teachers may facilitate discourse and position EBs by language brokering, they must also strive to make that revoicing comprehensible by leveraging other communicative resources, as will be described in the following sections.
Moreover, two studies [19,21] showed that revoicing could be employed to both legitimize what students were saying and model for them how they might convert their ideas into the academic register. Revoicing served to draw students' attention to important language features, as Khisty and Chval [19] observed with one fifth-grade teacher, who modeled how students' organic mathematical conversations in their groups could be reformulated into another register and thus expanded their mathematics discourse. One fifth-grade teacher also validated student strategies by repeating their counting gestures while also gesturing to correct the student's understanding that he was working with whole units rather than the appropriate half-units [39]. Additionally, students themselves responded to this positioning by taking opportunities to elaborate upon the responses of their peers, showing complicity with their teacher's positioning of them as mathematical thinkers with the ability to teach [19,43]. Students also took on roles of providing a narrative to one another's models and explaining the relationship between symbols like tally marks and quantities in the problem, further interactively positioning one another and showing esteem for their peers' knowledge [43]. Moreover, students' responses to their teachers' positioning show the scope of interactive positioning to eventually foster students' reflexive positioning of themselves as mathematical thinkers.
4.1.2. First-order positioning through task selection
In five of the studies, another first order, or initiating, interactive positioning move was providing rigorous problems and enacting a belief that students can be experts in mathematics discourse communities [1,25,27,31,44]. Contrastingly, teachers in another study were unable to position their students as mathematical thinkers by not entrusting them with responsibilities or rigorous tasks [37]. However, teachers from a 2009 study [1] moved away from acting as directors of knowledge and assigned their students activities such as convincing one another of a solution for a high-cognitive demand task, thus positioning them as experts.
Additionally, expectations of students to act as experts were enacted through teachers' decisions to use more rigorous, open-ended questions, to first-order position EBs across five of the studies [21,31,36,37,47]. A case study of a third-grade classroom by Hufferd-Ackles and colleagues [31] discussed the instructional changes used to create a math-talk learning community that would enhance the mathematics learning of all students. Even though this teacher began with closed-ended questions and having ownership of the mathematical knowledge in the classroom, she eventually made changes that positioned her students differently. She moved from the front of the room to the back and rather than being the questioner, she clarified student utterances as they moved up to the front of the room to explain to and question one another [31]. On the other hand, Banse and colleagues [21] attributed their study's students' lack of complex responses to the teachers' overuse of closed-ended questions, which may have made students think that detailed explanations were not a part of the teachers' expectations.
However, a uniform casting of closed-ended questions as detrimental to the facilitation of discourse amongst EBs is flawed. A bilingual first-grade teacher used closed-ended questions extensively but, rather than take away from the richness of explanations within this classroom, the closed-ended questions actually bridged the links between the verbalization of one's strategy and the action or gesture involved [36]. In one example with a story problem about pencils, the teacher sequenced her closed-ended questions so that students could clearly see how her questions and their answers correlated with what was being enacted upon the pencils [36]. Furthermore, she did not exclusively use closed-ended questions but interrupted her sequence of closed-ended questions with open-ended questions to elicit more extensive responses [36]. Combining the two question types allowed her students to understand how to independently conceive and defend solutions [36].
In contrast to the study that found varying usage of closed-ended and open-ended questions, a study of two middle school mathematics teachers revealed that one of the teachers did not actually position students as independent mathematical thinkers in the community because the teacher did not scaffold their attempts at high-level tasks [4]. At one point, the teacher asked the students to discuss why 12.5% was lower than 1 with their groups, but students were perplexed and had difficulty engaging in conversations. In this instance, this teacher's provision of opportunities for student interaction was an attempted application of the Sheltered Instruction Observation Protocol (SIOP), which is the prescribed teaching model in many states [49]. However, in this episode, there was haphazard application of the guide, resulting in lowered participation from EBs [4]. Although high expectations of students' abilities were imperative to position them as mathematical thinkers, teachers actually aptly positioned their students to attempt rigorous work by giving them closed-ended scaffolding questions [36].
4.1.3. First-order positioning through task selection
Alongside revoicing, a variety of modes of teacher talk were discussed in two of the studies, where teachers did not encourage student participation in discourse by not considering how their talk positioned students or accompanying their talk with rigorous tasks [21,37]. In the first study, the teachers' use of the SIOP strategy of self-talk, where a teacher narrated actions and moves, and think-aloud, where a teacher narrated a thought process, did not facilitate student discussion because it focused on the teacher as the expert [21]. Moreover, Petkova [37] observed the ineffectiveness of SIOP tenets surrounding the style of teacher talk when unaccompanied by high-level questioning. The usage of simplified speech, varying pitch, and slowed tempo did not necessarily increase either student understanding or participation because students did not have opportunities to provide rich explanations and justifications [37]. Though the intention of SIOP tenets, such as providing opportunities to discuss, comprehensible input, and open-ended questions [49], is to deepen student understanding of the content area, using any one of them in isolation or without thought to how it positions students may not yield benefits for EBs.
4.1.4. Second-order positioning through validation of fluid meanings
Two of the studies reviewed [7,34] explored teachers' facilitating mathematics discourse by positioning student communication with fluid word meanings as valid mathematical practice. Moschkovich [34] observed a teacher as she aided two middle school students in reaching a solution to a problem, which showed a table of the number of hours and the distance that a group had traveled at different time points. The teacher asked the students to draw a graph and to answer how far the group traveled in the first and second halves of the day. In discussing the problem, the students verbalized their ideas to one another and referred to graphs they had drawn [34]. In moving fluently amongst systems of words, mathematical symbols, and graphical representations, the students used the phrase "going by" to discuss their strategy and illustrate their engagement in mathematical practice. Furthermore, their definition of this word was fluid and morphed to match their needs in discussing the problem, but this did not cause a lapse in understanding for either the students or the teacher overseeing them [34]. At different times of the problem, the phrase "going by" followed by a number referred to the value of the interval between labeled tick marks on a graph, the number of segments between the labeled tick marks, or the numerical value of the interval contained between two tick marks [34]. The teacher did not see the students' use of vocabulary that was not traditionally recognized as mathematical vocabulary as a problem that needed correcting and did not resist the way they positioned themselves as they attempted to explain the problems to one another. Rather, the teacher asked questions to engage the students more deeply with their mathematical understanding of the problem, showing complicity in the viewpoint that "going by" is appropriate terminology. This study suggested that a teacher might engage students in mathematics discourse by not viewing technical vocabulary as a rigid construct necessary to shape all utterances but might position students' styles of expression as ways of doing mathematics. Even so, the findings from other studies indicate that modeling how to use academic mathematical language may accompany the growth of more sophisticated mathematical problem-solving [7] and that vocabulary development can bridge connections between mathematical thinking and everyday scenarios [45,47]. Moreover, the introduction of sophisticated mathematical vocabulary may enact the understanding that although students' extant communication is valid, the teacher believes in students' capabilities of fluency in multiple registers.
4.1.5. First- and second-order positioning through the use of nonlinguistic resources
In 12 articles, teachers' use of nonlinguistic resources to build meaning in mathematics discourse positioned students in the first order, by enabling their participation, and in the second order, by endorsing their extant practices [7,22,24,26,31,33,34,35,36,39,42,43]. In addition to highlighting students' visual representations to position EBs as mathematically competent in two previous studies [31,43], nonlinguistic resources from the literature included the use of visual representations to teach vocabulary [32,33] and build richer discussion [22], showing the teacher's expectation that students acquire a new register and construct elaborate explanations. For instance, in Celedón-Pattichis and Turner's [22] study, one kindergarten teacher who was encouraging her student to explain her process and who had seen other students use visual representations in the past, supplied her student with a model of a square with dots inside to represent a box of eggs. Because of the model, her student could point to the dots and count them to show how she had completed her subtraction, thereby demonstrating that rich explanations could be pieced together from combined verbal explanation, visual representation, and gestures such as pointing. The teacher both positioned her students through her expectation that they build rich explanations and positioned their use of diagrams to formulate coherent explanations as an appropriate means to do so. Furthermore, the use of physical resources and gestures enabled students of all language backgrounds to interact in the community [7,24,26,33,35,39,42], further demonstrating the teacher's value of these students' potential contributions.
The other nonlinguistic practice that was highlighted in the literature was the teachers' first-order and second-order positioning through the use of gestures to build mathematical meaning [24,26,33,35,39,42]. In a case study of elementary students in an after-school program, Dominguez [24] found that teachers positioned students' current gestures as valid through task selection. The researchers observed that students regulated their own cognition by using gestures to reenact operations from their problems, suggesting that teachers could further legitimize the use of gestures by using numbers that made it conceivable for students to use their fingers to perform actions on the numbers from the problems [24]. Planning tasks to elicit the use of nonlinguistic resources was also an aspect of one kindergarten teacher's practice as she used native language problems with relatable contexts and numerical values that students could physically model [35]. However, it should be noted that using small numbers that allowed for physical modeling of the problem did not detract from the rigor of the problems or expectations of students in this teacher's classroom [35]. She moved beyond the expected arithmetic operations for most kindergarteners to introduce them to and have them perform multiplication and division, showing how her drawing upon nonlinguistic resources fortified high expectations and positioned her students as advanced [35].
Moschkovich's [34] study of a teacher and two middle school students also suggested that gestures, verbalization, and visual representations could jointly work to demonstrate concepts and correct misconceptions, going beyond the scope of the pointing and counting observed by Celedón-Pattichis and Turner [22] and enacting high expectations of students while positioning their practices as valid. One student began by indicating the steepness of the graph he had drawn by moving his arm horizontally and then vertically to show the changes in the x- and y-coordinates, respectively. To correct her student's understanding, the teacher adopted these gestures to represent the x- and y-axes but then introduced a new gesture of holding her thumb and index finger to represent the scale of the axes. Whereas the teacher also utilized pointing and counting to help the student visualize his error, other gestures accompanied the image of the graph and verbal explanation to build students' understanding. Again, gestures were modeled by the teacher and positioned as valid parts of mathematics discourse, while she pressed her students to achieve more accurate understanding.
4.1.6. First- and second-order positioning of out-of-school knowledge
The literature also proposed validating the linguistic resources and outside knowledge of EBs to facilitate their participation in mathematics discourse [1,4,19,20,23,25,27,28,29,31,32,35,36,43]. In three of the articles discussed heretofore, native language use was described to conduct language brokering and make EBs' ideas accessible to the class, thereby positioning those ideas as valuable [28,29,43]. Findings also suggested the potential for native language use in showing the value of home practices [26,27,42,48], making space for students to contribute to discussions [25,32,38] and building mathematical vocabulary as well as mathematics discourse [19]. The value of students' other out-of-school knowledge was represented in teachers' task selection [23,25,26,27,35,36]. Elementary school teachers of EBs bridged the distance between outside knowledge and school in their support of vocabulary development by providing students with authentic contexts for their problems [23,27]. A teacher used the context of a t-shirt factory throughout multiple problems so that students could see the same context over and over, thereby having greater access to the vocabulary and the concepts therein [23]. Authentic contexts also characterized the tasks and problems that two other elementary school teachers provided [35,36] and the problems provided by a researcher, who first interviewed students' parents or the students themselves to learn about their interests and leverage their out-of-school knowledge [25,26]. By doing so, the researcher, who was facilitating an after-school program in an urban area, showed complicity by demonstrating esteem for the same things that the students did. In contrast, a study of two middle school teachers revealed difficulty with validating the cultural and linguistic contexts of students and integrating their contexts with new mathematical knowledge [4].
Finally, to draw on the understandings and prior knowledge of their students, teachers or facilitators from 17 studies drew on grouping or pairing as a strategy to promote discourse through first-order positioning [1,19,23,25,26,28,30,31,33,34,35,36,37,39,41,42,46]. In two instances, teachers positioned students as individuals upon whom their group members or partners should rely by preparing students to aptly communicate in their groups [19,46] One elementary school teacher modeled communication for her students by showing her students how to listen to one another [19]. Another teacher chose to group students with similar language proficiencies together to make space for native language use in her classroom and encourage all students to participate in mathematics discourse [46].
4.2. Teacher's reflexive positioning
As was discussed, a third-grade teacher positioned herself to make space for students to guide classroom learning instead of her [31], but other teachers in three studies also positioned themselves as mathematics learners, bilinguals, and facilitators rather than experts [1,29,35]. Two sixth-grade teachers made deliberate reflexive positioning moves to demonstrate the fluidity of those who held mathematical knowledge within their mathematics discourse community [29]. Though native language was used for language brokering in two of the classrooms described [28,43], one sixth-grade teacher also spoke the native language he shared with his students to position himself as a fellow bilingual learner [29]. Another teacher in the same study also removed herself from the static position of having complete mathematical knowledge by saying that she did not like doing a certain skill in her head, reminding her students that she, too, had to think about mathematics problems and wanted them to do the same [29]. These two teachers positioned themselves as growing learners of language and mathematics, giving students opportunities to see themselves alongside their teachers rather than beneath them in a knowledge hierarchy. However, the two teachers' self-positioning moves were deliberate, unlike the errors made in the English-language explanations of one bilingual high school teacher, whose mistakes in trying to paraphrase a question only confused her students rather than positioning her as a fellow learner [37].
4.2.1. Self-positioning as facilitator rather than expert
Drawing on community resources in task selection and grouping went beyond the use of authentic and relatable contexts and also took the form of entrusting the task of explaining and modeling to the students themselves, while teachers positioned themselves as facilitators, in five of the studies [1,29,31,35]. Even though Hansen-Thomas [29] found that students at beginner stages of English language development took on more peripheral roles, one talkative student with developed knowledge in both Spanish and English was often asked to come up to the board and aid his classmates' comprehension. Whereas the idealized mathematics discourse community aims at equitable participation from all students regardless of their English proficiency, the responsibilities given to this student showed the teacher's comfort with moving into a facilitator role while the students may move into the teacher's role [29]. Lastly, the elementary school teacher, who taught her students how to listen to one another, positioned herself as a connector to help students understand one another's ideas rather than as the provider of the ideas and the only one with sufficient knowledge to guide learning [35]. As a result of teachers' reflexive positioning as facilitators, some students began to reflexively position themselves as teachers in discourse [1].
4.3. Summary and limitations
The findings of this review suggest teachers can interactively position EBs in mathematics discourse by asking them conceptually focused questions and assigning them high-level tasks. In response, students may grow to see themselves as mathematically competent and participate further in classroom discourse. Teachers can further this positioning by drawing on communication, understanding, and ideas that EBs already have. They can group students and use their home language and out-of-school knowledge to make them feel esteemed and prepared to deepen their own understandings. Moreover, even as teachers employ nonlinguistic resources or encourage their usage in discourse, teachers can continue to build students' access to dominant academic discourse by teaching them to convert their ideas to the academic register. Lastly, teachers can reflexively position themselves as facilitators, making space for students to teach one another. A limitation of this review is that discourse beyond the K-12 context is not considered; even so, one goal of this work is that EBs view themselves as participants in the mathematics discourse community and that they will bring their mathematics identity into other spaces, feeling confident in their ability to contribute.
5.
Discussion
The need for researchers to consider how teachers position EBs to learn in a mathematics discourse community and how those students subsequently position themselves is not important because the population of EBs is growing or may even be a majority in U.S. schools one day [5]. The reality that U.S. classrooms do not serve all groups of students, regardless of the size of the population they comprise, makes it necessary for teachers to consider how to empower students from all marginalized groups. Even though research [29,39] has provided insights into how to support EBs, particularly Spanish-speaking students, the existence of students with needs that are not being served warrants future research regardless of how great or small of a group those students form. The findings of this review suggest the following action steps for teachers of EBs and areas of future research.
5.1. Suggestions for educators and potential challenges
Collectively, findings provide two key suggestions for teachers. Teachers must provide high-level tasks and questioning to enact a belief that their students are capable and that their varying proficiencies in English do not mean they cannot think mathematically. If their students seem not to know how to approach tasks, the onus is upon teachers to consider how to help students approach the task, not to lower the rigor. The teacher in Willey's [4] study once randomly implemented an unplanned prompt to have students discuss with their groups why 12.5% was lower than 1. Her groups were largely silent, and to many, her question did not make sense. Rather than deciding her students could not handle the independent reflection, this teacher might have broken down her original question by asking "What do we know about 12.5%?" [4, p. 109]. The teacher might have asked students to draw a representation of 12.5% to illustrate how it was lower than 1 as did the teacher who drew dots to represent chocolate eggs [22]. Aligning with the findings of Turner and colleagues [43] and Musanti and colleagues [36], this review recommends that teachers employ native language, nonlinguistic resources, scaffolding questions, and any other means to position their students as capable of advanced mathematics.
The review also suggests that teachers observe and seek knowledge of what students already know and how they participate in discourse to help teachers strengthen their growing knowledge and communicative practices. Though their identities have traditionally been cast as incompatible with learning and doing academic mathematics [15], EBs have knowledge, culture, and communicative practices that teachers must incorporate in their facilitation of discourse. By taking time to confer with students privately about their understanding [4], seeking out knowledge of student interests through interviews with them and their parents [25], and introducing, mirroring, and building upon students' use of nonlinguistic resources, teachers can build upon the strengths their students already have.
It should be noted that it may be challenging for teachers to implement these moves in their classrooms because of the difficulty of acting as a language broker for EBs as a monolingual teacher [3] or the difficulty of focusing on collaborative discourse in the era of high-stakes testing [50]. Possible professional development ideas might focus on how monolingual teachers can invite translanguaging into the classroom, including building their comfort level with this practice. Furthermore, in the era of high-stakes testing, teachers and school communities often put an emphasis on independent work and building student stamina for testing rather than building their discourse in the classroom [50]. Therefore, professional development can also focus on the inherent value of promoting discourse and belonging amongst EBs in U.S. classrooms as well as its potential to aid students' performance levels on standardized assessments.
5.2. Limitations and areas of future research
In this review, I described instructional moves that teachers can use to facilitate EBs' participation in mathematics discourse and mathematics discourse communities. I also identified some starting points for teachers of EBs to start building mathematics discourse within their classrooms. The review also demonstrates the value of positioning theory as a way to conceive how diverse students participate in mathematics classrooms. Enyedy and colleagues [28] as well as Turner and colleagues [43] have shown how positioning theory can be used to identify modes of facilitating agentive participation from diverse students. Future studies might also consider the positioning moves that teachers deploy in building discourse communities amongst EBs. Furthermore, the state of the literature is not at a point where different strategies can be advocated for students of different age groups, urban as opposed to rural environments, or classrooms with varying proportions of English-proficient and EBs. Out of the 30 studies, only 5 occurred in a high school, suggesting that a future direction for research is a more extensive study of older EBs. Moreover, the vast majority of the studies took place in urban environments, while EBs can be found in many different areas of the U.S. Finally, in the current U.S. context, K-12 settings can look different from school to school. While one class may be entirely populated with EBs, another class might only have a small percentage. Regardless of students' age or whether EBs' needs represent a majority or minority, teachers and researchers must continuously consider EBs' positionings, working to overturn extant inequities of access and considering how to ensure that their positioning moves do not create new inequities.
Use of Generative-AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors assert that they do not have any conflicts of interest.
Ethics declaration
The author declared that no ethics approval is required for the study.









 DownLoad:
DownLoad: