Bayesian extreme value modelling of annual maximum monthly rainfall in Somalia from 1901 to 2022

1.   Introduction

Extreme weather events, including heavy and low rainfall, are increasingly linked to climate change, giving rise to a spectrum of natural disasters such as floods, droughts, and ecological disruptions. These events, in turn, have profound impacts on human daily life and economic well-being. Numerous climate models predict a rise in extreme weather events due to global warming ^[1]. Hotter temperatures, heatwaves, and intense rainfall events are expected to become increasingly common, as highlighted by the United Nations Intergovernmental Panel on Climate Change (IPCC) in February 2023 ^[2].

Somalia, in particular, has witnessed a series of extreme weather-related catastrophes, including prolonged droughts, devastating floods, and locust invasions. Extreme rainfall frequently leads to perilous river overflows and flash floods. UNHCR reported that over 650,000 Somalis were displaced by river overflows and flash floods triggered by extreme rainfall in 2020, with Hirshabelle and southwest states among the hardest-hit regions ^[3]. The years 2018 and 2019 witnessed the displacement of an estimated 281,000 and 416,000 individuals from their homes, respectively. FAO reported that approximately 15,000 hectares were submerged under floodwaters in 2018, including 3500–4500 hectares of cultivated cereals ^[4]. Furthermore, floods destroyed approximately 500 tons of sorghum stored in underground pits. These recurring weather-related calamities have severe repercussions for societies heavily reliant on agriculture, particularly farming and livestock, for their livelihoods. These extreme events underscore the importance of meteorological, hydrological, and climate information for disaster risk reduction and early warning systems in Somalia ^[5]. Changes in the human-flood distance can mitigate flood fatalities and displacements, emphasizing the critical need for flood protection measures, especially in areas lacking adequate mitigation works ^[6]. The development of effective early warning systems in Somalia is critical for fostering livelihood resilience and preventing loss of lives and properties ^[5]. Therefore, it is recommended that Somalia implement further strengthening of existing disaster risk reduction and early-warning-system mechanisms at the national and regional levels through an integrated and cross-sectoral approach ^[5].

Extreme environmental events profoundly impact both a country's communities and its economy ^[7]. While these events may seem unpredictable, the consequences of extreme rainfall events can be mitigated through proactive measures informed by statistical analysis of extreme rainfall data ^[8]. The unpredictability of the events can be understood through the concept of predictability-time-windows ^[9]. Within a specific time-window, such as 10 minutes for high-resolution storm events, rainfall intensity can be predicted with a certain accuracy. Beyond this time-window, the predictability diminishes, and assumptions like persistence models become more relevant, where each value is assumed to be equal to the next. This underscores the importance of timely and accurate meteorological information for effective disaster preparedness and response strategies.

The behaviors of rainfall and extreme rainfall, both short-term and long-term, are crucial for understanding their impacts ^[10]. The fractal analysis quantifies short-term behavior through parameters like fractal dimension (D), indicating roughness ^[11]. A higher D signifies smooth behavior with more stable patterns, while a lower D suggests rough behavior with frequent changes. Long-term behavior is assessed by the Hurst parameter H, revealing the persistence and clustering of wet and dry periods ^[12]. An H value close to 0.5 denotes randomness, while values near 1 indicate strong memory and high dependence between periods ^[13]. Simulation of short-term (fractal) and especially long-term (persistence) behaviors of rainfall often challenges Markov Chain models. Therefore, a stochastic synthesis framework proposed by Dimitriadis and Koutsoyiannis (2018, section 4.2) ^[14] can be explored, which explicitly preserves these behaviors and marginal moments, including heavy-tail distributions representing the marginal probability distribution of the process.

In the last decades, numerous studies have been undertaken to study extreme weather events in various regions of the world ^{[15,16,17,18,19,20,21,22]}. A substantial historical dataset of extreme rainfall is essential to conduct such extreme value analysis. However, like many other countries, Somalia faces limitations in obtaining such data. In such cases, a Bayesian approach is often employed to estimate parameters for the generalized extreme value distribution (GEVD) and generalized Pareto distribution (GPD) ^[1,23,24]. Bayesian-based GEVD and GPD models offer the advantage of incorporating prior information through prior distributions. Previous research has utilized Markov chain Monte Carlo (MCMC) simulations to address computational challenges inherent in Bayesian-based approaches ^{[24,25,26,27,28]}.

Despite the existing studies on Bayesian extreme value modeling, research specific to Somalia remains limited ^[29,30]. This paper aims to analyze patterns in extreme rainfall data using Bayesian-based GEVD and GPD models. By examining the annual maximum average monthly rainfall in Somalia, this study seeks to enhance understanding of both short-term variability and long-term trends in extreme weather, contributing to improved disaster preparedness and mitigation strategies.

2.   Materials and methods

2.1.   Study area

The area of study is Somalia (located at approximately 5.5941182°N, 47.2192383°E), a country situated on the Horn of Africa, a peninsula in the northern region of Africa. Somalia shares its borders with Djibouti to the northwest, Ethiopia to the west, Kenya to the southwest, the Indian Ocean to the east and south, and the Gulf of Aden to the north. Somalia covers an area of 637,657 square kilometers and is home to approximately 12,000,000 inhabitants, with a population density of around 25 people per square kilometer. It boasts a coastline that stretches for 3025 kilometers, making it the longest coastline in Africa. Mogadishu serves as both the largest city and the capital of Somalia.

The northern region of Somalia is characterized by its mountainous terrain, with elevations ranging from 900 to 2000 meters above sea level. In contrast, the southern and central areas are predominantly flat, consisting mainly of plateaus with elevations of less than 180 meters above sea level. Somalia's geographical extremes include its lowest point, which lies at sea level in the Indian Ocean, and its highest point, Mount Shimbiris, which reaches an elevation of 2416 meters. The arid and semi-arid lands (ASALs) in Somalia, constituting over 80% of the nation's land area, are inherently susceptible to extreme weather conditions such as elevated mean surface temperatures, prolonged droughts, unpredictable rainfall patterns, and intense winds ^[31].

Within Somalia's meteorological landscape, the country experiences an arid and semi-arid climate that exhibits significant variations in both space and time. The primary climatic features include distinct wet and dry seasons, coupled with minimal temperature variations. Daily temperatures typically range from 24℃ to 30℃, with exceptions in higher altitude areas and along the coastline.

Rainfall holds crucial importance in Somalia's meteorology, significantly influencing livelihoods. Rainfall patterns exhibit substantial spatial and temporal variations. Agriculture production is heavily reliant on these variations, both between seasons and within seasons. Nevertheless, Somalia generally receives low rainfall with high variability. The northeastern regions typically receive less than 100 mm of annual rainfall, while the central plateaus receive an average of 200 to 300 mm. In contrast, the southwest and northwest regions receive approximately 500 to 600 mm of annual rainfall.

Flooding in Somalia manifests in two main forms: river floods and flash floods. River floods occur along the Juba and Shabelle rivers in southern Somalia, while flash floods are prevalent along intermittent streams in the north. Recent years have witnessed an increase in the frequency and intensity of flooding events in the country, resulting in loss of human life and significant economic damage.

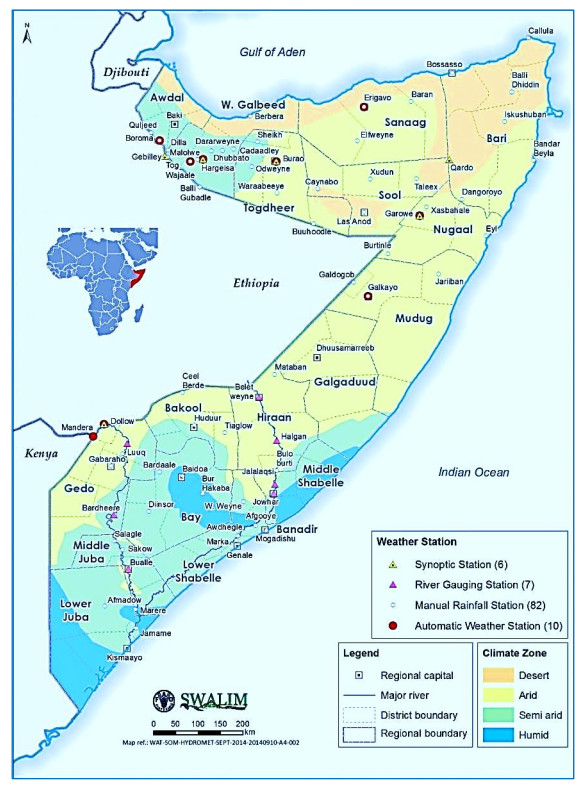
It is important to note that the country currently has 6 synoptic stations, 7 river gauging stations, 82 manual rainfall stations, and 10 automatic weather stations (see Figure 1). Most of the rainfall stations have data gaps spanning from 1991 to 2002 as a result of the collapse of the central government in 1991. Therefore, the available data from these stations is temporally limited and, for this reason, they cannot be used in this study for modeling and forecasting extreme rainfall events.

2.2.   Data description and source

The data utilized for the analysis in this study comprises high-resolution monthly gridded rainfall data obtained from the merged satellite-gauge product known as the Climatic Research Unit Time Series 4.0 (CRU TS 4.0) ^[32], with a spatial resolution of 0.5° × 0.5°. This dataset stands as a cornerstone in climate modeling research due to its widespread use. Over an extended timeframe, CRU TS 4.0 provides the most reliable estimates of month-to-month rainfall variations.

The CRU TS 4.0 dataset considered in this study covers the period from 1901 to 2022 and has been sourced from the Climate Knowledge Portal of the World Bank Group (https://climateknowledgeportal.worldbank.org). The creation of CRU TS 4.0 involves interpolating monthly climatic anomalies derived from an extensive network of weather station records. Prior to its release, CRU TS 4.0 undergoes a stringent quality control process. This process includes updating historical data from multiple weather stations, filling in missing records, addressing outliers, and implementing various data refinement procedures (refer to Harris et al. ^[32] for details).

Given the unavailability of continuous, long-term meteorological data with comprehensive spatial coverage within Somalia, the high-resolution gridded rainfall data (CRU TS 4.0) are employed as an alternative and previously scrutinized data source. Leveraging the extensive historical record of this rainfall-gridded dataset, we are equipped to proceed with estimating the parameters of the GEVD and GPD models employed in the present study.

While the CRU TS 4.0 dataset is a valuable resource for climate research, it is important to acknowledge potential limitations and biases that could impact the study results. The dataset's spatial resolution of 0.5° × 0.5° may be too coarse to capture localized extreme rainfall events accurately, potentially leading to underestimation or overestimation of rainfall extremes in specific areas. The interpolation methods used to create CRU TS 4.0 rely on available weather station data, which may be sparse in certain regions, including Somalia, introducing biases if the spatial distribution of stations is uneven or if there are significant data gaps. The quality of historical weather station data can vary, with issues such as changes in station locations, instrumentation, and observation practices over time introducing inconsistencies and potential biases. Additionally, the dataset may not always accurately capture the most extreme rainfall events due to the limitations of the interpolation methods and the resolution of the underlying data. These limitations could influence the precision of the estimated parameters of the GEVD and GPD models. However, by using a comprehensive and well-established dataset like CRU TS 4.0, we aim to mitigate some of these challenges and provide robust estimates of extreme rainfall events. Future studies could benefit from higher-resolution datasets and improved interpolation techniques to address these limitations further.

2.3.   Extreme value theory

The methodology and all of the formulae in this section are based on Coles ^[24]. Extreme value theory (EVT) is a statistical technique used to describe extreme events' asymptotic behavior. The block maxima method is a popular approach in EVT. Block maxima refers to the maximum value of observations in a length of the interval, T. The choice of the block is often made on an annual, monthly, or seasonal basis, with each block containing only one observation. As a consequence, independent and identically random variables appear. The following equation gives the GEVD as the limiting distribution of the block maxima:

where z represents the data, μ represents the location parameter ($-\infty < \mu < \infty$), σ represents the scale parameter ($\sigma > 0$), and $\xi$ stands for the shape parameter ($-\infty < \xi < \infty$). The GEVD studies the combined extreme value distributions of Weibull ($\xi < 0$), Gumbel ($\xi = 0$), and Fréchet ($\xi > 0$). Thus, the differences in the generalized extreme values of the three classes highlighted are determined by the value of shape parameter ξ only. Another popular technique in EVT is peaks over threshold (POT). The data that surpasses the threshold, u, is modeled by GPD which has the cumulative distribution:

where y > 0, and $\stackrel{~}{\sigma } = \sigma +\xi \left(u-\mu \right)$. The GPD consists of three types of distributions: exponential distribution ($\xi = 0$), ordinary Pareto distribution ($\xi > 0$), and Pareto-Ⅱ-type distribution ($\xi < 0$). In this study, we used a threshold of 30 mm to analyze the extreme rainfall data as the parameter estimates of the GPD become stable at u = 30 mm. For assessing the validity of GEVD and GPD models, probability plots, QQ plots, return level plots, and density plots can all be used. If the model is appropriate for the data, then the probability plot, QQ plot, and return level plot will be roughly linear and the fitted density plot will be approximately the same as the actual density of the data.

Estimates of the extreme quantiles of annual maxima are particularly useful in environmental extremes because they provide an estimate of the level that the process is likely to exceed once every n years on average. For GEVD, these quantiles are calculated as follows:

The quantity ${q}_{p}$ is the return level associated with the 1/p-year return period. It can be defined as the level that is expected to be exceeded on average once every 1/p years, or more precisely, the level exceeded by the annual maxima in any year with probability p. For GPD, the N-year return level is given by the formula:

where n_y is the number of observations per year and ${\zeta }_{u} = \mathit{Pr}\left(X > u\right)$, which has the natural estimator $\widehat{{\zeta }_{u}} = k/n$, the sample proportion of points exceeding u.

2.4.   Bayesian approach

The methodology and all of the formulae in this section are based on Coles ^[24] and Smith ^[27]. The Bayesian method enables us to make inferences from the likelihood function when the sample size of the annual maximum time series is small. As shown by Koutsoyiannis ^[33], even with larger samples of 100 years or more, estimating the shape parameter based on a single series is extremely difficult. Bayesian analysis has the advantage of reducing these drawbacks because it enables prior information to be incorporated into the likelihood to increase estimation reliability. Therefore, this study adopted the Bayesian approach as recommended by Annazirin et al. ^[34], Lazoglou and Anagnostopoulou ^[35], and Ahmad et al. ^[36]. As per this method, unlike the maximum likelihood estimation, a parameter of a distribution is not an undefined constant but is viewed as a random variable with zero mean and a certain variance with a prior probability density function $f\left(\theta \right)$.

If we suppose the data $x = \left({x}_{1}, ..., {x}_{n}\right)$ as independent realizations of a random variable with a density from the parametric family $F:\left\{f(x; \theta):\theta \in \Theta \right\}$, the Bayes Theorem states:

where $f\left(\theta \right)$ is the prior distribution, $f(\theta /x)$ is the posterior distribution, and $f(\theta /x) = \prod\limits_{i = 1}^n {f({x_i}/\theta)}$ is the likelihood. The EVT's function is to describe the observed process extremes in order to find the probability of future occurrence of extreme events. There are good reasons to choose Bayesian procedures if an appropriate prior can be specified. However, the denominator in (5) can be computationally complex in the case of several parameters such as the GEVD. MCMC is usually adopted to overcome this issue, using multiple simulations ^[37]. MCMC methods give the means to simulate complicated distributions by simulating from Markov chains that have the intended distributions as their stationary distributions. The Gibbs sampler is one type of MCMC method that offers a way to simulate multivariate distributions, given that it is possible to simulate full conditional distributions ^[37,38]. Simulating from these full conditions might not be easy, but Metropolis-Hastings systems offer a guide. These systems are based on studies by Metropolis et al. ^[39] and Hastings ^[40]. Suppose $\pi$ is a distribution of interest such that a reversible Markov chain, which has a stationary distribution, can be created. Simulating from such a reversible Markov chain can result in values from $\pi$.

The method is to create a transition kernel p ($\theta$, $\phi$) such that the distribution of the chain's equilibrium is $\pi$. This transition kernel is composed of two elements: the arbitrary transition q ($\theta$, $\phi$), also described as the distribution of the proposal, and the probability of acceptance a ($\theta$, $\phi$) defined as:

This was proposed by Hastings (1970). To find a chain with limiting distribution $\pi$, we use the following algorithm:

Step 1: Initialize the counter to j = 1 and the chain's state to θ⁽⁰⁾.

Step 2: Using the kernel $q\left({\theta }^{(j-1)}, \phi \right)$, simulate a proposed value $\phi$.

Step 3: Obtain the probability of acceptance of the proposed value $a\left({\theta }^{(j-1)}, \phi \right)$.

Step 4: With probability $a\left({\theta }^{(j-1)}, \phi \right)$, accept ${\theta }^{\left(j\right)} = \phi$ and otherwise take ${\theta }^{\left(j\right)} = {\theta }^{(j-1)}$.

2.4.1.   Prior specification

According to Coles, even if there is no prior information to work with, determining a prior distribution is an essential part of any Bayesian analysis ^[24]. In such cases, it is common to use priors with a high variance—or, to put it another way, priors that are near-flat—to represent the lack of genuine prior knowledge. There is a lot of literature on this subject, but in practice, studies are not typically sensitive to prior distribution choices with a wide enough variance. Sensitivity analysis may be used to analyze this aspect of any issue. Suppose the likelihood function for the maximum rainfall analysis is the GEVD given by:

where Z_i is the annual maxima for the year indexed by i. We might use the following prior density function with $\phi = \mathit{log}\sigma$:

where ${\pi }_{u}\left(\mu \right)$, ${\pi }_{\phi }\left(\phi \right),$ and ${\pi }_{\xi }\left(\xi \right)$ are normal density functions with zero means and ${v}_{\mu }$, ${v}_{\phi, }$ and ${v}_{\xi }$ are variances, respectively. The reason for using $\phi = \mathit{log}\sigma$ is that it is a simpler parameterization for preserving the positivity of $\sigma$. When the variance parameters are sufficiently large, the prior density (8) refers to the prior independence specification in the parameters of $\mu$, $\phi,$ and $\xi$, which can be rendered to be nearly flat. We used ${v}_{\mu } = {v}_{\phi } = \mathrm{10,000}$ and ${v}_{\xi } = 100$ for this analysis.

2.4.2.   MCMC algorithm

It is essential to select an MCMC algorithm for inference. We adopt a Metropolis$-$Hastings MCMC sampling scheme, in which the individual components of the vector $\left(\mu, \phi, \xi \right)$ are considered. We denote the resulted transition densities by ${q}_{\mu }$, ${q}_{\phi }$, and ${q}_{\xi }$ and we specify a random walk procedure to generate the proposed values, i.e.,

with ${\epsilon }_{\mu }$, ${\epsilon }_{\phi, }$ and ${\epsilon }_{\xi }$ being normally distributed random variables with zero means and variances ${w}_{\mu }$, ${w}_{\phi, }$ and ${w}_{\xi },$ respectively. The algorithm and its tuning parameters do not affect the model. However, it affects the algorithm's performance. The parameters of the algorithm were tuned to strive for a 30 percent overall acceptance performance. For GEVD, the values ${w}_{\mu }$ = 4.34, ${w}_{\phi }$ = 0.16, and ${w}_{\xi }$ = 0.19 were found to function fairly well in this data after some trial and error. For GPD, ${w}_{\phi }$ = 0.115 and ${w}_{\xi }$ = 0.07 were used.

2.5.   Model selection criteria

The assessment of the selection of the Bayesian-based GEVD and GPD overall fits is based on the deviance information criterion (DIC) ^[41]. The DIC is the generalization of the Akaike information criterion (AIC) for hierarchical modeling. It is especially useful in Bayesian model selection problems where the models' posterior distributions were obtained via MCMC simulations. DIC, like AIC, is an asymptotic approximation as the sample sizes get larger. The DIC is given by:

where y is the data, $\overline{D}\left(y, \theta \right)$ is the posterior mean deviance, and $D\left(y, \overline{\theta }\right)$ is the deviance at the posterior mean of $\theta$. The value of DIC is valid only when the posterior distribution is close to the multivariate normal distribution.

Prediction errors such as mean squared error (MSE) and mean absolute error (MAE), as well as k-fold cross-validation errors (MSE, MAE), were also considered to assess model performance. MSE is calculated as:

where ${y}_{i}$ are the observed values, $\widehat {{y_i}}$ are the predicted values, and n is the number of observations.

MAE is calculated as:

where $|·|$ denotes the absolute value.

In k-fold cross-validation, MSE and MAE are computed similarly across different folds of the data, providing an average performance metric across the validation process.

2.6.   Software used for data analysis

Data analysis was performed using the R statistical software, an open-source programming language widely used for statistical computing and graphics. Specifically, the extRemes 2.0 package was utilized for extreme value analysis ^[42]. The extRemes package provides a comprehensive suite of tools for the analysis of extreme values in environmental data. This includes functions for fitting extreme value distributions to data, calculating return levels, and conducting various diagnostics to assess model adequacy. In our study, we employed this package to analyze the extreme values of monthly rainfall data, allowing us to better understand the frequency and magnitude of extreme events within our data.

3.   Results and discussion

3.1.   Results

3.1.1.   Descriptive analysis

In this section, we conducted a detailed examination of the statistical properties of monthly rainfall data spanning from 1901 to 2022. These findings lay the foundation for subsequent Bayesian analysis. Table 1 (below) presents a comprehensive summary of key statistics for monthly rainfall (in millimeters) during the study period. The average monthly rainfall is calculated at 22.21 mm, representing a central tendency measure. The highest recorded monthly rainfall occurred in November 1961, reaching an impressive 125.66 mm, showcasing extreme variability. Conversely, the lowest reported monthly rainfall was observed in February 1967, with a mere 0.77 mm, highlighting the occurrence of extremely dry periods. Skewness, a measure of the data's asymmetry, stands at 1.50, indicating substantial positive skewness. This confirms that the distribution of monthly rainfall is highly skewed toward higher values. The estimated excess-kurtosis coefficient (kurtosis minus 3), measuring the data's peakedness, stands at 2.10. This value suggests a leptokurtic distribution, implying that the distribution has heavier tails and is more prone to extreme values.

The Hurst exponents calculated for the rainfall in Somalia showed values consistently above 0.5, indicating a degree of long-term persistence in the data. Specifically, the corrected empirical Hurst exponent of 0.562 was obtained, suggesting a slight but noticeable positive autocorrelation, meaning that periods of high rainfall are moderately likely to be followed by similar periods, and the same for low rainfall. This persistence points to a tendency in the rainfall patterns to maintain their behavior over time. The corresponding fractal dimensions, derived as D = 2 – H, range from approximately 1.39 to 1.46, reflecting moderate roughness and complexity. This complexity indicates that while the rainfall patterns are somewhat predictable in their persistence, they still exhibit significant variability and irregularity typical of natural phenomena.

To gain a more intuitive understanding of the monthly rainfall distribution, we present Figure 2, which displays the histogram of monthly rainfall. This graphical representation visually confirms the data's right-skewed nature, aligning with the skewness measure. The presence of heavier tails in the distribution is evident, further emphasizing the occurrence of extreme values.

Moreover, Figure 3 provides insights into the seasonal variability of monthly rainfall in Somalia from 1901 to 2022. The observed pattern reveals a rise in monthly rainfall from March to May and again from September to November, indicating distinct wet periods. Conversely, the monthly rainfall experiences a decline from December to February and from June to August, representing dry intervals. This observed pattern underscores the suitability of EVT in analyzing extreme rainfall events in Somalia.

3.1.2.   Bayesian analysis

In the following section, we leverage Bayesian estimation techniques to analyze and model rainfall extremes. Specifically, we focus on the GEVD and the GPD. These distributions are essential for characterizing extreme rainfall events.

Table 2 presents parameter estimates obtained through Bayesian estimation by fitting the GEVD model to annual maximum rainfall data. The parameter values, derived from the posterior means of MCMC samples, closely approximate maximum likelihood estimates due to the utilization of nearly flat and minimally informative priors. The estimated shape parameter (ξ) is observed to be close to zero, indicating a distribution close to the Gumbel type, as supported by the confidence interval that encompasses zero, suggesting symmetry in the tail behavior of the distribution.

For GEVD parameters, Bayesian inference using MCMC methods was employed to approximate the posterior densities, as depicted in Figure 4. The MCMC analysis was performed using the Metropolis-Hastings algorithm, which iterated 50,000 times in total. To ensure robust inference, the first 10,000 iterations were discarded as burn-in periods, during which the chains stabilized and reached convergence. Following this initial phase, the remaining 40,000 iterations were retained as realizations of the posterior's marginal distributions. Sensitivity analyses were conducted using different initial points to verify convergence across chains. All chains converged to consistent locations within the first 10,000 iterations, confirming the reliability and stability of the Bayesian estimates for the GEVD parameters.

The objective of fitting a statistical model to the annual maxima was to draw conclusions about the distribution parameters. Diagnostic plots were used to assess the adequacy of the Bayesian GEVD model. Figure 5 presents four diagnostic plots including a quantile-quantile plot, probability plot, density plot, and return level plot—which collectively indicate a satisfactory fit of the Bayesian GEVD model to the annual maxima. These diagnostic assessments are essential for validating the model's assumptions and ensuring its appropriateness for describing the distribution underlying the annual maxima.

Samples from the posterior distribution of return levels were generated by substituting observation vectors from the marginal posterior distributions with values in the range 0 < p < 1 into equation (3). This method was applied for probabilities of p = 0.10, 0.02, and 0.01 to estimate the posterior distributions of return levels corresponding to 10, 50, and 100 years. Figure 6 displays plots of the posterior densities, illustrating the distributions of return levels across these different return periods. These posterior distributions provide probabilistic estimates of extreme event magnitudes, incorporating uncertainties from the Bayesian framework used in the analysis.

Due to the positive skew observed in the posterior distributions, as depicted in Figure 6, the posterior medians are considered more suitable measures than the posterior means. Table 3 presents the posterior medians and their corresponding 95% credibility intervals for the 10-, 50-, and 100-year return levels. These intervals reflect the uncertainty in the estimation of extreme event magnitudes under a non-informative prior assumption. Notably, as indicated in Table 3, the return levels increase steadily with longer return periods. For instance, the 10-year return level has a posterior median of 94.383 mm with a 95% credibility interval ranging from 87.033 mm to 106.230 mm, while the 100-year return level shows a posterior median of 140.815 mm with a broader interval from 117.571 mm to 195.386 mm.

The Bayesian approach can also be effectively applied to the GPD. Similar to the procedure used for the GEVD, a random walk method serves as the proposal density function, while independent normal density functions act as the priors. This approach facilitates the estimation of GPD parameters through MCMC sampling. The parameter estimates, represented by the posterior means, are detailed in Table 4. Given the use of non-informative priors, the posterior means are anticipated to be very similar to the maximum likelihood estimates for the GPD parameters. This similarity underscores the minimal influence of the priors on the parameter estimates, thereby allowing the observed peaks over the threshold to primarily inform the posterior distributions.

Figure 7 depicts the estimated MCMC posterior densities and trace plots for the parameters obtained from fitting the GPD model to the peaks over the threshold using Bayesian estimation. The trace plots demonstrate the sampling paths of the parameters throughout the MCMC iterations, allowing for the assessment of convergence and mixing behavior. In this analysis, the Metropolis$-$Hastings algorithm was employed, and it was observed that all chains converged to the same parameter locations within the first 10,000 iterations. This convergence indicates that the algorithm successfully explored the posterior distributions and that the subsequent samples can be considered reliable representations of the true posterior densities. The posterior density plots provide a visualization of the distribution of parameter estimates, showing their central tendencies and spreads. These plots are crucial for understanding the uncertainty and variability in the parameter estimates derived from the Bayesian framework.

The diagnostic plots in Figure 8, including the quantile-quantile plot, density plot, return level plot, and probability plot, collectively validate the fitted Bayesian GPD model. The near-linear alignment in the quantile-quantile and probability plots indicates that the empirical data closely follows the theoretical distribution. The return level plot demonstrates that the model provides reasonable estimates for various return periods. However, the density plot shows some deviation between the predicted density and the observed data histogram, suggesting slight discrepancies. Despite this deviation, the overall diagnostic plots confirm that the Bayesian GPD model is generally well-calibrated and reliable for modeling extreme rainfall events.

To examine the effects of the non-informative prior on the return levels, we produced posterior density plots. These plots were generated by replacing observation vectors from the marginal posterior distributions of the location parameter (μ) and the scale parameter (σ) with values in the range 0 < p < 1. Specifically, this procedure was performed for probabilities p = 0.1, 0.02, and 0.01 to obtain the posterior distributions of the 10-year, 50-year, and 100-year return levels, respectively. Figure 9 displays the posterior density plots for these return levels under the non-informative prior assumption. These plots illustrate the uncertainty and variability in the estimated return levels, providing insights into the likely range of extreme rainfall events over different return periods.

Given the slight positive skewness observed in the posterior densities, we opted to use posterior medians rather than posterior means for our analysis. Table 5 presents the posterior medians and corresponding 95% credibility intervals for the 10-year, 50-year, and 100-year return levels using a non-informative prior in the GPD model. As the return period increases, the 95% credibility intervals slightly widen, reflecting increased uncertainty in the estimates due to fewer extreme events occurring over longer periods. This phenomenon is evident in the quite widening of the intervals from the 10-year to the 100-year return levels. The GPD model produced precise return levels and narrower credibility intervals compared to the GEVD, indicating reduced uncertainty associated with the estimated return levels. This precision is advantageous in assessing and planning for extreme events, ensuring reliable inference even in the presence of skewed distributions or limited data points.

3.1.3.   Comparative analysis

To determine the most suitable model between the GEVD and the GPD with Bayesian estimation for modeling extreme rainfall events in Somalia, we utilized multiple criteria. First, the deviance information criterion (DIC) was employed as a measure of model goodness of fit and complexity. Table 6 illustrates that the GEVD model exhibits a significantly lower DIC value compared to the GPD model (3130.044 vs. 9524.425, respectively). This indicates that the GEVD model provides a better balance between fit and complexity, suggesting superior performance in capturing the extreme tail behavior of rainfall distributions.

Further analysis of prediction errors and validation errors supports this finding. For instance, the mean squared error (MSE) and mean absolute error (MAE) from k-fold cross-validation (k = 5) were computed for both models. The GEVD model demonstrates lower prediction errors across both MSE (756.523) and MAE (21.261) compared to the GPD model (MSE = 957.576, MAE = 24.561). These results reaffirm that the GEVD model more accurately predicts extreme rainfall values, which is essential for long-term risk assessments and infrastructure planning in Somalia.

Figure 10 illustrates the observed values versus predicted values for rainfall extremes using block maxima and peaks-over-threshold methods. This figure visually represents how well each model—GEVD and GPD—captures extreme rainfall events. Ideally, the plot would show a close alignment of observed and predicted values, especially in the tail regions where extreme events occur. The GEVD model exhibited a closer fit to observed extreme values compared to the GPD model. This alignment is crucial for ensuring the reliability of predictions related to rare but severe weather events, infrastructure resilience, and flood management strategies.

3.2.   Discussion

This study aimed to model and predict annual maximum monthly average rainfall in Somalia by employing and comparing two statistical distributions, the GEVD and the GPD with the Bayesian approach. To estimate the parameters of these distributions, the study leveraged the MCMC technique, specifically utilizing the Metropolis–Hastings algorithm. An important aspect of this analysis was tuning the algorithm's parameters to achieve an acceptance rate of 0.3. According to Gamerman, the acceptance rate is recommended to fall within the range of 0.2 to 0.5, and the attainment of this rate suggests the efficiency of the proposed distribution ^[43]. To further justify the significance of this rate, it is important to consider its impact on algorithm efficiency and computational performance. Exploring alternative approaches, such as machine learning methods or advanced optimization techniques, may potentially yield improvements in achieving higher acceptance rates or optimizing the algorithm's performance metrics. These avenues warrant further investigation to enhance the effectiveness of the proposed distribution and its application in practical scenarios.

The results of this study reveal that the Bayesian GEVD model fits the data well and can be effectively employed to forecast extreme rainfall events in Somalia. This finding is in accordance with prior research, such as that conducted by Ahmad et al. ^[36], which supports the suitability of the GEVD for modeling extreme events in diverse contexts. Mohamed and Adam ^[29] also found that the GEVD is the best model for rainfall extremes in Somalia, emphasizing its robustness in capturing the magnitude and frequency of extreme rainfall.

Nonetheless, the choice of priors in Bayesian analysis requires careful consideration, especially in data-scarce environments like Somalia. Due to the lack of informative priors for this specific application, we employed non-informative and independent priors to estimate posterior densities. Non-informative priors are chosen to let the data primarily influence the posterior distribution, minimizing the introduction of subjective biases. This is particularly relevant when prior information is scarce or uncertain, ensuring that the resulting posterior is driven mainly by the observed data. However, it is crucial to recognize the potential impacts of this choice. Non-informative priors can lead to broader posterior distributions, reflecting higher uncertainty, but they are also more objective in the absence of strong prior knowledge. This approach is justified in our context as it allows a more transparent and data-driven inference process. When applying non-informative priors to the Bayesian analysis, it becomes evident that the return level densities exhibit a right-skewed distribution. This skewness may be attributed to the model's inherent uncertainty in estimating upper return levels, particularly for longer return periods. This phenomenon is consistent with the findings of Coles and Tawn ^[44], who noted that such skewness may arise when the model struggles to provide precise estimates for higher return levels, while lower return levels are more confidently estimated.

One of the key advantages of Bayesian analysis is its capacity to quantify uncertainty ^[27]. This is especially valuable in providing more accurate insights into what is likely to occur in a given year based on historical data. This quantification of uncertainty is achieved through various steps. These steps include the transformation of the sequence of simulated values $\left({\mu }_{i}, {\sigma }_{i}, {\xi }_{i}\right)$ and the extraction of a sample from the corresponding distribution of return levels ^[1]. This process enhances the precision of predictions and risk assessments, making it a valuable tool for decision-making in fields such as disaster preparedness and resource allocation.

In this study, particular attention was given to posterior median return levels, as they tend to minimize expected loss when compared to posterior mean return levels ^[45]. By calculating posterior medians along with their associated 95 percent credibility intervals, the study gained a more comprehensive understanding of the maximum rainfall return levels for Somalia. This information can prove invaluable for risk management and resource planning in the face of extreme weather events.

Furthermore, the study investigated the behavior of return levels as return periods increased. Notably, the study found that the widths of the credibility intervals for return levels expanded as return periods lengthened. This observation aligns with previous research, highlighting the increasing uncertainty associated with longer-term predictions. This underscores the importance of considering a wide range of scenarios and potential outcomes when planning for extreme rainfall events in Somalia.

Another significant finding of this study pertains to the efficiency of the GEVD over the GPD, particularly in modeling rainfall extremes. The GEVD was applied to block maxima (annual maxima), while the GPD was applied to peaks over threshold (POT) to capture the extreme rainfall tails ^[46]. Consequently, the GPD was observed to underestimate data points in some instances and overestimate them in others when extreme values were present in the data. This discrepancy contributes to the Bayesian GPD exhibiting a higher DIC value compared to the GEVD, along with elevated prediction and validation errors. However, the GPD excels in estimating return levels with precision compared to the GEVD model. For example, for a 100-year return period, the GPD estimated a quantile of 119.215 mm, whereas the GEVD provided a higher estimate of 140.815 mm, potentially indicating overestimation. The GPD's precision in return level estimation improves with longer return periods, highlighting its utility in Somalia for accurately assessing high return levels crucial for risk assessment and infrastructure planning. Generally, the GEVD demonstrates superior performance in accurately predicting quantile values, particularly for lower to moderate return periods. This capability is vital for designing resilient infrastructure and implementing effective flood management strategies.

In comparison to Mohamed and Adam's research on modeling the magnitude and frequency of extreme rainfall in Somalia using the maximum likelihood estimation (MLE) approach for the GEVD ^[29], our Bayesian approach yielded distinct findings for the return level estimation. For example, Mohamed and Adam reported a 100-year return level estimate of 168.111 mm using MLE for their study on Somali rainfall extremes. In contrast, our Bayesian analysis produced a more conservative estimate of 140.815 mm for the same return period, showcasing a significant difference in estimation precision. The Bayesian approach's incorporation of prior information and iterative sampling from the posterior distribution likely contributed to this discrepancy, providing a more nuanced and robust estimation framework. This highlights the advantages of Bayesian methods in capturing uncertainties and refining estimates crucial for effective risk assessment and infrastructure planning in regions prone to extreme rainfall events like Somalia.

In summary, the detailed analysis conducted in this study underscores the effectiveness of the GEVD model for forecasting extreme rainfall events in Somalia, particularly when utilizing Bayesian MCMC techniques. The study highlights the significance of considering uncertainty in risk assessment and decision-making, with a focus on posterior medians and credibility intervals. Additionally, the results emphasize the need to carefully select the distribution model based on the specific characteristics of the data, especially when dealing with extreme values and longer return periods. This comprehensive analysis contributes valuable insights for enhancing preparedness and resilience in the face of extreme weather events in Somalia.

4.   Conclusions

Extreme environmental hazards, such as heavy rainfall, carry significant potential for property damage and human life loss, underscoring the need for understanding and predicting these events. This study harnessed the power of Bayesian extreme value theory to model and forecast extreme rainfall, offering a valuable tool for effective rainfall-related management. Particularly in data-scarce regions like Somalia, our Bayesian approach presents a robust solution for modeling extreme climate events, using monthly rainfall data spanning from 1901 to 2022.

Our research has identified the Gumbel distribution within the GEVD family as the most suitable model for annual maximum monthly rainfall data in Somalia. Rigorous model diagnostics have further substantiated the GEVD's ability to capture extreme rainfall patterns. Additionally, our study has revealed that with increasing return periods, the associated return levels also escalate. Comparing the return levels generated by the GEVD and GPD models, we found that the GPD consistently predicts slightly smaller return levels than the GEVD, particularly for moderate to high return periods, and with higher precision (indicating less uncertainty).

Utilizing the Bayesian GEVD model, we have estimated extreme rainfall return levels exceeding 106 mm, 163 mm, and 195 mm for return periods of 10, 50, and 100 years, respectively. These return levels offer critical insights into the potential severity of future extreme rainfall events. Armed with this knowledge, decision-makers in Somalia can make informed choices to mitigate the potential impact on life, agriculture, and essential infrastructure.

These findings have crucial implications for urban planning, civil engineering, and policymaking in Somalia. Accurate estimation of extreme rainfall return levels empowers decision-makers to mitigate flooding risks and enhance climate resilience. Urban planners can optimize drainage systems and flood management strategies to accommodate projected increases in rainfall intensity. Civil engineers can integrate these estimates into critical infrastructure designs, fortifying structures like bridges, dams, and roads against future climate impacts. Policymakers can craft adaptive policies that foster sustainable development and bolster community resilience to climate-induced hazards. These findings thus contribute to resilient planning and policy frameworks that safeguard lives, livelihoods, and infrastructure amid escalating climate uncertainties.

As the impact of climate change continues to unfold, proactive measures in Somali communities become paramount. This study contributes to the development of early warning systems, preparedness strategies, effective management, timely response, and mitigation approaches to address flood risks and their repercussions. While Somalia has taken commendable steps in fostering climate change adaptation, ongoing efforts remain necessary to build resilience and protect vulnerable populations from the consequences of extreme rainfall.

Availability of data and software

The data that support the findings of this study are publicly available in the Climate Knowledge Portal of the World Bank Group at https://climateknowledgeportal.worldbank.org. The R code that supports the findings of this study is available from the corresponding author upon reasonable request.

Author contributions

All authors contributed to the preparation of the manuscript. Jama Mohamed performed data collection, analysis, first draft preparation, and organization of the manuscript. Dahir Abdi Ali wrote the Introduction of the manuscript. Abdimalik Ali Warsame contributed to the manuscript by participating in writing some of the Materials and methods section of the manuscript. Mukhtar Jibril Abdi contributed to the Methods section of the manuscript. Eid Ibrahim Daud read the first draft and gave intellectual comments that enriched the manuscript. Mohamed Mohamoud Abdilleh reviewed and commented on the first draft. All authors read and approved the final manuscript.

Use of AI tools declaration

The authors declare that Artificial Intelligence (AI) tools were not used in the creation of this article. ChatGPT was utilized solely for grammar correction purposes.

Conflict of interest

The authors declare no conflict of interest.