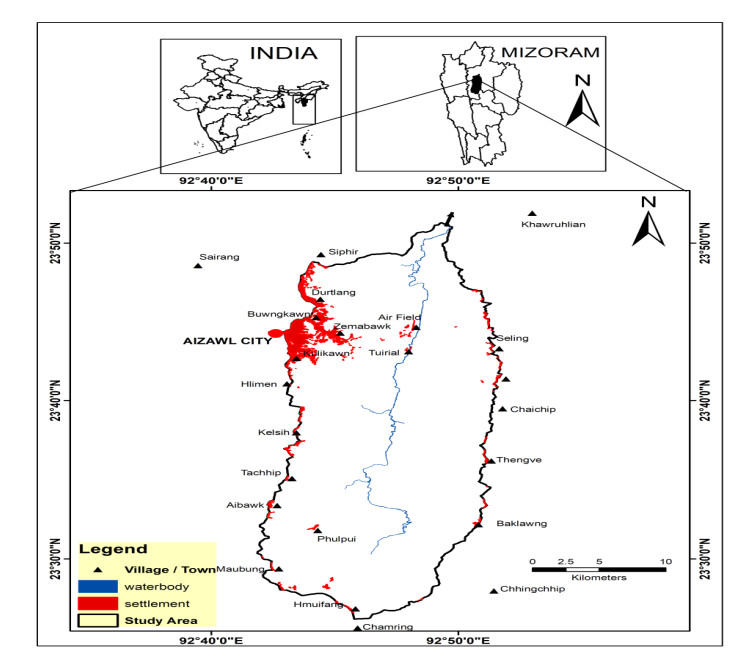
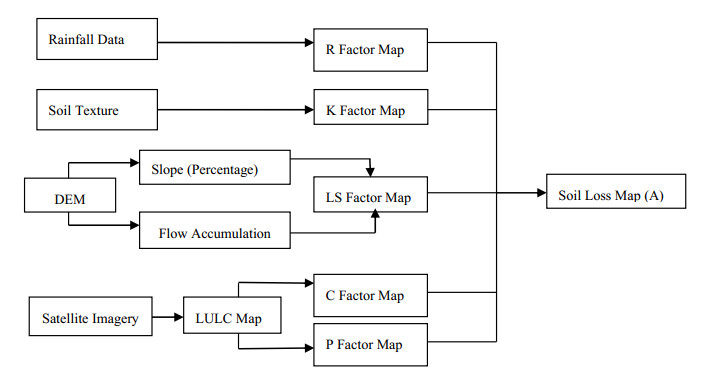
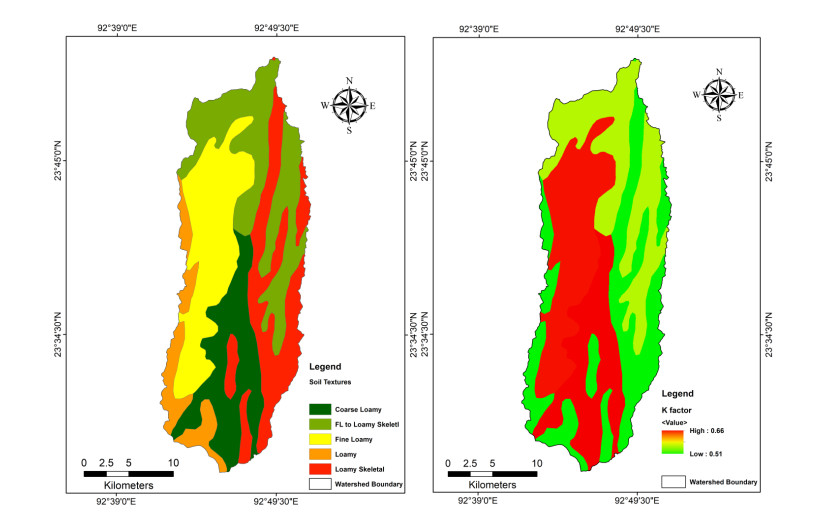
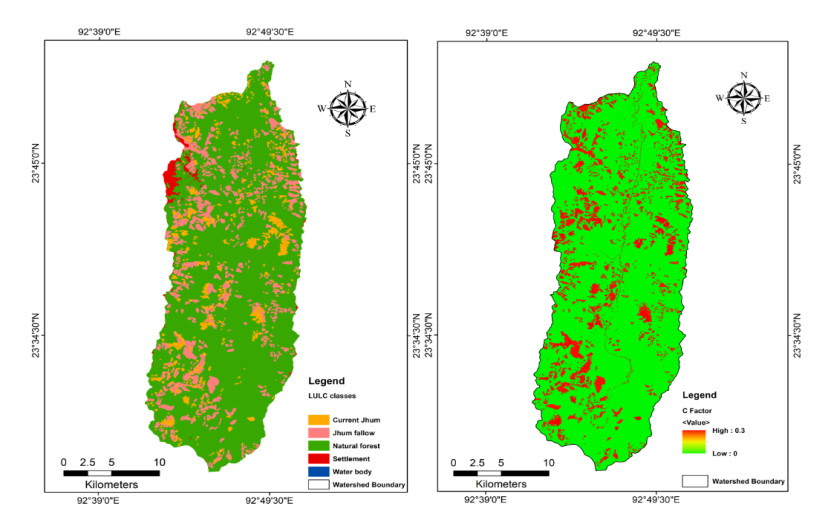
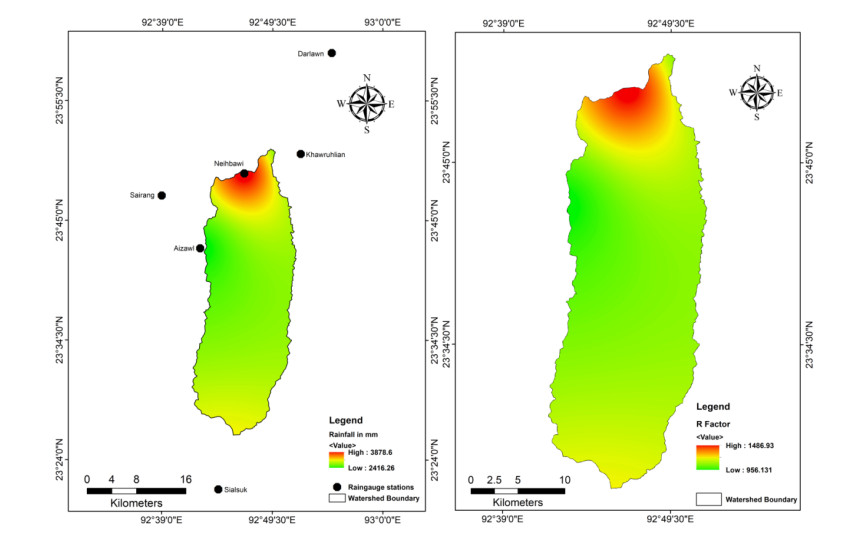
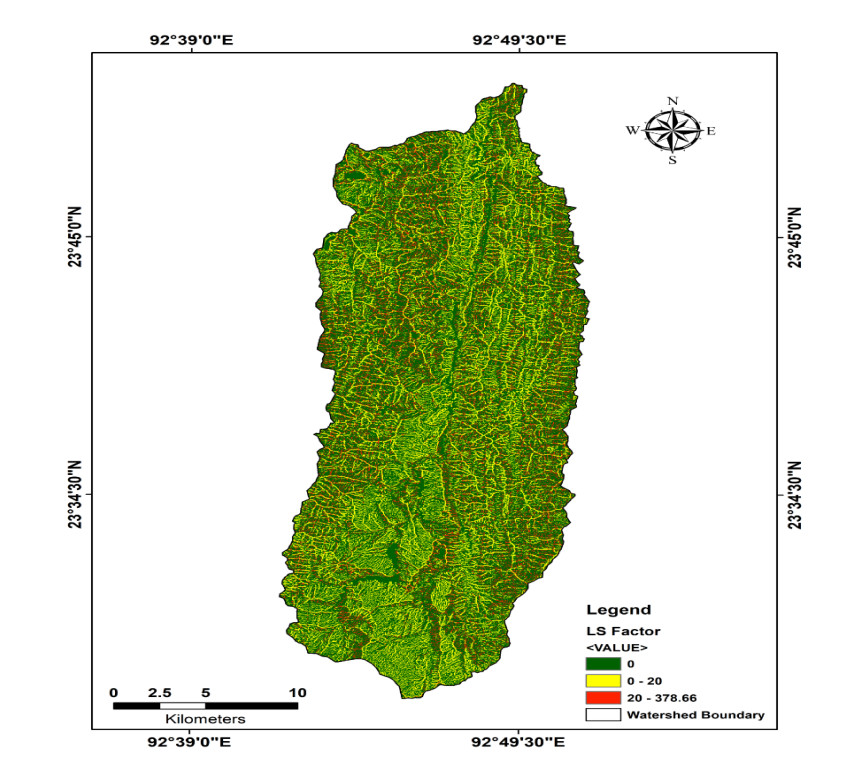
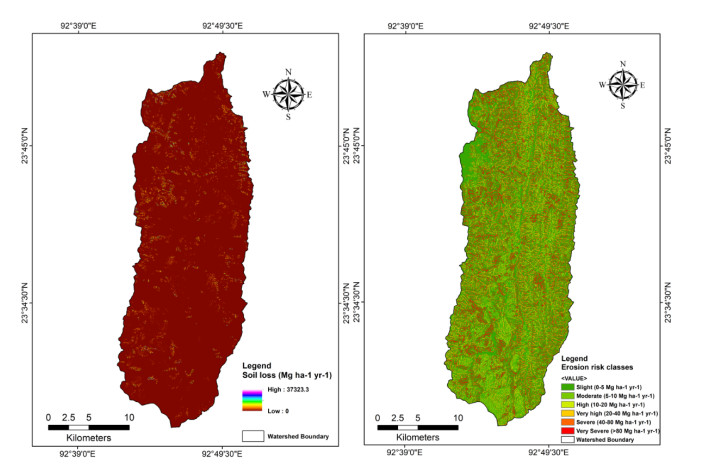
Soil erosion assessment using revised universal soil loss equation model and geo-spatial technology: A case study of upper Tuirial river basin, Mizoram, India

1.   Introduction 

Soil erosion is one of the major environmental problems worldwide which not only affect soil productivity, nutrient loss, siltation in water bodies ^[1] but also affect public health, and the livelihood of global marginal communities that largely depend on agriculture ^[2]. The Eastern Indian Himalayan region as a whole is experiencing serious problem of soil erosion and the rivers flowing through this region carries huge quantities of sediments and finally discharge into the Bay of Bengal. About 25% of the dissolved load is supplied to the World oceans by the Himalayan and Tibetan regions ^[3]. The foot hills of Himalayas, which extends in the northeastern part of Indian states like Arunachal Pradesh, Nagaland, Manipur, Mizoram, Meghalaya and Assam and this region, are no exception to huge soil erosion. The sediment load in the Himalayan rivers increased due to loss of forest cover, indiscriminate exploitation of other natural resources, intense monsoonal precipitations and the fragile river catchments of low water retention capacity ^[4,5]. Geologically the region is very weak and fragile due to its soil structure mostly composed of sandstones, siltstone and shales. Erosion worsens the physical, chemical and biological properties of soil by removing of natural nutrients, humus and top soil and making the soil unproductive for crop growth. Anthropogenic disturbances such as deforestation, expansion of agricultural land from forest cover, shifting cultivation (locally known as Jhum) on steep slopes, construction of roads, rapid urbanization and other developmental activities coupled with high rainfall, poor soil conservation and high soil erosivity induced by shallow soil depths, low structural stability are the main reasons for high rate of soil loss ^[6]. High seismicity is yet another factor in the region for high soil erosion and sedimentation in river reaches ^[7]. Soil erosion is nevertheless a major problem which affects the agricultural production ^[8], soil fertility ^[9,10], excessive siltation ^[11,12], and sedimentation in lakes and rivers, water quality and recreation. Each year, due to soil erosion, million tons of soil is eroded off mostly from agricultural practices in mountainous terrain ^{[13,14,15,16,17,18]}. Recent estimates indicate that nearly 39% of the Indian Himalayas has potential soil erosion rate of more than 40 Mg ha⁻¹ yr^−1[19]. Thus soil erosion is a major setback to the sustainable development of natural resources and environment and thus calls for urgent quantification.

Traditional method of conducting field studies to estimate soil loss may not be easy due to complex interactions of factors that affect the results, besides such exercise may be very time consuming and expensive. Furthermore correct prediction of soil loss may involve results drawn from several years. Soil erosion models that take into account various complex interactions and use of advance technology may make this process faster and estimate soil erosion more accurately ^[20]. There are several soil erosion models ranging from simple empirical models to more complicated physics-based models ^[21] used by various researchers in estimating soil erosion and basin sediment yields. A detailed review on various soil erosion models, their complexity and input requirements are provided ^[20]. Among the various models Revised Universal Soil Loss Equation (RUSLE), an improvised version of universal soil loss equation (USLE), that can be integrated with remote sensing and geospatial technique is now considered being a very reliable and practical model most suited to local condition ^[22]. Forest cover, rangelands, non-agricultural lands such as built up areas and disturbed areas are also included in RUSLE model's compared to USLE model. In this method the annual average soil loss of an area is calculated by multiplying five factors, viz. rainfall erosivity factor (R), soil erodibility factor (K), slope length and steepness factor (LS), cover management factor (C) and conservation practice (P) factor ^[23].Though RUSLE has also several limitations in the sense that it cannot estimate gulley erosion, dispersive soils and predict sediment pathways ^[21,24], nevertheless it is a simple empirical model which can easily be integrated into other soil erosion models to accurately estimate annual soil loss over a longer period of time ^[21] and therefore this model is very useful with management and decision making.

The state of Mizoram is basically a rugged mountain state where more than 60% of land under hilly terrain. The state is dominated by tribes who practice shifting cultivation for livelihood and food security. Due to increase in population over the years and reduced acreage of available land the shifting cultivation cycle which used to be 15–20 years is now drastically reduced to 4–5 years. The shortening of fallow period (intervening period between two shifting cultivation) cause severe soil erosion and land degradation. There are several studies carried out in the region that report shifting cultivation to be principal source of soil erosion. The practice of shifting cultivation in hill slope (60–70%) is reported to cause soil loss to tune of 147 Mg ha⁻¹ yr⁻¹ in the 1^st year of cultivation and with gradual increase in abandonment of land the rate of erosion is reduced to 30 Mg ha⁻¹ yr⁻¹ within a 3-years period ^[25]. The policy makers in the state have made several efforts to arrest soil erosion by creating different types of terraces, and adopting to alternate measures of land use, but these initiatives have not so far yielded significant results. Some case studies conducted in the region using RUSLE to predict soil erosion include that of Dikrong river basin of Arunachal Pradesh ^[11], Muhuri river basin ^[26], Dhalai river basin ^[27] of Tripura, Panchnoi river basin ^[28], Sadiya, Assam ^[29], different land use of Ri-bhoi district, Meghalaya ^[30], however in identifying areas more prone to soil erosion is completely lacking from the state of Mizoram. Tuirial river basin provides an important avenue for livelihood activities for the rural residents from natural forests and shifting cultivation lands. We therefore aimed to assess spatial distribution of soil loss across this small river basin so as prescribe suitable land management.

The aim of the present study was to estimate the annual soil loss in upper Tuirial river basin of Mizoram, NE India by using RUSLE and geo-spatial technology. The study is expected to contribute to adaptation of appropriate soil and water conservation measures in very high risk zones of the river basin and similar studies may also be extended to other unexplored areas for proper watershed management practices in hilly terrains of Mizoram state.

2.   Materials and methods 

2.1.   Description of study area 

Tuirial river basin covers 53,393.09 ha of land and lies between longitudes 92°42′E–92°52′E and latitudes 23°26′N–23°52′Nat an elevation of about 1690 m above MSL at the highest point and about 76 m above MSL at the lowest, in the state of Mizoram, which is basically a rugged mountainous state in India. The state reposes under direct influence of southwest monsoon with an annual average precipitation of about 2500 mm. The onset of monsoon is usually encountered during the early month of May while the months of July-August sustain the wettest months and December-January the driest months of the year. Rainfall and temperature data collected for a period of 2007 to 2016 at the study area gives the average annual rainfall of 2732 mm, average monthly temperature of 21.24 ℃ with maximum and minimum temperature of 15.39 ℃ and 27.19 ℃ respectively. The location map of the study area is shown in Figure 1.

Figure 1.  Location map of the study area.

DownLoad: Full-Size Img PowerPoint

2.2.   Data collection and source 

The various types of data and satellite imagery used for the present study are shown in Table 1. The method involved integration of different thematic layers such as land cover map, DEM, rainfall, and soil map in GIS environment (Figure 2). Soil textural map of 1:250,000 scale was collected from National Bureau of Soil Survey and Land Use Planning (NBSS & LUP) and were digitized in ArcGIS10.3.1 software to generate soil erodibility factor map (K). Rainfall data of 9 years collected from six stations located within the study area were improvised from Directorate of Agriculture and Crop Husbandry, Government of Mizoram. These point data were then interpolated using IDW interpolation method by GIS technique in order to generate the rainfall distribution map and finally the rainfall erosivity factor map. For generation of L and S factors CARTOSAT DEM of 30 m spatial resolution downloaded from bhuvan.nrsc.gov.in was used to generate slope and flow accumulation map using the Spatial Analyst toolbox of ArcGIS 10.3.1 software. Sentinel 2A multispectral satellite data of 10 m spatial resolution acquired on 30^th March 2019 (http://earthexplorer.usgs.gov/); was used to prepare land use and land cover map of the study area in order to generate the crop management factor and practice management factor.

Table 1.  Various types of data and satellite imagery used for the present study.

Sl. No.	Type of Data	Source	Purpose
1	Topo sheet	Survey of India	Base Map
2	Soil Map	NBSS & LUP	Soil Textural map
3	Satellite data Sentinel 2A (10 m resolution), 30/03/19	United States Geological Survey (USGS)	Land use/Land cover mapping
4	CARTOSAT DEM (30 m)	ISRO	Slope map and Flow accumulation map
5	Rainfall (2007–2016)	Directorate of Agriculture and Crop Husbandry, Government of Mizoram	Rainfall Distribution map

---

 | Show Table

DownLoad: CSV

Figure 2.  Flow chart showing the work procedure for RUSLE—based soil erosion modeling.

DownLoad: Full-Size Img PowerPoint

2.3.   Soil erosion model 

For estimation of average annual soil loss we used RUSLE model that is most widely accepted where multiple components responsible for soil erosion are integrated in GIS environment ^{[31,32,33,34,35]}. These components are rainfall runoff erosivity factor (R), soil erodibility factor (K), slope length (L), slope steepness (S), cover management factor or crop management factor (C), and practice management factor (P) ^[23]. This model is widely used in basin level analysis because of its simplicity and can be applied to broad areas with different land use patterns ^{[36,37,38,39,40,41,42]}. It is usually denoted by

where, A = Average annual soil loss (Mg ha⁻¹ yr⁻¹); R = Rainfall-runoff erosivity factor (M J mm ha⁻¹ h⁻¹ yr⁻¹); K = Soil erodibility factor (Mg ha⁻¹ MJ⁻¹ mm⁻¹); L = Slope length factor; S = Steepness factor; C = Cover and management factor and P = Conservation practices factor. Among these factors L, S, C and P are dimension less.

2.3.1.   Rainfall-runoff erosivity factor (R) 

The rainfall runoff erosivity factor represents the ability of rainfall and runoff to cause erosion on the surface of the earth and it also predicts the rate and amount of run-off which is directly interconnected with that precipitation event ^[43]. It is a function of the falling raindrop and the rainfall intensity, and is the product of kinetic energy of the raindrop and the 30-minute maximum rainfall intensity ^[22]. Extreme rainfall increases the amount of erosion and sedimentation in an area ^[18]. For this study average yearly rainfall data for 9 years (2007–2016) (Table 2) was used to estimate R factor following relationship developed for India ^[44].

where R = Rainfall runoff erosivity factor and P = Average annual rainfall in mm.

Table 2.  The average annual rainfall of 9 year period of Tuirial watershed during (2007–2016).

Rainfall(mm)	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	Average
Aizawl	2486	1570	1592	4378	2156	2544	2078	1914	2551	2844	2411
Sialsuk	4651	2987	2458	3276	3163	3606	3000	2993	3249	3163	3255
Neihbawi	4859	3784	3217	4404	3864	4057	4275	2976	3501	3849	3879
Darlawn	2923	2085	1922	2454	2287	3030	1697	1089	1691	2392	2157
Khawruhlian	2845	1894	1516	2485	1857	2128	2180	1997	2423	3010	2234
Sairang	2489	1661	1579	2679	2137	2266	2810	2733	2977	3217	2455

---

 | Show Table

DownLoad: CSV

2.3.2.   Soil Erodibility Factor (K) 

The soil erodibilty factor is the measure of the rate of soil detachment due to the impact of raindrops or surface runoffand manifest the change in soil erosion per unit area per applied external force. This factor is largely influenced by soil textures, soil structure, soil permeability and organic matter content.A soil textural map digitised by ArcGIS from the data provided by NBSS & LUP, Government of India was used to genarate a clear and distinct soil classification model for different locations of the study area (Figure 3). For this study soil erodibility factor value (Table 3) were calculated and were cross checked with the work of the different soil textures taken from published literature ^[15].

Figure 3.  Soil textural classification and soil erodibility (K) factor map of the study area.

DownLoad: Full-Size Img PowerPoint

Table 3.  Soil erodibility factor values assigned for different soil textures in the study area.

Soil Textures	"K" factor
Loamy soil	0.51
Fine loamy	0.57
Fine loamy to loamy skeletal	0.55
Loamy skeletal	0.54
Coarse loamy	0.66

---

 | Show Table

DownLoad: CSV

2.3.3.   Slope Length and Slope Steepness(LS) Factors 

Slope length (L) is defined as the distance from the origin of overland flow to where the slope gradually decreases such that deposition occurs and finally enters a defined channel ^[22,45]. Slope steepness (S) is a dimensionless quantity which refers to the angle of inclination of the slope or its gradient expressed in degree or percent.The risk for soil erosion increases with the increase in slope length as well as inclination of slope ^[22,23] as increase in these factors produces higher velocities of overland flow, thus resulting in higher erosion. LS factor was determined using CARTOSAT DEM data following ^[22] equation.

where, λ = Flow accumulation x Pixel size in m, Ɵ = Angle of slope in percentage, m = dependent on the slope, 0.5 if slope > 5%, 0.4 if slope is between 3.5% and 4.5%, 0.3 if slope is between 1% and 3%, 0.2 if slope is less than 1%. In this case the value of m is taken as 0.5 and the value of each pixel is 30 m.

2.3.4.   Crop Management Factor (C) 

Crop management or cover management factor is expressed as the ratio of soil loss of specific crop to the soil loss under the condition of continuous bare soil ^[46]. Depending upon the type and coverage of the land surfaces, the rate and amount of soil loss also vary because region with vegetation cover prevents the direct impact of raindrops on the soil particles resulting less erosion. Whereas region having bare surfaces will have more erosion due to direct impact of raindrops on the soil surface ^[32,38]. For the preparation of crop management factor map, Sentinel 2A multispectral satellite data of 10 m spatial resolution acquired on 30^th March, 2019 was used and thus land use and land cover map of the study area was prepared. Image classification was done based on visual interpretation of FCC image with limited field validation and also validated with Google earth pro image (https://earth.google.com/web/). Five types of land cover were identified in the study area such as Current Jhum, Settlement, natural forest, Jhum fallow and water body (Table 4, Figure 4). The C factor value corresponding to each land cover conditions were assigned as per the published literature ^[13,15] carried out in this region.

Table 4.  Satellite image classification for Land Use/Land Cover and the corresponding C and P factor values.

LULC	Descriptions	C factor	P factor
Settlement	Land covered by concrete, including airport runway, residential, industrial, commercial buildings, open-roof concrete structures, other human-made structures.	0.0	1
Current Jhum fallow	Areas characterized by grasses, herbs, and crops, including current Jhum	0.3	0.28
Jhum fallow	This category includes land with sparse vegetation, scrub land and land with barren rocks.	0.15	1
Natural forest	Land characterized by relatively moderate and thick forest vegetation.	0.005	1
Water body	Surface covered with river water only	0.280	1

---

 | Show Table

DownLoad: CSV

Figure 4.  LULU and Crop management factor (C) map of the study area.

DownLoad: Full-Size Img PowerPoint

2.3.5.   Practice management factor (P) 

Practice management factor is the ratio of soil loss with a specific conservation practice to the corresponding loss with up and down slope cultivation ^[13,46]. This factor helps in reducing the rate of soil erosion by altering the flow direction of runoff with the aid of some preventive measures such as contour bounding, terraces, silt fences and proper drainage systems which reduces the runoff rate ^[47]. The lower the P factor, the more effective will be the conservation practice in terms of reduction in the soil erosion ^[48,49]. In the study area, no major conservation practice was followed except for terrace farming activities in Jhum land in some areas. The values for P factor were assigned as 0.28 for area under Jhum cultivation and 1.0 for other area ^[13,14,15] (Table 4). The magnitude and the spatial distribution of P factor are shown in Figure 5 and the value ranged from 0.28 to 1.00 with a mean value of 0.971.

Figure 5.  Practice management (P) factor and slope map of the study area.

DownLoad: Full-Size Img PowerPoint

3.   Results 

3.1.   Rainfall erosivity factor (R) 

The average annual rainfall distribution for the years 2007 to 2016 varies from 2157 to 3879 mm and the (R) Factor ranges from 956.10 to 1486.93 MJ mm ha⁻¹ h⁻¹ yr⁻¹ with average value of 1116.77 MJ mm ha⁻¹ h⁻¹ yr⁻¹ as shown in Figure 6. The south (Siaksuk) and north (Neibawi) part of the river basin exposed to maximum rainfall while northwest part (Aizawl and Sairang) experienced low rainfall, and the rainfall erosivity was directly proportional to the amount of rainfall received in different parts of the river basin.

Figure 6.  Rainfall distribution and rainfall runoff erosivity (R) map of the study area.

DownLoad: Full-Size Img PowerPoint

3.2.   Soil erodibility factor (K) 

The calculated K factor varied from 0.51 to 0.66, Mg ha⁻¹ MJ⁻¹ mm⁻¹ with mean value of 0.57 Mg ha⁻¹ MJ⁻¹ mm⁻¹. Lower value of K indicates soils with least prone to erosion, while higher values indicate soils which are highly prone to erosion by water.

3.3.   Slope length and slope steepness factor (SL) 

The SL factor varied from 0 to 378.661, with a mean value of 5.719 with standard error of 11.586 (Figure 7). The spatial distribution map clearly shows the concentration of high SL values in steeper slope areas, where there is sudden change in relief and slope angle.

Figure 7.  Slope length and steepness (SL) factor map of the study area.

DownLoad: Full-Size Img PowerPoint

3.4.   Crop management factor (C) 

The magnitude and the spatial distribution of crop management factor are given in Figure 4. Crop management factor was found to be at the range of 0.0 to 0.3 with a mean value of 0.0327 as shown in Table 4.

3.5.   Average annual soil loss 

The value of soil loss generated from the thematic map ranges from 0 to 34323.3 Mg ha⁻¹ yr⁻¹ with mean value of 88.875 and standard deviation of 457.65. The highest value of 34323.3 does not represent the overall soil loss but it represents the value of one pixel only. The high value pixels are shown in areas such as barren land, Jhum fallows, and agricultural land and built-up areas and also in areas where the topography is highly dissected with steep slope value. Therefore current Jhum fallows are found to be more affected and sensitive in terms of soil erosion in this region.

3.6.   Erosion risk map 

Erosion risk has been grouped into six classes based on the rate of erosion (Table 5). Out of the total area of the watershed, 37489.71 ha (70.21%) falls under slight/very low erosion risk zone where the erosion rate is 0 to 5 Mg ha⁻¹ yr⁻¹. A total of 3484.96 ha (6.53 %) of the area falls under very high erosion risk zone with an erosion rate of 20 to 40 Mg ha⁻¹ yr⁻¹ and 5295.41 ha (9.92%) to very severe soil erosion risk (>80 Mg ha⁻¹ yr⁻¹) zone. These values in the erosion risk map (Figure 8) do not represent the actual rate of erosion rather these classes are the representation of the spatial distribution of erosion risk zones for each class.

Table 5.  Spatial distribution of soil loss and erosional risk classes.

Erosion Risk Classes	Soil Loss (Mg ha−1 yr−1)	Area (ha)	Area (%)
Slight	0–5	37489.71	70.21
Moderate	5–10	800.09	1.50
High	10–20	1877.81	3.52
Very high	20–40	3484.96	6.53
Severe	40–80	4445.08	8.33
Very severe	> 80	5295.41	9.92

---

 | Show Table

DownLoad: CSV

Figure 8.  Spatial distribution of soil erosion and soil erosion risk map of the study area.

DownLoad: Full-Size Img PowerPoint

4.   Discussion 

The degree of soil degradation depends on the soils susceptibility to degradative processes, land use and the duration of degraded land use, and the management. In the state of Mizoram, shifting cultivation is the predominant land use that has been practiced since time immemorial. The continuance of this practice without suitable soil conservation measures has made the soil more erodible. The high K value of the soil (0.57) suggests that the soils are intrinsically susceptible to erosion force of the rainfall. The steepness of hilly terrain, wide variations in slopes and the fragile ecosystems combined make the watershed more prone to soil erosion. Geologically the state of Mizoram is composed of sedimentary rocks of tertiary age, which are basically sandstone, siltstone and shale and their admixture in various proportions. The dynamic landscape coupled with widely practiced primitive shifting cultivation in sedimentary rock base without proper soil and water conservation measure is a cause of concern for the huge soil loss from the watershed in the state. The estimated annual soil loss of 91.357 Mg ha⁻¹ yr⁻¹is quite high, and much higher than the reported tolerable soil loss rate of 4.2–7.2 Mg ha⁻¹ yr⁻¹ for deep to very deep soil depth ^[50]. The threshold limit prescribed by ^[51] for soil tolerance is 1.5 Mg ha⁻¹ yr⁻¹ and beyond 5 Mg ha⁻¹ yr⁻¹ is considered to be high erosion and beyond the tolerance limit. Some studies carried out in the region reveal that shifting cultivation has highest erosion ratio (12.46) and can cause soil loss from 30.2 to as high as 170.2 Mg ha⁻¹ yr^{−1 [52]}, in Meghalaya the soil loss from cultivated field is reported to be 32–79 Mg ha⁻¹ yr^{−1 [52]}. Average annual soil loss in the neighboring states of northeast India varied from < 25 Mg ha⁻¹ yr⁻¹ under dense forest and intense rubber plantation to main course of river basin (>70 Mg ha⁻¹ yr⁻¹) ^[26], 5.45 Mg ha⁻¹yr⁻¹ in Sandiya region, Assam ^[29] and on average 51 Mg ha⁻¹ yr⁻¹ in Arunachal Pradesh ^[13]. In other parts of India, the soil loss is reportedly low like in Kerala it is 17.73 Mg ha⁻¹ yr^{−1 [38]} and 2.278 Mg ha⁻¹ yr⁻¹ in Western Deccan, India ^[53]. These results reveal that the higher rate of soil loss in northeast India compared to the rest of the country could be due attributable to high rainfall in the region. Severe rainfall in the region cause acidification and loss of vital metallic minerals such as calcium, magnesium, potassium, sodium etc. that is essential for crop production. About 28–38% of land in neighboring states of Manipur and Meghalaya are reported to be washed out due to torrential rain in the region ^[19]. The average annual loss of loss in the state of Mizoram is also quite high compared to average soil erosion rate of India i.e. 16.4 Mg ha⁻¹ yr^{−1 [50]}. Nevertheless the loss is a major factor for low crop productivity in the state of Mizoram. Soil erosion cause reduction in water holding capacity of soil, and depletion of soil organic matter thereby making the soil more acidic that is a characteristic feature of hilly soils. The spatial distribution of soil loss in the watershed revealed that very high, severe and very severe soil erosion area account 3484.96, 4445.08 and 5295.41 ha respectively and together contribute nearly one-fourth (24.75%) of the area in the watershed that necessitate protection and conservation of the existing vegetation cover and replanting forests in the cultivated areas or by bringing an improvement to the existing cultivation practice of the shifting cultivation. Either slope length or gradient was not found effective, however the combined LS factor was most significant causing soil loss from the watershed. In addition during the past few years the state has witnessed rapid land use changes, and other anthropogenic activities for high rate of soil erosion.

Soil loss is the resultant of all the factors (R, K, L, S, C, P) which are mostly interdependent on each other. In the minimal presence of C & P factors, the other factors were more prominent in governing the soil loss in the site. There was wide variation in topographic conditions (L, S factors) in the river basin that caused spatial variation in soil loss. R factor varied between the sites obviously due to variation in rainfall that mostly induced the K factor, while the soil structure and its characteristics being similar in the whole of the river basin. Soil erodibility factor (K) reported in the region varied from 0.039 to 0.55 Mg ha MJ⁻¹ mm⁻¹(Dikrong river basin, Arunachal Pradesh), 0.15 to 0.36 Mg ha MJ⁻¹ mm⁻¹ (Muhuri river basin, Tripura), 0.28 to 0.34 Mg ha MJ⁻¹ mm⁻¹ (Ri-Bhoi district of Meghalaya), these values are well within the range reported in the present study. The large variations in K factor was due to wide variations not in soil texture but also other soil parameters such as organic matter, soil permeability and soil structure. The presence of low organic matter in agriculture field than the forest and Jhum fallows attributed to higher K-values, an agreement in accordance with some other workers ^[28,30].

The excessive soil loss in and around areas with high SL factor (within the northern and northwestern part of the study area) and K factor (which is sparsely distributed within the whole basin) may not only increase the siltation rate but also leads to rise in water level of a river, further reducing the productivity of crop lands in such areas. Meanwhile these are the areas where P factor admittedly attain lower values. However, RUSLE modeling will succor upon taking up effective measures regarding with soil conservation for management and development of the watershed. Another contrasting factor that RUSLE model possess is its tendency to give detailed information of an area in terms of its erosivity that may be inaccessible for field verifications in areas like steep and rugged terrain to thick forest cover.

Nevertheless the causes of erosion are very complex, and in most cases poorly understood. Despite the previous uncovering through RUSLE model, the prominent factors such as high intensity of rainfall, the steeply sloped rugged mountainous terrain, the fine to coarse loamy nature of the soil as well as the unscientific practices of Jhum cultivation accounted for severe soil erosion within the study area. Moreover, the high rate of Jhum practices within the area hamper the soil content and left the soil barren and make them unsuitable for plants and crops, where most areas turns out to be high erosion risk zone. Therefore, an alternative way with a more logical and conventional techniques must be implemented upon these agricultural lands for the further welfare of the rural inhabitants.

The analysis of risk map suggests that fallow lands formed as a result of agricultural practices designate excessive erosion risk zone, eroded mainly due to gulling and over land flow with steep slopes being the other salient factor which increases the rate of erosion. Severe erosion risk areas were also observed within the vicinity river banks where the land is very steep and small channels (rills) gear up the process. Some of the areas prone to erosion are shown as field evidences in the river basin (Figure 9A–D). Nevertheless, low erosion risk zones maybe discerned around regions covered by thick forests. Improper planning and management of land use, seepage from the unlined water courses, non-conjunctive use of surface and ground water are some of the observed factors around the watershed. We suggest that the state government should adapt some mitigation techniques such as water harvesting, terracing, introduction of vegetative barriers using natural geotextiles, mulching, conservation agriculture, reforestation and horticulture development, agroforestry and integrated farming systems in order to minimize the soil erosion, and to provide sustainable livelihoods to the growing population around the watershed.

Figure 9.  A: A common phenomenon in the mountainous region shows the burning and clearing of forest cover through Jhum activity for cultivation. B: Terrace farming (Top of the Photo) is more common in the hilly terrain and current Jhum land (below the photograph) ready for cultivation. C: Manual sand seiving is common hilly river beds for construction purpose extracted form the Tuirial river bed in the study area. D: Encroachment of river bed is also more common in the hilly teraain forconstruction of sports stadium a tributary in Chite Lui sub-watershed, Eastern part of the Aizawl city area in the Tuirial basin.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions 

Contemplate observations and scrutiny of the above generated data as well as field credentials provided us an exemplary result with the average annual soil loss is 115.4 Mg ha⁻¹ yr⁻¹ and a total soil loss of 6.161 million Mg yr⁻¹ specifying zones of severe erosion. About one-fourth (24.78%) of the total basin area was projected to be very soil erosion risk area that need immediate conservation measures. Since there were no baseline field data available on soil erosion from the study area, hence no calibration/validation of the result could be made. It was also well observed that severe erosion zones are usually grounded upon areas with considerably unprotected areas like Jhum fallows and less vegetative areas with higher slope values while that of slight erosion in areas with almost negligible slope values with thick forest cover area.

Acknowledgements 

The authors wish to thank the anonymous reviewers for their constructive suggestions which helped in improving the quality of the manuscript. One of the authors (BKB) is grateful to the University Grants Commission (UGC), New Delhi—Mizoram University (UGC-MZU) for award of a Research Fellowship. The Head, Department of Geology provided necessary facilities to carry out this work.

Conflict of interests 

All authors declare no conflicts of interest in this paper.