Hopf bifurcation for a class of predator-prey system with small immigration

1.   Introduction

The predator-prey models describe the dynamics of populations in a predator-prey relationship. These kinds of models have become of great interest, especially for describing and solving many problems in biology, ecology, and medicine, among others. See, for instance, ^[1,2,3,4].

One special question in this area is related with the coexistence or not of the species. In this context the presence of nontrivial equilibrium points or limit cycles play an important role. A limit cycle typically occurs when the interactions between predators and prey lead to cyclic behavior in their population sizes. Many works in predator-prey differential systems have demonstrated that its dynamics can exhibit either cyclic oscillation or divergent extinction of one species.

In this context the presence of immigrants in the species is of biological interest because, in general, in nature most systems are not isolated.

Several authors have analyzed the effects of the presence of immigrants in one or more species. For example, in ^[5,6,7,8] the authors have used delay equations because delayed migration can occur when the individuals encounter some barriers. Also, in ^[9] the authors analyze the asymptotic stability in different predator-prey models with small immigration, and in ^[10] they study a two-dimensional problem that considers immigration in both species.

Also, in higher dimension, ^[11] studies the existence and stability of equilibrium points and Hopf bifurcation in a three-dimensional predator-prey with constant immigration rate in the predator, the prey, and the competitor of the prey species.

In this paper we study periodic orbits bifurcating from the two-dimensional family of the predator-prey system given by

where $x, y$ represent dynamical variables, the dot denotes derivative with respect to the time $t$, $d, a$ represent, respectively, the growth rate of prey and the death rate of predator, $a, b$ are the rate of predation and the conversion rate of eaten prey into new predator, and $c_1, c_2$ are the immigration rates of prey and predator, respectively. Due to biological meaning, all the parameters $a, b, d, n$ must be positive and the parameters $h, c_1, c_2$ can be positive or zero. The cases $c_1 = 0$ or $c_2 = 0$ represent the situation where there is no immigration in the respective species. Moreover, the dynamical variables $x, y$ are assumed to be no negative which means that our study will be restricted to the positive quadrant of the plane $\mathbb{R}^2$.

System (1.1) was considered in ^[12] where the author studies the global phase portrait restricted to the positive quadrant of the Poincaré disk when $m = h = 0.$ In that paper, numeric computations suggest the existence of a limit cycle for some choice of parameters. However, the author states that they were not able to obtain the result analytically.

In this paper, we study the Hopf bifurcation of system (1.1), which takes place for values of the parameters $h, c_1, c_2$ close to zero. This means that we are supposing, for $h > 0$ close to zero, small immigration in both species.

From direct computations, it follows that under the biological conditions $a, b, d, n,$ and $(h, c_1, c_2) = (0, 0, 0),$ system (1.1) has the equilibrium point $P_m = \left(\left(\frac{n}{b}\right)^{\frac{1}{m+1}}, \frac{d}{a}\left(\frac{b}{n}\right)^{\frac{m}{m+1}}\right)$ in the positive quadrant. Moreover, the origin is also an equilibrium point for all value of the parameters. We are interested in studying the Hopf bifurcation that may occur at the equilibrium point $P_m.$ Next, proposition provides conditions under which, for $m = h = c_1 = c_2 = 0,$ the point $P_0$ is a Hopf equilibrium point.

Proposition 1. Under the conditions $h = c_1 = c_2 = 0,$ system (1.1) has a Hopf equilibrium point at the point $P_m = \left(\left(\frac{n}{b}\right)^{\frac{1}{m+1}}, \frac{d}{a}\left(\frac{b}{n}\right)^{\frac{m}{m+1}}\right)$ if, and only if, $m = 0.$ In this case, the equilibrium point $P_m$ becomes $P_0 = \left(\frac{n}{b}, \frac{d}{a}\right).$

Proof. The result follows from the fact that, when $h = c_1 = c_2 = 0,$ the characteristic polynomial of the linear part of system (1.1) at $P_m$ has the form

As $d > 0,$ the equilibrium point $P_m$ has eigenvalues of the form $\pm i\omega$ if, and only if, $m = 0.$

Under the conditions of Proposition 1, we characterize the conditions for the existence of a Hopf bifurcation at the equilibrium point $P_0$ of system (1.1) using the averaging theory of second order.

As we are studying Hopf bifurcations for system (1.1) with $h, c_1, c_2$ close to zero, in order to apply the averaging theory of second order, we write the parameters $h, c_1, c_2$ of system (1.1) with $m = 0$ into the form

where $h(\varepsilon) = \varepsilon h_1+\varepsilon^2 h_2, \; c_1(\varepsilon) = \varepsilon^2 c_{12}, \; c_2(\varepsilon) = \varepsilon^2 c_{22},$ with $h_1 > 0,$ $c_{11}, c_{21}\geqslant0$ and $\varepsilon > 0$ sufficiently small. Doing this, we are studying the Hopf bifurcation of system (1.1) for the values of parameters $h, c_1, c_2$ close to $0.$

The main result of this paper is the following.

Theorem 2. Consider system (1.2) satisfying

(i) $(3d-n)(d-n) > 0;$

(ii) $(A_-^*-1)(A_+^*-1) < 0,$ with

(iii) $|2d-n|\sqrt{\dfrac{d+n}{(d-n)(3d-n)}}-(\sqrt{n}\cos\theta+\sqrt{d}\sin\theta) > 0,$ for all $\theta\in[0, 2\pi];$

(iv) $C_+ = \{2d-n > 0\mbox{ and}\; n^2-8dn+5d^2\neq0\}$ or $C_- = \{2d-n < 0\}.$

Then, for any $h_1 > 0$ and $c_{12}, \, c_{22}\geq0,$ system (1.2) exhibits a Hopf bifurcation at the equilibrium point $P_0.$ More precisely, under these conditions, for $\varepsilon > 0$ sufficiently small, system (1.2) admits a periodic orbit $(x(t, \varepsilon), v(t, \varepsilon))$ such that $(x(t, \varepsilon), v(t, \varepsilon))\rightarrow P_0$ as $\varepsilon\rightarrow 0.$ Moreover, under condition $\mathcal{C}_+$ of (iv), this periodic orbit is stable if $n^2-8dn+5d^2 > 0$, and unstable if $n^2-8dn+5d^2 < 0.$ On the other hand, under condition $\mathcal{C}_-$ of (iv), this periodic orbit is stable.

We observe that in this paper, we use the second order averaging theory for proving Theorem 2. For a general introduction to the averaging theory, see the books ^[13,14]. For completeness we present in the Appendix the main theorem on averaging theory that is used for obtaining Theorem 2.

2.   Proof of Theorem 2

In this section we provide the proof of Theorem 2. We observe that our result will provide the bifurcation of one limit cycle for the values of the parameters $h, c_1, c_2$ close to $0.$ The parameters that do not affect the Hopf bifurcation are not perturbed.

Proof of Theorem 2. In order to apply Theorem 5 of the Appendix, we must write system (1.2) in the normal form (3.3) of the averaging theory. That is, we must write system (1.2) as a nonautonomous time periodic system and expand it with respect to a small parameter $\varepsilon$ in Taylor series. For doing this we start translating the equilibrium $P_0$ at the origin of coordinates, and after we write the linear part of system (1.2) with $\varepsilon = 0$ at the origin of coordinates in its real Jordan normal form. After this we shall write the differential system in polar coordinates $(\varepsilon r, \theta).$ Then, we shall take as the new time the variable $\theta$ and the differential system becomes a differential equation of the form $\frac{dr}{d\theta} = \varepsilon f(\theta, r, \varepsilon)$. This differential equation will be in the normal form (3.3) for applying the averaging theory.

As the first step, we observe that for $\varepsilon = 0$ and $a, b, d, n > 0,$ the linear part of system (1.2) at the equilibrium point $P_0 = \left(\frac{n}{b}, \frac{d}{a}\right)$ has the form

Translating the equilibrium point $P_0$ when $\varepsilon = 0$ to the origin of coordinates by doing

and so writing the linear part of the new system in its real Jordan normal form, considering the change of coordinates

system (1.2) becomes

In order to put the previous system in the averaging normal form, we will write it in polar coordinates taking

Doing this, the system becomes

Finally, taking $\theta$ as the new time we obtain the equivalent differential system

where the prime denotes the derivative with respect to the new time $\theta.$ Writing the vector field associated with the previous differential system in the form

we observe that it is in normal form for applying Theorem 5.

Initially we have to compute the averaging equation of first order given by:

Doing this integral, we get:

where

We observe that for the first two cases, the unique simple zero of $f_1(r)$ is $r = 0,$ and this zero only provides an equilibrium point instead of a periodic orbit, so the averaging theory of first order does not provide any information about the periodic orbits that can bifurcate from the zero-Hopf equilibrium point.

On the other hand, under the hypothesis

it follows that the first averaging equation is identically zero. Therefore, we are able to apply the averaging of second order.

To do this, we have to consider the averaging function of second order:

Computing this integral under the hypothesis (ⅲ), we get

where

Now, solving the equation $A(b, d, n, h_1, r) = 0$ with respect to $r,$ we obtain

which are real numbers by assumption (ⅰ). Moreover, $r_+ > 0$ (resp., $r_- > 0$) under the hypothesis $\mathcal{C_+}$ (resp., $\mathcal{C}_-$) in the assumption (ⅳ) of the theorem.

Evaluating expression (2.4) at $r_\pm$ given in (2.5), we get

by hypothesis (ⅱ) of the theorem. This assures that condition (2.4) is satisfied for $\varepsilon > 0$ sufficiently small.

Moreover, the derivative of the averaging function $f_2(r)$ with respect to $r$ at the zero $r_+$ is

which is different from zero by assumption (ⅳ) of the theorem. Therefore, under the hypothesis (ⅰ)-(ⅳ), the averaging function of second order has a positive simple zero satisfying the assumptions of Theorem 5. Consequently we have a limit cycle bifurcating from the equilibrium point $P_0$ of differential system (1.1) when $m = 0$ and $h = c_1 = c_2 = 0,$ and this system is perturbed in the form (1.2).

Moreover, under condition $\mathcal{C}_+$ of (ⅳ), we have $r_+ > 0.$ In this case, $\dfrac{\partial f_2}{\partial r}(r_+)$ can be positive or negative depending on the choice of the parameters $d, n > 0.$ Therefore, the periodic orbit is stable if $n^2-8dn+5d^2 > 0$ and unstable if $n^2-8dn+5d^2 < 0.$

On the other hand, under condition $\mathcal{C}_-$ of (ⅳ), we have $r_- > 0.$ In this case, we have

and the periodic orbit is stable.

3.   Examples

Example 3. Consider the following differential system in $\mathbb{R}^4:$

This particular system has the form (1.2) with $a = b = d = c_{12} = 1,$ $n = \frac{1}{10},$ $h_1 = \frac{2}{100},$ $h_2 = 0,$ and $c_{22} = 2.$

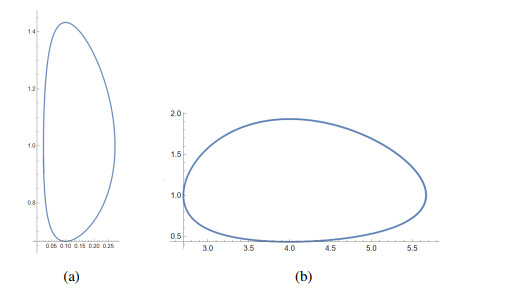
A direct computation shows that this choice of the parameters satisfies the hypothesis (ⅰ)–(ⅳ) of Theorem 2. Then, for $\varepsilon > 0$ sufficiently small, this differential system has a limit cycle in the positive quadrant. Moreover, as $2d-n = 1.9 > 0$ and $n^2-8dn+5d^2 = 4.21 > 0,$ this periodic orbit is stable. See this limit cycle in Figure 1(a).

Example 4. Consider the following differential system in $\mathbb{R}^4:$

In this case the system has the form (1.2) with $a = b = d = c_{12} = 1,$ $n = 4,$ $h_1 = \frac{2}{100},$ $h_2 = 0$ and $c_{22} = 2.$

A direct computation shows that this choice of parameter satisfies the hypothesis (ⅰ)–(ⅳ) of Theorem 2. Then, for $\varepsilon > 0$ sufficiently small, this differential system has a limit cycle in the positive quadrant. Moreover, as $2d-n = -2 < 0,$ this periodic orbit is stable. See this limit cycle in Figure 1(b).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author is partially supported by Fapeps grant number 2019/10269-3. The second author is partially supported by the Agencia Estatal de Investigación of Spain grant PID2022-136613NB-100, the H2020 European Research Council grant MSCA-RISE-2017-777911, AGAUR (Generalitat de Catalunya) grant 2021SGR00113, and by the Real Acadèmia de Ciències i Arts de Barcelona.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix

In this section, we briefly describe the basic results from the averaging theory that we shall need for proving the main result of this paper.

The averaging theory of second order provides a method for finding periodic orbits bifurcating from a Hopf equilibrium point of a differential system when the first averaging function $f_1({y})$ is identically zero. In the literature, this is called the second order averaging theory, and it is a particular case of the $k$–th order averaging theory that can be found in ^[15].

Theorem 5 (Second order averaging theory for computing periodic orbits). Consider the differential system

and suppose that $F_i(t, .)\in C^{2-i}$ for all $t\in\mathbb{R},$ $i = 1, 2,$ and $R$ and $F_2$ are locally Lipschtz with respect to ${x}.$ Assume that the first averaging function

is identically zero and that the second averaging function

where

Moreover, suppose that for $p\in D$ with $f_2(p) = 0,$ there exists a neighborhood $V\subset D$ of a such that $f_2({y})\neq0$ for all ${y}\in\bar{V}\setminus\{p\},$ and that the Brouwer degree $d_B(f_2({y}), V, p)\neq0.$

Then, for $\varepsilon$ sufficiently small, there exists a $T$–periodic solution ${x}(t, \varepsilon)$ of system (3.3) such that ${x}(t, \varepsilon)\rightarrow p$ when $\varepsilon\rightarrow 0^+.$

Remark 6. Let $f:D\rightarrow \mathbb{R}^n$ be a $C^1$ function, with $f(p) = 0,$ where $D$ is an open subset of $\mathbb{R}^n$ and $p\in D.$ Whenever $p$ is a simple zero of $f$ (i.e., the Jacobian $J_f(p)$ of $f$ at $p$ is not zero), then there exists a neighborhood $V$ of $p$ such that $f(z)\neq0$ for all $z\in\overline{V}\backslash\{p\}$ and $d_B(h, V, p)\in\{-1, 1\}.$ See ^[16] for the details.

The averaging theory provides information on the location of the periodic orbits. Thus if $p$ is a zero of the averaged function $f_2(z)$ with $d_B(f_2, V, p)\ne 0$, then there is a limit cycle ${x}(t, \varepsilon)$ of system (1.2) satisfying that ${x}(0, \varepsilon)\rightarrow p$ when $\varepsilon\rightarrow0.$ So, $p$ is an initial condition for the periodic orbit which bifurcates to the limit cycle ${x}(t, \varepsilon).$

As the first nonzero averaging function is the first nonzero coefficient (modulo a constant) in the displacement function for a $C^2$–differential system, the second order averaging theory also provides, in this case, the stability or unstability of the periodic orbits.