Positive periodic solutions for discrete Nicholson system with multiple time-varying delays

1.   Introduction

Flies are complete metamorphosis insects that contain various species, including Muscidae (houseflies), Calliphoridae (blowflflies) Drosophilae (fruitflies) and Scrcophagidae (fleshflies), etc. The life history of flies can be divided into egg, larva, pre-pupa, pupa and adult stages. Although the life span of flies is only about one month, they are very fertile and multiply rapidly in a short period ^[1]. The feeding habits of flies are very complex. They can feed on a variety of substances, such as human food, animal waste, kitchen scraps and other refuses. It is known to us that flies transmit various pathogens from filth to humans and cause many diseases ^[2,3,4]. On the other hand, flies are also beneficial to medical research, ecosystem food chain and pollen dispersal. Considering medical research, for example, fruit fly Drosophila is of great significance in studying the pathogenesis and therapy of human diseases. The nervous system of Drosophila is much simpler than that of human beings, but it also exhibits complex behavioral characteristics similar to humans ^[5,6]. Therefore, studying fly population dynamics is of crucial importance to both nature and human society.

The study of biological population growth model promotes the development of human society to a great extent. It has important applications in population control, social resource allocation, ecological environment improvement, species protection and human life and health ^[7,8,9]. To understand the population dynamics of the Australian sheep blowfly, Gurney et al. ^[10] constructed the autonomous delay differential equation

based on experimental data ^[11,12]. In this model, $x$ is the density of mature blowflies, $\delta$ is the daily mortality rate of adult blowflies, $P$ is the maximum daily spawning rate of female blowflies, $\tau$ is the time required for a blowfly to mature from an egg to an adult, $1/\gamma$ is the blowfly population size at which the production function $f(u) = ue^{-\gamma u}$ reaches the maximum value. Subsequently, this model and its modified extensions were continually used to describe rich fly dynamics.

Environmental changes play an important role in biological systems. The influence of a periodically changing environment on the system is different from that of a constant environment, and it can better facilitate system evolution. Moreover, delay is one of the important factors which can change the dynamical properties and result in more rich and complex dynamics in biological systems ^[13,14]. Many researchers have assumed periodic coefficients and time delays in the system to combine with the periodic changes of the environment ^{[15,16,17,18]}. For related literature, we refer to ^[19,20]. However, considering the fact that adult flies number is a discrete value that varies daily and the situations where population numbers are small and individual effects are important or dominate, a discrete model would indeed be more realistic to describe the population evolution in discrete time-steps ^[21,22,23].

Interactions between different species are extremely important for maintaining ecological balance. Such interactions are typically direct or indirect between multiple species, including positive interactions and negative interactions. Among them, the positive interactions can be divided into three categories according to the degree of action: commensalism, protocooperation and mutualism ^[24,25]. In the paper ^[9], a delay differential Nicholson-type system concerning the mutualism effects with constant coefficients was proposed. The existence, global stability and instability of positive equilibrium were obtained. Based on this system, Zhou ^[26] and Amster ^[27] considered periodic Nicholson-type system combined with nonlinear harvesting terms. The main research theme is the existence of positive periodic solutions. Recently, Ossandóna et al. ^[28] presented a Nicholson-type system with nonlinear density-dependent mortality to describe the dynamics of multiple species, the uniqueness and local exponential stability of the periodic solution are established. However, relatively few studies on discrete dynamical systems have explored the mutualism of flies. In this paper, we consider the mutualism relationship between two fly species and establish a two-dimensional discrete Nicholson system with multiple time-varying delays

We assume that $a_i\!: \mathbb{Z} \to (0, 1)$, $b_i\!: \mathbb{Z} \to (0, \infty)$, $c_{ij}\!: \mathbb{Z} \to (0, \infty)$, $\tau_{ij}\!: \mathbb{Z} \to \mathbb{Z}^+$ and $\gamma_{ij}\!: \mathbb{Z} \to (0, \infty)$ are $\omega$-periodic discrete functions for $1 \le i \le 2$ and $1 \le j \le n$. The period $\omega$ is a positive integer. Moreover, the interaction rate of second fly specie on first fly species and that of first fly specie on second fly species are represented by $b_1$ and $b_2$, respectively.

Because $\tau_{ij}$ $(1 \le i \le 2)$ have $\omega$-periodicity, we can find the maximum values

of $\{\tau_{i1}(k)\}$, $\{\tau_{i2}(k)\}$, $\dots$, $\{\tau_{in}(k)\}$ for $i = 1, 2.$ Note that $0 < a_i(k) < 1$ for $k \in \mathbb{Z}$. Then, the solution $x(\cdot, \phi) = (x_1(\cdot, \phi_1), x_2(\cdot, \phi_2))^T$ of system (1.1) that satisfies the initial condition

is a positive solution. The purpose of this paper is to present sufficient conditions for the existence of positive $\omega$-periodic solution of (1.1).

2.   Priori bounds for parametric system and auxiliary lemma

We discuss the parametric delay difference system

for each parameter $\lambda\in (0, 1)$. Let $\underline{a}_i = \min_{1 \le k \le \omega}a_i(k)$ and $\overline{b}_i = \max_{1 \le k \le \omega}b_i(k)$ for $i = 1, 2$. Then, an estimation of upper and lower bounds of positive $\omega$-periodic solution of (2.1) can be conducted.

Proposition 2.1. Suppose that

and there exists a constant $\gamma > 1$ such that

Then, every positive $\omega$-periodic solution $x = (x_1, x_2)^{T}$ of (2.1) is bounded. Specifically,

where

in which $\underline{\gamma}_{1j} = \min_{1 \le k \le \omega}\gamma_{1j}(k),$ $\underline{\gamma}_{2j} = \min_{1 \le k \le \omega}\gamma_{2j}(k),$ $\overline{c}_{1j} = \max_{1 \le k \le \omega}c_{1j}(k),$ $\overline{c}_{2j} = \max_{1 \le k \le \omega}c_{2j}(k),$ $\overline{\gamma}_1 = \max_{1 \le j \le n}\{\max_{1\le k\le\omega}\gamma_{1j}(k)\}$ and $\overline{\gamma}_2 = \max_{1 \le j \le n}\{\max_{1\le k\le\omega}\gamma_{2j}(k)\}$.

Remark 1. Note that $A_i$ and $B_i$ are the lower bound and upper bound of $x_i$, respectively. We can verify the fact that $A_i < B_i$ for $i = 1, 2$. From the definitions of $A_1$ and $A_2$, we see that

Hence, we obtain

Similarly, it follows that

Proof. Let $x = (x_1, x_2)^{T}$ be arbitrary positive $\omega$-periodic solution of (2.1) under the initial condition (1.2). For $i = 1, 2$, we define

Then $\underline{x}_i \le x_i(k) \le \overline{x}_i$ for $k \in \mathbb{Z}^+\!$. We can rewrite system (2.1) into

Taking the maximum on both sides of the first equation of (2.4) in one period, we have

Similarly, we obtain

Hence, it leads to

and

By (2.5) and (2.6), basic computations show that

Note that $1-\lambda a_i(k) > 0$ for all $k \in \mathbb{Z}$ and $i = 1, 2$. Multiplying both sides of the two equation of (2.1) by $\prod_{r = 0}^{k}1/(1-\lambda a_1(r))$ and $\prod_{r = 0}^{k}1/(1-\lambda a_2(r))$ respectively, we have

and

Choosing natural numbers $k_1$ and $k_2$ such that

Summing both sides of (2.7) and (2.8) over $k$ ranging from $k_1$ to $k_1+\omega-1$ and $k_2$ to $k_2+\omega-1$ respectively, by using $x_i(k_i+\omega) = x_i(k_i) = \underline{x}_i$, we obtain

and

Note that $a_i$ $(i = 1, 2)$ is positive $\omega$-periodic. It follws that

Hence, we obtain

and

Recall that $\overline{\gamma}_i = \max_{1 \le j \le n}\{\max_{1\le k\le\omega-1}\gamma_{ij}(k)\}$ for $i = 1, 2$. We define $f_1(u) = ue^{-\overline{\gamma}_1u}$ and $f_2(u) = ue^{-\overline{\gamma}_2u}$ for $u\ge 0.$ Since $\underline{x}_i \le x_i(k) \le \overline{x}_i$ for all $k \in \mathbb{Z}^+\!$, it turns out that

Note that $k_1 \ge \overline{\tau}_1$. By using (2.3) and (2.10), we have

Calculating by the same way, from (2.3) and (2.11), we obtain

Then, it follows from (2.9) that

It is natural to divide the argument into two cases: (ⅰ) $f_i(\underline{x}_i) \le f_i(\overline{x}_i)$; (ⅱ) $f_i(\underline{x}_i) > f_i(\overline{x}_i)$.

Case (ⅰ): It follows from (2.12) that $\underline{x}_i > \gamma\:\!f_i(\underline{x}_i)$. Specifically, we have

which imply that $\underline{x}_1 > \ln\gamma/\overline{\gamma}_1$ and $\underline{x}_2 > \ln\gamma/\overline{\gamma}_2.$

Case (ⅱ): Function $f_i$ is unimodal and takes the only peak value at $1/\overline{\gamma}_i$. Also, $f_i$ monotonically increases on $\left[0, 1/\overline{\gamma}_i\right]$ and monotonically decreases on $\left[1/\overline{\gamma}_i, \infty\right)$. If $\overline{x}_i \le 1/1/\overline{\gamma}_i$, then we see that $f_i(\underline{x}_i) \le f_i(\overline{x}_i) \le f_i(1/\overline{\gamma}_i)$, which is a contradiction. Hence, it follows that $\overline{x}_i > 1/\overline{\gamma}_i$. Note that $\overline{x}_i \le B_i$. From (2.12), we obtain

and

Thus, we estimate

and

Now, it can be concluded that each positive $\omega$-periodic solution $x = (x_1, x_2)^{T}$ of (2.1) satisfies

and

for $k \in \mathbb{Z}^+\!$. The proof is complete.

Suppose that $X$ is a Banach space and $L\!: {\rm{Dom}}\ L \subset X \to X$ is a linear operator. The operator $L$ is called a Fredholm operator of index zero if

$({\rm{i}})$ ${\rm{dim}}\ {\rm{Ker}}\ L = {\rm{codim}}\ {\rm{Im}}\ L < +\infty,$

$({\rm{ii}})$ ${\rm{Im}}\ L$ is closed in $X.$

If $L$ is a Fredholm operator of index zero and $P$, $Q\!: X \to X$ are continuous projectors satisfying

where $I$ is the identity operator from $X$ to $X$, then the restriction $L_P\!: {\rm{Dom}}\ L\cap{\rm{Ker}}\ P \to {\rm{Im}}\ L$ is invertible and has the inverse $K_P\!: {\rm{Im}}\ L \to {\rm{Dom}}\ L\cap{\rm{Ker}}\ P$.

Let $N\!: X \to X$ be a continuous operator and $\Omega$ an open bounded subset of $X$. The operator $N$ is $L$-compact on $\overline{\Omega}$ if

$({\rm{i}})$ $QN(\overline{\Omega})$ is bounded,

$({\rm{ii}})$ $K_P(I-Q)N\!: \overline{\Omega} \to X$ is compact.

We present the continuation theorem of coincidence degree theory (for example, see ^[29,30]) as follows:

Lemma 2.2. Let $L\!: {\rm{Dom}}\ L \subset X \to X$ be a Fredholm operator of index zero and let $N\!: X \to X$ be $L$-compact on $\overline{\Omega}.$ Suppose that

$\rm (i)$ every solution $x$ of $Lx = \lambda Nx$ satisfies $x \not\in \partial\Omega$ for $\lambda \in (0, 1)$;

$\rm (ii)$ $QNx \not = 0$ for $x \in \partial\Omega\cap{\rm{Ker}}\ L$ and

Then, $Lx = Nx$ has at least one solution in $X \cap\, \overline\Omega.$

3.   Positive $\omega$-periodic solution

Theorem 3.1. Suppose that (2.2) and (2.3) hold. If

then system (1.1) has at least one positive $\omega$-periodic solution $x^*$.

Proof. Let $X$ be a set of $\omega$-periodic functions $x = (x_1, x_2)^T$ defined on $\mathbb{Z}^+$ and denote the maximum norm $||x|| = \max\{\max_{1 \le k \le \omega}|x_1(k)|, \max_{1 \le k \le \omega}|x_2(k)|\}$ for any $x \in X$. Then, $X$ is a Banach space. Moreover, we define

and

It is not difficult to show that $L$ is a linear operator from $X$ to $X$ and $N$ is a continuous operator from $X$ to $X$.

From the definition of $L$, we see that

It turns out that ${\rm{dim}}\ {\rm{Ker}}\ L = 2 = {\rm{codim}}\ {\rm{Im}}\ L < +\infty$ and ${\rm{Im}}\ L$ is closed in $X$. Thus, $L$ is a Fredholm operator of index zero.

We define $P\!: X \to X$ by

and let $Q = P$. Then, $P$ and $Q$ are two continuous projectors such that ${\rm{Im}}\ P = {\rm{Ker}}\ L$ and ${\rm{Ker}}\ Q = {\rm{Im}}\ L = {\rm{Im}}\ (I-Q)$.

It can be shown that the restriction $L_P\!\!: {\rm{Dom}}\ L\cap{\rm{Ker}}\ P \to {\rm{Im}}\ L$ has the inverse $K_P\!\!: {\rm{Im}}\ L \to {\rm{Dom}}\ L\cap{\rm{Ker}}\ P$ given by

for $x = (x_1, x_2)^T \in {\rm{Im}}\ L$. In fact, for $i = 1, 2$, since

for all $k \in \mathbb{Z}^+\!$, we see that $K_P x\in {\rm{Dom}}\ L$. Moreover, it follows that

Hence, $K_Px \in {\rm{Ker}}\ P$.

For any $x \in {\rm{Im}}\ L$, one has

Furthermore, for any $x \in {\rm{Dom}}\ L\cap{\rm{Ker}}\ P$, one has

Since $x \in {\rm{Ker}}\ P = {\rm{Ker}}\ Q = {\rm{Im}}\ L$, we see that $\sum_{s = 1}^{\omega}x_i(s) = 0$. Hence, $(K_PL_Px)_i = x_i(k) = (Ix)_i$. We therefore conclude that $K_P = L_P^{-1}$.

We define

and prove that the operator $N$ defined above is $L$-compact on $\overline{\Omega}$. We first check that $QN(\overline{\Omega})$ is bounded.

Since $x_1(k) < B_1+1$ and $x_2(k) < B_2+1$ for $k \in \mathbb{Z}^+$, we obtain

and

for $x\in \overline{\Omega}$. Hence, the operator $QN$ is bounded on $\overline{\Omega}$.

We next show that $K_P(I-Q)N\!: \overline{\Omega} \to X$ is compact. From the definitions of $N$, $QN$ and $K_p$, we obtain

Meanwhile, we have

for $x \in X$. For any bounded subset $E\subset \overline{\Omega}\subset X$, it is a subspace of a finite dimensional Banach space $X$. Hence, $E$ is closed, and therefore $E$ is compact. By a straightforward calculation, it can be proven that $K_P(I-Q)N(E)$ is relatively compact.

An arbitrary $\omega$-periodic solution of (2.1) corresponds one-to-one to a solution of $Lx = \lambda Nx$ with parameter $\lambda \in (0, 1)$. Proposition 2.1 displays that each positive solution $x = (x_1, x_2)^T$ of $Lx = \lambda Nx$ satisfies that $A_1 < x_1 \le B_1$ and $A_2 < x_2 \le B_2$. It is obvious that if $y = (y_1, y_2)^T\in\partial\Omega$, then $y$ is never a solution of $Lx = \lambda Nx$. Hence, the condition (i) of Lemma 2.2 holds. If $x = (x_1, x_2)^T \in \partial\Omega\cap{\rm{Ker}}\ L$, then there are four cases to be considered: (1) $x = (A_1, x_2)^T$, (2) $x = (B_1+1, x_2)^T$, (3) $x = (x_1, A_2)^T$, (4) $x = (x_1, B_2+1)^T$.

Case (1): It follows from $x_1 \equiv A_1$ that

Since $A_1 \le \ln\gamma/\overline{\gamma}_1$, we see that $e^{A_1\overline{\gamma}_1}\le\gamma$. Hence, $(QNx)_{1} > 0$.

Case (2): Because of $x_1 \equiv B_1 + 1$, we have

Similarly, we can show that $(QNx)_{2} > 0$ in Case (3) and $(QNx)_{2} < 0$ in Case (4). We therefore conclude that $QNx = ((QNx)_{1}, (QNx)_{2})^T\not = 0$ for each $x\in \partial\Omega\cap{\rm{Ker}}\ L$.

Define a continuous operator $H\!: \Omega\cap{\rm{Ker}}\ L\times[0, 1] \to X$ by

Recall that the elements of $\partial\Omega\cap{\rm{Ker}}\ L$ are vectors satisfying $x = (A_1, x_2)^T$, $y = (B_1+1, y_2)^T$, $z = (z_1, A_2)^T$ and $w = (w_1, B_2+1)^T$. For $x = (A_1, x_2)^T$, we can check that

Moreover,

for $y = (B_1+1, y_2)^T$. Hence, $H(x, \mu) \not = 0$ and $H(y, \mu) \not = 0$. By similar computations, we have $H(z, \mu) \not = 0$ and $H(w, \mu) \not = 0$. Therefore, we see that $H(x, \mu) \not = 0$ for $(x, \mu) \in \partial\Omega\cap{\rm{Ker}}\ L\times[0, 1]$. Thus, $H$ is a homotopic mapping. Using the homotopy invariance, we have

Hence, the condition (ⅱ) of Lemma 2.2 holds. Therefore, the equation $Lx = Nx$ has at least one solution located in $X \cap\, \overline\Omega$. Thus, from Lemma 2.2, we obtain that there is a positive $\omega$-periodic solution of system (1.1). The proof is now complete. □

4.   Existence of positive 4-periodic solution

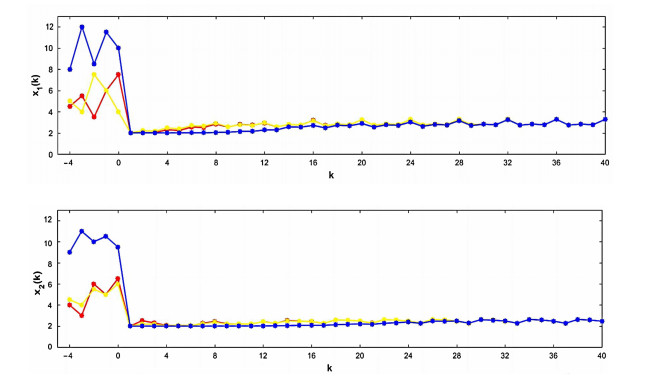
Consider the delay difference system

Here, we assume that

In addition, $a_i(k) = a_i(k+4)$, $b_i(k) = b_i(k+4)$, $c_{ij}(k) = c_{ij}(k+4)$ and $\gamma_{ij}(k) = \gamma_{ij}(k+4)$ for $k \in \mathbb{Z}$, $i = 1, 2$ and $j = 1, 2$. Theorem 3.1 shows that the system has at least one positive $4$-periodic solution.

It is clear that $\omega = 4$, $a_i$, $b_i$, $c_{ij}$, $\gamma_{ij}$ and $\tau_{ij}$ $(1 \le i \le 2, \, 1 \le j \le 2)$ are $\omega$-periodic discrete functions satisfying $0 < a_i(k) < 1$, $0 < b_i(k) < 1$, $c_{ij}(k) > 0$ and $\gamma_{ij}(k) > 0$ for $k\in\mathbb{Z}^+$. Since $\underline{a}_1 = 1/5$, $\underline{a}_1 = 1/2$, $\overline{b}_1 = 1/4$ and $\overline{b}_2 = 1/12$, we see that

Hence, condition (2.2) is satisfied. Let $\gamma = 11/10 > 1$. Then, we can easily check condition (2.3)

for $k = 1, 2, 3, 4$. Moreover, it can be calculated that

Namely, condition (3.1) holds. Therefore, from Theorem 3.1, it turns out that the system has at least one positive $4$-periodic solution.

5.   Conclusions

A discrete Nicholson system that describles the dynamics of two fly species is studied in this paper. The system considers the mutualism effect between fly species. Continuation theorem of coincidence degree theory is used effectively to seek sufficient conditions for the existence of a positive periodic solution. It is easy to check whether these sufficient conditions hold or not by using coefficients. The positive periodic solution indicates a cycle change in the adult fly populations. From the obtained result, we found that mutualistic interactions between species plays an important role in adult flies populations. But the increase in the flies populations resulting from maximum cumulative mutualism effect only should be less than the death of the flies populations because there is the natural generation of flies populations. Moreover, to avoid species extinction and maintain the coexistence of two fly species in a mutually beneficial environment, we see that (ⅰ) the adult fly population produced by maximum daily spawning should exceed a constant multiple of dead fly population for each fly species, and the multiple is greater than constant 1 and (ⅱ) the total population growth must be maintained more than the population loss for each fly species. In fact, the third sufficient condition (3.1) of Theorem 3.1 can be rewritten into the form

The left side of each inequality represents the production of one fly species in a period under the mutualism influence of another, and the right side represents the death of that species in a period. Hence, statement (ⅱ).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The paper is supported by College Students Innovations Special Project funded by Northeast Forestry University of China (Grant No. 202210225156) and Fundamental Research Funds for the Central Universities of China (Grant No. 41422003).

Conflict of interest

The authors declare that there is no conflicts of interest.