Predicting secondary school mathematics teachers' digital teaching behavior using partial least squares structural equation modeling

1.   Introduction

In the 21^st century, digital technologies are widely used in education. These technologies include but are not limited to general teaching software (e.g., PowerPoint), subject-specific teaching software (e.g., The Geometer's Sketchpad, GeoGebra), digital games (e.g., Morabaraba, Kahoot), various online education resources (e.g., learning websites and online courses) and various digital teaching devices (e.g., interactive whiteboard) ^[1]. The abilities to access, manage, understand, integrate, communicate, evaluate, create and disseminate information safely and appropriately through digital technologies ^[2] are becoming more and more important for each citizen, which is especially true for every teacher ^[3,4]. Effective use of digital technologies in teaching has been a concern in many educational systems ^[5,6]. In many countries, this has led to notable investment in educational technology facilities to enable their integration in the process of teaching and learning. In 2021, United Nations Educational, Scientific and Cultural Organization (UNESCO) issued a document named Reimagining our futures together: In a new social contract for education aiming to expand the time and space of education, strengthen digital infrastructure, manage digital learning spaces, and use digital technologies to support public and inclusive education for the future ^[7]. In 2022, the Chinese Ministry of Education released the Standards for Teacher's Digital Literacy, which clearly stated that teachers should enhance their awareness, ability and responsibility to utilize digital technologies to optimize, innovate and transform educational activities ^[1]. Teachers must be able to use digital technologies appropriately to improve their teaching effectiveness and efficiency. However, the situation of using digital technologies in teaching does not inspire optimism ^{[8,9,10,11,12,13,14]}. Therefore, it is critical to investigate the influential factors in the adoption of digital technologies aiming to improve the digital teaching of secondary school mathematics teachers.

Many previous studies have explored the effects of digital teaching behavior of secondary school mathematics teachers ^[15,16,17]. For example, some research revealed that dynamic mathematics software could promote teachers' professional development and students' understanding of mathematics content ^[18,19]. However, limited research explored what factors influence the digital teaching behavior of secondary school mathematics teachers ^[20,21,22]. The effective use of digital technologies in mathematics teaching depends on multiple factors. These factors can have different levels of analysis: the social, political, economic and cultural level, the mathematical and epistemological level, the school and institutional level and the classroom and didactical level ^[15]. Some possible factors have been mentioned, which include teachers' beliefs about, and attitudes towards the technology, as well as their perception of the nature of mathematical knowledge and how it should be learned ^[5]. Perceived usefulness (such as, how well using technology aligned with the goals of a lesson) and perceived ease of use have also been confirmed ^[16]. Some obstacles have been identified, such as a lack of time and supportive professional development, no access to appropriate digital technology and poor technical support ^[5,15,17]. The purpose of this study is to find out the main predictors of secondary school mathematics teachers' digital teaching behavior. Specifically, this study will try to answer the following two research questions based on the extended unified theory of acceptance and use of technology (UTAUT) model and the partial least squares structural equation modeling (PLS-SEM) method:

1) What factors positively affect the digital teaching behavior of secondary school mathematics teachers based on an extended UTAUT model?

2) Which is the biggest predictor of digital teaching behavior of secondary school mathematics teachers?

This paper has been divided into the following main sections: The first section is an introduction about the research background and previous studies closely related to teachers' digital teaching behavior. The second section is a literature review, in which a secondary school mathematics teachers' digital teaching behavior conceptual model is proposed based on the UTAUT model and also the concept of technological pedagogical content knowledge (TPACK) and attitude are integrated into it, followed by the relevant hypotheses. In the third section, the method and process for instrument development, data collection and data analysis are described in detail. The fourth section describes the results based on the standard procedure on how to report the results of partial least squares structural equation modeling, and the main findings are emphasized and explained. Finally, the conclusion section consists of a summary of results, practical and theoretical implications, limitations and suggestions for future research.

2.   Literature review

2.1.   Digital technologies in secondary school mathematics teaching

Digital technologies are more effective and efficient for secondary school content than elementary school content. Although research on digital technologies covers all stages of K-12, most of them focus on teaching at secondary school level ^[23]. With regard to mathematics education, the current studies have shown that digital technologies, combined with appropriate pedagogy, may have the potential to address some of the issues commonly associated with mathematics in secondary schools, having the capacity to facilitate realistic, problem-solving and collaborative approaches to teaching ^[24], thus providing coherency and context for the mathematics ^[25].

Digital technologies are adopted in various aspects of secondary school mathematics teaching. Online teaching platforms are frequently used for augmenting discussion and cooperation ^[26]. For example, Bozkurt and Ruthven's research showed how the teacher managed a number of aspects of classroom teaching related to using GeoGebra, such as including technology-mediated tasks aligned with his pedagogical goals, preparing his students to use the technology efficiently, and adapting formats for classroom activity ^[27]. Furthermore, digital games should also be noted as digital teaching tools because digital game-based learning has been perceived as a promising method for teaching mathematics ^[28]. It can be used in the mathematics classroom to promote the learning of mathematics ^[29]. Ortiz-Martínez et al. ^[30,31] found a game named Kahoot! has a direct effect on continuous learning. Other researchers also certified flipped learning with gamification promotes students' cognitive engagement ^[32]. The development of different innovative technologies has enabled the replication of mathematical experiences based on technology both within and external to the classroom ^[26]. Even though students prefer regular face-to-face teaching, they are content with the quality of their teachers' remote mathematics teaching ^[33]. There has been increased focus among educational scholars and practitioners on the utilization of mobile technologies (e.g., tablets) by teachers and learners in the field of mathematics because of their portability ^[34]. Digital technologies can support skills and strategies that are highly relevant in their mathematical content, such as real-world problem solving ^[35]. It can also support learning through interactive and scaffolded activities ^[36].

2.2.   UTAUT and digital teaching behavior

There were many theories and models to analyze user's technology acceptance, such as theory of planned behavior (TPB), technology acceptance model (TAM) and unified theory of acceptance and use of technology (UTAUT) ^[37,38]. Among them, the UTAUT model is preferred by many researchers because it integrates multiple models and theories ^[39], which has more powerful explanatory and predictive power for dependent variables. The UTAUT model contains four core independent variables: performance expectancy (PE), effort expectancy (EE), social influence (SI) and facilitating conditions (FC). Performance expectancy refers to the degree to which users believe that using technology can improve their job performance. The level of ease of use for a technology medium is defined as Effort expectancy. The degree to which a person feels that important people around him/her believe that someone should use technologies or a technological system is referred to as social influence. Facilitating conditions are the degree to which a person believes that an environment supports the use of technology. According to the UTAUT model ^[39], performance expectancy, effort expectancy and social influence directly affect users' behavioral intention; facilitating conditions directly affect usage behavior, and users' behavioral intentions directly affect usage behavior. The UTAUT model is widely used because its explanatory power of user behavior is nearly 70%, which is higher than other technology acceptance models ^{[9,40,41,42,43]}. The UTAUT model provides the main influential factors of technology usage behavior, so it may be used to explain and predict teachers' digital teaching behavior. In most previous studies, the UTAUT model was used to explain behavioral intention. A few researchers applied this model to predict the factors of technology usage behavior in the field of education ^{[44,45,46,47,48,49]}. This study adopted an extended UTAUT model to explore the predictors of the digital teaching behavior of secondary school mathematics teachers.

2.3.   Attitude towards the integration of technology

Attitude may refer to someone's judgment of something, which may be either positive or negative. On technology, attitude may refer to one's feelings, their likes and dislikes about technology ^[50,51]. It can help to clarify decisions that teachers make in teaching and how they prepare to teach with technology ^[52]. The attitudes of teachers are seen to play a significant role in technology usage in the educational field ^[53,54,55]. If educators desire to utilize technology effectively in their classrooms, they need to have positive attitudes about using it ^[56]. In the recent study, attitude towards technology directly influences four independent variables in the original UTAUT model ^[57]. In this study, mathematics teachers' attitude toward technology is one of the mediating variables assumed to influence behavioral intention and digital teaching behavior, which were measured by four items developed from the Standard for Teacher Digital Literacy issued by the Chinese Ministry of Education in 2022 ^[1].

2.4.   TPACK framework

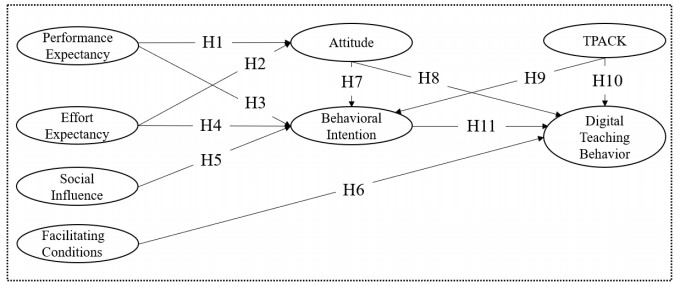
The famous framework of teacher knowledge was proposed by Shulman ^[58] who asserted that teachers need pedagogical (P) content (C) knowledge (K), now popularly referred to simply as PCK. With the infusion of technology in education, Mishra and Koehler ^[59] expanded the PCK concept by adding technology to represent the technological pedagogical content knowledge (TPACK) framework. Finally, TPACK was a form of knowledge that went beyond all three basic components of teacher knowledge (technology, pedagogy and content). The TPACK framework was used in various fields ^{[60,61,62,63,64]}. Besides, it had been used for the assessment of digital competence level of teachers ^[65,66]. There are three classifications for applying the TPACK framework to research. First, most research contains seven aspects, namely technological knowledge (TK), pedagogical knowledge (PK), content knowledge (CK), pedagogical content knowledge (PCK), technological content knowledge (TCK), technological pedagogical knowledge (TPK) and TPACK ^[67]. Second, several studies just include the core of the TPACK framework, which consists of four key components: (1) an overarching conception for the purpose of integrating information technology into subject teaching; (2) knowledge of curriculum resources and organization for integrating information technology into subject teaching; (3) knowledge of instructional strategies and representations for integrating information technology into subject teaching; (4) knowledge of students' understandings and misconceptions for integrating information technology into subject teaching ^[68,69]. Third, some research models focus on technology dimension, which only absorbed technological knowledge (TK), technological content knowledge (TCK), technological pedagogical knowledge (TPK) and TPACK into their models ^[70,71]. This study focused on teachers' digital teaching behavior. Therefore, the third classification was adopted. TPACK was usually regarded as the important external factor in the technology acceptance model, and a significant supplement to the UTAUT ^[70]. In this study, mathematics teachers' technological pedagogical content knowledge (TPACK) is one of the independent variables assumed to influence both behavioral intention and digital teaching behavior. The initial hypotheses are as follows: (1) performance expectancy, effort expectancy and social influence positively affect behavioral intention; (2) behavioral intention and facilitating conditions positively affect digital teaching behavior; (3) performance expectancy and effort expectancy positively affect attitude; (4) attitude positively affects both behavioral intention and digital teaching behavior; (5) TPACK positively affects both behavioral intention and digital teaching behavior. The extended UTAUT digital teaching behavior conceptual model for secondary school mathematics teachers is shown in Figure 1.

Figure 1.  An extended UTAUT digital teaching behavior conceptual model for secondary school mathematics teachers.

DownLoad: Full-Size Img PowerPoint

The following are the initial hypotheses that will be tested in this study.

H1: Performance expectancy affects secondary school mathematics teachers' attitude towards using digital technology.

H2: Effort expectancy affects secondary school mathematics teachers' attitude towards using digital technology.

H3: Performance expectancy affects secondary school mathematics teachers' behavioral intentions of using digital technology.

H4: Effort expectancy affects secondary school mathematics teachers' behavioral intentions of using digital technology.

H5: Social influence affects secondary school mathematics teachers' behavioral intentions of using digital technology.

H6: Facilitating conditions affect secondary school mathematics teachers' digital teaching behavior.

H7: Attitude affects secondary school mathematics teachers' behavioral intentions of using digital technology.

H8: Attitude affects secondary school mathematics teachers' digital teaching behavior.

H9: TPACK affects secondary school mathematics teachers' behavioral intentions of using digital technology.

H10: TPACK affects secondary school mathematics teachers' digital teaching behavior.

H11: Behavioral intention of using digital technology affects secondary school mathematics teachers' digital teaching behavior.

3.   Methodology

In order to investigate the main predictors of secondary school mathematics teachers' digital teaching behavior, a quantitative method was employed in this study. Six constructs, namely, performance expectancy, effort expectancy, social influence, facilitating conditions, behavioral intention and digital teaching behavior in the instrument, were adopted from the UTAUT model ^[39]. The instrument also included TPACK and attitude as two new constructs. The data were gathered using a self-designed questionnaire based on the extended UTAUT model. They were collected from 385 junior high school mathematics teachers in a state-level new area, which is located in a middle province of China. The data were analyzed using the partial least squares structural equation modeling (PLS-SEM) method.

3.1.   Instrument development

An instrument was developed to investigate the main predictors of digital teaching behavior of secondary school mathematics teachers. A number of papers were initially reviewed in order to assess the feasibility of questionnaire's items. A portion of the questionnaire was designed based on the items proposed by Venkatesh et al. ^[39,72] and the traits of digital teaching. In particular, the duration, frequency and number of tasks completed using digital technology were taken into consideration while designing the components of digital teaching behavior ^[73]. Additionally, several items based on the TPACK core component model ^[69] were also added into the questionnaire, and then a pilot study was conducted in a junior high school in Changsha on 10 May 2023. However, the discriminant validity was not satisfactory between TPACK and digital teaching behavior (DTB). Therefore, the items of TPACK were revised according to the TPACK framework ^[59]. Three items of TPACK were replaced with the following ones: "I am familiar with the illustration of various digital technology", "I can use appropriate digital technology to teach according to the different curriculum content" and "I know that some of the curriculum content will be replaced by other content due to the use of new digital technology". Then, the questionnaire items were consulted with two professors and nine other researchers for the evaluation of content validity. The final version of the questionnaire (Appendix A) was obtained after being revised due to suggestions for improvement. All 34 measurement items used a 5-point Likert scale ranging from strongly disagree (1 point) to strongly agree (5 points).

3.2.   Data collection

The questionnaire was made by the Wenjuanxing application (https://www.wjx.cn). Four hundred and six junior high school mathematics teachers filled in the questionnaire, which is more than 95 percent of all junior high school mathematics teachers in this state-level new area. Three hundred and eighty-five of them provided valid data. Because the respondents' data were anonymous, they were not forced to give their names and identities. The respondents were informed that the investigation was voluntary and all information was only for this study. These hints are supposed to reduce social desirability bias ^[74]. Since almost all junior high school mathematics teachers in the state-level new area participated in this survey study, the non-response bias is supposed to have no impact on the results. Also, we mentioned that the purpose of the research was to identify the predictors of secondary school mathematics teachers' digital teaching behavior.

According to Table 1, there are 134 male and 251 female teachers, and 366 and 19 teachers are of Han and minority nationality, respectively. 41.6% of teachers have an intermediate professional title, 52.7% of teachers have a junior professional title and 5.7% of teachers possess a senior professional title. It is worth noting that 77.4% of teachers hold a bachelor's or associate degree and 22.6% of teachers hold a master's degree. Most teachers report that they have taught for at least six years (65.5%). Nearly all of them work in urban schools (92.5%), and only 7.5% of these teachers work in rural schools. More specific demographic information about the teachers is shown in Table 1. The questionnaire was completed in 6 minutes on average, indicating that these teachers paid attention to details.

Table 1.  Demographics data of the secondary school mathematics teachers.

Demographic	Type	Number (N = 385)	Percentage (%)
Gender	Male	134	34.8
	Female	251	65.2
Nationality	Han	366	95.1
	Minor	19	4.9
Professional title	Primary	203	52.7
	Intermediate	160	41.6
	Senior	22	5.7
Level of education	Bachelor's or associate degree	298	77.4
	Master's degree	87	22.6
Teaching experiences	Less than 5 years	133	34.5
	6–15 years	165	42.9
	Over 15 years	87	22.6
School location	Urban	356	92.5
	Rural	29	7.5

---

 | Show Table

DownLoad: CSV

3.3.   Data analysis

The quantitative data were analyzed using SPSS 26, Mplus 8.3 and SmartPLS 4. First, data cleaning and descriptive analysis were conducted using SPSS 26. The Kolmogorov-Smirnov test ^[75] was then used to find out whether the data are normal distribution. Second, given that all the data comes from a single source, the presence of common method variance bias has been evaluated using Harman's single factor test ^[76], which tests the hypothesis that a single factor can account for all of the variance in their data. Confirmatory factor analysis (CFA) was conducted in Mplus 8.3 with a single factor model and an eight-factor model (performance expectancy, effort expectancy, social influence, facilitating conditions, technological pedagogical content knowledge, attitude, behavioral intention and digital teaching behavior). The fitting results showed that the eight-factor model (χ² = 989.040, df = 506, χ²/df = 1.95 < 3, RMSEA = 0.050 < 0.08, CFI = 0.940 > 0.9, TLI = 0.933 > 0.9, SRMR = 0.051 < 0.08) is much better than the single factor model (χ² = 3252.030, df = 527, χ²/df = 6.17 > 3, RMSEA = 0.116 > 0.08, CFI = 0.660 < 0.9, TLI = 0.638 < 0.9, SRMR = 0.097 > 0.08), which demonstrates that there is no problem of common method variance bias. Third, factors affecting secondary school mathematics teachers' digital teaching behavior were investigated by SmartPLS 4. When the purpose of the study focuses on the explanation and prediction, PLS-SEM is thought to be a more appropriate SEM approach than the traditional covariance-based structural equation modeling (CB-SEM) approach. It is especially true when the sample distribution is non-normal or the sample size is small ^[77]. Since the purpose of this study is to find the predictors of teachers' digital teaching behavior, and the sample data don't follow a normal distribution, PLS-SEM is more suitable to analyze the data ^[13]. Moreover, it is effective in performing traditional linear regression analyses for problems with complex correlations and exploring theoretical extensions of established theories ^[78,79,80]. The two stages of PLS-SEM, according to Hair et al. ^[77], are measurement model evaluation and structural model evaluation. The outcomes were obtained using the PLS-SEM algorithm, bootstrapping and PLSpredict algorithm in SmartPLS 4.

4.   Results

There are two parts to present the results. Initially, the reflective measurement model evaluation shows indicator reliability, internal consistency reliability, convergent validity and discriminant validity of the digital teaching behavior conceptual model for secondary school mathematics teachers. Then, the structural model evaluation additionally reveals the model's overall goodness of fit, the result of collinearity examination, the significance and relevance of the structural model relationships, the coefficients of determination (R²), the effect size (f²) and the PLSpredict results. Finally, the partial least squares important-performance map analysis (IPMA) confirmed the results of the biggest predictor of secondary school mathematics teachers' digital teaching behavior.

4.1.   Measurement model evaluation

The reflecting measurement model's reliability and validity tests are conducted. According to Hair et al. ^[81], indicator loading greater than 0.708 is more suitable. The lowest outer loading is TPACK3 at 0.743. Additionally, at a significance level of 0.01, the t values of indicators are all greater than 2.57, demonstrating the measurement model has a good indicator reliability. At the same time, the Cronbach's alpha, exact reliability coefficient (ρ_A) and composite reliability (CR) (ρ_C) of all constructs surpass 0.7. Social influence has the lowest Cronbach's alpha value, the lowest exact reliability coefficient and the lowest composite reliability value at 0.864, 0.874 and 0.908, respectively. This means the measurement model has an excellent internal consistency reliability ^[81]. Social influence also has the lowest average variance extracted (AVE), which is 0.711 and higher than the critical value of 0.5 ^[81]. Therefore, the measurement model has a good convergent validity.

Table 2.  Results of reliability and convergent validity test.

Constructs	Indicators	Outer Loadings	t Values	Cronbach's Alpha (α)	Exact Reliability Coefficients (ρA)	Composite Reliability (ρC)	Average Variance Extracted (AVE)
Performance Expectancy (PE)	PE1	0.922	41.521	0.951	0.951	0.964	0.871
	PE2	0.939	66.146
	PE3	0.939	68.701
	PE4	0.933	62.510
Effort Expectancy (EE)	EE1	0.909	66.950	0.937	0.938	0.955	0.840
	EE2	0.923	74.445
	EE3	0.914	73.357
	EE4	0.920	83.390
Social Influence (SI)	SI1	0.864	45.325	0.864	0.874	0.908	0.711
	SI2	0.878	36.738
	SI3	0.754	18.176
	SI4	0.870	44.711
Facilitating Conditions (FC)	FC1	0.838	34.915	0.916	0.921	0.941	0.799
	FC2	0.901	53.371
	FC3	0.893	61.196
	FC4	0.941	116.863
Technological Pedagogical Content Knowledge (TPACK)	TPACK1	0.884	50.326	0.941	0.946	0.954	0.775
	TPACK2	0.905	47.014
	TPACK3	0.743	21.539
	TPACK4	0.913	69.967
	TPACK5	0.908	69.033
	TPACK6	0.917	80.698
Attitude (ATD)	ATD1	0.805	31.281	0.896	0.896	0.928	0.763
	ATD2	0.897	55.972
	ATD3	0.892	53.061
	ATD4	0.897	57.613
Behavioral Intention (BI)	BI1	0.927	70.733	0.941	0.943	0.958	0.850
	BI2	0.909	27.583
	BI3	0.907	30.596
	BI4	0.944	100.480
Digital Teaching Behavior (DTB)	DTB1	0.913	60.576	0.945	0.945	0.960	0.859
	DTB2	0.931	102.529
	DTB3	0.948	126.025
	DTB4	0.914	75.214

---

 | Show Table

DownLoad: CSV

Additionally, the discriminant validity is evaluated via the Fornell-Larcker criterion ^[82]. The correlation coefficients between the constructs should be smaller than the square root of AVEs. In Table 3, the bolded square root of AVEs of each construct on the diagonal is greater than the correlation coefficients, indicating the measurement model has an excellent discriminant validity.

Table 3.  Results of the Fornell-Larcker test for assessing discriminant validity.

Constructs	ATD	BI	DTB	EE	FC	PE	SI	TPACK
Attitude (ATD)	0.874
Behavioral Intention (BI)	0.725	0.922
Digital Teaching Behavior (DTB)	0.646	0.662	0.927
Effort Expectancy (EE)	0.638	0.553	0.755	0.917
Facilitating Conditions (FC)	0.564	0.581	0.677	0.679	0.894
Performance Expectancy (PE)	0.804	0.750	0.610	0.588	0.548	0.933
Social Influence (SI)	0.696	0.772	0.584	0.596	0.610	0.780	0.843
TPACK	0.589	0.601	0.843	0.768	0.744	0.535	0.556	0.881

---

 | Show Table

DownLoad: CSV

The results of calculating the heterotrait-monotrait (HTMT) ratio of correlation are more suited to concomitant with the Fornell-Larcker criterion when evaluating the discriminant validity ^[81]. The largest HTMT value is 0.892 (Table 4), which falls below the limit of 0.90, confirming the measurement model's discriminant validity ^[83].

Table 4.  Results of the HTMT test for assessing discriminant validity.

Constructs	ATD	BI	DTB	EE	FC	PE	SI	TPACK
Attitude (ATD)
Behavioral Intention (BI)	0.787
Digital Teaching Behavior (DTB)	0.703	0.700
Effort Expectancy (EE)	0.696	0.585	0.803
Facilitating Conditions (FC)	0.623	0.624	0.726	0.732
Performance Expectancy (PE)	0.870	0.789	0.644	0.622	0.588
Social Influence (SI)	0.794	0.852	0.654	0.669	0.691	0.866
Technological Pedagogical Content Knowledge (TPACK)	0.640	0.639	0.892	0.817	0.799	0.564	0.624

---

 | Show Table

DownLoad: CSV

At this point, the indicator reliability, internal consistency reliability, convergent validity and discriminant validity have been tested and presented, and the data are all acceptable. This means that the results of the measurement model evaluation are satisfactory, and the next step is the structural model evaluation.

4.2.   Structural model evaluation

The steps for assessing the structural model, according to Hair et al. ^[77], are as follows: (1) assessing the structural model for collinearity, (2) assessing the significance and relevance of the structural model relationships, (3) assessing the model's explanatory power and (4) assessing the model's predictive power. Nevertheless, Henseler et al. ^[84] pointed out that the overall goodness of fit of the model should be the starting point for model evaluation. This is especially true for the reflective measurement model. The suitability and robustness of the model are frequently assessed using the SRMR (standardized root mean square residual) and NFI (normed fit index) values ^[85,86].

The overall model fits well when SRMR is less than 0.08. In addition, an NFI value over 0.90 for the model is excellent ^[84]. However, a value over 0.80 is also acceptable ^[86]. The NFI value is 0.856, which is close to 0.9, and the SRMR value is 0.051 < 0.08. Consequently, the conceptual model for this study is reasonable.

The majority of VIF (variance inflation factor) values, as showed in Table 5, are substantially below the threshold of 3. Only two VIF values are slightly over 3, and they are still less than 5, indicating that the structural model is not affected by collinearity issues ^[81].

Table 5.  Results of evaluating the collinearity problem (inner model's VIF values).

Constructs	ATD	BI	DTB	EE	FC	PE	SI	TPACK
Attitude (ATD)		3.281	2.313
Behavioral Intention (BI)			2.388
Digital Teaching Behavior (DTB)
Effort Expectancy (EE)	1.528	2.867
Facilitating Conditions (FC)			2.422
Performance Expectancy (PE)	1.528	3.858
Social Influence (SI)		2.819
Technological Pedagogical Content Knowledge (TPACK)		2.566	2.545

---

 | Show Table

DownLoad: CSV

A bootstrap (5000 samples) technique was used to obtain the path coefficients, t values, p values, 95% confidence intervals and total effects. As we can see from Table 6, all of the hypothesized path relationships are supported except for H4 and H6. Specifically, both performance expectancy (PE) (b = 0.656, p < 0.001) and effort expectancy (EE) (b = 0.252, p < 0.001) have a direct positive impact on attitude, which confirm the hypotheses H1 and H2. It also shows that there are direct positive influences on behavioral intention from performance expectancy (b = 0.212, p = 0.020), social influence (b = 0.400, p < 0.001), attitude (b = 0.221, p < 0.001) and TPACK (b = 0.237, p = 0.001), which support the hypotheses H3, H5, H7 and H9, respectively. The direct effect of effort expectancy (b = −0.133, p = 0.052) on behavioral intention is not significant. As a result, H4 is rejected. Attitude (b = 0.134, p = 0.029), TPACK (b = 0.649, p < 0.001) and behavioral intention (b = 0.161, p = 0.003) have a direct positive impact on digital teaching behavior. As it turned out, hypotheses H8, H10 and H11 are confirmed. The impact of facilitating conditions (b = 0.025, p = 0.706) on digital teaching behavior is not significant. Therefore, H6 is rejected.

Table 6.  Significance testing results of the structural model path coefficients.

Relationships	Path Coefficients (β)	t Values	p Values	95% Confidence Intervals	Significance (p < 0.05)
H1: Performance Expectancy ® Attitude	0.656	14.087	0.000	[0.560, 0.743]	Yes
H2: Effort Expectancy ® Attitude	0.252	4.902	0.000	[0.149, 0.354]	Yes
H3: Performance Expectancy ® Behavioral Intention	0.212	2.321	0.020	[0.031, 0.382]	Yes
H4: Effort Expectancy ® Behavioral Intention	−0.133	1.944	0.052	[−0.268, −0.001]	No
H5: Social Influence ® Behavioral Intention	0.400	4.634	0.000	[0.238, 0.578]	Yes
H6: Facilitating Conditions ®Digital Teaching Behavior	0.025	0.378	0.706	[−0.096, 0.162]	No
H7: Attitude ® Behavioral Intention	0.221	3.814	0.000	[0.107, 0.334]	Yes
H8: Attitude ® Digital Teaching Behavior	0.134	2.189	0.029	[0.016, 0.251]	Yes
H9: TPACK ® Behavioral Intention	0.237	3.322	0.001	[0.103, 0.382]	Yes
H10: TPACK ® Digital Teaching Behavior	0.649	10.430	0.000	[0.521, 0.770]	Yes
H11: Behavioral Intention ® Digital Teaching Behavior	0.161	2.987	0.003	[0.055, 0.267]	Yes

---

 | Show Table

DownLoad: CSV

The results of calculating the indirect effects (Table 7) show that all indirect effects are significant at a 5% level except for the relationships "Performance Expectancy → Behavioral Intention → Digital Teaching Behavior", "Effort Expectancy →Attitude → Digital Teaching Behavior" and "Effort Expectancy → Behavioral Intention → Digital Teaching Behavior". The results of calculating the total effects (Table 8) show that all total effects are significant at a 5% level except for the relationships "Effort Expectancy → Behavioral Intention" and "Facilitating Conditions → Digital Teaching Behavior".

Table 7.  Significance analysis of the indirect effects.

Relationships	Total Indirect Effects	Indirect Effects (β)	t Values	p Values	95% Confidence Intervals	Significance (p < 0.05)
Performance Expectancy® Attitude ®Behavioral Intention	0.145	0.145	3.587	0.000	[0.068, 0.226]	Yes
Effort Expectancy®Attitude® Behavioral Intention	0.056	0.056	3.035	0.002	[0.010, 0.169]	Yes
Performance Expectancy® Attitude ®Digital Teaching Behavior	0.145	0.088	2.131	0.033	[0.003, 0.081]	Yes
Performance Expectancy®Behavioral Intention ®Digital Teaching Behavior		0.034	1.684	0.092	[0.007, 0.046]	No
Performance Expectancy® Attitude ®Behavioral Intention®Digital Teaching Behavior		0.023	2.332	0.020	[0.238, 0.578]	Yes
Effort Expectancy®Attitude® Digital Teaching Behavior	0.022	0.034	1.932	0.053	[0.004, 0.071]	No
Effort Expectancy®Behavioral Intention®Digital Teaching Behavior		−0.021	1.626	0.104	[−0.050, 0.000]	No
Effort Expectancy®Attitude® Behavioral Intention®Digital Teaching Behavior		0.009	2.302	0.021	[0.003, 0.017]	Yes
Social Influence®Behavioral Intention®Digital Teaching Behavior	0.064	0.064	2.629	0.009	[0.021, 0.117]	Yes
Attitude®Behavioral Intention®Digital Teaching Behavior	0.036	0.036	2.442	0.015	[0.010, 0.068]	Yes
TPACK®Behavioral Intention®Digital Teaching Behavior	0.038	0.038	2.123	0.034	[0.010, 0.079]	Yes

---

 | Show Table

DownLoad: CSV

Table 8.  Significance testing results of the total effects.

Relationships	Total Effects (β)	t Values	p Values	95% Confidence Intervals	Significance (p < 0.05)
Performance Expectancy ® Attitude	0.656	14.087	0.000	[0.560, 0.743]	Yes
Effort Expectancy ® Attitude	0.252	4.902	0.000	[0.149, 0.354]	Yes
Performance Expectancy ® Behavioral Intention	0.357	3.949	0.000	[0.168, 0.521]	Yes
Effort Expectancy ® Behavioral Intention	−0.077	1.083	0.279	[−0.219, 0.057]	No
Social Influence ® Behavioral Intention	0.400	4.634	0.000	[0.238, 0.578]	Yes
Facilitating Conditions ® Digital Teaching Behavior	0.025	0.378	0.706	[−0.096, 0.162]	No
Attitude ® Behavioral Intention	0.221	3.814	0.000	[0.107, 0.334]	Yes
Attitude ® Digital Teaching Behavior	0.170	2.668	0.008	[0.047, 0.289]	Yes
TPACK ® Behavioral Intention	0.237	3.322	0.001	[0.103, 0.382]	Yes
TPACK ® Digital Teaching Behavior	0.687	11.537	0.000	[0.568, 0.800]	Yes
Behavioral Intention ® Digital Teaching Behavior	0.161	2.987	0.003	[0.055, 0.267]	Yes
Performance Expectancy ® Digital Teaching Behavior	0.145	2.901	0.004	[0.051, 0.245]	Yes
Effort Expectancy ® Digital Teaching Behavior	0.022	0.896	0.370	[−0.026, 0.068]	No
Social Influence ® Digital Teaching Behavior	0.064	2.629	0.009	[0.021, 0.117]	Yes

---

 | Show Table

DownLoad: CSV

The structural model's explanatory power is evaluated by the coefficient of determination (R²) value, which represents the amount of variance in the endogenous construct explained by all of the exogenous constructs linked to it [77 (p. 195)]. The R² is a measure of in-sample predictive power. As a standard, R² values of 0.75, 0.50 and 0.25 can be considered substantial, moderate and weak, respectively ^[81]. The results of using the PLS-SEM show the explained variance is 68.8% for attitude, 69.7% for behavioral intention and 75.6% for digital teaching behavior (Figure 2). This suggests that 75.6% of the variance affecting the digital teaching behavior of secondary school mathematics teachers can be explained by the model. Meanwhile, the variables outside of this model are responsible for the other 24.4% of the variance. Thus, the determination coefficient (R²) value of digital teaching behavior in this empirical model can be categorized as a substantial level. It means this model has covered the main predicators of digital teaching behavior of secondary school mathematics teachers.

Figure 2.  Final model with R², path coefficients and p values.

DownLoad: Full-Size Img PowerPoint

The effect size is indicated by the value of f². Considering that 0.02 ≤ f² < 0.15 is a small effect, that 0.15 ≤ f² < 0.35 is a medium effect, and that f² ≥ 0.35 is a large effect ^[81]. According to Table 9, performance expectancy (f² = 0.901) has a large effect size on attitude, while effort expectancy (f² = 0.133) has a small effect size on attitude. Social influence (f² = 0.187) has a medium effect size on behavioral intention, while performance expectancy (f² = 0.038), effort expectancy (f² = 0.020), attitude (f² = 0.049) and TPACK (f² = 0.072) have small effect sizes on behavioral intention. TPACK (f² = 0.678) has a large effect size on digital teaching behavior, attitude (f² = 0.032) and behavioral intention (f² = 0.044) have small effect sizes on digital teaching behavior, while facilitating conditions don't have an effect size on digital teaching behavior (f² = 0.001).

Table 9.  Results of calculating f² effect sizes.

Endogenous Construct	Predictor Construct
	Performance Expectancy	Effort Expectancy	Social Influence	Facilitating Conditions	Attitude	Behavioral Intention	TPACK
Attitude (R2 = 0.688)	0.901	0.133
Behavioral Intention (R2 = 0.697)	0.038	0.020	0.187		0.049		0.072
Digital Teaching Behavior (R2 = 0.756)				0.001	0.032	0.044	0.678

---

 | Show Table

DownLoad: CSV

The best approach for assessing the predictive power of a PLS path model is by means of Shmueli et al.'s ^[87] PLSpredict procedure. After running the PLSpredict algorithm with 10 folds and 10 repetitions in SmartPLS4, the Q_predict² values, the RMSE values of PLS-SEM analysis and the naïve linear regression model (LM) benchmark for all indicators of the endogenous constructs were obtained (Table 10). Since all indicators except for BI2 got negative values after calculating the differences of PLS-SEM_RMSE and LM_RMSE, the model had a medium predictive power ^[20].

Table 10.  Results of assessing the model's predictive power by using PLSpredict.

Indicator	Q²predict	PLS-SEM_RMSE	LM_RMSE	PLS-SEM_RMSE −LM_RMSE
ATD1	0.438	0.612	0.613	−0.001
ATD2	0.513	0.467	0.475	−0.008
ATD3	0.562	0.505	0.534	−0.029
ATD4	0.566	0.450	0.459	−0.009
BI1	0.527	0.423	0.445	−0.022
BI2	0.508	0.410	0.386	0.124
BI3	0.590	0.411	0.413	−0.002
BI4	0.615	0.392	0.396	−0.004
DTB1	0.596	0.535	0.564	−0.029
DTB2	0.665	0.547	0.567	−0.020
DTB3	0.603	0.578	0.624	−0.046
DTB4	0.650	0.522	0.549	−0.027

---

 | Show Table

DownLoad: CSV

Table 11 provides the results of the importance-performance map analysis (IPMA) for digital teaching behavior, which are graphically depicted in Figure 3. The IPMA results indicate that TPACK (0.687:70.265) is the biggest predictor of secondary school mathematics teachers' digital teaching behavior.

Table 11.  Importance-performance map analysis (IPMA) results of digital teaching behavior.

Constructs	Importance	Performances
Attitude	0.170	76.956
Behavioral Intention	0.161	79.724
Effort Expectancy	0.022	69.518
Facilitating Conditions	0.025	74.791
Performance Expectancy	0.145	79.386
Social Influence	0.064	77.038
TPACK	0.687	70.265

---

 | Show Table

DownLoad: CSV

Figure 3.  Importance-performance map for digital teaching behavior.

DownLoad: Full-Size Img PowerPoint

5.   Discussion

Digital technologies have been extensively used in mathematics teaching. However, there are many obstacles preventing teachers from using digital technology appropriately in teaching ^[56]. The teacher and the decisions he or she makes when integrating technology are critical to its successful implementation ^[21]. This study therefore sets out to find out the main predictors of secondary school mathematics teachers' actual digital teaching behavior.

One unexpected finding is that attitude significantly influenced both behavioral intention and digital teaching behavior, differing from previous studies ^[9,56,88]. Among those previous research models, attitude was not able to simultaneously affect behavioral intention and usage behavior. A possible explanation for this might be that there are other more important factors, such as self-efficacy, influencing behavioral intention and digital teaching behavior. However, in our research model, attitude is a strong mediating variable with nearly 69% explanatory power.

What stands out in the model is that TPACK significantly influences both behavioral intention and digital teaching behavior, and TPACK is the biggest predictor of teachers' digital teaching behavior. What's more, the explanatory power of digital teaching behavior in the final model is more than 75%, which is relatively high compared to other relevant studies. The main potential reason is that TPACK items in this study focus on technology distinguishing from other studies. TPACK helps teachers to acquire knowledge about integrating technology into their teaching, which promotes their professional development ^{[89,90,91,92,93]}. The result is similar to previous study, which shows that TPACK also significantly affects digital teaching behavior. Most importantly, the explanatory power of digital teaching behavior in the research model is beyond 75% ^[94]. However, the result is different from other studies ^[70,95]. For example, in Wijaya et al.'s ^[14] research model, TPACK did not have a significant influence on actual use of digital mathematics textbooks. This is possibly because that study just focused on one specific digital technology rather than other more general ones.

It is not surprising to see that performance expectancy significantly influences attitude. When teachers have higher performance expectancy, their attitudes toward digital technology will be more positive. There are several studies with similar results concerning the influence of performance expectancy on behavioral intention from other countries ^[96,97]. It is suggested that if school leaders want to enhance the digital competence of secondary school mathematics teachers, they need to help teachers have profound understanding of the usefulness of digital technology for their teaching ^[98].

Contrary to expectations, this study does not find a significant effect between effort expectancy and behavioral intention. The result is not in line with other studies ^[13,48,94]. Since the p value is close to 0.05, it may be that the sample size causes this situation. Moreover, China has adopted corresponding policies to improve teachers' digital competence, such as the information technology application ability improvement project for elementary and secondary school teachers ^[99]. Most teachers are more proficient in using digital technology than before, so it is not difficult for them to use most digital technologies. Therefore, effort expectancy is not the factor influencing behavioral intention.

Based on the results, the most influential factor of teachers' behavioral intentions to use digital technology is social influence. This is in line with several previous studies, which shows that social influence has a significant effect on teachers' behavioral intentions ^[100]. In the context of digital transformation in education, teachers' digital literacy must be improved quickly. Therefore, they care about the opinions of those around them and even are influenced by them.

Interestingly, facilitating conditions do not significantly influence the digital teaching behavior, which is totally different from previous studies ^{[12,13,72,101,102]}. For example, in Yuan et al.'s ^[20] study, facilitating conditions are the biggest factor affecting secondary school mathematics teachers' usage behavior of dynamic mathematics software. This is most likely because teachers in our study are from a state-level new area, in which conditions are best in Hunan province. Therefore, facilitating conditions no longer hinder their digital teaching behavior. In addition, dynamic mathematics software is a kind of a subject-specific digital technology, and the curriculum resources and supportive professionals are relatively lacking compared with other general digital technologies.

Based on the results, social influence is the factor that has the greatest influence on behavioral intention, which is aligned with the results of Yuan et al.'s study ^[20]. Although the results show behavioral intention improving the digital teaching of the teachers, it is less important in affecting the digital teaching behavior compared with TPACK.

Except for the direct effects mentioned above, some small indirect effects are also found in the digital teaching behavior conceptual model for secondary school mathematics teachers. For example, performance expectancy has two indirect effects on digital teaching behavior via attitude, and via attitude and behavioral intention, respectively. Effort expectancy has an indirect effect on digital teaching behavior via attitude and behavioral intention. Social influence, attitude and TPACK all have an indirect effect on digital teaching behavior via behavioral intention. These results proved the rationality of the conceptual model in this study.

6.   Conclusions

By using the PLS-SEM method, the extended UTAUT model is used in this study to figure out the main predictors of secondary school mathematics teachers' digital teaching behavior. It is concluded that technological pedagogical content knowledge (TPACK) was the biggest predictor of secondary school mathematics teachers' digital teaching behavior. Attitude, behavioral intention, performance expectancy, effort expectancy and social influence can also affect teachers' digital teaching behavior in direct and/or indirect ways. This study assists in advancing the digital teaching behavior of secondary school mathematics teachers by helping the government and schools to find out the main predictors. Schools should support teachers to improve their abilities of using digital technology and then effectively integrating them into the classroom. Teachers should make every effort to develop their TPACK. This study demonstrates that having facilitating conditions for mathematics teachers does not automatically affect their digital teaching behavior. Thus, to help secondary school mathematics teachers have actual digital teaching behavior, the government and schools should not only provide adequate facilities and resources and create a positive atmosphere for digital teaching, but also provide training for teachers to change their attitudes toward digital technology and improve their TPACK.

In addition to having shown the main predictors of digital teaching behavior of secondary school mathematics teachers, a new extended UTAUT model is proposed in this study. The in-sample predictive power or explanatory power of digital teaching behavior in this model is more than 75%, which is undoubtedly a powerful model. TPACK and attitude are added as two new constructs in this extended UTAUT model. Both of them can significantly influence behavioral intention and digital teaching behavior of secondary school mathematics teachers. TPACK is the biggest predictor of teachers' digital teaching behavior in this model. It lays a solid foundation for future study to explain and predict teachers' digital teaching behavior.

The results provided valid suggestions for government, school leaders and individual teachers. Since social influence is the most influential factor of behavioral intention, followed by TPACK, the government and schools should create a positive atmosphere to use digital technology in teaching. Developing an encouraging learning environment also contributes to the in-service teachers' TPACK development ^[103]. For example, they can organize related competitions regularly to enhance teachers' engagement. Meanwhile, teachers themselves should grasp more TPACK and then try to apply it into practice. If teachers do not have sufficient TPACK, it will be difficult to carry out digital teaching successfully. Furthermore, according to the TPACK-Practical model ^[104], the corresponding course is conducive to the improvement of teachers' TPACK. Therefore, it is suggested that schools should have experts to help teachers improve their TPACK and provide them with convenient support and guidance.

This study has some restrictions. First, the sample is from a state-level new area, which has good economic conditions and high education quality. The findings may not able to be broadly generalized in other regions. Future research on digital teaching behavior concerning more level of districts or countries would provide better illustrations of the research questions. Second, all participants are junior high school teachers in this study, future research should include senior high school teachers. Finally, it is necessary to include qualitative methods like in-depth interviews and classroom observations. Future study may adopt both quantitative and qualitative methodologies.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This study was funded by the Young Scholar Fund of Humanities & Social Science of Chinese Ministry of Education, grant number 18YJC880115. The authors extend their thanks to all junior high school mathematics teachers in the XiangJiang state-level new area who supported this study and to Professor Qiaoping Zhang for his suggestions on this article.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix A

Table A1.  Questionnaire items for investigating the predictors of secondary school mathematics teachers' digital teaching behavior.

Constructs	Code	Chinese Version	English Version	References
Performance Expectancy (PE)	PE1	使用数字技术进行教学能帮助我提高教学效率.	Digital technology helps me to enhance teaching efficiency.	[39,72]
	PE2	使用数字技术进行教学能帮助我提高教学效果.	Digital technology helps me to enhance teaching effectiveness.
	PE3	使用数字技术进行教学能帮助我更好地完成教学任务.	Digital technology helps me to complete teaching tasks better.
	PE4	总的来说, 数字技术对我的教学很有用.	In general, Digital technology is very useful for my teaching.
Effort Expectancy (EE)	EE1	我觉得数字技术很容易使用.	I find digital technology is easy to use.	[13,39,72]
	EE2	我觉得数字技术的操作过程很容易理解.	I find the illustration of digital technology is easy to understand.
	EE3	我能很灵活地使用数字技术完成我想做的事情.	I can flexibly use digital technology according to my wishes.
	EE4	总的来说, 我觉得使用数字技术进行教学并不困难.	In general, I find using digital technology in teaching is not difficult.
Social Influence (SI)	SI1	我相信领导会很乐意看到我在恰当的时候使用数字技术进行教学.	I believe the school leaders will encourage me to use digital technology at the right time.	[13,39,72]
	SI2	我相信学生会很乐意看到我在恰当的时候使用数字技术进行教学.	I believe students will be happy and encourage me to use digital technology to teach at the right time.
	SI3	我学校里那些使用数字技术进行教学的教师更受大家欢迎.	My fellow teachers who use digital technology are more popular with everyone.
	SI4	总的来说, 我所在的学校支持我在恰当的时候使用数字技术进行教学.	In general, my school supports the use of digital technology to teach when appropriate.
Facilitating Conditions (FC)	FC1	学校有较好的硬件设备支持我使用数字技术进行教学.	The school has good hardware facilities for me to use digital technology.	[13,39,72]
	FC2	我可以方便的得到使用数字技术进行教学的相关课程资源.	I can easily get curriculum resources for using digital technology to teach.
	FC3	我在使用数字技术进行教学时可以得到同事或专家的帮助.	When I teach using digital technology, some colleagues or experts are ready to help me.
	FC4	总的来说, 我具备使用数字技术进行教学的便利条件.	In general, I have the facilitating conditions to use digital technology in teaching.
Attitude (ATD)	ATD1	我喜欢在教学中使用数字技术.	I like using digital technologies in teaching.	[1]
	ATD2	我愿意投入时间去学习数字化教学的技能.	I am willing to spend time acquiring digital teaching skills.
	ATD3	我愿意克服困难在教学中使用数字技术.	I am willing to overcome obstacles to use digital technologies in teaching.
	ATD4	总的来说, 我非常乐意在教学中使用数字技术.	In general, I am very happy to use digital technologies in teaching.
TPACK	TPACK1	我对各类数字技术的操作都比较熟悉.	I am familiar with the illustration of various digital technologies.	[59]
	TPACK2	我能根据不同的课程内容选择恰当的数字技术进行教学.	I can use appropriate digital technology to teach according to the different curriculum content.
	TPACK3	我知道有些课程内容会由于新的数字技术的使用而被其它内容所取代.	I know that some of the curriculum content will be replaced by other content due to the use of new digital technology.
	TPACK4	我知道如何有效地组织数字化教学.	I know how to effectively organize digital teaching.
	TPACK5	我知道常用的数字化教学策略和教学内容呈现方式.	I know the common digital instructional strategies and representation.
	TPACK6	总的来说, 我具备使用数字技术进行教学的相关知识.	In general, I have the relevant knowledge about using digital technology to teach.
Behavioral Intention (BI)	BI1	如果我能获得数字技术, 我会考虑使用它.	If I have access to digital technology, I will consider using it.	[13,39,72]
	BI2	我愿意在合适的课程内容中使用数字技术进行教学.	I am willing to teach with digital technology in appropriate curriculum content.
	BI3	我打算在未来继续使用数字技术进行教学.	I intend to continue using digital technology to teach in the future.
	BI4	总的来说, 我愿意使用数字技术进行教学.	In general, I would like to use digital technology to teach.
Digital Teaching Behavior (DTB)	DTB1	我在课堂教学中经常使用数字技术.	I often use digital technology in classroom teaching.	[13,39,72,73]
	DTB2	我有丰富的使用数字技术进行教学的经验.	I have rich experience in using digital technology to teach.
	DTB3	我在很多课程内容的教学中都使用了数字技术.	I have used digital technology to teach in some curriculum content.
	DTB4	我对自己使用数字技术进行教学的效果非常满意.	I am very satisfied with the effectiveness of myself using digital technology to teach.

---

 | Show Table

DownLoad: CSV