Crashworthiness performance of gradient energy-absorbing structure for subway vehicles under quasi-static loading

1.   Introduction

Train collisions cannot be avoided entirely. In the event of collision, an energy-absorbing structure can absorb a large amount of impact energy and prevent it from causing significant damage to the car body and death to passengers ^[1]. As a result, it is critical to have an energy-absorbing structure that can disperse energy in an orderly and steady manner.

A good energy-absorbing structure's deformation is anticipated to be stable and controllable. But certain energy-absorbing structures show less-than-ideal deformation patterns throughout a variable range, which is not what the designer intended. Improper placement and design of materials and structures can have negative effects on energy-absorbing properties ^[2]. For example, composite energy-absorbing structure (CES) ^[3], lattice structure filled thin-walled tube (LSFT) ^[4], and corrugation reinforced multi cell square tube (CMST) ^[5,6] showed that all these structures produce unexpected deformation modes, as shown in Table 1.

Because of the instability and unpredictability of the deformation patterns of the thin-walled structure, the design idea of gradient energy absorption is gaining popularity. The notion of gradient energy absorption design refers to designing gradient changes of energy absorption material parameters or structural dimensions at different positions to achieve specific energy absorption requirements or energy absorption characteristics. The advantages of gradient energy absorbing structures versus classical energy absorbing structures are largely evident in the better adaptability and the smoothness of the mechanical parameter rise ^[7,8]. There has been some advancement in the optimization and modification of energy absorption structures using the gradient energy absorption idea. Baroutaji et al. ^[9] presented the circular-tube with gradient thickness that varied along the perimeter plane and identified the optimal thickness gradient parameters, thereby greatly enhancing the crashworthiness of the circular-tube. Liu et al. ^[10] introduced the structural size gradient into the honeycomb graded structure of continuous woven glass fibber reinforced laminated thermoplastic composites, and verified that the process of structural gradient induced deformation is well consistency with the results of experiment. Chang et al. ^[11] showed that incorporating graded honeycomb materials into energy absorbers can increase the crushing characteristics.

For the design of energy absorbers at the end of rail vehicles, scholars have made a series of efforts to realize the orderly and stable deformation of the structure from the initiation site to the end. In this regard, Xie et al. ^[12] planned thin-walled tubes into conical shapes, filled with honeycombs of uniform size between the diaphragms, and acquired the best structural configuration with multi-objective optimization. Zhao et al. ^[13] and Wang et al. ^[14] both filled the conical thin-walled tube with local gradient honeycomb. However, this local gradient design may still produce irregular deformation during the crushing process. In addition, there are certain gaps between the honeycomb and the outer wall of these structures, which not only limit the maximum energy absorption to a certain extent, but also may cause local instability.

To reduce the uncertainty of the energy-absorbing structure's deformation process and achieve stable and orderly deformation. To this end, this paper introduces the concept of gradient design, and proposes a honeycomb filled gradient energy-absorbing structure (HGES), whose honeycomb structure size, collapse-inducing grooves and diaphragms are all designed as gradients. The mechanical properties of HGES were investigated by quasi-static compression test. In addition, optimum design parameters are achieved through multi-objective optimization, and the crashworthiness of the optimal solution has been significantly improved compared with the baseline.

A reminder of the current work is organized below. Section 2 presents the geometrical configuration of HGES and gives a detailed description of the material and the quasi-static compression experiments. Section 3 provides the FE model of HGES and conducts experimental validation. Section 4 performs the parametric analysis for assessing the impact of geometric configuration on the crashworthiness of the structure. Section 5 hereafter applies multi-objective optimization method integrating entropy and the order preference by similarity to an ideal solution (TOPSIS) to choose the optimal configuration from the Pareto front. Lastly, Section 6 draws the conclusions of this paper.

2.   Materials and methods

2.1.   Geometric description

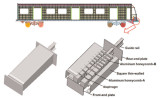
As shown in Figure 1, the HGESs at the front end of the subway are located on the two sides of head car body, which mainly play a role of absorbing energy and preventing climbing between trains. The HGES specifically consists of a front-end plate, a rear-end plate, diaphragms, honeycombs, an anti-climber, thin-walled tube, and guide. There are 10 honeycomb structures filling in the spaces formed by the diaphragms. There is a semi-circular arc-shaped collapse initiator groove on each side of the first honeycomb. Its function is to weaken the intensity of the first honeycomb at the end, so that the deformation of the honeycomb can be carried out accurately and gradually from front to back. In addition, there are three collapse-inducing grooves on the two sides of thin-walled tube. Intriguingly, the length of these collapse-inducing grooves decreases gradually from front to back. The gradient distribution of the collapse initiator grooves is also used to make the honeycomb deform in an orderly manner from front to back during the compression process. In addition, the diaphragm is connected to the thin-walled tube by welding.

The gradient idea is likewise utilized in honeycomb structure design. The concrete structural diagram of the honeycomb core is displayed in Figure 2(a), and its specific dimensional parameters are given in Table 2. In Figure 2(a), ${L}_{N}^{S}$, ${L}_{N}^{l}$ and ${S}_{N}$ represent the upper bottom length, lower bottom length and height of the Nth trapezoidal honeycomb core respectively.

The cell unit of the representative hexagonal honeycomb core is composed of two groups of single-layer and one group of double-layer cell walls, as displayed in Figure 2(b). Furthermore, t represents the single-layer thickness of cell unit, l denotes the edge length of the single thickness of the cell unit, w stands for the edge length of the double thickness of the cell unit, and θ is the wall angle of the cell unit. If with a regular cell unit, l = w and θ = 30°. The thin-walled tube is filled with honeycombs with gradient variations in size, where the taper of the thin-walled tubes and honeycombs is equal to 1.75°. In total, the length of honeycombs and diaphragms is 816 mm. The anti-climber has a thickness of 50 mm. The front and rear plates respectively have a thickness of 8 and 15 mm. The wall thickness is defined as 1.0 mm, while the diaphragm thickness is defined as 2 mm.

2.2.   Material test

2.2.1.   Tensile test of the steel structure

The diaphragm of the HGES sample is welded in thin-walled tube, and the honeycomb is filled between the diaphragms. The material of diaphragm and thin-walled tube is mild steel Q345. Tensile specimens shall undergo standard uniaxial tension tests according to GB/T 228.1-2010 (ISO 6892-1:2009, MOD) ^[15] to obtain the mechanical characteristics of relevant material (Figure 3(a)). The test sample is stretched uniaxially using MTS 647 testing equipment before its fracture is attained. The tensile test sample is illustrated in Figure 3(b). The average true stress-strain curves of Q345 mild steel taken from three replicate experiments are also displayed in Figure 3(b), while the average values of mechanical performances of Q345 mild steel are tabulated in Table 3.

2.2.2.   Compression test of the honeycomb

The aluminium honeycomb core was produced from 3003 alloy. Its detailed material properties are density of 2730 kg/m³, Young's modulus of 69 GPa, Poisson's ratio of 0.33, and yield stress of 115.8 MPa ^[16]. In order to acquire precise mechanical performance data on the platform intensity of honeycomb, axial compression tests were implemented on the samples of aluminium honeycomb cores. The overall length × width × height of the honeycomb core sample is 60 × 60 × 68 mm. In this study, the honeycomb cell size (t × l × w) is 0.32 × 4.0 × 4.0 mm. The deformations of the five aluminium honeycomb core samples before and after compression are respectively presented in Figure 4(a), (c). Figure 4(b) displays the five repeatable quasi-static axial compression tests on aluminium honeycomb core samples based on the standards GB/T 1453-2005 ^[17] as well as ASTM C365/C365M 2016 ^[18] under the same test conditions. The loading velocity was set as 2 mm/min. The average stress-strain curves taken from the five replicate trials are also displayed in Figure 4(c). Furthermore, the platform intensity of honeycomb is determined as a mean intensity over a compression range of 33–66% ^[13]. Here, the platform intensity of honeycomb is specified as 10.23 MPa.

2.3.   Quasi-static crush test of HGES

The test system employed in the experiments is consisted primarily of displacement transducers, hydraulic loading device and pressure sensors, as shown in Figure 5. HGES is completely fixed to the fixture device by four bolts to limit its movement. In the experiment, hydraulic cylinder is driven by the hydraulic loading device via an electromagnetic control system, and implements quasi-static axial loading at a slow and stable crushing velocity of 50 mm/min. The displacement transducer mounted on the hydraulic ram were utilized to measure the displacement data of the feed, and four pressure transducers connected to rigid wall were utilized for recording the resulting crushing force in HGES loading. Figure 6 reveals that the compressive displacement of a specimen determined with the displacement transducer is 540 mm, accounting for about 60% of the longitudinal length of the HGES. Additionally, from the measurement results before and after compression of the HGES (Figure 7), total HGES length prior to the test is 889 mm, and the length of the HGES after the test is 351 mm. The results show that the deformation length of the HGES is 538 mm, which is almost the same as the data measured by the displacement transducer. The error is within the allowable range.

The profile of HGES after compression is shown in Figure 8. Because the guide tube in the middle is too long, we first used flame cutting to intercept the too long guide tube, and then used wire cutting to cut the section. In addition, in order to save wire cutting time, I did not cut the section on the central symmetry plane. From the cross-sectional view of HGES, it can be seen that the honeycomb shape inside HGES is stepped, and decreases step by step from the loading end to the bottom.

2.4.   Crashworthiness indicators

The crushing performance of HGES was quantitatively assessed via crashworthiness indicators, which include peak crushing force (PCF), specific energy absorption (SEA) and energy absorption (EA) ^[19–21]. These three parameters are described as below.

Here we define EA as the area enclosed by the force-displacement curve within the effective compression stroke s.

where $f(x)$ represents the instantaneous crushing force and s denotes the effective displacement of crushing.

SEA is expressed as the total energy EA generated by the HGES within the effective compression stroke range divided by the total mass m of the structure, emphasizing the ability to absorb energy per unit mass.

In general, the initial peak force of ordinary straight thin-walled structures tends to occur in the early stages of compression ^[22]. However, the crushing force of HGES can be very distinct from ordinary straight thin-walled structures. Due to the gradient design of HGES, its crushing force increases with crushing displacement. Therefore, to reduce the risk of occupant casualties in the event of an accident, the PCF prior to densification should also be kept under control.

3.   Finite element (FE) modeling

3.1.   FE modeling of HGES

The numerical simulation model of HGES in the current work is constructed using LS-DYNA software to further explore the crashworthiness of the structure. The FE model of HGES consists of a moving plate and HGES, as displayed in Figure 9. Moreover, for accurately simulating the quasi-static loading of HGESs, the rear-end of the HGESs is restrained fixedly, and the moving plate performs axial extrusion on the HGES at a fixed velocity of 3m/s. It should be emphasized that the numerical simulation of quasi-static loading should provide a higher loading velocity than the experimental test, in order to trade off the accuracy of the numerical simulation and the computational cost ^[23]. In addition, it is proved to be feasible to adopt the method of increasing the loading velocity in the quasi-static simulation ^[24,25]. In fact, as long as the following two criteria ^[26] are met, it can be judged that the loading velocity used in the finite element simulation is feasible. (i) The total kinetic energy in the simulation should be much smaller than the total internal energy. (ii) The crushing force-displacement response was not significantly correlated with the increased loading velocity. To this end, we carried out verification on the quasi-static loading velocity of 3 m/s to pass the above two criteria. It can be seen from Figure 10(a) that the total kinetic energy of HGES in the finite element simulation is much smaller than its total kinetic energy. As shown in Figure 10(b), the force-displacement curves at different loading velocities tend to be similar, and do not change significantly as the loading velocity increases.

The models for the end plates, anti-climbers, and guide rails are assigned the attributes of MAT_RIGID because of the relatively high stiffness of these structures and the fact that they undergo little deformation during quasi-static axial crushing. The diaphragms and thin-walled tubes are modelled utilizing MAT_PIECEWISE_LINEAR_PLASTICITY. With the aim of improving the computational efficiency, an equivalent crushing model was introduced to construct the aluminium honeycomb structure. The detailed modeling method can well reflect the failure and evolution of the honeycomb. However, the model has a large number of units and nodes, and its solution time is long. Seriously, the computational time is catastrophic for large honeycombs in engineering problems with fine-grained models. MAT_26 with orthotropic mechanical properties (*MAT_HONEYCOMB) is a solid equivalent model for characterizing honeycomb structures. This modeling method can not only reflect the mechanical properties of the honeycomb well, but also greatly improve the calculation efficiency. Our previous research ^[13] and related scholars ^[27,28] have confirmed the feasibility of this modeling method. Both the diaphragms and the thin-walled tube are meshed through Belytschko-Tsay shell elements, and has five points of integration in the thickness direction.

The "AUTOMATIC_SURFACE_TO_SURFACE" surface contact algorithm is utilized to mimic the interaction between the anti-climber and the rigid wall. In order to avoid the occurrence of underlying penetration during extrusion, HGES adopts the "AUTOMATIC_SINGLE_SURFACE" contact algorithm to define self-contact. The comparison of force-displacement curves for different friction coefficients is shown in Figure 11. The PCFs with friction coefficients of 0.15, 0.3, and 0.45 are 766.23,786.92, and 923.10 kN, respectively. The experimental PCF is 862.79 kN. It can be easily found that the error between the PCF of the finite element model with a friction coefficient of 0.15 or the friction coefficient of 0.30 and the experimental PCF is greater than 10%. However, the crashworthiness indicator of the simulation model with the friction coefficient set to 0.3 is closer to that of the experiment. Therefore, coefficient of friction is set to 0.30 at all contact locations ^[29,30]. A range of shell element sizes and solid element sizes have been examined respectively in the grid convergence study to identify the appropriate grid size for HGES, as displayed in Figure 12. For balancing the calculation efficiency and accuracy, the optimal shell and solid element mesh sizes for this study are determined to be 10 mm and 10 mm, respectively.

3.2.   Validation of FE model

Figure 13 contrasts the buckling modes derived from FE simulations and compression tests in HGES, which is one of the fundamental criteria for confirming the correctness of FE model. HGES produces orderly and progressive deformation due to the presence of induced structures and stiffeners. In addition, there was no tearing of the weld seam during the test. The results demonstrate that the buckling process of HGES in the experiment is equivalent to these in the numerical simulation, displaying that the FE model built in this study can simulate the real compression process well.

The comparison between the FE and experimental results of the force-displacement curve is depicted in Figure 14. It reveals that the force of HGES fluctuates periodically and regularly with displacement, and the fluctuation amplitudes of the experiment and simulation are fundamentally the same. However, due to the influence of many uncertainties, for instance, test conditions, external environment, sample processing, manufacturing, and so on, the force-displacement at each stage cannot totally overlap.

To reflect the accuracy of the FE model more intuitively, Table 4 lists the results of EA and PCF obtained by experiments and FE simulations. The relative error values of the experiment and simulation of the two indicators are 2.66 and 8.79%, respectively, both within the acceptable error range. In general, FE model possesses acceptable accuracy in the prediction of the HGESs crushing behaviour and can be utilized for subsequent parametric analyses and optimization.

4.   Parametric analyses

4.1.   Effect of wall thickness

The wall thickness distribution exerts an essential impact on the crushing characteristics of the HGES. In this section, six thickness values T_t of HGES (namely, 0.5, 0.7 and 0.9, 1.1, 1.3 and 1.5 mm) are selected for comparative investigations. The masses of the effective energy-absorbing components corresponding to different wall thicknesses are 18.11, 19.36, 20.61, 21.86, 23.12 and 24.37 kg, respectively. Figure 15(a) exhibits the trend of force-displacement curves with various T_t. Obviously, the force-displacement curve shows a gradual transition from stable fluctuations to more violent fluctuations as wall thickness increases. The fluctuation of force-displacement curve raises as wall thickness increases. Figure 15(b) depicts the impact of having varying wall thicknesses on the values of PCF and SEA, the SEA is negatively linked to the varying trend of the wall thickness. The SEA reduces as the wall thicknesses raises. In addition, the larger thickness can enhance the property of energy absorption of structure, simultaneously resulting in the raise of overall mass and PCF of structure. In general, excessive wall thickness may threaten the life safety of drivers and passengers.

4.2.   Effect of diaphragm thickness

Figure 16 shows the results of changing diaphragm thickness (T_b) with other parameters fixed. T_b is respectively set as 1.0, 1.4, 1.8, 2.2, 2.6, and 3.0 mm. The masses of the effective energy-absorbing components corresponding to different diaphragm thicknesses are 17.42, 18.95, 20.47, 22.00, 23.53 and 25.06 kg, respectively. From force-displacement curves in Figure 16(a), it exhibits that the curve fluctuations under a variety of T_b are similar, and the peak-to-valley difference of the same wave does not change significantly. To more intuitively study the effects of different diaphragm thicknesses on SEA and PCF, Figure 16(b) plots the changing trends of these two responses with increasing diaphragm thickness. The SEA almost decreases linearly as diaphragm thickness raises. However, the PCF showed a trend of rising first and then falling. When the diaphragm thickness raised from 1.0 to 2.2 mm, the PCF increased almost linearly. Once the thickness exceeded 2.2 mm, the PCF showed a decreasing trend.

4.3.   Effect of platform intensity of honeycomb

For investigating the impact of platform intensity of the honeycomb (H_f) on crushing characteristic, the platform intensity of honeycomb is set as 5, 7, 9, 11, 13 and 15 MPa, respectively. Figure 17(a) reveals the force-displacement curves of HGES with the variety of platform intensities of honeycomb. As the platform intensity enhances, the platform slope of force-displacement curve increases in an orderly manner. It should be noted that when the platform intensity reaches 5 MPa, the force-displacement curve violently fluctuates and it is easy to become unstable. Comparing the wall thickness, it exhibits that the platform intensity possesses a greater influence on the crushing force compared with the wall thickness. To better understand the crushing performance of HGES, Figure 17(b) shows the dependence of PCF and SEA on diverse platform intensity. Obviously, there is nearly a linear positive association between the platform intensity and SEA, which fully reflects the lightweight and high-efficiency energy-absorbing performance of honeycomb. Although increasing the platform intensity will increase the SEA of HGES, it also increases the PCF. As a result, it is valuable to further optimize the crushing characteristics of HGES and to find the ideal structural configuration for engineering applications.

5.   Optimization and decision-making

5.1.   Definition of optimization problem

For enhancing the HGES crashworthiness, the crashworthiness indexes of HGES under the quasi-static loading are optimized in this section to acquire the best parameter configuration. In train collision scenarios, the peak impact force during the compression-density phase of the structure is vital to survival of the occupants. As the PCF increases, the probability of driver and occupant survival in the event of an impact is greatly reduced. The higher SEA is more conducive to achieving the original intention of a lightweight and efficient energy absorption structure, which in turn enables HGES to maximize energy absorption per unit mass. In addition, a lower limit of EA greater than 225 kJ is set as a constraint to ensure that the absorbing energy of HGES can meet the requirements of train collisions. To sum up, PCF minimization and SEA maximization are defined as optimization objectives to improve train crash safety while maximizing the energy absorption of the structure. Therefore, the formulation of the optimization problem of HGES is formulated as follows:

where T_t denotes the wall thickness of the HGES, T_b is the diaphragm thickness, and H_f represents the platform intensity of honeycomb.

5.2.   Design of experiment

The purpose of design of experiment is to generate sampling points. In the current study, Optimal Latin hypercube sampling (OLHS) provides a more homogeneous distribution of sample to capture higher order effects compared to Latin hypercube sampling (LHS). The design variables and their corresponding FE simulation results are exhibited in Table 5.

5.3.   Construction and comparison of approximate models

Approximate models use mathematical models in place of complex physical relationships to capture correlations between responses and design variables in a computationally inexpensive and computationally efficient manner. For the crashworthiness problem, there are four frequently employed approximate models, including Moving Least Squares (MLS), Least Squares Regression (LSR), Radial Basis Function (RBF) and Kriging (KRG). The accuracy of the fitting of the surrogate model is the critical factor for identifying the approximate model, since the higher the accuracy of the fitting of the surrogate model, the more reliable the optimization results derived from the approximate model will be.

To this end, two assessment parameters, that is, Relative Mean Absolute Error (RAAE) together with R-squared (R²), are combined to further evaluate and validate the accuracy of approximate model. R² and RAAE are used to measure the overall error and local region error of the approximate model for the three responses (PCF, SEA and EA), respectively. If R² and RAAE is close to 1 and 0, respectively, implying that the stated approximate model is fitted with high accuracy. The mathematical expressions are shown in Eqs (4) and (5), respectively.

where $\kappa$ represents the number of the cross-validation points, ${y_i}$ denotes the actual response value, ${\hat y_i}$ represents the predicted response value, and $\bar y$ is the average value of actual response.

In this study, the OLHS method ^[31,32] was used to produce 25 homogeneously distributed points for the samples. Additionally, another DOE matrix comprising five points was formed with the LHS method ^[33] to compare and assess the fitting accuracy of these four approximate models.

Table 6 presents the comparison of the evaluation indicators for different approximation models. Notably, the approximate model is considered to have a high fit if the evaluation index RAAE is less than 0.2 as well as R² is greater than 0.9. Therefore, PCF constructed by KRG model reflects a higher model accuracy, while SEA and EA show better results by choosing RBF model. Figure 18 depicts the response surfaces in space for SEA and PCF under different design variables.

5.4.   Optimization method

The multi-objective genetic algorithm (MOGA) takes full advantage of the features of genetic algorithms that is easy to handle large-scale problem to solve differentiable, continuous and linear the multi-objective optimization problems ^[34]. The multi-objective structural optimization in this paper is based on the reliable approximate model obtained in Section 5.3 combined with the MOGA algorithm.

5.5.   Multicriteria decision-making method

5.5.1.   Entropy method for weighting

Step 1: Data standardization. For a multicriteria decision-making problem, the raw decision matrix ${{\bf{X}}}$ is described as:

Here ${{\bf{X}}}$ represents decision matrix and $x$ denotes the raw response value. As evaluation criteria frequently vary in units and size, it is not possible to directly compare different criteria. Therefore, the original responses need to be normalized and converted to comparable standard values. A cost criterion can be defined by the following formula:

In addition, a benefit criterion can be expressed by the following formula:

Here we take ${\min _j}$ and ${\max _j}$ to denote the minimum and maximum response values of the jth response, respectively. Thus, $0 \leqslant {p_{ij}} \leqslant 1$. In accordance with Eqs (8) and (9), the standardised decision matrix can be acquired as ${\bf{P}} = {({p_{ij}})_{\upsilon \kappa }}$.

Step 2: Decision matrix normalization. Each row of the normalized decision matrix can be represented as follows:

Step 3: Acquire the entropy value. Next the entropy value for each objective can be expressed as:

Step 4: Obtain the weight factor. The entropy weight of each objective is calculated as:

5.5.2.   Ranking with the TOPSIS method

Step 1: Construction of the weighted decision matrix.

Here ${z_{ij}}$ refers to the weighted normalized attribute value.

Step 2: Acquisition of negative and positive ideal solutions. The ideal solutions are obtained as:

We adopt ${{Z} ^ - }$ and ${{Z} ^ + }$ to denote the negative and positive ideal solutions, respectively.

Step 3: Computation of the Euclidean distance for each alternative.

We define $D_i^ +$ and $D_i^ -$ as the distance of each alternative to positive and negative ideal solution, respectively.

Step 4: Determination of the relative proximity of each alternative.

If the value of ${H_i}$ is higher, it implies that the alternative is closer to the most desirable solution.

5.6.   Results analysis

The Pareto front formed by the optimized two objectives is revealed in Figure 19. It shows that the PCF and SEA are always in conflict with each other, and the optimization goals cannot be achieved simultaneously. As the PCF increases, the SEA must also increase, which poses a challenge to choose the best parameter combination.

The Pareto front enables the HGES to obtain optimal configurations under the conditions of strict constraints. The criteria applied for assessing the crashworthiness of the HGES are the PCF and SEA. The SEA and PCF are the benefit and cost criterion, respectively. Finally, the weight values of PCF and SEA determined by the entropy weight method in Section 5.5.1 are 0.7976 and 0.2024, respectively. It can be seen that the weight of PCF is much greater than that of SEA, revealing that PCF has a more significant impact on crashworthiness. The entropy weights of the two performance objectives are combined with the TOPSIS method to obtain the optimal performance configuration of HGES.

The optimal point is shown as the red dot in Figure 15. Compared with the initial design geometric configuration (H_f = 10.23 MPa, T_b = 2.0 mm, T_t = 1.0 mm), the optimized HGES geometric configuration (H_f = 10.87 MPa, T_b = 1.01 mm, T_t = 0.53 mm) have changed to a certain extent to meet higher crushing requirements. In addition, we can also find that the selection of the optimal geometric configuration completely follows the parameter change law obtained in Section 4. Compared with the initial design, the optimized HGES improves PCF and SEA by 25.28 and 19.81%, respectively.

Table 7 shows the comparison of the results obtained by the approximate model and the FE simulation for the two optimization objectives under the optimal configuration. The errors of PCF and SEA computed using finite element model and approximate model are determined to be 1.73 and 2.55%, respectively. The two errors are clearly less than 5%, confirming the great accuracy of the generated approximate model.

6.   Conclusion remarks

In the current work, FE model validation and quasi-static tests were conducted on the HGES. The sensitivity of the associated structural parameters of HGES to its crashworthiness was investigated, which include the diaphragm thickness (T_b), the wall thickness (T_t), and the platform intensity of honeycomb (H_f). A multi-objective optimization is conducted for improving HGES crashworthiness with maximum SEA and minimum PCF as design objectives. The major findings are as follows:

1) The increase of the three parameters T_t, T_b, and H_f all lead to the increase of EA. Improvements to the platform intensity of honeycomb H_f have the most effects on the crashworthiness of HGES, presuming that all other dimensions stay the same. Smaller wall thicknesses are beneficial for producing a smoother force-displacement curve.

2) The SEA decreased with the increase of T_t and T_b, but raised as H_f increases. In addition, the increase of T_b is not always positive and monotonous for the PCF. The Pareto front in the form of SEA versus PCF diagram was derived by multi-objective optimization and its optimal solution is chosen on the basis of a multicriteria decision-making method.

3) The optimized design parameters, namely, H_f = 10.87 MPa, T_b = 1.01 mm, T_t = 0.53 mm, were obtained under the constraint of EA ≥ 225 kJ. In comparison to the initial design (that is, H_f = 10.23 MPa, T_b = 2.0 mm, T_t = 1.0 mm), the SEA and PCF of optimized HGES were enhanced by 19.81 and 25.28%, respectively.

Acknowledgments

This work was supported by the Hunan Provincial Natural Science Foundation of China (grant number 2022JJ40619), the Changsha Municipal Natural Science Foundation (grant number kq2202102), the Scientific Research Project of Hunan Provincial Education Department (grant number 22C1496), the National Key Research and Development Program of China (grant number 2021YFB3703801), and the Scientific Research Foundation for Young Scholars of Central South University (grant number 202044019).

Conflict of interest

The authors declare there is no conflict of interest.