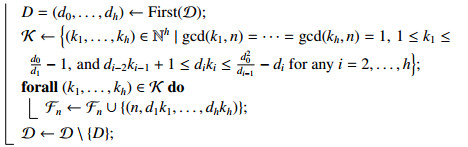1.
Introduction
Suzuki [1] and Abhyankar and Moh [2] proved independently that the affine line can be embedded in a unique way, up to ambient automorphisms, in the affine plane. Let us indicate some details of this fact. Let K be an algebraically closed field of arbitrary characteristic. A polynomial mapping σp,q:K⟶K2 defined as σp,q(x,y)=(p(x,y),q(x,y)) is a polynomial embedding of the line K if there is a polynomial map g:K2⟶K such that g(p(t),q(t))=t in K[t]. This is equivalent to the equality K[p(t),q(t)]=K[t].
An affine curve C⊂K2 is an embedded line if there exists a polynomial embedding σp,q such that σp,q(K)=C. It is easy to check that any embedded line is an irreducible affine curve.
Let C be an embedded line with a minimal equation f(x,y)=0. After [2], the curve C has only one place at infinity, that is, the closure ¯C of C in the projective plane has only one point O∞ on the line at infinity, and it is unibranch at O∞ (the polynomial f(x,y) is irreducible as an element of the formal power series ring K[[x,y]]). In this case, associated with ¯C we have a numerical semigroup S(¯C) consisting of zero and all intersection numbers of ¯C with all algebroid curves not having ¯C as an irreducible component. By the Bresinsky-Angermüller Theorem ([3] for zero characteristic and [4] for arbitrary characteristic) there exists a (unique) sequence (v0,…,vh), called the characteristic at infinity of C, generating S(¯C) where v0 is the degree of C.
Assume that C is an affine irreducible curve of degree greater than 1 with one branch at infinity and let (v0,…,vh) be its characteristic at infinity. Suppose that gcd(degC,ordO∞¯C)≢0 (mod char K). Then, after [2]
The condition gcd(degC,ordO∞ˉC)≢0 (mod char K) is automatically satisfied when the characteristic of K is zero, but otherwise it is essential.
The inequality (1.1) is called the Abhyankar-Moh inequality. Originally, this inequality appears linked to the Puiseux expansion of the given branch at the infinite place (see [2, equality (35)]). The semigroups of integers associated with branches and satisfying the Abhyankar-Moh inequality are called Abhyankar-Moh semigroups of degree v0 (the order of the branch). The Abhyankar-Moh semigroups were studied in [5], where these semigroups with maximum possible conductor, which is equal to (v0−2)(v0−1), were described. Later, in [6], a geometric interpretation of the branches with Abhyankar-Moh semigroup and maximum possible conductor was given. It is well known that the conductor of an Abhyankar-Moh semigroup of degree v0 is an even integer belonging to the interval [v0−1,(v0−1)(v0−2)]. Our main result is the following:
Theorem A. Let n>2 be an even natural number. For any even number c with n−1≤c≤(n−1)(n−2), there is an Abhyankar-Moh semigroup of degree n and conductor equal to c.
In order to prove Theorem A, we start by computing in Section 3, in an algorithmic way, the set of all Abhyankar-Moh semigroups of a fixed degree (see Algorithm 2). Section 4 is devoted to the proof of Theorem A. This proof is constructive, and the algorithms of Section 3 play a fundamental role in it.
From the computational point of view, it remains, as an open question, to determine the values of conductors reached by the Abhyankar-Moh semigroups of odd degree, but it seems that this poses new computational challenges. From the geometric point of view, the next step would be to geometrically characterize the branches with Abhyankar-Moh semigroups of even degree, studied in this paper, following the line given in [6] for those with the maximum possible conductor.
2.
Preliminaries
A numerical semigroup S is an additive submonoid of N with finite complement in N. It is well known that numerical semigroups are finitely generated, and their minimal generating sets are unique. The largest integer in N∖S is called the Frobenius number of S. The conductor of S is the Frobenius number of S plus 1.
Given a finite set A={a1,…,at}⊂N, A is the generating set of S when S=Na1+⋯+Nat. In this work, when A is the minimal generating set of S, we assume that a1<⋯<at. When we write S=⟨A⟩, we imply that A is the minimal set of generators of S. The cardinality of the minimal generating set of S is called the embedding dimension of S.
A sequence of positive integers (v0,…,vh) is called a characteristic sequence if it satisfies the following two properties:
(CS1) Put ek=gcd(v0,…,vk) for 0≤k≤h. Then, ek<ek−1 for 1≤k≤h and eh=1.
(CS2) ek−1vk<ekvk+1 for 1≤k≤h−1.
We put nk=ek−1ek for 1≤k≤h. Therefore, nk>1 for 1≤k≤h and nh=eh−1. If h=0, the only characteristic sequence is (v0)=(1). If h=1, the sequence (v0,v1) is a characteristic sequence if and only if gcd(v0,v1)=1 and v0>1. Property (CS2) plays a role if and only if h≥2.
Lemma 1. ([5, Lemma 1.1]) Let (v0,…,vh) be a characteristic sequence with h≥2. Then,
(i) v1<⋯<vh, and v0<v2.
(ii) Let v1<v0. If v0≢0, (mod v1), then (v1,v0,v2,…,vh) is a characteristic sequence. If v0≡0, (mod v1) then (v1,v2,…,vh) is a characteristic sequence.
A semigroup S⊆N is strongly increasing (SI-semigroup) if S≠{0} and it is generated by a characteristic sequence, that is, S=Nv0+⋯+Nvh. We will denote by S=S(v0,v1,…,vh) the numerical semigroup generated by the characteristic sequence (v0,v1,…,vh).
A SI-semigroup S(v0,v1,…,vh)⊆N is an Abhyankar-Moh semigroup (A-M semigroup) of degree n=v0>1 if it satisfies the Abhyankar-Moh inequality
Observe that the semigroup N=S(n,1) for any n∈N, so N is an Abhyankar-Moh semigroup of any degree.
The conductor of the A-M semigroup S=S(v0,v1,…,vh) is
where ni=ei−1ei for i∈{1,…,h}. Moreover c(S) is an even integer (see [5, Proposition 1.2]).
Remark 2. If S=S(v0,v1,…,vh) is an A-M semigroup of degree n=v0>1, then v0>v1, since e0v1<e1v2<⋯<eh−1vh<n2=v20.
Let S=S(v0,v1,…,vh) be an A-M semigroup of degree n=v0>1. If c(S) is the conductor of S, then, by [5, Theorem 2.2],
Moreover,
Hence, if S≠N is an A-M semigroup of degree n>1, its conductor c(S) is an even integer satisfying the inequalities
By Remark 2 we get that the only A-M semigroup of degree 2 is generated by the characteristic sequence (2, 1). Such a semigroup achieves the upper bound for the conductor, given in (2.2).
After [5, Proposition 1.2], if (v0,v1,…,vh) is a characteristic sequence and S=S(v0,v1,…,vh), then {min(v0,v1),v2,…,vh−1,vh} is a subset of the minimal generating set of S, and v2∉Nv0+Nv1. Furthermore, for every w∈S, (v0,v1,…,vi,w,vi+1,…,vh) is not a characteristic sequence, for every i=0,…,h−1.
Let S=S(v0,v1,…,vh) be a SI-semigroup. By Lemma 1, the characteristic sequences generating S are the following:
● (v0,v1,v2,…,vh).
● If v0<v1, (v1,v0,v2,…,vh).
● If v1<v0 and v0≢0 (mod v1), (v1,v0,v2,…,vh).
● If v1<v0 and v0≡0 (mod v1), (v1,v2,…,vh) and (v2,v1,…,vh).
● (kv′0,v′0,v′1,v2,…,vh) for every integer k∈[2,v′1/v′0] where v′0=min(v0,v1), v′1=max(v0,v1), and v′1≢0 (mod v′0).
As a consequence, we determine the characteristic sequences generating a SI-semigroup given by its minimal generating set.
Let S=⟨a1,…,at⟩ be a SI-semigroup. Then, from [5, Corollary 1.4], the characteristic sequences generating S are the following:
Similarly, the possible characteristic sequences generating an A-M semigroup given by its minimal generating set can be described: Let S=⟨a1,…,at⟩ be a SI-semigroup. If S is an A-M semigroup, then
for every integer k∈(√gcd(a1,…,at−1)ata1,a2a1). For the first case, S should be an A-M semigroup of degree a2, and it should be of degree ka1 for the second (see [5, Proposition 2.1]).
Notice that if you want to check whether the semigroup ⟨a1,…,at⟩ is an A-M semigroup, you only need to check whether it is an A-M semigroup of degree a2.
3.
Computing Abhyankar-Moh semigroups
The A-M semigroups minimally generated by two elements are easy to describe. Whenever b>a>1 are two coprime integers, ⟨a,b⟩=S(b,a) is an A-M semigroup of degree b. Furthermore, ⟨a,b⟩=S(ka,a,b) is also an A-M semigroup of degree ka for every k∈(√b/a,b/a)∩N.
A-M semigroups of higher embedding dimensions are completely characterized by gluings: The gluing of S=⟨a1,…,at⟩ and N with respect to the positive integers d and f with gcd(d,f)=1 (see [7, Chapter 8]) is the numerical semigroup Nda1+⋯+Ndat+Nf. We denote it by S⊕d,fN.
Proposition 3. The set ˉS is an A-M semigroup with embedding dimension t≥3 if and only if ˉS=S⊕d,fN where S=⟨b1,…,bt−1⟩ is an A-M semigroup of degree m, and f,d are two coprime integers such that dm2>f>dgcd(b1,…,bt−2)bt−1. Moreover, the degree of ˉS is dm.
Proof. Consider ˉS=⟨a1,…,at⟩. Put d=gcd(a1,…,at−1), f=at, bi=ai/d for all i=1,…,t−1, and the SI-semigroup S=⟨b1,…,bt−1⟩. Trivially, ˉS=S⊕d,fN. Since ˉS is a SI-semigroup,
By (2.6), the degree of ˉS equals a2, or ka1 for some integer k>1. If we assume that the degree is a2, then (a2,a1,a3,…,at) is a characteristic sequence generating ˉS, and a22>gcd(a1,…,at−1)at. Thus, (b2,b1,b3,…,bt−1) is a characteristic sequence generating S, and
Hence, S is an A-M semigroup of degree m=b2.
Similarly, for the degree ka1, (kb1,b1,b2,…,bt−1) is a characteristic sequence generating S, and (kb1)2=(ka1/d)2>gcd(b1,…,bt−2)bt−1, so S is an A-M semigroup of degree m=kb1. For both of the previous possibilities, the inequality dm2>f is satisfied.
Conversely, let S=⟨b1,…,bt−1⟩ be an A-M semigroup of degree m∈N and f,d be two coprime integers such that dm2>f>dgcd(b1,…,bt−2)bt−1. Since f>dgcd(b1,…,bt−2)bt−1, ˉS=S⊕d,fN=⟨db1,…,dbt−1,f⟩ is a SI-semigroup ([8, Theorem 3]). Again, by (2.6), the possible characteristic sequences generating S are (b2,b1,b3,…,bt−1) and (kb1,b1,b3,…,bt−1), with degrees b2 and kb1, respectively. Hence, the characteristic sequences generating ˉS are (db2,db1,db3,…,dbt,f) and (kdb1,db1,db2,…,dbt,f); and by hypothesis, we have the Abhyankar-Moh inequality (dm)2>df. Thus, ˉS is an A-M semigroup of degree dm.
Let S be an A-M semigroup of degree m, and f>d>1 are two coprime integers such that S⊕d,fN is also an A-M semigroup of degree dm. Then, by [9, Proposition 10],
where c(S) denotes the conductor of S.
Denote by M(A) the largest element of the minimal system of generators of the numerical semigroup ⟨A⟩, and s(A)=min(A∖{min(A)}), that is, the second element in A. Algorithm 1 computes all the A-M semigroups with conductor less than or equal to a fixed non-negative integer.
Table 1 illustrates Algorithm 1: We collect all the A-M semigroups with conductor less than or equal to 18. We also give the characteristic sequences associated with the given semigroups.
Let n>1 be an integer. A sequence of integers (d0,…,dh) will be called a sequence of divisors of n if di divides di−1 for 1≤i≤h and n=d0>d1>⋯>dh−1>dh=1. In particular, if (v0,v1,…,vh) is a characteristic sequence, then (e0,…,eh) is a sequence of divisors of n=v0, where ei=gcd(v0,…,vi). In this case we will say that (e0,…,eh) is the sequence of divisors associated with (v0,…,vh).
Using sequences of divisors, in [5, Proposition 2.3] it was proved that
is a characteristic sequence, and the semigroup generated by it is an A-M semigroup of degree n and conductor (n−1)(n−2) (which is the maximal possible conductor after (2.2)). Inspired by this idea, using sequences of divisors, we introduce an algorithm for computing all the A-M semigroups for a given degree (Algorithm 2). The following proposition is the key for providing this algorithm.
Proposition 4. Let n≥2 be an integer and D=(d0,…,dh) be a sequence of divisors of n=d0. Then, the characteristic sequence of any A-M semigroup with degree n and sequence of divisors equal to D is of the form (n,d1k1,…,dhkh), with 1≤k1≤d0d1−1, di−2ki−1+1≤diki≤d20di−1−di for any i=2,…,h, and gcd(di−1di,ki)=1 for i=1,…,h.
Proof. Notice that the condition gcd(di−1di,ki)=1 for i=1,…,h guarantees that the characteristic sequence (n,d1k1,…,dhkh) has associated sequence of divisors equal to D. It remains to check the bounds on the ki. The case h=1 is trivially verified. Suppose h≥2. Let v0=d0 and vi=diki for any i=1,…,h, and assume that (v0,…,vh) is the characteristic sequence of an A-M semigroup S of degree n=v0 and associated sequence of divisors (d0,…,dh). Since A-M semigroups are SI-semigroups, by the definition of vi, di−1ki<di+1ki+1 for all i∈{1,…,h−1}. Hence, di−1ki+1≤di+1ki+1. Moreover, since 1<v1<v0, 1≤k1≤d0d1−1; and since dh−1kh<d20 and kh≤d20dh−1−1, this is enough to finish the proof when h=2. Consider now that h≥3. By Proposition 3, S=Sh−1⊕dh−1,khN where Sh−1 is the A-M semigroup of degree d0dh−1 generated by the characteristic sequence (d0dh−1,d1dh−1k1,…,dh−2dh−1kh−2,kh−1). So, dh−2dh−1kh−1<(d0dh−1)2. Then kh−1≤d20dh−1dh−2−1, and hence dh−1kh−1≤d20dh−2−dh−1. In general, using this process, for any i∈{3,…,h−1}, Si=Si−1⊕di−1,kiN, where Si−1 is the A-M semigroup of degree d0di−1 generated by the characteristic sequence (d0di−1,d1di−1k1,…,di−2di−1ki−2,ki−1). For any i, the condition that Si−1 is an A-M semigroup implies that di−2di−1ki−1<(d0di−1)2, and di−1ki−1≤d20di−2−di−1.
Algorithm 2 provides a computational method to compute all A-M semigroups with fixed degree. Note that this algorithm supports parallel deployment.
Table 2 shows all the A-M semigroups with degree eight. Note that, in this example, all the even integers in [n−1,(n−1)(n−2)] are the conductor of some A-M semigroup of degree n=8. In this work, we prove that this is true for all even degrees.
If n>2, (d0,…,dh=1) is a sequence of divisors of degree n=d0, and we consider values ki as in Proposition 4, then, by (2.1), the conductor of the A-M semigroup S(n,d1k1,…,dhkh) is
Note that the characteristic sequence given in (3.2) is (n,d1k1,…,dhkh) for the maximum values of ki obtained in Proposition 4. Moreover, as a consequence of that, we have the following corollary.
Corollary 5. Let n>2 be a natural number. Fix a sequence of divisors (d0=n,d1,…,dh) of n. The A-M semigroup of the form S(n,d1k1,…,dhkh) having the minimum conductor is given by k1=1 and ki=di−2diki−1+1, for i∈{2,…,h}, and its conductor is ∑h−2i=0di(di+1−1).
Proof. By (3.3) and according to Proposition 4, the minimum value of conductors of A-M semigroups of the form S(n,d1k1,…,dhkh) holds for the minimum values of ki for i=1,…,h.
For h=1, the sequence of divisors (d0,d1,…,dh) is (n,1). So, S(n,1)=N, and its conductor is zero, which is equal to the empty sum ∑−1i=0di(di+1−1).
Assume that h≥2. Put k1=1, and for any i∈{2,…,h}, we put ki=⌈di−2ki−1+1di⌉=di−2ki−1di+1. Notice that, since di−1di is a divisor of di−2di, we have gcd(di−1di,di−2ki−1di+1)=1. Thus, the integers k1=1 and ki=di−2diki−1+1, for i∈{2,…,h}, satisfy Proposition 4; and then, S(n,d1k1,…,dhkh) is the A-M semigroup having the minimum conductor for the sequence of divisors (d0=n,d1,…,dh).
Note that, for k1=1 and kq=dq−2kq−1dq+1, we have k2=d0d2+1, and, in general, kq=1dq−1dq∑q−3i=0didi+1+dq−2dq+1 for q∈{2,…,h}.
After (3.3), we get c(S(n,d1k1,…,dhkh))=∑hi=1(di−1−di)ki−n+1. Thus,
Remark 6. Given an integer n=pα11⋯pαtt≥2 with p1>p2>⋯>pt prime integers, the maximum length of any sequence of divisors of n is Λ(n)=∑ti=1αi. Moreover, if we fix h, a length of the sequences of divisors of n, then it allows us to provide a lower bound for the integers which could be realizable as the conductor of an A-M semigroup of degree n with an associated sequence of divisors with length greater than or equal to h: Let us consider that with ch:=min{∑h−2i=0di(di+1−1)∣(d0,d1,…,dh)isasequenceofdivisorsofn}, if c<ch, then c is not realizable as the conductor of an A-M semigroup of degree n with an associated sequence of divisors with length greater than or equal to h.
Fix n∈N, and let Th be the set of sequences of divisors of n with length h. Consider two sequences D,D′∈∪Λ(n)h=1Th. If D and D′ have different lengths, we add zeros to the end of the one with the smallest length so that D and D′ have the same length ℓ, and we can compare D and D′ with the lexicographical order <lex as elements of Nℓ. We have
Proposition 7. Let n∈N and D=(d0=n,d1,…,dh),D′=(d′0=n,d′1,…,d′h′)∈∪Λ(n)h=1Th with D<lexD′. Then, the value ∑h−2i=0di(di+1−1) is at most ∑h′−2i=0d′i(d′i+1−1).
Proof. Let D=(d0=n,d1,…,dh) and D′=(d′0=n,d′1,…,d′h′) be two sequences of divisors of n such that D<lexD′. We may further assume that d1<d′1 (otherwise, d1=d′1 and we can truncate both sequences, removing n, and see them as sequences of divisors of d1 instead). Since d1 and d′1 are both divisors of n, then they are of the form d1=n/a1 and d′1=n/a′1 with a′1<a1. Now, notice that, since D is a sequence of strictly decreasing divisors of n, we have
for every i∈{1,…,h}. Thus,
However, ∑i∈N1/22i−1 is a convergent series bounded above by 1. Therefore,
We now prove the inequality
which is equivalent to proving that
We prove a slightly stronger inequality, that is, we have the following inequality:
However remember that a′1<a1. Hence, a′1(a1+1)≤(a1−1)(a1+1)=a21−1≤a21, so the inequality (3.5) follows. If we plug this in to the inequality (3.4), we obtain
as we wanted to show.
Table 3 illustrates Proposition 7 for n=105.
4.
Conductors of A-M semigroups of even degree
Let Fn be the set of Abhyankar-Moh semigroups of degree n>2. Let En=[n−1,(n−1)(n−2)]∩2Z. The cardinality of En is
For any c∈En, is there an S∈Fn such that c(S)=c? We will prove that the answer is positive when n is even. However, if n is odd, then this is not true. Indeed, suppose that S is an A-M semigroup of a prime degree n>2. In this case, S=S(v0,v1), where n=v0 is greater than v1, v1>1, and gcd(v0,v1)=1. Hence,
and the cardinality of Fn is n−2. By (4.1), the cardinality of En is (n−1)(n−3)2+1. Observe that (n−1)(n−3)2+1>n−2 for any n>3. So, for n>3, we conclude that there are values in En which are not realizable as conductors of an A-M semigroup of degree n. Remember that the only A-M semigroup of degree 2 is N. Suppose that n is an even integer greater than 2. First, we will prove that for any c∈[n−1,n2−22)∩2N there is an A-M semigroup of degree n and conductor c.
Lemma 8. Let n≥4 be an even integer. The only A-M semigroup S of degree n with c(S)=n is the semigroup generated by the characteristic sequence (n,2,n+1).
Proof. The characteristic sequence (n,2,n+1) determines an A-M semigroup with conductor n. Let us prove the uniqueness. Let S be an A-M semigroup of degree n=c(S) determined by the characteristic sequence (v0=n,v1,v2,…,vh). By [5, Proposition 1.2], c(S)=∑hi=1(ni−1)vi−v0+1 with ni>1 for 1≤i≤h. Suppose that h≥3. Since v1<n<v2<v3<⋯<vh, we get c(S)≥∑3i=1(ni−1)vi−n+1>n. On the other hand, if h=1, then c(S)=nv1−n−v1+1. Since n>v1≥3, c(S)≥3n−n−v1+1>n+1.
Let us suppose that h=2, so e2=1. Since v2≥n+1, c(S)>(n1−1)v1+(n2−2)n. Observe that for n2>2 we get c(S)>n. So, n2=e1=2, n1=n/2, and v1 is an even integer. If v1≥4 then c(S)≥2n−2>n. Hence, v1=2, and consequently, c(S)=n if and only if v2=n+1.
Lemma 9. Let n≥4 be an even integer. For any q∈[0,(n−1)(n−2)+n4−1), the semigroup generated by (n,2,n+1+2q) is an A-M semigroup of conductor n+2q.
Proof. The characteristic sequence (n,2,n+1+2q) determines an A-M semigroup for any even integer q<(n−1)(n−2)+n4−1 with sequence of divisors (n,2,1) and c(S(n,2,n+1+2q))=n+2q.
Corollary 10. For any even integer n≥4 and c∈[n−1,n2−22)∩2N, there is at least one A-M semigroup of degree n and conductor c.
Now, the target will be to prove that, if n≥4 is an even integer and c∈[n2−22,(n−1)(n−2)]∩2N, there is an A-M semigroup of degree n and conductor c. We will do it in several steps.
Lemma 11. Let n be a natural number such that n=2r≥4, where r is odd. Let k∈N be co-prime with r and 1≤k≤r−1. The sequence (n,2k,v2) determines an A-M semigroup of degree n if and only if it satisfies the following conditions:
1. v2 is an odd number,
2. kn+1≤v2≤2r2−1.
Proof. It follows directly from the definition of an A-M semigroup.
Suppose that (n=2r,2k,v2) defines an A-M semigroup of degree n, where 1≤k≤r−1 with gcd(r,k)=1, so e0=n=2r>e1=2>e2=1. Denote this semigroup by S(k,v2). The conductor of S(k,v2) equals (r−1)2k+v2−2r+1. Hence, if S(k,v2) and S(k,v′2) are two A-M semigroups of degree n with v2<v′2, then c(S(k,v2))<c(S(k,v′2)). If we fix k, varying v2 we get A-M semigroups attaining the following values for their conductor:
Define Il:=[2ln−2(l+r)+2,ln−2(l+r)+2r2]∩2N for any 1≤l≤r−1. Note that for any l1,l2∈N with l1<l2, Il1∩Il2 is the empty set if and only if l2≥r2+l1r−l12r−1. Since r2+l1r−l12r−1>r+l12, we obtain that Il1∩Il2≠∅ for every l1∈N and l2∈(l1,r+l12]∩N. We want to show that by also varying the values of k, we construct A-M semigroups covering all possible conductors. For that, we prove the following lemma.
Lemma 12. Let r,l∈N where r is odd, l≤r−2 and gcd(l,r)=1. There is a k∈(l,l+r2]∩N coprime with r.
Proof. Let m:=min{n∈N:r−2n≤l+r2}. Notice that such an integer exists since l≤r−2 by hypothesis. We claim that k:=r−2m∈(l,l+r2] and is coprime with r. Indeed, gcd(r−2m,r)=gcd(2m,r)=1, due to r being odd. Moreover, by definition of m, k≤l+r2. Assume by contradiction that k=r−2m≤l and then 2r−2m≤l+r, that is, r−2m−1≤l+r2, which contradicts the minimality of m. Hence, k∈(l,l+r2]∩N is as desired.
Therefore, we conclude the following:
Proposition 13. Let n be a natural number such that n=2r, where r>1 is odd. For any even number c with n−1≤c≤(n−1)(n−2) there is an A-M semigroup of degree n whose conductor is equal to c.
Proof. It is enough to consider the characteristic sequences (n=2r,2k,v2) defining A-M semigroups. Indeed, take L:={l∈[1,r−1]∩N∣gcd(l,r)=1}={l1,l2,…,ls}, with lt<lt+1 for any t∈{1,…,s}. Lemma 4 and its following discussion tell us that, by considering these characteristic sequences, we construct A-M semigroups whose conductors cover all the values in Il1∪…∪Ils. Moreover, by Lemma 5, we know that Ili∩Ili+1≠∅ for every i∈{1,…,s−1}. Hence, we cover all even integers from the minimum value in Il1 to the maximum value in Ils. Since l1=1 and ls=r−1, these values are n and (n−1)(n−2), respectively. This concludes the proof.
Remark 14. After Algorithm 1, we get that the A-M semigroups of degree 4 are S1=S(4,2,5), S2=S(4,3) and S3=S(4,2,7), where c(S1)=4 and c(S2)=c(S3)=6. Hence, any c∈E4 is the conductor of an A-M semigroup of degree 4. Observe that the sequence of divisors of S1 and S3 is (4,2,1), and the sequence of divisors of S2 is (4,1).
Proposition 15. Let n be a natural number such that n=2kr, where k≥1, and r>1 is odd. For any even number c with n−1≤c≤(n−1)(n−2) there is an A-M semigroup of degree n whose conductor is equal to c.
Proof. We use induction over k. Notice that for k=1, the statement holds by Proposition 13.
Let us assume that k≥2 and that the proposition holds for k−1. In addition, Remark 14 already covers the case n=4, and thus we can further assume that n≥8.
We first observe that, by Corollary 10, for every even c∈I1:=[n−1,n2−22), there exists an A-M semigroup of degree n and conductor c. Thus, it remains to prove that the same is true for any c∈[n2−22,(n−1)(n−2)].
On the one hand, as explained in Lemma 3, S′=⟨n2,2,n2+1⟩ is an A-M semigroup with conductor c(S′)=n2. One can check that the gluing S=S′⨁2,dN=⟨n,4,n+2,f⟩ is an A-M semigroup for every odd number f∈[2n+5,n22−1]. Furthermore, (3.1) tells us that
Hence, through this gluing we have shown that for any even number c belonging to I2:=[3n+4,n22+n−2], the semigroup S=⟨n,4,n+2,c+1−n⟩ is an A-M semigroup with conductor c.
On the other hand, by the induction hypothesis, for m=n2=2k−1r, we can guarantee that, for every even number c′∈[m−1,(m−1)(m−2)], there exists an A-M semigroup S′c′ of degree m and conductor c′. It is not hard to check that the gluing
is an A-M semigroup of degree 2m=n, for both values: f1=n22−1 and f2=n22−3. In addition, again by (3.1), the conductor c(c′,fi) of S(c′,fi) is
Now, notice the relations
and
These imply that, by making this gluing and recursively decreasing the value of c′, alternating it with both f1 and f2, we can assure the existence of an A-M semigroup of degree n and conductor c, for every even number from the maximum possible value, that is,
and all the way down to
Overall, we have shown that, for any even number c∈I1∪I2∪I3 there exists an A-M semigroup of degree n and conductor c, where I3=[n22+n−4,(n−1)(n−2)]. Clearly, I2 and I3 overlap, and we have that I1∪I2∪I3=[n−1,(n−1)(n−2)] as long as n≥8. Thus, the statement follows.
Let p>1 be a prime number and k be an integer greater than or equal to two. Note that, for every A-M semigroup S of degree n=pk, c(S) is a multiple of p−1 (see equation (2.1)). So, c(S)∈[n−1,(n−1)(n−2)]∩(p−1)N.
Now, we will study the A-M semigroups of degree n=pk, where p is a prime number and k∈N, k>1. For any natural number k1 with 1≤k1≤pk−1−1, we define Ik1:=[1,p2k−1−pkk1−1], and
In the following proposition, we prove that for a fixed n=2k, every value in [n−1,(n−1)(n−2)]∩2N is the conductor of some A-M semigroup of degree n. Furthermore, the conductors of the A-M semigroups of degree n=pk are provided explicitly for any odd prime integer p, and the sequences of divisors of n that determine these conductors are made explicit.
Proposition 16. Let p≥2 be a prime number, and k≥2 is an integer. Any conductor of an A-M semigroup with degree n=pk is obtained from, at most, two types of sequences of divisors:
1. For p, a prime odd number, the sequences are (pk,1) and (pk,p,1);
2. For p=2 and k=2, the sequence is (4,2,1);
3. For p=2 and k=3, the sequences are (8,2,1) and (8,4,2,1);
4. For p=2 and k≥4, the sequence is (2k,2,1).
Moreover, for any odd prime number p, the set of the conductors of A-M semigroups of degree n is
Proof. Let (pk,pk1,v2) be a characteristic sequence where gcd(p,k1)=gcd(p,v2)=1. Note that the semigroup S(pk,pk1,v2) is an A-M semigroup if and only if pkk1<v2<p2k−1. So, we assume that k1∈[1,pk−1−1] and v2∈[pkk1+1,p2k−1−1], with k1 and v2 coprime with p. Consider v2=pkk1+i with i∈Ik1=[1,p2k−1−pkk1−1] and such that i≠0modp.
Thus, c(S)=(pk−1)(pk1−1)+i(p−1). Define c(pk,pk1,pkk1+i)=(pk−1)(pk1−1)+(p−1)i. This even value belongs to C(k1)∩(p−1)N, where C(k1)=[(pk−1)(pk1−1)+(p−1),(pk−1)(pk1−1)+(p−1)(p2k−1−pkk1−1)], for any i∈Ik1. Note that, for p=2, c(2k,2k1,2kk1+i) takes all the even numbers in C(k1). In addition, for any integer k′1 such that k1<k′1, we have that
if and only if minC(k′1)≤maxC(k1)+max{2,p−1}.
Assume that p≥3 and suppose gcd(p,k1+1)=1. In that case, the condition (4.2) holds for k1+1≤pk−1−1 iff minC(k1+1)≤maxC(k1)+p−1, that is, iff (p−1)(p2k−1−pkk1−1)−p(pk−1)≥0. Since k1≤pk−1−2,
Thus, the condition (4.2) holds when gcd(p,k1+1)=1. In the case where p and k1+1 are not coprime, we have that gcd(p,k1+2)=1, and the inequality minC(k1+2)≤maxC(k1)+p−1 is equivalent to (p−1)(p2k−1−pkk1−1)−2p(pk−1)≥0. Again, since k1+2≤pk−1−1, (p−1)(p2k−1−pkk1−1)−2p(pk−1)≥pk(p−3)+p+1>0. We conclude that, for p≥3, the condition (4.2) always holds. That means that, for every k1∈[1,pk−1−1] and i∈Ik1 with imodp≠0, c(pk,pk1,pkk1+i)=(pk−1)(pk1−1)+i(p−1)∈A=[minC(1),maxC(pk−1−1)]∩(p−1)N=[n(p−1),(n−1)(n−2)]∩(p−1)N. Note that A is the union of the disjoint sets
and
The elements of A′k1 are not the conductors of any A-M semigroup of degree n. Suppose there exists an A-M semigroup S′ of degree n such that its conductor belongs to A′k1. If the characteristic sequence of S′ is (pk,v1) with gcd(p,v1)=1, then c(S′)=(pk−1)(v1−1)=(pk−1)(pk1−1)+i(p−1), and (pk−1)v1=(pk−1)pk1+i(p−1). However this is not possible since gcd(pk−1,p)=gcd(p,v1)=1. If the length of the characteristic sequence of S′ is greater than or equal to three, by Proposition 3, there exists an A-M semigroup S″, and with and , such that . Thus, by equality (3.1), , and . Since , it does not hold.
Note that, by Proposition 3 and the equality (3.1), is the smallest conductor of an A-M semigroup of degree that can be obtained from characteristic sequences of length greater than or equal to three. Moreover, the set of the conductors of the A-M semigroups of degree with a characteristic sequence of length two is .
Summarizing, we have just proved that, for every prime odd number and , the conductor of any A-M semigroup with degree is equal to with satisfying , or it is equal to where and such that . For the first type, their sequences of divisors are , and we have for the second one.
For , , but . Hence, the condition (4.2) holds if and only if . Using the upper bound of , . It is easy to prove that for any . Therefore, for , every even number in is realizable as the conductor of an A-M semigroup with the sequence of divisors . The particular cases , and are showed in Remark 14 and Table 2, respectively.
By Proposition 15 and Proposition 16, for , we have the following,
Theorem A. Let be an even natural number. For any even number with , there is an A-M semigroup of degree and conductor equal to .
Open question: Characterize the values of conductors of A-M semigroups of odd degree. Note that Proposition 16 solves this question for degree with any prime integer.
Acknowledgments
The second and fourth-named authors were supported partially by Junta de Andalucía research groups FQM-343. The first-named author was supported by the grant PID2019-105896GB-I00 funded by MCIN/AEI/10.13039/501100011033. The first and third-named authors were supported partially by MACACO (ULL research project).
Conflict of interest
The authors declare there are no conflicts of interest.









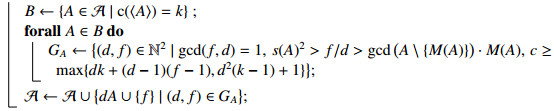
 DownLoad:
DownLoad: