Introduction
The study of Hom-algebras can be traced back to Hartwig, Larsson and Silvestrov's work in [1], where the notion of Hom-Lie algebra in the context of q-deformation theory of Witt and Virasoro algebras [2] was introduced, which plays an important role in physics, mainly in conformal field theory. Hom-algebras and Hom-coalgebras were introduced by Makhlouf and Silvestrov [3] as generalizations of ordinary algebras and coalgebras in the following sense: the associativity of the multiplication is replaced by the Hom-associativity and similar for Hom-coassociativity. They also defined the structures of Hom-bialgebras and Hom-Hopf algebras, and described some of their properties extending properties of ordinary bialgebras and Hopf algebras in [4,5]. In [6], Caenepeel and Goyvaerts studied Hom-bialgebras and Hom-Hopf algebras from a categorical view point, and called them monoidal Hom-bialgebras and monoidal Hom-Hopf algebras respectively, which are different from the normal Hom-bialgebras and Hom-Hopf algebras in [4]. Many more properties and structures of Hom-Hopf algebras have been developed, see [7,8,9,10] and references cited therein.
Later, Yau [11,12] proposed the definition of quasitriangular Hom-Hopf algebras and showed that each quasitriangular Hom-Hopf algebra yields a solution of the Hom-Yang-Baxter equation. The Hom-Yang-Baxter equation reduces to the usual Yang-Baxter equation when the twist map is trivial. Several classes of solutions of the Hom-Yang-Baxter equation were constructed from different respects, including those associated to Hom-Lie algebras [11,13,14,15], Drinfelds (co)doubles [16,17,18], and Hom-Yetter-Drinfeld modules [19,20,21,22,23,24,25,26].
It is well-known that classical nonlinear equations in Hopf algebra theory including the quantum Yang-Baxter equation, the Hopf equation, the pentagon equation, and the Long equation. In [27], Militaru proved that each Long dimodule gave rise to a solution for the Long equation. Long dimodules are the building stones of the Brauer-Long group. In the case where H is commutative, cocommutative and faithfully projective, the Yetter-Drinfeld category HHYD is precisely the Long dimodule category HHL. Of course, for an arbitrary H, the categories HHYD and HHL are basically different. In [28], Chen et al. introduced the concept of Long dimodules over a monoidal Hom-bialgebra and discussed its relation with Hom-Long equations. Later, we [29] extended Chen's work to generalized Hom-Long dimodules over monoidal Hom-Hopf algebras and obtained a kind solution for the quantum Yang-Baxter equation. For more details about Long dimodules, see [30,31,32,33] and references cited therein.
The main purpose of this paper is to construct a new braided monoidal category and present solutions for two kinds of nonlinear equations. Different to our previous work in [29], in the present paper we do all the work over Hom-Hopf algebras, which is more unpredictable than the monoidal version. Since Hom-Hopf algebras and monoidal Hom-Hopf algebras are different concepts, it turns out that our definitions, formulas and results are also different from the ones in [29]. Most important, we associate quantum Yang-Baxter equations and Hom-Long equations to the Hom-Long dimodule categories.
This paper is organized as follows. In Section 1, we recall some basic definitions about Hom-(co)modules and (co)quasitriangular Hom-Hopf algebras.
In Section 2, we first introduce the notion of (H,B)-Hom-Long dimodules over Hom-bialgebras (H,α) and (B,β), then we show that the Hom-Long dimodule category BHL forms an autonomous category (see Theorem 2.6) and prove that the category is equivalent to the category of left B∗op⊗H-Hom-modules (see Theorem 2.7).
In Section 3, for a quasitriangular Hom-Hopf algebra (H,R,α) and a coquasitriangular Hom-Hopf algebra (B,⟨|⟩,β), we prove that the Hom-Long dimodule category BHL is a subcategory of the Hom-Yetter-Drinfeld category H⊗BH⊗BHYD (see Theorem 3.5), and show that the braiding yields a solution for the quantum Yang-Baxter equation (see Corollary 3.2).
In Section 4, we prove that the category HM over a triangular Hom-Hopf algebra (resp., HM over a cotriangular Hom-Hopf algebra) is a Hom-Long dimodule subcategory of BHL (see Propositions 4.1 and 4.2). We also show that the Hom-Long dimodule category BHL is symmetric in case (H,R,α) is triangular and (B,⟨|⟩,β) is cotriangular (see Theorem 4.3).
In Section 5, we introduce the notion of (H,α)-Hom-Long dimodules and obtain a solution for the Hom-Long equation (see Theorem 5.10).
1.
Preliminaries
Throughout this paper, k is a fixed field. Unless otherwise stated, all vector spaces, algebras, modules, maps and unadorned tensor products are over k. For a coalgebra C, the coproduct will be denoted by Δ. We adopt a Sweedler's notation △(c)=c1⊗c2, for any c∈C, where the summation is understood. We refer to [34,35] for the Hopf algebra theory and terminology.
We now recall some useful definitions in [3,4,5,12,36,37].
Definition 1.1. A Hom-algebra is a quadruple (A,μ,1A,α) (abbr. (A,α)), where A is a k-linear space, μ:A⊗A⟶A is a k-linear map, 1A∈A and α is an endmorphism of A, such that
are satisfied for a,a′,a″∈A. Here we use the notation μ(a⊗a′)=aa′.
Definition 1.2. Let (A,α) be a Hom-algebra. A left (A,α)-Hom-module is a triple (M,⊳,ν), where M is a linear space, ⊳:A⊗M⟶M is a linear map, and ν is an endmorphism of M, such that
are satisfied for a,a′∈A and m∈M.
Let (M,⊳M,νM) and (N,⊳N,νN) be two left (A,α)-Hom-modules. Then a linear morphism f:M⟶N is called a morphism of left (A,α)-Hom-modules if f(h⊳Mm)=h⊳Nf(m) and νN∘f=f∘νM.
Definition 1.3. A Hom-coalgebra is a quadruple (C,Δ,ϵ,β) (abbr. (C,β)), where C is a k-linear space, Δ:C⟶C⊗C, ϵ:C⟶k are k-linear maps, and β is an endmorphism of C, such that
are satisfied for c∈C.
Definition 1.4. Let (C,β) be a Hom-coalgebra. A left (C,β)-Hom-comodule is a triple (M,ρ,μ), where M is a linear space, ρ:M⟶C⊗M (write ρ(m)=m(−1)⊗m(0),∀m∈M) is a linear map, and μ is an endmorphism of M, such that
are satisfied for all m∈M.
Let (M,ρM,μM) and (N,ρN,μN) be two left (C,β)-Hom-comodules. Then a linear map f:M⟶N is called a map of left (C,β)-Hom-comodules if f(m)(−1)⊗f(m)(0)=m(−1)⊗f(m(0)) and μN∘f=f∘μM.
Definition 1.5. A Hom-bialgebra is a sextuple (H,μ,1H,Δ,ϵ,γ) (abbr. (H,γ)), where (H,μ,1H,γ) is a Hom-algebra and (H,Δ,ϵ,γ) is a Hom-coalgebra, such that Δ and ϵ are morphisms of Hom-algebras, i.e.,
Furthermore, if there exists a linear map S:H⟶H such that
then we call (H,μ,1H,Δ,ϵ,γ,S) (abbr. (H,γ,S)) a Hom-Hopf algebra.
Definition 1.6. ([36]) Let (H,β) be a Hom-bialgebra, (M,⊳,μ) a left (H,β)-module with action ⊳:H⊗M⟶M,h⊗m↦h⊳m and (M,ρ,μ) a left (H,β)-comodule with coaction ρ:M⟶H⊗M,m↦m(−1)⊗m(0). Then we call (M,⊳,ρ,μ) a (left-left) Hom-Yetter-Drinfeld module over (H,β) if the following condition holds:
where h∈H and m∈M.
When H is a Hom-Hopf algebra, then the condition (HYD) is equivalent to
Definition 1.7. ([36]) Let (H,β) be a Hom-bialgebra. A Hom-Yetter-Drinfeld category HHYD is a pre-braided monoidal category whose objects are left-left Hom-Yetter-Drinfeld modules, morphisms are both left (H,β)-linear and (H,β)-colinear maps, and its pre-braiding C−,− is given by
for all m∈(M,μ)∈HHYD and n∈(N,ν)∈HHYD.
Definition 1.8. A quasitriangular Hom-Hopf algebra is a octuple (H,μ,1H,Δ,ϵ,S,β,R) (abbr. (H,β,R)) in which (H,μ,1H,Δ,ϵ,S,β) is a Hom-Hopf algebra and R=R(1)⊗R(2)∈H⊗H, satisfying the following axioms (for all h∈H and R=r):
where Δcop(h)=h2⊗h1 for all h∈H. A quasitriangular Hom-Hopf algebra (H,R,β) is called triangular if R−1=R(2)⊗R(1).
Definition 1.9. A coquasitriangular Hom-Hopf algebra is a Hom-Hopf algebra (H,β) together with a bilinear form ⟨|⟩ on (H,β) (i.e., ⟨|⟩∈ Hom(H⊗H,k)) such that the following axioms hold:
for all h,g,l∈H. A coquasitriangular Hom-Hopf algebra (H,⟨|⟩,β) is called cotriangular if ⟨|⟩ is convolution invertible in the sense of ⟨h1|g1⟩⟨g2|h2⟩=ϵ(h)ϵ(g), for all h,g∈H.
2.
Hom-Long dimodules over Hom-bialgebras
In this section, we will introduce the notion of Hom-Long dimodules and prove that the Hom-Long dimodule category is an autonomous category.
Definition 2.1. Let (H,α) and (B,β) be two Hom-bialgebras. A left-left (H,B)-Hom-Long dimodule is a quadruple (M,⋅,ρ,μ), where (M,⋅,μ) is a left (H,α)-Hom-module and (M,ρ,μ) is a left (B,β)-Hom-comodule such that
for all h∈H and m∈M. We denote by BHL the category of left-left (H,B)-Hom-Long dimodules, morphisms being H-linear B-colinear maps.
Example 2.2. Let (H,α) and (B,β) be two Hom-bialgebras. Then (H⊗B,α⊗β) is an (H,B)-Hom-Long dimodule with left (H,α)-action h⋅(g⊗x)=hg⊗β(x) and left (B,β)-coaction ρ(g⊗x)=x1⊗(α(g)⊗x2), where h,g∈H,x∈B.
Proposition 2.3. Let (M,μ),(N,ν) be two (H,B)-Hom-Long dimodules, then (M⊗N,μ⊗ν) is an (H,B)-Hom-Long dimodule with structures:
for all m∈M,n∈N and h∈H.
Proof. From Theorem 4.8 in [21], (M⊗N,μ⊗ν) is both a left (H,α)-Hom-module and a left (B,β)-Hom-comodule. It remains to check that the compatibility condition (2.1) holds. For any m∈M,n∈N and h∈H, we have
as desired. This completes the proof.
Proposition 2.4. The Hom-Long dimodule category BHL is a monoidal category, where the tensor product is given in Proposition 2.3, the unit I=(k,id), the associator and the constraints are given as follows:
for u∈(U,μ)∈BHL,v∈(V,ν)∈BHL,w∈(W,ω)∈BHL.
Proof. Straightforward.
Proposition 2.5. Let H and B be two Hom-Hopf algebras with bijective antipodes. For any Hom-Long dimodule (M,μ) in BHL, set M∗=Homk(M,k), with the (H,α)-Hom-module and the (B,β)-Hom-comodule structures:
and the Hom-structure map μ∗ of M∗ is μ∗(f)(m)=f(μ−1(m)). Then M∗ is an object in BHL. Moreover, BHL is a left autonomous category.
Proof. It is not hard to check that (M∗,θM∗,μ∗) is an (H,α)-Hom-module and (M∗,ρM∗,μ∗) is a (B,β)-Hom-comodule. Further, for any f∈M∗, m∈M, h∈H, we have
Thus M∗∈BHL.
Moreover, for any f∈M∗ and m∈M, one can define the left evaluation map and the left coevaluation map by
where ei and ei are dual bases in M and M∗ respectively. Next, we will show that (M∗,evM,coevM) is the left dual of M.
It is easy to see that evM and coevM are morphisms in BHL. For this, we need the following computation
Similarly, we get
So BHL admits the left duality. The proof is finished.
Theorem 2.6. The Hom-Long dimodule category BHL is an autonomous category.
Proof. By Proposition 2.5, it is sufficient to show that BHL is also a right autonomous category. In fact, for any (M,μ)∈BHL, its right dual (∗M,~coevM,~evM) is defined as follows:
∙ ∗M=Homk(M,k) as k-modules, with the Hom-module and Hom-comodule structures:
where f∈∗M, m∈M, and the Hom-structure map μ∗ of ∗M is μ∗(f)(m)=f(μ−1(m));
∙ The right evaluation map and the right coevaluation map are given by
where ai and ai are dual bases of M and ∗M respectively. By similar verification in Proposition 2.5, one may check that BHL is a right autonomous category, as required. This completes the proof.
Recall from [17] that for any finite dimensional Hom-Hopf algebra B, B∗ is also a Hom-Hopf algebra with the following structures
where x,y∈H, f,g∈B∗.
Theorem 2.7. If B is a finite dimensional Hom-Hopf algebra, then the Hom-Long dimodule category BHL is identified to the category of left B∗op⊗H-Hom-modules, where B∗op⊗H means the usual tensor product Hom-Hopf algebra.
Proof. Define the functor Ψ from B∗op⊗HM to BHL by
where (M,μ,⇁) is a B∗op⊗H-Hom-module, f:M→N is a morphism of B∗op⊗H-Hom-modules. Further, the H-action on M is defined by
and the B-coaction on M is given by
where ei and ei are dual bases of B and B∗ respectively.
First, we will show (M,μ,⋅) is a left (H,α)-Hom-module. Actually, for any m∈M, h,g∈H, we have 1H⋅m=(ϵB⊗1H)⇁m=μ(m), and
which implies (M,μ,⋅)∈HM.
Second, one can show that (M,μ)∈BM in a similar way.
At last, for any m∈M, h∈H, we have
which implies (M,μ)∈BHL.
Conversely, for any object (M,μ), (N,ν), and morphism f:U→V in BHL, one can define a functor Φ from BHL to B∗op⊗HM
where the (B∗op⊗H,β∗⊗α)-Hom-module structure on M is given by
for all p∈B∗,h∈H,m∈M. It is straightforward to check that (M,μ,⇁) is an object in BHL to B∗op⊗HM, and hence Φ is well defined.
Note that Φ and Ψ are inverse with each other. Hence the conclusion holds.
3.
New braided momoidal categories over Hom-Long dimodules
In this section, we will prove that the Hom-Long dimodule category BHL over a quasitriangular Hom-Hopf algebra (H,R,α) and a coquasitriangular Hom-Hopf algebra (B,⟨|⟩,β) is a braided monoidal subcategory of the Hom-Yetter-Drinfeld category H⊗BH⊗BHYD.
Theorem 3.1. Let (H,R,α) be a quasitriangular Hom-Hopf algebra and (B,⟨|⟩,β) a coquasitriangular Hom-Hopf algebra. Then the category BHL is a braided monoidal category with braiding
for all m∈(M,μ)∈BHL and n∈(N,ν)∈BHL.
Proof. We will first show that the braiding CM,N is a morphism in BHL. In fact, for any m∈M,n∈N and h∈H, we have
The third equality holds since ⟨|⟩ is β-invariant and the fifth equality holds since R is α-invariant. So CM,N is left (H,α)-linear. Similarly, one may check that CM,N is left (B,β)-colinear.
Now we prove that the braiding CM,N is natural. For any (M,μ),(M′,μ′), (N,ν),(N′,ν′) ∈BHL, let f:M→M′ and g:N→N′ be two morpshisms in BHL, it is sufficient to verify the identity (g⊗f)∘CM,N=CM′,N′∘(f⊗g). For this purpose, we take m∈M,n∈N and do the following calculation:
The sixth equality holds since f,g are left (B,β)-colinear. So the braiding CM,N is natural, as needed.
Next, we will show that the braiding CM,N is an isomorphsim with inverse map
For any m∈M,n∈N, we have
The second equality holds since ρ(R(2)⋅ν−2(n(0)))=β−1(n(0)(−1))⊗α(R(2))⋅n(0)(0) and the fifth equality holds since R−1=S(r(1))⊗r(2).
Now let us verify the hexagon axioms (H1,H2) from Section XIII. 1.1 of [38]. We need to show that the following diagram (H1) commutes for any (U,μ),(V,ν),(W,ω)∈BHL:
For this purpose, let u∈U,v∈V,w∈W, then we have
and
Since r=R, it follows that aV,U,W∘CU,V⊗W∘aU,V,W=(idV⊗CU,W)∘aV,U,W∘(CU,V⊗idW), that is, the diagram (H1) commutes.
Now we check that the diagram (H2) commutes for any (U,μ),(V,ν),(W,ω)∈BHL:
In fact, for any u∈U,v∈V,w∈W, we obtain
Also we can get
So the diagram (H2) commutes since r=R. This ends the proof.
Corollary 3.2. Under hypotheses of Theorem 3.1, the braiding C is a solution of the quantum Yang-Baxter equation
Proof. Straightforward.
Lemma 3.3. Let (H,R,α) be a quasitriangular Hom-Hopf algebra and (B,⟨|⟩,β) a coquasitriangular Hom-Hopf algebra. Define a linear map
for any h∈H,x∈B and m∈(M,μ)∈BHL. Then (M,μ) becomes a left (H⊗B)-Hom-module.
Proof. It is sufficient to show that the Hom-module action defined above satisfies Definition 1.2. For any h,g∈H,x,y∈B and m∈M, we have
That is, (1H⊗1B)⇀m=μ(m). For the equality μ((h⊗x)⇀m)=(α(h)⊗β(x))⇀μ(m), we have
as required. Finally, we check the expression ((h⊗x)(g⊗y))⇀μ(m)=(α(h)⊗β(x))⇀((g⊗y)⇀m). For this, we calculate
So (M,μ) is a left (H⊗B)-Hom-module. The proof is completed.
Lemma 3.4. Let (H,R,α) be a quasitriangular Hom-Hopf algebra and (B,⟨|⟩,β) a coquasitriangular Hom-Hopf algebra. Define a linear map
for any m∈(M,μ). Then (M,μ) becomes a left (H⊗B)-Hom-comodule.
Proof. We first show that ¯ρ satisfies Eq (HCM2). On the one side, we have
On the other side, we have
Since R is α-invariant, we have Δ(m[−1])⊗μ(m[0])=(α⊗β)(m[−1])⊗¯ρ(m[0]), as needed.
For Eq (HCM1), we have
as desired. And this finishes the proof.
Theorem 3.5. Let (H,R,α) be a quasitriangular Hom-Hopf algebra and (B,⟨|⟩,β) a coquasitriangular Hom-Hopf algebra. Then the Hom-Long dimodules category BHL is a monoidal subcategory of Hom-Yetter-Drinfeld category H⊗BH⊗BYD.
Proof. Let m∈(M,μ)∈BHL and h∈H. Here we first note that ρ(h⋅μ−1(m(0)))=m(0)(−1)⊗α(h)⋅μ−1(m(0)(0)). It is sufficient to show that the left (H⊗B)-Hom-module action in Lemma 3.3 and the left (H⊗B)-Hom-comodule structure in Lemma 3.4 satisfy the compatible condition Eq (HYD). Indeed, for any h∈H, x∈B, m∈M, we have
So (M,μ)∈H⊗BH⊗BHYD. The proof is completed.
Proposition 3.6. Under hypotheses of Theorem 3.5, BHL is a braided monoidal subcategory of H⊗BH⊗BHYD.
Proof. It is sufficient to show that the braiding in the category BHL is compatible to the braiding in H⊗BH⊗BHYD. In fact, for any m∈(M,μ) and n∈(N,ν), we have
as desired.This finishes the proof.
4.
Symmetries in Hom-Long dimodule categories
In this section, we obtain a sufficient condition for the Hom-Long dimodule category BHL to be symmetric.
Let C be a monoidal category and C a braiding on C. The braiding C is called a symmetry [38,39] if CY,X∘CX,Y=idX⊗Y for all X,Y∈C, and the category C is called symmetric.
Proposition 4.1. Let (H,R,α) be a triangular Hom-Hopf algebra and (B,β) a Hom-Hopf algebra. Then the category HM of left (H,α)-Hom-modules is a symmetric subcategory of BHL under the left (B,β)-comodule structure ρ(m)=1B⊗μ(m), where m∈(M,μ)∈HM, and the braiding is defined as
for all m∈(M,μ)∈HM,n∈(N,ν)∈HM.
Proof. It is clear that (M,ρ,μ) is a left (B,β)-Hom-comodule under the left (B,β)-comodule structure given above. Now we check that the left (B,β)-comodule structure satisfies the compatible condition Eq (2.1). For this purpose, we take h∈H,m∈(M,μ)∈HM, and calculate
So, Eq (2.1) holds. That is, (M,ρ,μ) is an (H,B)-Hom-Long dimodule.
Next we verify that any morphism in HM is left (B,β)-colinear, too. Indeed, for any m∈(M,μ)∈HM and n∈(N,ν)∈HM. Assume that f:(M,μ)→(N,ν) is a morphism in HM, then
So f is left (B,β)-colinear, as desired. Therefore, HM is a subcategory of BHL.
Finally, we prove that HM is a symmetric subcategory of BHL. Since CM,N(m⊗n)=R(2)⋅ν−1(n)⊗R(1)⋅μ−1(m), for all m∈(M,μ)∈HM and n∈(N,ν)∈HM, we have
It follows that the braiding CM,N is symmetric. The proof is completed.
Proposition 4.2. Let (B,⟨|⟩,β) be a cotriangular Hom-Hopf algebra and (H,α) a Hom-Hopf algebra. Then the category BM of left (B,β)-Hom-comodules is a symmetric subcategory of BHL under the left (H,α)-module action h⋅m=ϵ(h)μ(m), where h∈H,m∈(M,μ)∈BM, and the braiding is given by
for all m∈(M,μ)∈BM,n∈(N,ν)∈BM.
Proof. We first show that the left (H,α)-module action defined above forces (M,μ) to be a left (H,α)-module, but this is easy to check. For the compatible condition Eq (2.1), we take h∈H,m∈(M,μ)∈BM and calculate as follows:
So, Eq (2.1) holds, as required. Therefore, (M,ρ,μ) is an (H,B)-Hom-Long dimodule.
Now we verify that any morphism in BM is left (H,α)-linear, too. Indeed, for any m∈(M,μ)∈BM and n∈(N,ν)∈BM. Assume that f:(M,μ)→(N,ν) is a morphism in BM, then
So f is left (H,α)-linear, as desired. Therefore, BM is a subcategory of BHL.
Finally, we show that BM is a symmetric subcategory of BHL. Since CM,N(m⊗n)=⟨m(−1)|n(−1)⟩ν−1(n(0))⊗μ−1(m(0)), for all m∈(M,μ)∈BM and n∈(N,ν)∈BM, then
where the fourth equality holds since ⟨|⟩ is β-invariant. It follows that the braiding CM,N is symmetric. The proof is completed.
Theorem 4.3. Let (H,α) be a triangular Hom-Hopf algebra and (B,⟨|⟩,β) a cotriangular Hom-Hopf algebra. Then the category BHL is symmetric.
Proof. For any m∈(M,μ)∈BHL and n∈(N,ν)∈BHL, we have
as desired. This finishes the proof.
5.
New solutions of the Hom-Long equation
In this section, we will present a kind of new solutions of the Hom-Long equation.
Definition 5.1. Let (H,α) be a Hom-bialgebra and (M,μ) a Hom-module over (H,α). Then R∈End(M⊗M) is called the solution of the Hom-Long equation if it satisfies the nonlinear equation:
where R12=R⊗μ,R23=μ⊗R.
Example 5.2. If R∈End(M⊗M) is invertible, then it is easy to see that R is a solution of the Hom-Long equation if and only if R−1 is too.
Example 5.3. Let (M,μ) be an (H,α)-Hom-module with a basis {m1,m2,⋯,mn}. Assume that μ is given by μ(mi)=aimi, where ai∈k,i=1,2,⋯,n. Define a map
where bij∈k,i,j=1,2,,⋯,n. Then R is a solution of Eq (5.1). Furthermore, if ai=1, for all i=1,2,⋯,n, then R is a solution of the classical Long equation.
Proposition 5.4. Let (M,μ) be an (H,α)-Hom-module with a basis {m1,m2,⋯,mn}. Assume that R,S∈End(M⊗M,μ⊗μ−1) given by the matrix formula
and μ(ml)=zilmi, where xijkl,yijkl,zil∈k. Then S12∘R23=R23∘S12 if and only if
for all k,p,q,u,v,w=1,2,⋯,n. In particular, R is a solution of the Hom-Long equation if and only if
Proof. According to the definition of R,S,μ, we have
It follows that S12∘R23=R23∘S12 if and only if ziuxjkvwypqij=zpixqkjwyijuv. Furthermore, R12∘R23=R23∘R12 if and only if ziuxjkvwxpqij=zpixqkjwxijuv. The proof is completed.
In the following proposition, we use the notation: for any F∈End(M⊗M), we denote F12=F⊗μ,F23=μ⊗F,F13=(id⊗τ)∘(F⊗μ)∘(id⊗τ), and τ(123)(x⊗y⊗z)=(z,x,y).
Proposition 5.5. Let (M,μ) be an (H,α)-Hom-module and R∈End(M⊗M). The following statements are equivalent:
(1) R is a solution of the Hom-Long equation.
(2) U=τ∘R is a solution of the equation:
(3) T=R∘τ is a solution of the equation:
(4) W=τ∘R∘τ is a solution of the equation:
Proof. We just prove(1)⇔(2), and similar for (1)⇔(3) and (1)⇔(4). Since R=τ∘U, R is a solution of the Hom-Long equation if and only if R12∘R23=R23∘R12, that is,
While τ12∘U12∘τ23=τ23∘τ13∘U13 and τ23∘U23∘τ12=τ23∘τ12∘U13, (5.2) is equivalent to
which is equivalent to U13∘U23=τ(123)∘U13∘U12 from the fact τ23∘τ12=τ(123).
Next we will present a new solution for Hom-Long equation by the Hom-Long dimodule structures. For this, we give the notion of (H,α)-Hom-Long dimodules.
Definition 5.6. Let (H,α) be a Hom-bialgebra. A left-left (H,α)-Hom-Long dimodule is a quadruple (M,⋅,ρ,μ), where (M,⋅,μ) is a left (H,α)-Hom-module and (M,ρ,μ) is a left (H,α)-Hom-comodule such that
for all h∈H and m∈M.
Remark 5.7. Clearly, left-left (H,α)-Hom-Long dimodules is a special case of (H,B)-Hom-Long dimodules in Definition 2.1 by setting (H,α)=(B,β).
Example 5.8. Let (H,α) be a Hom-bialgebra and (M,⋅,μ) be a left (H,α)-Hom-module. Define a left (H,α)-Hom-module structure and a left (H,α)-Hom-comodule structure on (H⊗M,α⊗μ) as follows:
for all h,g∈H and m∈M. Then (H⊗M,α⊗μ) is an (H,α)-Hom-Long dimodule.
Example 5.9. Let (H,α) be a Hom-bialgebra and (M,ρ,μ) be a left (H,α)-Hom-comodule. Define a left (H,α)-Hom-module structure and be a left (H,α)-Hom-comodule structure on (H⊗M,α⊗μ) as follows:
for all h,g∈H and m∈M. Then (H⊗M,α⊗μ) is an (H,α)-Hom-Long dimodule.
Theorem 5.10. Let (H,α) be a Hom-bialgebra and (M,⋅,ρ,μ) be a (H,α)-Hom-Long dimodule. Then the map
is a solution of the Hom-Long equation, for any m,n∈M.
Proof. For any l,m,n∈M, we calculate
So we have R12M∘R23M=R23M∘R12M, as desired. And this finishes the proof.
Acknowledgement
The work of S. Wang is supported by the Anhui Provincial Natural Science Foundation (No. 1908085MA03) and the Key University Science Research Project of Anhui Province (No. KJ2020A0711). The work of X. Zhang is supported by the NSF of China (No. 11801304) and the Young Talents Invitation Program of Shandong Province. The work of S. Guo is supported by the NSF of China (No. 12161013) and Guizhou Provincial Science and Technology Foundation (No. [2019]1050).
Conflict of interest
The authors declare there is no conflict of interest.









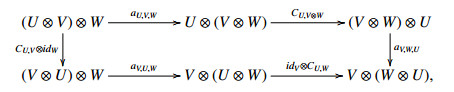
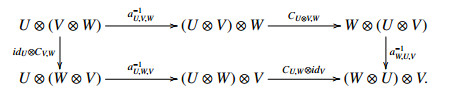



 DownLoad:
DownLoad: