Spanish business commitment to the 2030 Agenda in uncertain times

1.   Introduction

A non-empty set together with one or more binary operations is called an algebraic structure. Algebraic structures have various applications in mathematics, including physics, control engineering, topological spaces, computer science, and coding theory ^[1]. It was Lehmer ^[2] who firstly studied the concept of ternary algebraic system. Ternary semigroups are important because of their applications to modern mathematical physics, algebraic, functional, and analytical methods ^[3]. Theory of ternary semigroups was established by Santiago, and Bala ^[4]. Los ^[5] proved a semigroup can be embedded to ternary semigroup but every ternary semigroup cannot necessarily be reduced to a semigroup. Here, illustrating an example, $\left\{\iota , -\iota , 0\right\}$ with ternary operation of multiplication in complex numbers is ternary semigroup, but it is not a semigroup under usual binary multiplication. Also, there are various structures that are not handled by binary multiplication, so we have used the ternary operation to solve these problems. For instance consider the set of rational numbers $Q$ is a semigroup but its subset ${Q}^{-}$ is not a subsemigroup of $Q$ because with the binary multiplication, it is not closed. But, under the ternary product ${Q}^{-}$ is closed. Sioson defined the notions of ideals in ternary semigroups ^[6]. For more detail, see ^{[7,8,9,10,11,12,13,14,15]}.

Theory of fuzzy set is well-known presented by Zadeh ^[16]. It has a variety of applications in different fields including medical diagnosis, digital communications, artificial intelligence, social, management sciences, decision-making challenges, and many more. A fuzzy set is established by a membership function whose range is the unit interval $\left[\mathrm{0, 1}\right]$. Theory of bipolar fuzzy set is an extension of fuzzy set which deals with the uncertain, and complex problems, both in positive, and negative aspects with membership degree range of $\left[-\mathrm{1, 1}\right]$. For more applications of fuzzy set and bipolar fuzzy set, see ^{[17,18,19,20,21,22,23,24]}.

Chen proposed bipolar fuzzy sets and 2-polar fuzzy sets are cryptomorphic mathematical concepts. By using the idea of one-to-one correspondence, the bipolar fuzzy sets are extended to $m$-PF sets ^[25]. Sometimes, different objects have been monitored in different ways. This led to the study of $m$-PF set. To assign the membership degrees to several objects regarding multi-polar information, $m$-PF set works successfully. Here, no membership degree will be assumed as negative as $m$-PF set provides only positive degree of memberships of each element.

The $m$-PF sets are applicable when a company decides to construct an item, a country elects its political leader, or a group of mates wants to visit a country with various options. It can be used to discuss the confusions, and conflicts of communication signals in wireless communication. Thus, $m$-PF set can be implement in both real world problems, and mathematical theories. For example, a fuzzy set "good leader" can have different interpretations among politicians of particular area. Multi-polar information, weighted games, multi-attributes, multi-index, multi-objects, multi-valued interactions, and multi-agent are only a few examples of real world applications for $m$-PF set. For more and recent applications, see ^[25,26].

We will give an example to demonstrate it.

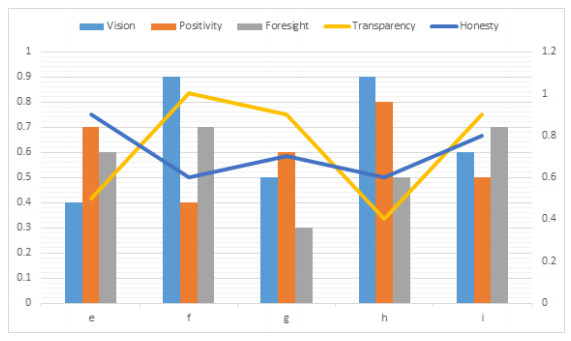
Let $H = \left\{e, f, g, h, i\right\}$ be a set of 5 candidates for the selection of appropriate political leader. We have characterized them according to five qualities in the form of $5$-PFS given in Table 1. Also, the graphical representation of a $5$-PFS is shown in Figure 1.

Thus, we get a $5$-PFS $\psi :H\to {\left[\mathrm{0, 1}\right]}^{5}$ of $H$ such that

Here, the value 1 represents good remarks, 0.5 represents average, and 0 represents bad remarks. When we combine the technique of $m$-PF set to ternary semigroup, it will be more useful. Many works have been done on m-PF set. Some previous work is given below.

1) In 2019, Al-Masarwah worked on m-polar fuzzy ideals of BCK/BCI-algebras ^[27,28]. Al-Masarwah & Ahmad studied the m-polar $\left(\alpha , \beta \right)$-fuzzy ideals in BCK/BCI-algebras ^[29] and he also worked on normality of m-PF subalgebras in BCK/BCI-algebra ^[30].

2) In 2020, Muhiuddin et al. introduced m-polar fuzzy q-ideals in BCI-algebras ^[31].

3) In 2021, Muhiuddin et al. introduced interval valued m-polar fuzzy BCK/BCI-algebras and interval-valued m-polar fuzzy positive implicative ideals in BCK-algebras ^[32,33].

4) In 2021, Shabir et al. studied m-polar fuzzy ideals in terms of LA-semigroups ^[34].

5) Later on, Bashir et al. initiated the concept of regular and intra-regular semigroups in terms of m-polar fuzzy environment ^[35].

In this paper, we have introduced the concept of $m$-PFIs in ternary semigroups, also characterized regular and intra-regular ternary semigroups by the properties of these $m$-PFIs.

The paper is organized as follows: In Section 2, we define the fundamental notions of $m$-PF sets in ternary semigroups. The main part of this paper is Section 3, in which $m$-PFTSSs and $m$-PFIs of ternary semigroups with examples are discussed. In Section 4, we have characterized regular, and intra-regular ternary semigroups with the properties of $m$-PFIs. A comparison of this paper to previous work is given in Section 5. In the last, we discuss the conclusions of this work and our future work.

The list of acronyms used here, is given in Table 2.

2.   Preliminaries

In this phase, we show some fundamentals but necessary ideas, and preliminary results based on ternary semigroups that are important in their own right. These are prerequisite for later sections. A mapping () : $D\times D\times D\to D$ is called a ternary operation for any non-empty set $D$. A non-empty set $D$ with ternary operation $($ $)$ is called ternary semigroup if it fulfills associative law such as $\left(\left({d}_{1}{d}_{2}{d}_{3}\right){d}_{4}{d}_{5}\right) = \left({d}_{1}\left({d}_{2}{d}_{3}{d}_{4}\right){d}_{5}\right) = \left({d}_{1}{d}_{2}\left({d}_{3}{d}_{4}{d}_{5}\right)\right)$ for all ${d}_{1}, {d}_{2}, {d}_{3}, {d}_{4}, {d}_{5}\in D$. Throughout this paper, $D$ will indicate ternary semigroup, unless otherwise specified, and subsets indicate non-empty subsets. A subset $H$ of $D$ is called ternary subsemigroup of $D$ if $HHH\subseteq H$. A right ideal (resp. lateral or middle ideal, and left ideal) of $D$ is a subset $H$ of $D$ satisfying $HDD\subseteq H\left(\text{resp.}\;DHD\subseteq H, DDH\subseteq H\right)$. A subset $H$ is called an ideal if it is right ideal, lateral ideal, and left ideal ^[36]. A subset $H$ of $D$ is called generalized bi-ideal of $D$ if $HDHDH\subseteq H$. A subset $H$ of $D$ is called bi-ideal of $D$ if $HHH\subseteq H$, and $HDHDH\subseteq H$ ^[37]. A subset $H$ of $D$ is called quasi-ideal of $D$ if $HDD\cap DHD\cap DDH\subseteq H$ and $HDD\cap DDHDD\cap DDH\subseteq H$ ^[38]. A subset $H$ of $D$ is called an interior ideal of $D$ if $DDHDD\subseteq H$ ^[39]. A mapping $\psi :D\to {\left[\mathrm{0, 1}\right]}^{m}$ is an $m$-PFS or a (${\left[\mathrm{0, 1}\right]}^{m}$-set) on $D$. The $m$-PFS is an $m$-tuple of membership degree function of $D$ that is $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right),$ where ${\psi }_{\kappa }:D\to \left[\mathrm{0, 1}\right]$ is a mapping for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ The $m$-PF set is a generalization of BFS. Similar to the case of BFS, an $m$-PF set can be presented as $m$ different fuzzy sets. Therefore, in this situation each input is characterized by an $m$-dimensional vector of numbers from the close interval $\left[\mathrm{0, 1}\right],$ each presenting a confidence degree. Assume that the set $\kappa = \left\{\mathrm{1, 2}, ..., m\right\}$ is the set of context. The degree of satisfaction for each element with respect to the ${\kappa }^{th}$ context will thus be represented by an $m$-PF set for each $\kappa \in N$ ^[40]. The $m$-PF set is an $m$-tuple of membership degree function of $D$ that is $\psi = \left\{{\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right\},$ where ${\psi }_{\kappa }:D\to \left[\mathrm{0, 1}\right]$ is a mapping for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

The set of all $m$-PFSs of $D$ is called an $m$-PF power set of $D$ and presented as $m\left(D\right)$. We define relation $\le$ on $m$-PF power set ($m\left(D\right)$) as follows: $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ are $m$-PFSs of $D, \psi \le \daleth \le \mho$ means that ${\psi }_{\kappa }\left(l\right)\le {\daleth }_{\kappa }\left(l\right)\le {\mho }_{\kappa }\left(l\right)$ for all $l\in D,$ and $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. The symbols $\psi \wedge \daleth \wedge \mho$ and $\psi \vee \daleth \vee \mho$ indicates these $m$-PFSs of $D$. $\left(\psi \wedge \daleth \wedge \mho \right)\left(l\right) = \psi \left(l\right)\wedge \daleth \left(l\right)\wedge \mho \left(l\right), (\psi \vee \daleth \vee \mho )\left(l\right) = \psi \left(l\right)\vee \daleth \left(l\right)\vee \mho \left(l\right)$ that is $\left({\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }\right)\left(l\right) = {\psi }_{\kappa }\left(l\right)\wedge {\daleth }_{\kappa }\left(l\right)\wedge {\mho }_{\kappa }\left(l\right)$ and $\left({\psi }_{\kappa }\vee {\daleth }_{\kappa }\vee {\mho }_{\kappa }\right)\left(l\right) = {\psi }_{\kappa }\left(l\right)\vee {\daleth }_{\kappa }\left(l\right)\vee {\mho }_{\kappa }\left(l\right)$ for all $l\in D$ and $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right)$, and $\mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ be $m$-PFSs of $D$. The ternary product of $\psi , \daleth , \mho$ is denoted as $\left(\psi \circ \daleth \circ \mho \right) = \left({\psi }_{1}\circ {\daleth }_{1}\circ {\mho }_{1}, {\psi }_{2}\circ {\daleth }_{2}\circ {\mho }_{2}, ..., {\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }\right)$, and defined as

for some $g, h, i\in D,$ and for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Example 1 shows the multiplication of $m$-PFSs of $\psi , \daleth ,$ and $\mho$ of $D$ for $m = 3.$

Example 1. Consider a ternary semigroup $D = \left\{0, {d}_{1}, {d}_{2}\right\}$. The multiplication of $m$-PFSs $\psi , \daleth , \mho$ of $D$ are given in Tables 3–5 for $m = 3.$

We define $3$-PFSs $\psi = \left({\psi }_{1}, {\psi }_{2}, {\psi }_{3}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, {\daleth }_{3}\right)$ and $\mho = \left({\mho }_{1}, {\mho }_{2}, {\mho }_{3}\right)$ of $D$ as follows:

Then, we have

Hence, the product of $\psi = \left({\psi }_{1}, {\psi }_{2}, {\psi }_{3}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, {\daleth }_{3}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, {\mho }_{3}\right)$ is defined by: $\left(\psi \circ \daleth \circ \mho \right)\left(0\right) = \left(\mathrm{0.3, 0.3, 0.3}\right), \left(\psi \circ \daleth \circ \mho \right)\left({d}_{1}\right) = \left(\mathrm{0.3, 0.1}, 0.5\right)$ and $\left(\psi \circ \daleth \circ \mho \right)\left({d}_{2}\right) = \left(\mathrm{0.3, 0.1, 0.2}\right).$

3.   Ternary semigroups by ${m}$-polar fuzzy ideals

This is a significant part because in this section we have done our major contributions. In this part, the notions of $m$-PFTSSs, $m$-PFIs, $m$-PFGBIs, $m$-PFBIs, $m$-PFQIs and $m$-PFIIs of ternary semigroups are explored by using various examples and lemmas. We have proved that, every $m$-PFBI of $D$ is an $m$-PFGBI of $D$ but the converse does not hold. This result was previously proved for semigroup by Bashir et al. ^[35]. We have generalized the results of ^[35] for ternary semigroups. Ternary semigroup is more general than semigroup. Throughout the paper, $\delta$ is the $m$-PFS of $D$ that maps every element of $D$ on $\left(\mathrm{1, 1}, ..., 1\right)$.

Definition 1. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFS of $D$.

1) Define ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ for all $\alpha$, where $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in {\left(\mathrm{0, 1}\right]}^{m}$, that is ${\psi }_{\kappa }\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Then ${\psi }_{\alpha }$ is called an $\alpha$-cut or a level set. This indicates ${\psi }_{\alpha } = \bigcap _{\kappa = 1}^{m}{\left({\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}.$

2) The support of $\psi :D\to {\left[\mathrm{0, 1}\right]}^{m}$ is defined as a set $Supp\left(\psi \right) = \left\{l\in D|\psi \left(l\right) > \left(\mathrm{0, 0}, ..., 0\right), m\text{-tuple}\right\}$ that is ${\psi }_{\kappa }\left(l\right) > 0$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$.

Definition 2. An $m$-PFS $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ of $D$ is called an $m$-PFTSS of $D$ if for all $g, h, i\in D$, $\psi \left(ghi\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right)$ that is ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Definition 3. An $m$-PFS $\psi = \left({\psi }_{1}, {\psi }_{2}, ...{\psi }_{m}\right)$ of $D$ is called an $m$-PFRI $($ resp. $m$-PFMI, and $m$-PFLI $)$ of $D$ if for all $g, h, i\in D, \psi \left(ghi\right)\ge \psi \left(g\right)($ resp. $\psi \left(ghi\right)\ge \psi \left(h\right), \psi \left(ghi\right)\ge \psi \left(i\right))$ that is, ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(g\right)($ resp. ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(h\right), {\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(i\right))$ for all $\kappa \in \left\{\mathrm{1, 2}, .., m\right\}.$

1) If $\psi$ is together $m$-PFRI and $m$-PFLI of $D$ then $\psi$ is called an $m$-PF two-sided ideal of $D$;

2) If $\psi$ is together $m$-PFRI, $m$-PFMI, and $m$-PFLI of $D$ then $\psi$ is called an $m$-PFI of $D$.

The Example 2 is of $3$-PFl of $D$.

Example 2. Consider the ternary semigroup $D = \left\{0, {d}_{1}, {d}_{2}\right\}$ given in Table 3, Table 4 and Table 5 of Example 1. We define $3$-PFS $\psi = \left({\psi }_{1}, {\psi }_{2}, {\psi }_{3}\right)$ of $D$ as follows: $\psi \left(0\right) = \left(\mathrm{0.9, 0.9, 0.6}\right), \psi \left({d}_{1}\right) = \psi \left({d}_{2}\right) = \left(\mathrm{0.5, 0.3, 0.1}\right).$ Clearly, $\psi = \left({\psi }_{1}, {\psi }_{2}, {\psi }_{3}\right)$ is $3$-PFRI, $3$-PFMI and $3$-PFLI of $D.$ Hence $\psi$ is $3$-PF ideal of $D.$

Definition 4. Let $H$ be a subset of $D$. Then the $m$-polar characteristic function $\chi :H\to {\left[\mathrm{0, 1}\right]}^{m}$ of $H$ is defined as

Lemma 1. Let $H, I$ and $J$ be subsets of $D$. Then the following conditions are true:

1) ${\chi }_{H}\wedge {\chi }_{I} = {\chi }_{H\cap I};$

2) ${\chi }_{H}\vee {\chi }_{I} = {\chi }_{H\cup I};$

3) ${\chi }_{H}\circ {\chi }_{I}\circ {\chi }_{J} = {\chi }_{HIJ}.$

Proof. The proof of (1) and (2) are obvious.

(3) Let $H, I$ and $J$ be subsets of $D.$

Case 1: Let $l\in HIJ$. This implies that $l = ghi$ for some $g\in H, h\in I,$ and $i\in J$. Thus, ${\chi }_{HIJ}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Since $g\in H, h\in I, i\in J,$ we have ${\chi }_{H}\left(g\right) = \left(\mathrm{1, 1}, ..., 1\right) = {\chi }_{I}\left(h\right) = {\chi }_{J}\left(i\right).$ Now,

Thus, ${\chi }_{H}\circ {\chi }_{I}\circ {\chi }_{J} = {\chi }_{HIJ}.$

Case 2: Let $l\notin HIJ$. This implies that ${\chi }_{HIJ}\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right).$ Since, $l\ne ghi$ for all $g\in H, h\in I$ and $i\in J$. Thus,

Hence, ${\chi }_{H}\circ {\chi }_{I}\circ {\chi }_{J} = {\chi }_{HIJ}.$

Lemma 2. Consider a subset $H$ of $D$. Then the following assertions are true.

1) $H$ is ternary subsemigroup of $D$ if and only if ${\chi }_{H}$ is an $m$-PFTSS of $D;$

2) $H$ is an ideal of $D$ if and only if ${\chi }_{H}$ is an $m$-PFI of $D.$

Proof. (1) Consider, $H$ is a ternary subsemigroup of $D$. We have to show that ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right)$ for all $g, h, i\in D$. We observe the following eight cases:

Case 1: Let $g, h, i\in H$. Then ${\chi }_{H}\left(g\right) = \left(\mathrm{1, 1}, ..., 1\right) = {\chi }_{H}\left(h\right) = {\chi }_{H}\left(i\right)$. So, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Since $H$ is ternary subsemigroup of $D,$ so $ghi\in H$ implies that ${\chi }_{H}\left(ghi\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 2: Let $g, h\in H$ and $i\notin H$. Then ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(h\right) = \left(\mathrm{1, 1}, ..., 1\right)$ and ${\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right).$

Case 3: Let $g, h\notin H$ and $i\in H$. Then ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(h\right) = \left(\mathrm{0, 0}, ..., 0\right)$ and ${\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge \left(\mathrm{0, 0}, ..., 0\right) = {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 4: Let $g, i\in H,$ and $h\notin H$. Then ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right),$ and ${\chi }_{H}\left(h\right) = \left(\mathrm{0, 0}, ..., 0\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge \left(\mathrm{0, 0}, ..., 0\right) = {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 5: Let $g, i\notin H$ and $h\in H$. Then ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$ and ${\chi }_{H}\left(h\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge \left(\mathrm{0, 0}, ..., 0\right) = {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 6: Let $h, i\in H$ and $g\notin H$. Then ${\chi }_{H}\left(h\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$ and ${\chi }_{H}\left(g\right) = \left(\mathrm{0, 0}, ..., 0\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge \left(\mathrm{0, 0}, ..., 0\right) = {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 7: Let $h, i\notin H$ and $g\in H$. Then ${\chi }_{H}\left(h\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$ and ${\chi }_{H}\left(g\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge \left(\mathrm{0, 0}, ..., 0\right) = {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Case 8: Let $g, h, i\notin H$. Then ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(h\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. This implies that, ${\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right).$

Conversely, let ${\chi }_{H}$ is an $m$-PFTSS of $D$. Let $g, h, i\in H$. Then, ${\chi }_{H}\left(g\right) = {\chi }_{H}\left(h\right) = {\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$. By definition, ${\chi }_{H}\left(ghi\right) = \left(\mathrm{1, 1}, ..., 1\right)\ge {\chi }_{H}\left(g\right)\wedge {\chi }_{H}\left(h\right)\wedge {\chi }_{H}\left(i\right)$ we have ${\chi }_{H}\left(ghi\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that $ghi\in H,$ so $H$ is a ternary subsemigroup of $D.$

$\left(2\right)$ Consider, $H$ is a left ideal of $D$. We have to show that ${\chi }_{H}$ is an $m$-PFLI of $D,$ that is ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(i\right)$ for all $g, h, i\in D$. Now, we observe these two cases:

Case 1: Let $i\in H\mathrm{a}\mathrm{n}\mathrm{d}g, h\in D$. Then, ${\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Since $H$ is left ideal of $D,$ so $ghi\in H$ implies that ${\chi }_{H}\left(ghi\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(i\right).$

Case 2: Let $i\notin H$ and $g, h\in D$. Then ${\chi }_{H}\left(i\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Clearly, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(i\right).$

Conversely, let ${\chi }_{H}$ is an $m$-PFLI of $D$. Assume that $g, h\in D$ and $i\in H$. Then, ${\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right)$. By definition, ${\chi }_{H}\left(ghi\right)\ge {\chi }_{H}\left(i\right) = \left(\mathrm{1, 1}, ..., 1\right),$ we have ${\chi }_{H}\left(ghi\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that $ghi\in H$, that is $H$ is a left ideal of $D.$

Similarly, we can prove for lateral ideal and right ideal of $D$.

Lemma 3. Consider $\psi$ is an $m$-PFS of $D$. Then the following properties hold.

1) $\psi$ is an $m$-PFTSS of $D$ if and only if $\psi \circ \psi \circ \psi \le \psi ;$

2) $\psi$ is an $m$-PFLI of $D$ if and only if $\delta \circ \delta \circ \psi \le \psi ;$

3) $\psi$ is an $m$-PFMI of $D$ if and only if $\delta \circ \psi \circ \delta \le \psi , \delta \circ \delta \circ \psi \circ \delta \circ \delta \le \psi ;$

4) $\psi$ is an $m$-PFRI of $D$ if and only if $\psi \circ \delta \circ \delta \le \psi ;$

5) $\psi$ is an $m$-PFI of $D$ if and only if $\delta \circ \delta \circ \psi \le \psi , \delta \circ \psi \circ \delta \le \psi , \psi \circ \delta \circ \delta \le \psi ,$ where $\delta$ is an $m$-PFS of $D$ mapping every element of $D$ on $\left(\mathrm{1, 1}, ..., 1\right)$.

Proof. $\left(1\right)$ Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFTSS of $D,$ that is ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Let $l\in D$. If $l$ cannot be written as $l = ghi$ for some $g, h, i\in D$ then $\left(\psi \circ \psi \circ \psi \right)\left(l\right) = 0$. Hence, $\psi \circ \psi \circ \psi \le \psi$. But if $l$ is expressible as $l = ghi$ for some $g, h, i\in D,$ then

Hence, $\psi \circ \psi \circ \psi \le \psi$. Conversely, let $\hspace{0.33em}\psi \circ \psi \circ \psi \le \psi$ and $g, h, i\in D$. Then $\hspace{0.33em}\;\text{for all}\;\;\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$.

Hence, $\psi \left(ghi\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right)$. Thus, $\psi$ is an $m$-PFTSS of $D.$

$\left(2\right)$ Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFLI of $D$ that is, ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}\mathrm{a}\mathrm{n}\mathrm{d}g, h, i\in D$. Let $l\in D,$ if $l$ cannot be written as $l = ghi$ for some $g, h, i\in D$ then $\left(\delta \circ \delta \circ \psi \right)\left(l\right) = 0$. Hence, $\delta \circ \delta \circ \psi \le \psi$. But if $l$ is expressible as $l = ghi$ for some $g, h, i\in D.$

Hence, $\delta \circ \delta \circ \psi \le \psi$. Conversely, let $\delta \circ \delta \circ \psi \le \psi$ and $g, h, i\in D$. Then,

Hence, $\left(ghi\right)\ge \psi \left(i\right)$. Thus $\psi$ is an $m$-PFLI of $D$.

Similarly, we can prove the parts $\left(3\right), \left(4\right)\mathrm{a}\mathrm{n}\mathrm{d}\left(5\right).$

Lemma 4. The following assertions are true in $D$.

1) Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right)$, and $\mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ be $m$-PFTSSs of $D$. Then $\psi \wedge \daleth \wedge \mho$ is also an $m$-PFTSS of $D;$

2) Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right)$, and $\mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ be $m$-PFIs of $D$. Then $\psi \wedge \daleth \wedge \mho$ is also an $m$-PFI of $D.$

Proof. Straightforward.

Proposition 1. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFS of $D$. Then $\psi$ is an $m$-PFTSS $($ resp. $m$-PFI $)$ of $D$ if and only if ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ is a ternary subsemigroup $($ resp. ideal $)$ of $D$ for all $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in \left(\mathrm{0, 1}\right].$

Proof: Let $\psi$ be an $m$-PFTSS of $D$. Let $g, h, i\in {\psi }_{\alpha }$. Then ${\psi }_{\kappa }\left(g\right)\ge {\alpha }_{\kappa }, {\psi }_{\kappa }\left(h\right)\ge {\alpha }_{\kappa }$ and ${\psi }_{\kappa }\left(i\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Since, $\psi$ is an $m$-PFTSS of $D,$ we have

Thus, $\left(ghi\right)\in {\psi }_{\alpha }$. Hence, ${\psi }_{\alpha }$ is a ternary subsemigroup of $D.$

Conversely, let ${\psi }_{\alpha }$ is a ternary subsemigroup of $D$. On contrary assume that $\psi$ is not an $m$-PFTSS of $D.$ Suppose $g, h, i\in D$ such that ${\psi }_{\kappa }\left(ghi\right) < {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for some $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Take ${\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right) = {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Then $g, h, i\in {\psi }_{\alpha }$ but $ghi\notin {\psi }_{\alpha },$ which is contradiction. Hence, ${\psi }_{\kappa }\left(ghi\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$. Thus $\psi$ is an $m$-PFTSS of $D.$

Further cases can be prove on the same lines.

3.1.   $m$-polar fuzzy generalized Bi-ideal in ternary semigroups

Definition 5. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFS of $D$. Then $\psi$ is called an $m$-PFGBI of $D$ if for all $g, {d}_{1}, h, {d}_{2}, i\in D, \psi \left(g{d}_{1}h{d}_{2}i\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right)$ that is ${\psi }_{\kappa }\left(g{d}_{1}h{d}_{2}i\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Example 3. Let $D = \left\{e, f, g, h, i\right\}$ be a ternary semigroup and its multiplication table is defined in Table 6.

Let $\psi = \left\{{\psi }_{1}, {\psi }_{2}, {\psi }_{3}, {\psi }_{4}\right\}$ be a $4$-PFS of $D$ such that $\psi \left(e\right) = \left(\mathrm{0.7, 0.8, 0.8, 0.9}\right), \psi \left(f\right) = \left(\mathrm{0.1, 0.2, 0.3, 0.4}\right),$ $\psi \left(g\right) = \left(0.2, \mathrm{0.3, 0.4, 0.5}\right), \psi \left(h\right) = \left(\mathrm{0, 0}, \mathrm{0, 0}\right),$ $\psi \left(i\right) = \left(\mathrm{0.3, 0.4, 0.5, 0.6}\right).$ Then simple calculations shows that $\psi$ is a $4$-PFGBI of $D.$

Lemma 5. A subset $H$ of $D\hspace{0.33em}$ is a generalized bi-ideal of $D$ if and only if ${\chi }_{H}$ is an $m$-PFGBI of $D.$

Proof. The proof follows from the proof of Lemma 2.

Lemma 6. An $m$-PFS $\psi$ of $D$ is an $m$-PFGBI of $D$ if and only if $\psi \circ \delta \circ \psi \circ \delta \circ \psi \le \psi$, where $\delta$ is the $m$-PFS of $D$ mapping every element of $D$ on $\left(\mathrm{1, 1}, ..., 1\right).$

Proof. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFGBI of $D$ that is, ${\psi }_{\kappa }\left(g{d}_{1}h{d}_{2}i\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$ and $g, {d}_{1}, h, {d}_{2}, i\in D$. Let $l\in D,$ if $l$ cannot be written as $l = ghi$ for some $g, h, i\in D$ then $\left(\psi \circ \delta \circ \psi \circ \delta \circ \psi \right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Hence, $\psi \circ \delta \circ \psi \circ \delta \circ \psi \le \psi$. Suppose $l$ is expressible as $l = ghi$ for some $g, h, i\in D$. Then

Hence, $\left(\psi \circ \delta \circ \psi \right)\circ \delta \circ \psi \le \psi$. Conversely, let $\left(\psi \circ \delta \circ \psi \right)\circ \delta \circ \psi \le \psi$ and $g, h, i\in D$. Then,

Hence, $\psi \left(g{d}_{1}h{d}_{2}i\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right)$. Thus $\psi$ is an $m$-PFGBI of $D$.

Proposition 2. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ...., {\psi }_{m}\right)$ be an $m$-PFS of $D$. Then $\psi$ is an $m$-PFGBI of $D$ if and only if ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ is a generalized bi-ideal of $D$ for all $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in {\left(\mathrm{0, 1}\right]}^{m}.$

Proof. Suppose $\psi = \left({\psi }_{1}, {\psi }_{2}, ...., {\psi }_{m}\right)$ is an $m$-PFGBI of $D$. Let $g, h, i\in {\psi }_{\alpha }$ and ${d}_{1}, {d}_{2}\in D$. Then, ${\psi }_{\kappa }\left(g\right)\ge {\alpha }_{\kappa }, {\psi }_{\kappa }\left(h\right)\ge {\alpha }_{\kappa }$ and ${\psi }_{\kappa }\left(i\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Since, $\psi$ is an $m$-PFGBI of $D$, so

Thus $g{d}_{1}h{d}_{2}i\in {\psi }_{\alpha },$ that is ${\psi }_{\alpha }$ is a generalized bi-ideal of $D.$

Conversely, let ${\psi }_{\alpha }$ is a generalized bi-ideal of $D$. On contrary suppose that $\psi$ is not an $m$-PFGBI of $D$. Let $g, {d}_{1}, h, {d}_{2}, i\in D$ such that ${\psi }_{\kappa }\left(g{d}_{1}h{d}_{2}i\right) < {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for some $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Take ${\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right) = {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Then $g, {d}_{1}, h, {d}_{2}, i\in {\psi }_{\alpha }$ but $\left(g{d}_{1}h{d}_{2}i\right)\notin {\psi }_{\alpha }$ which is a contradiction. Thus, ${\psi }_{\kappa }\left(g{d}_{1}h{d}_{2}i\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$. Hence $\psi$ is an $m$-PFGBI of $D$.

3.2.   $m$-Polar fuzzy Bi-ideal in ternary semigroups

Definition 7. An $m$-PFTSS $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ of $D$ is called an $m$-PFBI of $D$ if for all $g, {d}_{1}, h, {d}_{2}, i\in D, \psi \left(g{d}_{1}h{d}_{2}i\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right)$ that is ${\psi }_{\kappa }\left(g{d}_{1}h{d}_{2}i\right)\ge {\psi }_{\kappa }\left(g\right)\wedge {\psi }_{\kappa }\left(h\right)\wedge {\psi }_{\kappa }\left(i\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Lemma 7. A subset $H$ of $D$ is a BI of $D$ if and only if ${\chi }_{H}$ the $m$-polar characteristic function of $H$ is an $m$-PFBI of $D.$

Proof. Follows from Lemmas 2 and 5.

Lemma 8. An $m$-PFTSS $\psi$ of $D$ is an $m$-PFBI of $D$ if and only if $\psi \circ \psi \circ \psi \le \psi$ and $\psi \circ \delta \circ \psi \circ \delta \circ \psi \le \psi$.

Proof. Follows from Lemmas 3 and 6.

Proposition 3. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ...., {\psi }_{m}\right)$ be an $m$-PFTSS of $D$. Then $\psi$ is an $m$-PFBI of $D$ if and only if ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ is a bi-ideal of $D$ for all $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in {\left(\mathrm{0, 1}\right]}^{m}.$

Proof. Follows from Propositions 1 and 2.

Remark 1. Every $m$-PFBI of $D$ is an $m$-PFGBI of $D.$

The Example 4 proves that the converse of the Remark 1 may not be true.

Example 4. Consider $D = \left\{e, f, g, h, i\right\}$ is a ternary semigroup as given in Example.3 and $\psi = \left\{{\psi }_{1}, {\psi }_{2}, {\psi }_{3}, {\psi }_{4}\right\}$ is $4$-PFGBI of $D.$ Then simple calculations shows that $\psi$ is not a bi-ideal of $D$ as $\psi \left(h\right) = \psi \left(fig\right) = \left(\mathrm{0, 0}, \mathrm{0, 0}\right)\ngeqq \left(\mathrm{0.1, 0.2, 0.3, 0.4}\right) = \psi \left(f\right)\wedge \psi \left(i\right)\wedge \psi \left(g\right)$.

3.3.   $m$-Polar fuzzy quasi-ideal in ternary semigroups

Definition 8. An $m$-PFS $\psi$ of $D$ is called an $m$-PFQI of $D$ if $\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \psi \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\le \psi , \left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\le \psi$ that is $\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\wedge \left({\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\le {\psi }_{\kappa }$ and $\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\le {\psi }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\},$ where $\delta$ is fuzzy subset of $D$ mapping every element of $D$ on $\left(\mathrm{1, 1}, ..., 1\right)$.

Example 5. Let $D = \left\{e, f, g, h\right\}$ be a ternary semigroup and its multiplication table is defined in Table 7.

Define a $5$-PFS $\psi = \left({\psi }_{1}, {\psi }_{2}, {\psi }_{3}, {\psi }_{4}, {\psi }_{5}\right)$ of $D$ as follows: $\psi \left(e\right) = \psi \left(g\right) = \left(\mathrm{0.9, 0.8, 0.7, 0.7, 0.6}\right),$ $\psi \left(f\right) = \left(\mathrm{0.3, 0.2, 0.2}, \mathrm{0.1, 0.3}\right), \psi \left(h\right) = \left(\mathrm{0, 0}, \mathrm{0, 0}, 0\right)$. Then simple calculations proves that ${\psi }_{\alpha }$ is a quasi-ideal of $D$. As the result of Proposition 4, $\psi$ is a $5$-PFQI of $D$.

Lemma 9. Let $H$ be a subset of $D$. Then $H$ is a quasi-ideal of $D$ if and only if the $m$-polar characteristic function ${\chi }_{H}$ of $H$ is an $m$-PFQI of $D.$

Proof. Let $H$ be a quasi-ideal of $\hspace{0.33em}D$ that is $HDD\cap DHD\cap DDH\subseteq H, HDD\cap DDHDD\cap DDH\subseteq H$. Now we have to show that, $\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\le {\chi }_{H}$, $\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\le {\chi }_{H}$ that is $\left(\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\right)\left(l\right)\le {\chi }_{H}\left(l\right)$ and $\left(\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\right)\left(l\right)\le {\chi }_{H}\left(l\right)$. This implies that $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right)\le {\chi }_{H}\left(l\right)$ and $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right)\le {\chi }_{H}\left(l\right)$ for all $l\in D.$

We observe the following two cases:

Case 1: If $l\in H$ then ${\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)\ge \left(\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\right)\left(l\right)$. So, $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right)\le {\chi }_{H}\left(l\right)$. Also, $\left(\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\right)\left(l\right)\le {\chi }_{H}\left(l\right)$. Hence, $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right)\le {\chi }_{H}\left(l\right).$

Case 2: If $l\notin H$ then $l\notin HDD\cap DHD\cap DDH$. This implies that $l\ne muv$ or $l\ne wnx$ or $l\ne yzo$ for some $m, n, o\in H$ and $u, v, w, x, y, z\in D$. Thus either $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ or $\left(\delta \circ {\chi }_{H}\circ \delta \right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ or $\left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ that is $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)\le {\chi }_{H}\left(l\right)$. Hence $\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ {\chi }_{H}\circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\le {\chi }_{H}.$

Also, if $l\notin H$ then $l\notin HDD\cap DDHDD\cap DDH.$ This implies that $l\ne mst$ or $l\ne uvnwx$ or $l\ne yzg$ for some $m, n, o\in H$ and $s, t, u, v, w, x, y, z\in D.$ Thus either $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ or $\left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ or $\left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$ that is $\left({\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\left(l\right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)\le {\chi }_{H}\left(l\right).$ Hence, $\left({\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ {\chi }_{H}\right)\le {\chi }_{H}.$

Conversely, let $\hspace{0.33em}l\in HDD\cap DHD\cap DDH$ and $l\in HDD\cap DDHDD\cap DDH.$

Firstly, if $l\in HDD\cap DHD\cap DDH$ then $l = muv, l = wnx, l = yzo$ for all $m, n, o\in H$ and $u, v, w, x, y, z\in D$. As ${\chi }_{H}$ is an $m$-PFQI of $D$. We have

Thus, ${\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, $l\in H$. So, $HDD\cap DHD\cap DDH\subseteq H.$

Now, secondly if $l\in HDD\cap DDHDD\cap DDH$ then $l = mst, l = uvnwx, l = yzo$ for all $m, n, o\in H$ and $s, t, u, v, w, x, y, z\in D$. As ${\chi }_{H}$ is an $m$-PFQI of $D,$ we have

Thus, ${\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, $l\in H$. So, $HDD\cap DDHDD\cap DDH\subseteq H.$ This shows that $H$ is a quasi-ideal of $D.$

Proposition 4. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFS of $D$. Then $\psi$ is an $m$-PFQI of $D$ if and only if ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ is a QI of $D$ for all $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in {\left(\mathrm{0, 1}\right]}^{m}$.

Proof. Consider $\psi$ is an $m$-PFQI of $D$. To show that ${\psi }_{\alpha }DD\cap D{\psi }_{\alpha }D\cap DD{\psi }_{\alpha }\subseteq {\psi }_{\alpha }$ and ${\psi }_{\alpha }DD\cap DD{\psi }_{\alpha }DD\cap DD{\psi }_{\alpha }\subseteq {\psi }_{\alpha }.$

Firstly, let $l\in {\psi }_{\alpha }DD\cap D{\psi }_{\alpha }D\cap DD{\psi }_{\alpha }$. Then $l\in {\psi }_{\alpha }DD, l\in D{\psi }_{\alpha }D$ and $l\in DD{\psi }_{\alpha }$. So, $l = muv, l = wnx, l = yzo$ for some $u, v, w, x, y, z\in D$ and $m, n, o\in {\left({\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}$. Thus, ${\psi }_{\kappa }\left(m\right)\ge {\alpha }_{\kappa }, {\psi }_{\kappa }\left(n\right)\ge {\alpha }_{\kappa }$ and ${\psi }_{\kappa }\left(o\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Now,

So, $\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ Now,

So, $\left({\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Now,

So, $\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ Thus,

So, $\psi \left(l\right)\ge \left(\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \psi \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\right)\left(l\right)\ge \alpha$. This implies that $l\in {\psi }_{\alpha }$. Hence, ${\psi }_{\alpha }$ is a quasi-ideal of $D.$

Now secondly, let $l\in {\psi }_{\alpha }DD\cap DD{\psi }_{\alpha }DD\cap DD{\psi }_{\alpha }$. Then $l\in {\psi }_{\alpha }DD, l\in DD{\psi }_{\alpha }DD, l\in DD{\psi }_{\alpha }$. So $l = mst, l = uvnwx,$ $l = yzo$ for some $s, t, u, v, w, x, y, z\in D$ and $m, n, o\in {\psi }_{\alpha }$. Thus, ${\psi }_{\kappa }\left(m\right)\ge {\alpha }_{\kappa }, {\psi }_{\kappa }\left(n\right)\ge {\alpha }_{\kappa },$ and ${\psi }_{\kappa }\left(o\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Now,

So, $\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ Now,

Thus, $\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ Now,

So, $\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)\ge {\alpha }_{\kappa }$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ Thus,

So, $\left(\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\right)\left(l\right)\ge \alpha .$ Since, $\psi \left(l\right)\ge \left(\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\right)\left(l\right)\ge \alpha$. So, $l\in {\psi }_{\alpha }.$

Conversely, on contrary consider that $\psi$ is not an $m$-PFQI of $D$. Let $l\in D$ be such that ${\psi }_{\kappa }\left(l\right) < \left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)$ for some $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Choose ${\alpha }_{\kappa }\in \left(\mathrm{0, 1}\right]$ such that ${\alpha }_{\kappa } = \left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. This implies that $l\in {\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)}_{{\alpha }_{\kappa }}, l\in {\left({\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ and $l\in {\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ but $l\notin {\left({\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ for some $\kappa$. Hence, $l\in {\left(\psi \circ \delta \circ \delta \right)}_{\alpha }, l\in {\left(\delta \circ \psi \circ \delta \right)}_{\alpha }$ and $l\in {\left(\delta \circ \delta \circ \psi \right)}_{\alpha }$ but $l\notin {\left(\psi \right)}_{\alpha },$ which is a contradiction. Hence, $\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \psi \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\le \psi .$

Also, on contrary consider that $\psi$ is not an $m$-PFQI of $D.$ Let $l\in D$ be such that ${\psi }_{\kappa }\left(l\right) < \left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)$ for some $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. Choose ${\alpha }_{\kappa }\in \left(\mathrm{0, 1}\right]$ such that ${\alpha }_{\kappa } = \left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)\left(l\right)\wedge \left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)\left(l\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}$. This implies that, $l\in {\left({\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)}_{{\alpha }_{\kappa }}, l\in {\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\circ {\delta }_{\kappa }\circ {\delta }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ and $l\in {\left({\delta }_{\kappa }\circ {\delta }_{\kappa }\circ {\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ but $l\notin {\left({\psi }_{\kappa }\right)}_{{\alpha }_{\kappa }}$ for some $\kappa$. Hence, $l\in {\left(\psi \circ \delta \circ \delta \right)}_{\alpha }, l\in {\left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)}_{\alpha }$ and $l\in {\left(\delta \circ \delta \circ \psi \right)}_{\alpha }$ but $l\notin {\left(\psi \right)}_{\alpha },$ which is a contradiction. Hence, $\left(\psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \psi \right)\le \psi .$

Lemma 10. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ be $m$-PFRI, $m$-PFMI and $m$-PFLI of $D$ respectively. Then $\psi \wedge \daleth \wedge \mho$ is an $m$-PFQI of $D.$

Proof. Suppose $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ is $m$-PFRI, $m$-PFMI and $m$-PFLI of $D$ respectively. Let $l\in D,$ if $l\ne ghi$ for some $g, h, i\in D$. Then, $\left(\left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \circ \delta \right)\wedge \left(\delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \right)\wedge \left(\delta \circ \delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\right)\le \psi \wedge \daleth \wedge \mho$. If $l = ghi$ for some $g, h, i\in D$. Then,

Hence, $\left(\left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \circ \delta \right)\wedge \left(\delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \right)\wedge \left(\delta \circ \delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\right)\le \left(\psi \wedge \daleth \wedge \mho \right)$, that is $\left(\psi \wedge \daleth \wedge \mho \right)$ is an $m$-PFQI of $\mathrm{D}.$ Similarly, $\left(\left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\circ \delta \circ \delta \right)\wedge \left(\delta \circ \delta \circ \left(\psi \wedge \daleth \wedge \mho \right)\right)\le \left(\psi \wedge \daleth \wedge \mho \right).$ Hence, $\left(\psi \wedge \daleth \wedge \mho \right)$ is an $m$-PFQI of $D.$

Lemma 11. Every $m$-PF one-sided ideal of $D$ is an $m$-PFQI of $D$.

Proof. The proof follows from Lemma 3.

In the Example 6, it is shown that the converse of the Lemma 11 may not be true.

Example 6. Consider $D = \left\{e, f, g, h\right\}$ is a ternary semigroup in Example 5 and $\psi$ is a $5$-PFQI of $D$. Now, by calculations $\psi \left(fhh\right) = \psi \left(h\right) = \left(\mathrm{0, 0}, \mathrm{0, 0}, 0\right)\stackrel{̸}{\ge }\psi \left(f\right) = \left(\mathrm{0.3, 0.2, 0.3, 0.1, 0.3}\right)$. So, $\psi$ is not a $5$-PFRI of $D.$

3.4.   $m$-Polar fuzzy interior ideals in ternary semigroups

Definition 9. An $m$-PFTSS $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ of $D$ is called an $m$-PFII of $D$ if for all $g, h, l, i, j\in D, \psi \left(ghlij\right)\ge \psi \left(l\right)$ that is, ${\psi }_{\kappa }\left(ghlij\right)\ge {\psi }_{\kappa }\left(l\right)$ for all $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

Lemma 12. Let $H$ be a subset of $D$. Then $H$ is an interior ideal of $D$ if and only if $m$-polar characteristic function ${\chi }_{H}$ of $H$ is an $m$-PFII of $D.$

Proof. Consider $H$ is an interior ideal of $D$. From Lemma 2, ${\chi }_{H}$ is an $m$-PFTSS of $D$. Thus, we have to show that ${\chi }_{H}\left(\left(ghl\right)ij\right)\ge {\chi }_{H}\left(l\right)$ for all $g, h, l, i, j\in D$. We observe these two cases:

Case 1: Let $l\in H$ and $g, h, i, j\in D$. Then ${\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Since, $H$ is an interior ideal of $D$. So, $\left(ghlij\right)\in H$. Then ${\chi }_{H}\left(ghlij\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, ${\chi }_{H}\left(ghlij\right)\ge {\chi }_{H}\left(l\right).$

Case 2: Let $l\notin H$, and $g, h, i, j\in D$. Then ${\chi }_{H}\left(l\right) = \left(\mathrm{0, 0}, ..., 0\right)$. Clearly, ${\chi }_{H}\left(ghlij\right)\ge {\chi }_{H}\left(l\right).$ Hence, the $m$- polar characteristic function ${\chi }_{H}$ of $H$ is an $m$-PFII of $D.$

Conversely, let ${\chi }_{H}$ is an $m$-PFII of $D$. Then by Lemma 2, $H$ is a ternary subsemigroup of $D$. Suppose $g, h, i, j\in D$, and $l\in H$ then ${\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. By the hypothesis, ${\chi }_{H}\left(ghlij\right)\ge {\chi }_{H}\left(l\right) = \left(\mathrm{1, 1}, ..., 1\right)$. Hence, ${\chi }_{H}\left(ghlij\right) = \left(\mathrm{1, 1}, ..., 1\right)$. This implies that $\left(ghlij\right)\in H,$ that is $H$ is an interior ideal of $D.$

Lemma 13. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFTSS of $D$. Then $\psi$ is an $m$-PFII of $D$ if and only if $\delta \circ \delta \circ \psi \circ \delta \circ \delta \le \psi .$

Proof. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFII of $D$. We have to show that, $\left(\left(\delta \circ \delta \circ \psi \right)\circ \delta \circ \delta \right)\le \psi .$ Let $l\in D$. Then,

Thus, $\left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\le \psi$. Conversely, let $\left(\delta \circ \delta \circ \psi \circ \delta \circ \delta \right)\le \psi$. We only have to show that ${\psi }_{\kappa }\left(ghlij\right)\ge {\psi }_{\kappa }\left(l\right)$ for all $g, h, l, i, j\in D$ and $\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$

So, $\left(ghlij\right)\ge \psi \left(l\right)$. Hence, $\psi$ is an $m$-PFII of $D$.

Proposition 4. Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFS of $D$. Then $\psi$ is an $m$-PFII of $D$ if and only if ${\psi }_{\alpha } = \left\{l\in D|\psi \left(l\right)\ge \alpha \right\}$ is an interior ideal of $D$ for all $\alpha = \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{m}\right)\in {\left(\mathrm{0, 1}\right]}^{m}$.

Proof. The proof is same as the proof of Propositions 1 and 2.

4.   Characterization of regular and intra-regular ternary semigroups by ${m}$-polar fuzzy ideals

In this section, various important results of regular and intra-regular ternary semigroups under the $m$-PFSs, $m$-PFIs of $D$ are presented. Many theorems of Shabir et al. ^[34]. Bashir et al. ^[35] are examined and generalized in the form of $m$-PFIs of $D$. Regular and intra-regular ternary semigroups have been studied by several authors see ^[6,38,41].

4.1.   Regular ternary semigroups

Definition 10. An element $l$ of $D$ is called regular if there exists $y, z\in D$ such that $l = lylzl$. $D$ is regular if all elements of $D$ are regular ^[6].

Theorem 1. ^[38] The listed below assertions are equivalent for $D$.

1) $D$ is regular;

2) $H\cap I\cap J = HIJ$ for all left ideal $H,$ all lateral ideal $I$ and all right ideal $J$ of $D$;

3) $H = HDHDH$ for all quasi ideal $H$ of $D$.

Theorem 2. Every $m$-PFQI of $D$ is an $m$-PFBI of $D.$

Proof. Suppose $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ is an $m$-PFQI of $D$. Let $g, h, i\in D$. Then

So, $\psi \left(ghi\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right).$ Also,

So, $\psi \left(g{d}_{1}h{d}_{2}i\right)\ge \psi \left(g\right)\wedge \psi \left(h\right)\wedge \psi \left(i\right).$ Hence, $\psi$ is an $m$-PFBI of $D.$

Theorem 3. For $D$ the given conditions are equivalent.

1) $D$ is regular;

2) $\psi \wedge \daleth \wedge \mho = \psi \circ \daleth \circ \mho$ for all $m$-PFRI $\psi ,$ all $m$-PFMI $\daleth$ and all $m$-PFLI $\mho$ of $D.$

Proof. $\left(1\right)\Rightarrow \left(2\right)\hspace{0.33em}:$ Suppose that $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ is $m$-PFRI, $m$-PFMI and $m$-PFLI of $D$ respectively. Let $l\in D,$ we have

Hence, $\left({\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }\right)\left(l\right)\le \left({\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }\right)\left(l\right)\;\text{for all}\;\kappa \in \left\{\mathrm{1, 2}, ..., m\right\}.$ So, $\left(\psi \circ \daleth \circ \mho \right)\le \left(\psi \wedge \daleth \wedge \mho \right).$ Since $D$ is regular, so for all $l\in D$ there exists $y, z\in D$ such that $l = lylzl.$

Thus, $\left(\psi \circ \daleth \circ \mho \right)\ge \left(\psi \wedge \daleth \wedge \mho \right).$ Therefore, $\left(\psi \circ \daleth \circ \mho \right) = \left(\psi \wedge \daleth \wedge \mho \right).$

$\left(2\right)\Rightarrow \left(1\right):$ Let $l\in D$. Then $H = lDD$ is a left ideal of $D, I = DlD$ is a lateral ideal of $D$ and $J = DDl$ is a right ideal of $D$. Then by using Lemma 2, ${\chi }_{H}, {\chi }_{I}, {\chi }_{J}$, the $m$- polar characteristic function of $H, I, J$ are $m$-PFLI, $m$-PFMI and $m$-PFRI of $D$ respectively. Now, by given condition

Thus, $H\cap I\cap J = HIJ.$ Hence, it follows from Theorem 1 that $D$ is regular.

Theorem 4. For $D$ the listed below conditions are equivalent.

1) $D$ is regular;

2) $\psi = \psi \circ \delta \circ \psi \circ \delta \circ \psi$ for every $m$-PFGBI $\psi$ of $D;$

3) $\psi = \psi \circ \delta \circ \psi \circ \delta \circ \psi$ for every $m$-PFQI $\psi$ of $D.$

Proof. $\left(1\right)\Rightarrow \left(2\right):$ Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right)$ be an $m$-PFGBI of $D$ and $l\in D$. As $D$ is regular, so there exist $y, z\in D$ such that $l = lylzl$. So, we have

Hence, $\psi \circ \delta \circ \psi \circ \delta \circ \psi \ge \psi .$ Since, $\psi$ is an $m$-PFGBI of $D$. So, we have

So, $\psi \circ \delta \circ \psi \circ \delta \circ \psi \le \psi$. Thus $\psi \circ \delta \circ \psi \circ \delta \circ \psi = \psi .$

$\left(2\right)\Rightarrow \left(3\right):$ It is obvious.

$\left(3\right)\Rightarrow \left(1\right):$ Let $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ be $m$-PFRI, $m$-PFMI and $m$-PFLI of $D$ respectively. Then $\left(\psi \wedge \daleth \wedge \mho \right)$ is an $m$-PFQI of $D$. Then by hypothesis,

So, ${\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }\le {\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }.$ But, ${\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }\le {\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }.$ This implies that ${\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa } = {\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }$. That is $\psi \circ \daleth \circ \mho = \psi \wedge \daleth \wedge \mho$. Thus $D$ is regular ternary semigroup by Theorem 3.

4.2.   Intra-regular ternary semigroups

Definition 11. An element $l$ of $D$ is called intra-regular if there exists $y, z\in D$ such that $l = y{l}^{3}z$. $D$ is intra-regular if all elements of $D$ are intra-regular ^[41].

Theorem 5. ^[41] If $D$ is an intra-regular ternary semigroup then $H\cap I\cap J\subseteq HIJ$ for any left ideal $H$, lateral ideal $I$ and right ideal $J$ of $D$.

Theorem 6. $D$ is intra-regular if and only if $\psi \wedge \daleth \wedge \mho \le \psi \circ \daleth \circ \mho$ for every $m$-PFLI $\psi , \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{y}m$-PFMI $\daleth$ and every $m$-PFRI $\mho$ of $D.$

Proof. Suppose, $\psi = \left({\psi }_{1}, {\psi }_{2}, ..., {\psi }_{m}\right), \daleth = \left({\daleth }_{1}, {\daleth }_{2}, ..., {\daleth }_{m}\right), \mho = \left({\mho }_{1}, {\mho }_{2}, ..., {\mho }_{m}\right)$ is $m$-PFLI, $m$-PFMI and $m$-PFRI of $D$ respectively. Let $l\in D$. Then, there exists $y, z\in D$ such that $l = y{l}^{3}z = y\left(y{l}^{3}z\right)\left(y{l}^{3}z\right)\left(y{l}^{3}z\right)z$. Thus

So, $\left({\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }\right)\ge \left({\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }\right)$. That is $\psi \wedge \daleth \wedge \mho \le \psi \circ \daleth \circ \mho .$

Conversely, suppose that $\left({\psi }_{\kappa }\circ {\daleth }_{\kappa }\circ {\mho }_{\kappa }\right)\ge \left({\psi }_{\kappa }\wedge {\daleth }_{\kappa }\wedge {\mho }_{\kappa }\right),$ for $m$-PFLI $\psi , m$-PFMI $\daleth$ and $m$-PFRI $\mho$ of $D$. Let $H, I, J$ are left, lateral and right ideal of $D$. Then by using Lemma 2, ${\chi }_{H}, {\chi }_{I}, {\chi }_{J}$ the $m$- polar characteristic functions of $H, I, J$ are $m$-PFLI, $m$-PFMI and $m$-PFRI of $D,$ respectively. Now, by our supposition

Thus, $H\cap I\cap J\subseteq HIJ$. Therefore by Theorem 5, $D$ is intra-regular.

5.   Comparative study

In the current section, we will describe a connection between this paper and previous papers ^[34,35]. Shabir et al. ^[34] worked on $m$-PFIs and $m$-PFBIs for the characterizations of regular LA-semigroups. Bashir et al. generalized ^[34] to ^[35]. We have extended this work to the structure of $m$-PFIs of ternary semigroups, regular ternary semigroups and intra-regular ternary semigroups. Our results are more general than the results in ^[34,35] because associative property does not hold in LA-semigroup. For example let $\psi \left(ghi\right) = g$ is not an LA-semigroup but it is ternary semigroup. Also, there are many structures that are not handled by binary multiplication but handled by ternary multiplication, such as ${Z}^{-}, {R}^{-}$ and ${Q}^{-}$. To get rid of this difficulty, we operate the ternary operation, and generalize all results in ternary semigroups. Hence, the technique used in this paper is more general than previous.

6.   Conclusions

The definition of an $m$-PF set is applied to the structure of ternary semigroups in this paper. When data comes from $m$ factors then $m$-PF set theory is used to deal such problems. We have converted the basic algebraic structure of ^[34,35] to ternary semigroup by using $m$-PF set. A huge number of uses and needs of ternary operation of $m$-PF set theory are given in this paper. Also, it is proved that every $m$-polar fuzzy bi-ideal of ternary semigroup is an $m$-polar fuzzy generalized bi-ideal of ternary semigroup but converse is not true in general shown by example. We have studied the characterization of regular and intra-regular ternary semigroups by $m$-PFIs.

In future, we will apply this technique for gamma semigroups and near rings. Thus, the roughness of $m$-PFIs of ternary semigroups, gamma semigroups and near-rings will be defined.

Acknowledgement

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (19-130-35-RG). The authors, therefore, gratefully acknowledge DSR technical and financial support.

Conflict of interest

The authors declare that they have no conflict of interest.