Rapid urbanization poses major challenges to the mankind with huge impact on the society and the economy. This paper aims to review relevant literature, mainly recent studies, focused on significant aspects of the interrelations of urban forests and terrestrial carbon sequestration, discussing their implications with reference to urban forests and their roles in climate mitigation, given that the real challenge lies in understanding the integration of carbon sequestration having huge pollution mitigating potentials with other mitigation options. Findings suggest that despite indications of studies that urban forests play significant mitigation roles; they have not been accorded adequate importance vis-à-vis management of ecological disturbances. Findings also suggest that urban forests significantly contribute to terrestrial carbon sequestration and these contributions are in addition to their multiple social-economic-cultural-aesthetic benefits. This paper underscoring the significant contributions of urban forests in maintaining ecological equilibrium, and managing balance between emissions and sequestration to ensure sustainability, offers usefulness to the future researchers, academics, urban-planners and policymakers.
1.
Introduction
In this paper, the object under investigation is a triple (M,g0,u) satisfying the following two conditions:
(a) (M,g0) is a smooth, connected, noncompact, complete, asymptotically flat, n-dimensional Riemannian manifold, with n≥3, with one end, and with nonempty smooth compact boundary ∂M, which is a priori allowed to have several connected components.
(b) u∈C∞(M) satisfies the system
where Ricg0, Dg0 and Δg0 are the Ricci tensor, the Levi–Civita connection, and the Laplace operator of the metric g0, respectively.
If the equality holds in the first equation of (1.1), the triple (M,g0,u) is said static. For clarity, we recall the definition to which we refer for asymptotically flat manifolds.
Definition 1.1. A smooth, connected, noncompact, n-dimensional Riemannian manifold (with or without compact boundary) (N,h), with n≥3, is said to be asymptotically flat if there exists a compact subset K⊂N such that N∖K is a finite disjoint union of ends Nk with the following properties. Every Nk is diffeomorphic to Rn minus a closed ball by a coordinate chart ψk and, if ˜h:=(ψk)∗h=˜hijdxi⊗dxj, we have
for some p>(n−2)/2. Here, δ is the Kronecker delta, and the coordinate charts ψk are called charts at infinity.
Throughout the paper, we will refer to a triple (M,g0,u) that satisfies conditions (a) and (b) as to a sub-static harmonic triple. A fundamental sub-static harmonic triple is the so called Schwarzschild solution, which is given by
It is well–known that both the metric g0 and the potential u, which a priori are well defined only in ˚M, extend smoothly up to the boundary and (M,g0) is called (spatial) Schwarzschild manifold. The parameter m>0 is the ADM mass mADM of the Schwarzschild manifold. We refer the reader to Section 5 for the definition of the mADM associated with a general asymptotically flat manifold. Here, we limit ourselves to recall that the decay conditions (1.2)–(1.5) guarantee that mADM is a geometric invariant [4,8].
Associated with a sub-static harmonic triple, specifically with the potential u ranging in [0,1), let us consider the following family of functions depending on the parameter β≥0:
In [2] it was proven that if (M,g0,u) is a static triple, then, for every β≥2, the function Vβ is strictly nonincreasig unless (M,g0,u) is the Schwarzschild solution. The main purpose of this paper is to extend this result to the sub-static case and to the optimal threshold β=n−2n−1. This is the content of Theorem 3.1, where the monotonicity of the above family - equipped with a corresponding rigidity statement - is expressed in terms of the functions Fβ(τ), where τ=1+t21−t2≥1, to be consistent with [3] and in light of the more advanced analysis contained therein. This generalisation suggests that our approach is robust enough and likely to be exported to other contexts. In a similar way, S. Brendle shows in [7] how some structure conditions for the metric are sufficient to prove an Alexandrov-type theorem and how such structure generalises to the sub-static case.
Let us now be slightly more detailed on how our Theorem 3.1 is proved. We adopt the main strategy proposed in [2], which essentially consists in obtaining the monotonicity as a consequence of a fundamental integral identity derived in a suitable conformally-related setting (see Proposition 4.3). A delicate point is justifying such identity in a region where critical points of the potential are present. One of the main differences with [2] is that, whereas in the static case the analyticity of the potential guarantees the local finiteness of the singular values, which made the argument simpler in many occurrences, in the present sub-static setting the metric and in turn the potential are not a priori analytic. Nevertheless, standard measure properties of the critical set of harmonic functions (summarised in Theorem 2.3) are enough to obtain the fundamental integral identity, which in turn implies the monotonicity of Fβ and, coupled with Sard's Theorem, also its differentiability.
Observe that the difficulty in treating the critical points under the threshold β=1 can be read off directly from formulæ (3.2) and (4.5), the first one displaying the derivative of Fβ and the second one expressing the mean curvature on a equipotential set in terms of the Hessian of the potential itself. In fact, calling Φβ the conformal version of Fβ and looking at formula (4.26) containing the equivalent characterisation of Φ′β derived from the integral identity (4.18), one realises that problems arise already when β<2.
Let us stress that the monotonicity is obtained from the nonnegativity of the right-hand side of our fundamental integral identity. It is above the threshold β=n−2n−1 that this is guaranteed, thanks to the Refined Kato Inequality for harmonic functions. The optimality of such inequality reflects a corresponding optimality of β=n−2n−1 in our result. Moreover, let us remark that the (nonnegative) right-hand side of (4.18) is obtained as the divergence of a suitable modification of a specific vector filed with nonnegative divergence (see (4.19)), in the limit of a vanishing neighbourhood of the critical set. The crucial point in the construction is to maintain the divergence of the modified vector field nonnegative. It would be interesting to see whether a similar construction can be performed for other families of metrics, including special solutions as rigid case.
A straightforward application of the monotonicity of Fβ is comparing Fβ(1) with Fβ(+∞), in turn yielding a "capacitary version" of the Riemannian-Penrose inequality (Theorem 1.1 below). The capacity comes naturally into play when computing Fβ(1) and Fβ(+∞), the latter value via the asymptotic expansions of the metric and of the potential. We recall that the capacity Cap(∂M,g0) of ∂M is defined as
Throughout the paper, we will use the short–hand notation C for the capacity. Comparing (1.6) with either (2.1) or (2.2), it is straightforward, in the case of the Schwarzschild solution, that mADM=C. For a general sub-static harmonic triple, the following inequality holds.
Theorem 1.1 (Capacitary Riemannian Penrose Inequality). Let (M,g0,u) be a sub-static harmonic triple with associated capacity C and suppose that ∂M is connected. Then
Moreover, the equality in (1.7) holds if and only if (M,g0) is isometric to the Schwarzschild manifold with mADM=C.
Whereas the above inequality has been obtained as a consequence of the monotonicity of Fβ, at every fixed β≥n−2n−1, we remark that one could possibly push the above described analysis one step forward, at the same time exploiting the full power of the optimality threshold. Indeed, we believe that considering p-harmonic functions defined at the exterior of a bounded domain Ω lying in M, it may be possible to derive, as done in [1] for the Euclidean case and in the simultaneous limit as β↓n−2n−1 and p↓1, a Minkowski-like inequality for ∂Ω (see [21] for a Minkowski-like inequality in the static, asymptotically flat case and [5] for the nonnegative Ricci case).
Concerning the treatment of general sub-static metrics and the derivation of related geometric inequalities, besides the already cited [7] we also would like to mention [19], where an integral formula is obtained and applied to prove Hentze-Karcher-type inequalities. For the case of asymptotically hyperbolic sub-static manifolds (specifically, for adS-Reissner-Nordström manifolds), we refer the interested reader to [13] and [27].
We remark that our results are not based on the Positive Mass Theorem. By contrast, we observe that using this celebrated result, more precisely a consequence of it contained in [17,Theorem 1.5], one can prove the following uniqueness statement. We refer the reader to Definition 1.1 for the notation and terminology.
Theorem 1.2 (Uniqueness Theorem for sub-static harmonic triples). Let (M,g0,u) be a sub-static harmonic triple with associated capacity C. Suppose that there is a chart at infinity such that
for some q>n. Then (M,g0) is the Schwarzschild manifold with associated ADM mass given by C.
It remains an open question to see whether it is possible to remove the assumption on the decay of R˜g0 and get the same conclusion.
The paper is organised as follows. In Section 2, we recall and discuss some preparatory material, namely the asymptotic expansions of the metric and of the potential, and classical measure properties of the critical set of the potential, with a close look on related integral quantities. In Section 3, we prove the Monotonicity and Outer Rigidity Theorem 3.1, and the consequent Capacitary Riemannian Penrose Inequality contained in Theorem 1.1. To do this, we use from Section 4 some corresponding results obtained in a suitable conformally-related setting. The biggest technical effort is contained in such section. In the Appendix we also provide an alternative proof of the monotonicity of our monotone quantities. Finally, Section 5 is devoted to the proof of Theorem 1.2.
2.
Preliminaries
Let (M,g0,u) be a sub-static harmonic triple. We observe, as a first consequence of system (1.1), that the scalar curvature Rg0 is nonnegative. Since u satisfies the last three conditions of system (1.1), by the Maximum Principle we have
Also, by the forth condition in (1.1), each level set of u is compact. Moreover, from the Hopf Lemma, it follows that |Dg0u|g0>0 on ∂M. In particular, zero is a regular value of u. Furthermore, from the first two conditions in (1.1) restricted to ∂M it is easy to deduce that D2g0u≡0 on ∂M. In turn, the function |Dg0u|g0 attains a positive constant value on each connected component of ∂M, and the boundary ∂M is a totally geodesic hypersurface in M.
We now deal with the asymptotic behaviour of the potential u at ∞. By Theorem 2.2 below, this is given by:
being
Here, σg0 is the canonical measure on the boundary ∂M seen as a Riemannian submanifold of (M,g0), and we have used the standard notation o2, which means that, in any chart at infinity ψ, denoted by ˜u the function u∘ψ−1, the following conditions hold true.
Let us remark that we can always suppose, without loss of generality, that the considered chart at infinity admits a diffeomorphic extension to the closure of the coordinate domain. We will make this implicit assumption throughout the paper, so that ∂K (see Definition 1.1) is a connected hypersurface of M and the quantities related to the metric can be pushed–forward in Rn outside an open ball and be smooth here. We also observe that formula (2.2) is nothing but an equivalent characterisation of the capacity of ∂M.
2.1. Asymptotic expansions
Let (N,h) be a smooth, connected, noncompact, complete, asymptotically flat, n-dimensional Riemannian manifold, with n≥3, with one end and with nonempty smooth compact boundary ∂N. We adopt the following notation.
● B and BR a generic open ball and the open ball of radius R>0 centred in the origin of (Rn,de), respectively;
● |⋅| the euclidean norm of Rn;
● |Sn−1| the hypersurface area of the unit sphere inside Rn with the canonical metric;
● De and Δe the Levi–Civita connection and the Laplace operator of (Rn,gRn), respectively;
● Dh and Δh the Levi–Civita connection and the Laplace operator of (N,h), respectively;
● σe the canonical measure on a Riemannian submanifold of (Rn,gRn);
● σh the canonical measure on a Riemannian submanifold of (N,h);
● |⋅|e the norm induced by gRn on the tangent spaces to the manifold Rn;
● |⋅|h the norm induced by h on the tangent spaces to the manifold N.
● If ψ is a chart at infinity of (N,h) according to Definition 1.1, we denote by ˜h the push–forward metric ψ∗h of h by ψ, having coordinate expression ˜hij(x)dxi⊗dxj. In this context, D˜h and Δ˜h denote the Levi–Civita connection and the Laplace operator of ˜h, respectively, while σ˜h is the canonical measure on a Riemannian submanifold of (Rn∖B,˜h) and |⋅|˜h is the norm induced by ˜h on the tangent spaces. Moreover, Ric˜h and R˜h are the Ricci tensor and the scalar curvature of ˜h, respectively.
Proposition 2.1. Let ψ be a chart at infinity of N (according to Definition 1.1). The decays
hold true for some p>n−22. Moreover,
where νe is the ∞–pointing unit normal with respect to the Euclidean metric and σe the associated canonical measure on ∂BR, while ν˜h is the ∞–pointing unit normal with respect to ˜h and σ˜h the associated canonical measure on ∂BR.
Proof. From ˜hik˜hkj=δij it is easy to get
These formulae coupled with (1.2), (1.3) and (1.4) give (2.6). Decay (2.7) is another direct consequence of Definition 1.1, keeping in mind that
Decays (2.8)–(2.9) are obtained by contractions of the Riemannian tensor. Now, observe that
and that
Observe also that
for some C>0, for any x∈Rn∖B. Since trivially |xkxl|≤|x|2, from (2.13) and (2.14), coupled with (2.6), we get decay (2.10). Concerning decay (2.11), recall first that, using a coordinate chart (y1,…,yn−1) on ∂BR, we have that dσ˜h=√det˜h∂BRdy1…dyn−1 with ˜h∂BR=˜h∂BRαβdyα⊗dyβ, where ˜h∂BRαβ=˜h(∂∂yα,∂∂yβ). Now, using the specific local parametrization x=x(y1,…,yn−1) of ∂BR, given by the inverse of stereographic projection from its north pole with the diffeomorphism p∈Sn−1→Rp∈∂BR, we have that
because
Hence, on ∂BR,
where in the last identity we have used the Leibniz formula for the determinant and Taylor–expanded the square root.
The following result is well–known. For completeness, we provide the statement, along with its proof, which is an extension of [20,Lemma A.2.] to every n≥3.
Theorem 2.2. Let (N,h) be a smooth, connected, noncompact, complete, asymptotically flat, n-dimensional Riemannian manifold, with n≥3, with one end, and with nonempty smooth compact boundary ∂N. If v∈C∞(N) is the solution to
then
We remark that the asymptotic behaviour of the potential u at ∞, given by formula (2.1), is a simply consequence of the above theorem observing that u=1−v when (N,h)=(M,g0).
Proof. Step 1: Construction of a barrier function. Let ψ be a chart at infinity for N. From now on by C we will denote some positive constant, which may change from line to line. By Definition 1.1, there exist p>(n−2)/2 and R1≥1 such that
for every x∈Rn∖BR1. By (2.6), the same conditions as in (2.17) are satisfied by ˜hij(x) for all x∈Rn∖BR1. Then, for every f∈C∞(Rn∖BR1), writing
where
we have that
in Rn∖BR1. For a fixed 0<ε<p and for a>0 to be chosen later, consider the function
By direct computation one can check that
and in turn that
Therefore, by (2.18) and (2.19), we obtain that
and hence there exists R2>R1 independent of a such that Δ˜hϕa<0 in Rn∖BR2, for every a>0. We now choose a>0 so that ϕa=1 on ∂BR2, that is a=[1Rn−22−1Rn−2+ε2]−1. Since ϕa is ˜h–superharmonic in Rn∖BR2 and since ˜v:=v∘ψ−1<1 on ∂BR2, by the Maximum Principle
Step 2: Asymptotic expansion of v. Note that from (2.20) one gets in particular that ˜v≤C|x|2−n. We now apply Shauder's Interior estimates ([12,Lemma 6.20]) to Δ˜h˜v=0 in Rn∖¯BR2, where the operator Δ˜h is defined as in (2.18) and its coefficients satisfy the estimates in (2.19). Recalling that the Hölder norms are weighted by the (Euclidean) distance de(⋅,∂BR2) from ∂BR2 and since de(x,∂BR2)≃|x| when |x|>>1, from such estimates we get
in Rn∖BR2 (up to a bigger R2). Combining (2.19) and (2.21), the equation Δ˜h˜v=0 can be equivalent written as Δe˜v=f where
We consider a smooth extension of ˜v on Rn, still denoted by ˜v, which is zero in a ball centred in the origin, and the smooth extension of f given by Δe˜v, still denoted by f. By a classical representation formula and due to (2.22), the function
is well–defined and fulfils Δew=f on Rn. Now, one can rewrite w in Rn∖{O} as
and show that each summand can be bounded by C|x|−(n−2+γ), where γ=min{1,p} if p≠1 and γ∈(1/2,1) if p=1, except the first one. Therefore, we have that
in Rn∖{O}. Since the function ˜v−w is harmonic and bounded on Rn, then it is constant and this constant is zero, using the fact that ˜v−w→0 for |x|→∞. Hence
in Rn∖BR2. We observe that
and that
Therefore, applying Shauder's Interior estimates to Δ˜hz=−Cˆz in Rn∖¯BR2, we get
in Rn∖BR2 (up to a bigger R2). From (2.23) and (2.24) we obtain in particular (2.16).
Step 3: Characterization of C. First of all we remark that 0<v<1 on ˚N, v:N→(0,1] is proper, and, from the Hopf Lemma, |Dhv|h>0 on ∂N. In particular, 1 is a regular value of v. Let K be the compact set on the complement of which the chart ψ is defined. For every R>R2, applying the Divergence Theorem to the function v on K∪{|ψ|<R} we obtain that
where νh is the outward unit normal vector field with respect to h along ∂N and {|ψ|=R}. Then, it follows that
where ˜v=v∘ψ−1. Now, thanks to (1.2), (2.6), (2.10) and (2.11), which are true for γ too, and also by identity (2.23) and the second in (2.24), and keeping in mind that |∂i˜v|≤C|x|1−n, we have that
Hence
2.2. Measure of and integration on the level sets of the potential
Let (N,h) and ι:S↪N be respectively a m–dimensional Riemannian manifold and a s–dimensional Riemannian submanifold of N. Let k be a positive real number. We set
B(S) the smallest σ–algebra containing all open sets of S;
(S,Λ(S),μι∗h) the canonical space of measure on the Riemannian manifold (S,ι∗h) (see [14,Section 3.4]);
HkS the k-dimensional Hausdorff measure on (S,dS), being dS the distance function of S;
HkS;N the k-dimensional Hausdorff measure on (S,dS;N) where dS;N is the distance function of N restricted to S×S;
HkN⌞S the k-dimensional Hausdorff measure of N restricted to S.
By definition of the Hausdorff measure and by [26,Proposition 12.7], HkS;N, HkN⌞S and HkS coincide on B(S), and by [26,Proposition 12.6] and by [25,Proposition 2.17], HsS and μι∗h coincide on Λ(S). The same results still hold when N is a manifold with boundary.
For the ease of the reader, we collect in the next theorem some results about the measure of the level sets of the potential u and
which are well–known in the Euclidean setting (see, e.g., [15,16]).
Theorem 2.3. Let (M,g0,u) be a sub-static harmonic triple. Then the following statements hold true.
(i) For every t∈[0,1), the level set {u=t} is compact and has finite (n−1)–Hausdorff measure in M;
(ii) Crit(u) is a compact subset of M and its Hausdorff dimension in M is less than or equal to (n−2);
(iii) The set of the critical values of u has zero Lebesgue measure, and for every t∈[0,1) regular value of u there exists ϵt>0 such that (t−ϵt,t+ϵt)∩[0,1) does not contain any critical value of u.
Proof. Each level set of u is compact, due to the forth condition in (1.1), while the compactness of Crit(u) follows by (2.4). Now, consider the nontrivial case where Crit(u)≠∅ and let p be a point of a critical level set {u=t}. Take a chart (Up,ψp) centred at the point p with ψp(Up)=B1. Setting ˜g0=(ψp)∗g0=˜g0;ijdxi⊗dxj, there exists C>0 such that
for each (v1,…,vn)∈Rn and for each x∈¯B12. The same condition is satisfied by the coefficients ˜gij0. In particular, setting ˜u=u∘ψ−1p, we have that
We observe that Δ˜g0v=aij∂i∂jv+bi∂iv=0 is an elliptic partial differential equation with coefficient C∞ in ¯B12. We recall that if v is a C∞–solution of the above equation and if v vanishes to infinite order at a point x0∈B12, i.e., for every k>0
then v is identically zero in B12 (see [11,Theorem 1.2]). Applying this fact to ˜u−t, one can argue that ˜u−t has finite order of vanishing at O. Then, by using [16,Theorem 1.7], there exists 0<ρ<12 such that
Since ˜u is nonconstant in B12 and by the structure and regularity of Δ˜g0, [15,Theorem 1.1] yields
Hence, since the restriction of ψp to ψ−1p(B1/2) is bilipschitz due to (2.25) and since the measures Hkψ−1p(B1/2) and HkM⌞ψ−1p(B1/2) coincide on borel sets, statements (i) and (ii) are true locally. In turn, by compactness of {u=t} and Crit(u), they are true globally. To prove (iii), observe that by Sard's Theorem, the set of the critical values of u has zero Lebesgue measure. Now, suppose by contradiction that there exists ¯t∈[0,1) regular value such that, for all m≥¯m with 1¯m<1−¯t, the interval (¯t−1m,¯t+1m)∩[0,1) contains critical values. Hence there is a sequence {tm}m≥¯m of critical values such that tm→¯t. In particular, there exists a sequence {pm}m≥¯m of critical points contained in the set {0≤u≤¯t+1m} and such that u(pm)=tm. Then, by compactness and up to a subsequence, pm→p. In turn, 0=|Dg0u|g0(pm)→|Dg0u|g0(p) and tm=u(pm)→u(p). Hence |Dg0u|g0(p)=0 and u(p)=¯t, which is absurd. This concludes the proof of (iii).
Remark 2.1. It is useful to observe that:
(i) for every t∈(0,1), the set {u≥t} is connected;
(ii) for every t≈1, the level set {u=t} is regular and diffeomorphic to Sn−1;
(iii) For every t∈(0,1), {u≥t}=¯{u>t} and {0≤u≤t}=¯{0<u<t}.
We check (ii) first. We start by observing that due to (2.1) |Dg0u|g0≠0 in {u≥t0}, for some 0<t0<1. This fact establishes a diffemorphism between {u≥t0} and {u=t0}×[t0,1) and tells us at the same time that the level sets {u=t} are pairwise diffeomorphic, for every t≥t0. It is thus sufficient to show that {u=t0} is connected. Suppose by contradiction that this is not the case. Without loss of generality we can assume that {u=t0} can be decomposed into the disjoint union of two connected sets C1 and C2, indeed the same argument works a fortiori if the connected components are more than two. Now, note that by definition of asymptotically flat manifold, there exists a compact set K⊂M such that M∖˚K is diffeomorphic to Rn∖˚B by a chart at infinity ψ, where B is a suitable ball, and we can suppose, up to a bigger t0, that {u≥t0}⊆M∖˚K. Now, in view of the asymptotic expansion of u, there exist two positive constants A<B such that
In particular, setting R0=[B/(1−t0)]1/(n−2), we have that
At the same time, we have that {|x|>R0} is connected and each Ci×[t0,1) is a closed set of M, so that indeed {|x|>R0}⊆Ci×[t0,1), for some i∈{1,2}.Therefore, we have that
which gives the contradiction that the noncompact set {Cj×[t0,1)}, where j∈{1,2}∖{i}, is contained into the compact one (M∖˚K)∩{|x|≤R0}. Therefore, {u=t0} is connected. Now, setting ˜u:=u∘ψ−1, we have that, up to a bigger t0 and due to (2.5), the set {˜u=t0} is a compact and connected hypersurface of Rn having strictly positive sectional curvature, as a Riemannian submanifold of (Rn,gRn). Hence, {˜u=t0} is diffeomorphic to Sn−1 by the Gauss map (see [10,Section 5.B] for more details). Statement (ii) thus follows, being {u=t0} and {˜u=t0} diffeomorphic.
To see (i), observe first that if t is a regular value of u, then Et:={u≥t} is a n–dimensional submanifold with boundary {u=t}. By Theorem 2.3 and by the Maximum Principle, every connected component C of Et is unbounded. Since u→1 at ∞, we have that u(C)=[t,1), and hence C∩{u=t0}≠∅, for every t0∈(t,1). Then, Et is connected by (ii). If t is a critical value of u, we let ¯t>t be a regular value of u such that {u=¯t} is connected and let {tm} be a nondecreasing sequence of regular value of u such that tm<t and tm→t. Hence, {{tm≤u≤¯t}}m∈N is a nonincreasing family of connected and compact sets in M, which is Hausdorff, and in turn the intersection {t≤u≤¯t} is still connected. In particular, we deduce that Et={t≤u≤¯t}∪{u≥¯t} is connected.
To check (iii), note first that for every t∈(0,1) regular value of u, the equalities are always true. If t∈(0,1) is a critical value of u, by Theorem 2.3 and by the Maximum Principle the interior of {0≤u≤t} and the interior of {u≥t} are both disjoint from {u=t}, so that (iii) is still true.
Let (M,g0,u) be a sub-static harmonic triple, and let t∈[0,1) be a real number. We consider the spaces of measure
Let f:S→R be a continuous and consider the zero–extension ˚f of f defined on {u=t} as
By Theorem 2.3 and by definition of the Lebesgue integral, we have that ˚f∈L1(Hn−1M⌞{u=t}) iff f∈L1(σg0) and
Similarly, if f:{u=t}→R is a continuous function, then f∈L1(Hn−1M⌞{u=t}) iff f|S∈L1(σg0) and
In the rest of this paper, we will confuse the integrals of cases (2.26) and (2.27), denoting both by ∫{u=t}fdσg0.
3.
Monotonicity and Outer Rigidity Theorem
In this section, we state and prove our Monotonicity and Outer Rigidity Theorem, which is then used to prove the Capacitary Riemannian Penrose Inequality (1.7). From now on and unless otherwise stated, (M,g0,u) will always be a sub-static harmonic triple, and, when referring to such triple, the subscript g0 will be dropped. The only exception is |Sn−1|, which always stands for the Euclidean volume of Sn−1.
Theorem 3.1 (Monotonicity and Outer Rigidity Theorem). Let (M,g0,u) be a sub-static harmonic triple, and let Fβ:τ∈[1,+∞)→[0,+∞) be the function defined by
for every β≥0. Then, the following properties hold true.
(i) Differentiability, Monotonicity and Outer Rigidity: for every β>n−2n−1, the function Fβ is continuously differentiable with nonpositive derivative in (1,+∞). Moreover, if there exists τ0∈(1,+∞) such that F′β(τ0)=0 for some β>n−2n−1, then, setting t0=√τ0−1τ0+1, the Riemannian submanifold {u≥t0}
is isometric to
(ii) Convexity: for every β>n−2n−1, the function Fβ is convex on [1,∞).
We remark that the functions Fβ are well–defined, in view of Theorem 2.3 and since the integrand function in (3.1) is bounded on every level set of u. Note that, from Theorem 3.1 and by a simple argument based on the Dominated Convergence Theorem, the monotonicity and the convexity of Fβ extend to the case β=n−2n−1. Moreover, on the values τ such that {u=√τ−1τ+1} is regular and thus on a.e. τ>1 due to Theorem 2.3 (iii), the function Fβ is twice differentiable for each β>n−2n−1, with first and second derivative given by
In the computation, we have used the first normal variation of the volume and the mean curvature of \{u = t\} , and the Divergence Theorem. The symbols \mathrm{H} and \mathrm{h} stand respectively for the mean curvature and the second fundamental form of the smooth (n-1) –dimensional submanifold \big\{u = \sqrt{\frac{\tau-1}{\tau+1}}\, \big\} , with respect to the \infty –pointing unit normal vector field \nu = \frac{\mathrm{D}u}{\vert \mathrm{D}u \vert} . Also, \mathrm{D}^{\mathrm{T}} denotes the tangential part of the gradient, that is
for every f\in C^{1}(M) .
To prove Theorem 3.1, we use the results of Section 4, which are obtained in the conformal setting defined by
Denoting by \nabla and \Delta_{g} the Levi–Civita connection and the Laplace–Beltrami operator of g , the triple (M, g, \varphi) satisfies the following system.
Moreover, we have that
as we will see in the proof of Lemma 4.1.
Remark 3.1. Since \mathrm{Crit}(\varphi) = \mathrm{Crit}(u) = \{\vert \nabla \varphi \vert_{g} = 0\} by the equality in ( \star ) and since \{\varphi = s\} = \{u = \tanh\big(\frac{s}{2}\big)\} by (3.4), using Theorem 2.3 and Remark 2.1 we deduce that: \mathrm{Crit}(\varphi) has zero \mu_{g} –measure and zero (n-1) –Hausdorff measure in (M, g) ; the level sets of \varphi have finite (n-1) –Hausdorff measure in (M, g) and in particular the smooth (n-1) –dimensional submanifolds \{\varphi = s\}\setminus\mathrm{Crit}(\varphi) have finite g –area, i.e., finite \sigma_{g} –measure. Moreover, \{\varphi\geq s\} is connected for every s\geq 0 and there exists s_0\geq0 such that \{\varphi = s\} is regular and diffeomorphic to \mathbb{S}^{n-1} , for every s\geq s_0 . Similar comments as those at the end of Subsection 2.2 can be made, regarding the relation between integration and \mathrm{Crit}(\varphi) .
Let \Phi_{\beta}:[0, \infty)\to \mathbb{R} be the function defined by formula
for every \beta\geq 0 . For the convenience of the reader, we anticipate from Section 4 the properties of \Phi_{\beta} that we are going to use.
( \circ ) For every \beta\geq0 , the function \Phi_{\beta}(s) is continuous in [0, +\infty) .
( \diamond ) For every \beta > \frac{n-2}{n-1} , the function \Phi_{\beta} is continuously differentiable in (0, +\infty) . The derivative \Phi'_{\beta} is nonpositive, satisfies for every S > s > 0
and admits for every s > 0 the integral representation
where Q is defined in (4.10).
( \diamond\, \diamond ) If there exists s_{0} > 0 such that \Phi'_{\beta}(s_{0}) = 0 for some \beta > \frac{n-2}{n-1} , then \{\varphi = s_{0}\} is connected and (\{\varphi\geq s_{0}\}, g) is isometric to \big([0, +\infty)\times \{\varphi = s_{0}\}, d\rho\otimes d\rho+g_{\{\varphi = s_{0}\}}) , where \rho is the g –distance function to \{\varphi = s_{0}\} and \varphi is an affine function of \rho in \{\varphi\geq s_{0}\} . If \Phi_{\beta} is constant for some \beta > \frac{n-2}{n-1} , then \partial M is connected and (M, g) is isometric to \big([0, +\infty)\times \partial M, d\rho\otimes d\rho+g_{\partial M}) , where \rho is the g –distance function to \partial M and \varphi is an affine function of \rho .
In the above list we have gathered and summarised the results contained in Lemma 4.5, Proposition 4.6, and Corollary 4.7.
Proof of Theorem 3.1. Step 1 : Differentiability, Monotonicity and Convexity. For every \beta\geq0 and for all \tau \in[1, +\infty) , we note that
Consequently, by (\circ) , we deduce that for every \beta\geq0 the function F_{\beta} is continuous in [1, +\infty) . By (\diamond) and by (3.7), we obtain immediately that for every \beta > \frac{n-2}{n-1} the function F_{\beta} is continuously differentiable in (1, +\infty) , with
In particular, from (\diamond) we get F'_{\beta}\leq 0 . As for the convexity, noticing that
and that the function \log\big(\, \frac{\sqrt{\tau+1}+\sqrt{\tau-1}}{\sqrt{\tau+1}-\sqrt{\tau-1}}\, \big) is nondecreasing, from (3.6) we obtain that F'_{\beta}\, is nondecreasing in (1, +\infty) . Therefore also by the continuity of F_{\beta} at 1 , F_{\beta} is convex in [1, +\infty) .
Step 2 : Outer Rigidity. Let us assume that there exists \tau_{0} \in (1, \infty) such that F'_{\beta}(\tau_{0}) = 0 for some \beta > \frac{n-2}{n-1} . Then, by equality (3.8), \Phi'_{\beta}(s_{0}) = 0 for s_{0} = \log\big(\, \frac{\sqrt{\tau_{0}+1}+\sqrt{\tau_{0}-1}}{\sqrt{\tau_{0}+1}-\sqrt{\tau_{0}-1}}\, \big) , and hence, by (\diamond\, \diamond) , (\{\varphi\geq s_{0}\}, g) is isometric to \big([0, +\infty)\times \{\varphi = s_{0}\}, d\rho\otimes d\rho+g_{\{\varphi = s_{0}\}}) , where \rho is the g –distance function to \{\varphi = s_{0}\} and \varphi = (n-2)\, (2\mathcal{C})^{-\frac{1}{n-2}}\rho+s_{0} , because \vert \nabla \rho\vert_{g}\equiv1 and in view of the limit in (\star) . Setting t_{0} = \tanh \frac{s_{0}}{2} , consider N the submanifold with boundary \{\varphi\geq s_{0}\} = \{u\geq t_{0}\} . Writing
the Riemannian manifolds in the first row, whose metrics are indicated in the second row, are pairwise isometric through the applications written in the third row. We recall that the application p\to (\rho, q) in the third row is the inverse of the diffeomorphism given by the normal exponential map, i.e., the application which associates to every point p of N the couple having as first coordinate the g –distance of p from \partial N and as second coordinate the point q of \partial N that realizes such distance. Then, in view of (3.4) and with the same notation as above, the following Riemannian manifolds are isometric.
where r_{0} = \big(\frac{2\mathcal{C}}{1-t_{0}^{2}}\big)^{\frac{1}{n-2}} . Doing some computations, we obtain that
where the convection followed for the Riemannian curvature tensor is that given in [23], c is a suitable positive constant and q is the point of \partial N that realizes the g –distance of p from \partial N . Denoting by \Theta the diffeomorphism from N to [r_{0}, +\infty)\times \partial N introduced in (3.9), for every q_{0}\in \partial N we consider the curve
and observe from (3.10) that
At the same time, we have that
This is because g_{0} is asymptotically flat according to Definition 1.1 and by (2.3), which yields in particular
for some p > \frac{n-2}{2} . Combining (3.11) and (3.12), the arbitrariness of the point q_{0} in \partial N gives that
Hence the sectional curvature of the Riemannian manifold (\partial N, g_{\partial N}) is constant and identically equal to (2\mathcal{C}\, )^{-\frac{2}{n-2}} . Then, being all the level sets \{u = t\} with t\approx1 regular and diffeomorphic to \mathbb{S}^{n-1} as observed in Remark 2.1, for [10,Section 3.F] (\partial N, g_{\partial N}) and (\mathbb{S}^{n-1}, (2\mathcal{C}\, )^{\frac{2}{n-2}}g_{ \mathbb{S}^{n-1}}) are isometric. Then, (\{u\geq t_{0}\}, g_{0}) is isometric to the submanifold \big(\, [r_{0}, +\infty)\times \mathbb{S}^{n-1}\, , \frac{dr \otimes dr}{1-2\mathcal{C}r^{2-n}}+r^{2}g_{ \mathbb{S}^{n-1}} \big) of the Schwarzschild manifold with associated ADM mass given by \mathcal{C} .
Proof of Theorem 1.1. Spep 1 : Inequality. By Theorem 3.1, we have that F_{\beta}(\tau_{0})\geq \lim_{\tau\to+\infty}\, F_{\beta}(\tau) , for every \tau_{0} > 1 . In particular, since F_{\beta} is continuous in [1, +\infty) due to the step 1 of Theorem 3.1, we have that
for every \beta > \frac{n-2}{n-1} . Since \mathrm{D}^{2}u \equiv 0 on \partial M and since \partial{M} of M is connected, \vert \mathrm{D} u \vert is constantly equal to \frac{(n-2)\, \mathcal{C}\, \vert \mathbb{S}^{n-1}\vert\, }{\vert \partial M\vert}\, , by formula (2.2). In particular, we have that
By (\star) , we know that
Therefore, fixed \varepsilon > 0 , there exists 1 < \tau_{0} < +\infty such that
in \big\{u\geq\sqrt{\frac{\tau_{0}-1}{\tau_{0}+1}}\, \big\} and the level sets \big\{u = \sqrt{\frac{\tau-1}{\tau+1}}\, \big\} are regular for all \tau\geq \tau_{0} . Therefore, for every \tau\geq \tau_{0} we have that
where in the second equality we have used the Divergence Theorem couple with the fact that u is harmonic, and in the third equality we have used formula (2.2). Since \varepsilon is arbitrary, we get
In a similar way we can obtain the reverse inequality, so that
Joining the formulas in (3.13), (3.14) and (3.15), we obtain the desired inequality (1.7).
Step 2 : Rigidity. If (M, g_{0}) is isometric to the Schwarzschild manifold with ADM mass m > 0 , then the right–hand side and the left–hand side of (1.7) are both equal to m , by direct computation.
Suppose now that the equality holds in (1.7). Then, by Step 1 and for every \beta > \frac{n-2}{n-1} , the function F_{\beta} is constant. In turn, \Phi_{\beta} is constant, being
Finally, (\diamond\, \diamond) and the very same argument of the proof of the Outer Rigidity in Theorem 3.1 imply first that (M, g) is isometric to
where \rho is the g –distance to \partial M and \varphi is an affine function of \rho , and secondly that (M, g_{0}) is isometric to the Schwarzschild manifold with ADM mass \mathcal{C} .
4.
Conformal setting
Let us consider the conformal change g of the metric g_0 introduced in (3.4) which is well–defined being 0\leq u < 1 in M . The metric g is complete, since any g –geodesic \gamma parametrized by g –arc length defined on a bounded interval [0, a) can be extended to a continuous path on [0, a] . Indeed, if \gamma has infinity length with respect to g_{0} , there exists a sequence \{t_{m}\}_{m\in \mathbb{N}} such that \gamma(t_{m})\to \infty (being \gamma not contained in any compact set) and using, in the computation of g –length of \gamma , the passage from g to g_{0} , the asymptotic flatness of (M, g_{0}) and the asymptotic expansion of u in (2.3) we obtain that \gamma has infinity length with respect to g . Hence \gamma has finite length with respect to g_{0} and, being g_{0} complete, it follows that g is complete (see [24,Section 1.1] and [9]). We also recall that the metric g is asymptotically cylindrical (see [2,Section 3.1]). The other main element of the conformal setting is the C^{\infty} –function \varphi , defined in (3.4). Now, the reverse changes are
Recalling that we denote by the symbols \nabla and \Delta_{g} the Levi–Civita connection and the Laplace–Beltrami operator of g , by the formulas in [6,Theorem 1.159], we obtain
Translating system (1.1) in terms of g and \varphi , we get system (3.5). Moreover, on \{\varphi = s\}\setminus\mathrm{Crit}(\varphi) we consider the \infty –pointing normal unit vector fields
the mean curvatures
and the second fundamental forms
for any X, Y tangent vector fields to the considered submanifold.
Reversing formulas (4.1), (4.2) and (4.3), we get
These equalities, jointly with the asymptotic flatness of (M, g_{0}) and the asymptotic expansion of u given in Section 2, allow us to obtain an upper bound for the functions \vert \nabla \varphi \vert_{g} and \vert \nabla^{2} \varphi \vert_{g} , and for the g –areas of the level sets of \varphi sufficiently "close" to infinity. This is the content of the following lemma.
Lemma 4.1. There exists 0\leq s_{0} < +\infty such that
Proof. Let \psi be a chart at infinity. Considering \widetilde{g}_{0} = \psi_{*}g_{0} = \widetilde{g}_{0;ij}dx^{i}\otimes dx^{j} , by formulas (2.6) and (2.4), the coordinate expression of
is
Hence
Moreover, by limit (4.6) there exist a constant L > 0 and a value s_{0} > 0 of \varphi such that every s\geq s_{0} is a regular value of \varphi and (1-u^{2})^{\frac{n-1}{n-2}}\leq L\, \, \vert \mathrm{D}u \vert on \{\varphi\geq s_{0}\} . Then
where in the last equality we have applied the Divergence Theorem. Consequently, we have that \sup\limits_{s\geq s_{0}}\int\limits_{\{\varphi = s\}}d\sigma_{g} < +\infty . Similarly, we have that
due to formulas (2.6), (2.5) and (5.3). Moreover,
All in all,
which gives
In particular, since \varphi is smooth, we have that
Remark 4.1. Note that \sup\limits_{s\geq 0}\int\limits_{\{\varphi = s\}}d\sigma_{g}\in(0, +\infty] , since we cannot a priori exclude that there exist a critical value \overline{s} > 0 and a sequence \{s_{m}\}\subset (0, +\infty) such that s_{m}\to\overline{s} and
As it will be clear in the proof of the integral identity (4.17), which is at the core of the conformal–monotonicity result (Proposition 4.6), it is useful to introduce a suitable vector field with nonnegative divergence. To do this, let us focus on the set \mathring{M}\setminus\mathrm{Crit}(\varphi) and notice first that the classical Bochner formula, applied to the g –harmonic function \varphi , becomes
Then, we obtain
where in the third equality we have used (4.7). Now, observe from the nonnegativity of the tensor
(see (3.5)) that
Therefore, by adding and subtracting the term \beta\, \vert\nabla \varphi \vert^{\beta-2}_{g}\, \coth(\varphi)\, \nabla ^{2}\varphi(\nabla \varphi, \nabla \varphi) on the right–hand side of (4.8), we get
Since
and since, setting
there holds
from (4.11) we get
Note that, by the refined Kato inequality for harmonic function
we have that
whenever \beta\geq\frac{n-2}{n-1} . Hence, \mathrm{div}_{g}\, Y_{\beta}\geq 0 for every \beta\geq\frac{n-2}{n-1} . This fact will be heavily used in the proof of the forthcoming results. It will also be useful to have a precise estimate of \int\limits_{\{\vert \nabla \varphi \vert_{g} = \delta\}}\big\vert\, \nabla\vert \nabla \varphi \vert_{g}\, \, \big\vert_{g}\, d\sigma_{g} in terms of a suitable power of \delta , close to \mathrm{Crit}(\varphi) , that is when \delta\to 0^{+} . This is the content of the following lemma.
Lemma 4.2. There exists \delta_{0} > 0 such that
We recall that the set of the critical values of \vert \nabla \varphi \vert^{2}_{g} has zero Lebesgue measure by Sard's Theorem, whereas we have no information regarding the local \mathcal{H} –dimension of \mathrm{Crit}(\vert \nabla \varphi \vert^{2}_{g}) .
Proof. Applying Sard's Theorem to the smooth function \vert \nabla \varphi \vert^{2}_{g} there exists \varepsilon_{0} > 0 such that \varepsilon_{0} is a regular value of \vert \nabla \varphi \vert^{2}_{g} and
where the limit in the previous expression is the (finite and positive) value computed in (4.6). In particular, \{\vert \nabla \varphi \vert^{2}_{g}\leq \varepsilon_{0}\} is compactly contained in \mathring{M} , and for every 0 < \delta < \delta_{0} regular value of \vert \nabla \varphi \vert_{g} we have that
Now, consider the smooth vector field
with \mathrm{div}_{g}Z\geq0 . Set
Then, for every 0 < \varepsilon < \varepsilon_{0} regular value of the function \vert \nabla \varphi \vert^{2}_{g} , we apply the Divergence Theorem to the smooth vector field Z on U_{\varepsilon_{0}} \setminus \overline{U_{\varepsilon}} , and we get
Then, it follows
Therefore, setting
we obtain
Consequently, the desired statement follows keeping in mind that: if \delta is a regular value of \vert \nabla \varphi \vert_{g} , then \delta^{2} is a regular value of \vert \nabla \varphi \vert_{g}^{2} ; in M\setminus\mathrm{Crit}(\varphi) we have \nabla\vert \nabla \varphi \vert^{2}_{g} = 2\vert \nabla \varphi \vert_{g}\nabla\vert \nabla \varphi \vert_{g} .
We underline that from now on we will use Remark 3.1 widely.
The following proposition contains the integral identity which is the main tool of our analysis.
Proposition 4.3. Let (M, g_{0}, u) be a sub-static harmonic triple, and let g and \varphi be the metric and the function defined in (3.4). Then, for every \beta > \frac{n-2}{n-1} and for every S > s > 0 regular values of \varphi , it holds
where the tensor Q is defined as in (4.9).
Proof. The case \beta\geq 2 is an easy adaptation of the argument used in [2] but it is anyway a consequence of the following argument. We focus on the unknown case \frac{n-2}{n-1} < \beta < 2 . In \mathring{M}\setminus\mathrm{Crit}(\varphi) we consider the smooth vector field Y_{\beta} , defined in (4.12) and satisfying
as already explained. Set
When E_{s}^{S}\cap \mathrm{Crit}(\varphi) = \emptyset , then the statement is a straightforward application of the Divergence Theorem. Now, suppose that E_{s}^{S}\cap \mathrm{Crit}(\varphi)\neq\emptyset . In this case we consider, for every \varepsilon > 0 sufficiently small, a smooth nondecreasing cut–off function \chi_{\varepsilon}:[0, +\infty)\to [0, 1] satisfying the following conditions
where c is a positive real constant independent of \varepsilon . We then define the smooth function \Xi_{\varepsilon}:M\to [0, 1] as
and apply the Divergence Theorem to the smooth vector field \Xi_{\varepsilon}\, Y_{\beta} in E_{s}^{S} . In this way, we get
where U_{\mu} is defined in (4.16). Note that \{\chi_{\varepsilon}\} can always be chosen to be nondecreasing in \varepsilon so that, in turn, \{\Xi_{\varepsilon}\} is nondecreasing. Therefore, applying the Monotone Convergence Theorem, when \varepsilon\to 0^+ , the first term on the right of the second equality tends to
For obtaining the desired statement, we show
First we observe that
where, keeping in mind the properties satisfied by \chi_{\varepsilon} , in the first inequality we have used the nonnegativity of the integrand function and in the last one the Coarea Formula. Note that there exist \varepsilon_{0}, \, c_{1} > 0 such that the inequality
is true a.e. s\in[\frac{1}{2}\varepsilon, \frac{3}{2}\varepsilon] for every 0 < \varepsilon < \frac{2}{3}\varepsilon_{0} , by both Sard's Theorem applied to the smooth function \vert \nabla \varphi \vert^{2}_{g}\, and by Lemma 4.2. Then, we get
where c_{2} > 0 is sufficiently big constant. This implies the limit in (4.19), because \beta > \frac{n-2}{n-1} .
Corollary 4.4. For every S > s > 0 regular values of \varphi there exists r_{s, S}\geq0 such that
Proof. Let \{\beta_{m}\}_{m\in \mathbb{N}} be a sequence such that \beta_{m} > \frac{n-2}{n-1} and \beta_{m}\to\frac{n-2}{n-1} . Due to Proposition 4.3, we have
where the first equality is consequence of the Dominate Converge Theorem keeping in mind that s and S are regular values of \varphi while the inequality follows from Fatou's Lemma. Since \{\beta_{m}\}_{m\in N} is arbitrary, the quantity
is well–defined. Moreover, it is nonnegative as above and therefore we get the statement.
Remark 4.2. For every \beta > \frac{n-2}{n-1} and for every s > 0 regular value of the function \varphi :
For every S big enough, which is a regular value of \varphi , by Lemma 4.5 with (4.6) we have
In particular,
Therefore, the desired identity can be obtained by the Monotone Convergence Theorem, by passing to the limit as S\to+\infty in (4.17).
Remark 4.3. For every \beta > \frac{n-2}{n-1} , as consequence of integral identity (4.17), we have
Since
for every K\subset \mathring{M} compact, by Hölder's Inequality from (4.21) with (4.14) we get that
We need a final lemma before stating the (last and) most important result of this section.
Lemma 4.5. Let (M, g_{0}, u) be a sub-static harmonic triple, and let g and \varphi be the metric and the function defined in (3.4). Then, the following statements hold true.
(i) For every \beta\geq0 and for every S > s > 0 :
(ii) For every \beta\geq0 and for every s > 0 :
(iii) The function \Phi_{\beta}:[0, \infty)\to \mathbb{R} , defined by formula
for every \beta\geq0 , is continuous and admits for every s > 0 the integral representation
This lemma can be proved as [2,Proposition 4.1]. In the Appendix we provide an alternative proof which is self contained and does not make use of any fine property of the measure of \mathrm{Crit}(\varphi) : we just need to know very classical properties of it (see Remark 3.1).
Proposition 4.6. Let (M, g_{0}, u) be a sub-static harmonic triple, let g and \varphi be the metric and the function defined in (3.4), and let \Phi_{\beta}:[0, \infty)\to \mathbb{R} be the function defined by formula (4.24) for every \beta\geq0 . Then for every \beta > \frac{n-2}{n-1} , the function \Phi_{\beta} is continuously differentiable. The derivative \Phi'_{\beta} is nonpositive and admits for every s > 0 the integral representation
Moreover, if there exists s_{0} > 0 such that \Phi'_{\beta}(s_{0}) = 0 for some \beta > \frac{n-2}{n-1} , then (\{\varphi\geq s_{0}\}, g) is isometric to \big([0, +\infty)\times \{\varphi = s_{0}\}, d\rho\otimes d\rho+g_{\{\varphi = s_{0}\}}) , where \rho is the g –distance function to \{\varphi = s_{0}\} and \varphi is an affine function of \rho in \{\varphi\geq s_{0}\} .
The following proof is essentially the same as in [2]. For completeness, we include it here, in a slightly refined version.
Proof. Step 1 : Continuous Differentiability and Monotonicity. Let \beta > \frac{n-2}{n-1} . Note that the boundary \partial M is a regular level set of \varphi and then, by Theorem 2.3 and the relationship between \mathrm{Crit}(u) and \mathrm{Crit}(\varphi) , there exists \epsilon_{0} such that the interval [0, \epsilon_{0}] doesn't contain critical values of the function \varphi . Therefore, for every 0 < \epsilon\leq\epsilon_{0} , applying first the Divergence Theorem to the smooth vector field \vert \nabla \varphi \vert^{\beta}_{g}\, \nabla \varphi in \{0 < \varphi < \epsilon\} and later the Coarea Formula, we get
Being
for every 0\leq s_{1} < s_{2}\leq \epsilon_{0} , by the Dominated Convergence Theorem the function
is continuous and therefore, by the Fundamental Theorem of Calculus \Phi_{\beta} is continuously differentiable on the closed interval [0, \epsilon_{0}] .
Let s_{0} be a regular value of the function \varphi . By Remark 4.3, we can define the function \Psi_{\beta}:(0, +\infty)\to \mathbb{R} by
which satisfies the following properties
(i) for every s > 0 regular value of the function \varphi , we have \Psi_{\beta}(s) = \int\limits_{\{\varphi = s\}} \frac{\vert \nabla \varphi \vert^{\beta}_{g}\, \, \mathrm{H}_{g}}{\sinh\varphi}\, d\sigma_{g} ;
(ii) the function \Psi_{\beta} is continuous on its definition interval (0, +\infty) .
The first statement follows immediately from Proposition 4.3. As for the second statement, we first observe that
for every couple 0 < s < \overline{s} < +\infty . Always by Remark 4.3 and by the Dominated Convergence Theorem, we can deduce the right and the left continuity of \Psi_{\beta} on the interval (0, +\infty) .
We consider \Upsilon_{\beta}:s\in(0, +\infty)\to\frac{\Phi_{\beta}(s)}{\sinh s}\in \mathbb{R}\, . For every (s, \overline{s}) couple of real number such that 0 < s < \overline{s} < +\infty , we have
where the first equality follows from Lemma 4.5 (i) , the second equality from the Coarea Formula keeping in mind (4.22). Moreover, the last equality follows from (i) and from Sard's Theorem. Using the continuity of both the functions \Upsilon_{\beta} and \Psi_{\beta} , passing to the limit in (\star) for either s\to \overline{s} or \overline{s}\to s yields that the function \Upsilon_{\beta} is C^{1} , and
Since \Phi_{\beta}(s) = \sinh(s)\Upsilon_{\beta}(s) for every s > 0 , then \Phi_{\beta}\in C^{1}(0, +\infty) and \Phi'_{\beta}(s) = -\beta\, \sinh(s)\Psi_{\beta}(s) . Moreover, by (4.26), we can see
for every 0 < s < S < +\infty .
Finally the integral representation (4.25) follows in the limit as S\to +\infty of the above identity, by using the Monotone Convergence Theorem, and by the fact that
Step 2 : Outer Rigidity. Let \beta > \frac{n-2}{n-1} and suppose \Phi'_{\beta}(s_{0}) = 0 for some s_{0} > 0 . By (4.25) with (4.14) we deduce that
Consequently \nabla^{2} \varphi\equiv 0 in \{\varphi\geq s_{0}\} being \mu_{g}\big(\mathrm{Crit}(\varphi)\, \big) = 0 , and hence \vert \nabla \varphi \vert_{g}^{2}\equiv a^{2} with a > 0 since \{\varphi\geq s_{0}\} is connected, due to Remark 3.1. Then, \{\varphi\geq s_{0}\} , with the induced Riemanninan metric, is a noncompact, connected and complete Riemannian manifold (being properly embedded in M ), with smooth, compact and totally geodesic boundary, and with \mathrm{Ric}_{g}\geq0 (from the inequality in (3.5)). Applying [18,Theorem C], we can thus deduce that the level set \{\varphi \, = \, s_{0}\} is connected (this is true in general and not only in the rigid case, if s_0\gg0 , as observed in Remark 3.1), and that \{\varphi\geq s_{0}\} is isometric to the product [0, + \infty)\times\{\varphi \, = \, s_{0}\} . Moreover, the isometry from the product [0, + \infty)\times\{\varphi \, = \, s_{0}\} to \{\varphi\geq s_{0}\} is given by the normal exponential map.
Now we want to prove that \varphi is an affine function of \rho on \{\varphi\geq s_{0}\} . First, we remark that every integral curve \gamma_{p} of \nabla \varphi outgoing from a point p of \{\varphi \, = \, s_{0}\} is defined on the interval [0, +\infty) , and it is contained in \{\varphi\geq s_{0}\} , by the completeness and since \vert\nabla \varphi\vert_{g} > 0 . Furthermore, \varphi \circ \gamma_{p}(t) = a^{2}t+s_{0} for every t\in[0, +\infty) , and all the curves \gamma_{p} realize the distance between the hypersurfaces \{\varphi = s_{0}\} and \{\varphi = s_{1}\} with s_{1} > s_{0} . Indeed, for any curve \sigma:[0, l]\to \{\varphi\geq s_{0}\} parametrized by arc–length joining a point of \{\varphi = s_{0}\} to a point of \{\varphi = s_{1}\} we have
where s_{1}, s_{0} and t satisfy s_{1} = a^{2}t+s_{0} . Since \xi = \frac{\, \nabla \varphi }{a} is the unit inner normal vector field of the boundary \{\varphi \, = \, s_{0}\} and we just know that the normal exponential map is a diffeomorphism, \exp^{\bot}(t\xi_{p}) is a point having distance from \{\varphi = s_{0}\} equal to t\, , and therefore
This tell us that \varphi is an affine function of \rho on \{\varphi\geq s_{0}\} .
While the previous proposition contains an outer rigidity result, with the following corollary we provide a global rigidity result.
Corollary 4.7. Let (M, g_{0}, u) be a sub-static harmonic triple, let g and \varphi be the metric and the function defined in (3.4), and let \Phi_{\beta}:[0, \infty)\to \mathbb{R} be the function defined by formula (4.24) for every \beta\geq0 . If \Phi_{\beta} is constant for some \beta > \frac{n-2}{n-1} , then \partial M is connected and (M, g) is isometric to \big([0, +\infty)\times \partial M, d\rho\otimes d\rho+g_{\partial M}) , where \rho is the g –distance function to \partial M and \varphi is an affine function of \rho .
Proof. We obtain immediately that \Phi_{\beta}'(s) = 0 for every s > 0 . Thus, by formula (4.25) with (4.14) we have that
for every s > 0 . In turn, by the Monotone Convergence Theorem, we get
Then, we deduce that
due to Kato Inequality for harmonic functions (4.13) and by (4.10). Consequently \nabla^{2} \varphi\equiv 0 in M . The very same argument of the proof of Outer Rigidity in Proposition 4.6 implies that \partial M is connected and (M, g) is isometric to
where \rho is the g –distance to \partial M and \varphi is an affine function of \rho .
5.
A Black–Hole uniqueness theorem for sub-static manifolds
This section is devoted to the proof of the Black–Hole uniqueness result for a sub–static harmonic triple, Theorem 1.2. We first recall the classical definition of ADM mass, together with an alternative characterization of it.
Let (N, h) and \psi be an asymptotically flat manifold with one end and a chart at infinity of N , respectively. We consider \widetilde{h}: = \psi_{*}h = \widetilde{h}_{ij}dx^{i}\otimes dx^{j} and we set
where \nu_{e} and \sigma_{e} are the \infty –pointing unit normal and the canonical measure on \partial B_{r} as Riemannian submanifold of (\mathbb{R}^{n}\setminus \overline{B}, g_{ \mathbb{R}^{n}}) , respectively, and \nu_{\widetilde{h}} and \sigma_{\widetilde{h}} are the \infty –pointing unit normal and the canonical measure on \partial B_{r} as Riemannian submanifold of (\mathbb{R}^{n}\setminus \overline{B}, \widetilde{h}) , respectively. Also, \mathrm{Ric}_{\widetilde{h}} and \mathrm{R}_{\widetilde{h}} are the Ricci tensor and the scalar curvature of \widetilde{h} respectively, and X is the Euclidean conformal Killing vector field x^{i}\, \frac{\partial }{\partial x^{i}} . The ADM mass is well defined as
and independent of the chosen chart at infinity. Moreover (see [22]), it can be equivalently expressed as
From the alternative definition of ADM mass, given by (5.1), and using the Positive Mass Theorem, more precisely a consequence of it contained in [17,Theorem 1.5], one can prove the following uniqueness statement. For the notation and terminology, we refer the reader to Definition 1.1 and Section 2.
Proof of Theorem 1.2. By condition (1.8) and by the fact that \mathrm{D}_{g_{0}}^{2}u\equiv 0 on \partial M , which in turn implies \mathrm{H}_{\partial M}^{g_{0}}\equiv 0 , we have that the hypothesis of [17,Theorem 1.5] are fulfilled, so that
Now, we want to show that the reverse inequality holds. Let \psi be a chart at infinity of M (according to Definition 1.1) and consider \widetilde{g}_{0} = \psi_{*}{g_{0}} . Recalling that \widetilde{u} stands for u\circ\psi^{-1} , we rewrite characterization (5.1) as
We note first that since \nu_{e} = \frac{x^{i}}{\vert x\vert}\, \frac{\partial }{\partial x^{i}} = \frac{1}{\vert x\vert}\, X and \widetilde{u}\, \mathrm{Ric}_{\widetilde{g}_{0}}-\mathrm{D}_{\widetilde{g}_{0}}^{2}\widetilde{u} \geq 0 from the first equation in (1.1), we have
Secondly, recalling that (\mathrm{D}_{\widetilde{g}_{0}}^{2}\widetilde{u})_{ij} = \partial_{i}\partial_{j}\widetilde{u}-\Gamma_{ij}^{k}\partial_{k}\widetilde{u} , where \Gamma_{ij}^{k} are the Christoffel symbols related to \widetilde{g}_{0} , and using (1.3), (2.12), and the asymptotic expansions of \widetilde{u} , we get
Decay (5.4) coupled with (2.8) (2.10) and (2.11) yields
being p > \frac{n-2}{2} . Thirdly, we observe that
Indeed
and one can show, with similar estimates as before, that the first two terms of this sum tend to 0 for r\to+\infty . It is also easy to see, using (2.5) and (2.11), that
Hence, (5.6) is proven. Gathering (5.2), (5.5), and (5.6), we have finally obtained
We remark that the above inequality is true for any \psi chart at infinity of M . From now on we assume that \psi satisfies condition (1.8) regarding the decay rate of \mathrm{R}_{\widetilde{g}_{0}} at \infty . Since
also using (2.11) we obtain
The fact that m_{\mathrm{ADM}}\leq \mathcal{C} thus follows from (5.7). All in all, the rigidity case m_{\mathrm{ADM}} = \mathcal{C} of [17,Theorem 1.5] holds, which implies that (M, g_{0}) is the Schwarzschild manifold.
Acknowledgments
The authors are members of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA), which is part of the Istituto Nazionale di Alta Matematica (INdAM), and they are partially funded by the GNAMPA project "Aspetti geometrici in teoria del potenziale lineare e nonlineare". F. O. thanks L. Benatti and C. Mantegazza for useful discussions during the preparation of the manuscript.
Conflict of interest
The authors declare no conflict of interest.
A.
Appendix
In this appendix we provide a proof of Lemma 4.5 which is alternative and more self contained than the corresponding in [2]. We underline that we will use Remark 3.1 widely.
Proof of Lemma 4.5 (i). In \mathring{M}\setminus\mathrm{Crit}(\varphi) and for every \beta\geq 0 , we consider the smooth vector field
which is such that
If \{s\leq \varphi\leq S\}\cap \mathrm{Crit}(\varphi) = \emptyset , then the statement is a straightforward application of the Divergence Theorem. Now, suppose that \{s\leq \varphi\leq S\}\cap \mathrm{Crit}(\varphi) \neq\emptyset . Since there always exists \overline{s}\in (s, S) regular value of \varphi , up to splitting the right–hand side of (4.23) into two subintegrals, we can suppose without loss of generality that one among s and S is a regular value of \varphi . To fix the ideas, suppose that S is the regular value. We are going to change the function \varphi in a neighbourhood of the set \mathrm{Crit}(\varphi) . To do this, for every \varepsilon > 0 sufficiently small, applying Sard's Theorem to the smooth function \varphi , we can fix a positive real number \delta(\varepsilon) such that s+\delta(\varepsilon) < S is a regular value of \varphi and \delta(\varepsilon) < d\, \varepsilon , where d > 0 will be specified later. Then, considering a smooth nonincreasing cut–off function \zeta_{\varepsilon}:[0, +\infty)\to [0, 1] satisfying the conditions
where c is a positive real constant independent of \varepsilon , we define
Clearly,
and
Note that s is a regular value for the function \varphi_{\varepsilon} . To see this, let p be a point of \{\varphi_{\varepsilon} = s\} and distinguish the two cases
In the first case, \zeta_{\varepsilon}(\vert \nabla \varphi\vert^{2}_{g})\equiv 1 so that s = \varphi_{\varepsilon}(p) = \varphi(p)-\delta(\varepsilon) and \nabla \varphi_{\varepsilon}(p) = \nabla \varphi(p) . Since s+\delta(\varepsilon) is a regular value for \varphi , \nabla \varphi_{\varepsilon}(p)\neq 0 . In the second case, observing that s\leq\varphi(p)\leq s+\delta(\varepsilon) and therefore p\in\{s\leq \varphi\leq S\} , we have from (A.2) that in p
where c is the constant appearing in (A.1). Now, observe that \max\limits_{\{s\leq \varphi\leq S\}}\big\vert\nabla\vert \nabla \varphi \vert_{g}\, \big\vert_{g}\, > 0 , since otherwise, due to the presence of critical points in \{s\leq \varphi\leq S\} , there should be a connected component of \{s\leq \varphi\leq S\} where \nabla \varphi\equiv0 . But this is impossible because \{s\leq \varphi\leq S\} = \overline{\{s < \varphi < S\}} (by Remark 2.1) and by the size of \mathrm{Crit}(\varphi) . Hence, choosing
from above we obtain \vert\nabla \varphi_{\varepsilon}\vert_{g}(p)\geq \frac{\vert\nabla \varphi\vert_{g}}{2}(p) . In particular, from (\bigstar) we get that \vert\nabla \varphi_{\varepsilon}\vert_{g}(p) > \frac{\varepsilon}{4} .
Now, we apply the Divergence Theorem to the smooth vector field \Xi_{4\varepsilon} X_{\beta} on \{s < \varphi_{\varepsilon} < S\} , where
Recalling that U_{\mu} is defined as in (4.16), we obtain
Note that \{\varphi = S\} is compactly contained in \{\vert \nabla \varphi\vert^{2}_{g} > \frac{3}{2}\, \varepsilon\} for every \varepsilon sufficiently small, and \Xi_{4\varepsilon}\equiv0 in \{\vert \nabla \varphi\vert^{2}_{g}\leq2\, \varepsilon\}\supset \{\vert \nabla \varphi\vert^{2}_{g}\leq\frac{3}{2}\, \varepsilon\} . Then, by (A.3) we get
Looking at the left–hand side of (A.4), note that
where in the second inequality we have used Lemma 4.1 and the fact that U_{\varepsilon} is contained in a compact set for every \varepsilon < < 1 (which is a consequence of (4.6)). Moreover, by the Dominated Convergence Theorem, we have that
Finally, note that \{\zeta_{\varepsilon}\} can always be chosen to be nonincreasing in \varepsilon so that, in turn, \{\Xi_{\varepsilon}\} in nondecreasing. Therefore, looking at the left–hand side of (A.4), we have that
by the Monotone Convergence Theorem. All in all, passing to the limit as \varepsilon\to 0^+ in (A.4), yields the desired identity.
Proof of Lemma 4.5 (ii). Lemma 4.1 implies
Note that
because its absolute value belongs to L^{1}_{\rm{loc}}\big(\{\varphi\geq s\}, \mu_{g}\big) immediately and to L^{1}\big(\{\varphi\geq S\}, \mu_{g}\big) for S sufficiently big, applying the Coarea Formula coupled with (4.6) and Lemma 4.5. Therefore, passing to the limit as S\to +\infty in (4.23) and using the Dominated Convergence Theorem gives the desired identity.
Proof of Lemma 4.5 (iii). Let \beta\geq0 . We are assuming that the boundary \partial M is a regular level set of \varphi so that there exists \epsilon > 0 such that [0, \epsilon]\cap\mathrm{Crit}(\varphi) = \emptyset . Therefore, applying the Divergence Theorem to the smooth vector field \vert \nabla \varphi \vert^{\beta}_{g}\, \nabla \varphi in \{0 < \varphi < \epsilon\} yields
In turn, the absolute continuity of the integral implies the continuity of \Phi_{\beta} at 0 . By point (i) and again by the absolute continuity of the integral, we obtain the right and the left continuity of the function
Hence, \Phi_{\beta} is continuous also in (0, +\infty) . The integral representation of \Phi_{\beta} follows directly from point (ii) .









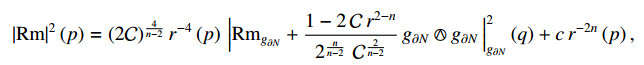
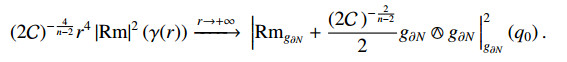
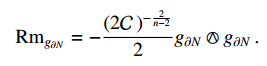




 DownLoad:
DownLoad: