Contactless temperature and distance measuring device: A low-cost, novel infrared ―based "Badge"-shaped structural model for measuring physical distance and body temperature

1.   Introduction

As we all know, the membership grades of type-1 fuzzy sets (T1 FSs) are crisp numbers as 0 or 1, therefore, the membership functions (MFs) of T1 FSs are not inherently uncertain and they can only measure uncertainties in a limited scope. The membership grades of interval type-2 fuzzy sets (IT2 FSs) are intervals, so the IT2 FSs are capable of better model uncertainties ^[1,2]. In the past decades, great progresses have been made transiting from type-1 fuzzy logic systems (T1 FLSs) to interval type-2 fuzzy logic systems (IT2 FLSs). IT2 FLSs based on IT2 FSs can approximate real continuous functions defined on compact sets with arbitrary accuracy. Furthermore, IT2 FLSs have been successfully applied in many fields with uncertainty, nonlinearity and time-varying characteristics like autonomous mobile robots ^[3,4], intelligent controllers ^[5], financial systems ^[6], power systems ^[7,8], permanent magnetic drive ^[9,10,11], edge detection ^[12], medical systems ^[13] and hot strip mill ^[14,15] and so on.

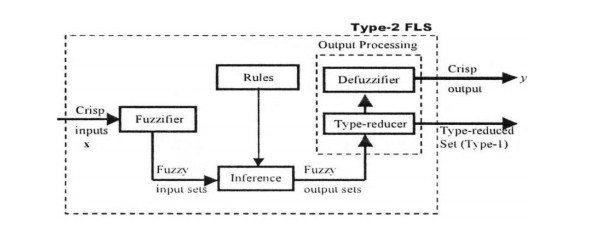
Generally speaking, IT2 FLSs (see Figure 1) are composed of fuzzifier, rules, inference ^[16], type-reducer and defuzzifier. Among which, the block of type-reduction (TR) under the guidance of inference plays the central role, and its main function is to transform the IT2 FS to the T1 FS. Then the defuzzification changes the T1 FS to the crisp output. The operations in TR are the differences between T1 and IT2 FLSs, which makes the latter with more challenges.

Currently, the computationally intensive iterative Karnik-Mendel (KM) algorithms and enhanced Karnik-Mendel (EKM) algorithms ^[18,19,20] are the most popular approaches for performing the TR. These two types of algorithms have the advantages of preserving the uncertainties flow in the systems and converge in super-convergence speed. However, the initializations of KM and EKM algorithms are usually given by trial and error of extensive simulation experiments. This paper analyzes the initializations ^[21] of KM and EKM algorithms, and provides reasonable initialization EKM (RIEKM) algorithms for performing the centroid TR and defuzzification of IT2 FLSs. According the accurate benchmark CNT algorithms ^[22], the proposed RIEKM algorithms have smaller absolute errors and faster convergence speeds compared with the EKM algorithms.

The rest of this paper is organized as follows. Section 2 gives the background of IT2 FLSs. Section 3 provides the RIEKM algorithms, and how to adopt them to perform the centroid TR of IT2 FLSs. In Section 4, four computer simulation experiments are used to illustrate and analyze the performances of RIEKM algorithms. Finally the conclusions and expectations are given in Section 5.

2.   IT2 FLSs

The rules uncertainties of IT2 FLSs generate from numerical or language uncertainties in knowledge, while these uncertainties can be solved by T2 FSs. In fact, the concept of T2 FSs can be viewed as the extension of concept of T1 FSs.

Definition 1. A T2 FS $\tilde A$ can be characterized by its T2 MF ${\mu _{\tilde A}}(x, u)$, i.e.,

in which the primary variable $x \in X$, and the secondary variable $u \in [0, 1]$, here equation (1) is usually referred to as the point-value expression, and whose compact form is as:

Definition 2. A vertical slice of ${\mu _{\tilde A}}(x, u)$ is the secondary MF, i.e.,

Definition 3. The two dimensional support of ${\mu _{\tilde A}}(x, u)$ is called as the footprint of uncertainty (FOU), i.e.,

here the upper and lower bounds of ${\rm{FOU}}(\tilde A)$ are referred to as the upper MF (UMF) and lower MF (LMF), respectively, i.e.,

For any IT2 FSs, they can be completely characterized by their UMFs and LMFs. That’s because the secondary membership grades of IT2 FSs must be equal to 1, i.e., ${f_x}(u) \equiv 1$.

From the aspect of inference structure, IT2 FLSs can be divided into Mamdani type ^[7,11,14] and Takagi-Sugeno-Kang (TSK) type ^[10,15]. Without loss of generality, consider a Mamdani IT2 FLS with $p$ inputs ${x_1} \in {X_1}, {x_2} \in {X_2}, \cdots, {x_p} \in {X_p}$ and one output $y \in Y$, there are a total of $M$ fuzzy rules, where the $lth$ rule is of the form:

In order to simplify the expressions, we model the input measurements as crisp sets, i.e., singleton fuzzifier is adopted. Then the process of fuzzy reasoning ^[7,16,23] is given as follows:

The fuzzy relation of each fuzzy rule is as:

whose MF is as:

where the sign $\cap$ is the product or minimum t-norm ^[24].

The T2 output of each fuzzy rule is ${\tilde B^l} = {A_x} \circ {\tilde R^l}$, and whose MF is as:

in which $\circ$ is the composition operation, and $\cup$ is the maximum t-norm. ${F^l}(x')$ is the defined firing interval, i.e.,

Here the most popular centroid TR approach ^[21] is selected, i.e., the output IT2 FS ${\tilde B^l}$ of each rule (which generates by merging each fuzzy rule and its corresponding consequent IT2 FS) is described as:

where $*$ denotes the product or minimum t-norm.

Then agammaegating all the firing rule IT2 FS ${\tilde B^l}$ to obtain the final output $\tilde B$, i.e.,

where $\vee$ represents the maximum operation. Then the type-reduced set ${Y_C}$ can be obtained by computing the centroid ${C_{\tilde B}}$ of $\tilde B$, i.e.,

where ${l_{\tilde B}}$ and ${r_{\tilde B}}$ can be computed by KM types of algorithms as:

where $N$ is the number of sampling of primary variable $y$, and $k$ is the switch point.

Finally the crisp output is computed by taking the arithmetic average of ${l_{\tilde B}}$ and ${r_{\tilde B}}$, i.e.,

3.   RIEKM algorithms

First of all, we derive the theoretical interpretations of initialization of KM and EKM algorithms. Let $a = {y_1} < {y_2} < \cdots < {y_N} = b$, then the continuous KM and EKM algorithms compute as (see Eqs (14) and (15)):

In addition, the specific computation steps of CKM and CEKM algorithms are given in Tables 1 and 2. According to the notations ${F_l}$ in (17) and ${F_r}$ in (18), from Steps 2 and 4 in Table 1, we can find:

When iterations terminate, ${l_{\tilde B}} = {\xi _l}$ and ${r_{\tilde B}} = {\xi _r}$, therefore

here ${l_{\tilde B}}$ and ${r_{\tilde B}}$ are the fixed points of ${F_l}(\xi)$ and ${F_r}(\xi)$, respectively. In like manner, the relations of (21) still hold for the CEKM algorithms as in Table 2.

In order to set the initialization of the algorithms, let ${\underline \mu _{\tilde B}}(y) = {\overline \mu _{\tilde B}}(y) = \theta (y)$ for all $y \in [a, b]$, then $\theta (y) = [{\underline \mu _{\tilde B}}(y) + {\overline \mu _{\tilde B}}(y)]/2$. In this case, Eqs (17) and (18) become the same, so that,

Equation (22) is the initialization approach of CKM algorithms given in Table 1, denoted here as ${\xi ^{(1)}}$, i.e.,

in which $\theta (y) = [{\underline \mu _{\tilde B}}(y) + {\overline \mu _{\tilde B}}(y)]/2$.

The specific computation steps of discrete KM and EKM algorithms are provided in Tables 3 and 4. And the discrete form of ${\xi ^{(1)}}$ is established in Steps 1 and 2 in Table 3, i.e.,

this KM initialization approach can provide excellent results as ${\underline \mu _{\tilde B}}(y)$ and ${\overline \mu _{\tilde B}}(y)$ are very close to each other, that’s because it becomes the exact optimal solution of (14) or (15) when ${\underline \mu _{\tilde B}}(y) = {\overline \mu _{\tilde B}}(y)$.

For the EKM algorithms, the initialization approach is based on the difference between ${\underline \mu _{\tilde B}}(y)$ and ${\overline \mu _{\tilde B}}(y)$. Let’s make an assumption that

Attention that $\rho \geqslant 1$, because ${\overline \mu _{\tilde B}}(y) \geqslant {\underline \mu _{\tilde B}}(y)$ for all $y \in [a, b]$.

In order to initialize the EKM algorithms, suppose that both ${\underline \mu _{\tilde B}}(y)$ and ${\overline \mu _{\tilde B}}(y)$ be constants for $y \in [a, b]$, i.e., ${\underline \mu _{\tilde B}}(y) = n > 0$, and ${\overline \mu _{\tilde B}}(y) = \rho n > 0$, according to Eq (14), so that

Then find the derivative of ${F_l}(\xi)$, so that

Setting ${F'_l}(\xi) = 0$, therefore

Solving Eq (28) for $\xi$, we can obtain

For the Eq (27), ${\xi _l}$ is the minimum value of ${F_l}(\xi)$. Because ${F'_l}(\xi) < 0$ for $\xi \in [a, {\xi _l})$, and ${F'_l}(\xi) > 0$ for $\xi \in ({\xi _l}, b]$. Therefore, ${l_{\tilde B}} = {F_l}({\xi _l}) = {\xi _l}$.

In like manners, it can be obtained:

Therefore,

Setting ${F'_r}(\xi) = 0$, it follows that:

Solving Eq (30) for $\xi$, we can obtain

For the Eq (30), ${\xi _r}$ is the maximum value of ${F_r}(\xi)$. Because ${F'_r}(\xi) > 0$ for $\xi \in [a, {\xi _r})$, and ${F'_r}(\xi) < 0$ for $\xi \in ({\xi _r}, b]$. Therefore, ${r_{\tilde B}} = {F_r}({\xi _r}) = {\xi _r}$. Considering the Eqs (29) and (33) together, the new initialization approach for $\xi$ can be denoted as ${\xi ^{(2)}}$, i.e.,

Here $\rho \geqslant 1$, therefore, ${\xi ^{(2)}} \leqslant a + \frac{1}{2}(b - a)$ for ${l_{\tilde B}}$, and ${\xi ^{(2)}} \geqslant a + \frac{1}{2}(b - a)$ for ${r_{\tilde B}}$.

Comparing the initializations of EKM algorithms in Table 4 and CEKM algorithms in Table 2, the discrete form of Eq (34) can be as:

where $N$ denotes the number of sampling of primary variable, and this $\rho = [\sum\limits_{i = 1}^N {{{\overline \mu }_{\tilde B}}(y)}]/[\sum\limits_{i = 1}^N {{{\underline \mu }_{\tilde B}}(y)}].$

Interestingly, when $\rho = 2$, it can be obtained that$1 + \sqrt \rho = 1 + \sqrt 2 \approx 2.4$, and $1 + \sqrt {1/\rho } = 1 + \sqrt {1/2} \approx 1.7$, therefore, the equation (35) becomes:

Equation (36) is just the initialization approach of EKM algorithms, which generates from empirical extensive simulation experiments. For the proposed reasonable initialization EKM (RIEKM) algorithms, we should determine each specific $\rho$ for the corresponding simulations. Finally the specific computation steps of discrete RIEKM algorithms are provided in Table 5.

4.   Simulation experiments

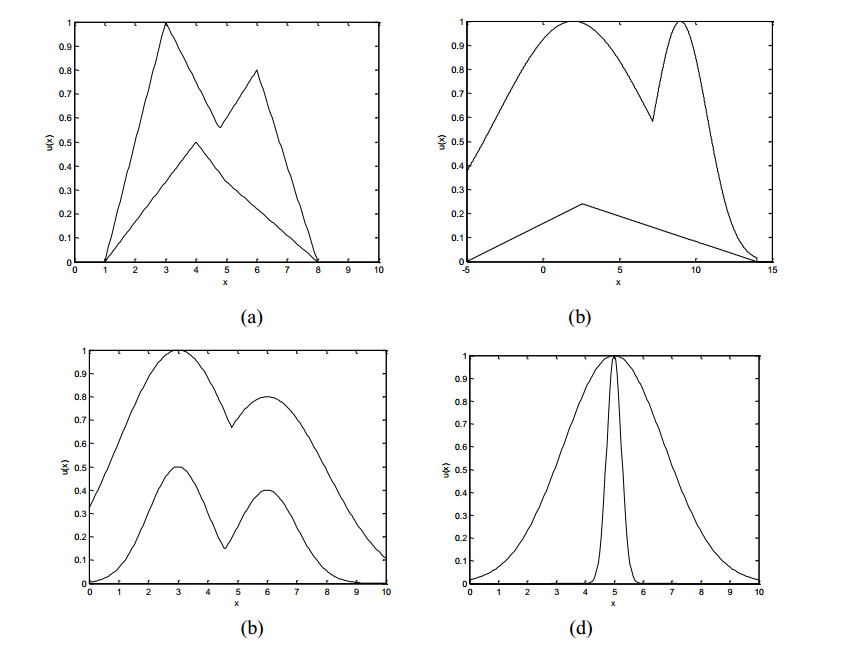
Four computer simulation examples are provided in this section to illustrate the performances RIEKM algorithms. Before performing the centroid TR, suppose that the FOU of centroid output IT2 FS be known by weighting and agammaegating all the fuzzy rules under the guidance of inference. Here the primary variable of centroid output IT2 FS is denoted by the letter $x$, $x$ is uniformly sampled, and the number of sampling is chosen as $N = 50:50:9000$.

In the first example, the FOU is bounded by the piecewise linear functions ^{[21,22,23,25,26]}. In the second example, the FOU is bounded by both the Gaussian functions and piecewise linear functions ^{[20,21,22,27,28,29,30,31]}. In the third example, the FOU is bounded by the Gaussian functions ^{[21,22,23,25,26]}. In the last example, the FOU is a Gaussian IT2 MF with uncertainty standard deviation ^{[20,21,22,27,28,29,30,31]}. Then the Figure 2 and Table 6 provide the defined FOUs for four examples.

In examples 1, 2 and 4, let the primary variable $x \in [0, {\rm{ }}10]$. In addition, let the primary variable $x \in [- 5, {\rm{ }}14]$in example 2. The accurate continuous Nie-Tan (CNT) algorithms ^[22,25] compute the centroid output of IT2 FS $\tilde A$ as:

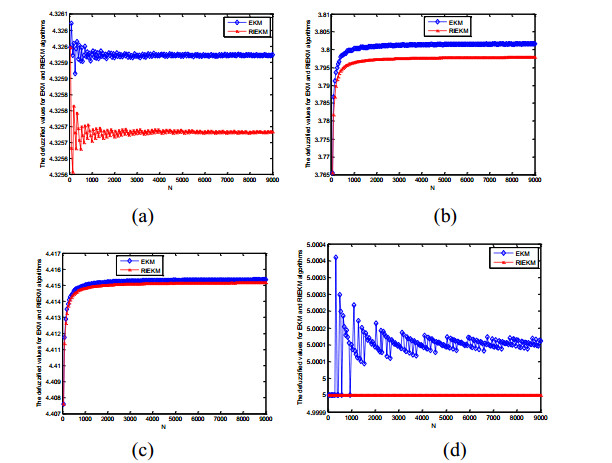
Therefore, the CNT algorithms are firstly considered as the benchmark to compute the defuzzified values for four examples as: $y_1^ * = 4.320794$, $y_2^ * = 3.714087$, $y_3^ * = 4.395260$, and $y_4^ * = 4.999999$. Then graphs of defuzzified values computed by two types of discrete EKM algorithms are shown in Figure 3.

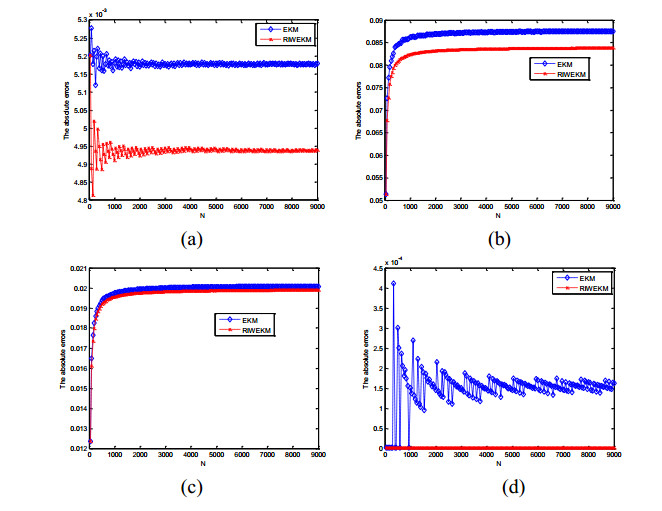
Furthermore, the absolute errors between the benchmark CNT algorithms and two types of discrete EKM algorithms are provided in Figure 4.

In order to further measure the performances of two types of algorithms, here we define the absolute errors sum $\sum\limits_{i = 1}^{180} {|y_{CN{T_i}}^ * - {y_{EK{M_i}(RIEK{M_i})}}|}$ of defuzzified values for four examples, and they are shown in Table 7, in which the last column denotes the total average of absolute errors sum for the EKM algorithms and RIEKM algorithms.

Observing from the Figures 3, 4 and the Table 7, the following conclusions can be made:

1) As the number of sampling increases, these two types of discrete EKM algorithms all converge to certain values. The absolute errors of RIEKM algorithms are always less than the EKM algorithms in these four examples (as the red error curves of RIEKM algorithms are under the corresponding blue error curves of EKM algorithms).

2) In example 1, the RIEKM algorithms can obtain the result that is closed to the benchmark value with the number of sampling of 150. In other three examples, the RIEKM algorithms can almost get the optimal value just at the number of sampling of 50 (starting number of sampling).

3) As $N = 50:50:9000$, the RIEKM algorithms can obtain smaller absolute errors sum than the EKM algorithms in all four examples. In addition, the total average absolute errors sum of RIEKM algorithms is less than the EKM algorithms.

4) According to the items one to three, it is evidence that the proposed RIEKM algorithms can obtain better calculation accuracy than the EKM algorithms.

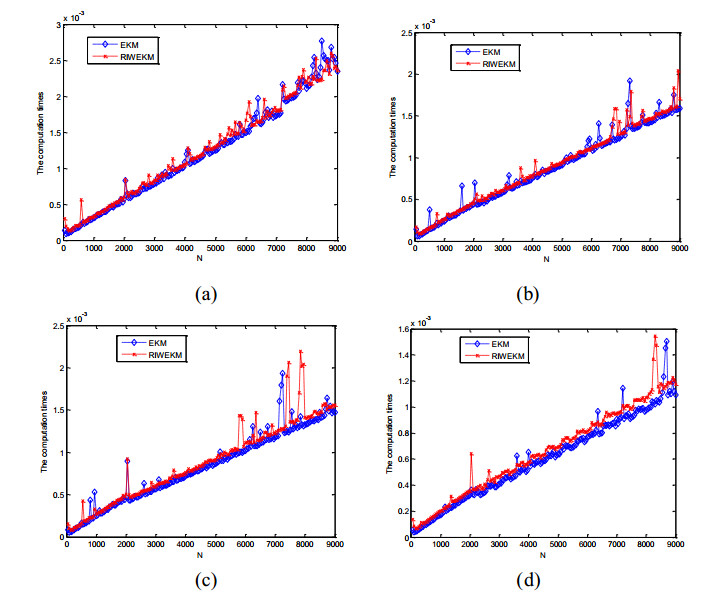
For the sake of applying these algorithms, next we study the specific unrepeatable computation times that depend on the hardware and software environments. Here the computer simulation platform is a dual CPU desktop with the Microsoft Windows XP operating system, E5300@2.6GHz and 2.00GB memory. All the programs are performed by the Matlab 2013a. Then Figure 5 gives the computation times for four examples, and the unit of time is the second (s).

For the sake of applying these algorithms, next we study the specific unrepeatable computation times that depend on the hardware and software environments. Here the computer simulation platform is a dual CPU desktop with the Microsoft Windows XP operating system, E5300@2.6GHz and 2.00GB memory. All the programs are performed by the Matlab 2013a. Then Figure 5 gives the computation times for four examples, and the unit of time is the second (s).

As shown in Figure 5, except for some fluctuations, the computation times of two types of discrete EKM algorithms emerge linear variation. In most number of sampling, the computation times of EKM algorithms are slightly better than the RIEKM algorithms. In other words, the convergence speeds of RIEKM algorithms are faster than the EKM algorithms in general. When the number of sampling is fixed, the computation times of two types of EKM algorithms are as: RIEKM > EKM for all four examples. This may because the initialization of RIEKM algorithms is more complex than the simple EKM algorithms.

Here we should point out that the paper focuses on the theoretical performances of RIEKM algorithms compared with the EKM algorithms. Four computer simulation examples show the advantages of RIEKM algorithms on high computation accuracy requirement. However, if the requirement of calculation accuracy is not very high, the simple EKM algorithms will complete with slightly faster computation speeds.

5.   Conclusions

This paper gives the fuzzy reasoning process of IT2 FLSs, and discusses the initializations of EKM algorithms. And the reasonable initialization EKM (RIEKM) algorithms are provided to perform the centroid TR and defuzzification of IT2 FLSs. For computing the defuzzified values of IT2 FLSs, the proposed RIEKM algorithms can obtain better absolute errors and faster convergence speeds than the EKM algorithms.

Many interesting works still lie ahead, including extending and weighting the RIEKM algorithms to perform the centroid TR ^{[17,27,28,31,32,40,41,42,43,44,49,50]} of general type-2 fuzzy logic systems, and studying the center-of-sets TR of T2 FLSs ^[33], and the relations between discrete and continuous TR algorithms ^{[18,21,28,29,30]}. Future studies will also be focused on designing and applying IT2 or GT2 FLSs based on intelligent optimization algorithms ^{[3,7,8,9,10,11,12,34,35,36,37,38,39,45,46,47,48,53]} for forecasting, control ^[51,52] and identification.

Acknowledgments

The paper is sponsored by the National Natural Science Foundation of China (No. 61973146, No. 61773188, No. 61903167, No. 61803189), the Liaoning Province Natural Science Foundation Guidance Project (No. 20180550056), and Talent Fund Project of Liaoning University of Technology (No. xr2020002). The author is very grateful for professor Jerry Mendel, who has given the author some valuable suggestions.

Conflict of interest

The authors declare that they have no conflict of interest.