Sustainability and innovation in 3D printing: Outlook and trends

1.   Introduction

Oscillation is a phenomenon found in various situations and in different areas, and is therefore a phenomenon of fundamental importance in the sciences. The study of the harmonic oscillator problem with damping is a paradigm in the study of oscillations and one of the most important examples of applications of differential equations. In engineering, oscillations play such a central role that, if on the one hand their study is important because we are interested in avoiding them as in excessive vibrations in structures, on the other hand we are sometimes interested in inducing them very precisely, as for example in the use of forced oscillations for the rheological characterization of materials. The investigation of possible generalizations of the mathematical description of damped oscillations is consequently a problem of practical and theoretical interest.

Fractional calculus ^[1,2,3,4] is a branch of mathematical analysis that has been shown to be very useful in the study of generalizations of differential equations, the so called fractional differential equations ^[5,6,7]. Accordingly it is not a surprise that some authors ^{[8,9,10,11,12,13,14,15]} studied generalizations of the damped harmonic oscillator equation using the concept of fractional derivative. In ^[16] the different approaches to fractional generalizations of the damped harmonic oscillator equation have been classified into three classes. Class Ⅰ contains models for which a fractional derivative of order $\alpha$ ($1 < \alpha \leq 2$) appears in the inertial term $m d^\alpha x(t)/dt^\alpha$, like in ^[8,9,10,11]; class Ⅱ contains models for which a fractional derivative of order $\beta$ ($0 < \beta \leq 1$) appears in the damping term $\gamma d^\beta x(t)/dt^\beta$, like in ^[12,13]; and class Ⅲ includes models for which a fractional derivative appears both in the mass term and in the damping term, like in ^[14,15]. Closed form solutions for fractional oscillator models in class Ⅰ are well-known, but not in class Ⅱ and Ⅲ. A closed from solution of a model in class Ⅲ have been provided recently in ^[14] for the case when $\alpha = 2\beta$, where $\alpha$ and $\beta$ are the order of the fractional derivatives of the mass and damping terms, respectively.

In this paper we will study a model in class Ⅱ called fractional Kelvin-Voigt oscillator ^[17,18]. A subject where the Kelvin-Voigt oscillator is a relevant model is viscoelasticity ^[19,20]. The basic model for the study of viscoelasticity consists of the combination of a spring and a dashpot; if this combination is made in series it is called Maxwell model, and if it is done in parallel, it is called Kelvin-Voigt model. Based on molecular theories for the description of viscoelastic materials, in ^[21,22] Bagley and Torvik established the basis for the use of fractional calculus in describing the behaviour of viscoelastic damping ^[23,24]. An element with constitutive law described by a fractional derivative of order $\alpha \in (0, 1)$ is placed between the behaviour of a spring and a dashpot, being called therefore a springpot ^[24]. A fractional Kelvin-Voigt oscillator is an oscillator model where the dashpot is replaced by a springpot in parallel with the spring. In our opinion, this is the most orthodox choice of all when compared with the classical model of an harmonic oscillator with damping; indeed there is a term associated with Hooke's law and another term corresponding to the usual definitions of momentum and mass, and the change is made only in the form of the damping term. However, to the best of our knowledge, this is the less studied type of model, and we believe that this is due to the mathematical difficulties in expressing its solution, as the functions necessary in the problem are the least known compared to those of the other classes. Indeed typical models in class Ⅰ and Ⅲ have solutions that can be expressed in terms of Mittag-Leffler functions of one and two parameters, while the case we will study requires a generalization of these functions called multivariate Mittag-Leffler functions (see Section 3).

We organized this paper as follows. In Section 2 we introduce the concept of Caputo fractional derivative and use it to write the damping force term in our fractional differential equation. There are some different definitions of fractional derivative ^[25,26], and the Caputo one is particularly suitable for initial value problems. In Section 3 we recall the definition of the Mittag-Leffler functions with one and two parameters and discuss the lesser-known multivariate Mittag-Leffler function, and some of its properties. In Section 4 we provided the solution of the initial value problem for our fractional damped oscillator in terms of the bivariate Mittag-Leffler function and explore some of its properties. In Section 5 we consider some specific examples of our fractional oscillator and compare them with the classical damped harmonic oscillator. In the Appendix we prove some results used throughout the text, the proof of which has technical details whose discussion we believe would not be necessary in a first reading.

2.   The Caputo fractional derivative and fractional viscoelastic friction

The Caputo fractional derivative (also called Caputo-Dzhrbashyan fractional derivative) of order $\alpha$, with $(n-1) < \alpha < n$ ($n \in \mathbb{N}$), is defined as ^[27]

where $f^{(n)}$ denotes the derivative of order $n$ of $f(t)$ and $\Gamma(\cdot)$ is the gamma function. The Caputo derivative has two very interesting properties for its use in differential equations. One property is the fact that $D^\alpha_t[1] = 0$, unlike other definitions as Riemann-Liouville's one, for which the $\sideset{_\rm{RL}^{}}{_t^{\alpha}}{\operatorname{\mathit D}} [1] = t^{-\alpha}/\Gamma(1-\alpha)$ for $0 < \alpha < 1$. The other property is related to the fact that its Laplace transform involves only the initial values of derivatives of integer orders of the original function, that is,

where $F(s) = \mathcal{L}[f(t)](s)$. One important characteristic of Caputo fractional derivative is the presence of the initial value of integer order derivatives $f^{(n-k-1)}(0)$ in the right hand side of Eq (2.2), unlike, for example, in the Riemann-Liouville definition ^[25,26].

Among the differential equations where the Caputo derivative finds interesting applications, as for example the relaxation equation (see ^[27] and references therein), we are interested in the harmonic oscillator equation. As commented in the Introduction, our approach is conservative, with the difference in relation to the classic expression for the damped harmonic oscillator given only by a modification in the damping term. Our fractional oscillator equation is

where $0 < \alpha \leq 1$, with initial conditions

and $f(t)$ is an external force. The damping force is therefore $2 m \gamma D^\alpha_t [x(t)]$. For $\alpha = 1$ we have the usual damping term $2 m \gamma x^\prime(t)$. The model based on Eq (2.3) is the fractional Kelvin-Voigt oscillator ^[17].

Although Eq (2.3) seems to be a simple modification of the classical damped harmonic oscillator equation, its solution is more obscure than the ones for other apparently more difficult equations, like for example

whose solution can be expressed in terms of Mittag-Leffler functions of two parameters. In fact, our equation is as difficult as

with $\beta \neq 2 \alpha$, but we will keep our attention in Eq (2.3) because a fractional inertial term lacks a natural interpretation in our opinion.

3.   The Mittag-Leffler function and some of its generalizations

The Mittag-Leffler function is a generalization of the exponential function, and is discussed, for example, in ^[28,29], as well as some of its generalizations. Let us recall the main definitions and results.

The Mittag-Leffler function $E_{a}(z)$ is defined as

where $\Gamma(\cdot)$ is the gamma function. This series converges for all values in the complex plane provided $\operatorname{Re}a > 0$. A very useful result is the Laplace transform of $E_a(-\sigma t^a)$, which can be easily calculated from its definition, that is,

The two-parametric Mittag-Leffler function $E_{a, b}(z)$ is defined as

for $\operatorname{Re}a > 0$ and $b \in \mathbb{C}$. The Laplace transforms involving $E_{a, b}(z)$ is ^[28]

Another generalization of the Mittag-Leffler function is the multivariate Mittag-Leffler function $E_{(a_1, \ldots, a_n)}(z)$, defined as ^[29]

From this definition we see that

for any $i$ and $j$, and

When two indexes are equal, a $n$-variate Mittag-Leffler function reduces to a $(n-1)$-variate one; in fact, considering, without loss of generality, that $a_{n-1} = a_n = a$, we have (see Appendix)

We have a special interest in the particular case $z_i = -A_i t^{a_i}$ ($i = 1, 2, \ldots, n$) since in this case we can define a one variable function $E_{(a_1, \ldots, a_n), b} (-A_1 t^{a_1}, \ldots, -A_n t^{a_n})$ with the Laplace transform

whose proof is given in the Appendix. This is a fundamental result for the application of the multivariant Mittag-Leffler functions in the study of fractional differential equations. A comparison with Section 5.6 of ^[5] clearly indicates that the function $E_{(a_1, \ldots, a_n), b} (-A_1 t^{a_1}, \ldots, -A_n t^{a_n})$ can be expressed in terms of a series involving three-parameter Mittag-Leffler functions ^[28].

The bivariate Mittag-Leffler function, that is,

plays a major role in this work. We see in Eq (3.9) that for $z_1 = -A_1 t^{a_1}$ and $z_2 = -A_2 t^{a_2}$ we have the Laplace transform

A particularly important case is the one where $a_2 = 2 a_1$. Let us denote in this case $a_1 = a$, and consider the function

In the Appendix we prove that

or, equivalently,

where

4.   Analytical solution of the harmonic oscillator with fractional viscoelastic friction

Our objetive is to find the analytical solution of the initial value problem given by the fractional differential equation (2.3) with the initial conditions given by Eq (2.4), that is,

where $0 < \alpha \leq 1$ and $f(t)$ is an external force. Using the Laplace transform and denoting $X(s) = \mathcal{L}[x(t)](s)$, the transformed equation gives

where $F(s) = \mathcal{L}[f(t)](s)$. The solution $x(t)$ of the problem is therefore

with $t > 0$ and where we denoted

for $\beta = \{\alpha - 1, 0, 1\}$ and $\ast$ denotes the convolution product.

We can see from Eq (3.11) that the inverse Laplace transform in Eq (4.5) can be expressed in terms of the bivariate Mittag-Leffler function. Comparing Eqs (4.5) and (3.11), we see that, with the identifications

we have

In eq.(4.4) we have the terms $G_{\alpha, 0}$ and $G_{\alpha, 1}(t) + 2\gamma G_{\alpha, \alpha-1}(t)$. The first one is

The term $G_{\alpha, 1}(t) + 2\gamma G_{\alpha, \alpha-1}(t)$ in Eq (4.4) can be simplified using the identity

which is the generalization of Eq (B.12) for $E_{a, b}(z)$ (see Appendix), and whose proof follows directly from the definition of $E_{(a_1, a_2), b}(z_1, z_2)$. Using this identity and Eq (4.7), we obtain

Consequently, we have

or

The solution of Eq (2.3) is given by Eq (4.4) with $G_{\alpha, 0}(t)$ and $G_{\alpha, 1}(t) + 2\gamma G_{\alpha, \alpha-1}(t)$ given by Eq (4.8) and Eq (4.11), respectively.

Properties of the derivative of $\boldsymbol{G_{\alpha, \beta}(t)}$. There is one interesting property involving the derivative of $G_{\alpha, \beta}(t)$, which follow directly from its definition, namely

The cases $\beta = \{1, 2, 3, \ldots\}$ can be handled using Eq (4.10). We must remember, however, that in Eq (4.4) we are considering $t > 0$. It may be appropriate in this case to work with the Heaviside step function $H(t)$, and then we can deal with the term $t^{1-\beta}/\Gamma(2-\beta)$ in Eq (4.10) using the definition of the Gelfand-Shilov distribution $\mathcal{G}_\nu(t)$ ^[33,34]

for which we have

and

However, since we are interested in $t > 0$, we can work with derivatives of functions instead of derivative of functions; in other words, we will simply write, for example, the derivative $1^\prime = 0$ instead of considering the derivative $H^\prime(t) = \delta(t)$ when calculating the derivative in Eq (4.10) for $\beta = 1$, and analogously for $\beta = \{2, 3, \ldots\}$.

Using $\beta = 1$ in Eq (4.10) it follows that

For the cases $\beta = \{2, 3, \ldots\}$, we use, for $\beta = 2$,

and then

For $\beta = \{3, 4, \ldots\}$ the calculation is analogous.

Equation (4.13) can be generalized, for $\beta < 1$ and $0 < \mu \leq 1$, as

which follows using the definition of $G_{\alpha, \beta}(t)$ and $D^\mu t^\nu = (\Gamma(\nu+1)/\Gamma(\nu-\mu+1)) t^{\nu-\mu}$ with $\nu > 0$ and $D^\mu 1 = 0$.

The velocity of the oscillator can be easily calculated using the above properties of the time derivative of $G_{\alpha, \beta}(t)$. From Eqs (4.4) and (4.13) we obtain

Moreover, since our fractional oscillator model has the same inertial term of the classical one, the momentum $p$ is $mv$, where $v = v(t)$ is given by Eq (4.21).

Examples of responses to external forces. For the simple case of an impulsive external force $f(t) = f_0 \delta(t)$, we have

where the response function $G_{\alpha, 0}(t)$ is the Laplace transform of $H(s)$,

Let us also consider sinusoidal external forces. For an external force $f(t)$ of the form

the convolution $f\ast G_{\alpha, 0} = f_0 \cos{\omega t} \ast G_{\alpha, 0}(t)$ can be written as

Comparing the above expression with Eq (3.9), we can conclude that

The case of an external force of the form

is completely analogous, and the result is

Therefore, the response to an arbitrary sinusoidal force is given in terms of a combination of 4-variate Mittag-Leffler functions.

4.1.   The particular case ${\alpha = 1}$

The case $\alpha = 1$ corresponds to the usual harmonic oscillator with frictional force $-2\gamma dx/dt$. This corresponds to $\alpha = 1$ in Eq (4.8) and in Eq (4.11), that is,

and

Now we can use Eq (3.13) or Eq (3.14). In order to use the latter equation, we need ^[28]

This gives

and

where we denoted

Using the above expressions in Eq (4.29) and in Eq (4.30) give the well-known solution of the harmonic oscillator with frictional force $-2\gamma dx/dt$ for the overdamped and underdamped cases, while the critically damped solution follows from the limit $\Omega \to 0$ in these solutions.

5.   Numerical solutions

In this section we will study speficic solutions for some values of $\gamma$, $\omega_0$ and $\alpha$. Although, as we will see, the classification of cases as overdamped, underdamped and critically damped is justified only for $\alpha = 1$, we will continue using it for preciseness.

5.1.   Solutions for the underdamped case

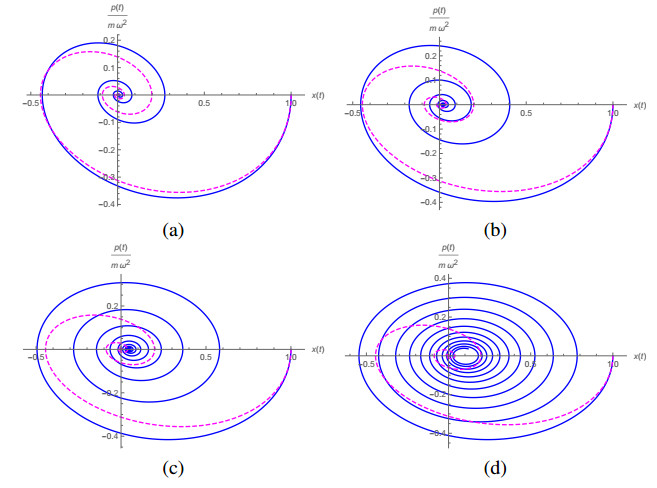
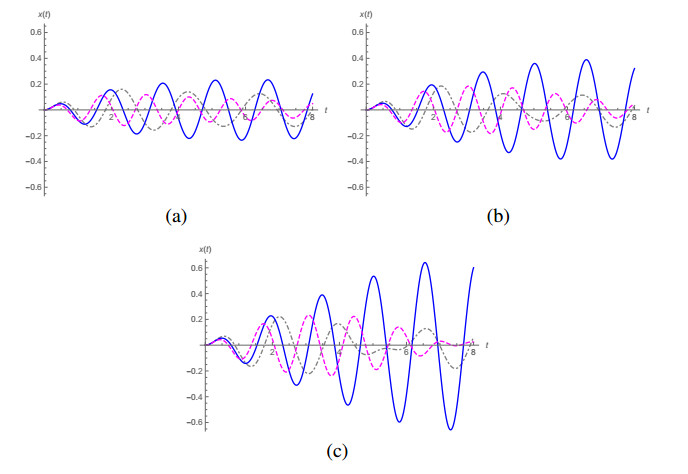
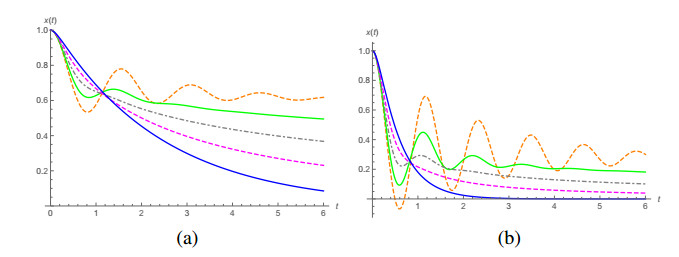
Let us consider the case with $x_0 = 1$ and $v_0 = 0$. The plots corresponding to the solutions for $\alpha = \{1, 0.8, 0.6, 0.4, 0.2\}$ are given in Figure 1 for (a) $\gamma = 1/2$ and $\omega_0 = 2$ and for (b) $\gamma = 1/2$ and $\omega_0 = 4$. In Figure 2 we plot the curves in phase space for the fractional oscillator with $\gamma = 1/2$ and $\omega = 2$ for (a) $\alpha = 0.8$, (b) $\alpha = 0.6$, (c) $\alpha = 0.4$ and (d) $\alpha = 0.2$, and compare these curves with the one for $\alpha = 1$. We used in Figure 2 the vertical axis as $p/m \omega_0^2$ in order to have the direct identification of this quantity with $-G_{\alpha, 0}(t)$. The plots in Figure 1 have been done using Mathematica 12.2 and were based on the inversion of the Laplace transform as in Eq (4.5), for which we employed the numerical inversion codes provided in ^[35] for Mathematica. The code used in these plots is based on the Post-Widder inversion formula ^[35,36]. However, the plots in Figure 2 have been done using the inverse Laplace transform routine in Mathematica 12.2, as it produces better results in this case.

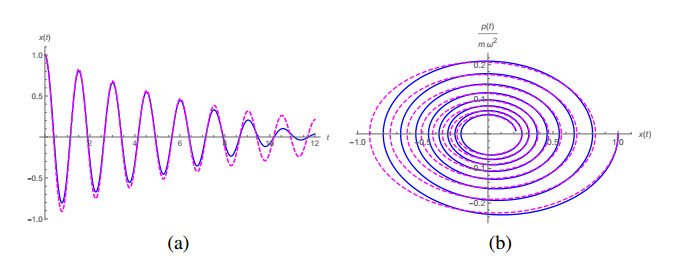
Although all curves in Figure 1 show a decay of an oscillatory amplitude, only the curve for $\alpha = 1$ has an exponential decay envelope. We can expect to find a damped oscillator with $\alpha = 1$ such that for given values $\gamma^\ast$ and $\omega_0^\ast$ the behaviour of its solution resembles the solution for a given $\alpha \neq 1$ for small values of $t$, but not for larger values due to deviations from the exponential decay behaviour. For example, let us consider the case $\alpha = 0.4$, $\gamma = 1/2$ and $\omega_0 = 4$. The poles of Laplace transform $\mathcal{L}[G_{\alpha, \beta}(t)](s)$ are located in $s_{0.4} = -0.126764 - 4.17572 i$ and $s_{0.4}^\ast = -0.126764 + 4.17572 i$. If we choose $\gamma^\ast = -(s_{0.4}+s_{0.4}^\ast)/2$ and $\omega_0^\ast = \sqrt{s_{0.4}s_{0.4}^\ast}$, we obtain a solution for the case $\alpha = 1$ which can be compared with the solution for the $\alpha = 0.4$, $\gamma = 1/2$ and $\omega_0 = 4$ case, as in plot (a) in Figure 3. The phase space plot of the corresponding curves are in plot (b). The plot of $x(t)$ clearly shows the similar behaviour of the solutions for small values of $t$, and the deviation of the decaying behaviour as $t$ increases. Notwithstanding, the solution with $\alpha = 0.4$ approaches zero for large $t$ with a rate slower than the exponential one. This can be seen from the asymptotic expansion of $G_{\alpha, \beta}(t)$ for $\alpha \neq 1$. We show in the Appendix that for $t\to \infty$ we have $G_{\alpha, 1}+2\gamma G_{\alpha, \alpha-1}(t) \sim t^{-\alpha}$ – see Eq (C.7). In other words, and borrowing a jargon from the study of statistical distributions, we can say that the solution for $\alpha = 0.4$ has a heavy tailed profile.

5.2.   Solutions for the overdamped case and the critically damped case

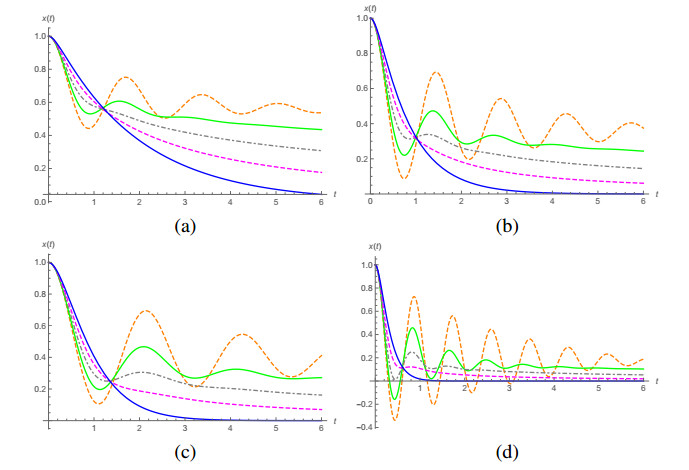
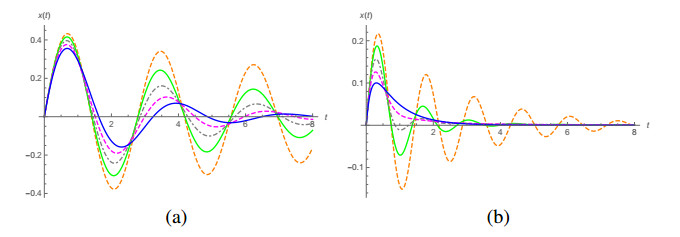
We proceed like the underdamped case, with $x_0 = 1$ and $v_0 = 0$. The plots corresponding to the solutions for $\alpha = \{1, 0.8, 0.6, 0.4, 0.2\}$ are given by the top plots in Figure 4 for (a) $\gamma = 4$ and $\omega_0 = 2$ and (b) for $\omega_0 = 3$. Figure 5 shows the plots of the curves in phase space corresponding to the case $\gamma = 4$ and $\omega_0 = 3$ for (a) $\alpha = 0.8$, (b) $\alpha = 0.6$, (c) $\alpha = 0.4$ and (d) $\alpha = 0.2$, and compare these curves with the one for $\alpha = 1$.

The overdamped case has a distinguished characteristic, that is, while with $\alpha = 1$ we have real solutions of $s^2 + 2 \gamma s + \omega_0^2 = 0$ (when $\gamma > \omega_0$), this is not the case for $\alpha \neq 1$ since we have complex conjugated solutions $s_0$ and $\bar{s}_0$ for $s^2 + 2 \gamma s^\alpha + \omega_0^2 = 0$ for $0 < \alpha < 1$. We expect, therefore, to see an oscillatory behaviour, which is suggested by the plots in Figure 4, where we see the presence of a small oscillation for $\alpha = 0.6$ when $\gamma = 4$ and $\omega_0 = 3$ but apparently none for $\gamma = 4$ and $\omega_0 = 2$, as well as the presence of higher oscillation amplitudes for $\gamma = 4$ and $\omega_0 = 3$ than for $\gamma_4$ and $\omega_0 = 2$ for the cases $\alpha = 0.4$ and $\alpha = 0.2$. We also see that, when we have a clear oscillatory behaviour, the local wavelength inscreases with inscreasing $t$, while the amplitude of the oscillations decreases with increasing $t$. Let us consider, for example, the case $\alpha = 0.2$, $\gamma = 4$ and $\omega_0 = 2$, represented by the dashed orange curve in the left plot in Figure 4. If we measure the local wavelength by the difference between successive minima $m_1 = 0.884$, $m_2 = 2.558$, $m_3 = 4.239$, $m_4 = 5.926$ and $m_5 = 7.623$, we obtain, for $\lambda_i = m_{i+1}-m_i$, $\lambda_1 = 1.674$, $\lambda_2 = 1.681$, $\lambda_3 = 1.687$ and $\lambda_4 = 1.707$, while the decreasing in the amplitude of the oscillations is clear in the plots. The values of the local minima were obtained using the FindMinimum routine in Mathematica. For $\alpha = 0.2$, $\gamma = 4$ and $\omega_0 = 3$ (dashed orange curve in the right plot), we have $m_1 = 0.741$, $m_2 = 2.167$, $m_3 = 3.596$, $m_4 = 5.026$ and $m_5 = 6.460$, we have $\lambda_1 = 1.426$, $\lambda_2 = 1.429$, $\lambda_3 = 1.430$, $\lambda_4 = 1.434$, so the increase in the local wavelength is slower than in the previous case, as well as the rate in which the amplitude of the oscillations decreases.

The plots in Figures 4 and 5 suggest that there may be a critical value $\alpha^\ast$ such that for $\alpha < \alpha^\ast$ an oscillatory behaviour appears. It is reasonable to suppose that such critical value depends on $\gamma$ and $\omega_0$. On the other hand, the presence of singularities in the complex plane for $\alpha \neq 1$ with a non-null imaginary part suggests that this may not be the case, that is, we can always have an oscillatory behavior for $\alpha < 1$, although in some cases with a very small amplitude. This is an issue that deserves attention but it is outside the scope of the present work.

In relation to the critically damped case, in the bottom plots in Figure 4 we have the plots of the solutions for the cases (c) $\gamma = 2$ and $\omega_0 = 2$ and (d) $\gamma = 6$ and $\omega_0 = 6$. As we see, the concept of critical damping makes sense only in the case $\alpha = 1$. The behaviour of the solutions is similar to the overdamped case. In fact, we can see a deviation of the pure decaying solution even in the case $\alpha = 0.8$ in plot (d).

5.3.   Solutions with external term

Equation (4.26) gives the response of a damped harmonic oscillator to an external force of the form $\cos{\omega t}$ and initial conditions $x_0 = 0$ and $v_0 = 0$. In Figure 6 we show the plots of the response in the case $\gamma = 1/2$, $\omega_0 = 4$, and driving frequency (a) $\omega = 3$, (b) $\omega = 4$ and (c) $\omega = 5$. As suggested in the previous plots, as $\alpha$ decreases, so the damping decreases and the response increases, and the effect of resonance is clearly manifested when the driving frequency equals the natural frequency.

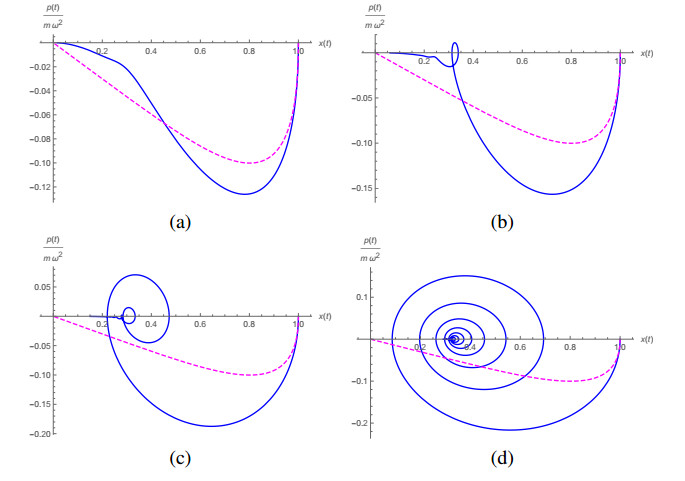
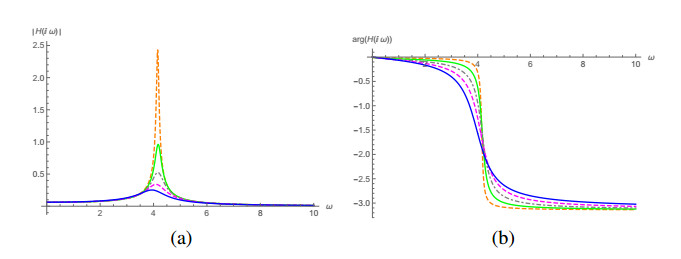
In Figure 7 we have plots for the response to an unit impulse force with $x_0 = 0$ and $v_0 = 0$ for the cases (a) $\gamma = 1/2$ and $\omega_0 = 2$ and (b) $\gamma = 4$ and $\omega_0 = 3$. As in this case the response function is the Laplace inverse transform of the transfer function $H(s)$ in Eq (4.23), it is interesting to look in more details the profile of $H(s)$ for different values of $\alpha$. Let us take case $\gamma = 4$ and $\omega_0 = 3$ as an example. Using the frequency $\omega$ as a variable through $s = i\omega$, in Figure 8 we have the plots of $|H(i\omega)|$ and $\operatorname{arg}H(i\omega)$ in terms of $\omega$.

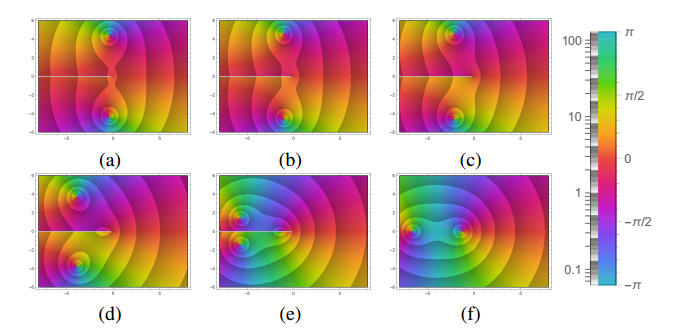
It is also interesting to observe how the poles of the $H(s)$ function move through the complex plane. In Figure 9 we have the phase portraits (made with Mathematica 12) of $H(s)$ for (a) $\alpha = 0.2$, (b) $\alpha = 0.4$, (c) $\alpha = 0.6$, (d) $\alpha = 0.8$, (e) $\alpha = 0.95$ and (f) $\alpha = 1$, in the rectangular region $|\operatorname{Re}s| \leq 8$ and $|\operatorname{Im}s| \leq 6$. In the HSL color model, the hue is an angular variable with values in $[0, 2\pi]$ or $[-\pi, \pi]$, and this fact is used in the phase portrait of a function $H(s)$ where points of the plane are colored according to relation between hue and the angle associated with the argument $\operatorname{arg}H(s)$, as shown in the plot legend in Figure 9. The absolute value $|H(s)|$ can be illustrated using contour lines, and this is done by means of a gray coloring in a logarithmic scale, as shown in the plot legend in Figure 9, which creates an effect of contour lines of constant values of $|H(s)|$ – for more details about the illustration of complex functions, see ^[37]. The white line segment in the plots in Figure 9 is the branch cut of $H(s)$. The analysis of the phase portraits clearly shows the localization of the poles of $H(s)$ as the center of closed curves with an approximate circular shape. We have two poles, and for small values of $\alpha$ (in plot (a) $\alpha = 0.2$), these two poles are located close to the imaginary axis. As the value of $\alpha$ increases, they move away from the imaginary axis towards the real negative direction, with the imaginary part of the poles decreasing, as can be seen in the sequence of plots. As $\alpha \to 1$, these two poles approach each other, while in a region along the branch cut (where we can see the emergence of a curve that resembles an ellipse) the values of $|H(s)|$ increase. When $\alpha = 1$ these two poles merge into a single pole along the negative imaginary axis, while in the region where $|H(s)|$ increased, a new pole appeared on the real negative axis, which is no longer a branch cut.

6.   Conclusions

In this paper we described a model of fractional oscillator with the fractional derivative appearing in the damping term. This is, to the best of our knowledge, the model of a fractional oscillator less discussed in the literature, although in our opinion it is the most natural and conservative one because it keeps the inertial and restoring force terms with their usual form. Our approach used the so called bivariate Mittag-Leffer function. Some properties of this function have been discussed and proved, and numerical examples of some particular solutions of the model for different values of the order $\alpha$ of the fractional derivative were provided, and compared with the usual $\alpha = 1$ damped oscillator. The examples show that the damping decreases as the order of the fractional derivative decreases, so that for certain values, even in the cases classically classified as overdamped or critically damped, oscillations may appear. The existence and identification of a value for the order of the fractional derivative below which oscillations can be noticed even in overdamped cases is an issue that deserves further investigations.

Conflict of interest

The authors declare no conflict of interest.

A.   Proof of some results

A.1.   Proof of Eq (3.8)

Equation (3.5) with $a_{n-1} = a_n = a$ is

Replacing the summation index $k_{n-1}$ by $m = k_{n-1} + k_n$, we have

and since

we obtain Eq (3.8).

A.2.   Proof of Eq (3.9)

Using the definition of the multivariate Mittag-Leffler function as in Eq (3.5), we have

with

where we used the notation of the Pochhammer symbol $(\alpha)_n$, that is,

It is well-known ^[30] that

Therefore, for $|s| > |A_n|^{1/a_{n}}$ we have

and then

where

For $|s| > (2 |A_n|)^{1/a_n}$ the condition for Eq (A.8) holds, and with $|s| > (2|A_{n-1})^{1/a_{n-1}}$ it follows, from the triangle inequality, that $|A_{n-1}s^{-a_{n-1}}/(1+A_n s^{-a_n})| < 1$, and then

which gives

We repeat the same procedure for $T_{n-2}$ given by

For $|s| > (3 |A_n|)^{1/a_n}$, $|s| > (3|A_{n-1})^{1/a_{n-1}}$ and $(3|A_{n-2}|)^{1/a_{n-2}}$, we still have the validity of Eqs (A.8) and (A.11), and it follows, from the triangle inequality, that $|A_{n-2}s^{-a_{n-2}}/(1+A_n s^{-a_n}+A_{n-1} s^{-a_{n-1}})| < 1$, and then

and then

After performing the same calculation for $T_{n-3}, \ldots, T_2$, we obtain

For $|s| > \operatorname{max}\{(n|A_1|)^{1/a_1}, \ldots, (n|A_n|)^{1/a_n}\}$, the conditions for the validity of $T_n, \ldots, T_2$ are still satisfied, and the triangle inequality gives $|A_1/s^{a_1}(1+ A_n s^{-a_n} + \cdots + A_2 s^{-s_2})| < 1$, and consequently

which is the result we want to prove.

B.   Proof of Eqs (3.13) and (3.14)

We can prove Eqs (3.13) and (3.14) from Eq (3.12) using the same series manipulations done in ^[31]. Let us define $A_+$ and $A_-$ as in Eq (3.15), that is, $A_\pm = (A_1/2) \pm \sqrt{\left(A_1/2\right)^2 - A_2}$, in such a way that

Equation (3.12) can be written as

Using the binomial theorem in $(A_+ + A_-)^{k_1}$ we obtain

Using the summation index $m$ defined as $k_1 = n+m$ we can write

Employing the summation index $m^\prime = k_2 + m$ we have

where we have used $(m^\prime - k_2)! = 0$ for $k_2 > m^\prime$. Using the summation index $n^\prime = k_2 + n$ we have

The last series is

where we have used ^[32] (Eq (56), page 619)

with $m = n$. Then

and using the summation index $r = m^\prime + n^\prime$,

where we used the sum of the geometric series. Using the definition of $E_{a, b}(z)$ as in Eq (3.3), we obtain

which is Eq (3.13). From the definition of $E_{a, b}(z)$ it follows the identity

which in Eq (B.11) gives

which is Eq (3.14).

C.   Asymptotic behaviour of ${G_{\alpha, \beta}(t)}$

In Appendix A.2 we showed that, for $|s| > \sigma = \operatorname{max}\{(n|A_1|)^{1/a_1}, \ldots, (n|A_n|)^{1/a_n}\}$, the Laplace transform of the series in Eq (3.5), multiplied by $t^{b-1}$, can be written as

where we supposed that $a_n > a_j$ ($j = 1, \ldots, n-1$). This function $\mathcal{H}_{(a_1, \ldots, a_n), b}(s)$ is the analytical continuation of the Laplace transformed series to other regions with $|s| \leq \sigma$, particularly in the neighbourhood of $s = 0$.

Let us now consider $n = 2$ and suppose that $a_2 > a_1 > 0$. We know, from Watson's lemma ^[36], that the behaviour of a function $f(t)$ for $t\to \infty$ is related to the behaviour of its Laplace transform for $s \to 0$. Then, using Eq (3.11), we have, for $s\to 0$ and $a_2 > a_1$,

and therefore, for $t\to \infty$,

We also assume $b - a_2 -1 > 0$.

After using the above expression in Eq (4.7) we obtain

for $t\to \infty$. We are interested in the cases $\beta = 0$ as in Eq (4.8) and $\beta = -1$ as in Eq (4.12). For $\beta = 0$ we have

and for $\beta = -1$ we have

which gives