Energy production potential of organic fraction of municipal solid waste (OFMSW) and its implications for Nigeria

1.   Introduction

A contraction is a self-mapping $F$ defined on a metric space $(M, d)$ satisfying the inequality $d(Fu, Fv)\leq \xi d(u, v)$ for every $u, v\in M$, where $\xi\in [0, 1)$ is a constant. The famous Banach fixed point theorem ^[1], also called the Banach contraction principle, states that if $(M, d)$ is a complete metric space and $F$ is a contraction defined on $M$, then $F$ possesses a unique fixed point. Moreover, starting from any element $u_0\in M$, the Picard sequence $\{F^nu_0\}$ converges to the fixed point. This theorem provides an important tool for studying the existence of solutions for various kinds of nonlinear problems such as integral equations, differential equations, partial differential equations, and evolution equations.

A natural question to ask is whether it is possible to obtain a similar result to that of Banach for non-contraction mapping $F: M\to M$, where $(M, d)$ is a metric space. For instance, if $F$ is not continuous on $(M, d)$, then $F$ is not a contraction. This question attracted the attentions of several mathematicians. {For instance, Kannan ^[2] considered the class of mappings $F: M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi\in \left[0, \frac{1}{2}\right)$ is a constant. Namely, Kannan proved that Banach's fixed point result holds true for this class of mappings. Motivated by the work of Kannan, Chatterjea ^[3] established the same result for the class of mappings $F:M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi\in \left[0, \frac{1}{2}\right)$} is a constant. Reich ^[4,5] investigated the class of mappings $F:M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi_1, \xi_2, \xi_3\geq 0$ and $\xi_1+\xi_2+\xi_3 < 1$. In ^[6], Ćirić introduced and studied the class of quasi-contraction mappings. Namely, the class of mappings $F:M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi\in [0, 1)$ is a constant. Berinde ^[7] introduced and studied the class of almost contractions. Namely, the class of mappings $F:M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi\in [0, 1)$ and $L\geq 0$ are constants. In ^[8], Khojasteh et al. unified several fixed point theorems by introducing the class of contractions involving simulation functions. In ^[9], Górnicki established various extensions of Kannan's fixed point theorem. Petrov ^[10] introduced and studied the class of mappings contracting perimeters of triangles. Recently, Pǎcurar and Popescu ^[11] investigated a new class of generalized Chatterjea-type mappings. We also refer to Branga and Olaru ^[12], where new fixed point results for generalized contractions in spaces with altering metrics were established.

Another kind of contribution was concerned with the study of fixed points when the set $M$ is equipped with a generalized metric, such as a $b$-metric ^[13], cone $E_b$-metric ^[14], $G$-metric ^[15], $F$-metric ^[16], hemi metric ^[17], non-triangular metric ^[18,19], or suprametric ^[20].

Assume now that $(M, d)$ is a metric space and $F: M\to M$ is a contraction. Then, for all $p\geq 1$ and $u, v\in M$, we have

that is,

where $\xi_p = \xi^p\in [0, 1)$ is a constant. We remark that (1.1) provides a new type of contractions. Notice that a mapping $F$ satisfying (1.1) is not necessarily a contraction (see Example 2.12). Based on this observation, for a metric space $(M, d)$, we introduce in Section 2 the class of mappings $F: M\to M$ satisfying the inequality

for every $u, v\in M$, where $\xi\in[0, 1)$ is a constant and $\{S_i\}_{i = 1}^k$ is a family of mappings $S_i: M\times M\to M$. A mapping $F$ satisfying the above condition is called a $p$-contraction with respect to $\{S_i\}_{i = 1}^k$. Notice that in the special case $k = 1$ and $S_1(u, v) = Fu$ for every $u, v\in M$, a $p$-contraction with respect to $\{S_1\}$ is a mapping $F$ satisfying (1.1). A fixed point theorem for $p$-contractions with respect to a family of mappings is established in Section 2. Our obtained result is a generalization of the Banach fixed point theorem. The result is supported by some examples where the Banach fixed point theorem is not applicable. We also provide an application to the study of fixed points for single-valued mappings defined on the set of positive integers.

On the other hand, it is well known that special functions arise in numerous applications. Indeed, various classical problems of physics can be solved by making use of such functions. In particular, the famous Euler Gamma function is one of the most important special functions, which plays a crucial role in various branches of mathematics; see, e.g., ^[21,22,23]. Motivated by this fact, in Section 3, we are concerned with the study of fixed points for mappings $F: M\to M$ satisfying contractions involving the ratio

where $(M, d)$ is a metric space, $\Gamma$ is the Euler Gamma function, $\psi:[0, \infty)\to [0, \infty)$ is a function satisfying a certain condition, and $\alpha\in (0, 1)$ is a constant. We call this class of mappings as the class of $(\psi, \Gamma, \alpha)$-contractions. Our obtained result is supported by an example where the Banach fixed point theorem is not applicable.

We end this section by fixing some notations that will be used throughout this paper. By $\mathbb{N}$ (resp. $\mathbb{N}^*$), we mean the set of nonnegative (resp. positive) integers. We denote by $M$ an arbitrary nonempty set. For a given mapping $F: M\to M$, we denote by $\{F^n\}$ the sequence of mappings $F^n: M\to M$ defined by

for all $u\in M$. By ${\rm{Fix}}(F)$, we mean the set of fixed points of $F$, that is,

Similarly, for a mapping $S: M\times M\to M$, we denote by ${\rm{Fix}}(S)$ the set of fixed points of $S$, that is,

2.   The class of $p$-contractions with respect to a family of mappings

In this section, we introduce the class of $p$-contractions with respect to a family of mappings, and study the existence and uniqueness of fixed points for such mappings.

Let $(M, d)$ be a metric space. Let $k\in \mathbb{N}^*$, $p\geq 1$ be constants, and $\{S_i\}_{i = 1}^k$ be a family of mappings $S_i: M\times M\to M$.

Definition 2.1. A mapping $F: M\to M$ is called a $p$-contraction with respect to $\{S_i\}_{i = 1}^k$ if there exists $\xi\in [0, 1)$ such that

for every $u, v\in M$.

Definition 2.2. We say that a mapping $F: M\to M$ is weakly Picard continuous on $(M, d)$ if the following condition holds: If for $u, v\in M$ and

then there exists a subsequence $\{F^{n_j}u\}$ of $\{F^nu\}$ such that

Remark 2.3. It can be easily seen that if $F: M\to M$ is continuous on $(M, d)$, then $F$ is weakly Picard continuous on $(M, d)$. However, the converse is not necessarily true, as demonstrated in the following example.

Example 2.4. Let $d$ be the Euclidean metric on $[0, 1]$, that is,

Suppose that $F: [0, 1]\to [0, 1]$ is the function defined by

It is clear that $F$ is not continuous at $u = 1$. Notice that for every $n\in \mathbb{N}^*$, it follows that

which shows that

Thus, $F$ is weakly Picard continuous on $([0, 1], d)$.

We recall below the famous Jensen inequality (see ^[24]) that will be used later.

Lemma 2.5. Let $J: [0, \infty)\to \mathbb{R}$ be a convex function. Then, for every $q\in \mathbb{N}^*$ and $\{x_1, x_2, \cdots, x_q\}$, $\{a_1, a_2, \cdots, a_q\}\subset [0, \infty)$ with $\sum\limits_{i = 1}^q a_i > 0$, we have

2.1.   Fixed point results

In this subsection, we give a fixed point theorem and several corollaries. Moreover, we provide some nontrivial examples to illustrate that our results can be used, but that Banach fixed point theorem is not applicable.

Our first main result is the following fixed point theorem.

Theorem 2.6. Let $(M, d)$ be a complete metric space and $F: M\to M$ a mapping. Suppose that the following conditions hold:

${\rm{(i)}}$ $F$ is a $p$-contraction with respect to $\{S_i\}_{i = 1}^k$;

${\rm{(ii)}}$ $F$ is weakly Picard continuous on $(M, d)$.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}}$ F possesses a unique fixed point $u^*$ in $M$;

${\rm{(III)}}$ $u^*\in \bigcap\limits_{i = 1}^k {\rm{Fix}}(S_i)$.

Proof. (I) For an arbitrary $u_0\in M$, let us consider the sequence $\{u_n\}\subset M$ defined by

By (i), taking $(u, v) = (u_0, u_1)$ in (2.1), we obtain

that is,

Repeating the same process with $(u, v) = (u_1, u_2)$, we obtain

that is,

Thus, in view of (2.2) and (2.3), we have

Continuing in the same way, we obtain

for every $n\in \mathbb{N}$, where

On the other hand, by the triangle inequality, we obtain that, for all $n\in \mathbb{N}$,

which yields

Furthermore, since the function $x\mapsto x^p$ is convex on $[0, \infty)$, using Lemma 2.5, we obtain

which implies by (2.5) that

The above inequality yields

Thus, it follows from (2.4) and (2.6) that

where

Next, thanks to (2.7) and (2.8), we obtain by the triangle inequality that, for all $n\in \mathbb{N}$ and any $m\in \mathbb{N}^*$,

which implies that $\{u_n\}$ is a Cauchy sequence. Then, due to the completeness of $(M, d)$, we infer that there exists $u^*\in M$ such that

and by (ii) it follows that there exists a subsequence $\{F^{n_j}u_0\}$ of $\{F^nu_0\}$ such that

Thus, in view of (2.9) and (2.10), we have $u^* = Fu^*$, that is, $u^*\in {\rm{Fix}}(F)$. This proves part (I) of Theorem 2.6.

(II) By (I), it follows that $u^*\in {\rm{Fix}}(F)$. If there still exists $v^*\in {\rm{Fix}}(F)$, then by (2.1), we obtain

that is,

Since $\xi\in [0, 1)$, the above inequality implies that

which yields $u^* = v^*$. Consequently, $F$ admits a unique fixed point $u^*$ in $M$, which proves part (II) of Theorem 2.6.

(III) From (II), we know that $F$ admits a unique fixed point $u^*\in M$. Taking $(u, v) = (u^*, u^*)$ in (2.1), we obtain

that is,

Since $\xi\in [0, 1)$, the above inequality implies that

Consequently, we obtain

that is, $u^*\in \bigcap\limits_{i = 1}^k {\rm{Fix}}(S_i)$. This proves part (III) of Theorem 2.6. □

We now discuss some special cases of Theorem 2.6. Taking $k = 1$ in Theorem 2.6, we obtain the following result.

Corollary 2.7. Let $(M, d)$ be a complete metric space, $p\geq 1$ a constant, and $S_1: M\times M\to M$ a mapping. Suppose that $F: M\to M$ is a mapping satisfying the following conditions:

${\rm{(i)}}$ There exists a constant $\xi\in [0, 1)$ such that

for every $u, v\in M$;

${\rm{(ii)}}$ $F$ is weakly Picard continuous on $(M, d)$.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}} F$ possesses a unique fixed point $u^*$ in $M$;

${\rm{(III)}}$ $u^*\in {\rm{Fix}}(S_1)$.

Taking $S_1(u, v) = Fu$ for every $u, v\in M$, we deduce from Corollary 2.7 the following result.

Corollary 2.8. Let $(M, d)$ be a complete metric space, $p\geq 1$ a constant, and $F: M\to M$ a mapping. Suppose that the following conditions hold:

${\rm{(i)}}$ There exists a constant $\xi\in [0, 1)$ such that

for every $u, v\in M$;

${\rm{(ii)}}$ $F$ is weakly Picard continuous on $(M, d)$.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}}$ F possesses a unique fixed point $u^*$ in $M$.

Taking $k = 2$ in Theorem 2.6, we obtain the following result.

Corollary 2.9. Let $(M, d)$ be a complete metric space, $S_1, S_2: M\times M\to M$ two mappings and $p\geq 1$ a constant. Suppose that $F: M\to M$ is a mapping satisfying the following conditions:

${\rm{(i)}}$ There exists a constant $\xi\in [0, 1)$ such that

for every $u, v\in M$;

${\rm{(ii)}}$ $F$ is weakly Picard continuous on $(M, d)$.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}} F$ possesses a unique fixed point $u^*$ in $M$;

${\rm{(III)}}$ $u^*\in {\rm{Fix}}(S_1)\cap {\rm{Fix}}(S_2)$.

If $F$ is continuous on $(M, d)$ (see Remark 2.3), then we deduce from Theorem 2.6 the following result.

Corollary 2.10. Let $(M, d)$ be a complete metric space and $F: M\to M$ a mapping. Suppose that the following conditions hold:

${\rm{(i)}}$ $F$ is a $p$-contraction with respect to $\{S_i\}_{i = 1}^k$;

${\rm{(ii)}}$ $F$ is continuous.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}}$ F possesses a unique fixed point $u^*$ in $M$;

${\rm{(III)}}$ $u^*\in \bigcap\limits_{i = 1}^k {\rm{Fix}}(S_i)$.

We now show that Theorem 2.6 includes the Banach fixed point theorem.

Corollary 2.11. (Banach fixed point theorem) Let $(M, d)$ be a complete metric space and $F: M\to M$ a mapping. Suppose that there exists a constant $\xi\in [0, 1)$ such that

for every $u, v\in M$. Then, $F$ possesses a unique fixed point $u^*$ in $M$. Moreover, for every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to $u^*$.

Proof. Let $k = p = 1$ and $S_1: M\times M\to M$ be the projection mapping defined by

In this case, (2.1) reduces to

that is, (2.13). This shows that, if $F$ satisfies (2.13), then $F$ satisfies (2.1) with $k = p = 1$ and $S_1$ is the mapping defined above. On the other hand, due to (2.13), the mapping $F$ is continuous. Thus, by Corollary 2.10, the desired result is completed. □

We provide below three examples illustrating our obtained results. In all the presented examples, the Banach fixed point theorem is not applicable.

Example 2.12. Let $F: [0, 1]\to [0, 1]$ be the mapping defined by

We consider the Euclidean metric on $[0, 1]$, that is,

Notice that $F$ is not continuous at $u = 1$, which implies that $F$ is not a contraction. Thus, the Banach fixed point theorem is not applicable in this example. Let us now estimate the ratio

We distinguish four cases as follows.

Case 1. $0\leq u, v < 1$. In this case, we obtain

Case 2. $u = v = 1$. In this case, we have

Case 3. $0\leq u < 1$ and $v = 1$. In this case, we have

Case 4. $u = 1$ and $0\leq v < 1$. In this case, we have

Generally speaking, from the above estimates, we deduce that

for every $u, v\in M$, which shows that $F$ satisfies (2.12) with $p = 1$.

On the other hand, for all $u\in [0, 1]$, we have

which shows that $F$ is weakly Picard continuous. Consequently, Corollary 2.8 applies. Notice that

which confirms Corollary 2.8.

Example 2.13. Let $M = \{m_1, m_2, m_3\}$ and $F: M\to M$ be the mapping defined by

Let $d$ be the discrete metric on $M$, that is,

Notice that

which shows that there is no $\xi\in [0, 1)$ such that (2.13) holds for every $u, v\in M$. Consequently, the Banach fixed point theorem is not applicable in this example.

Let us introduce the mapping $S_1: M\times M\to M$ defined by

and

We claim that $F$ satisfies (2.11) with $p = 1$ and $\xi = \frac{1}{2}$, that is,

for every $i, j\in \{1, 2, 3\}$.

Indeed, notice that for all $i\in\{1, 2, 3\}$, we have

which shows that (2.15) holds for all $i = j\in\{1, 2, 3\}$.

On the other hand, due to the symmetry of $S_1$, we just have to show that (2.14) holds for $(i, j)\in\{(1, 2), (1, 3), (2, 3)\}$. For this purpose, we divide it into three cases below.

Case 1. $(i, j) = (1, 2)$. In this case, we have

which shows that (2.15) is satisfied for $(i, j) = (1, 2)$.

Case 2. $(i, j) = (1, 3)$. In this case, we have

which confirms (2.15).

Case 3. $(i, j) = (2, 3)$. In this case, we have

which shows that (2.15) is also satisfied for $(i, j) = (2, 3)$.

From the above discussions, we deduce that (2.15) holds for every $i, j\in\{1, 2, 3\}$.

Since $F$ is continuous (because $M$ is a finite set), then $F$ is weakly Picard continuous on $(M, d)$. Consequently, Corollary 2.7 applies. Notice that

and

which confirms Corollary 2.7.

Example 2.14. Let us consider the mapping $F: [0, 1]\to [0, 1]$ defined by

Let $d$ be the metric on $[0, 1]$ defined by

Notice that $F$ is not continuous at $u = 1$, which implies that $F$ is not a contraction. Then, the Banach fixed point theorem is not applicable in this case.

Let us introduce the mapping $S: [0, 1]\times [0, 1]\to [0, 1]$ defined by

We consider the following four cases.

Case 1. $0\leq u, v < 1$. Taking into consideration that

and $F([0, 1))\subset [0, 1)$, we obtain by the mean value theorem that

Case 2. $0\leq u < 1$, $v = 1$. In this case, on the one hand, using that $F1 = F0$ and (2.16), we obtain by the mean value theorem that

On the other hand,

which implies that

Consequently, we have

Case 3. $u = 1$, $0\leq v < 1$. In this case, we obtain

Moreover, we have

Consequently, we arrive at

Case 4. $u = v = 1$. In this case, we have

Thus, from the above discussion, we deduce that $F$ satisfies (2.11) with $p = 1$, $S_1 = S$, and $\xi = \frac{1}{2}$. Furthermore, for all $u\in [0, 1]$, we have $\{F^nu\}\subset [0, \frac{1}{2}]$. Then, by the continuity of $F$ on $[0, \frac{1}{2}]$, if for some $u, v\in [0, 1]$ we have

so $v\in [0, \frac{1}{2}]$, and

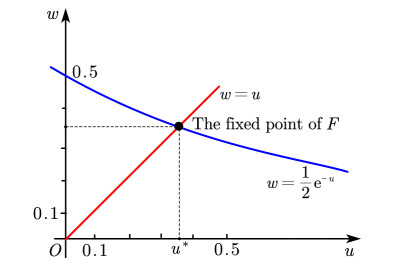
This shows that $F$ is weakly Picard continuous on $([0, 1], d)$. Finally, by Corollary 2.7, we deduce that $F$ has one and only one fixed point $u^*\approx 0.3517$. Figure 1 confirms our conclusion.

2.2.   An application: A discrete fixed point result

In this subsection, as an application of Theorem 2.6, we obtain sufficient conditions under which a mapping $F: \mathbb{N}^*\to \mathbb{N}^*$ admits a unique fixed point.

Theorem 2.15. Let $F: \mathbb{N}^*\to \mathbb{N}^*$ be a mapping satisfying the inequality

for every $n, m\in \mathbb{N}^*$ with $F(n)\neq F(m)$, where $\xi\in [0, 1)$ is a constant. Then, $F$ possesses a unique fixed point.

Proof. Let us consider the mapping $S_1: \mathbb{N}^*\times \mathbb{N}^*\to \mathbb{N}^*$ defined by

We claim that

for every $n, m\in \mathbb{N}^*$. To this end, we discuss two cases.

Case 1. $F(n) = F(m)$. In this case, by the definition of $S_1$, we obtain

which shows that (2.18) holds in this case.

Case 2. $F(n)\neq F(m)$. In this case, $n\neq m$. By the definition of $S_1$, we obtain

which implies by (2.17) that

Note that

that is,

Thus, by (2.19) and (2.20), we get (2.18). Consequently, $F$ satisfies (2.11) with $k = p = 1$, $M = \mathbb{N}^*$, and

On the other hand, since $F$ is defined on $\mathbb{N}^*$, then $F$ is continuous on $(M, d)$, which shows that condition (ii) of Corollary 2.7 is satisfied. Therefore, by Corollary 2.7, we obtain that $F$ possesses a unique fixed point. This completes the proof of Theorem 2.15. □

We now illustrate Theorem 2.15 by an example in which the Banach fixed point theorem is not applicable.

Example 2.16. Let us consider the mapping $F: \mathbb{N}^*\to \mathbb{N}^*$ defined by

First, notice that

which shows that there is no $\xi\in [0, 1)$ such that

for every $n, m\in \mathbb{N}^*$. Consequently, $F$ is not a contraction on $(\mathbb{N}^*, d)$, where $d(n, m) = |n-m|$ for every $n, m\in \mathbb{N}^*$. Thus, the Banach fixed point theorem is not applicable in this example.

Now, we show that $F$ satisfies (2.17) for every $n, m\in \mathbb{N}^*$ with $F(n)\neq F(m)$. Notice that for every $n, m\in \mathbb{N}^*$, we have

where

and

Due to the symmetry of (2.17), without restriction of the generality, we may assume that $(n, m)\in V$. So, we have two possible cases.

Case 1. $n = 1$ and $m\geq 3$. In this case, we have

Case 2. $n > m\geq 2$. In this case, we have

From the above estimates, we deduce that

for every $n, m\in \mathbb{N}^*$ with $F(n)\neq F(m)$. Thus, $F$ satisfies (2.17) with $\xi = \frac{1}{2}$, and Theorem 2.15 applies. On the other hand, we have ${\rm{Fix}}(F) = \{1\}$, which confirms Theorem 2.15.

3.   The class of $(\psi, \Gamma, \alpha)$-contractions

Before introducing the class of $(\psi, \Gamma, \alpha)$-contractions, let us briefly recall some properties related to the Euler gamma function. For more details, we refer to Abramowitz and Stegun ^[21].

The Euler gamma function is the function $\Gamma$ defined by

An integration by parts shows that

In particular, when $s = k\in \mathbb{N}^*$, we obtain

For all $n\in \mathbb{N}$, we have

The function $\Gamma$ is $\ln$-convex, i.e.,

Let us denote by $\Psi$ the set of functions $\psi: [0, \infty)\to [0, \infty)$ satisfying

where $c, \tau > 0$ are constants. Remark that by (3.4), if $\psi\in \Psi$, then

Notice that no continuity assumption is imposed on $\psi\in \Psi$.

Definition 3.1. Let $(M, d)$ be a metric space and $F: M\to M$ a mapping. We say that $F$ is a $(\psi, \Gamma, \alpha)$-contraction, if there exist $\alpha, \beta\in (0, 1)$ and $\psi\in \Psi$ such that

for every $u, v\in M$ with $Fu\neq Fv$.

Our second main result is the following fixed point theorem.

Theorem 3.2. Let $(M, d)$ be a complete metric space and $F: M\to M$ a mapping. Suppose that the following conditions hold:

${\rm{(i)}}$ $F$ is a $(\psi, \Gamma, \alpha)$-contraction;

${\rm{(ii)}}$ $F$ is weakly Picard continuous on $(M, d)$.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}} F$ possesses a unique fixed point.

Proof. (I) For an arbitrary $u_0\in M$, let

We distinguish two cases as follows:

Case 1. There exists $m\in\mathbb{N}$ such that

In this case, we obtain $u_{m} = Fu_m$ and

which shows that $u_m\in {\rm{Fix}}(F)$ and $\{u_n\}$ converges to $u_m$.

Case 2. For all $n\in\mathbb{N}$, we have

that is,

In this case, using (3.6) with $(u, v) = (u_0, u_1)$, we obtain

that is,

Again using (3.6) with $(u, v) = (u_1, u_2)$, we obtain

that is,

Then, it follows from (3.7) and (3.8) that

Repeating the same argument, we obtain by induction that

On the other hand, by (3.4), we have

which implies together with (3.9) that

Furthermore, by the $\ln$-convexity of $\Gamma$ (see (3.3)), for any $n\in\mathbb{N}$, we have

Subsequently, by (3.1), we have

which yields

Hence, from (3.11), we deduce that

which implies that

Now, using both inequalities (3.10) and (3.12), we obtain

which is equivalent to

where

and

Next, using (3.13) and the triangle inequality, we obtain that for all $n\in\mathbb{N}$ and $q\in\mathbb{N}^*$,

which shows (since $0 < \sigma < 1$) that $\{u_n\}$ is a Cauchy sequence. Then, by the completeness of $(M, d)$, we infer that there exists $u^*\in M$ such that

Thus, using the weakly Picard continuity of $F$ and proceeding as in the proof of Theorem 2.6, we obtain that $u^*\in {\rm{Fix}}(F)$. This proves part (I) of Theorem 3.2.

(II) From part (I), we know that $u^*\in{\rm{Fix}}(F)$. Assume that there exists another different $v^*\in {\rm Fix}(F)$ (so, $d(Fu^*, Fv^*) > 0$). Then, using (3.6), we obtain

that is,

Moreover, since

it follows immediately from (3.5) that

Then, from (3.14), we reach a contradiction with $\beta\in (0, 1)$. Therefore, $u^*$ is the unique fixed point of $F$. This proves part (II) of Theorem 3.2. □

In the special case when $F$ is continuous on $(M, d)$, we deduce from Theorem 3.2 the following result.

Corollary 3.3. Let $(M, d)$ be a complete metric space and $F: M\to M$ a mapping. Suppose that the following conditions hold:

${\rm{(i)}}$ $F$ is a $(\psi, \Gamma, \alpha)$-contraction;

${\rm{(ii)}}$ $F$ is continuous.

Then:

${\rm{(I)}}$ For every $u_0\in M$, the sequence $\{F^nu_0\}$ converges to a fixed point of $F$;

${\rm{(II)}} F$ possesses a unique fixed point.

We now give an example to illustrate Theorem 3.2.

Example 3.4. Let $M = \left\{q_1, q_2, q_3\right\}$ and $F: M\to M$ be the mapping defined by

Let $d: M\times M\to [0, \infty)$ be the mapping defined by

and

Observe that

which shows that $d$ is a metric on $M$.

Notice that

which shows that there is no $\xi\in [0, 1)$ such that

for all $i, j\in\{1, 2, 3\}$. Consequently, the Banach fixed point theorem is not applicable in this case.

Consider now the function $\psi: [0, \infty)\to [0, \infty)$ defined by

It can easily be seen that

which shows that $\psi\in \Psi$ (indeed, $\psi$ satisfies (3.4) with $c = \dfrac{5\sqrt\pi}{32}$ and $\tau = 1$).

From the definition of $F$, for all $i, j\in\{1, 2, 3\}$, we have

Moreover, by (3.15), the definition of $\psi$, and (3.2), we obtain

and

Then, by (3.16), the above calculations, and the symmetry of $d$, we deduce that for all $i, j\in\{1, 2, 3\}$ and $\dfrac{1}{2}\leq \beta < 1$,

which means that $F$ satisfies (3.6) with $\alpha = \dfrac{1}{2}$ and $\dfrac{1}{2}\leq \beta < 1$. Furthermore, since $M$ is a finite set of elements, then $F$ is continuous on $M$ with respect to the metric $d$. This shows that Theorem 3.2 (or, more precisely, Corollary 3.3) applies. On the other hand, we have

which confirms Theorem 3.2.

4.   Conclusions

The Banach fixed point theorem is a very important result in fixed point theory that has numerous applications in nonlinear analysis. However, when the mapping does not belong to the class of contractions, the theorem is inapplicable. Thus, the development of fixed point theory for non-contraction mappings is of great importance. Motivated by this fact, two new classes of self-mappings defined on a complete metric space $(M, d)$ are introduced in this work. The first one is the class of $p$-contractions with respect to a family of mappings $\{S_i\}_{i = 1}^k$, where $S_i: M\times M\to M$. For such a class of mappings, a fixed point theorem was established (see Theorem 2.6). Namely, we proved that, if $F: M\to M$ is weakly Picard continuous on $(M, d)$ and $F$ is a $p$-contraction with respect to $\{S_i\}_{i = 1}^k$, then $F$ possesses a unique fixed point, which is also a common fixed point of the mappings $S_i$ ($i = 1, 2, \cdots, k$). Moreover, for any $u_0\in M$, the Picard sequence $\{F^nu_0\}$ converges to this fixed point. We also proved that our obtained result recovers the Banach fixed point theorem. The second class introduced in this work is the class of $(\psi, \Gamma, \alpha)$-contractions, where $\Gamma$ is the Euler gamma function, $\psi: [0, \infty)\to [0, \infty)$ satisfies condition (3.4), and $\alpha\in (0, 1)$. A fixed point theorem was proved for this class of mappings (see Theorem 3.2). Namely, as for the previous class of mappings, we proved that, if $F: M\to M$ is weakly Picard continuous on $(M, d)$ and $F$ is a $(\psi, \Gamma, \alpha)$-contraction, then $F$ admits a unique fixed point, and for any $u_0\in M$, the sequence $\{F^nu_0\}$ converges to this fixed point.

Some questions related to this work need to be investigated. For this purpose, we provide below some interesting questions for further studies:

I. Consider the class of mappings $F: (M, d)\to (M, d)$ satisfying the inequality

for all $u, v\in M$ with $d(Fu, Fv) > 0$, where $\alpha\in (0, 1)$ and $\beta > 0$ are constants. Is it possible to obtain sufficient conditions on $\beta$ and $\psi$ so that $F$ admits one and only one fixed point?

II. We reiterate the previous question for the class of mappings $F: (M, d)\to (M, d)$ satisfying

III. It would be also interesting to study the multi-valued version of Theorem 3.2 by considering the class of multi-valued mappings $F: M\to CB(M)$, where $CB(M)$ denotes the family of all nonempty bounded and closed subsets of $M$, satisfying the inequality

where $H$ is the Hausdorff-Pompeiu metric on $CB(M)$.

Author contributions

All authors contributed equally in this work. All authors have read and agreed to the submitted version of the manuscript.

Acknowledgments

The first author acknowledges the financial support from the Initial Funding of Scientific Research for High-level Talents of Chongqing Three Gorges University of China (No. 2104/09926601). The second author is supported by Researchers Supporting Project number (RSP2024R4), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.