Stokes-Dirac structures for distributed parameter port-Hamiltonian systems: An analytical viewpoint

1.   Introduction

The theory of port-Hamiltonian systems is an ever-growing area of research ^{[1,2,3,4,5,6,7]}, as it provides a powerful framework for the modeling ^{[8,9,10,11,12,13,14,15,16,17,18]}, control ^[19,20,21] and simulation ^{[22,23,24,25]} of complex physical systems. Its versatility allows us to describe subsystems independently, and to interconnect them through ports ^{[26,27,28,29,30]}. It models physical exchanges between subsystems, making use of physically meaningful quantities.

The geometric characterization of port-Hamiltonian systems is not univocal in the literature. Port-Hamiltonian systems can be defined using two approaches:

● calculus of variation for field theories and the jet bundle formalism ^[31,32],

● Dirac structures ^{[28,33,34,35,36]}.

The jet bundle and Dirac structure formalism are likely connected by a unifying geometrical description of port-Hamiltonian systems. Nevertheless, such a connection is yet to be found in the literature.

In the jet bundle case, port-Hamiltonian systems are obtained like in the classical Hamiltonian formalism of symplectic geometry, i.e., by converting the Euler-Lagrange equations via the Legendre transform. The boundary ports are deduced by accounting for non-trivial variations on the boundary. This approach is applicable to finite- and infinite-dimensional systems. In the latter case, the Hamiltonian is a functional over a field and its derivatives, commonly named a jet bundle in field theories. This construction has the advantage of being very structured and in direct association with the Lagrangian formalism. However, deducing boundary ports is a non-trivial task in higher-order problems ^[37].

Dirac structures generalize Hamiltonian systems defined on symplectic manifolds (basic examples of integrable Dirac structures include Poisson and presymplectic manifolds ^[33]). They describe the energy routing inside and outside of a given system and are strictly connected with graph and network theory ^[38]. Solutions of a port-Hamiltonian system lie in the Dirac structure at all times. More specifically, this structure encodes the power balance satisfied by the Hamiltonian along trajectories. Twenty years ago, lumped-parameter port-Hamiltonian systems have been generalized to distributed-parameter port-Hamiltonian systems ^[39], allowing us to model in a structured manner the physical exchanges occurring at the boundary of physical domains. This construction easily allows for the identification of the boundary ports of a given distributed system^*. However, unlike the jet bundle description (that relies on the Lagrangian description and its Legendre transform), it is still unclear how to systematically construct port-Hamiltonian systems in the Dirac structure framework; particularly, an overarching geometric definition of port-Hamiltonian systems based on Dirac structures is yet to be established, and this is especially true in the infinite-dimensional case. Many authors have attempted to provide such a unifying definition, starting either from (Stokes-)Dirac structures ^[20,40], or from physically meaningful examples ^{[41,42,43,44]}. For the moment, no general consensus can be found in the literature. In particular, the geometric formulation of problems arising from continuum mechanics is, to the best of our knowledge, open.

^*The term Stokes-Dirac structure has been coined in ^[39], as the boundary variables are provided by the Stokes theorem.

The present contribution aims at providing a unifying functional analytic framework for linear port-Hamiltonian systems defined by means of a (Stokes-)Dirac structures. The presented formulation encompasses many engineering examples and relies on the well-known boundary control system theory, or, more generally, on well-posed linear systems ^{[45,46,47,48,49,50,51]}, to define (Stokes-)Dirac structures. Such an approach has already been used for this purpose ^[40,41,42]. The major novelty compared to previous work is that the algebraic structure is clearly separated from the dynamics satisfied by the trajectories. This is achieved by assuming a particular decomposition of the operators together with an abstract integration by parts formula. An abstract Stokes-Dirac structure is then constructed by means of an auxiliary boundary control system. To demonstrate well-posedness, only a subclass of linear constitutive relations are considered (namely, for undamped linear port-Hamiltonian systems, also called lossless port-Hamiltonian systems). Our framework allows us to properly describe examples stemming from continuum mechanics, like general elastodynamics and plate models. In the considered physical examples, we highlight the connection between the operator included in the Dirac structure and the associated Hilbert complexes. This connection is important, as it establishes a link between algebraic, topological and geometric properties and has important consequences for discretization ^[52].

The paper is organized as follows. Section 2 defines the general framework proposed in this work. It is divided into five parts. Section 2.1 recalls some useful definitions for lumped-parameter port-Hamiltonian systems. Then, the definition of Stokes-Dirac structures is given as the direct extension to infinite-dimensional port-Hamiltonian systems in Section 2.2. The definition of distributed-parameter port-Hamiltonian systems is detailed in Section 2.3. Section 2.4 deals with the auxiliary boundary control system enabling the construction of a Stokes-Dirac structure from differential and boundary operators. The class of lossless linear port-Hamiltonian systems are proved to be well-posed in Section 2.5. Section 3 gives four meaningful physical examples coming from continuum mechanics and physics. Section 4 concludes this work.

2.   A general framework

2.1.   Port-Hamiltonian systems in the finite dimension

A common way to define finite-dimensional port-Hamiltonian systems on $\mathbb{R}^N$, borrowed from ^[7], is port-based modeling, which relies on a Dirac structure.

The definition of Dirac structures is given in [7,Definition 2.1], but the equivalent definition given by [7,Proposition 2.1] is better suited for an extension to infinite-dimensional spaces.

Definition 1 (Bond space). Let $\mathcal{E}$ be a Hilbert space and $\mathcal{F} : = \mathcal{E}'$ be its topological dual. The space $\mathcal{B} : = \mathcal{F} \times \mathcal{E}$ endowed with the bilinear form

is called a bond space. $\mathcal{E}$ is called the effort space, and $\mathcal{F}$ is called the flow space.

Here, $\left\langle f, e \right\rangle _{\mathcal{F}, \mathcal{E}} : = f(e)$, i.e., the linear form $f \in (\mathcal{E})'$ applied to the vector $e \in \mathcal{E}$. This notation is classical for general Hilbert spaces, and it is known as the duality bracket between $\mathcal{F} : = (\mathcal{E})'$ and $\mathcal{E}$. In finite dimensions, identification between $(\mathcal{E})'$ and $\mathcal{E}$ is safe since all norms are equivalent. Unfortunately, this is no longer the case in the infinite dimension, and continuity of linear maps is norm-dependent; hence, a norm has to be chosen and fixed once and for all to define the topological dual $(\mathcal{E})'$ of $\mathcal{E}$.

Definition 2 ((Stokes-)Dirac structure). Let $\mathcal{B}$ be a bond space. A subspace $\mathcal{D} \subset \mathcal{B}$ is called a Dirac or Stokes-Dirac structure if and only if $\mathcal{D}^{[\perp]} = \mathcal{D}$, where $\mathcal{D}^{[\perp]}$ is the orthogonal companion of $\mathcal{D}$ in $\mathcal{B}$, defined by

In the real-valued finite-dimensional case, it is common to talk about Dirac structures. In the general framework, we often emphasize the infinite-dimensional setting by talking about the Stokes-Dirac structure, as it makes use of the so-called Stokes divergence theorem in practice, see ^[4].

Definition 3 (Port-Hamiltonian systems ^[7]). Consider a solution space^† $\mathcal{Z}$, a resistive space $\mathcal{R}$, a control space $\mathcal{U}$ and $\mathcal{H} : \mathcal{Z} \rightarrow \mathbb{R}$, a Hamiltonian defining energy-storage, as a function of the energy variable $\alpha$. A port-Hamiltonian system on $\left(\mathcal{Z}, \mathcal{R}, \mathcal{U}\right) \simeq \left(\mathbb{R}^{d_s} \times \mathbb{R}^{d_r} \times \mathbb{R}^{d_u} \right)$ is defined by a Dirac structure:

^†Note that this is not the usual state space, which is usually determined by the "energy" norm of the solutions, but a strict subspace. This terminology follows that in ^[49].

and dynamics (i.e., trajectories depending on the initial value $\alpha(0)$ and on the control $u(t)$) evolving in the following Dirac structure:

together with a constitutive relation for the resistive port $(f_r, e_r) \in \mathcal{S} \subset \mathcal{R}' \times \mathcal{R}$.

In [7,Definition 2.3], the Dirac structure depends on the energy variable $\alpha$; the Dirac structure is modulated. Modulated Stokes-Dirac structures for distributed port-Hamiltonian systems are discussed in ^[10,11]. In the present work, only constant Stokes-Dirac structures are considered.

Proposition 1 (Power balance). The Hamiltonian of a port-Hamiltonian system satisfies the following power balance along the trajectories:

In particular, $\mathcal{H} \in \mathcal{C}^1([0, \infty); \mathbb{R})$.

In practice, the constitutive relation $\mathcal{S}$ is given and the term $\left(f_r, e_r(t) \right)_{ \mathbb{R}^{d_r}}$ leads to a fully determined power balance, as given by (2.3).

Proposition 2 (Extended structure matrix). Consider a port-Hamiltonian system and assume that the trajectories are solutions of the following system:

where $J$ is a skew-symmetric matrix and $B$ is a control matrix, with appropriate sizes.

Then, the Dirac structure is given as the graph^‡ of the $\textrm{extended structure matrix}$:

^‡Rigorously speaking, the Dirac structure is given by the graph of the inverse $\mathcal{J}^{-1}$ of the extended structure matrix since it is regarded in $\mathcal{F} \times \mathcal{E}$ and not in $\mathcal{E} \times \mathcal{F}$. Nevertheless, to avoid mentioning details on the inverse, by abuse of language, we will only say graph throughout this paper, since it perfectly fits the definition of [7,Exercise 1,p. 17].

Proof. See [7,Exercise 1,p. 17]. □

2.2.   Stokes-Dirac structure over complex Hilbert spaces

This section aims at providing a sufficient condition for an operator on complex Hilbert spaces to generate a Stokes-Dirac structure as its graph. The definition of a bond space extends from finite to infinite dimensions. However, for an infinite-dimensional system, it is compulsory to consider complex spaces, and to consider a weaker topology on the flow space $\mathcal{F} : = \mathcal{E}'$, as will be seen in the sequel. This dictates the following complex^§ definition of a sesquilinear form to be a bond product on $\mathcal{B} : = \mathcal{E}' \times \mathcal{E}$:

^§With the topological dual $\mathcal{F}$ of $\mathcal{E}$ being the vector space of continuous linear forms on $\mathcal{E}$, $\left\langle f, e \right\rangle _{\mathcal{F}, \mathcal{E}} : = f(e)$ is antilinear in its first variable, and linear in its second.

Theorem 1. Let $\mathcal{E}$ be a Hilbert space, $\mathcal{F} = \mathcal{E}'$ be its topological dual and $\mathcal{J} \in \mathcal{L}(\mathcal{E}, \mathcal{F})$. If the following holds^¶:

^¶This identity is a skew-symmetry-like property of $\mathcal{J}$. The classical skew-symmetry would require that $\mathcal{J}$ has its range in $\mathcal{E}$, and that it is necessary to make use of the Hermitian product of $\mathcal{E}$ instead of the duality bracket between $\mathcal{F}$ and $\mathcal{E}$.

then

is a Stokes-Dirac structure in $\mathcal{B} : = \mathcal{F} \times \mathcal{E}$.

The operator $\mathcal{J}$ is called the extended structure operator of $\mathcal{D}$.

Proof. Let $\begin{pmatrix} f^1 \\ e^1 \end{pmatrix} \in \mathcal{D}$. Then, for all $\begin{pmatrix} f^2 \\ e^2 \end{pmatrix} \in \mathcal{D}$, one has

This shows that $\mathcal{D} \subset \mathcal{D}^{[\perp]}$, i.e., that $\mathcal{D}$ is a Tellegen structure.

Reciprocally, let $\begin{pmatrix} f^1 \\ e^1 \end{pmatrix} \in \mathcal{D}^{[\perp]}$. Then, for all $\begin{pmatrix} f^2 \\ e^2 \end{pmatrix} \in \mathcal{D}$, one has

This is true for all $e_2 \in \mathcal{E}$; hence, $f^1 - \mathcal{J} e_1 \in \mathcal{E}^\perp : = \left\{ f \in \mathcal{F} \, \mid \, \left\langle f, e \right\rangle _{\mathcal{F}, \mathcal{E}} = 0 \text{ for all } e \in \mathcal{E} \right\} \equiv \{ 0 \}$, i.e., $\begin{pmatrix} f^1 \\ e^1 \end{pmatrix} \in \mathcal{D}$, which concludes the proof. □

Remark 1. Let us consider the following example to fix the ideas: $\mathcal{J} : = \frac{\rm d}{\rm d x}$, as defined from the Sobolev space $H^1_0(0, 1)$ to $L^2(0, 1)$. There are two ways of considering this operator: either as a closed and densely defined unbounded operator from $L^2(0, 1)$ to $L^2(0, 1)$, or as a bounded operator from $H^1_0(0, 1)$ to $L^2(0, 1)$. If one takes $\mathcal{E} : = L^2(0, 1) = \mathcal{F}$, the graph of $\mathcal{J}$ would only be a Tellegen structure on $\mathcal{F} \times \mathcal{E} = L^2(0, 1) \times L^2(0, 1)$. Indeed, for the reciprocal part of the above proof to hold, one would require $\mathcal{J}$ to be skew-adjoint, which would be too restrictive for our purpose. On the other hand, if one takes $\mathcal{E} : = H^1_0(0, 1)$ and $\mathcal{F} : = (H^1_0(0, 1))' \simeq H^{-1}(0, 1) \supset L^2(0, 1)$, one obtains a Dirac structure on $\mathcal{F} \times \mathcal{E} = H^{-1}(0, 1) \times H^1_0(0, 1)$, as expected. The price to pay is having a weaker topology on the flow space $\mathcal{F}$, and a stronger one on the effort space $\mathcal{E}$.

Remark 2. Equivalently, the skew-symmetric-like property (2.5) can be rewritten as follows:

Remark 3. Theorem 1 gives a kernel representation of the infinite-dimensional Stokes-Dirac structure $\mathcal{D}$, as defined in [7,Chapter 5] for finite-dimensional port-Hamiltonian systems.

2.3.   Port-Hamiltonian systems on Hilbert spaces

Assuming $\mathcal{Z}$, $\mathcal{R}$ and $\mathcal{U}$ to be Hilbert spaces, Definition 3 directly translates to the infinite-dimensional setting, provided that the gradient of the Hamiltonian ${\bf{grad}}_{\alpha} \mathcal{H}$ is replaced by the variational derivate $\delta_{\alpha} \mathcal{H}$, whose definition can be directly extended to our framework from [53,Definition 4.1,p. 245]. In particular, Proposition 1 admits a straightforward generalization.

Proposition 3 (Power balance). Let $\mathcal{Z}$, $\mathcal{R}$, and $\mathcal{U}$ be three Hilbert spaces, and a functional $\mathcal{H} : \mathcal{Z} \rightarrow \mathbb{R}$ be a Hamiltonian, as a function of the energy variable $\alpha$ defining energy storage.

Consider a port-Hamiltonian system on $\left(\mathcal{Z}, \mathcal{R}, \mathcal{U}\right)$ defined by a Stokes-Dirac structure:

and trajectories (depending on the initial value $\alpha(0)$ and on the control $u$):

together with a resistive constitutive relation for the resistive port $(f_r, e_r) \in \mathcal{S} \subset \mathcal{R}' \times \mathcal{R}$.

Then, the Hamiltonian $\mathcal{H}(\alpha(t)) \in \mathcal{C}^1([0, \infty); \mathbb{R})$ satisfies the following power balance along the trajectories:

Remark 4. As in the finite-dimensional setting given by (2.3), the resistive constitutive relation is needed to relate $f_r$ and $e_r$, and to reach the final power balance. This supplementary constitutive relation often models dissipation through a proportional law (i.e., Ohm's law, Fourier's law, etc.). Indeed, assume that $\mathcal{R}' \simeq \mathcal{R}$ and there exists $S \in \mathcal{L}(\mathcal{R}, \mathcal{R})$ such that $e_r = S f_r$, where $S$ is symmetric and positive. $S^\star = S$ and $\left(f_r, S f_r \right)_{\mathcal{R}} \ge 0$ for all $f_r \in \mathcal{R}$; then, $\Re {\rm e} \left\langle f_r(t), e_r(t) \right\rangle _{\mathcal{R}', \mathcal{R}} = \left(f_r(t), S f_r(t) \right)_{\mathcal{R}} \ge 0$ and the power balance then becomes

which stands for lossy port-Hamiltonian systems.

2.4.   Formal skew-symmetry with boundary control and structure operators

This section is devoted to the description of a class of operators that generate a Stokes-Dirac structure as its graph thanks to Theorem 1. The aim is to obtain an infinite-dimensional counterpart of Proposition 2, namely, Theorem 3.

As a starting point, boundary control systems are considered as infinite-dimensional analogous systems of the form of (2.4).

More precisely, we consider systems of the form

where $J$ is formally skew-symmetric and $G$ is a boundary control operator. The output will be defined accordingly to $G$ in order to obtain the desired Stokes-Dirac structure.

An important point to keep in mind for this section is that the focus is set on the Stokes-Dirac structure, and not on the trajectories of a port-Hamiltonian system. Therefore, there is no need to distinguish the solution space $\mathcal{Z}$ from the resistive space $\mathcal{R}$, or to consider the time evolution.

Furthermore, many examples coming from physics, as will be seen in Section 3, lead us to introduce some notations and propose the following assumptions:

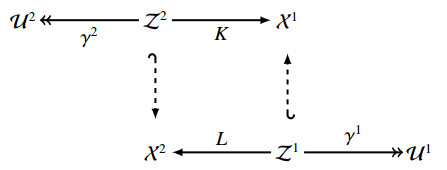
$\textbf{(A1)}$ $\mathcal{X}^1$ and $\mathcal{X}^2$ are two Hilbert spaces, identified by their respective duals;

$\textbf{(A2)}$ $J$ can be decomposed as $\begin{bmatrix} 0 & - K \\ L & 0 \end{bmatrix}$ on $\mathcal{X} : = \mathcal{X}^1 \times \mathcal{X}^2$;

$\textbf{(A3)}$ $L$ is a closed and densely defined operator from $\mathcal{X}^1$ into $\mathcal{X}^2$, with domain $\mathcal{Z}^1$. Endowed with the graph norm, $\mathcal{Z}^1$ is a Hilbert space, continuously and densely embedded in $\mathcal{X}^1$ [49,Section 2.2], and $L \in \mathcal{L}(\mathcal{Z}^2, \mathcal{X}^1)$; and, $K$ is a closed and densely defined operator from $\mathcal{X}^2$ into $\mathcal{X}^1$, with domain $\mathcal{Z}^2$. The Hilbert space $\mathcal{Z}^2$ is also endowed with the graph norm, and $K \in \mathcal{L}(\mathcal{Z}^1, \mathcal{X}^2)$. Furthermore, their domains satisfy $\mathcal{Z}^1 \times \mathcal{Z}^2 = \mathcal{Z} \times \mathcal{R}$;

$\textbf{(A4)}$ $G$ can be decomposed as $\begin{bmatrix} \gamma^1 & 0 \\ 0 & \gamma^2 \end{bmatrix} \in \mathcal{L}(\mathcal{Z}^1\times\mathcal{Z}^2, \mathcal{U}^1\times\mathcal{U}^2)$, with $\mathcal{U}^1$ and $\mathcal{U}^2$ being two other Hilbert spaces satisfying $\mathcal{U} = \mathcal{U}^1 \times \mathcal{U}^2$.

Figure 1 shows the interactions between the different spaces of our setting.

Finally, it has been assumed in system (2.7) that $J$ is formally skew-symmetric, which translates with the above decomposition of $J$ by $L$ and $K$ being formal adjoints with respect to $G$:

This identity can be seen as an abstract formulation of the usual definition of formal adjoints that is often encountered in the port-Hamiltonian formalism for differential operators and using $\mathcal{C}^\infty_0$ test functions; see [54,Def. 5.80].

In the framework of this paper, a slightly more general assumption is being made:

$\textbf{(A5)}$ There exist two operators $\beta^1 \in \mathcal{L}(\mathcal{Z}^1, (\mathcal{U}^2)')$ and $\beta^2 \in \mathcal{L}(\mathcal{Z}^2, (\mathcal{U}^1)')$ such that the following abstract Green's identity holds:

It is clear that this abstract Green's identity implies that $L$ and $K$ are formal adjoints with respect to $G$.

Remark 5. The abstract integration by parts formula (2.8) has an important connection with differential geometry. When dealing with the de Rham complex, it corresponds to the topological integration by parts formula of differential forms [52,Eq. 2.4]. When the elasticity complex is considered, the corresponding formula is based on the exterior covariant derivative (see, for instance, [55,Eq. 32]).

To retrieve the notations of the previous sections, we may consider either $\mathcal{Z} = \mathcal{Z}^1 \times \mathcal{Z}^2$ and $\mathcal{R} = \emptyset$, or $\mathcal{Z} = \mathcal{Z}^1$ and $\mathcal{R} = \mathcal{Z}^2$. The former will be our setting for well-posedness (see Theorem 4) and most examples treated in Section 3. An example with $\mathcal{R}$ being neither $\emptyset$ nor $\mathcal{Z}^2$ is provided in Section 3.4.

Remark 6. In this work, the abstract Green's identity given by (2.8) is assumed from the very beginning, which is contrary to the point of view that, although equivalent, was developed in [46,Def. 2.1], [42,Def. 2.1], or [56,Def. 4.1]. As an example, if $L = \operatorname{div}$ on $H^{ \operatorname{div}}$ and $K = -\boldsymbol{grad}$ on $H^1$, we assume

rather than

for the computation of the scalar product $\quad \left(\begin{pmatrix} {\boldsymbol{f}} \\ f \end{pmatrix}, J\, \begin{pmatrix} {\boldsymbol{g}} \\ g \end{pmatrix} \right)_{L^2(\Omega; \mathbb{R}^3) \times L^2(\Omega)}$, where $J : = \begin{bmatrix} 0 & \boldsymbol{grad} \\ \operatorname{div} & 0 \end{bmatrix}$.

Before going further in the port-Hamiltonian framework, let us show that the above assumptions allow the definition of the skew-adjoint operator, which will be the $C_0$-semi-group generator of the boundary control system generating the Stokes-Dirac structure.

Theorem 2. Assume that $\mathcal{X}^i_1 : = \ker \gamma^i$ is dense in $\mathcal{X}^i$ for $i = 1, 2$, and denote $\mathcal{X}_1 : = \mathcal{X}^1_1 \times \mathcal{X}^2_1$. Let us define the operator $A$ as the restriction of $J$ to $\mathcal{X}_1$, i.e., $A : = J|_{\mathcal{X}_1}$. If $\mathcal{X}^1_0 : = \ker \gamma^1 \cap \ker \beta^1$ is dense in $\mathcal{X}^1$ and $\beta^1$ restricted to $\mathcal{X}^1_1$ is onto, then $A$ is skew-adjoint on $\mathcal{X}$.

Remark 7. Regarding the symmetric role played by $L$ and $K$, the latter hypothesis may be replaced by the following: $\mathcal{X}^2_0 : = \ker \gamma^2 \cap \ker \beta^2$ is dense in $\mathcal{X}^2$ and $\beta^2$ restricted to $\mathcal{X}^2_1$ is onto, taking care of the obvious reversal needed in the following proof. Furthermore, if both $\mathcal{X}^1_0$ and $\mathcal{X}^2_0$ are dense in $\mathcal{X}^1$ and $\mathcal{X}^2$, respectively, then both $\mathcal{X}^1_1$ and $\mathcal{X}^2_1$ are dense in $\mathcal{X}^1$ and $\mathcal{X}^2$, respectively. If $L$ and $K$ belong to the de Rham complex, this symmetrical construction finds its explanation in the Hodge duality, which converts a strong differential operator, i.e., the exterior derivative, into a weak one, i.e., the codifferential. A more involved notion of Hodge duality arises if one considers the elasticity complex [55,Section 5].

Proof. By hypothesis, $A$ is densely defined on $\mathcal{X}$. Furthermore, (2.8) implies that $A$ is skew-symmetric. Indeed, one has the following, for all $z = \begin{pmatrix} z_1 \\ z^2 \end{pmatrix} \in \mathcal{X}_1 : = \mathcal{X}^1_1 \times \mathcal{X}^2_1 : = \ker \gamma^1 \times \ker \gamma^2$:

since $z^1 \in \ker \gamma^1$ and $z^2 \in \ker \gamma^2$.

The aim is to apply [49,Proposition 3.7.3.] to conclude that $A$ is skew-adjoint on $\mathcal{X}$. Let us show that both $(I-A)$ and $(I+A)$ are onto.

● $I-A$ is onto:

Let $f^1 \in \mathcal{X}^1$ and $f^2 \in \mathcal{X}^2$; we are seeking for a solution $v = \begin{pmatrix} v^1 \\ v^2 \end{pmatrix} \in \mathcal{X}_1 : = \mathcal{X}^1_1 \times \mathcal{X}^2_1 : = \ker \gamma^1 \times \ker \gamma^2$ to

Let us first assume that (2.9) admits a solution. Then, for all $\varphi^1 \in \mathcal{X}^1_1$, one has

Since $\gamma^1$ is continuous from $\mathcal{Z}^1$ in $\mathcal{U}^1$, its kernel $\mathcal{X}^1_1$ is a closed subspace of $\mathcal{Z}^1$ and inherits the graph norm of $L$. Hence, the above equality reads as

In summary, (2.9) implies (2.10).

Applying the Riesz representation theorem, there exists a unique $v^1 \in \mathcal{X}^1_1$ satisfying (2.10).

Consider the linear continuous extension $\widetilde{K} \in \mathcal{L}(\mathcal{X}^2, (\mathcal{X}^1_0)')$ of $K \in \mathcal{L}(\mathcal{Z}^2, \mathcal{X}^1)$, defined thanks to (2.8) restricted to $\mathcal{X}^1_0 \times \mathcal{Z}^2$:

where the dual $(\mathcal{X}^1_0)'$ is taken with respect to the pivot space $\mathcal{X}^1$.

Now, let us denote $v^2 : = L v^1 + f^2 \in \mathcal{X}^2$; then,

By the density of $\mathcal{X}^1_0$ in $\mathcal{X}^1$, the right-hand side extends to all $\varphi^1 \in \mathcal{X}^1$, which implies that $\widetilde{K} v^2 = K v^2 \in \mathcal{X}^1$; hence, $v^2 \in \mathcal{Z}^2$ and $v^1 + K v^2 = f^1$ in $\mathcal{X}^1$.

It remains to be verified that, indeed, $\gamma^2 v^2 = 0$ in $\mathcal{U}^2$. From (2.8), for all $\varphi^1 \in \mathcal{X}^1_1$, one has

because $v^1$ is a solution of (2.10). Since $\beta^1$ restricted to $\mathcal{X}^1_1$ is assumed to be onto, this shows that $\gamma^2 v^2 = 0$ in $\mathcal{U}^2$, i.e., that $v^2 \in \mathcal{X}^2_1 : = \ker \gamma^2$.

Hence, for all $f^1 \in \mathcal{X}^1$ and $f^2 \in \mathcal{X}^2$, we found that $v^1 \in \mathcal{X}^1_1$ and $v^2 \in \mathcal{X}^2_1$ are solutions of (2.9), showing that $I-A$ is indeed onto.

● $I+A$ is onto: The same proof is adapted straightforwardly.

We conclude by applying [49,Proposition 3.7.3.]. □

The main result of this section is the following infinite-dimensional analogue of Proposition 2.

Theorem 3. With the notations, definitions and assumptions of the beginning of this section, assume furthermore the following

(A1) $\gamma^i \in \mathcal{L}(\mathcal{Z}^i, \mathcal{U}^i)$ is onto, $i = 1, 2$;

(A2) $\mathcal{X}^i_1 : = \ker \gamma^i$ is dense in $\mathcal{X}^i$, $i = 1, 2$;

(A3) either $\mathcal{X}^1_0 : = \ker \gamma^1 \cap \ker \beta^1$ is dense in $\mathcal{X}^1$ and $\beta^1$ restricted to $\mathcal{X}^1_1$ is onto, or $\mathcal{X}^2_0 : = \ker \gamma^2 \cap \ker \beta^2$ is dense in $\mathcal{X}^2$ and $\beta^2$ restricted to $\mathcal{X}^2_1$ is onto.

Let us denote $A|_{\mathcal{X}}$ the continuous extension of $A$ to $\mathcal{X}$, with value in $\mathcal{X}_{-1}$, which is the completion of $\mathcal{X}$ endowed with the norm $\left\| (I-A)^{-1} \cdot \right\|_{\mathcal{X}}$.

Denote furthermore $\mathcal{X}^i_{-1}$ as the projection of $\mathcal{X}_{-1}$ on the $i$-th component for $i = 1, 2$.

Then, there exists:

● a unique control operator $B^1 \in \mathcal{L} (\mathcal{U}^1, \mathcal{X}_{-1}^2)$ associated with^‖ $\gamma^1$;

^‖By "associated with", it is meant that $B^1$ is constructed from the operator $\gamma^1$.

● a unique control operator $B^2 \in \mathcal{L} (\mathcal{U}^2, \mathcal{X}_{-1}^1)$ associated with $\gamma^2$;

such that the graph of $\mathcal{J} \in \mathcal{L}(\mathcal{E}, \mathcal{F})$, $\mathcal{F} : = \mathcal{E}'$, defined by

is a Stokes-Dirac structure $\mathcal{D}$ in the bond space $\mathcal{B} : = \mathcal{F} \times \mathcal{E}$.

Proof. The complete proof is available in Appendix B. It consists of the three following steps:

1. prove that $\left(J, G \right)$ is a boundary control system on $\left(\mathcal{Z}^1\times\mathcal{Z}^2, \mathcal{X}^1\times\mathcal{X}^2, \mathcal{U}^1\times\mathcal{U}^2\right)$;

2. prove that $\mathcal{J}$ satisfies (2.5);

3. prove that the control operator associated with $\left(J, G \right)$ is of the form $\begin{bmatrix} 0 & B^2 \\ B^1 & 0 \end{bmatrix}$, with $B^i$ associated with $\gamma^i$, $i = 1, 2$. □

Remark 8. It is important to notice that $A|_{\mathcal{X}}$ is the linear continuous extension to $\mathcal{X}$ of $J$ restricted to $\mathcal{X}_1$, i.e., $A$, which is a priori not identifiable with $J$ defined on $\mathcal{Z}^1 \times \mathcal{Z}^2$. Indeed, they differ on $(\mathcal{X}^1_1)^{\perp_{\mathcal{Z}^1}} \times (\mathcal{X}^2_1)^{\perp_{\mathcal{Z}^2}}$ since $\mathcal{X}_1^i$ is not dense in $\mathcal{Z}^i$, $i = 1, 2$, in general. This difference is exactly the way the control operators are exhibited. See the proof of [49,Proposition 10.1.2] for more details.

Remark 9. In this work, we do not consider a non-zero feedthrough operator $D \in \mathcal{L}(\mathcal{U}, \mathcal{U}')$ in $\mathcal{J}$. However, as soon as $D$ satisfies $\Re {\rm e} \left\langle D u, u \right\rangle _{\mathcal{U}', \mathcal{U}} = 0$ for all $u \in \mathcal{U}$, the results would follow as well.

2.5.   Well-posed linear port-Hamiltonian systems

This section is devoted to the problem of existence and uniqueness of solutions in the particular case where the Hamiltonian is of quadratic form, and without a resistive port, i.e., when $\mathcal{Z} = \mathcal{Z}^1 \times \mathcal{Z}^2$ and $\mathcal{R} = \emptyset$.

This is clearly a restrictive case; however, sufficient for the lossless port-Hamiltonian systems of Section 3.

Theorem 4 (Well-posed linear port-Hamiltonian system). Let us consider a port-Hamiltonian system as in Proposition 3, whose Stokes-Dirac structure is given as in Theorem 3. Assume furthermore that the Hamiltonian $\mathcal{H}$ is given by a self-adjoint positive-definite operator $Q \in \mathcal{L}(\mathcal{X})$ as $\mathcal{H}(\alpha) = \frac{1}{2} \left(\alpha, Q \alpha \right)_{\mathcal X}$, with $\mathcal{X} = \mathcal{X}^1 \times \mathcal{X}^2$, $\mathcal{R} = \emptyset$ and $\mathcal{U} = \mathcal{U}^1 \times \mathcal{U}^2$.

Then, the following holds: for all $\alpha_0 \in \mathcal{X}$, and all $u \in H^2_{\rm \ell oc}([0, \infty); \mathcal{U})$ such that $\begin{pmatrix} Q \alpha_0 \\ u(0) \end{pmatrix} \in \mathcal{E}$, there exists a unique trajectory satisfying

Such a system is said to be a well-posed linear port-Hamiltonian system.

Proof. Uniqueness is clear by linearity.

Let us denote

where $B = \begin{bmatrix} 0 & B^2 \\ B^1 & 0 \end{bmatrix}$ and $C = \begin{bmatrix} 0 & \beta^2 \\ \beta^1 & 0 \end{bmatrix}$. From Theorem 2, $A$ is skew-adjoint on $\mathcal{X}$. Since $Q$ is bounded, self-adjoint and positive-definite on $\mathcal{X}$, $Q^\frac{1}{2} A Q^\frac{1}{2}$ is also skew-adjoint on $\mathcal{X}$, with domain $Q^{-\frac{1}{2}} \mathcal{X}_1$. Therefore, it is the generator of a strongly continuous group on $\mathcal{X}$ [49,Theorem 3.8.6.].

It is clear that $Q^\frac{1}{2} B \in \mathcal{L}(\mathcal{U}, Q^\frac{1}{2} \mathcal{X}_{-1})$.

For all $\begin{pmatrix} Q \alpha_0 \\ u(0) \end{pmatrix} \in \mathcal{E}$, $A Q \alpha_0 + B u(0) \in \mathcal{X}$. Denoting $z_0 : = Q^\frac{1}{2} \alpha_0$ and multiplying by $Q^\frac{1}{2}$ gives $Q^\frac{1}{2} A Q^\frac{1}{2} z_0 + Q^\frac{1}{2} B u(0) \in \mathcal{X}$.

Applying [49,Proposition 4.2.11], there exists a unique solution $z$ to

that satisfies $z \in \mathcal{C}^1([0, \infty); \mathcal{X})$.

Defining $\alpha : = Q^{-\frac{1}{2}} z$, one has

satisfying $\alpha \in \mathcal{C}^1([0, \infty); \mathcal{X})$.

To conclude, $(I-A) Q \alpha(t) = Q \alpha(t) - \dot \alpha(t) + B u(t)$ for all $t\ge0$ implies that $(I-A) Q \alpha \in \mathcal{C}([0, \infty); \mathcal{X} + B \mathcal{U})$. In other words, $Q \alpha \in \mathcal{C}([0, \infty); \mathcal{Z})$ by Proposition 4, point 4. In particular, the observation operator $C \in \mathcal{L}(\mathcal{Z}, \mathcal{U}')$ can be applied to $Q \alpha$ and $y \in \mathcal{C}([0, \infty); \mathcal{U}')$.

All together, and since $H^2_{\rm \ell oc}([0, \infty); \mathcal{U}) \subset \mathcal{C}([0, \infty); \mathcal{U})$, the result follows. □

Remark 10. The regularity assumption on $u$ can be relaxed with the less stringent condition $u \in H^1_{\rm \ell oc}([0, \infty); \mathcal{U})$, provided that $Q^\frac12 B$ is an admissible control operator for the semi-group generated by $Q^\frac{1}{2} A Q^\frac{1}{2}$. See [49,Chapter 4] for more details.

3.   Some useful examples

This section provides four examples dealing with different differential operators. For the sake of completeness, a case of lossy port-Hamiltonian systems is included: the electrodynamical problem with the Joule effect, although well-posedness has not been proved for this case.

3.1.   Scalar wave: $(\operatorname{div}, -{\bf{grad}})$ case

Let us begin with the classical scalar wave equation, defined on a bounded set $\Omega \subset \mathbb{R}^3$. The governing partial differential equation reads as follows:

where $w$ denotes the deflection from the equilibrium, $\rho$ is the mass density, bounded from above and below, and ${\boldsymbol{T}}$ is Young's modulus; a rank-2 tensor field, symmetric and positive-definite almost everywhere.

Choosing the total mechanical energy, i.e., kinetic plus potential, as Hamitlonian, one has to select the energy variables to express it. Let us take the linear momentum and the strain as follows:

The Hamiltonian functional is then a quadratic form with these variables:

The co-energy variables are given by the variational derivatives of $\mathcal{H}$ with respect to the energy variables:

that is, the velocity and the stress, respectively.

Assuming smooth solutions, the power balance satisfied by the Hamiltonian reads as follows:

giving us information on the boundary controls and obervations that are allowed in the formalism, which must lead to trajectories lying in the Stokes-Dirac structure according to Proposition 3.

Let us choose a simple causality and control the velocity at the boundary. The port-Hamiltonian formulation then reads as follows:

where $\gamma_0$ denotes the Dirichlet trace operator.

In this first example, the spaces and operators defining the operator $J$ are as follows:

where the following Sobolev spaces have been used:

From the de Rham cohomology, it is known that the following complex holds [57,Chapter 3]:

Hence, $L$ and $K$ are indeed closed and densely defined, as expected. The spaces and boundary operators defining $G$ are given as follows:

where, by definition, $H^\frac{1}{2}(\partial\Omega) \simeq {\rm Ran}\gamma_0$; hence, $\gamma^1$ is trivially surjective.

Now, it is a well-known result that $H_0^1(\Omega) : = {\rm ker} \gamma_0$ is dense in $L^2(\Omega)$.

Finally, thanks to the (usual) Green's formula, $L$ and $K$ are formal adjoints with respect to $G$, and $C$ is identified as the normal trace operator $\gamma_\perp : = {\boldsymbol{n}} \cdot \gamma_0 : H^{ \operatorname{div}}(\Omega; \mathbb{R}^3) \rightarrow H^{-\frac{1}{2}}(\partial\Omega) = (\mathcal{U}^1)'$, where ${\boldsymbol{n}}$ is the outward unit normal to the boundary.

Thus, by virtue of Theorem 3, the operators $L$, $K$ and $G$ generate a Stokes-Dirac structure.

If, furthermore, we define the multiplicative operator of constitutive relations:

then Theorem 4 proves that the scalar wave problem with velocity boundary control is a well-posed linear port-Hamiltonian system, with the normal trace of the stress as a collocated boundary observation.

3.2.   Three-dimensional elasticity: $({\rm{Div}}, - {\rm{Grad}})$ case

We consider the linear elastodynamics problem, described by the vector-valued partial differential equation defined on the bounded set $\Omega \subset \mathbb{R}^3$:

where $\rho$ is the mass density and the stiffness tensor ${\boldsymbol{\mathcal{D}}} : \mathbb{R}^{3\times 3}_{\text{sym}} \rightarrow \mathbb{R}^{3\times 3}_{\text{sym}}$ is a rank-4 tensor that is bounded, symmetric and positive definite almost everywhere. The operator ${\rm{Div}}$ is the columnwise divergence of a tensor field, whereas ${\rm{Grad}} : = \frac{1}{2}(\nabla + \nabla^{\top})$ is the symmetric gradient. This system of equations is formulated as a port-Hamiltonian system by respectively selecting as energy variables the linear momentum and the strain tensor:

The Hamiltonian functional is quadratic for these variables:

where ${\boldsymbol{A}} : {\boldsymbol{B}} = \sum_{ij} A_{ij} B_{ij}$ denotes the tensor contraction. The co-energy variables are given by the variational derivative of $\mathcal{H}$ (see ^[22] for the definition of the variational derivative in the tensorial case):

Since the characterization of mixed control spaces for elasticity is involved, we consider, for simplicity, the case of uniform boundary control of the normal trace of the Cauchy stress tensor ${\boldsymbol{\Sigma}}$. The port-Hamiltonian formulation including the boundary input then reads as follows (cf. [24,page 40]):

where $\boldsymbol\gamma_{\perp}$ denotes the normal trace of a tensor field over the boundary, namely, $\boldsymbol\gamma_{\perp} {\boldsymbol{E}}^2: = {\boldsymbol{E}}^2 \cdot {\boldsymbol{n}}\vert_{\partial\Omega}$. For this case, the spaces and operators are as follows:

where the following Sobolev spaces have been introduced:

The operator $-{\rm{Div}} : L^2(\Omega, \mathbb{R}^{3\times 3}_{\text{sym}}) \rightarrow L^2(\Omega, \mathbb{R}^3)$ is a closed densely defined operator with domain $H^{{\rm{Div}} } (\Omega, \mathbb{R}^{3\times 3}_{\text{sym}})$, while ${\rm{Grad}} : L^2(\Omega, \mathbb{R}^3) \rightarrow L^2(\Omega, \mathbb{R}^{3\times 3}_{\text{sym}})$ is a closed densely defined operator with domain $H^{\rm{Grad}} (\Omega, \mathbb{R}^3)$. More precisely, these operators are part of the following elasticity complex ^[58]:

where the homogeneous boundary conditions, denoted by a ($\circ$) above the functional space, are defined within each Sobolev space. The corresponding dual domain complex is given by

The boundary input operator spaces for this example are as follows:

The space

is defined to be the range of the Dirichlet trace^** ${\boldsymbol{\gamma}}_0$ on the Sobolev space $H^{\rm{Grad}} (\Omega, \mathbb{R}^{3})$. The space

^**The bold notation here distinguishes the vectorial case of elasticity from the scalar case of the wave equation.

is isomorphic to the range of the normal trace operator on the space $H^{{\rm{Div}} }(\Omega, \mathbb{R}^{3\times 3}_{\text{sym}})$. The kernel of the trace operator $\gamma_n$ corresponds to the space

which is dense in the space $L^2(\Omega, \mathbb{R}^{3\times 3}_{\text{sym}})$, since it contains $\mathcal{C}_0^\infty(\Omega, \mathbb{R}^{3\times 3}_{\text{sym}})$.

It is assumed that, for the linear elastodynamics problem with boundary control of the normal trace of the Cauchy stress tensor, the following Green formula holds:

where the observation operator $C^1 = {\boldsymbol{\gamma}}_0$ corresponds to the (vector) Dirichlet trace of the velocity, and $C^2 = 0$. The duality product corresponds to the duality product between $H^{1/2}(\partial\Omega, \mathbb{R}^3)$ and $H^{-1/2}(\partial\Omega, \mathbb{R}^3)$. By Theorem 3, a Stokes-Dirac structure is defined for the linear elastodynamic problem. The multiplicative constitutive operator

leads to a well-posed linear port-Hamiltonian system by Theorem 4.

3.3.   Kirchhoff-Love thin plates: ${\rm{(div \;Div, Grad \;}}\bf{grad}{\rm{) }}$ case

In this example, we consider the mechanical vibrations of thin plates by using the Kirchhoff-Love model, expressed by the following PDE defined on the bounded set $\Omega \subset \mathbb{R}^2$:

where $\mu$ is the mass density per unit area and the bending stiffness tensor ${\boldsymbol{\mathcal{D}}}_b : \mathbb{R}^{2\times 2}_{\text{sym}} \rightarrow \mathbb{R}^{2\times 2}_{\text{sym}}$ is a rank-4 tensor that is bounded, symmetric and positive definite almost everywhere. The port-Hamiltonian structure of this PDE can be exposed if the linear momentum and the strain tensor are selected as energy variables:

The Hamiltonian functional is quadratic with these variables:

The co-energy variables are given by

In this case, we consider uniform boundary conditions, given by the linear and angular velocities. The port-Hamiltonian formulation reads as follows (cf. [24,page 57]):

where $\gamma_{0}$ denotes the trace operator over the boundary, and $\gamma_1$ denotes the normal derivative trace, i.e., $\gamma_1 e^1 = \partial_{{\boldsymbol{n}}} e^1\vert_{\partial\Omega}$. For this case, the spaces and operators are as follows:

where ${\rm{Grad}}\; {\bf{grad}}\;$ corresponds to the Hessian operator and the following Sobolev spaces have been introduced:

The operator $\operatorname{div}{\rm{Div}} : L^2(\Omega, \mathbb{R}^{2\times 2}_{\text{sym}}) \rightarrow L^2(\Omega, \mathbb{R}^3)$ is a closed densely defined operator with domain $H^{ \operatorname{div}{\rm{Div}} } (\Omega, \mathbb{R}^{2\times 2}_{\text{sym}})$, while ${\rm{Grad}}\; {\bf{grad}}: L^2(\Omega) \rightarrow L^2(\Omega, \mathbb{R}^{2\times 2}_{\text{sym}})$ is a closed densely defined operator with domain $H^{2}(\Omega)$. This is known from the more general fact that the Hessian (i.e., the Gradgrad operator) and divDiv operators are part of the Hessian-Hilbert complexes and its corresponding adjoint complex, the divDiv complex, respectively ^[58,59,60]. The Hessian complex in two dimensions reads as follows:

where the homogeneous boundary conditions are defined within each Sobolev space. The corresponding dual domain complex (the divDiv complex) is given by

Since the problem is of second differential order, the input boundary space consists of a Cartesian product:

The space $H^{3/2}(\partial\Omega)$ is taken to be the space of traces of functions belonging to $H^2(\Omega)$. The normal derivative trace can be extended as a linear continuous surjective mapping [49,Th. 3.6.6]:

As a consequence, the $G$ operator is surjective. Furthermore, the kernel of $\gamma$ corresponds to the space

which is dense in $L^2(\Omega)$; see [49,Def. 13.4.6 and Prop. 3.6.7.]. By assumption, the following Green formula holds:

This Green formula is also reported in [61,Th. 2.2.] for $C^\infty(\Omega, \mathbb{R}^{2\times 2}_{\text{sym}})$ tensor fields and $H^2(\Omega)$ vector fields. The observation operator

corresponds to effective the shear force and bending momentum definitions, with ${\boldsymbol{t}}$ being the unit tangent vector to the boundary. The duality boundary product is given both by the duality product between $H^{1/2}(\partial\Omega)$ and $H^{-1/2}(\partial\Omega)$, and between $H^{3/2}(\partial\Omega)$ and $H^{-3/2}(\partial\Omega)$.

So, by virtue of Theorem 3, a Stokes-Dirac structure is defined for the Kirchhoff-Love model of this plate. Finally, defining the multiplicative constitutive operator

by Theorem 4, the Kirchhoff-Love model for thin plates with Dirichlet and Neumann boundary controls of the vertical displacement is a well-posed linear port-Hamiltonian system, with an effective shear force and bending momentum as collocated observations at the boundary.

3.4.   Maxwell equations: $({\bf{curl}}, {\bf{curl}})$ case

As the last example, we propose the Maxwell equations, which have already been treated in ^[7,62].

Let us denote ${\boldsymbol{E}}$ and ${\boldsymbol{B}}$ as the electric and magnetic fields, respectively, of a domain $\Omega\subset\mathbb{R}^3$, and ${\boldsymbol{D}}$ and ${\boldsymbol{H}}$ as the respective auxiliary fields ^[57]. The governing system is composed of the Maxwell-Ampère and Maxwell-Faraday dynamical equations:

where ${\boldsymbol{J}}$ is the free current density. Following ^[39], we do not consider the two static equations explicitly, namely, Maxwell-Gauss $\operatorname{div}({\boldsymbol{D}}) = \rho$ in the presence of a charge density, or Maxwell-flux $\operatorname{div}({\boldsymbol{B}}) = 0$.

The total electromagnetic energy is given in terms of the energy variables ${\boldsymbol{D}}$ and ${\boldsymbol{B}}$:

where $\epsilon$ is the electric permittivity and $\mu$ is the magnetic permeability.

The co-energy variables are then

Thanks to the following Green's formula (see e.g. [57,Theorem 3.31]):

where $\wedge$ denotes the vector product in $\mathbb{R}^3$, the electromagnetic power is computed as

where ${\boldsymbol{\Pi}} : = \gamma_0\left({\boldsymbol{E}} \wedge {\boldsymbol{H}} \right)$ is known as the Poynting vector. Using Ohm's law, i.e., ${\boldsymbol{J}} = \eta^{-1} {\boldsymbol{E}}$, with $\eta$ being the resistivity, the second term of the power balance is negative: $- \int_\Omega {\boldsymbol{E}} \cdot {\boldsymbol{J}} = - \int_\Omega \eta^{-1} \|{\boldsymbol{E}}\|^2 \le 0$. This is actually the Joule effect, which corresponds to a loss of energy in the thermal domain ^[17].

Regarding the boundary control, we again avoid mixed boundary conditions for the sake of simplicity because of the difficulty associated with the determination of the boundary functional spaces. Let us choose to control the twisted tangential trace of the magnetic field ${\boldsymbol{u}} = \gamma_t({\boldsymbol{H}}) : = {\boldsymbol{n}} \wedge \gamma_0 ({\boldsymbol{H}})$, and to observe the tangential trace of the electric field ${\boldsymbol{y}} = \gamma_T ({\boldsymbol{E}}) : = \left({\boldsymbol{n}} \wedge \gamma_0 ({\boldsymbol{E}}) \right) \wedge {\boldsymbol{n}}$. One may indeed verify that ${\boldsymbol{u}} \cdot {\boldsymbol{y}} = {\boldsymbol{\Pi}} \cdot {\boldsymbol{n}}$.

To summarize, the port-Hamiltonian formulation reads as follows:

together with the constitutive relations:

Using again the de Rham complex (3.1), one gets closed and densely defined $L$ and $K$ operators by setting

Also,

where:

We refer to [57,Chapter 3] for more details on $Y(\partial\Omega)$. For our purpose, we only use [57,Theorem 3.31], stating that $G$ is surjective. Furthermore, $\ker\gamma_t = \overline{\mathcal{C}^\infty_0(\Omega; \mathbb{R}^3)}$, with the closure being taken in $H^{{\bf{curl}}}(\Omega; \mathbb{R}^3)$, from [57,Theorem 3.33]. In particular, the kernel contains $\mathcal{C}^\infty_0(\Omega; \mathbb{R}^3)$, which is dense in $L^2(\Omega; \mathbb{R}^3)$. Hence, the kernels of $\gamma^i$, $i = 1, 2$, are dense in $\mathcal{X}^i$, $i = 1, 2$, respectively.

From (3.21), Theorem 3 applies: the electromagnetic problem with twisted tangential control of the magnetic field generates a Stokes-Dirac structure on the bond space $\mathcal{B} = \mathcal{E} \times \mathcal{F}$, with

Remark 11. Note that $\mathcal{Z}^i$, $i = 1, 2$ are not identifiable with the $\mathcal{Z}$ and $\mathcal{R}$ spaces that define the port formulation used in Proposition 3. Indeed, the former spaces have been used to prove that $\mathcal{J}$ generates a Stokes-Dirac structure on $\mathcal{B}$, while the latter consider the dynamics of the energy variables ${\boldsymbol{D}}$ and ${\boldsymbol{B}}$.

The splitting of $\mathcal{V}$ is then chosen based on either the algebraic point of view (considering flows and efforts), or the dynamical systems point of view (considering the energy and co-energy variables together with the resistive port). In this example, we either consider

for the algebraic point of view, or

for the dynamical systems point of view.

Note that, since $\mathcal{R} \neq \emptyset$, Theorem 2.4 cannot apply directly to this example; further work is needed to achieve the well-posedness of this constrained system, i.e., that $\eta^{-1} \not\equiv 0$ or $\not\equiv \infty$ (at the physical level, $\eta^{-1} = 0$ models a perfect insulator, whereas $\eta^{-1} = \infty$ models a perfect conductor). However, this system has already been proven to be well-posed for many kinds of boundary controls. See ^[62] and the references therein.

It is furthermore possible to define the linear multiplicative operator $Q : = \begin{bmatrix} \epsilon^{-1} & {\boldsymbol{0}} \\ {\boldsymbol{0}} & \mu^{-1} \end{bmatrix}$ relating the energy and co-energy variables, as well as the linear multiplicative operator $S : = \eta^{-1}$ accounting for the resistive constitutive law $\mathcal{S} \subset \mathcal{R} \times \mathcal{R}$, defined by Ohm's law: ${\boldsymbol{e}}_{{\boldsymbol{J}}} = S {\boldsymbol{f}}_{{\boldsymbol{J}}}$.

3.5.   Summary of the examples

Let us summarize the above examples in Table 1.

4.   Perspectives and conclusion

The proposed construction shows how linear wave-like systems can be associated with the Stokes-Dirac geometric structure via the theory of boundary control systems. In particular, linear elastodynamic problems fit into this framework. This extends the canonical Stokes-Dirac structure defined in ^[39], which includes the case of scalar and electromagnetic waves only. This allows one to deduce the well-posedness of the considered class of port-Hamiltonian systems.

The correct specification of the functional analytic framework is crucial for discretization purposes. For instance, in a finite-element context, discrete spaces for the variables are chosen in suitable subspaces of the infinite-dimensional functional spaces. The assumed structure of the systems under consideration can be readily discretized using mixed finite-element strategies. In particular, the employment of mixed finite elements for port-Hamiltonian systems has been explored in ^[63], where it is shown how several systems, linear and nonlinear, can be structurally discretized via finite elements. A complete proof of convergence of mixed finite elements with boundary control is presented in ^[64], where it is proven that several families of finite elements, beyond those satisfying a de Rham subcomplex property, lead to convergence. A geometric viewpoint is instead presented in ^[65], where the discretization mimetically represents the continuous weak formulation via finite-element differential forms that constitute a de Rham subcomplex. This approach leads to a primal-dual formulation that is capable of retaining the power balance at the discrete level. Finite-element exterior calculus provides a framework for the discretization of partial differential equations, unifying concepts from topology, geometry and algebra. For this reason, a natural extension of this work would consist of combining the functional analytic setting with the geometric one.

The inclusion of unbounded dissipation operators that occur in, e.g., Rayleigh damping, represents another important development of the present work. Furthermore, extending the presented analysis to nonlinear constitutive relations is also of fundamental interest for applications. In this case, convexity of the Hamiltonian constitutes a fundamental hypothesis to establish well-posedness.

Aknowledgment

The authors would like to thank Pr. Jean-Pierre Raymond, from Université de Toulouse, for fruitful discussions and helpful advice about functional analysis. Moreover, the authors would like to thank the anonymous reviewers who helped to correct and improve the original version of the manuscript.

This study was funded in part by the European Research Council, the PortWings Project, grant no. 787675, and by the Agence Nationale de la Recherche (France), IMPACTS, grant no. ANR-21-CE48-0018.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there is no conflict of interest.