Global existence and stability of temporal periodic solution to non-isentropic compressible Euler equations with a source term

1.   Introduction

Modern industrial systems are frequently created with exacting criteria of quality. There are many different methods used to improve system reliability. A redundant structure is a method for further developing system reliability. For instance, a cloud storage server typically has a minimum of one backup to assist users in protecting sensitive data. In the same vein, a commercial aircraft is equipped with a backup engine for use in the event of unexpected malfunctions. In many industrial products, such as production systems, pump systems, power generation systems, etc., the reliability of systems is impacted by a number of factors when they are added to be used within the actual environment, including operating environments, outdoor shocks, operators, and so on. One way to look at these factors is as stresses the system experiences while it is operating. In such situations, the stress-strength (S-S) model is normally used to evaluate the parallel machine's reliability. The S-S version, first offered through Birnbaum and McCarty ^[1], is one of the most widely used reliability fashions. For this model, it fails if its stress exceeds its strength. Therefore, device reliability can be described as the probability that the device's strength exceeds its stress. That is expressed mathematically in the form $R = P(Y < X)$, where $X$ stands for the stress variable and $Y$ for the system's strength. Numerous statistical issues, including those involving quality control, engineering, clinical, and biostatistics, have found use for the S-S model. In the context of medical research, for instance, the variable $R$ quantifies the efficacy of a novel treatment in relation to its control; in this case, $X$ and $Y$ stand for the new treatment's and the control's respective effects. Similar to this, in engineering studies, $R$ stands for the likelihood that a system component's strength ($Y$) will exceed the system's external stress ($X$). An overview of all the techniques and consequences related to the S-S version is provided by Kotz et al. ^[2].

Evaluating the reliability of the S-S model using different statistical techniques has been the focus of a lot of research lately. For example, Ghitany et al. ^[3] presented point and interval estimates of the reliability of the S-S model under a Lindley power distribution. They used maximum likelihood estimators (MLEs) as well as parametric and nonparametric bootstrapping techniques. Using recorded samples from two parameter generalized exponential distribution, Asgharzadeh et al.^[4] estimated the S-S model $P(Y < X)$. The process of establishing a generalized inference on the S-S model based on the unknown parameters of the generalized exponential distribution was carried out by Wang et al ^[5]. With the growing interest in this system and the importance of Chen distribution, which has become evident in the past two decades, in order to obtain point and interval estimates for a multicomponent $R$ of an $S$-out-of-$j$ system, Kayal et al. ^[6] used classical and Bayesian methods under the assumption that both the S-S variables follow a Chen distribution with a common shape parameter. The reliability estimation of $R$ when the failure times are progressively Type-Ⅱ censored and both the latent strength and stress variables originate from the inverse exponential Rayleigh distribution was discussed by Ma et al. ^[7]. Moreover, Agiwal ^[8] developed a Bayesian estimation method to estimate $R$ where $X$ and $Y$ are inverse Chen random variables. Recently, Sarhan and Ahlam ^[9] have given attention to the estimation of $R$ for step-stress partial acceleration life testing, when the stress and strength additives are independent random variables generated from Weibull distributions with specific shape and scale parameters.

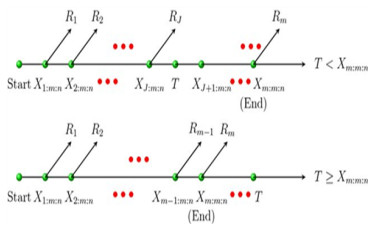
To gather information about the lifetime and reliability characteristics of products (Contreras-Reyes et al. ^[10]), various units are typically used during life testing experiments. In actuality, it is sometimes not possible to finish experiments until all failures are noted due to time and financial constraints. To increase test efficiency in this regard, several censoring schemes and testing techniques are suggested. In practice, the most commonly used methods in the literature are type Ⅰ and type Ⅱ control. According to these methods, life tests terminate or stop after a specified time or a specified number of failures, respectively. Through various life testing experiments, there are many different challenges that experimenters face in order to be able to control the testing time as well as keep the experimental units intact, so stopping the experiment before all experimental units fail is one of the solutions to achieve these goals. This is done through the use of control structures that rely on deferring some active devices from the experiment. The progressive censoring system is considered one of the experimental designs commonly used in recent years, as through this system, survival units are arbitrarily removed from the test at any stage of the test. As a result, it is more adaptable and efficient than conventional censoring techniques. Over time, numerous models of progressive censorship have been discussed. According to this model, censoring has been divided into two parts: When the experiment ends after a specific time, this section is called progressive censoring of the first type, while the second part is progressive censoring of the second type, and in this section the experiment stops after a predetermined number of failures appear. Through both sections, experimenters will be able to freely remove test units during the experiment at nonterminal times. Whithin a type-Ⅱ progressive censoring scheme, to test the life of units, the experimenter puts $n$ units through the test at time zero, and only $m$ units that fail completely are observed. With the primary failure, which may take the shape $X_{1}$, $R_{1}$ is randomly eliminated from the final devices within the test. At the time of the second failure $X_{2}$, the experimenter selects a random number of final units, let it be $R_{2}$, and they are removed from the experiment. Finally, in the same sequence, at the time of the $m$th failure, $X_{m}$ the experimenter removes all remaining units $R_{m}$ from the experiment, where

When test units are highly reliable, the long testing time represents one of the main drawbacks of the progressive type-Ⅱ censoring model. For this reason, Ng et al. ^[11] suggested an improved model (see Figure 1) that allows for adjustments to the censoring scheme throughout the experiment.

This improved model is known in the literature as the adaptive type-Ⅱ progressive censoring model. The technique of this model can be explained as follows:

(1) First, the effective sample size $m$, the number of units to be tested $n$, the progressive censoring scheme ($R_{1}, R_{2}, ..., R_{m}$), and the time point $T$ must be determined in advance before the beginning of the experiment.

(2) As indicated by the preceding progressive censoring strategy, $R_{1}$ units are arbitrarily eliminated from the test at the moment of the first failure $X_{1:m:n}$. $R_{2}$ units are also arbitrarily removed from the test at the moment of the second failure, $X_{2:m:n}$, and so on.

(3) When the $m$th failure occurs before time $T$ (i.e., $X_{m:m:m} < T$), the test ends at this point with the unchanged progressive censoring scheme

and we will have the standard progressive type-Ⅱ censoring.

(4) In the event where $X_{J:m:n} < T < X_{J+1:m:n}$, where $J < m$ and $X_{J:m:n}$ is the $J$th failure time to occur before the time $T$, no surviving item will be removed from the test by placing

and at the time $X_{m:m:n}$, all remaining units $R_{m}^{\ast }$ are removed, where

Because of this, the progressive censoring scheme that is being used in this instance is ($R_{1}, R_{2}, ..., R_{J}, 0, 0, ..., 0, n-m-\sum\limits_{i = 1}^{J}R_{i}$).

(5) After running the previously specified test, we may get the following adaptive progressive type-Ⅱ censored observation data

For more details on recent developments using the adaptive type-Ⅱ progressive censoring, one may refer to Almuqrin et al. ^[12], Al-Essa et al. ^[13], Dutta et al. ^[14], and Lv et al. ^[15].

Many scientific and engineering applications use a variety of distributions, including gamma, exponential, Rayleigh, normal, Weibull, and others, to model the lifetime characteristic of products. Among the various probabilistic models, bathtub-shaped failure rate distributions have drawn a lot of attention. These models are highly helpful for studying complex systems or subsystems and for making decisions, particularly when the target product's entire life cycle needs to be modeled. Regarding this, numerous authors have proposed and discussed in literature a variety of probability models featuring bathtub-shaped failure rate functions. The bathtub-shaped hazard function offers a suitable conceptual model for the lifespan of humans as well as certain mechanical and electronic products. Xie and Lai ^[16], Wang et al.^[17], and Xie et al. ^[18] are only a few of the writers whose articles contain references to the earlier comprehensive work on parametric probability distributions with bathtub-shaped failure rate function. The Chen distribution is considered one of the most important distributions that contain bathtub curves.

Chen ^[19] introduced a distribution that is often called the Chen or bathtub-shaped distribution with two parameters in the literature. It is a significant probability model that is frequently applied to lifetime analysis. This probability model is truly crucial for studying physical events for which the hazard rate function predicts bathtub-shaped behavior. It gives complex systems whose failure rates vary over time a flexible way to be modeled. One of the primary features of the Chen distribution is its bathtub-shaped failure rate curve, which has three unique phases (decreasing, constant, and ascending) and may be used to describe a wide range of systems. This curve has a wide range of potential applications, including researching the efficacy of medications or therapies across various age groups. It can be helpful when analyzing mortality data as well. When modeling the reliability of items or systems that are prone to wear and tear, one might employ the Chen distribution. For the Chen distribution, these are the probability density function (PDF) and cumulative density function (CDF):

and

Here, both $\alpha$ and $\beta$ are known as shape parameters. The Chen distribution's hazard rate function (HRF) is presented in the manner shown below:

The Chen distribution's HRF (3) has a bathtub form with a minimum at $(\frac{ 1-\beta }{\beta })^{1/\beta }$, when $\beta < 1$. It increases when $\beta \geq 1$. This distribution may be used to describe many kinds of failure-time data quite well since it is fairly adaptable. For example, if we select $\beta = 1$ in (1), this distribution further transforms into a Gompertz distribution with parameters 1 and $\alpha$. When $\alpha = 1$, the exponential power distribution results. If $x\sim$Ch($\alpha, \beta$) and we take

the distribution turns into a Weibull distribution with parameters $\alpha$ and $\theta$.

Some important characteristics of the Chen distribution distinguish it from other two-parameter models: The hazard rate function has a bathtub shape, and the joint confidence regions and shape parameter confidence intervals are closed-form. As a result, researchers have paid close attention to this distribution in recent years due to its broad applicability in simulating a variety of real-life phenomena. For a brief review, using progressive type-Ⅱ censoring, Wu ^[20] calculated the MLEs of the unknown parameters and approximated their intervals. Rastogi et al. ^[21] achieved the Bayesian inference of this distribution against various symmetric and asymmetric loss functions. Using data that was progressively censored, Kayal et al. ^[22] looked at the Bayesian one and two sample prediction. Ahmed et al. ^[23] observed the Chen distribution for a competitive risk model with progressive type-Ⅱ censored data.

Here, we derive the expression of the S-S reliability coeficient defined by

when the independent random variables $X$ and $Y$ follow the Chen distributions Ch($\alpha _{1}, \beta$) and Ch($\alpha _{2}, \beta$), respectively. Since Chen's distribution contains two shape parameters, we will assume that for both $X$ and $Y$, the second shape parameter, $\beta$, is the same. Two reasons of this condition are (ⅰ) the reliability parameter cannot be obtained explicitly when the two shape parameters are different; (ⅱ) the condition $\beta _{1}\neq \beta _{2}$ increases the complexity of the likelihood function under adaptive progressive censored samples. After a linear integral is expanded, we obtain

It is important to note from Eq (4) that the S-S reliability parameter $R$ is in a closed form, and it is a function of $\alpha _{1}$ and $\alpha _{2}$. Also, as the strength parameter $\alpha _{1}$ increases, $R$ decreases for the fixed values of the stress parameter $\alpha _{2}$. Since $R$ is independent of the common shape parameter $\beta$, utilizing Eq (4) to derive $R$ is an easy task. This is only possible if the values of the parameters $\alpha _{1}$ and $\alpha _{2}$ are known or can be calculated using various estimation techniques.

It is worth noting that the evaluation depends on whether this probability ($R = P\left(Y < X\right)$) is less than or greater than $0.5$. The result is evaluated and interpreted as follows:

(1) The lifetime of the two products or any two units is equal if $R = 0.5$.

(2) If $R > 0.5$, the lifetime of Unit/Product 1 exceeds that of Unit/Product. For example, if $R = 0.7$, Unit/Product 1 is better than Unit/Product 2 with a probability of 70%.

(3) If $R < 0.5$, the lifetime of Unit/Product 2 exceeds that of Unit/Product 1. For example, if $R = 0.20$, Unit/Product 2 is better than Unit/Product 1 with an $80\%$ probability.

We discover several examples of efforts that have been done in the literature to estimate the $R$ parameter when the variables follow the Chen distribution: Sarhan et al. ^[24] used the maximum likelihood and Bayes procedures to determine the reliability $R$ in the case of two independent r.v.s., $X$ and $Y$, using a two-parameter Chen distribution. Based on upper record values, Tarvirdizade and Ahmadpour ^[25] and Raqab et al. ^[26] have investigated the calculation of the S-S reliability for the two-parameter Chen model. Shoaee and Khorram ^[27] examined the S-S reliability of this lifetime distribution using type-Ⅱ progressively censored data. According to Wang et al. ^[28], a multicomponent system is reliable when its strength and stress follow Chen distribution.

Although the inference procedures of S-S models under complete samples have been well-studied in the literature, the issue of censored data, specifically, adaptive type-Ⅱ progressive censored data has received less attention. In this work, we study the problem of estimating the S-S parameter $R$ where $X$ and $Y$ are independent Chen random variables with distinct shape parameters, using adaptive progressive type-Ⅱ censored samples. Our problem is motivated by the fact that adaptive progressive type-Ⅱ censored samples have some additional advantages in life testing experiments. Where in this censoring scheme, we can ensure the final effective sample size, and that the experiment will end as soon as possible. The main contributions are:

(1) To derive the MLE of $R$.

(2) To derive the Bayes estimators of $R$ based on different general loss functions.

(3) To examine $R$'s statistical inference using the delta approach.

(4) We perform numerical simulations to assess the accuracy of Bayesian and frequentist procedures.

(5) In order to show how the suggested inferences may be applied by analyzing actual datasets.

The following describes the paper's methodology: First, we'll estimate $R$ using the ML technique. Next we will discuss the asymptotic confidence interval of $R$. The delta approach is used to estimate the variance of the $R$ estimator in order to achieve the required confidence interval. Second, the balanced loss function is taken into account in order to compute Bayesian estimates of $R$, with special attention paid to the balanced square error loss function (BSEL) and the balanced exponential loss function (BLINEX). In the last ten years, the Markov chain Monte Carlo (MCMC) technique has become a popular solution to the Bayesian approach to deal with the problem of many integrals arising in the posterior distribution. Using this technique, we calculate the Bayes estimates and credible intervals for $R$. A comprehensive numerical comparison of the presented estimates with respect to means squared errors, coverage probabilities, and confidence lengths is carried out.

The structure of the paper is as follows after this introduction. In Section 2, we give the expression for $R$ of Chen distribution. The MLE of $R$ and the associated approximate confidence interval as will as boot-p confidence interval are also discussed. In Section 3, we derive the Bayesian estimate $R$ and the its credible interval using the Gibbs technique within Metropolis-Hastings (MH). In Section 4, we present an examination of an actual dataset. In Section 5, we do a Monte Carlo simulation analysis to compare the suggested values of $R$. In Section 6, we finally bring the article to a close.

2.   MLE of $R$

Suppose

is an adaptive type-Ⅱ progressive censored sample from Ch($\alpha _{1}, \beta$) with the scheme $\{m_{1}, n_{1}, T_{1}, R_{1}, R_{2}, ..., R_{m_{1}} \}$ such that

Additionally,

is an adaptive type-Ⅱ progressive censored sample from Ch($\alpha _{2}, \beta$) under the scheme $\{ m_{2}, n_{2}, T_{2}, S_{1}, S_{2}, ..., S_{m_{2}} \}$ such that

For

according to the two independent random samples $X$ and $Y$, the likelihood function (LF) is provided by

where

and

Wu ^[20] provides the LF (5) for $R$ in the progressive censored sample case, which is produced in the situation $T_{1} = T_{2} = \infty$. Moreover, the LF for $R$ in the complete sample is reached when $T_{1} = T_{2} = \infty$ and $R_{i} = S_{i} = 0$, as reported by Sarhan et al. ^[24]. The following may be used to represent the LF for the observed sample data, $X$ and $Y$, using Eqs (1), (2), and (5):

Ignoring the additive constants $C_{J_{1}}$and $C_{J_{2}}$, the log-LF, say,

is given by:

The first order derivatives of the log-LF, with respect to $\alpha _{1}$, $\alpha _{2}$, and $\beta$ are

and

From (8) and (9), we obtain

where,

and

In the case that the parameter $\beta$ is known, the MLE of $\alpha _{1}$ and $\alpha _{2}$ can be obtained directly from the Eq (11). However, when the all parameters are unknown, the parameter $\beta$ will be estimated by maximizing the profile log-likelihood function $\mathcal{L} (\hat{\alpha}_{1}\left(\beta \right), \hat{\alpha}_{2}\left(\beta \right), \beta)$, with respect to $\beta$ by solving the following nonlinear equation:

where

and

The nonlinear Eq (14) has a fixed point solution at $\hat{\beta}$, which may be found by using the following straightforward iterative method:

where,

Since $\hat{\beta}$ is the fixed point solution of Eq (17), it may be derived by applying an iterative approach as follows:

where $\beta ^{\left(k\right) }$ denotes the $k^{th}$ iterate value of $\hat{\beta}$. Once $\vert\beta _{\left(k\right) }-\beta _{\left(k+1\right) } \vert$ is little enough, the iteration process should end. In the real data application, we use the fixed point method to obtain the MLE of unknown parameter $\beta$. This technique's starting value is established by drawing the two functions $z = \beta$ and $z = h\left(\beta \right)$ and observing their intersection, where $z = h\left(\beta \right)$ is defined in Eq (18).

Using $\hat{\beta}$, we can now apply Eq (11) to obtain $\hat{\alpha}_{1}$ and $\hat{\alpha}_{2}$ as $\hat{\alpha}_{1}(\hat{\beta})$ and $\hat{\alpha} _{2}(\hat{\beta})$, respectively. Thus, the MLE of $R$ under the common parameter situation may be derived from Eq (4) using the invariance property as

2.1.   Approximate confidence interval estimation of $R$

In this section, we construct asymptotic confidence interval (ACI) of $R$ using the asymptotic distribution of MLE $R$. The Fisher information matrix of

is

where

for $i, j = 1$, $2$, $3$, is the observed information matrix defined by

From the log-LF (7), we have the second derivatives of $\mathcal{L}$ with respect to $\alpha _{1}$, $\alpha _{2}$, and $\beta$, which are illustrated in the following:

and

The expectations of the entries of the observed information matrix cannot be obtained analytically. Therefore, the Fisher information matrix

can be obtained by using numerical methods.

Theorem 1. When $n\rightarrow \infty$, one has

where $I^{-1}(\hat{\Theta})$ is the inverse of Fisher information matrix $\mathbf{I}(\Theta)$, given by

Proof. The multivariate central limit theorem and the asymptotic condition of MLE may be used to show the outcome. □

Theorem 2. When $n\rightarrow \infty$, one has $\sqrt{n}\left(\hat{R}-R\right) \overset{d}{\rightarrow }N(0, nVar(R))$, where

where,

Proof. Wang et al. ^[28] provides the complete proof of this theorem. □

We would like to point out here that all the theories and their proofs for the asymptotic normality of the obtained estimators are included in ^[28]. As an immediate consequence, substituting $\Theta$ by its MLE, $\hat{\Theta}$, and for arbitrary $0 < \gamma < 1$, a two-sided $100(1-\gamma)\%$ ACI of $R$ is given by

where $z_{\frac{\gamma }{2}}$ is the upper $\frac{\gamma }{2}$th quantile of the standard normal distribution,

and

The ACI derived in Eq (24) can have a negative bottom bound in some circumstances. To overcome this issue, Wang et al. ^[17], for instance, explained how to use the logarithmic transformation and delta techniques to obtain the asymptotic normality distribution of $\ln \hat{R}_{ML}$, where,

With this in mind, a $100(1-\gamma)\%$ ACI of $R$ obtained can be constructed as

where

2.2.   Bootstrap confidence interval of $R$

Based on the asymptotic results, it is evident that a small sample size decreases the confidence interval's performance. For this, we use the percentile parametric bootstrap technique to generate a confidence interval; see Efron and Tibshirani ^[29] for further details. The following process illustrates how to find $R$'s percentile Boot-p confidence interval.

Step 1. The initial values are established for the following: $\alpha _{1}$, $\alpha _{2}$, $\beta$, $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$, $T_{1}$, $T_{2}$, and progressive censoring schemes ($R_{1}, R_{2}, ..., R_{m_{1}}$) and ($S_{1}, S_{2}, ..., S_{m_{2}}$).

Step 2. Using the previous initial inputs, independent samples ($x_{1:m_{1}:n_{1}}, x_{2:m_{1}:n_{1}}, ..., x_{m_{1}:m_{1}:n_{1}}$) and ($y_{1:m_{2}:n_{2}}, y_{2:m_{2}:n_{2}}, ..., y_{m_{2}:m_{2}:n_{2}}$) are generated from Ch($\alpha _{1}, \beta$) and Ch($\alpha _{2}, \beta$), respectively. The procedures listed below are used to create the adaptive progressively type Ⅱ censored datasets from Chen lifetime (see to Kundu and Gupta ^[30]).

ⅰ) From a typical uniform distribution $U(0, 1)$, generate $m_{1}$ independent and identical observations $W_{1}, W_{2}, ..., W_{m_{1}}$ of size $m_{1}$.

ⅱ) Establish

for $i = 1, ..., m_{1}$.

ⅲ) For each $i = 1, 2, ..., m_{1}$, evaluate

Thus, the progressive Type-Ⅱ censored sample $\{ Z_{1}, Z_{2}, ..., Z_{m_{1}} \}$ originates from the $U(0, 1)$ distribution.

ⅳ) To compute the sample data from $Ch$($\alpha _{1}, \beta$) of the progressive type-Ⅱ censoring scheme, given the starting values of $\alpha _{1}$ and $\beta$, one may set

where $i = 1, 2, ..., m_{1}$.

ⅴ) Determine the value of $J_{1}$, which satisfies $X_{J_{1}:m_{1}:n_{1}} < T_{1} < X_{J_{1}+1:m_{1}:n_{1}}$, and remove the sample $X_{J_{1}+2:m_{1}:n_{1}}, ..., X_{m_{1}:m_{1}:n_{1}}.$

ⅵ) Using the truncated distribution $\frac{f(x, \alpha _{1}, \beta)}{1-F(x_{J_{1}+1:m_{1}:n_{1}})}$, get the first $m_{1}-J-1$ order statistics ($X_{J_{1}+2:m_{1}:n_{1}}, ..., X_{m_{1}:m_{1}:n_{1}}$), where the sample size is $n_{1}-m_{1}-1-\sum_{i = 1}^{J_{1}}R_{i}$.

ⅶ) Using steps i-vi, we generate two adaptive progressive type-Ⅱ censoring data ($x_{1}, x_{2}, ..., x_{m_{1}}$) and ($y_{1}, y_{2}, ..., y_{m_{2}}$) from Ch($\alpha _{1}, \beta$), Ch($\alpha _{2}, \beta$), respectively.

Step 3. The generated data is used to calculate the MLEs for $\alpha _{1}$, $\alpha _{2}$, $\beta$, and then using Eq (19), the MLE for $R$ is estimated.

Step 4. Bootstrap samples from Ch($\hat{\alpha}_{1}, \hat{\beta}$) and Ch($\hat{\alpha}_{2}, \hat{\beta}$) were created using the preceding stages. These samples may be expressed as ($x_{1}^{\ast }, x_{2}^{\ast }, ..., x_{m_{1}}^{\ast }$) and ($y_{1}^{\ast }, y_{2}^{\ast }, ..., y_{m_{2}}^{\ast }$).

Step 5. With the bootstrap samples provided, calculate bootstrap estimates $\hat{\alpha}_{1}^{\ast }$, $\hat{\alpha} _{2}^{\ast }$, and $\hat{\beta}$. Subsequently, compute the bootstrap estimate of $R$, say $R^{\ast }.$

Step 6. Steps 3 and 4 can be repeated $B$ times to provide $B$ numbers of $R$'s bootstrap estimators, let it be$\ R^{\ast (b)}$, $b = 1$, $2$, $...$, $B$.

Step 7. After the preceding step, the bootstrap estimates of $R$ need to be ordered as follows: $R^{\ast \left[ 1\right] }, \ R^{\ast \left[ 2\right] }, ..., \ R^{\ast \left[ B\right] }$.

Step 8. For the variable $R$, the two-sided $100(1-\gamma)\%$ bootstrap confidence interval is provided

3.   Bayes estimation of $R$

The Bayes estimator and associated credible interval of $R$ are constructed in this section.

3.1.   Prior and posterior distributions

Because of its simplicity and ease of computation, the gamma prior is taken into consideration for the parameter in a variety of lifetime models as an informative prior. It is a distribution with a peak close to zero and a tail that extends to infinity. This means that we can actually simplify the solution to the posterior distribution. Consequently, it is believed that we have separate gamma priors for the unknown parameters $\alpha _{1}$, $\alpha _{2}$, and $\beta$. Mathematically, the independent prior distributions will take the following forms:

In this case, the values of $a_{1}$, $b_{1}$, $a_{2}$, $b_{2}$, $a_{3}$, and $b_{3}$ are selected to represent past understandings of $\alpha _{1}$, $\alpha _{2}$, and $\beta$. It should be noted that if the hyper-parameters are taken to be zero ($a_{1} = b_{1} = a_{2} = b_{2} = a_{3} = b_{3} = 0$), then gamma prior reduces to non-informative form.

The joint prior distribution and the LF $L(\Theta |data)$ are used in the Bayesian technique to create the posterior distribution of any parametric space ($\Theta$). Thus, the following joint posterior density of $\alpha _{1}$, $\alpha _{2}$, and $\beta$ is derived from Eqs (6) and (28)–(30).

where, $\ U(X, \beta)$ and $V(Y, \beta)$ are given by (12) and (13), respectively. Below is the definition of the standardizing constant $A$:

where

In decision theory, defining a loss function is essential to determine the optimal estimator and utilize it to express the lowest statistical error (risk) connected to each potential estimate. To make the computations easier, a squared error loss function is used by several writers to generate Bayesian estimates. However, this loss function's primary critique is that it gives equal weight to overestimation and underestimating, which is at odds with real-world practices. In the literature, a number of asymmetric loss functions have been put out to deal with this situation. We mention the linear exponential (LINEX) (Varian ^[31] and generalized entropy (Calabria and and Pulcini ^[32]) loss functions as some of the asymmetric loss functions that are used in the literature.

To calculate the posterior distribution of $R$, we have the following transformation: $\alpha _{2} = W$. Then from (4), we have

The posterior distribution of $R$ and $W$ can be calculated by the following formula:

In the above formula, $J$ is called Jacobian and is calculated as follows

In the next subsection, we will focus on a more general loss function, which is the balanced loss function to estimate $R$ via the Bayesian approach. It includes several symmetric and nonsymmetric loss functions. Both the BLINEX and BSE loss functions may be obtained from it.

3.2.   Balanced loss function

A generalized loss function known as the balanced loss function (refer to Jozani et al.^[33]) has the following form:

where $\rho$ represents an arbitrary loss function, a previously chosen "target" estimator of $\Theta$ is $\delta _{0}$, which can be determined by the MLE or any other estimator. The weight $\omega$ has values in the interval $[0, 1)$.

Selecting

allowed (36) to be simplified to the BSE loss function, which Ahmadi et al. ^[34] utilized in the following form:

and the associated Bayes estimate for the unidentified parameter $\Theta$ is provided by

The loss function for BLINEX with shape parameter $c$ ($c\neq 0$) may be derived by selecting

$c\neq 0$ (Zellner ^[35]).

Thus, under the BLINEX loss function, the Bayes estimate of $\Theta$ is provided by

Keep in mind that balanced loss functions are more widely applicable; as special cases, they consist of the MLE and the symmetric and asymmetric Bayes estimates. Equation (38) may be used to get the MLE for $\omega = 1$, as well as the squared error loss function (symmetric) when $\omega = 0$. Furthermore, the Bayes estimator under the BLINEX loss function in (40) reduces to MLE when $\omega = 1$, and when $\omega = 0$, it leads to the LINEX loss function (asymmetric) situation.

Based on the BSE loss function, the Bayes estimator for $R$ may be obtained from (38) by

and from (40), which yields the Bayes estimator for $R$ under the BLINEX loss function,

It is well-known that assuming the BSE loss function, the Bayesian estimator of $R$ can be obtained also from (34) and (38) by

Additionally, the Bayesian estimator of $R$ under the BLINEX loss function is given as follows:

where $c\neq 0,$ $\pi ^{\ast }(R, W, \beta |data)$ is given by (34).

Since it is often difficult to discover the analytical solution, the Bayes estimators in Eqs (43) and (44) require many integrations, for which computational and numerical approaches are required to confront the integrals. Therefore, in the next subsection, the MCMC approach is considered to approximate these integrations. The MH algorithm (Hastings ^[36]) will be implemented to compute the Bayes estimates and credible intervals width of $R$ under BSE and BLINEX loss functions.

3.3.   Bayes estimation via MCMC approach

Sampling from the posterior is done directly for complex functions using the MCMC method, which was suggested by Robert and Casella ^[37]. Using the preceding value from the specified function, this creates a chain or sequence of random samples. Thus, sampling methodology is the foundation of this process in order to compute and encounter the high-dimensional function. The Gibbs sampler and the MH algorithm are two main techniques utilized in this procedure. The Gibbs sampler, initially introduced by Casella and George ^[38], is among the most precisely described MCMC sampling algorithms. Wherein the conditional posterior distribution, a lower-dimension functional form is obtained from the high-dimensional parametric model. The Gibbs approach must decompose the joint posterior distribution into full conditional distributions for each parameter in the model. Computing Bayesian estimates of $\Theta$, as well as any function of $\Theta$, requires sampling from each of these conditional distributions.

Specifically, (31) shows that it is not possible to get explicit forms for the marginal posterior distributions for each parameter. It can be demonstrated that given $\alpha _{2}$, $\beta$, and data, the conditional density of $\alpha _{1}$ is given by

Given $\alpha _{1}$, $\ \beta$, and data, the conditional density of $\alpha _{2}$ is

and, correspondingly, given $\alpha _{1}$, $\alpha _{2}$, and data, the conditional density of $\beta$ is

Evidently, samples of $\alpha _{1}$ and $\alpha _{2}$ using (45) and (46), respectively, are readily produced with any procedure for producing gamma. Unfortunately, standard techniques cannot sample the conditional posterior distribution of $\beta$ (Eq (47)) directly since it cannot be analytically reduced to a known distribution. A standard alternative that does not require completion and an increase in the dimension is the MH algorithm. It is more straightforward to use in high dimensions, applicable without an envelope, and has a normalizing effect compared to other iterative techniques. The major difference with the Gibbs sampler is that we need to choose the proposal distribution, which can be a priori anything. In order to get random numbers from (43), here we apply the MH algorithm within Gibbs sampler algorithm to compute Bayes estimate as well as credible intervals of $R$ under adaptive progressive type Ⅱ censoring. We estimate the marginal posterior density $\pi _{3}(\beta |\alpha _{1}, \alpha _{2}, data)$ by using normal proposal distribution $N(\beta ^{\left(p-1\right) }$, Var$(\hat{\beta}))$, where Var$(\hat{\beta})$ represents the variance of $\beta$ and $\beta ^{\left(p-1\right) }$ is the current value of $\beta$.

The following procedures illustrate how the MH algorithm functions within Gibbs sampling to simulate posterior samples:

(1) Use the MLEs of ($\alpha _{1}, \alpha _{2}, \beta$) as the initial point of the iteration, denoted by ($\alpha _{1}^{\left(0\right) }, \alpha _{2}^{\left(0\right) }, \beta ^{\left(0\right) })$.

(2) Set $p = 1$.

(3) Generate $\alpha _{1}^{\left(p\right) }$ and $\alpha _{2}^{\left(p\right) }$ from Gamma($m_{1}+a_{1}, b_{i}+U(X, \beta ^{\left(p-1\right) }))$, and Gamma($m_{2}+a_{2}, (b_{2}+V(Y, \beta ^{\left(p-1\right) })$), respectively, where $U(X, \beta ^{\left(p-1\right) })$ and $V(Y, \beta ^{\left(p-1\right) })$ are given, respectively by

and

(4) With a normal proposal distribution, $N(\beta ^{\left(p-1\right) }$, Var$(\hat{\beta}))$, create $\beta ^{\left(p\right) }$ from $\pi (\beta ^{\left(p-1\right) }|\alpha _{1}^{\left(p\right) }, \alpha _{2}^{\left(p\right) }, data)$ using the flowing MH:

ⅰ) Compute the acceptance probabilities

ⅱ) Generate $u$ from uniform distribution.

ⅲ) If $u < \beta ^{\ast }$, accept the proposal and set $\beta ^{\left(p\right) } = \beta ^{\ast }$; otherwise, put

(5) Compute the S-S reliability measure

(6) Place $p = p+1$.

(7) Go through steps 3–6 $N$ times.

To ensure convergence and eliminate any bias in the initial value selection, the first $M$ simulated variates are eliminated. Then, for sufficiently big $N$, the selected sample, $R^{\left(p\right) }, p = M+1, ..., N$ creates an estimated posterior sample that may be utilized to construct the Bayesian inference of $R$.

Using the BSE loss function provided by (41), the estimated Bayes estimate of $R$ is obtained as follows:

Also, the approximate Bayes estimate for $R$, under BLINEX, from (42) is subsequently provided by

Additionally, the approximated/estimated $100(1-\gamma)\%$ credible intervals for $R$ are given by $\left(R_{\left[ \gamma /2\right] }, \ R_{ \left[ 1-\gamma /2\right] }\right)$, which may be obtained by sorting $R^{\left(p\right) }, p = M+1, ..., N$ in ascending orders; see Chen and Shao ^[39]. The number in the burn-in phase is $M$ here. In the same way, the Bayes estimator for $R$ can be found from relations (43) and (44).

The purpose of the next section is to clarify how to apply the previously suggested approaches to actual occurrences that occur in the real world.

4.   Carbon fiber data application

Carbon fiber is composed of strong, thin crystalline carbon strands, which are effectively extended chains of carbon atoms joined by a bond. Since fibers are light, robust, and extremely durable, they are employed in several processes to create excellent structural materials. They are currently employed as steel and plastic substitutes. Therefore, we used actual carbon fiber data from Badr and Priest ^[40], which expresses the draw of impregnated carbon fibers at 1000 GPa (gigapascals) and the strength of single carbon fibers. Single fibers with gauge lengths of 20 mm (dataset Ⅰ) and 10 mm (dataset Ⅱ) underwent tension testing. The appropriate sample sizes are $N_{1} = 69$ and $N_{2} = 63$, in that order. After deducting 0.75 from each of the datasets, Kundu and Gupta ^[30] examined the changed datasets and fitted the Weibull models to each of them independently. Similarly, Çetinkaya and Genç ^[41] fit the power model for each dataset independently after multiplying them by 1/3 and 1/5, respectively. Then, they used Bayesian and MLE techniques to investigate the $R$ estimation problem. The same data transformed by ^[41] will be used here. Tables 1 and 2 present the transformed datasets, respectively, for gauge lengths of 20 mm and 10 mm.

The random variables that produce the strength measurements in dataset Ⅰ and the stress measurements in dataset Ⅱ are represented by $X$ and $Y$, respectively. We apply the MLE process and fit the Chen distribution to these complete data sets. To avoid the problem of initial values when using the Newton-Raphson (N-R) method, we propose to use the fixed point iteration algorithm to obtain an initial value $\beta$ from (17). First, we get the MLEs of the unknown parameters using the fixed point approach. Drawing the two functions,

and noting their intersection, where

is specified in Eq (17), we yield the starting value for this method. Figure 2 displays the results. This figure indicates that the starting value of $\beta$ should be around between 3.5 and 4. Our starting approximation of $\beta$ is 3.5, and the iterative procedure ends when the difference between two successive iterations is smaller than 10^-5. The Mathematica routines can also be utilized to solve Eq (17), where the function NMaximize from Mathematica 11 was used to derive the MLEs as solutions of the likelihood equations. For $\alpha _{1}$, $\alpha _{2}$, $\beta$, and $R$, the corresponding MLEs are

We want to see whether a Chen distribution can be used to fit each dataset independently before moving forward. According to the one-sample Kolmogorov-Smirnov (K-S) test, the K-S statistic for $X$ is 0.0619 with a $p$ -value of 0.9541 and for $Y$ is 0.080 with a $p$-value of 0.8149. Since the $p$-values of the K-S test are more than the 5% significance level, it is evident that these data closely follows the Chen distribution. Figure 3a, c illustrates how well Chen's density matched the histograms when we plotted the histograms of the two datasets. Additionally, the quantile-quantile (Q-Q) plots of the two datasets shown in Figure 3b, d. Using all available datasets, the estimated/empirical CDFs of the Chen distributions are displayed in Figure 4. The findings show that the fitted distribution functions for datas 1 and 2 are quite comparable to the corresponding empirical distribution functions.

Because it demands a simple null hypothesis, the one-sample K-S test is not very helpful in real-world situations. That is, the distribution must be completely specified with all parameters known. To get around this issue, a K-S bootstrap test was suggested; for more information, see Sheldon ^[42]. The $p$-values are accurately approximated asymptotically using this strategy. In this effort, the fit of the Chen distribution to each dataset will be evaluated using this bootstrapped version. The following stages are included in this method:

Step 1. Estimate the parameters $\Theta = \{\theta _{1}, \theta _{2}, ..., \theta _{k}\}$ and construct the theoretical CDF: $F_{n}\left(X, \hat{\Theta}\right)$, based on an initial sample for the variable $X = \{x_{1}, x_{2}, \ldots, x_{n}\}$.

Step 2. Determine

where $\hat{F}_{n}\left(x_{i}\right)$ is the empirical CDF.

Step 3. Create fresh samples for $X$ using the estimations from the first step, that is, $\{x_{1l}^{\ast }, x_{2l}^{\ast }, \ldots, x_{nl}^{\ast }\}$. Using these new samples, compute the bootstrap sample estimate of $\Theta$, say,

Step 4. Step 3 should be repeated $B$ times. A high number of bootstrap samples $B$ is necessary to guarantee a reliable estimate.

Step 5. Evaluate

If $D_{0} > D_{(B\left(1-\gamma \right) +1)}^{\ast }$ for a significance level $\gamma$, we reject the null hypothesis. An approximate $p$-value can be computed using

where $\#\left\{ D_{l}^{\ast } > D_{0}\right\}$ denotes the amount of $D_{l}^{\ast }$ ($l = 1, \ldots, B$) that exceeded $D_{0}$.

Using the above algorithm, based on bootstrap samples $B = 5000$, the K-S distances and the corresponding $p$-values are $0.07472(0.7421)$ and $0.07749(0.3957)$ for the strength and stress real life data, respectively. The results also suggest that the Chen distribution fits the transformed dataset well.

Based on the complete carbon fiber data ($X, Y$), several adaptive type-Ⅱ progressive censoring samples are generated with different choices of $m_{1}$, $m_{2}, T_{1}$, $T_{2}$ and censoring schemes $R$ and $S$. Table 3 presents these samples. The different estimators for $R$ are computed using the previously described techniques based on these generated samples. After calculating the MLE of $R$ using the N-R procedure, we calculate Bayes estimates of $R$ under both BSE and BLINEX loss functions, and the MH approach. Here, a non-informative prior is employed in the Bayes estimates, where $a_{i} = b_{i} = 0, i = 1, 2, 3$ because we lack previous knowledge about the parameters. The values of

are initialized when samples from the posterior distribution are created using MH, where, $\hat{\alpha} _{1}, \hat{\alpha}_{2}$, and$\ \hat{\beta}$ indicate the MLEs of the parameters $\alpha _{1}$, $\alpha _{2}$, and $\beta$, respectively. From a total of $21,000$ samples produced by the posterior density, we then remove the first $1000$ burn-in samples. Then, as specified by Eqs (43) and (44), the Bayes estimates of $R$ are obtained using various loss functions, such as BSE and BLINEX with $c = (-5, 0.5, 5)$ and $\omega = (0, 0.25, 0.5, 0.95)$.

The convergence of the chains must be verified in accordance with the Bayesian technique. Thus, Figure 5a displays the MCMC trace plot with sample mean, and 95% highest posterior density (HPD) credible interval for $R$. Also, using the Gaussian kernel, Figure 5b displays the marginal posterior density estimate of $R$ and its histogram based on samples of size 20000.

The graphic clearly shows how nearly symmetrical the marginal distribution is. Therefore, these charts demonstrate how the sample data from the Chen model displays a suitable mixture for the Bayes estimate. Table 4 shows the estimated outcomes for $R$ based on ML's approach. Table 4 also shows the results of Bayes estimates of $R$ with respect to the BSE and BLINEX loss functions, over a range of values of $\omega$ and a variable value of the LINEX parameter $c$. It is worth mentioning that, for different schemes, the bootstrap estimate of $R$ and its 95% confidence interval were generated using a bootstrap sample of size 1000. Furthermore, Table 5 displays the lower and higher lengths of confidence intervals for $R$ using the normal approximation interval, Log normal confidence interval, Boot p, and Bayes procedures. A 95% confidence level is used in this process.

Analysis of an earlier real dataset illustrates the significance and use of the adaptive type-Ⅱ progressive censoring and the inferential methods based on it. It is demonstrated that the estimate of the S-S reliability model and the associated varied confidence intervals is highly dependent on the number of failures and a predefined number of inspection times. The performance of the various estimating techniques may also be observed to be rather similar to one another. Table 4's numerical findings substantiate our understanding that, for $R$, all Bayes estimation outcomes under the BSEL and BLINEX loss functions are equal to the respective MLEs as $\omega$ approaches unity. The results also show that the default estimators within the SE and LINEX loss functions, respectively, are derived from the default estimators based on both BSEL and BLINEX, when $\omega = 0$. Thus, it is evident to us how important it is to use balanced loss functions in the Bayes approach. Table 5 indicates that the Bayes estimator is the best based on the length of the confidence interval. The estimators of approximate normal and approximate log-normal are next in order of preference, and the bootstrap estimator is the last one. Additionally, the values of the lengths of the confidence intervals based on the interval estimators of approximate normal and approximate log-normal exhibit a substantial convergence.

In summary, the results of point estimates and interval estimates do not change significantly between different schemes. It is evident that, as predicted in Tables 4 and 5, the estimates produced using the type-Ⅱ censored data are nearer to the estimates produced with the complete sample. Although the adaptive type-Ⅱ progressive censoring scheme shortens the testing time, the accuracy cannot be determined from a single sample, therefore for better comparison we will create a simulation study in the next section.

5.   Simulation and comparisons

Numerous simulation tests are conducted to evaluate the accuracy of our estimations using MC simulations. While the coverage percentage (CR) and interval mean length (IML) are used to evaluate interval estimation, the mean square error (MSE) and biases are used to evaluate point estimation. Smaller MSE and closer estimation value indicate better estimation performance for point estimation. Furthermore, in the context of interval estimation, better estimates are produced with greater coverage rates and shorter interval mean lengths.

First and foremost, the algorithm (Steps 2 and 3) provided in Subsection 2.2 must be used to construct adaptive type-Ⅱ progressive censored data from a Chen distribution ($Ch(\alpha _{1}, \beta)$, $Ch(\alpha _{2}, \beta)$). It is established that the real values of ($\alpha _{1}$, $\alpha _{2}$, $\beta$) are ($1.5, 2.0, 0.75$). To facilitate comparison, we take into account

and

Three separate censoring schemes (CS) are selected for each combination of sample sizes and times $T_{1}\ $and $T_{2}$. We simplify the censoring schemes by abbreviating them. For instance, ($5^{\ast 2}, 0^{\ast 3}$) is the representation of ($5, 5, 0, 0, 0$). Every scenario involves $1000$ iterations of the simulation. Mathematica software may then be used to do MC simulations in order to obtain the corresponding MSEs and bias for the point estimate and the related mean lengths and coverage rates for the interval estimation of $R$.

Based on these repeated samples, the following formulae are used to calculate the estimators' bias, MSE, and lower bound:

and

The solutions of likelihood equations for the MLE are found by applying the N-R technique. Additionally, we calculate the predicted length and coverage probability (CP) for the log-normal interval (Log-NCI), the percentile bootstrap interval (Boot-p), and the ACI. We utilize $1000$ bootstrap iterations to generate the bootstrap confidence intervals. It is configured with

as the significance threshold. Furthermore, two different prior types are taken into consideration to produce the Bayes estimates of

represent the non-informative prior scenario, whereas Prior 1 values

represents the informative prior scenario, which are chosen such that the prior means match the original means. We have computed the Bayes estimates of $R$ under balanced (BSE, BLINEX) loss functions with different values of $\omega$ ($0, 0.25, 0.5, 0.95$) and LINEX constant $c$ ($-3, 3$). The Bayes estimates and corresponding credible intervals are calculated using

samples, and the first

values are discarded as the burn-in phase. The simulation results are reported in Tables 6 and 7. Based on the simulation results, we can conclude that:

● According to the outcomes of our simulation, biases and MSEs are found to decrease with increasing sample sizes ($N_{1}, N_{2}, m_{1}, m_{2}$).

● Overall, none of the three censoring schemes performs better than the others when compared, although the random scheme (Scheme 3 in Tables 6–8) performs better when it comes to minimal MSEs than the other two schemes. In most cases shown in Tables 6–8, in terms of minimal MSEs, schemes 1–3 are the schemes that perform the best through worst. This is true in several $m$ and $N$ cases.

● The results indicate that the different estimations are successful since the estimated values are near to the actual values and the bias and MSEs generally decrease as sample sizes ($N_{1}, N_{2}, m_{1}, m_{2}$) grow.

● The Bayes estimators seem to be sensitive to the assumed values of the prior parameters, based on the performance of the estimators based on Prior 0 and 1.

● The Bayes estimate under LINEX with $\omega = 0$ and $c = -3$ provides better estimates for $R$ because of having the smallest MSEs.

The interval average lengths (ALs) and CPs are used in Table 9 to compare the suggested confidence intervals. The following conclusions are drawn from these tables:

● For various censoring schemes, in terms of interval length, the bootstrap interval is the largest, while the Bayesian credible intervals under both prior 0 and priors 1 are the smallest. Moreover, the ACIs are the second-best ones.

● By expanding the sample size, the ALs and the CPs for ML, bootstrap and Bayesian approaches have improved.

● When comparing the confidence/credible interval lengths based on schemes 1 and 2 to those based on scheme 3, it is evident that the second scheme's intervals in most cases for $N$ and $m$ have the shortest.

● When the sample size increases, the coverage probabilities approach $1-\gamma$, indicating that the ACIs will get more accurate. Through a comparison of the various credible and confidence intervals, it is clear that, in the majority of cases that are taken into consideration, the Bayes intervals offer the highest coverage percentages. Based on the Prior 1, the Bayes credible interval performs best. Further, in the case of traditional asymptotic intervals, the CPs are less than 0.95 and always more than 0.95 under Prior 1, but for Bayesian intervals they remain close to 0.95 under Prior 0. While the bootstrap confidence intervals are bigger than the other confidence intervals, they perform well in terms of coverage probability.

6.   Conclusions and further works

In this work, S-S reliability of the Chen distribution is statistically inferred with the assumption that the data is adaptive type-Ⅱ progressively censored. The point and interval estimates of the S-S reliability are determined by applying the ML technique. Additionally, the approximated confidence intervals for the S-S reliability as well as the parametric percentile bootstrap confidence interval are produced. The delta approach is used to approximate the variance of the S-S reliability estimators in order to achieve the approximation normal/log-normal intervals. By taking into consideration balanced squared error and balanced LINEX loss functions under informative gamma prior, the Bayes estimates are obtained. The Bayes estimates and credible intervals for the S-S reliability are obtained using the MCMC approach. Using a comprehensive numerical analysis, we analyze the supplied estimates with respect to their MSE, confidence lengths, and CPs. Additionally, a case study is conducted to offer background information on the suggested methods. The numerical findings show that the Bayes estimates perform better than estimates obtained by applying the ML method. The Bayesian estimations produce more accurate estimates when the asymmetric loss function is used instead of the symmetric loss.

In general, the strengths of this work may be summed up as follows:

(1) When $X$ and $Y$ follow the Chen distribution, several estimators for $R = P(X < Y)$ are determined analytically. This is a crucial subject in statistical modeling and reliability engineering.

(2) Adaptive progressive type-Ⅱ censored data is highly versatile and may be used in survival analysis in medical research, electronic component reliability testing, and clinical trials with little funding.

(3) The Chen distribution is a great choice for computing a reliability system when adaptive progressive type-Ⅱ censored data is available. This contributes to the corpus of knowledge already present in the literature.

(4) The suitability of Chen's distributions to the model of a real dataset is demonstrated through a case study.

(5) MC simulations were used to establish the validity of the expressions and the overall methodological framework.

On the other hand, the most important weakness of this research is that the amount of data used to clarify the methodology and equations developed in the research is limited, and therefore the superiority of Chen's distributions over other potential models needs to be evaluated on a case-by-case basis.

The findings presented in this study might, with slight modifications, be applied to additional forms of failure data: jointly adaptive progressive type-Ⅱ, progressive first-failure data, and joint progressive Type-Ⅱ censored data. Inference for the

reliability for Chen systems with dependent components appears to be an interesting and practical area of study in the future. In addition to the techniques described in this study, other estimate techniques including Expectation Maximization (EM) and Stochastic EM algorithms will be used. The assessment of the S-S dependability based on the Chen distribution with a common second shape parameter is the only topic of our investigation. We'll look at the situation of unequal form parameters in the future. Moreover, the strength random variables are assumed to be independently and identically distributed, which could not fully reflect some real-world scenarios. Thus, future research will take into account the analysis of multicomponent S-S systems with different strength factors.

Author contributions

E. A. Ahmed: conceptualization, methodology, software, formal analysis, data curation, writing the original draft preparation, writing the revision and editing, visualization; L.A. Al-Essa: methodology, validation, resources, writing the revision and editing, visualization. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to express their gratitude to the reviewer and editor for their thoughtful remarks, which have significantly improved a previous draft of the manuscript. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R443), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Use of AI tools declaration

The authors did not use any AI tools or techniques to prepare this paper.

Conflict of interest

The authors declare no conflicts of interest.