How Mediterranean winegrowers perceive climate change

1.   Introduction

Reliability is a function, which always varies with time. To affirm the reliability of any designed system, it must be able to perform decently under the desired conditions over a specified period. The definition of reliability has four basic parts: probability, adequate performance, time, and operating conditions. Moreover, reliability refers to the probability of a system/device performing its purpose adequately for the period intended under the operating conditions encountered ^[1,2]. Reliability ends when the system stops to perform its intended function, and then unreliability occurs. Under specified system conditions, how reliably power can be transferred from one area to another though all transmission lines of interconnected electric systems is known as transfer capability. The whole concept of reliability is based on probabilistic characterization. The measurement of the amount of dispersion of a set of values is done by the standard deviation and the standard deviation of uncertainty helps to obtain the result of Transmission Reliability Margin (TRM). In all Available Transfer Capability (ATC) determinations, transmission provider (TP) uses TRM to provide a sensible level of assurance that the unified transmission web will be guarded. TRM is not notably used for the shipment of energy; it is retained as a reliability margin to echo the unpredictability of the operation of an electric system. Therefore, an accurate estimation of transmission reliability margin (TRM) is required to ensure effective power transfer over the transmission lines during the occurrence of uncertainties ^[3]. The bootstrap technique has been used for estimating TRM for the uncertainties of line outages and system parameters ^[4]. Besides, several approaches to compute TRM have been proposed ^[5,6]. For better transmission systems, one of the crucial points is to gauge the transfer capability for multi-transaction in a deregulated power system environment, which is known as ATC. ATC is a measure of the transfer capability remaining in the physical transmission network for further commercial activity over and above the base case flows. ATC is estimated by considering the outages of critical transmission line and critical generator unit and the TRM ^[7]. For the computation of ATC, AC Power Transfer Distribution Factor (ACPTDF) based approach has been proposed for multi-transaction cases using power transfer sensitivity and Jacobian calculated with three different methods ^[8,9]. ATC is determined considering PTDFs using AC load flow in case of multi transactions and the results have been obtained for single transaction cases; line outages are also considered for ATC determination ^[10], contingency analysis, and in combination with economic emission dispatch (CEED) environment ^[11]. Moreover, MATLAB software is used to determine the ATC between any buses in deregulated power systems without violating system constraints ^[12]. Besides, Voltage Distribution Factors (VDF) are used to consider voltage limits for ATC calculation ^[13]. Uncertainty in each transfer capability is known as sensitivity and can be computed for a wide range of parameters for DC/AC load flow ^[14,15]; paper describes a novel approach of the application of sensitivity analysis with ATC determination ^[16]. Security margins to voltage collapse blackouts, oscillatory instability, generator limits, voltage constraints, and line overloads are considered; the usefulness of computing the sensitivities of these margins concerning inter-area transfers, loading parameters, generator dispatch, transmission line parameters, and VAR support is established for networks as large as 1500 buses ^[17]. It illustrates the use of loading margin sensitivities for the avoidance of voltage collapse ^[18]. The whole world is suffering from a power crisis ^{[19,20,21,22,23]} and the researchers are always trying to develop the easiest way to calculate the transmission reliability margin, which will subsequently minimize the power outage ^[5,6].

Many system models have been described for online computation of voltage collapse sensitivity indices ^[24]. Margin sensitivity is useful in determining the effectiveness of different parameters for enhancing system loading margin ^[25]. The Stochastic response surface method (SRSM) is an effective method, which uses statistics and probability distributions concept to estimate TRM accurately ^[26]. All necessary statistics concepts are discussed in detail ^[27]. The probability of failure of a system can be estimated by reliability analysis. So, a logical-and-probabilistic method was developed in the MATLAB software package to establish an algorithm for calculating reliability ^[28]. An analytical study was evaluated by intensive simulations using MATLAB by MTM (Multi-taper method) to derive mathematical terms of probability density function ^[29]. The probability of failure and reliability index is used for evaluating reliability analysis for steel beam. On top of that, the pseudo-random variables which depend on its statistical characteristics are generated by Matlab software ^[30].

This paper explains the method of TRM calculation by AC load flow obtained from ATC and sensitivity with respect to ATC of each parameter for both Normal and Rayleigh distributions. In most of the previous work, ATC determination was presented for real power ^[8,9], but in this paper, both real and reactive power have been considered for ATC calculation. Besides, three parameters such as load, voltage, and line impedance, are taken into consideration to calculate sensitivity. Moreover, previous works calculated sensitivity of transfer capability considering load and voltage while this paper determines the sensitivity of available transfer-capability for all those three parameters which are discussed above. The whole TRM calculation is done for multi-transactions considering the standard IEEE 6 bus system ^[31,32]. Section-2 explains the calculation of ATC from AC load flow by using AC Power Transfer Distribution Factors (ACPTDFs) and Q-AC Power Transfer Distribution Factors (QACPTDFs). At the same time, these two factors are combined for calculating SPTDFs (Apparent power distribution factors); for load and transmission line impedance parameters. Later, the results are compared for two distinct Jacobian approaches, and Voltage Distribution Factors (VDFs) for voltage level have also been discussed. Subsequently, section-3 describes the sensitivity of ATC. Section-4 explains TRM calculation for both Normal and Rayleigh distributions. In Section-5, the algorithm of the proposed technique is presented. Validation and conclusion are given in sections 6 and 7 respectively.

2.   ATC Computation by SPTDF and VDF Method

2.1.   Methodology for ATC determination in case of multi-transactions for load and line impedances by SPTDF method

In any power system network, power must be injected at a point by generator (seller bus) and extracted by a load (buyer bus) at another point. This phenomenon is known as a transaction. Moreover, an interconnection between two or more countries (bidding zone) or cross border in which some valuable service is exchanged for some remuneration is known as commercial transactions. A physical connection between various power systems that represent both monitoring and potential congestion in the system is known as flow-gates. The PTDFs (Power Transfer Distribution Factors) ensure that the commercial transactions between zones (e.g., countries as well as individual nodes) do not jeopardize network operation by observing the variation occurring on each flow-gate (e.g., borders but also individual branches). Besides, it can be defined as the coefficient of the linear relationship between the amount of transaction and the flow on a line. For AC load flow, this factor is known as ACPTDFs; in this paper, ACPTDFs denote for real power and QACPTDFs denote for reactive power. This calculation has been performed using the data of Tables 1 and 2. The determination of ATC for both load and line impedances are discussed below:

Full Jacobian approach:

Step 1: Run the N-R load flow to get updated voltage and angle values.

Step 2: Calculate the bus admittance matrix (${\mathrm{Y}}_{\mathrm{b}\mathrm{u}\mathrm{s}}$${Y_{bus}}$) using those update voltage and angle magnitudes.

Step 3: Determine the power flow equation for both real and reactive power between two buses are ^[8]:

Here, ${V}_{i}\;and\;{V}_{j}$ are the bus voltage magnitudes, ${G}_{ij}\; and \; {B}_{ij}$ are the real and imaginary part of ${Y}_{bus}$ matrix and finally ${\delta }_{ij}$ is the voltage angle.

Step 4: Calculate the Jacobian matrix using new updated voltage and angle magnitudes from the first step.

Here, $J1 = \frac{{\partial P}}{{\partial \delta }};$$J2 = \frac{{\partial P}}{{\partial V}};$$J3 = \frac{{\partial Q}}{{\partial \delta }};$$J4 = \frac{{\partial Q}}{{\partial V}}$

Step 5: The sensitivity of real and reactive power flow equation can be written in a matrix form as shown below ^[8]:

Here, n = total no. of buses; start from ${\delta _2}$ and ${V_2}$ because assuming bus number one is the reference bus.

Now, Q/ACPTDFs for any transaction between a seller (k) and buyer (l) bus, for a transmission line between two buses i & j can be represented as ^[8]:

${P_t} = {Q_t} =$Transacted power

ATC for a transaction is:

${LL}_{max}$ = maximum power flow limit through a line i-j.

Decoupled Jacobian based approach:

Step 1: In N-R load flow new update angle and voltage magnitudes have been obtained from the following equation:

Use these updated values to calculate:

Now,

Other equations remain as before.

For line impedances, change the value of line impedances for each transaction and follow the above steps.

2.2.   Methodology of ATC determination in case of multi-transactions for voltage magnitudes by VDF method

For ATC determination bus, voltage magnitude is considered in this work.

Step 1: Run N-R load flow to calculate the new voltage magnitude (${V_{m, kl}}$) for each bus ‘m’ and for each transaction (∆kl) between a seller and buyer bus.

Here, $\Delta {V_m} = {V_{m, kl}} - V_m^0$; $V_m^0$ = base case voltage magnitude for a bus ‘m’; ${V_{m, kl}}$ = voltage at bus ‘m’ under a change in a transaction.

Step 2: Determine ATCV considered voltage level:

Here, $V_{\min }^m$ = minimum voltage limit at bus ‘m’.

This ATC is also done for both full and decoupled Jacobian matrix.

3.   Sensitivity calculation for each parameter

For any transaction, how the increase of load for any bus affects the transaction is known as sensitivity. The sensitivity of transfer capability for some parameters is explained in ^[14]. In this paper, the sensitivity of available transfer capability concerning each parameter has been analyzed. To calculate the sensitivity, we need to increase or decrease any parameter magnitudes; in this paper, all magnitudes are increased because one of the parameters is the voltage which is very crucial to study. The calculated ATC shown in section 2 is going to be the old ATC and new ATC will be obtained after increasing the level, running the load flow, and following each step. Finally, the sensitivity of ATC for each parameter can be determined from the following formula:

For load: an increasing load of 30 MW in a bus the sensitivity of ATC with respect to S (apparent power) can be written as ^[14]:

$ATC{S_{old}}$ = Base case ATC value before increased load.

$ATC{S_{new}}$ = ATC value after increased load.

$\frac{{dATCS}}{{dS}}$ = sensitivity w.r.t apparent power.

For voltage: change of 5% voltage level for a bus with the sensitivity of ATC in respect to V can be written as:

$ATC{V_{old}}$ = Base case ATC value before increased voltage magnitudes.

$ATC{V_{new}}$ = ATC value after increased voltage magnitudes.

$\frac{{dATCV}}{{dV}}$ = sensitivity w.r.t voltage.

For line impedance: change of line impedance to 10% with the sensitivity of ATC in respect Y can be written as:

$ATC{Y_{old}}$ = Base case ATC value before increased line impedances.

$ATC{Y_{new}}$ = ATC value after increased line impedances.

$\frac{{dATCY}}{{dY}}$ = sensitivity w.r.t line impedance.

In reference ^[14], the sensitivity formula is done for transfer capability but in this work, it is calculated for ATC.

4.   Calculation of TRM for normal and Rayleigh distribution

System parameters that are generally correlated with reliability are explained by probability distributions because all elements of a given category, assemble, structure and operating condition will not breakdown after the same managing time but will fail at distinct times in the future. Therefore, these time-to-failure adhere to a probability distribution that may or may not be known and which illustrates the probability that a given component declines within a certain specified time or sustains beyond a certain specified time. If the operating condition changes or components are attained from a different environment, the times-to-failure is likely to be changed too because probability distributions describe different values of probability of failure within a given specified time.

For this reason, the probability distribution concept is very crucial for reliability evaluation; in this work, Normal and Rayleigh's distribution have been used for TRM determination because these two distributions are continuous probability distribution for random variables that can correlate with AC load flow method.

4.1.   Methodology of TRM determination for normal distribution

Reliability is a probabilistic calculation; for this reason, to determine the TRM, the normal distribution is considered which is also known as bell curve; it is very useful because of the central limit theorem.

We have considered those sensitivity values from Eqs 28, 29, 30 to determine TRM ^[3]:

Reference ^[3], states the TRM formula only for load, where bus voltage magnitudes, as well as line impedances, are included.

Here, $\frac{{dATCS}}{{dS}}$ = sensitivity w.r.t apparent power.

$\frac{{dATCV}}{{dV}}$ = sensitivity w.r.t voltage.

$\frac{{dATCY}}{{dY}}$ = sensitivity w.r.t line impedance.

$\sigma (g)$ = parameter distribution.

= 0.1→ for load

= 0.05→ for voltage

= 0.0029→ for line impedances

Finally, we have summed-up all these sensitivity values multiplying with a certain number (U) which is the tolerance intervals for normal distribution, calculated from z-table with confidence (1-α)100% to determine the Transmission Reliability Margin. Here, U = 1.65, 1.96 and 2.57 for 90%, 95% and 99% probability respectively ^[3].

4.2.   Methodology of TRM determination for Rayleigh distribution

Rayleigh distribution is a chi distribution with two degrees of freedom and it’s a special case of Weibull distribution. The expected value or the mean of the Rayleigh distribution for every transaction is: $\sum\limits_{i = 1}^n {\sigma \sqrt {\frac{\pi }{2}} } {x_i}$;

Here, 𝜎 = parameter distribution,

= 0.1→ for load

= 0.05→ for voltage

= 0.0029→ for line impedances

${x_i}$ = sensitivities for each parameter, i = 1, 2, .., n.

After that, the variance and standard deviation are: $\sum\limits_{i = 1}^n {{\sigma ^2}(\frac{{4 - \pi }}{2}){x_i}}$ and $\sum\limits_{i = 1}^n {\sqrt {{\sigma ^2}(\frac{{4 - \pi }}{2}){x_i}} }$ respectively.

For Rayleigh distribution U is: 2.4 for 90%, 2.72 for 95% and 3.7 for 99%. These values are calculated from the chi-square distribution table for two degrees of freedom; besides, Rayleigh distribution is a chi distribution. So, we need to square root the value in the table to get the correct value of U, which keeps the margin greater than the standard deviation of uncertainty.

5.   Algorithm of the proposed technique

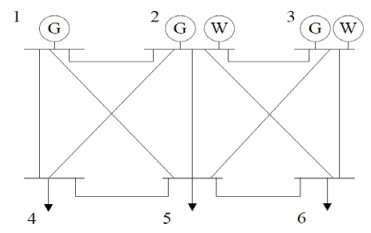
In this work, the IEEE 6 bus system is used to determine the TRM as shown in Figure 1. The system consists of three sellers (generator) buses (buses 1, 2, 3), and three buyers (load) buses (buses 4, 5, 6) ^[31]. The whole process is done for nine multi-transactions which are given below:

T14: a transaction between seller bus 1 and buyer bus 4.

T15: a transaction between seller bus 1 and buyer bus 5.

T16: a transaction between seller bus 1 and buyer bus 6.

T24: a transaction between seller bus 2 and buyer bus 4.

T25: a transaction between seller bus 2 and buyer bus 5.

T26: a transaction between seller bus 2 and buyer bus 6.

T34: a transaction between seller bus 3 and buyer bus 4.

T35: a transaction between seller bus 3 and buyer bus 5.

T36: a transaction between seller bus 3 and buyer bus 6.

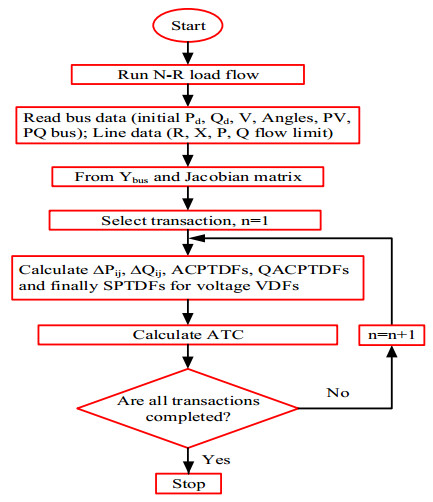
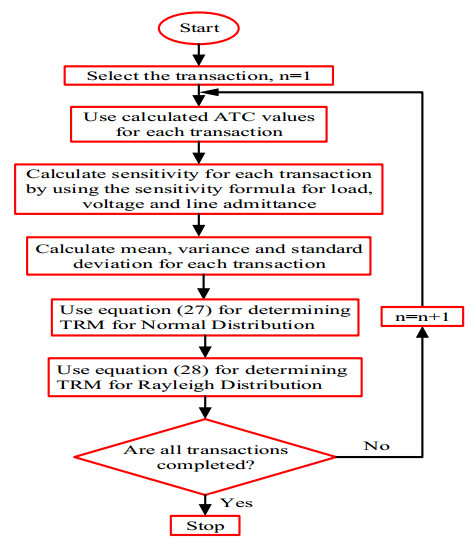
For making it simple, the algorithm of the proposed system is represented as a flow chart. Figure 2 shows the flow chart of the determination of ATC by AC load flow; applying the N-R load flow to calculate real and reactive power for each transaction as well as for full and decoupled Jacobian approaches. After that, we have determined the ACPTDFs, QACPTDFs, SPTDFs, and VDFs to calculate ATC for each case and each transaction. These steps have elaborately been discussed in section-2. On the other hand, Figure 3 illustrates the determination of TRM by AC load flow in the following processes: Firstly, we have calculated the sensitivity for each parameter (load, voltage, and line impedance). Secondly, the standard deviation of these sensitivities for each transaction has been identified. It is mentionable here that the standard deviation is needed in the measurement of sensitivity because, through standard deviation, the distribution of data can be measured about the mean. Finally, the calculation of TRM from Eqs 31 and 32 for Normal and Rayleigh distributions has been done. The whole steps are discussed briefly in section-4.

Now, the new voltage magnitudes and angles are calculated from N-R load flow and those values are later used to calculate ATC by AC load flow method. The final values of ATCs are represented in Table 3. According to ^[14], ATC values decrease with the increases of load values in the load bus. The proposed technique also gives the decreased ATC values with the increases of load for both load and generator bus, which validate the effectiveness.

Tables 3, 4, 5 present the base ATC values and new ATC values after increasing each parameter like load, voltage magnitudes, and line impedances. In this work, the load is increased by 30 MW, voltage magnitude is increased by 5% and line impedances are increased by 10%. Table 3 shows that after increasing load for both PV and PQ buses, the new ATC values become decreased which indicates that disruption occurred. In the same manner, Table 4 depicts that after increasing the bus voltage magnitudes for PV and PQ buses, the new ATC values become decreased for the PV bus and increased for the PQ bus which means that the disturbance occurred in both cases. Moreover, Table 5 presents that the new ATC values are decreased after increasing line impedances which also indicates the distress.

Table 6 represents the sensitivity values for load, bus voltage magnitudes, and line impedances. These values represent the effect of increased magnitudes for each parameter on ATC, where the sign is the indication for understanding whether the ATC values have increased or decreased; negative sign indicates the reduction and positive sign indicates the rise. In this table, only the sensitivity values for voltage of PQ bus 5 is positive whereas all the others are negative which means if voltage magnitude is increased for any load bus, the ATC values are increased because of the Ferranti effect. The whole sensitivity values are done for both full and decoupled Jacobian approaches and the values are quite close.

Tables 7 and 8 demonstrate the TRM values respectively for both Normal distribution and Rayleigh distribution with the characteristics of both full and decoupled Jacobian approaches. Here, the TRM values get increased for each transaction with the rise of the probabilities of uncertainties (90%, 95%, and 99%) which means if any disturbance occurs in the system, the margin must be set up in such a manner that the whole network will act securely. Even though these distributions are continuous, the values of TRM are slightly different. For example, in Rayleigh distribution, all values are less than one. On the other hand, in Normal distribution, some values are greater than one and some are less than one. This discrimination happens because the values of the Rayleigh probability density function for distinct standard deviation values are greater than the Normal probability density function. Here, the probability density function defines probability distribution. So, greater PDF values require fewer TRM values to secure the system. Besides, as reliability is a probabilistic calculation, three distinct probabilities of uncertainties (90%, 95%, and 99%) are considered in this work. From the table, we can deduce that whenever the probability of uncertainty is increased, the margin increases too ^[28] for both Normal and Rayleigh distributions.

6.   Validation

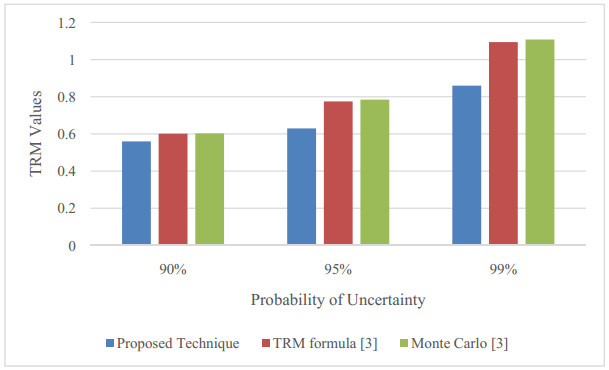
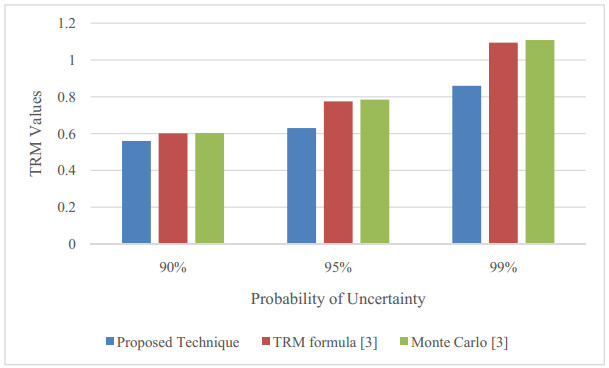
TRM results obtained from the proposed technique are compared with the results of ^[3] and ^[26] which are quite close. Besides, in previous work only Normal distribution was applied but, in this work, both Normal and Rayleigh distributions are applied. Figures 4 and 5 present the TRM values for 90%, 95%, and 99% probability of uncertainty which state that lifting-up in the probability of failure also lifts-up the TRM which proves system reliability. The crucial point here is to focus on the variation of each TRM value with the variation of the probability of uncertainty even though there is little difference in the values of the proposed technique and the TRM formula as well as Monte Carlo, all values are rising with the increase in the probability of uncertainty.

7.   Conclusions

In any power system network, secured functioning is very crucial, because when the disturbances occur, it must make sure that, under a reasonable range of uncertainty the system works confidently. As a consequence, the estimation of the Transmission Reliability Margin needs to be done properly. Most of the calculation of Available Transfer Capability involves a determination of TRM but in the proposed technique, TRM is incorporated with ATC and sensitivity of the system parameters. The research finds that the proposed technique can satisfactorily calculate the secure margin considering the uncertain system parameters when available power is transferred. The proposed technique also calculates the reliability margin by incorporating the key parameters such as load, voltage magnitudes, and line impedances that are correlated with the ATC and sensitivity. Moreover, ATC is calculated by AC load flow considering both real and reactive power. The validation of the technique in comparison with different other approaches clearly shows that the results obtained using the proposed technique are close to the published ones. The whole process is accomplished through MATLAB software for an existing standard IEEE 6 bus system. The validation is also done with a standard IEEE bus system.

Conflict of interest

The authors declare no conflicts of interest in this paper.