Clustering district heating customers based on load profiles

1.   Introduction

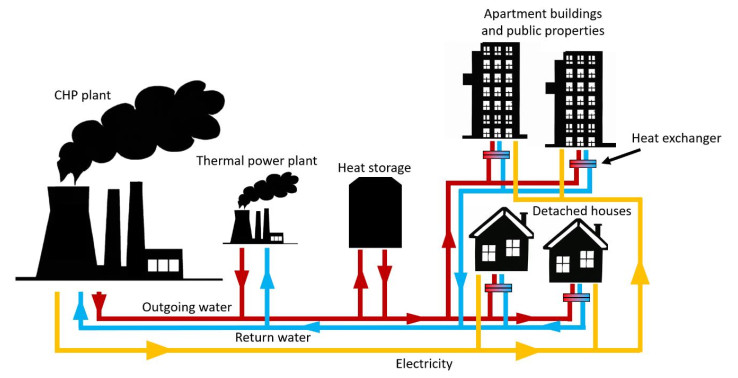
District heating is the most common form of heating of buildings and their water with a 45% share in Finland ^[1,2]. The operating principle is that water is heated in one or more thermal power plants and transported to customers via the district heating network with the help of water or steam (Figure 1). Typical customers are residential, industrial, commercial, and public buildings. The cooled water is directed back to the heater.

Heat can be produced by solar, geothermal, wind, nuclear, and local fuels, as well as thermal power produced from combined heat and power plants. Wasted heat resources, including industrial waste heat, recycled heat from burning household waste, and biomass such as forestry waste wood, are also commonly used.

The system may include heat storage to provide flexibility of the system by reducing the demand for heat production during peak load, and by balancing the difference between demand and supply ^[3,4,5,6]. However, they are nowadays rare and heat consumption is allocated directly to the heating network.

The cost of district heating systems consists of production and distribution costs. The production cost depends on fuel costs, excise tax, emission rights costs, and other variable costs. The distribution cost originates from the investments, maintenance, and temperature and pressure losses in the network. To be economically feasible, the total cost must be lower than the local heat generation alternative ^[7].

The most important factor in the efficiency of district heating systems is to lower the distribution temperatures ^[8]. This requires intelligent control systems, and strategies to identify operating errors that cause high return temperatures. To plan such strategies, it is important to know the customer's behavior and predict their future needs.

The competitiveness of district heating arises from the combination of heat production and heat distribution conditions. One important condition for heat distribution is that the heat demand must be centralized to minimize distribution costs and heat losses ^[9]. Low heat density in sparsely populated areas generates higher distribution costs and losses ^[10,11]. In a smart fourth-generation district heating system, the heating system and the distribution network must interact ^[12,13].

The consumption is measured by smart meters remotely which send data directly to the district heating company. This is an important property that allows the analysis of past and prediction of future heat use of customers. ^[14,15] listed several potential benefits: reducing peak energy use, optimizing indoor temperature and energy production, continuous network monitoring, accurate billing, and reducing fraud.

The data can also be used for detecting heat load patterns ^[16], analyzing the factors affecting energy consumption, and forecasting future use ^[17]. Heat load patterns are the most typical behavior patterns that reveal how different customer groups use heat. Analyzing such patterns is essential for efficient operation and management of the system ^[18]. A better understanding of heat use at the customer level can help to improve the efficiency of the system. District heating companies can optimize their operations, introduce new control strategies, and personalize demand management for certain customer groups ^[16].

The data can also be used to identify abnormal consumption because even one problematic customer can affect the performance of the network ^[16]. However, recognizing typical and abnormal heat uses is a complex task in a system consisting of customers with different types and characteristics.

Heat demand is determined by outside temperature, inside temperature, building materials, building structure, weather conditions, and individual behavior ^[19]. Individual behavior can include a secondary heating system such as a fireplace or an air source heat pump, hot water consumption, the number of people in the building, electrical devices producing heat, the building's ventilation, and the wind directed at the building. ^[20] estimated that 40% of heating is spent on room heating, 35% on ventilation heating, and 25% on domestic water heating in a residential building.

Clustering is one of the most popular exploratory data mining methods for analyzing heat load patterns ^[21]. It has been successfully used for analyzing large-scale building operational data ^[22], recognizing consumption profiles ^[23], and as a preprocessing step when using other data mining techniques to predict future energy use ^[24,25].

In this work, we analyze the heat consumption profiles of district heat customers in Kuopio, Finland. We constructed two consumption profiles of the users. The first is the average hourly use on weekdays, and the second one is the average hourly use on weekends. The profiles are then clustered to construct four average profiles.

These clusters provide useful information about the most common consumption profiles. They can be used for a better prediction of heat use and for intelligent heat control, which could reduce heat consumption without the customer noticing the effect. The consumption models can be used to alert when the consumption of a customer is significantly higher than the average usage in the cluster. It can be the first indication of a problem like heat leaking. Such a warning system can reduce the possibility of water damage.

The rest of the paper is organized as follows. The data is first given in Section 2. The clustering process is described in Section 3 including pre-processing to fill in missing values, removing erroneous data, feature extraction, normalization, and the clustering algorithm. The resulting clusters are presented in Section 4 and their content is analyzed. Conclusions are drawn in Section 5.

2.   District heating data

We use two data sources: customer consumption measures and weather data. The consumption measures come from Kuopio district heating customers in Finland during 2021. The weather data is provided by the Finnish Meteorological Institute for Kuopio's Savilahti area in Kuopio.

The consumption data consists of 54, 657, 082 measurements in megawatt-hours (MWh) from 6089 customers. Each measurement has a status value that indicates the quality of the measurement. The statuses are in accordance with metered service consumption report (MSCONS) message service codes: successful reading (136), uncertain reading (Z02), and failed reading (Z03) ^[26]. The distribution of the readings for different statuses is shown in Table 1. The measurements are made once every hour, so there are 24 daily energy consumption measures for every customer. In total, 733, 885 readings were missing from the database; they were left out of the final data. We also filtered out five customers with uncertain data or failed reading. The distribution of the 6084 used customers is summarized in Table 2 according to the building type.

3.   Clustering customer profiles

To form daily consumption habits characteristic of customers, we use clustering. The clustering algorithm divides the data into groups (clusters) where customers in the same cluster are more similar than customers in other clusters. The overall process is shown in Figure 2. The details of the cluster analysis process are described in the following sub-sections.

3.1.   Pre-processing

We pre-processed the data to detect and fix errors. There were a relatively large number of missing values. When more than four measures from the customer's data were missing on the same day, the entire day was deleted from the data. In other cases, missing readings are created by linear interpolation. Unrealistically large values were also filtered out. Missing outdoor temperature data were recovered using the open data service of the Finnish Meteorological Institute ^[27].

3.2.   Consumption profiles

We extract daily consumption patterns (12 measurements per day) separately for weekdays and weekends. The result is a 24-dimensional feature vector normalized according to the outdoor temperature.

Figure 3 shows the daily heat consumption of customers of two different building types. Weekdays are marked in red and weekend days in blue. For service properties, heating peaks are most often at two and six o'clock, while for residential buildings, three significant heating moments are at 2, 5, and 17 o'clock. The morning peak in residential building customers' data is due to people using hot water in the shower (the evening peak exists but is less visible). Both customer types have slightly lower usage during the weekend, but besides this, there is very little we can observe from the averages. The consumption varies a lot between individual customers for both customer types.

The biggest common affecting factor is the outside temperature. Figure 4 shows the total consumption of district heating by month and the average temperature for the months. The consumption closely follows the outside temperature and is roughly 7 times higher in the peak winter months (December, January, and February) than in the mid-summer months (June and July). In the summer months, the heating is mainly used for hot water.

Figure 5 shows the effect of outdoor temperature. The consumption decreases linearly when the outside temperature increases until it reaches 15 ℃. This is the temperature value when the heating of the building is turned off. The remaining consumption is mainly for hot water heating, and in some humid spaces, floor heating is continuous regardless of the weather. The further decrease of consumption beyond 15 ℃ in residential buildings can be explained by using less warm water when the weather becomes warmer.

To eliminate the effect of outdoor temperature, we construct two models of the daily consumption relative to the outside temperature by linear regression as suggested ^[28]. One model is for the cases when the average outdoor temperature is below 15 ℃, and the other for those above 15 ℃. The resulting modified daily load profile is 0/1-normalized so that normalized measurements have zero mean and unit variance.

3.3.   Clustering algorithm

K-means is the most widely used clustering algorithm despite its sensitivity to random initialization. However, this deficiency can be compensated by better initialization and repeating the algorithm multiple times ^[29], or by using an additional random swap step as a wrapper around the k-means ^[30]. K-means has also been generalized to graphs ^[31], sets ^[32], and time series ^[33].

The customer profiles are essentially time series. For this reason, we use the k-Shape algorithm ^[33] which is essentially a k-means variant adopted for time series. It operates iteratively like k-means but with distance function and centroid calculation tailored for time series. Its advantages are fast speed, available implementation, and well-known properties ^[34]. We use the implementation available in the tslearn-library ^[35].

To compensate the sensitivity of k-means by repeating the algorithm 1000 times with different (random) initialization and choose the best according to the optimization function (sum-of-squared error) following the principle presented in ^[31]. The algorithm stops when the error decreases less than a threshold value (10^-6), or the number of iterations reaches a maximum value of 2000.

For selecting the number of clusters, we ran the algorithm from 2 to 40 clusters. The results were compared with five cluster validity indexes: Calinski-Harabasz-index (CHI) ^[36], Davies-Bouldin index (DBI) ^[37], Silhouette Coefficient (SC) ^[38], Sum of Squared Distances (SSD), and Gap statistic (GS) ^[39]. For a more detailed analysis of these measures, we refer to ^[40].

None of the indexes indicated that there would be natural clusters in the data, see Figure 6. The number was therefore left to us, the researchers, to decide. Since our goal is to create average customer profiles that can be manually analyzed, the number of clusters was kept relatively small: four.

4.   Results

After the pre-processing, five of the 6084 customers did not have enough data and were therefore dropped out. Four clusters were then created from the remaining 6079 customer profiles.

Figure 7 summarizes the average heat profiles of the four clusters. Figure 8 shows the distribution building types and consumption profiles of the customers. Small houses are the most common building type in every cluster. Despite being mostly used for living, they have different heat use profiles. Terraced and apartment buildings are in all clusters, but mostly in cluster 3, which is formed mainly of residential buildings and almost completely lacking services and industrial buildings.

Clusters 1 and 3:

All profiles have the smallest consumption at night and then increase in the morning but only clusters 1 and 3 have a clear peak in the evening around 18-20 o'clock. On the weekend, the consumption profiles are similar, but the morning peak appears about two hours later than on weekdays.

It is likely that the residents of cluster 3 work outside the home since the peaks align well with traditional working hours. There is less variation in cluster 3 than in cluster 1 having more residents in the same building, which smooths the variations.

Cluster 2:

Many service and industrial buildings belong to cluster 2, where the consumption profile follows the working hours. It is likely determined by the ventilation, and the use is flat throughout the normal opening hours.

Cluster 4:

The profile of cluster 4 decreases steadily from morning to evening and is constant on weekends. The cluster consists mostly of non-residential buildings where the most heat consumption typically takes place in the morning on weekdays and is flat on weekends. Many of the buildings are used only on weekdays.

The total energy use in each cluster is shown in Figure 9 according to the building type. Clusters 1 and 3 contain the most customers (2201 and 1995), yet the total consumption of customers in cluster 1 is the smallest. For the district heating company, clusters 2 and 3 are the most interesting because of the largest energy consumption. The number of service buildings is small, but they constitute a significant part of the energy consumption, especially in cluster 2. The terraced and multi-story buildings dominate the energy consumption in clusters 1 and 3. The total energy use of the small houses is insignificant in all clusters. In cluster 1, they make up more than a quarter of all building types; yet their heat consumption is less than a third of the total heat consumption in the cluster.

5.   Conclusions

We constructed four average customer profiles of district heating customers in Kuopio by clustering their daily heat use profiles. These clusters provided useful information about the most common consumption profiles. They can be used for predicting future heat use and intelligent heat control, which could reduce heat consumption without the customer even noticing it. The models could also identify deviations from the normal (average) consumption to alert if the customer's consumption is significantly higher than the average usage. It can be the first indication of a heat leak or other problem. Such a warning system could reduce the extent of possible water damage.

Limitations: The shape-based measure was shown superior in ^[33], but the results later in ^[41] did not favor this measure as strongly. Our data has fixed length where all measurements have recorded at the same time of day. It might be worth to take closer look whether Euclidean distance or dynamic time warping would be more accurate.

Another limitation is that our study did not consider the energy stored in the building's structures. Solar radiation and previous heating are stored in the structures, which are later released to the interior. As a future work, this thermal inertia could be used in the model to create a more sophisticated prediction model.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools for this article.

Conflict of interest

Pasi Fränti is an Editor-in-Chief for Applied Computing and Intelligence and was not involved in the editorial review and the decision to publish this article.