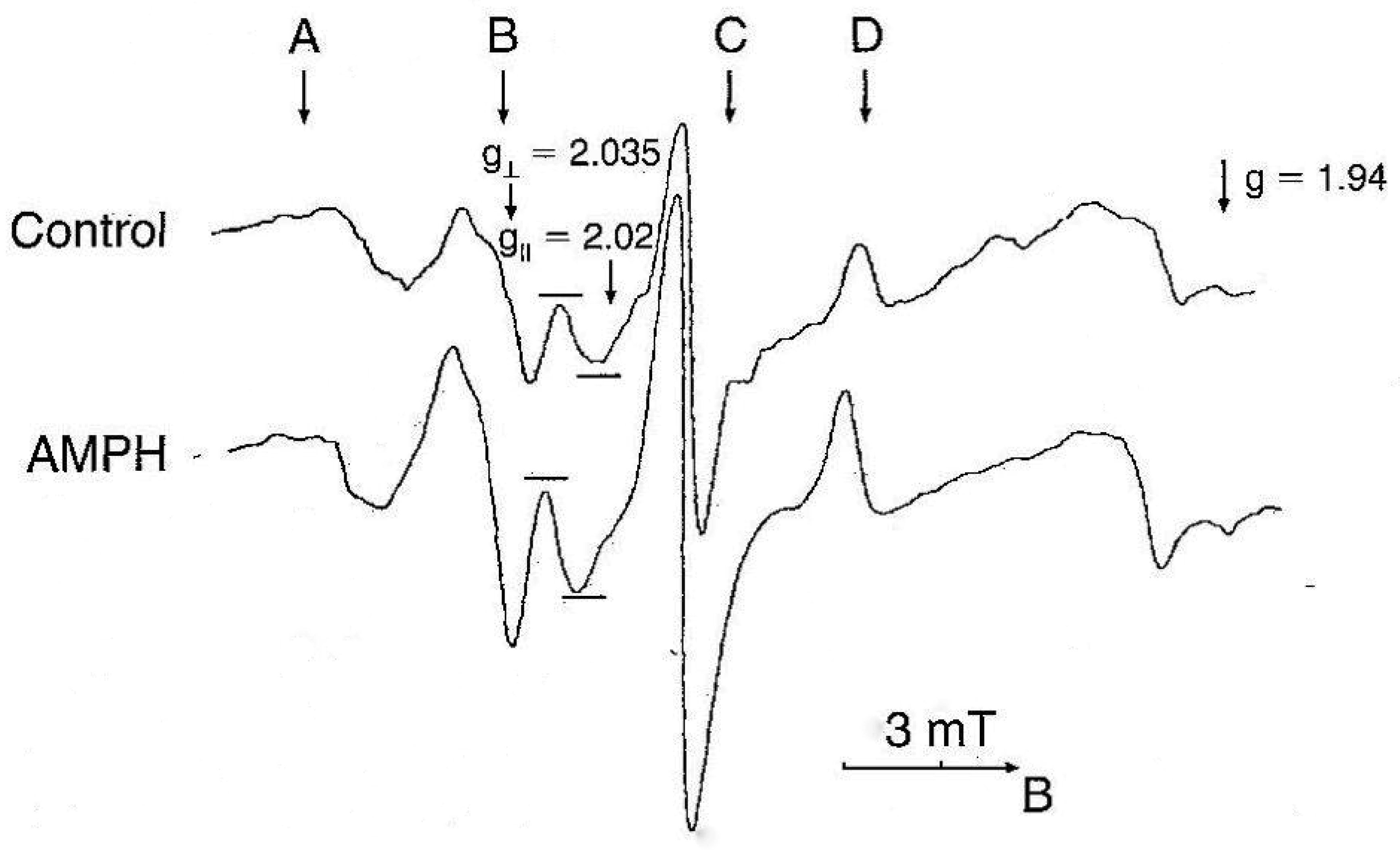
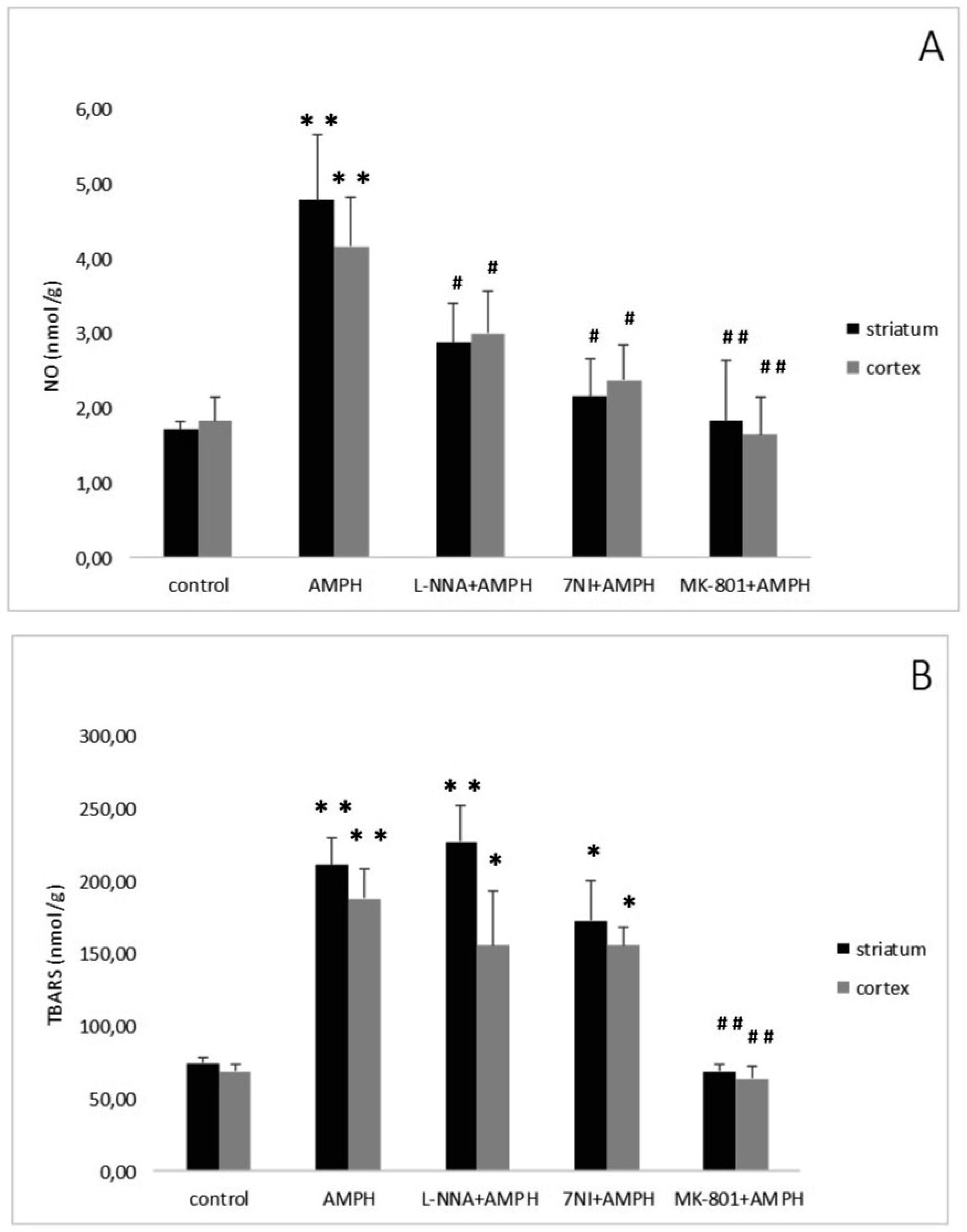
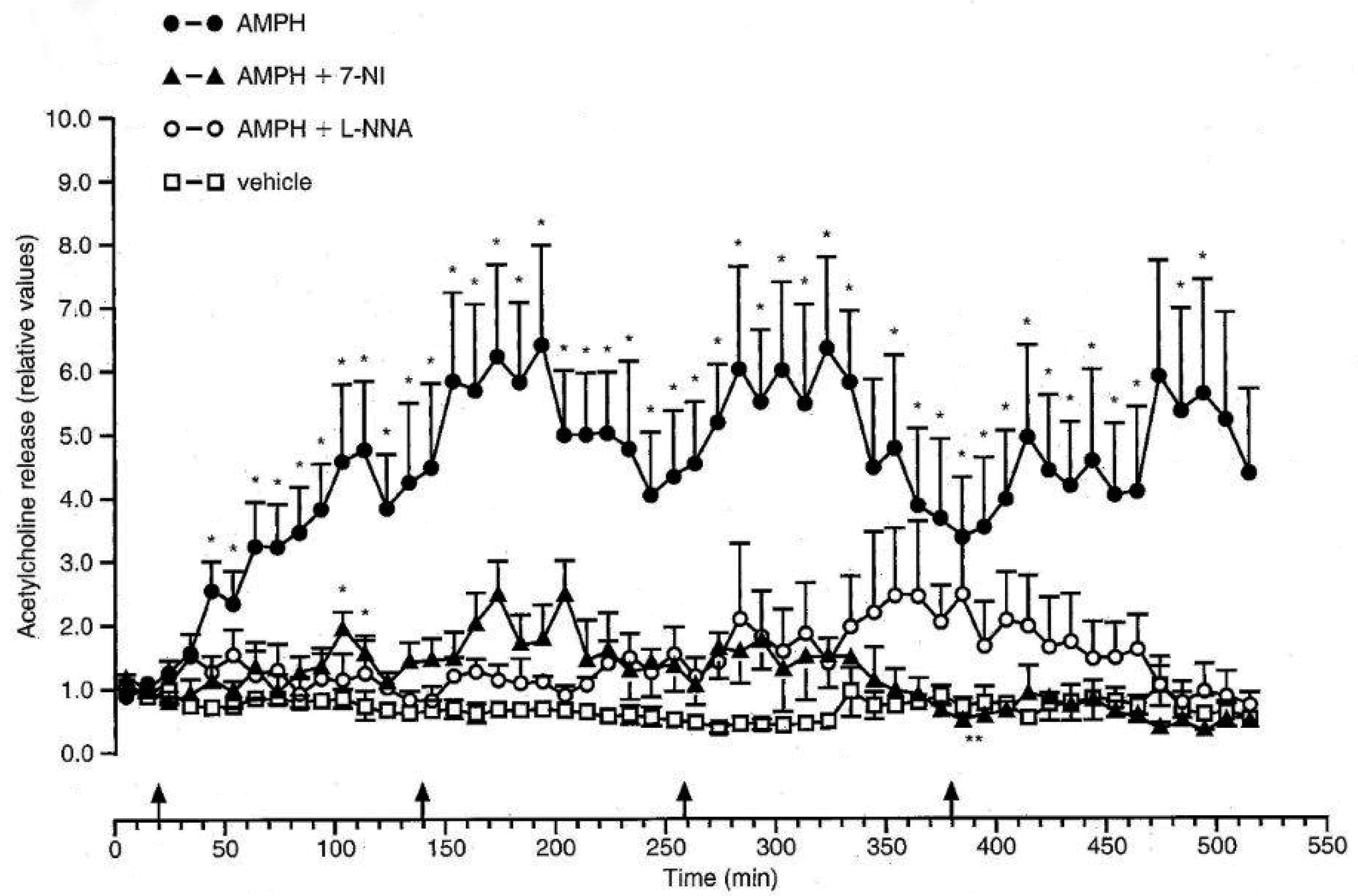
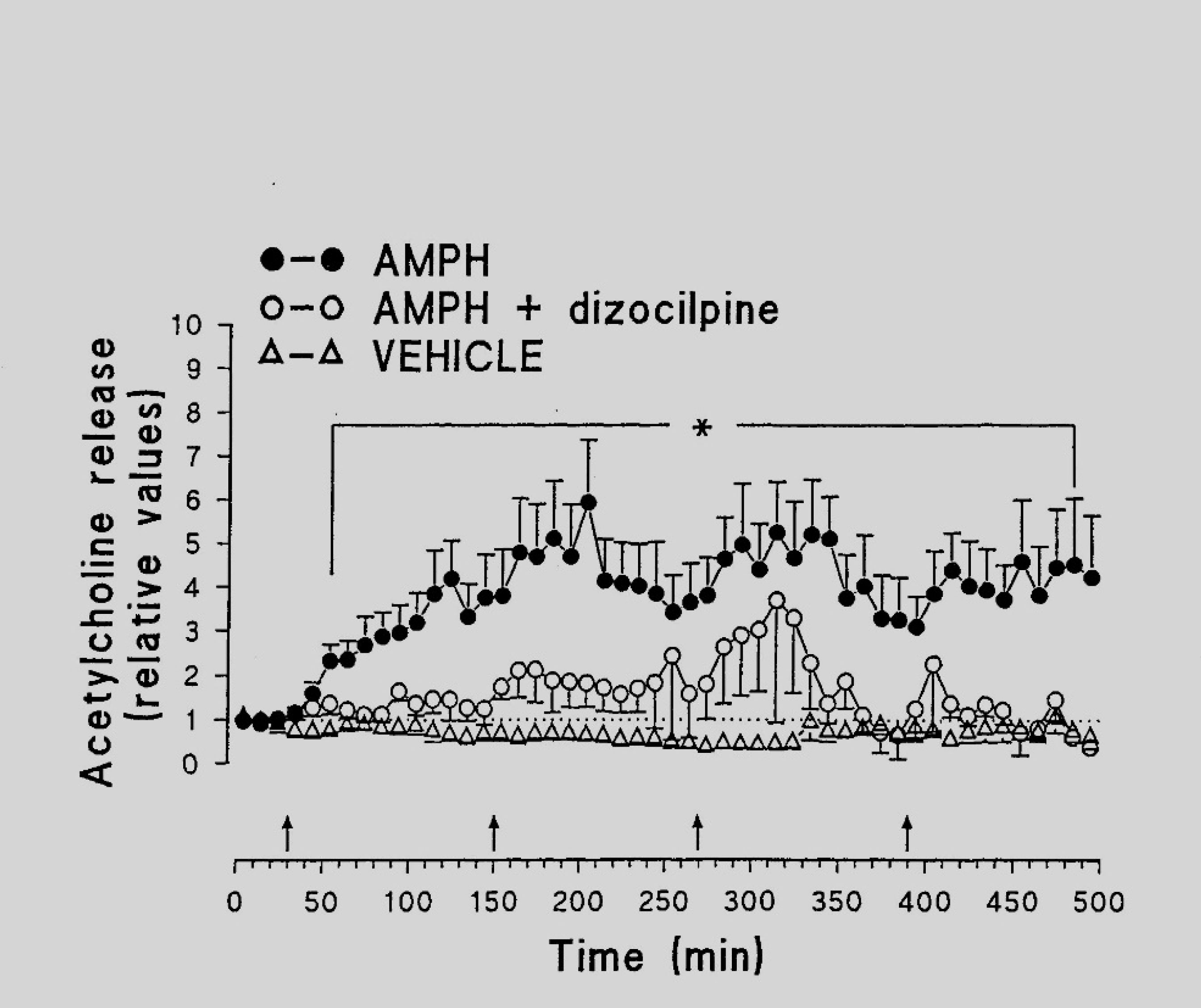
In recent decades, consumption of psychostimulants has been significantly increased all over the world, while exact mechanisms of neurochemical effects of psychomotor stimulants remained unclear. It is assumed that the neuronal messenger nitric oxide (NO) may be involved in mechanisms of neurotoxicity evoked by psychomotor stimulants. However, possible participation of NO in various pathological states is supported mainly by indirect evidence because of its short half- life in tissues. Aim of this review is to describe the involvement of NO and the contribution of lipid peroxidation (LPO) and acetylcholine (ACH) release in neurotoxic effects of psychostimulant drugs. NO was directly determined in brain structures by electron paramagnetic resonance (EPR). Both NO generation and LPO products as well as release of ACH were increased in brain structures following four injections of amphetamine (AMPH). Pretreatment of rats with the non-selective inhibitor of NO- synthase (NOS) N-nitro-L-arginine or the neuronal NOS inhibitor 7-nitroindazole significantly reduced increase of NO generation as well as the rise of ACH release induced by AMPH. Both NOS inhibitors injected prior to AMPH had no effect on enhanced levels of LPO products. Administration of the noncompetitive NMDA receptor antagonist dizocilpine abolished increase of both NO content and concentration of LPO products induced by of the psychostimulant drug. Dizocilpine also eliminated the influence of AMPH on the ACH release. Moreover, the neurochemical and neurotoxic effects of the psychostimulant drug sydnocarb were compared with those of AMPH. Single injection of AMPH showed a more pronounced increase in NO and TBARS levels than after an equimolar concentration of sydnocarb. The findings demonstrate the crucial role of NO in the development of neurotoxicity elicited by psychostimulants and underline the key role of NOS in AMPH-induced neurotoxicity.
1.
Introduction
Within numerous control systems, various measures are implemented to mitigate costs or curtail energy consumption. For some special cases, specific control values are deliberately maintained at zero for designated durations using handoff control strategies, thereby effectively minimizing the associated control costs. In [1], a novel control methodology was introduced to solve the maximum hands-off control problem characterized by $ L^{0} $ norm, which is to find the sparsest control among all permissible controls. This control methodology holds significant utility in minimizing electricity or fuel consumption, showcasing its practical relevance and applicability. In [1], within the car's start-stop system, the engine is automatically deactivated when the vehicle comes to a halt or operates at speeds below a predetermined threshold. This deliberate shutdown serves to diminish CO$ _2 $ emissions and decrease fuel consumption as part of the system's efficiency measures. Handoff control demonstrates effectiveness within networked control systems as well [2].
Sparse optimization has emerged as a prominent subject of interest among scholars in recent years. The technology of sparse optimization has garnered extensive attention and exploration across various domains, including compressed sensing [3], image and signal processing [4,5], machine learning [6,7], Alzheimer's disease biomarkers [8], and other fields. Maximum hands-off control shares a relationship with sparsity, a characteristic pertinent to numerous optimization problems. In the realm of sparse optimization, sparsity refers to a condition where a substantial portion of elements within a matrix or vector assumes zero values. Leveraging sparsity offers the potential to economize on both time and compression expenses. Moreover, it serves as a mechanism to sift through extensive datasets, extracting pertinent information and thereby streamlining the complexity of the problem [9]. Within various optimization problems, the $ L^{0} $ norm of a vector commonly serves as a means to quantify and define sparsity [10,11]. Due to its non-convex and non-continuous nature, the $ L^{0} $ norm presents inherent complexity in analysis. Consequently, numerous scholars resort to exploring the variational property of the $ L^{0} $ norm and employing subdifferentiation techniques to address its intricacies. In [12], a technique known as convex relaxation was introduced as a substitute for the $ L^{0} $ norm, employing the more tractable $ L^{1} $ norm. This transformation enables the formulation of the problem in a linear programming paradigm, amenable to resolution using methods such as the interior point method or the simplex method. In [13,14], the approach revolves around the non-convex relaxation method, leveraging the $ L^{p} $ relaxation technique, where $ 0\leq p\leq 1 $, to yield solutions with increased sparsity. In [15,16], a focus is directed toward the Difference of Convex functions (DC) algorithm. This method entails the representation of the $ L^{0} $ norm as a difference between two convex functions. Subsequently, leveraging the DC algorithm facilitates the resolution of the resultant relaxation model. In [17], by addressing the non-convex nature of the logarithmic function, a proposal was made to substitute the logarithm function for the $ L^{0} $ norm. In [18], the resolution involves addressing a sparse optimization problem that encapsulates two competing objectives: measurement error minimization and sparsity maximization. This problem is approached and solved through the utilization of a multi-objective evolutionary algorithm. In [19], an effective fault diagnosis framework was constructed by integrating $ L^{0} $ norm sparse constraint optimization with principal component analysis, aimed at mitigating the extent of sparsity. However, in [12,13,14,15,16,17,18,19], the sparse optimization problems do not take into account the constraints of the dynamical system. The focus of the study presented in [20] revolves around the $ L^{1} $ objective optimal control problem specifically tailored for linear discrete systems. This formulation leads to diverse sparse solutions based on the selection of distinct problem parameters. The study detailed in [21] introduces a methodical approach for synthesizing sparse optimal control structures governed by linear discrete systems. This method guarantees sparsity within solutions, enabling the specification of a predetermined count of zero elements within the control structure. In [22], the utilization of the Smith iteration and Altering-Direction-Implicit (ADI) iteration methods was explored for obtaining numerical solutions in a large sparse optimal control problem governed by linear discrete-time Riccati equations, leveraging Newton's method. In [23], provably optimal sparse solutions to overdetermined linear systems with non-negativity constraints were researched in a least-squares sense by implicit enumeration. Nevertheless, in [20,21,22,23], the sparse optimal control problem governed by the linear dynamical system failed to incorporate the constraints associated with the nonlinear dynamical system. The work presented in [24] delved into the examination of the Newton-like method of undetermined equations. This exploration led to the discovery of sparse solutions pertaining to sparse optimal control problems governed by an affine nonlinear system. The analysis of optimal control using the value function was conducted employing the dynamic programming method. In [25], a dynamic programming approach was introduced to effectively approximate the sparse optimal control problem governed by an affine nonlinear system in a numerical context. The maximum hands off control problem governed by the class of affine nonlinear systems was studied in [26]. Nonetheless, in [24,25,26], the nonlinear dynamical systems involved in the sparse optimal control problem are affine nonlinear systems, where the state variables and control inputs are separable. This paper delves into the investigation of the sparse optimal control problem governed by a general nonlinear dynamical system where the state variables and control inputs are inseparable.
The conventional approach to optimal control involves determining the most effective control strategy within specified constraints [27]. This strategy aims to either maximize or minimize the performance index. Typically, deriving an analytical solution for the optimal control problem governed by a nonlinear dynamic system proves challenging. Therefore, the resolution of such problems often necessitates numerical methods to obtain an effective solution [28]. The numerical solutions to optimal control problems can be divided into two solution strategies: first optimize then discretize (indirect methods), and first discretize then optimize (direct methods) [29]. For problems that do not contain inequality constraints, indirect methods derive the first-order necessary conditions for the optimal control problem, namely, the Euler-Lagrange equations that include the initial and boundary value conditions. The solution to this initial-boundary value problem mainly involves two types of methods: the control vector iteration method and methods such as multiple shooting and collocation [30]. The direct method encompasses techniques such as the direct collocation method and control parameterization [31,32]. Control parameterization involves discretizing solely the control function, approximating it using fixed basis functions within specific subintervals [33]. The coefficients within this linear combination of basis functions serve as the optimal decision variables. Typically, predetermined switching times govern the transitions between values for each control component, often evenly divided within specified intervals [34]. To enhance solution accuracy, the time range of the control function is frequently subdivided more finely, leading to a greater number of decision variables. However, this denser division amplifies computational costs. Simultaneously, to mitigate the need for extensive time range subdivisions, one must consider incorporating the switching times as additional decision variables [35]. The traditional time-scaling transformation operates by mapping variable switching times with fixed points within a redefined time horizon. This process yields an optimization problem wherein the revised switching times remain constant. The application of the time-scaling transformation finds extensive utility across diverse domains, including mixed integer programming [36] and singular optimal control [37]. Yet, in practical scenarios, simultaneous switching of time poses notable challenges [38]. The sequential adaptive switching time optimization technique (SASTOT) presented by [39], suggests that the interval for control switching times can vary, affording the flexibility to freely select the number of segments for each approximate control component. The method initiates by applying control parameterization and the time-scaling transformation to a single control component initially, leaving the remaining components untouched. Subsequently, within the newly introduced time range, the time-scaling transformation introduces a subsequent new time range. This iterative process continues until the final control component undergoes processing in a similar manner. This modification introduces a significant level of flexibility into the control strategy. Compared with the traditional time-scale transformation techniques, the SASTOT can accurately identify sparse positions for each control.
In this study, our focus lies on the maximum hands-off control problem governed by a nonlinear dynamical system (MHCPNDS) with a maximum hands-off control constraint characterized by the $ L^{0} $ norm. The optimization variables encompass the count of segments for each control component and the respective switching times for each of these components. The examination of the MHCPNDS poses challenges in obtaining an analytical solution. Hence, the adoption of a numerical solution becomes imperative. In practical scenarios, simultaneous switching of all control components is not optimal. Addressing this, this paper introduces the SASTOT, which allows for a flexible selection of the number of segments and switching times for each individual control element. The integration of control parameterization with the SASTOT serves as a transformative approach to addressing the MHCPNDS. The non-smooth term that involves the maximum operator is approximated through a smoothing function, and we further illustrate the convergence of this approximation technique. The attainment of a sparse solution for the MHCPNDS involves the utilization of a gradient-based algorithm. Empirical assessments through numerical experiments substantiate the efficacy of the algorithm put forth in the study.
The contributions of the paper are three-fold:
1) Distinguished from the above-mentioned sparse optimization problem, which is amenable to analytical solutions, we consider the sparse optimal control problem within a nonlinear dynamic system. Given the intrinsic complexity of the nonlinear dynamic system, pinpointing an analytical solution poses a significant challenge. Taking these into consideration, we propose a numerical solution method, based on the gradient formulae of the cost function (Theorems 5–8) and the gradient-based algorithm, without requiring the linearization of the nonlinear dynamical systems.
2) A smoothing function has been introduced to mitigate the roughness of the non-smooth term involving the maximum operator. Several significant theorems (Theorems 1–4) have been established, illustrating that the smoothing function effectively addresses the shortcomings associated with constraint qualification noncompliance.
3) Setting itself apart from the time-scaling transformation technique, this paper introduces the SASTOT method that enables flexible determination of the number of segments and the specific switching times for each control element individually.
The rest of the paper is organized as follows. In Section 2, we present the MHCPNDS. In Section 3, the MHCPNDS is transformed by using control parameterization and the SASTOT. In Section 4, we deal with the nonsmoothness of the objective function by using the smoothing technique. In Section 5, the gradient-based algorithm is used to solve the resulting smooth problem. In Section 6, numerical results are presented. In Section 7, we draw some conclusions and suggest some future research directions.
2.
Maximum hands-off control problem
Let $ I_n $ be the set of $ \{1, 2, ..., n\}. $ For a continuous time control $ v:[0, T]\rightarrow R $, the $ L^{p} $ norm is defined by
The $ L^{0} $ norm is defined by
where $ q_{M} $ is the Lebesgue measure and the set $ {\rm{supp}}(v) $ is called a support set of $ v $ defined by
In some cases, it is possible to significantly reduce the control effort by keeping the control value at exactly zero over a time interval. Maximum hands-off control can be called sparse control, which means that the more zeros the control value is in unit time, the more sparse it is. It makes the time interval of the control completely zero.
In order to obtain the sparse solution of maximum hands-off control, we consider a nonlinear dynamical system defined by
where $ \boldsymbol{x}(t): = (x_1(t), ..., x_n(t))^\mathrm{T}\in \mathbb{R}^{n} $ denotes the state vector at time $ t $, $ \boldsymbol{u}(t): = (u_1(t), ..., u_m(t))^\mathrm{T}\in \mathbb{R}^{m} $ denotes control input vector at time $ t $, $ \xi $ denotes the initial state value, $ T \ge 0 $ denotes a given terminal time, and $ \boldsymbol{f}(t, \boldsymbol{x}(t), \boldsymbol{u}(t)) $ denotes a nonlinear function vector defined on $ \mathbb{R}^{n} $.
Let $ \boldsymbol {x}(\cdot|\boldsymbol{u}) $ denote the solution of system (2.4) satisfying
For all $ t $ on $ [0, T] $, there is also the following constraint on each component of the control input vector $ \boldsymbol{u}(t) $
A control input vector $ \boldsymbol{u}(t)\in \mathbb{R}^m $ that satisfies constraint (2.6) is called a candidate control input vector. Let $ \mathcal L[T, \xi] $ be the set consisting of all candidate control input vectors.
Definition 1. The maximum hands-off control constraint characterized by the $ L^{0} $ norm is defined by
where $ \lambda_{i}\ge 0, i\in I_m, $ are given weights, $ \boldsymbol{u}\in \mathcal L[T, \xi] $ denotes the admissible control, and $ \mu $ is a small positive number.
Definition 1 is used to characterize the sparsity of maximum hands-off control. The cost functional is defined by
where $ \pi_{0}: \mathbb{R}^m\rightarrow \mathbb{R} $ and $ \vartheta: \mathbb{R}^m\rightarrow \mathbb{R} $ are continuously differentiable functions.
Then, our maximum hands-off control problem can be formulated as follows.
Problem A: Given system (2.4), choose an admissible control $\boldsymbol{u} \in \mathcal L[T, \xi]$ to minimize the cost functional defined in (2.8) subject to boundary condition (2.6) and maximum hands-off control constraint (2.7).
3.
Solution to maximum hands-off control problem
The $ L^{0} $ norm, owing to its non-convex and discontinuous characteristics, inherently introduces complexity into analytical procedures. The $ L^{0} $ norm can be well approximated by the $ L^{1} $ norm [20]. The maximum hands-off control constraint characterized by the $ L^{0} $ norm is approximated by Definition 2.
Definition 2. The maximum hands-off control constraint characterized by the $ L^{1} $ norm is defined by
where $ \lambda_{i}\ge 0, i\in I_m, $ are given weights, $ \boldsymbol{u}\in \mathcal L[T, \xi] $ denotes the admissible control, and $ \mu $ is a small positive number.
Definition 2 serves to delineate the computationally efficient sparsity of maximum hands-off control. By Definition 2, Problem A can be well approximated by the following Problem B.
Problem B: Given system (2.4), choose the control $ \boldsymbol{u} \in \mathcal L[T, \xi] $ to minimize the objective functional defined in (2.8) subject to boundary condition (2.6) and maximum hands-off control constraint (3.1).
Control parameterization stands as an effective methodology for resolving the optimal control problem, commonly approached through approximation via piecewise constant functions [29,40,41,42]. Increasing the level of detail in the time level partition leads to greater accuracy as it allows for a more intricate and nuanced representation of the time-dependent processes or phenomena under consideration [43]. Employing control parameterization enables the derivation of a finite-dimensional approximation for Problem B. Ultimately, the gradient-based algorithm is employed to resolve the resultant approximation problem.
The conventional time-scaling transformation necessitates simultaneous switching of all control components, a condition challenging to attain in practical applications [44]. Hence, the introduction of SASTOT emerges as a solution, combining both time-scaling transformation and control parameterization methodologies [39]. Within this methodology, each control component possesses the capability to adaptively adjust and independently select its switching time, allowing for diverse switching points across components. Empirical validation showcases a notable reduction in computational complexity alongside an improvement in the accuracy of calculations. For a clearer exposition of this approach, this article examines two distinct control inputs. Let $ \boldsymbol{\tilde{u}}(t) = [\tilde{u}_{1}(t), \tilde{u}_{2}(t)]^\mathrm{T} $. Then, the dynamical system is
3.1. Control parameterization and time-scale transformation for $ \tilde{u}_{1}(t) $.
The interval $ [0, T] $ is divided into $ q_{1} $ subintervals $ [\delta_{1}^{l_{1}-1}, \delta_{1}^{l_{1}}] $, $ l_{1}\in I_{q_{1}} $, where $ \boldsymbol{\sigma}_{1}: = [\delta_{1}^{1}, \delta_{1}^{2}, \dots, \delta_{1}^{q_{1}}]^\mathrm{T} $ are variable switching time vector, and
The control component $ \tilde{u}_1(t) $ can be approximated by
where $ \eta_{1}^{l_{1}} $ is the piecewise constant function value on the $ l_{1} $th subinterval of the control component $ u_{1}(t) $ satisfying
and $ \chi _{[\delta_{1}^{l_{1}-1}, \delta_{1}^{l_{1}})}(t) $ is an indicator function defined by
Then, we obtain the following system:
Let $ \boldsymbol{\tilde{x}}(\cdot|\boldsymbol {\eta_{1}}, u_{2}) $ denote the solution of system (3.7).
After applying the time-scaling transformation [45] to $ \tilde{u}_{1}(t) $ and mapping the variable switching times $ \left\{\delta_{1}^{0}, \delta_{1}^{1}, \dots, \delta_{1}^{q_{1}}\right\} $ to a fixed number of switching times $ \left\{0, 1, \dots, q_{1}\right\} $ in the new time horizon, we define the vector $ \boldsymbol{\phi}_{1}: = [\phi_{1}^{1}, \dots, \phi_{1}^{q_{1}}]^\mathrm{T} \in \mathbb{R}^{q_{1}} $, where $ \phi_{1}^{l_{1}} = \delta_{1}^{l_{1}}-\delta_{1}^{l_{1}-1}\geq \rho $, $ \rho $ is an extremely small positive number, $ l_{1}\in I_{q_{1}} $, and $ \phi_{1}^{1}+\phi_{1}^{2}+\dots+ \phi_{1}^{q_{1}} = T $.
Then, we introduce a new time variable $ p $ and define a time scaling function $ \nu_{1}(p, \phi_{1}) $
where $ \theta (p) = \tilde{u}_{2}(\nu_{1}(p, \boldsymbol{\phi}_{1})) = \tilde{u}_{2}(t) $ and $ {\lfloor p \rfloor} $ is a floor function of the time variable $ p $. With the new time variable $ p $, the dynamical system is redefined on the subinterval $ [l_{1}-1, l_{1}), \ l_{1}\in I_{q_{1}}, $
Let $ \hat{\boldsymbol{x}}(\cdot|\boldsymbol {\eta_{1}, \theta }) $ denote the solution of system (3.9).
3.2. Control parameterization and time-scaling transformation for $ \tilde{u}_{2}(t) $.
The interval $ [0, q_{1}] $ is divided into $ q_{2} $ subintervals $ [p_{2}^{l_{2}-1}, p_{2}^{l_{2}}], \ l_{1}\in I_{q_{2}}, $ where $ \boldsymbol{\sigma}_{2} = [p_{2}^{0}, p_{2}^{1}, \dots, p_{2}^{q_{2}}]^\mathrm{T} $ is the variable switching time vector, and
The control component $ \tilde{u}_{2}(t) $ can be approximated by
where $ \eta_{2}^{l_{2}} $ is the piecewise constant function value on the $ l_{2} $th subinterval of the control component $ \theta(p) $ satisfying
With the new time variable $ p $, system (3.9) is redefined on the subinterval $ [p_{2}^{l_{2}-1}, p_{2}^{l_{2}}), \ l_{2}\in I_{q_{2}}, $
After applying a time-scaling transformation to $ \check{u}_{2}(t) $ and mapping the variable switching times $ \left\{\delta_{2}^{0}, \delta_{2}^{1}, \dots, \delta_{2}^{q_{2}}\right\} $ to a fixed number of switching times $ \left\{0, 1, \dots, q_{2}\right\} $ in the new time horizon, we define the vector $ \boldsymbol{\phi}_{2}: = [\phi_{2}^{1}, \dots, \phi_{2}^{q_{2}}]^\mathrm{T} \in \mathbb{R}^{q_{2}} $, where $ \phi_{2}^{l_{2}} = \delta_{2}^{l_{2}}-\delta_{2}^{l_{2}-1}\geq \rho $, $ \rho $ is an extremely small positive number, $ l_{2}\in I_{q_{2}}, $ and $ \phi_{2}^{1}+\phi_{2}^{2}+\dots+ \phi_{2}^{q_{2}} = T $.
Then, we introduce a new time variable $ w $ and define a time scaling function $ \nu_{2}(w, \phi_{2}) $
where $ {\lfloor w \rfloor} $ is the floor function of the time variable $ w $. System (3.13) is redefined on the subinterval $ [l_{2}-1, l_{2}), l_{2}\in I_{q_{2}}, $
Let $ \check{\boldsymbol{x}}(\cdot|\boldsymbol {\eta_{1}, \eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $ be the solution of system (3.15). Then the continuous state constraint (2.5) becomes
The cost function (2.8) and the maximum hands-off control constraint (3.1) become
With these in mind, Problem B can be approximated by the following Problem C.
Problem C: Given system (3.15), choose the quadruple $ (\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} })\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}} $ to minimize the objective function defined by (3.17) subject to continuous inequality constraints (3.16), boundary conditions (3.5) and (3.12), and maximum hands-off control constraint (3.18).
Because of $ |\eta_{1}^{\lfloor \nu_{2}(w) \rfloor}| = 2{\max}\Big\{\eta_{1}^{\lfloor \nu_{2}(w) \rfloor}, 0\Big\}-\eta_{1}^{\lfloor \nu_{2}(w) \rfloor}, |\eta_{2}^{l_{2}}| = 2{\max}\Big\{\eta_{2}^{l_{2}}, 0\Big\}-\eta_{2}^{l_{2}}, $ the maximum hands-off control constraint (3.18) can be equivalently transformed as $ A_{3}(\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} }) $ defined in (3.19).
Define
where $ \rho $ is the penalty parameter and
Thus, Problem C can be equivalently transformed into Problem D.
Problem D: Given system (3.15), choose the quadruple $ (\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} })\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}} $ to minimize the objective function defined in (3.20).
Remark 1. According to [29], it has been established that when the penalty parameter $ \rho $ exceeds its threshold value $ \rho^* $, the solution derived for Problem D represents an exact solution for Problem C.
4.
Smoothing process
4.1. Smoothing technique
The fundamental concept underlying the smooth technique involves the approximation of the non-smooth maximum operator through the utilization of a smoothing function [46], which is defined by
where $ \rho $ is a penalty factor, $ q $ is the number of continuous inequality constraints, and $ \varepsilon > 0 $ is the smoothing parameter.
Theorem 1. ([46]) For $ \varepsilon > 0 $, we have
By the smoothing process, the maximum hands-off control constraint $ A_{3}(\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} }) $ defined in (3.19) can be approximated by
Based on the smoothing function (4.1), the cost function (3.20) can be approximated by
where
Based on the smoothing function (3.20), Problem D can be approximated by Problem E.
Problem E: Given system (3.15), choose the quadruple $ (\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} })\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}} $ to minimize the cost function defined in (4.4).
4.2. Error analysis
The application of smoothing techniques may introduce discrepancies between Problems D and E. This section entails the derivation of errors between Problems D and E concerning the smoothing function (3.20). It has been demonstrated that for a sufficiently small smoothing parameter $ \varepsilon $, the solution to Problem D can be acquired by sequentially solving a series of Problem E while incrementing the values of the penalty factor $ \rho $.
Theorem 2. If $ \rho > 0, \ q > 0 $, and $ \varepsilon > 0 $, then
Proof. Based on Theorem 1, we have for $ \rho > 0, \ q_{1}, \ q_{2} > 0 $, and $ \varepsilon > 0 $,
Then,
which completes the proof.
Theorem 3. Let $ (\boldsymbol {\eta_{1}^{*}}, \boldsymbol {\eta_{2}^{*}}, \boldsymbol{\phi_{1}^{*}}, \boldsymbol{\phi_{2}^{*}}) $ be the solution of Problem D, and let $ (\boldsymbol {\eta_{1}^{**}}, \boldsymbol {\eta_{2}^{**}}, \boldsymbol{\phi_{1}^{**}}, \boldsymbol{\phi_{2}^{**}}) $ be the solution of Problem E. Then,
Proof. Based on Theorem 2, we have
Since $ (\boldsymbol {\eta_{1}^{*}}, \boldsymbol {\eta_{2}^{*}}, \boldsymbol{\phi_{1}^{*}}, \boldsymbol{\phi_{2}^{*}}) $ is the solution of Problem D, we have
which yields
Since $ (\boldsymbol {\eta_{1}^{**}}, \boldsymbol {\eta_{2}^{**}}, \boldsymbol{\phi_{1}^{**}}, \boldsymbol{\phi_{2}^{**}}) $ is the solution of Problem D, we obtain
which yields
Based on (4.7) and (4.8), we have
which completes this proof.
Remark 2. Theorem 3 states that when the smoothing parameter $ \varepsilon $ assumes a sufficiently small value, the solution of Problem E tends to approximate the solution of Problem D.
To obtain an error estimation between the solutions of Problems E and C outlined in Theorem 4, the definition of $ \varepsilon $-feasibility to Problem D is given in Definition 3.
Definition 3. A vector $ (\boldsymbol {\eta_{1}^{\varepsilon}}, \boldsymbol {\eta_{2}^{\varepsilon}, \boldsymbol{\phi_{1}^{\varepsilon}}, \boldsymbol{\phi_{2}^{\varepsilon}})\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}}} $ is called $ \varepsilon $-feasible to Problem D if
Theorem 4. Let $ (\boldsymbol {\eta_{1}^{*}}, \boldsymbol {\eta_{2}^{*}}, \boldsymbol{\phi_{1}^{*}}, \boldsymbol{\phi_{2}^{*}}) $ and $ (\boldsymbol {\eta_{1}^{**}}, \boldsymbol {\eta_{2}^{**}}, \boldsymbol{\phi_{1}^{**}}, \boldsymbol{\phi_{2}^{**}}) $ be the solution of Problems D and E, respectively. Furthermore, let $ (\boldsymbol {\eta_{1}^{*}}, \boldsymbol {\eta_{2}^{*}}, \boldsymbol{\phi_{1}^{*}}, \boldsymbol{\phi_{2}^{*}}) $ be feasible to Problem D and $ (\boldsymbol {\eta_{1}^{**}}, \boldsymbol {\eta_{2}^{**}}, \boldsymbol{\phi_{1}^{**}}, \boldsymbol{\phi_{2}^{**}}) $ be $ \varepsilon $-feasible to Problem D. Then
Proof. Since $ (\boldsymbol {\eta_{1}^{*}}, \boldsymbol {\eta_{2}^{*}}, \boldsymbol{\phi_{1}^{*}}, \boldsymbol{\phi_{2}^{*}}) $ is the solution of Problem D, we have
where
Since $ (\boldsymbol {\eta_{1}^{**}}, \boldsymbol {\eta_{2}^{**}}, \boldsymbol{\phi_{1}^{**}}, \boldsymbol{\phi_{2}^{**}}) $ is $ \varepsilon $-feasible to Problem D, we obtain
Based on Theorem 3, we get
which completes this proof.
Remark 3. In this scenario, as outlined in Theorem 4, an error estimation between the solutions of Problems E and C is provided, specifically under the condition of $ \rho > \rho^* $. Consequently, the solution for SOP (Sum of Optimization Problems) can be approximately obtained by iteratively solving a sequence of Problem E.
5.
Gradient computation
In this section, we will derive the gradient formulae of the cost function $ J_{2}(\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}}, \rho, q_1, q_2, \varepsilon) $ with respect to the quadruple $ (\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} })\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}} $ based on Theorems 5–8, whose proofs are similar to the proofs of Theorems 1 and 2 in [39].
Theorem 5. For each $ (\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $, we have
where $ \boldsymbol{M}_{1}(\cdot|\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $ is the solution to the following system on $ w\in[l_{2}-1, l_{2}], l_{2}\in I_{q_{2}}: $
On the basis of Theorem 5, the gradient of $ J_{2} $ with respect to $ \boldsymbol{\eta_{1}} $ is given as follows:
Theorem 6. For each $ (\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $,
where $ \boldsymbol{M}_{2}(\cdot|\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $ is the solution to the following system on $ w\in[l_{2}-1, l_{2}], \ l_{2}\in I_{q_{2}}: $
On the basis of Theorem 6, the gradient of $ J_{2} $ with respect to $ \boldsymbol{\eta_{2}} $ is given as follows:
Theorem 7. For each $ (\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $, we have
where $ \boldsymbol{N}_{1}(\cdot|\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $ is the solution to the following system on $ w\in[l_{2}-1, l_{2}], \ l_{2}\in I_{q_{2}}: $
Based on Theorem 7, the gradient of $ J_{2} $ with respect to $ \boldsymbol{\phi_{1}} $ is given as follows:
Remark 4. For this, we introduce the inverse of $ \nu_{2}(w) $. The gradient of $ J_{2} $ with respect to $ \boldsymbol{\phi}_{2} $ is complicated to derive because the switching time is in the time range of $ w $. $ \nu_{2}^{-1}(p) $ is a function of $ \boldsymbol{\phi}_{2} $, and at every connection point, this inverse function is not differentiable. $ \nu_{2}^{-1}(r), r\in I_{q_{1}} $ is represented by $ w_{r} $, and the gradient of $ w_{r} $ with respect to $ \phi_{2}^{l_{2}}, \ l_{2}\in I_{q_{2}} $ at $ r\in I_{q_{1}-1} $ is given in Remark 1 as follows.
Remark 5. If point $ w_{r} $ coincide with $ w\in I_{q_{2}-1}, $ then we have
and
Remark 6. If point $ w_{h} $ does not coincide with $ w\in I_{q_{2}-1} $, then we have $ \frac{\partial w_{r}^{+}}{\partial \phi_{2}} = \frac{\partial w_{r}^{-}}{\partial \phi_{2}} $.
With the above discussion, the gradient of states with respect to $ \boldsymbol{\phi_{2}} $ is given below.
Theorem 8. For each $ (\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $, we have
where $ \boldsymbol{N}_{2}(\cdot|\boldsymbol{\eta_{1}}, \boldsymbol{\eta_{2}}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}) $ is the solution to the following system on $ w\in[l_{2}-1, l_{2}], \ l_{2}\in I_{q_{2}}: $
with
$ H_{r, \boldsymbol{f}, \boldsymbol{h}}^{-} = \phi_{1}^{\lfloor \nu_{2}(w_{h}^{-}) \rfloor}\phi_{2}^{\lfloor w_{h}^{-} \rfloor} \Big[\boldsymbol{f}(\tilde{\boldsymbol{x}}(w_{h}^{-}))+h_{1}(\tilde{\boldsymbol{x}}(w_{h}^{-}))\eta_{1}^{\lfloor \nu_{2}(w_{h}^{-}) \rfloor}+ h_{2}(\tilde{\boldsymbol{x}}(w_{h}^{-}))\eta_{2}^{\lfloor w_{h}^{-} \rfloor}\Big] \frac{\partial w_{r}^{-}}{\partial \phi_{2}} $ and
$ H_{r, \boldsymbol{f}, \boldsymbol{h}}^{+} = \phi_{1}^{\lfloor \nu_{2}(w_{h}^{+}) \rfloor}\phi_{2}^{\lfloor w_{h}^{+} \rfloor} \Big[\boldsymbol{f}(\tilde{\boldsymbol{x}}(w_{h}^{+}))+h_{1}(\tilde{\boldsymbol{x}}(w_{h}^{+}))\eta_{1}^{\lfloor \nu_{2}(w_{h}^{+}) \rfloor}+ h_{2}(\tilde{\boldsymbol{x}}(w_{h}^{+}))\eta_{2}^{\lfloor w_{h}^{+} \rfloor}\Big] \frac{\partial w_{r}^{+}}{\partial \phi_{2}} $.
Based on Theorem 8, the gradient of $ J_{2} $ with respect to $ \boldsymbol{\phi_{2}} $ is given as follows:
where $ H_{r, \lambda_{i}}^{+} $ and $ H_{r, \lambda_{i}}^{-} $ are defined as $ H_{r, \boldsymbol{f}, \boldsymbol{h}}^{+} $ and $ H_{r, \boldsymbol{f}, \boldsymbol{h}}^{-} $, respectively.
Remark 7. The gradient formulae of the cost function $ J_{2}(\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}}}, \rho, q_1, q_2, \varepsilon) $ with respect to the quadruple $ (\boldsymbol {\eta_{1}, \eta_{2}, \boldsymbol{\phi_{1}}, \boldsymbol{\phi_{2}} })\in \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{1}}\times \mathbb{R}^{q_{2}}\times \mathbb{R}^{q_{2}} $ is calculated by the variational method (Theorems 5–8). Therefore, the gradient-based algorithm easily obtains the optimal solution for Problem E.
6.
Numerical results
We consider a nonlinear maximum hands-off control problem with the cost functional defined by
governed by the nonlinear dynamical system
with the maximum hands-off control constraint
and the bound constraints of the control inputs
Case 1: The optimal control problem governed by nonlinear dynamical system (6.2) without the maximum hands-off control constraint (6.3).
Case 2: The optimal control problem governed by nonlinear dynamical system (6.2) with the maximum hands-off control constraint (6.3).
For Cases 1 and 2, the number of segments for the two controls are, respectively, 10 and 20. For Cases 1 and 2, by using the proposed method we respectively obtain the optimal control strategies $ {\mathbf u}^{1*} $ and $ {\mathbf u}^{2*} $ plotted in Figures 1 and 2. Their corresponding optimal cost and sparsity levels are given in Table 1. From Figure 2, it is observed that for the first control, sparse control happened in the first and from the fourth to the tenth segments. For the second control, sparse control occurred in the second, the sixteenth, from the ninth to the thirteenth, and from the eighteenth to the twentieth segments.
The graphical representation in Figure 1 illustrates that the optimal control strategies demonstrate a considerable density. In contrast, Figure 2 portrays these strategies with a noticeable level of sparsity. Nevertheless, it is essential to highlight that the inclusion of the maximum hands-off control constraint (6.3) results in a marginal increase in the cost function value compared to the scenario without this constraint (6.3). Specifically, the cost function slightly exceeds its counterpart when the maximum hands-off control constraint is imposed.
The observed trend in Figure 2 reveals a noteworthy pattern in the sparsity of the sparse optimal control strategies. It becomes evident that there is a rapid initial increase in sparsity, accompanied by a relatively minor escalation in cost. Therefore, based on the findings presented in this paper, it can be inferred that the proposed method exhibits the capability to generate solutions of superior quality.
Furthermore, from Table 1, it is pertinent to note that the value of the cost function, specifically $ h_0({\mathbf u}^{2*}) $, slightly exceeds that of $ h_0({\mathbf u}^{1*}). $ The smaller the value of $ A_1({\mathbf u}^{*}) $, the sparser $ {\mathbf u}^{*} $ becomes. From Table 1, it follows that $ {\mathbf u}^{2*} $ is sparser than $ {\mathbf u}^{1*} $. So, we can conclude that this proposed method achieves a balance between system performance and sparsity, thereby suggesting its efficacy in providing solutions that optimize both aspects effectively.
7.
Conclusions
Solving the sparse optimal control problem within the framework of linear dynamical systems often allows for an analytical solution. However, when addressing the maximum hands-off control problem within the domain of nonlinear dynamical systems, obtaining an analytical solution proves to be considerably challenging. This paper necessitates the numerical solution of the sparse optimal control problem which is governed by nonlinear dynamical systems. We employ control parameterization in conjunction with the sequential adaptive switching time optimization technique to approximate the maximum hands-off control problem by a sequence of finite-dimensional optimization problem. This approach allows for varying control switching times without imposing uniformity and offers flexibility in selecting control components. The resolution of the sparse optimal control problem relies on a gradient-based algorithm. To showcase the efficacy of the proposed methodology, an illustrative example is provided.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgements
This work was supported in part by the National Key Research and Development Program of China under Grant 2022YFB3304600; in part by the National Natural Science Foundation of China under Grants 11901075, 12271307 and 12161076; in part by the China Postdoctoral Science Foundation under Grant 2019M661073; in part by the Fundamental Research Funds for the Central Universities under Grants 3132022201, 3132023206, 3132023535 and DUT22LAB305; in part by the Guandong Province Natural Science Foundation of China under Grant 2022A1515011761; in part by Chongqing Natural Science Foundation Innovation and Development Joint Fund (CSTB2022NSCQ-LZX0040); in part by Ministry of Higher Education (MoHE) Malaysia through the Foundation Research Grant Scheme (FRGS/1/2021/STG06/SYUC/03/1); in part by the Shandong Province Natural Science Foundation of China under Grant ZR2023MA054; in part by the Fundamental Scientific Research Projects of Higher Education Institutions of Liaoning Provincial Department of Education under JYTMS20230165 (General Project); and in part by the Xinghai Project of Dalian Maritime University.
Conflict of interest
The authors declare there is no conflict of interest.










 DownLoad:
DownLoad: