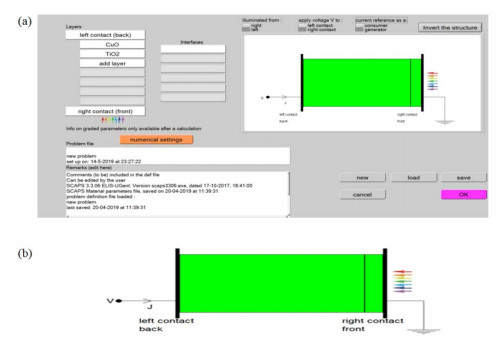
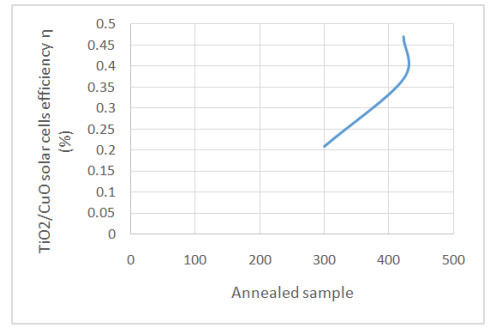
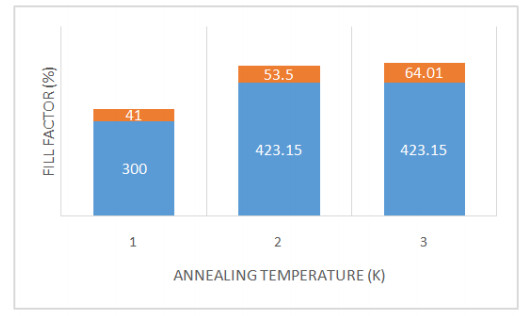
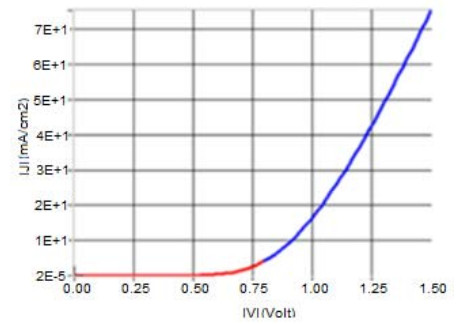
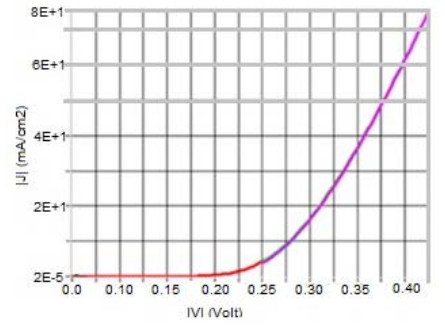
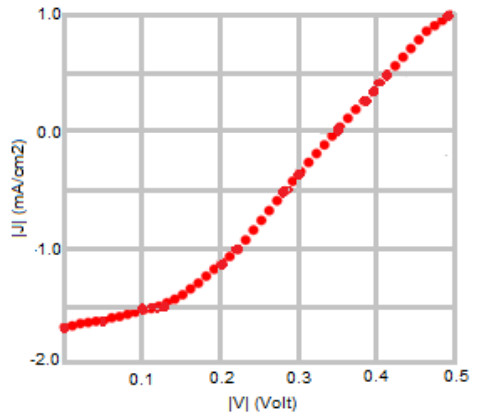
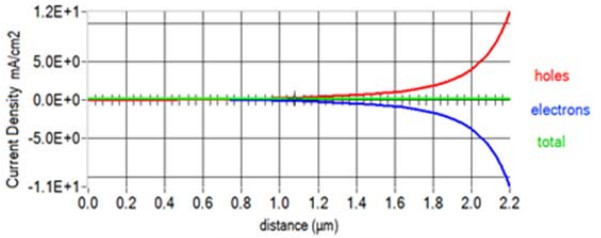
The problem of global warming has led to increased research on solar energy and other renewable energy. Solar cells are a building block of solar energy. Different materials for solar cells fabrication exist with silicon-based being commercially viable and common. The bulk of the alternate materials aimed at providing cheap, efficient and sustainable solar cells. Nanostructured Metal oxides solar cells goes a step further to providing a clean, affordable, sustainable solar cells although the efficiency is still low. This study examined the numerical modelling of the annealing effect on the efficiency of nanostructured CuO/TiO2 pn heterojunction using SCAPS. The motivation for the study is to provide a basis for experimental design of affordable, non-toxic and efficient alternate material for silicon solar cells. The modelling was performed using Solar cells capacitance simulator (SCAPS). The input parameters, obtained from literature, include a working point of 300 K for the as-deposited CuO/TiO2 which was compared with air and nitrogen annealed (423.15 K) nanostructured CuO/TiO2 pn heterojunction. Other working condition included simulated sunlight using illumination of AM 1.5G with a 500 W Xenon lamp, silver was used as the electrode/contact. Film thickness of 2000 nm and 200 nm for absorber and buffer respectively. The results gave an optimum efficiency of 0.47 obtained from Nitrogen annealed CuO/TiO2 pn heterojunction. Also, the optimum Fill Factor was obtained to be 64.01% from Nitrogen annealed. The annealed samples performed better than the as-deposited CuO/TiO2 pn heterojunction. This result will help in the experimental fabrication of improved efficiency metal oxide-based solar cells.
1.
Introduction
Periodically perturbed issues or seasonal variations of environment have been confirmed to bring diversity and complexity to population communities. Several seasonality parameters were analyzed in detail by means of bifurcation diagrams demonstrated that even a relatively simple dynamic behavior of the system with constant parameters become very complex when they were periodically perturbed [1]. For instance, their results showed that the prey-predator system can give rise to multiple attractors under periodically varying parameters while only one attractor was generated when the parameters in the constant case. Moreover, the limit cycle of the unperturbed system can be converted into the quasi-periodic one owing to the introduction of the seasonality. Abundant chaotic solutions were found in the prey-predator ecosystem subjected to periodic forcing of the intrinsic growth rate of the prey, which in its unforced state has a globally stable focus [2]. Incorporating periodic forcing in the prey-predator system with age structure for predator also exhibited further quasi-periodic solution and chaotic solution [3]. The chaotic solution was detected in a seasonally perturbed ratio-dependent prey-predator system through Lyapunov exponents, Lyapunov dimension and Poincare section [4]. Frequency lockings and resonant patterns were observed in a spatial version of prey-predator model with the appearance of periodic forcing and noise [5], which indicate that the phenomena may partly result from periodic forcing and noise instead of deterministic factors. In article [6] it was found that the addition of periodic forcing to the semi-Kolmogorov ecological system can produce pullback attractors.
These above results indicated that the periodic forcing usually brings systems to more complex dynamical behaviors such as chaos, which are often undesirable attributes of the ecosystems, especially for the ecosystems related to pest populations. Forest pests have caused huge ecological damage and significant economic losses to forests either through the consumption of leaves or fluids by defoliators or chewing phloem by bark beetles [7]. Most of insects rarely caused the whole tree to die directly, but they resulted in defoliation across wide areas [8]. Other defoliators such as the eastern spruce budworm in North America can cause a great quantity of trees dead if they were destroyed for several years [9]. Most of the literatures that deal with this issue were largely at the descriptive and phenomenological levels. Although the association between forest damage and insects outbreak has been frequently explored from the quantitative point of view, nevertheless the corresponding mathematical models did not been put forward. Chen-Charpentier developed a tree-beetle system to qualitatively analyze the effect of interaction between forest damage and pest outbreaks [10]. The constructed two-dimensional mathematical model described the temporal dynamics of the tree-beetle system and the potential for the existence of positive feedback between wildfire and insect outbreak disturbances, which was consistent with the previous experimental data available. Nevertheless, this article did not further address the multiple attractors coexistence, quasiperiodic and chaotic phenomena.
In the history of battles against pests, human combat strategies and tactics have been evolving with the society development, becoming more and more ingenious and effective to a large extent [11]. Initially, humans used hand picking, swatting and other methods to catch pests, and later changed the environment to eliminate pests, such as burning fields to kill insects, and using scarecrows to drive away birds. The introduction of natural enemies to eliminate pests is an important control referred to "biological control". The superiority of biological control is that biological control does not pollute fields and environments, but the disadvantage is that it may cause the natural enemies outbreak. In the 1940s, chemical control began to dominate in the control policies because of the adoptation of insecticide DDT, which was effective, cheap and long-lasting. Insecticides were so effective that entomologists and pest managers even held the view that the extinction of pests was doomed. However, large-scale use of insecticides was prone to cause pests resistance to insecticides and injure some innocent insects imprudently, the pests soon multiplied in large numbers.
Nevertheless, it is impossible to eradicate the pests completely, nor is it biologically or economically desirable. Recently, a new comprehensive approach termed integrated pest management(IPM) has been put forward. Integrated pest management relies heavily on natural mortality factors such as natural enemies, whether or not adopts the chemical pesticides only after evaluating the potential interaction among various control tactics. IPM considers all available pest control strategies including biological, cultural and chemical action to reduce pest populations to tolerable levels when the pests reach or exceed an economic threshold(ET). For example, people combined chemical and biological control methods to control aphids [12,13], adopted IPM to eliminate the parasitoids in a host-parasitoid model [14] and reduce the density of pests in prey-predator models [15,16]. That is, to avoid economic loss, the number of pests should be less than the economic injury level (EIL) where an ET is approximately 75 % or 80 % of EIL [13,17,18]. This shows that the main aim of IPM is to reduce the density of pest population below the EIL, rather than eliminate it.
Threshold policy control (TPC) is a control strategy that divides the whole system into several subsystems according to the presetting threshold [19,20,21], and different subsystems adopt distinct control strategies, i.e., if the number of pest population does not reach ET, no control strategy need to be adopted and allow the number of pests to continue to grow. If the number of pest population is larger than ET, the corresponding control measure will be implemented, such as releasing natural enemies, spraying pesticides and etc. In traditional biological control or pesticide-dominated control systems, pest managers release natural enemies or spray pesticides at fixed time or by seasonality regardless of whether the number of pests reaches ET or not. Although threshold policy control was also adopted in the pest control systems with state-dependent impulse where the control policy was related to ET, it was not reasonable for people to carry out control policy and make the number of pests less than ET instantaneously. Actually, the control strategies cannot be finished at a moment and the control effect will take a certain period of time to appear. Consequently, a class of Filippov pest management systems combining IPM and TPC have attracted the attention of scholars. Periodically forced Filippov population systems by taking advantage of IPM and TPC have been considered in References [21,22,23]. The Filippov system is a kind of discontinuous/non-smooth system [25,26] and applied in mechanical systems [27,28], prey-predator models [29,30,31], pest-natural enemy system [32], braking system [33], electro-mechanical system [34], epidemic models [35,36,37], neuronal model [38]. In this paper, integrated IPM with TPC, a novel Filippov forest-pest system with periodic forcing is proposed.
The organization of this paper is as follows. In section 2, based on the classical tree-beetle model, a periodically forced Filippov forest-pest model integrated IPM with TPC is proposed. The theoretical preliminary of switching dynamics of the proposed system will be given in section 3. In section 4, numerical investigations of the Filippov system are studied, which includes bifurcation analysis of the periodic forcing amplitude γ, the periodic forcing frequency ω and economic threshold ET, four cases of the coexisting attractors and key parameters sensitivity analysis on the dynamics of the system and the corresponding biological significance are discussed. Concluding remarks are presented in the last section.
2.
Model formulation
Chen-Charpentier [10] proposed the tree-beetle system model
where V(t) represents the number of susceptible trees, rv and kv are its intrinsic growth rate and carrying capacity, respectively. B(t) represents the density of mountain pine beetles, its intrinsic growth rate is rb and the carrying capacity kb is assumed to depend on the amount of foliage or phloem available. The growth of the trees is density limited as given by a logistic self-interaction without beetles. m(B) accounts for the mortality of trees caused by the attack of beetles. The term
is the Holling type Ⅲ functional response, which defines the tree defense ability depends on the number of beetles per tree where α=0 denotes the trees have no defense and saturates for high number of beetles. Based on model (2.1), Liu and Xiang et al. proposed the following forest-pest model to elaborate the relationships of trees and pests [24]
where δ represents the mortality rate of tree consumed by beetle; η is the conversion coefficient of the beetles; ηδB(t)V(t) denotes the number of beetles additional increases after they comsumed trees. To explore the effects of periodic forcing on population communities in this paper, when B(t)<ET, the forest-pest system with periodic forcing term γ(1−cosωt) is considered where the periodic forcing follows the idea in References [2,3,22].
where S(t)=ωt, γ and ω are its amplitude and frequency of periodic forcing term. Rearrange the second equation of model (2.3), it can be written as
IPM strategies are adopted to control pests when the density of pest population reaches or exceeds the economic threshold. Some anthropogenic disturbances are also considered which includes planting trees or releasing natural enemies of pests. Compared to the entire forest, the effect of anthropogenic disturbance is limited. Thus, when B(t)>ET, spraying pesticides and some anthropogenic disturbances are taken into account simultaneously, supposing that control strategies are applied, then model (2.3) becomes
where τ(t) could be regarded as newly planted trees, q1B(t) could be viewed as the number of pests reduced after adopting control strategy. Therefore, the Filippov system [25,34] combines model (2.3) and (2.4) is
with
Denote H(Z)=B(t)−ET with column vector Z=(V,B,S)T, and the column vector is defined in G=R2+×T1 with T1=R+/2πN (N is positive integer) [39]. Models (2.5) and (2.6) describe the TPC referred to as an on-off control. Then, it should be noted that the discontinuity boundary set Σ={Z∈G|H(Z)=0} separates G into two regions
where G1={Z∈G|H(Z)<0}, G2={Z∈G|H(Z)>0}, the specific expressions FG1(Z) and FG2(Z) take the form of
and
The sliding region and sliding mode dynamics of Filippov system (2.7) can be determined by means of the Filippov convex method [25] or the Utkin's equivalent control method [34]. Denote
where ⟨⋅⟩ is the standard scalar product and HZ denotes a non-vanishing gradient of the smooth scale function on Σ. Then, the sliding mode domain can be defined as
Meanwhile, the sliding mode domain ΣS can be distinguished as the following regions
(ⅰ) Escaping region: if ⟨HZ(Z),FG1(Z)⟩<0 and ⟨HZ(Z),FG2(Z)⟩>0,
(ⅱ) Sliding region: if ⟨HZ(Z),FG1(Z)⟩>0 and ⟨HZ(Z),FG2(Z)⟩<0.
3.
Sliding region and sliding mode dynamics of Filippov system (2.7)
In this section, the sliding region and sliding mode dynamics of Filippov system (2.7) are investigated. According to the definitions of σ(Z) and the switching surface H(Z) in section 2, we have
The sliding regions exists on the discontinuity boundary Σ if the sign of the vector in subsystem SG1 is positive while in subsystem SG2 is negative. Then, the sliding region can be obtained by solving the following inequalities related to V and S
The two inequalities can be combined as follows
Substituting S=ωt into (3.2), which can be rewritten as
where
Therefore, the sliding segment of Filippov system (2.7) can be defined as
We further introduce the sliding mode dynamics of Filippov (2.7) by employing Utkin's equivalent control method [34]. Since ˙H=0
where B=ET. Then, solve the above equation with respect to ε yields
So the dynamics on Σs (i.e., the sliding region) can be determined by the following equations
Denote
Hence, equations (3.3) can be represented as follows
A correlation equation is then defined, namely,
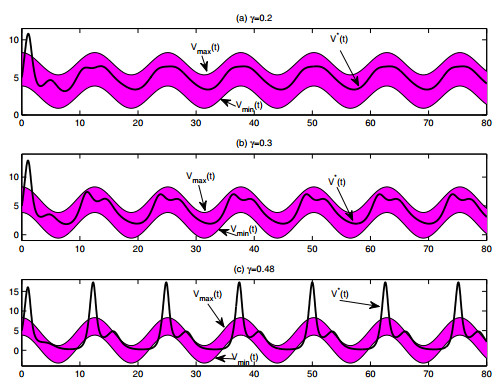
where we denote the solution of equation (3.5) as V∗(t). Numerical simulation of sliding periodic solution at low value of γ(0.2) are illustrated in Figure 1 (a) and Figure 2, respectively. The sliding periodic solution is refers to the periodic solution completely oscillates in the sliding domain except for finite time out of the sliding domain. In other words, the density of the trees fluctuates between Vmin(t) and Vmax(t) and the density of pest population always does not reach and exceed the ET. In this case, the pests are completely controllable. When the amplitude γ of periodic forcing increases to 0.3, the density of trees still fluctuates within the expected range which is showed in Figure 1(b). However, in Figure 1(c), when γ take the larger value 0.48, the system's periodic solution is out of the boundary of the sliding domain, which is not the sliding periodic solution, thus the pest population become unpredictable and may outbreak in this case.
From Figure 1 we argue that this numerical evidence supports the fact that the larger γ, then Vmin(t) tend to the smaller. In a biological sense, if the pests outbreak, the more trees will be destroyed and the density of trees will be lower. The existence of sliding periodic solution of the system is vital to achieve the pest control. If the amplitude γ of periodic forcing below a certain critical value such as 0.48 and other parameters are fixed as Figure 1(a), the initial densities of the two populations are random, then the system still has a sliding periodic solution depicted in Figure 2, indicating that pests are under controllable range.
4.
Complexity of the dynamic behaviors and simulation
To gain deeper understanding of the rich dynamic behaviors brought about by parameter space of Filippov system (2.7), some special numerical cases are considered in this section. We first show the bifurcation diagrams of key parameters (i.e., γ, ET and ω), it is observed that period-adding bifurcation, multiple attractors coexistence and quasi-periodic phenomenon exist in the Filippov system. Coexisting attractors are compared through wavelet coherence, and parameter sensitivity analysis also be provided to address the influence of parameters in biological pest control.
4.1. Bifurcation analysis of key parameters
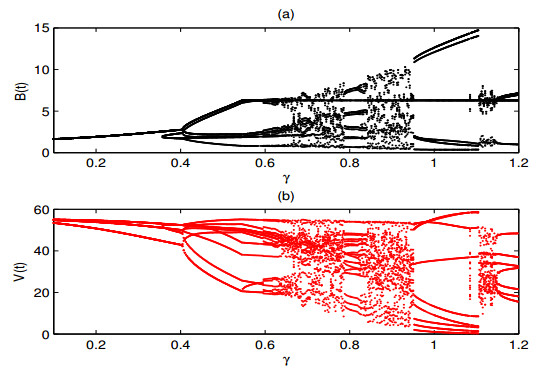
We first choose the amplitude γ of periodic forcing term as a bifurcation parameter and fix all other parameter values as those in Figure 3, bifurcation diagram about γ for pest population (B(t)) is showed in Figure 3(a). The results indicate that if 0.1<γ<0.6, the pest population oscillates and the local maximum values do not exceed the ET, which is a favourable case for pest control. When γ>0.6, the number of pests will exceed the threshold ET at sometimes and fall below the threshold ET at other cases, which implies the system will switch between two subsystems. If the density of pests above ET but below EIL, the density of pests is still under controllable range. From Figure 3(b) we can find the density of trees (V(t)) shows periodic windows and chaos rhythm similar to pests. The Filippov system experiences stable state with period-1 to period-n and then chaos, period-n and chaos occur alternately. Especially, it follows from Figure 3(b) that multiple attractors can coexist in the interval around (1.1,1.2).
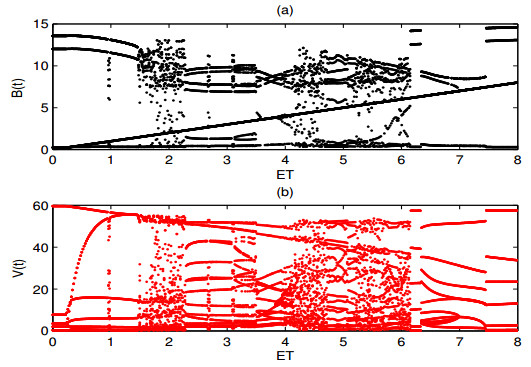
Bifurcation structures of states variables about economic threshold ET are showed in Figure 4(a) and (b), respectively. It is noted that period-adding bifurcations interchanging with regions of chaos are observed since ET in a wide range (0,8). Theoretically, the lower ET, the more intensive pest control measures should be taken. However, the densities of pests and trees are affected by various factors. When the parameter in term of pest control policy is large such as q1=0.6, we didn't find the number of pests drop dramatically as expected. Part of the reason may be that seasonal variation leads to a sharp increase in the number of pests such as the amplitude of periodic forcing γ=0.6. Moreover, two attractors can coexist if ET∈(2.6,3.2) or ET∈(6.1,6.3). Multiple attractor coexistence indicates that the pest outbreak patterns not only depend on the parameters of Filippov system but also the initial densities of pests and trees.
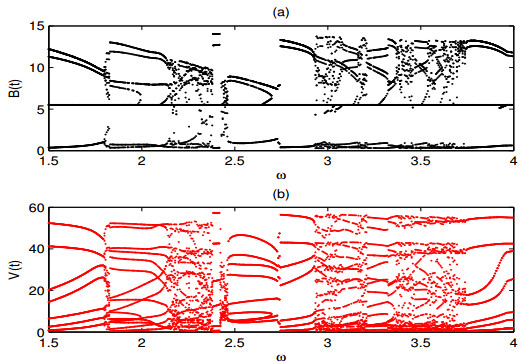
The two bifurcation diagrams presented in Figure 5 related to the frequency ω of periodic forcing term for the pests and trees, respectively. The value of ω can also affect the implementation of the control strategy. Like the amplitude γ and the threshold ET, the frequency ω is not a simple linear relationship with the densities of pests and trees. The bifurcation diagram about pest population in Figure 5(a) shows the density of pests exhibits the phenomenon in which multiple periods and chaos occur alternately, if the density of pests exceeds the threshold ET, and fluctuates at a high level, it is likely to exceed the EIL, which increases the difficulty of pests control. Compared with the bifurcation diagram in Figure 5(a), the bifurcation period of V(t) in Figure 5(b) is more complex than that of B(t) in Figure 5(a) with the same frequency ω. In addition to bifurcation and chaos, there also exist several multiple attractors in interval (1.8,1.9) and (2.2,2.8). For example, when ω=2.422 four attractors can coexist and if ω increases to 2.738, where the four attractors turn to three attractors. Besides, ω=1.824 or ω=2.513, two attractors can coexist although their phase planes are completely distinct. In the next subsection, the four cases of attractors coexistence mentioned above and their real biological implications will be restated.
4.2. Attractors coexistence
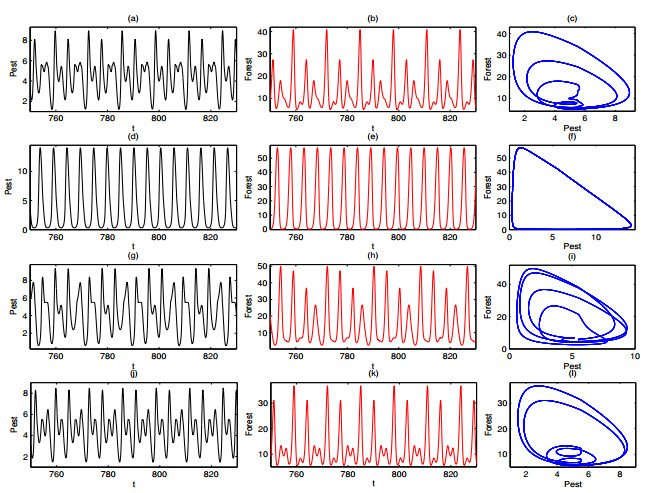
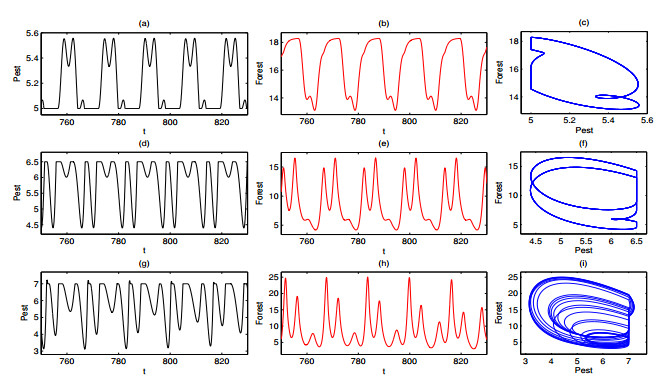
For a dynamical system described by a set of autonomous ODEs, an attractor can be viewed as a stable equilibrium point, a periodic limit cycle, or even a strange chaotic attractor. Among which a point and a limit cycle are the most common attractors with integer dimension while an attractor is referred to be strange if it has a noninteger dimension [40]. According to the bifurcation analysis of Filippov system (2.7), several cases of coexisting attractors are further shown in this subsection. When ω=2.422, Figure 6 presents four coexisting attractors. Subfigures (a)-(c) of Figure 6 show the first attractor, and the maximum amplitudes of the pest population and forest are 8.9317 and 40.8495, respectively. Another attractor is shown in Figure 6(d)-(f) and the maximum amplitudes are 14.0361 and 57.2602, respectively. We use black curves and red curves represent time series diagrams of the pest population and forest(left panel and middle panel), their corresponding phase portraits are plotted by the blue curves(right panel). Subplots (g)-(i) and (j)-(l) of Figure 6 are the time series and phase diagrams of other two attractors where the sliding segments showed in Figure 6(g) and (j), which means that the pest population density would be stable at the ET for some time. The maximum amplitudes of subfigures (g) and (h) of Figure 6 are 9.3571 and 49.8862, respectively. The maximum amplitudes as shown in Figure 6(j) and (k) are 8.4677 and 36.7320, respectively. The phase diagram of the second attractor is a standard limit cycle while the first, third and fourth attractors are periodic attractors with varying degrees of amplitude attenuation. The four coexisting attractors demonstrate that the Filippov system (2.7) with different initial values have different oscillation patterns, in other words, if the initial densities of two populations locate at the attraction basin of their attractors, then the two populations will be eventually stable at the corresponding attractor after a finite time.
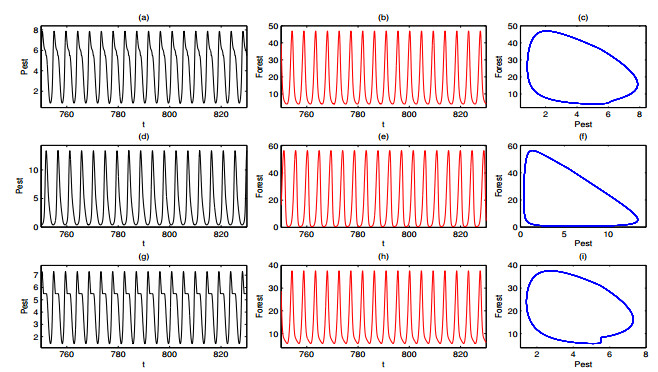
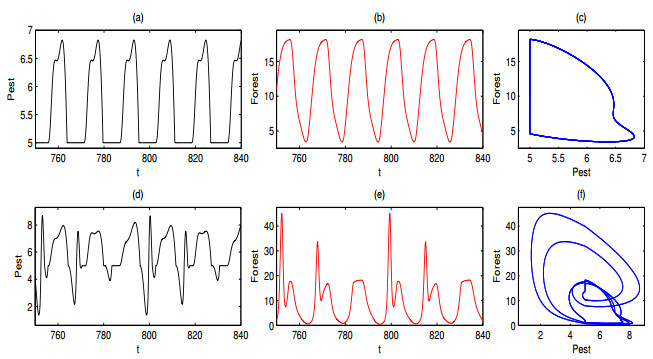
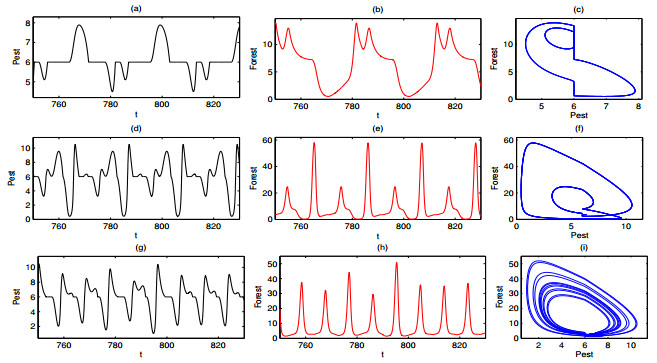
When ω=2.738, three coexisting attractors are elaborated in Figure 7. Subfigures (a)-(c) and (d)-(f) of Figure 7 are the first and second attractors, they are very similar except for a slight differ in amplitude. Figure 7(g)-(i) show the third attractor where it has sliding segments at ET=5.5. Obviously, the three attractors are all periodic attractors. The second attractor has the local maximum amplitude for pest population while the amplitude of the third sliding limit cycle is minimum. Therefore, if the initial densities of two populations start at the attraction basin of the third attractor, the density of pest population will keep at lower level compared with the other two attractors, which is desired results of pest control.
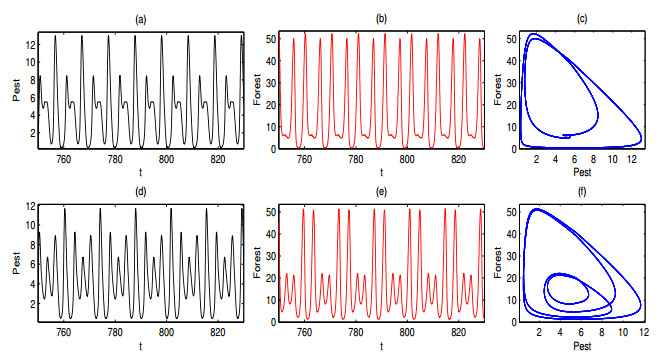
An illustrative example of two periodic attractors is shown in Figure 8 when ω=1.824. The oscillation periods of two coexisting attractors are 10.3 and 13.8, respectively. In particular, the sliding segments appear in Figure 8(a). If the other parameters are identical to those in Figure 5, the system trajectory will follow one of the two attractors and switch from one to another according to different initial values. The other case of two coexisting attractors is shown in Figure 9 supposing ω=2.513, they are also periodic attractors. The time series and phase diagrams of the two coexisting attractors are similar to the second and the third attractors of Figure 7. The oscillation periods of these two attractors are both 5.
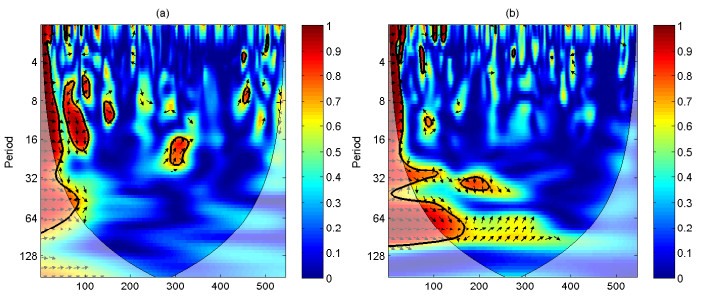
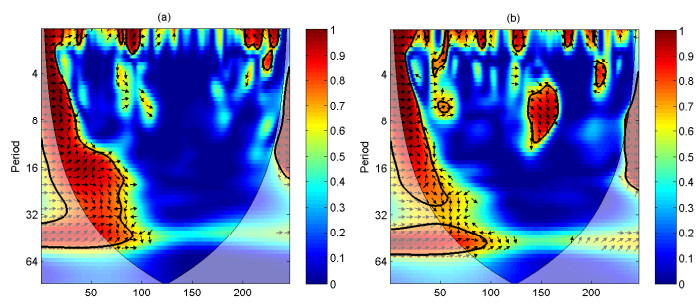
The relationship between the time series of two coexisting attractors can be compared by time frequency space through wavelet coherence. Figure 10 present the wavelet coherence for the pests and forests of two coexisting attractors of Figure 8. The wave coherence of the two coexisting attractors of Figure 9 is depicted in Figure 11. As shown in Figure 10, the significance level regions at a level of about 5% are denoted by the black contour lines. Lighter shadows indicate that edge effects can distort the picture. A color scale shows strong or weak power for specific time and period. The arrows indicate the phase difference between the two coexisting attractors where the left arrows indicate phase and the right arrows indicate anti-phase, the upward arrows indicate that the first attractor leads the second attractor, and the downward arrows indicate that the second attractor leads the first attractor [41,42,43].
4.3. Parameter sensitivity analysis
In this subsection, we also choose ET, γ and ω as varying parameter and fix other parameters to analyze the effects of key parameters on the dynamics of Filippov system (2.7). Note that the periodic attractor with smaller amplitude can switch to a larger amplitude of periodic attractor if the threshold ET change from 5 to 6.5 which showed in Figure 12(a) and Figure 12(b). From the perspective of pest control, a larger threshold ET allows a certain amount of pest grow over a larger range without adopting excessive pest control strategies. However, the pests may outbreak or be difficult to control since the threshold is at a critical value leading to quasi-periodic feature such as Figure 12(c) where ET=7.
The Filippov system (2.7) exhibits sliding periodic orbits indicated in Figure 13(a)-(c) when γ=0.5 and the pest population density always over the ET. The transition from the periodic motion to another periodic motion can be noticed in Figure 13 (d)-(f) when the amplitude γ increase to 0.59.
Similarly, it is found from Figure 14 that the population densities of system (2.7) seem to be sensitive to the parameter ω. Although there exists both sliding periodic solutions when ω=0.2 and ω=0.6, the amplitude, period and phase diagram vary greatly. The sliding time in per-period of Figure 14(a) when ω=0.2 keep longer than that of Figure 14(d) when ω=0.6. When there is a little change for ω, such as ω=0.68, the state of system (2.7) will be transferred from periodic transition to quasi-periodic solution which showed in Figure 14(g)-(i).
5.
Discussion
In this paper, non-smooth bifurcations, multiple attractors coexistence, quasi-periodic phenomenon and chaotic dynamics are investigated for the Filippov forest-pest model with periodic forcing. The classical beetle-tree model studied the effects of intrinsic growth rate, mortality and other parameters on the dynamic behaviors of the system. Our model mainly focused on the influence of external factors such as economic threshold and periodic forcing on the system. The phenomena such as period-adding bifurcations, quasi-periodic feature, multi attractor coexistence that our model exhibits were not discussed in the classical beetle-tree model. Considering economic threshold can avoid taking single pest control policy, when the density of pests does not reach the economic threshold, biological control and other methods with less environmental pollution can be adopted. When the density of pests reaches or exceeds the economic threshold, spraying insecticides can be used to control the outbreak of pests, so as to reduce the frequency of pest control and the dosage of insecticides.
From the results of theoretical analysis and numerical simulation, it is observed that sliding periodic solution can completely oscillate in the sliding domain. Once the system has sliding segments, which can reveal that the pest population density would be stable at the ET for some time. As long as the maximum amplitude of pest population does not exceed EIL, the sliding periodic solution is an ideal state for pest control, that is, to allow pests to grow in a certain range. Nevertheless, in most cases, the periodic solution does not necessarily locate in the sliding domain. Bifurcation diagrams with respect to the economic threshold ET, the amplitude γ, the frequency ω of periodic forcing term clarify that the Filippov system could have very complex dynamics including alternating period-adding bifurcations and chaos regions. In our paper, the feature of period-adding bifurcation is not strictly increased from period-k to period-(k+1), but may be from period-k to period-(k+n). Note that there exist several cases of coexisting attractors in term of the parameter ω and the number of attractors varies from two to four. For instance, when ω=2.422, four periodic attractors coexist. The coexistence of multiple attractors shows that the state of the system depends not only on the parameters but also on the initial value. For pest control, even with the same intrinsic growth rate, mortality rate and other system parameters, different initial densities of pests and trees will trigger diverse pests outbreak patterns such as multiple periodic attractors with different amplitude and frequency. The wavelet coherence for the pests and forests of two coexisting attractors when ω=1.824 and ω=2.513 are presented to further distinguish the phase difference between the time series of two populations of coexisting attractors. Furthermore, sensitivity analysis about the key parameters ET, the periodic forcing amplitude γ and the periodic forcing frequency ω reveal that the overall trend was that the higher the setting ET and γ, the higher the maximum pest density, that is, the number of pests is large. However, there is a complex relationship between ω and the density of pests, which may be caused by the periodicity of the forcing term. Therefore, in order to keep the pests at a low level, we need to take control measures when the pest density reaches at the critical ET. It's hoped that the analysis presented here will prove beneficial in studies of pests control problems.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 11961024, in part by Youth Project of Scientific and Technological Research Program of Chongqing Education Commission(KJQN201901203), and in part by the Special Funds for "Double First-Class" Construction in Hubei Province.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: