The Bilingual Cognitive Advantage: No Smoke without Fire?

1.   Introduction

Even though the roots of fractional calculus are in the late 17th century ^[1], the subject has received significant attention from researchers only in recent decades. The importance of fractional calculus and fractional differential equations (FDEs) is evidenced by the emergence of fractional-order models for real-world phenomena, which has lead to a plethora of applications of FDEs ^[2]. A short review of the areas in which FDEs are applied is given below.

The advantage of fractional-order models is that they can be used to model systems with the memory effect, under which the current state of the system at time $ t = t_0 $ is affected by an interval of states at time $ t < t_0 $. Thus, such models lend themselves naturally to the description of viscoelastic materials ^[3,4]. It can be noted that most biological tissues possess viscoelastic properties ^[5] which has lead to the use of FDEs to describe the evolution of various biomedical systems ^[6,7,8]. In physics, fractional-order models are widely used to study dielectric materials ^[9,10,11] and Bose-Einstein condensates ^[12]. FDEs have also been used to describe the memory effect in economic models ^[13,14].

Due to the applicability of fractional-order models, a wide variety of methods have been developed to construct solutions to FDEs. The Q-homotopy analysis transform is applied in order to obtain analytical solutions to the fractional coupled Ramani equation in ^[15]. The solutions of integer-order differential equations are used to construct the solutions to the models of cooling and spread of epidemic diseases ^[16]. An Adams-type predictor-corrector method for the construction of numerical solutions to FDEs is discussed in ^[17]. A new family of predictor-corrector methods for FDEs is discussed in ^[18]. A Legendre operational matrix approach is used to numerically solve FDEs in ^[19,20].

The homotopy analysis method is adapted to FDEs for the computation of approximate solutions to various equations, including fractional Korteweg-de-Vries, Burgers and Boussinesq models in ^[21]. A class of rational Krylov methods for the construction of numerical solutions to partial fractional differential equations is considered in ^[22]. The traditional reproducing kernel method is adapted to be applicable to FDEs in ^[23]. A restricted transform technique is used to solve irrational order FDEs in ^[24]. Artificial neural networks are used to construct approximate solutions to FDEs in ^[25].

The main objective of this paper is to present a novel framework for the extension of the solutions to fractional differential equation (FDEs) to negative argument values. The main idea of this procedure is to construct the ordinary differential equation (ODE) that has a solution which can be transformed to the solution of the considered FDE. Since the solution of the ODE also exists for negative argument values, it can be used to extend the solution of the FDE for such argument values as well. This results in complex-valued solutions to FDEs for negative argument values. Such extension is a novel viewpoint into the solutions to FDEs, as they can be analyzed not only in the set $ x \in \mathbb{R}_+ $, but in the entire real line $ x \in \mathbb{R} $. This goes beyond the current state-of-the-art, as with current algorithms the solutions to FDEs cannot be considered in the negative $ x $-axis.

2.   Preliminaries

2.1.   Fractional power series and functions

In this paper we consider functions defined via power series:

where $ v_j \in \mathbb{R} $ are coefficients of the series and the base functions $ w^{(n)}_j; n \in \mathbb{N}, j = 0, 1, \dots $ are defined as:

The usual notation $ \Gamma(x) $ is used to denote the gamma function ^[26].

The number $ n $ which denotes the order of the basis of fractional power series is selected with respect to the fractional derivative order which is analyzed. If the fractional derivative is of order $ \alpha = \frac{k}{m} $, and $ \gcd(k, m) = 1 $, it is taken that $ n = m $ ^[27].

Consider $ x > 0 $ and let $ \sqrt[n]{x} \in \mathbb{R} $. Using the substitution $ t : = \sqrt[n]{x} $, (2.1) can be rewritten as:

For subsequent computations it is required that $ \widehat{f}(t) $ be analytic (except for some finite number of singularity points) and non-singular at $ t = 0 $. Thus, there exists a convergence radius $ |t| < T_0; \, T_0 > 0 $. The function $ \widehat{f} $ will be referred to as the characteristic function of $ f $.

For any given $ n \in \mathbb{N} $, the set of all functions defined by (2.1) and meeting the requirements stated above is denoted as $ {}^C \mathbb{F}_n $. Conventional addition and multiplication operations on functions belonging to $ {}^C \mathbb{F}_n $ are defined. For example, given two series $ f = \sum_{j = 0}^{+\infty} v_j w^{(n)}_j $ and $ g = \sum_{j = 0}^{+\infty} b_j w^{(n)}_j $, the product is defined as:

Note that the sum above obeys the finite summation principle: all coefficients of the above series are given by finite sums, not series ^[28].

The set $ {}^C \mathbb{F}_n $ with addition and multiplication operations forms an algebra over $ \mathbb{C} $. The properties of algebra $ {}^C \mathbb{F}_n $ are discussed in detail in ^[27] and ^[29].

2.2.   Caputo fractional differentiation operator

Let $ f = \sum_{j = 0}^{+\infty} v_j w^{(n)}_j \in {}^C \mathbb{F}_n $. Caputo differentiation operator of order $ \frac{1}{n} $ is then defined as ^[30]:

Note the Caputo derivatives of basis functions ^[27]:

Derivatives of rational order $ \frac{k}{n}; k \in \mathbb{N} $ are defined by higher powers of operator $ \, {}^{C} \mathit{\boldsymbol{\mathrm{{D}}}}^{(1/n)} $ ^[29]:

In the special case of $ k = m\cdot n; m\in \mathbb{N} $, (2.7) reads:

2.3.   Riemann extension algorithm for Caputo functions

It is well-known that analytic functions can be extended beyond their convergence radius ^[31]. The same idea is adapted for series of the type (2.1). Let $ f = \sum_{j = 0}^{+\infty} \gamma_j \left(\sqrt[n]{x}\right)^j $ and choose $ \sqrt[n]{x_0} $ such that $ x_0 $ is nonzero and in the characteristic function's convergence radius, $ 0 < x_0 < T_0^n $. Then (2.1) can be rearranged:

Coefficients $ \widehat{\gamma}_j $ are defined as:

Note that coefficients (2.10) are finite, because the non-extended series $ f $ converges in its convergence radius $ 0 < x_0 < T_0^n $. The convergence radius for (2.9) is $ |\sqrt[n]{x}-\sqrt[n]{x_0}| < T_1, \, T_1 > 0 $. Furthermore, if the same procedure is repeated for $ x_1 \neq x_0 $ that also satisfies $ 0 < x_1 < T_0^n $, then:

as long as $ x $ is such that series on both sides of the equation converge.

This procedure can be applied to extend a function from the set $ {}^C \mathbb{F}_n $ between two singularity points (or singularity and infinity, if no other singularities are present) by rewriting the function in different basis $ \left(\sqrt[n]{x} - \sqrt[n]{x_k}\right)^j, k = 0, 1, \dots $. Note that these extended series coincide for $ x $ that lies in all of their convergence radii, thus the extensions are unique.

Note that computational operations, such as the Caputo differentiation operator are only defined for basis $ \left(\sqrt[n]{x}\right)^j $ (in the neighbourhood of $ x = 0 $). For this reason, all computations are first performed in this neighbourhood and then extended throughout the entire function domain. Thus, the zero neighbourhood of $ x $ is called the algebraic operation neighbourhood. The concept of this neighbourhood is introduced in ^[28].

2.4.   Generalized differential operator technique

In the subsequent sections of this paper, constructing series solutions to ordinary differential equations (ODEs) is necessary. The generalized differential operator technique is used for this task. A short description of this method is given in this section. A detailed overview can be found in ^[32,33].

Let us consider an ordinary differential equation in the explicit form:

where $ P $ is an arbitrary bivariate analytic function. The following generalized differential operator is associated with the ODE (2.12) ^[34]:

where $ \mathit{\boldsymbol{\mathrm{{D}}}}_{\lambda} $ denotes the partial differentiation operator with respect to variable $ \lambda $.

The series solution to (2.12) can then be written in the form ^[32]:

where $ p_j(c, s) = \mathit{\boldsymbol{\mathrm{{D}}}}_{cs}^j s $.

3.   Solutions to fractional differential equations with polynomial nonlinearity

The following fractional differential equation is considered in this section:

where $ y_n \in {}^C \mathbb{F}_n $ and $ Q_m $ is an arbitrary $ m $th order polynomial:

In the remainder of this section, solutions in the operation neighbourhood of $ x = 0 $ will be constructed directly and later extended into different neighbourhoods using the procedure described in previous sections.

3.1.   Construction of solutions to (3.1) in the neighbourhood of $ x=0 $

Consider a series $ y_n = \sum_{j = 0}^{+\infty} v_j w^{(n)}_j = \sum_{j = 0}^{+\infty} \gamma_j \left(\sqrt[n]{x}\right)^j \in {}^C \mathbb{F}_n $. Inserting the function into (3.1) yields:

Let $ \sqrt[n]{x} = t $ and $ \widehat{y}_n = \sum_{j = 1}^{+\infty} \gamma_j t^j $. Then, (3.3) yields:

Rearranging the sums in (3.4) yields:

It can be noted that adding $ \sum_{j = 1}^{n-1} j \gamma_j t^{j-1} $ to both sides of (3.5) transforms the right side to an ordinary derivative of $ \widehat{y}_n $:

Noting that $ \gamma_j = \frac{v_j}{\Gamma\left(\frac{j}{n}+1\right)} $ yields a different form of (3.6):

Adding the initial condition $ y_n(c) = s $, Equation (3.7) can be solved using the method described in 2.4. The generalized differential operator for (3.7) reads:

The solution to (3.7) (taking values of $ t $ for which the series converges) has the form:

where $ p_j(c, s) = \mathit{\boldsymbol{\mathrm{{D}}}}_{cs}^j s $. Noting that $ y_n(x) = \widehat{y}_n\left(\sqrt[n]{x}\right) $ yields Theorem 3.1.

Theorem 3.1. The fractional differential equation (3.1) admits the following general solution for any parameter values $ u_0; v_1, v_2, \dots, v_{n-1}; \; x_0 \ge 0 $:

where

and

if $ x $ satisfies $ \left|\sqrt[n]{x}-\sqrt[n]{x_0}\right| < T_{x_0} $. Here $ T_{x_0} > 0 $ denotes the convergence radius of (3.10).

Note that the results of this section can be extended to analytic functions. Taking $ Q(x) = \sum_{k = 0}^{+\infty} a_k x^k $ instead of $ Q_m(x) $ and following the steps outlined above would yield a theorem that is analogous to Theorem 3.1. However, the analysis of such equations is not the focus of this paper, thus we will consider only polynomial $ Q_m(x) $ in the remainder of the text.

3.2.   Cauchy initial value problems on (3.1) formulated at the origin point

Based on Theorem 3.1, the Cauchy initial value problem for (3.1) can be formulated at point $ x = 0 $:

Note that since $ \sqrt[n]{x} $ in general possesses $ n $ branches, in these computations we select the branch with a minimum value of $ \arg{x} $.

By the results obtained in the previous section, in the neighbourhood of $ x = 0 $, the problem (3.13)–(3.15) has the solution:

This solution can be extended by applying the algorithm discussed in section 2.3. First, choose a sequence $ x_0 = 0 < x_1 < x_2 < \dots $ and freely choose $ u_0^{(0)} \in \mathbb{R} $. Then, compute parameters $ u_0^{(1)}, u_0^{(2)}, \dots $ as:

The general solution to (3.13)–(3.15) can then be written for any $ k $:

for $ \left|\sqrt[n]{x}-\sqrt[n]{x_k}\right| < T_{x_k} $, $ T_{x_k} > 0, x_k \ge 0 $.

3.3.   Cauchy initial value problems on (3.1) not formulated at the origin point

The rearrangements described in the previous section can be applied to construct a more general Cauchy initial value problem, where the first initial condition can be formulated at nonzero $ x $:

Analogously to problem (3.13)–(3.15), the solution reads:

Note that initial conditions that correspond to fractional derivative values still must be formulated at $ x = 0 $ for solution (3.22) to hold true.

4.   Solutions to fractional differential equations with polynomial nonlinearity for negative values of $ x $

As stated earlier, the main objective of this paper is to extend the solutions to FDEs so that they would exist for negative values of argument $ x $. This extension results in complex-valued fractional power series, which are defined in the following subsection. Note that this extension is not possible when considering fractional derivatives in the traditional Caputo sense, as they are defined via integrals only for non-negative values of $ x $.

4.1.   Complex fractional power series

Let us consider an extension to the power series basis presented in section 2.1:

where $ x\in \mathbb{R} $, $ k = 0, \dots, n-1; j = 0, 1, \dots $ and $ \sqrt[n]{|x|} \in \mathbb{R} $ denotes the root with the lowest value of $ \arg{x} $. The basis with $ k = 0 $ corresponds to $ w^{(n)}_j $ presented in section 2.1, while $ k = 1, 2, \dots, n-1 $ result in complex-valued functions $ \left(w^{(n)}_j\right)_k $.

Using (4.1), the standard fractional power series (2.1) can be extended into $ n $ complex-valued series:

4.2.   Extension of solutions to FDEs with polynomial nonlinearity

By Theorem 3.1, the solution to

reads:

where coefficients $ p_j $ are generated via the generalized differential operator technique as described in previous sections. Using the basis defined in the previous section, the solution (4.4) can extended into the complex plane:

Denoting $ \alpha : = \arg{x_0} $ and $ \beta_n^{(k)}(\alpha) : = \exp\left(i \frac{\alpha+2\pi k}{n}\right) $, series (4.5) can be rewritten as:

where

Expression (4.6) allows the consideration of solutions for $ x < 0 $, however, these solutions are multi-valued (a total of $ n $ branches corresponding to the number of distinct roots $ \sqrt[n]{x} $) and take complex values.

4.3.   Riemann extension scheme for solutions of FDEs with negative argument values

A refinement of the procedure described in section 3.2 is needed to construct particular solutions to FDEs (4.3). Two sequences of numbers are chosen: $ \dots < x_{-r} < \dots < x_{-1} < 0 $; $ 0 < x_1 < x_2 < \dots $ and $ x_0 = 0 $. For any $ k = 0, \dots, n-1 $, the initial condition $ s_0^{(k)} \in \mathbb{R} $ can be taken freely.

Sequences $ s^{(k)}_{-r} $ and $ s^{(k)}_{r} $ are computed using relations:

Here $ \widehat{y} $ denotes the solution of the ODE that the FDE (4.3) is transformed to, as given by Theorem 3.1.

Then the particular solution to (4.3) corresponding to the $ k $th branch of the root $ \sqrt[n]{x} $ reads:

where $ r = 0, \pm 1, \pm 2, \dots $.

Note that the sequence $ \dots < x_{-1} < x_0 < x_1 < \dots $ must be chosen in such a way that the series generated by $ \widehat{y} $ are convergent in both $ \mathbb{R} $ and $ \mathbb{C} $. Also, the point $ x = 0 $ is a branching point for the solution to the FDE, thus the functions $ \left(y_n(x)\right)_k $ are non-differentiable at this point.

5.   Computational experiments

Let us consider the non-fractional Riccati equation:

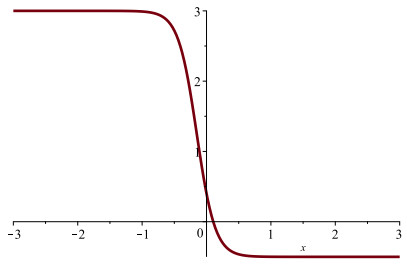
It is well-known that (5.1) admits the kink solitary solution:

where $ \alpha_{1} = 3, \alpha_{2} = -\frac{1}{2} $ are the roots of polynomial $ 2y^2 - 5y - 3 $. Solution (5.3) is depicted in Figure 1.

Suppose that $ n = 2 $, $ x_0 = 0 $ and let us consider the fractional Riccati equation:

As stated earlier, the initial conditions read:

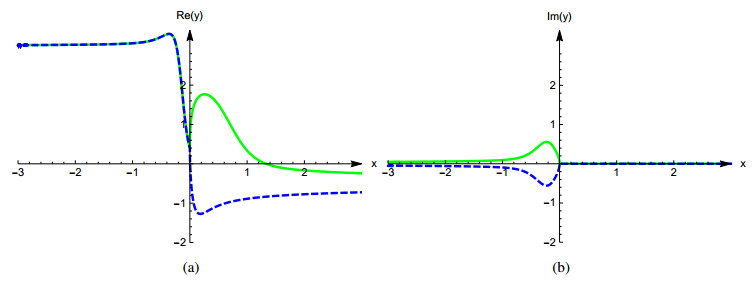
The solution to (5.4), (5.5) is constructed using the algorithm described in section 4.3. Note that since $ \sqrt{x} $ possesses two branches, two solutions exist. The real and imaginary parts of these solutions are shown in Figure 2. Note that solution is purely real for $ x \ge 0 $ – the imaginary parts appears only for negative values of $ x $.

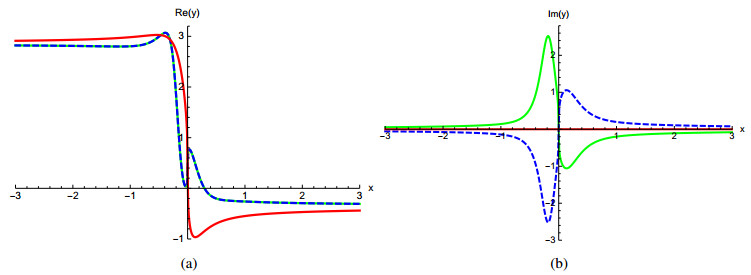
It can be seen in Figure 3 that as $ v_1 $ approaches zero, the solutions to (5.4) approach the kink solitary solution (5.3).

Taking $ n = 3 $ results in the fractional Riccati equation:

The number of initial conditions for (5.6) increases to three:

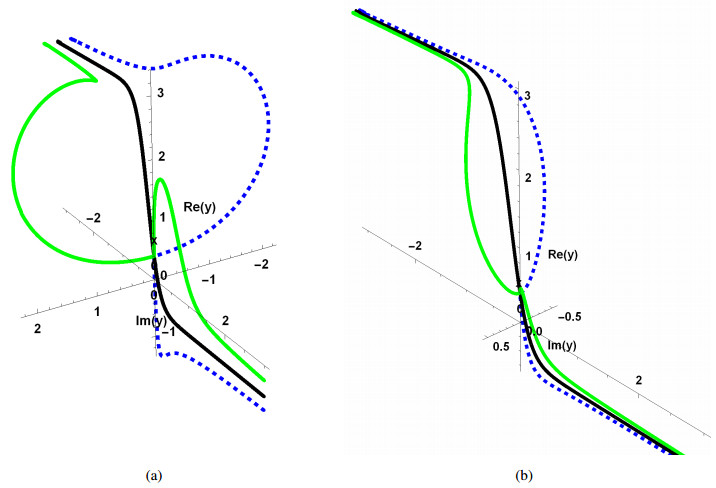
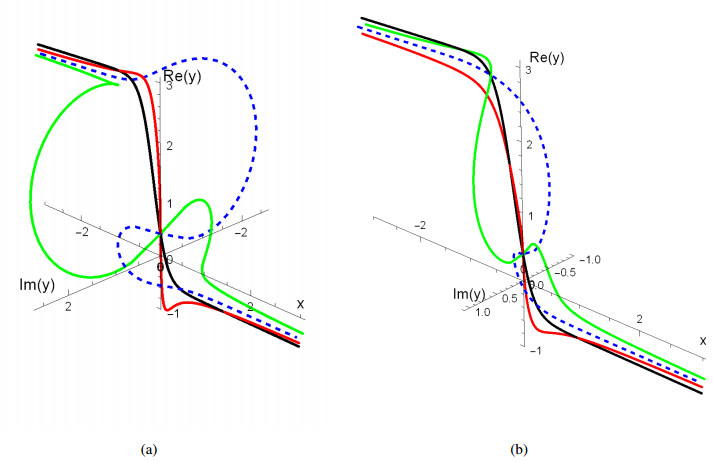
Riccati equation (5.6) has three solutions: two of them are complex-valued and one is a real-valued solution. The real and imaginary parts of these solutions are depicted in Figure 4. A spatial plot for two different sets of initial conditions is shown in Figure 5.

Note that the as $ x\to \pm \infty $, the fractional solitary solutions approach the non-fractional kink solitary solution. This is due to the properties of the characteristic equation (3.6). Thus, the limits of the fractional and non-fractional coincide as $ x \to \pm \infty $.

6.   Conclusions

An analytical framework for the extension of solutions to FDEs into the negative half-line is presented in this paper. The main idea of this extension is the construction of a characteristic differential equation for a given FDE. The solution to the characteristic equation is used to construct a fractional power series solution to the FDE. This solution is then extended using classical Riemann extension techniques to enable the consideration of the solution at a neighbourhood different than the origin $ x = 0 $. Furthermore, this extension is valid for both positive and negative values of $ x $, which extends the solution to the entire real line.

As demonstrated by computational experiments, the solution to the FDE is complex-valued for negative values of $ x $. Furthermore, there exist $ n $ branches of solutions, where $ n $ is the denominator of the fractional differentiation order. If the initial conditions (3.20) that correspond to fractional derivatives tend to zero, the solution to the FDE tends to the non-fractional solution of the same equation.

The presented technique provides a solid foundation for the construction of solutions to FDEs on the negative half-line. In particular, this allows to travel backwards in time from the initial conditions of a FDE – such a possibility has not been reported previously. It is well-known that fractional order derivatives help to model memory effects in dynamical systems. Therefore it would be tempting to extend the available coronavirus pandemic models ^[35,36] by introducing fractional derivatives. However, the results of this paper show that such an extension would eliminate the possibility of the unique backwards extrapolation. These questions as well as the physical interpretation of the extensions to the negative half-line remain a definite objective of future research.

Acknowledgments

This research was funded by a grant (No. S-COV-20-8) from the Research Council of Lithuania.

Conflict of interest

All authors declare no conflicts of interest in this paper.