Double total domination number in certain chemical graphs

1.   Introduction

Graph dominations are important since they occur in various applications such as dominating queens, computer network, school bus routing, social networks problems and in chemistry ^{[1,2,3,4,5,6,7,8,9]}. Chemical structures can be represented by graphs. Vertices represent atoms, while edges represent chemical bonds. Because of such similarity, many physical and chemical properties of molecules are connected with graph theoretical invariants. One such invariant is the total (double) domination number ^{[1,2,3,5,6,10,11,12,13,14,15,16]}.

We explore double total dominations on pyrene network and hexabenzocoronene, and we give upper bounds for double total dominating number on pyrene network and upper and lower bounds for double total dominating number on hexabenzocoronene. Also, we give some exact values for the double total domination number on these graphs. This work is connected with our previous work ^[16] where we have also studied total and double total dominations, but on the hexagonal grid. At the moment there are only a few publications on total and double total domination on chemical graphs ^[1,2,5,6,16].

Pyrene networks and hexabenzocoronene are benzenoid hydrocarbons ^[2,8,17]. Benzenoid hydrocarbons and their derivates are an important class of organic compounds that have, apart from their chemical importance, big technical and farmaceutical importance as well and belong to the group of the most serious polluters of the environment. Pyrene has interesting photophysical properties and it is used to make dyes, plastics and pesticides.

Apart from this introduction, the rest of the paper is organized as follows. Section 2 lists preliminaries about the total and double domination, dominating sets and hexagonal systems. Section 3 gives an upper bound for the double total domination number $\gamma_{2t}$ on pyrene network $PY(n)$ dimension $n\geq 3$ and the exact value for the double total domination number on $PY(1)$ and $PY(2)$.

Section 4 gives the upper and lower bound for the double total domination number on hexabenzocoronene $XC(n)$ dimension $n\geq 3$ and the exact value for the double total domination number on $XC(2)$.

2.   Preliminaries

Let $G$ be a graph with the vertex set $V(G)$. A set $D \subset V(G)$ is a dominating set of a graph $G$ if every vertex $y$ in $V(G) \setminus D$ has neighbour in $D$. The domination number $\gamma (G)$ is the cardinality of the smallest dominating set. Total domination is the stronger version of domination. A set $D \subset V(G)$ is a total dominating set of a graph $G$ if every vertex $y$ in $V(G)$ has a neighbour in $D$. The total domination number $\gamma_t (G)$ is the cardinality of the smallest total dominating set.

A set $D\subseteq V(G)$ is a $k$-dominating set, if every vertex $v\in V(G)\setminus D$ has at least $k$ neighbours in $D$. The $k$-domination number $\gamma_{k}(G)$ is the cardinality of the smallest $k$-dominating set. A set $D\subseteq V(G)$ is a total $k$-dominating set if every vertex $v\in V(G)$ has at least $k$ neighbours in $D$. In such case, it must be $k\le \delta(G)$ where $\delta(G)$ is the minimum degree of vertices on $G$ and $|D|\ge k+1$. The total $k$-domination number $\gamma_{kt}(G)$ is the cardinality of the smallest total $k$-dominating set. For $k = 2$ the total 2-dominating set is called double total dominating set.

Each vertex in hexagonal system is either of degree 2 or of degree 3. It follows that on a hexagonal grid there is no total $k$-dominating set for $k \geq 3$.

3.   Double total domination number of pyrene network

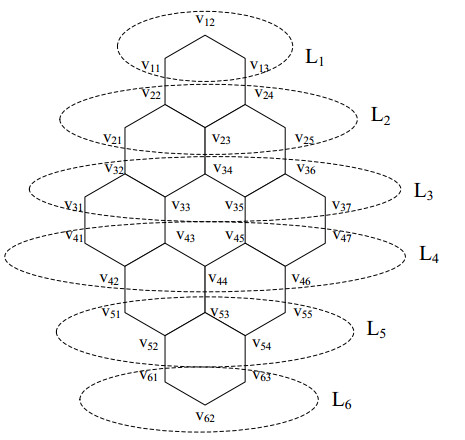
Benzenoid graphs are geometric figures that are composed of congruent hexagons. The hexagons are arranged according to certain rules. We denote by $PY(n)$ pyrene network of dimension $n$. Pyrene network $PY(n)$ is a simple connected 2-D planar benzenoid graph. $PY(n)$ has $3n^2 +4n -1$ edges, where $n$ is the number of rings in the center of the graph. See Figure 1 for $n = 3$.

Pyrene network of dimension $1$ has just a single hexagon. In $PY(n)$ any zigzag line not containing vertical edges is called horizontal zigzag line. The set of horizontal zigzag lines of $PY(n)$ are denoted by $L_i$, $1 \leq i \leq 2n$. More precisely, $L_i$ is the subgraph of $PY(n)$ formed by the $i$-th horizontal zigzag line of $PY(n)$ and $V(L_i)$ is its set of vertices, with $1 \leq i \leq 2n$.

Vertices on $L_i$ are

Lemma 3.1. For pyrene network of dimension $1$ and $2$ it holds

Proof. Because we consider double total domination, each vertex adjacent to a vertex with degree 2 must be in any double total dominating set $T$.

Let $T$ be double total dominating set on $PY(n)$. For $n \in \{1, 2\}$ all boundary vertices from $PY(n)$ must be in $T$ because each boundary vertex is adjacent to at least one vertex with degree 2. See Figure 2. There is $8n-2$ boundary vertices on $PY(n)$ (3 on $L_1$, 3 on $L_n$ and 4 on each remaining $2n-2$ zig zag lines).

It follows that $\gamma_{2t}(PY(1)) \geq 6, \phantom{a} \gamma_{2t}(PY(2)) \geq 14.$ On the other hand, boundary vertices double total dominate all vertices on $PY(1)$ and $PY(2)$. Then $\gamma_{2t}(PY(1)) \leq 6$, $\gamma_{2t}(PY(2)) \leq 14.$

Theorem 3.1. For pyrene network $PY(n)$, $n\geq 3$ it holds

Proof. First, we will consider case $n\equiv 1 \bmod 2.$ Graph $PY(n)$ is axially symetric. See Figure 3 for double total dominating set on $PY(5)$.

(ⅰ) $i \leq n$

For $i$ is odd we define

For $i$ is even

(ⅱ) $n+1 \leq i\leq 2n$

For $i$ is odd we define

For $i$ is even

$T_i \subset V(L_i)$ and it holds $\vert T_i\vert = \vert T_{2n+1-i} \vert$, $i \leq n$. Because of symmetry, we will consider lines $i \leq n$ and multiply the result by 2.

Hence, for $i \leq n$, $\vert T_i\vert = 3\lceil\frac{2i+1}{4}\rceil = 3(\frac{i+1}{2})$ if $i$ is odd and $\vert T_i\vert = 3\lceil\frac{2i-1}{4}\rceil = 3(\frac{i}{2})$ if $i$ is even. $T = T_1 \cup T_2...\cup T_n...\cup T_{2n}$ is double total dominating set on $PY(n)$ and

Now, we consider the case $n\equiv 0 \bmod 2.$ The same as for the previous case, the graph is axially symetric. So, we will consider lines $i \leq n$ and multiply the result by 2. See Figure 4 for the double total dominating set on $PY(6)$.

(ⅰ) For $i$ is odd we define

It follows that $\vert T_i\vert = 3(\frac{i+1}{2}).$

(ⅱ) For $i$ is even and $2 \leq i < n$

Thereby $\vert T_i\vert = 3(\frac{i}{2})$. But

Therefore $\vert T_n\vert = 3(\frac{n}{2}) + 2$.

$T = T_1 \cup T_2...\cup T_n...\cup T_{2n}$ is the double total dominating set on $PY(n)$ and

4.   Double total domination number of hexabenzocoronene

We denote by $XC(n)$ hexabenzocoronene of dimension $n \geq 2$. This graph is also called a ring type benzenoid graph $R(n)$. $XC(n)$ has $27n^2 - 33n + 12$ edges, where $n$ is the number of rings from the center of the graph to the bottom or top. See Figure 5 for $n = 2$ and Figure 6 for $n = 5$.

Again, any zigzag line in $XC(n)$ not containing vertical edges is called a horizontal zigzag line. The horizontal zigzag line of $XC(n)$ are denoted by $L_i$, $1 \leq i \leq 4n-2$. More precisely, $L_i$ is the subgraph of $XC(n)$ formed by the $i$-th horizontal zigzag line of $XC(n)$ and $V(L_i)$ is its set of vertices, with $1 \leq i \leq 4n-2$.

From definition of hexabenzocoronenes it follows that

Theorem 4.1. For hexabenzocoronene of dimension $n \geq 2$ it holds

Proof. Because we consider the double total domination, each vertex adjacent to a vertex with degree $2$ must be in any double total dominating set $D$. From this follows that all boundary vertices on $XC(n)$ must be in $D$.

On $XC(n)$ there are two lines with 3 boundary vertices ($L_1$ and $L_{4n-2}$), $2n-2$ lines with 8 boundary vertices ($L_2$, ..., $L_n$ and $L_{4n-3}$, ..., $L_{4n-n-1}$) and on all remaining $2n-2$ lines there are 4 boundary vertices on each. Therefore at least

vertices must be in $D$. If there were only $24n -18$ boundary vertices in the double total dominating set $D$ on $XC(n)$, inner vertices on this graph distance $\geq 2$ from boundary would not be double total dominated. Thus

Lemma 4.1.

Proof. Let set $T$ contain all marked vertices from Figure 5. $T$ is double total dominating set and $\vert T \vert = 36.$ It follows

From the previous theorem it follows that all boundary vertices must be in $T$ and $\vert T \vert > 30$. If we take only boundary vertices in $T$, all vertices on $XC(2)$ are double total dominated except vertices $\{ v_{3, 4}, v_{3, 5}, v_{3, 6}, v_{4, 6}, v_{4, 5}, v_{4, 4} \}$. These vertices make one hexagon $PY(1)$ and none of them is adjacent to vertices from $T$. To double total dominate them from Lemma 3.1 we need at least 6 more vertices. Hence

Theorem 4.2. For hexabenzocoronene of dimension $n \geq 3$ it holds

Proof. First, we will consider the case $n\equiv 1 \bmod 2, n \geq 3.$ The graph $XC(n)$ is axially symmetric. So we will consider the lines $i \leq 2n -1$ and multiply the result by 2 as there are $4n-2$ zigzag lines.

By $T_i$ we denote the subset of the double total dominating set $T$ on the $L_i$. See Figure 6 for the double total dominating set on $XC(5)$.

For $4 \leq i \leq n$ we consider 2 subcases, $i$ is even and $i$ is odd.

(ⅰ) $i$ is even

Because $n$ is odd it follows that $4 \leq i \leq (n-1)$. We define

Then

(ⅱ) $i$ is odd

Because $n$ is odd we have $5 \leq i \leq n$. We define

Then

For $n+1\leq i \leq 2n-1$ we define

Then

$T_1 \cup T_2 \cup T_3 \cup... \cup T_{2n-1}$ double total dominates all vertices on $L_1 \cup L_2 \cup L_3 \cup... \cup L_{2n-1}$. Therefore for $n\equiv 1 \bmod 2, n \geq 3$ follows

For $n\equiv 1 \bmod 2, n \geq 5$

And for $n = 3$

Now we consider the case $n\equiv 0 \bmod 2, n \geq 4.$ Again, the graph $XC(n)$ is axially symmetric. So we will consider the case $i \leq 2n -1$ and multiply the result by 2.

By $T_i$ we denote the subset of the double total dominating set $T$ on the $L_i$. We define $T_1, ...T_n$ the same as for $n$ is odd. Then $\vert T_1 \vert = 3$, $\vert T_2 \vert = 8$, $\vert T_3 \vert = 14$ and for $4 \leq i \leq n$, if $i$ is even $\vert T_i \vert = \frac{9i}{2}$, and if $i$ is odd $\vert T_i \vert = \frac{9i}{2} + \frac{1}{2}.$ For $n+1\leq i \leq 2n-1$ we define

Then

$T_1 \cup T_2 \cup T_3 \cup... \cup T_{2n-1}$ double total dominate all vertices on $L_1 \cup L_2 \cup L_3 \cup... \cup L_{2n-1}$. Therefore for $n\equiv 0 \bmod 2, n \geq 4$ it follows

Conflict of interest

The authors declare there is no conflict of interest.