Double total domination number of Cartesian product of paths

1.   Introduction

Throughout this article, we only deal with finite and simple graphs. For the undefined notation and terminology, one may refer to ^[4]. Let $G = (V(G), E(G))$ be a graph. The open neighborhood of a vertex $v\in V$ is denoted by $N_{G}(v) = \{u\in V: uv\in E(G)\}$, and the $degree$ of $v$ in $G$ is denoted by $d(v) = |N_{G}(v)|$. A graph $G$ is $k$-regular if every vertex has degree $k$ in $G$. We use $\delta(G)$ and $\Delta(G)$ denote the minimum degree and the maximum degree among the vertices of $G$, respectively. For a subset $S\subseteq V(G)$, let $G[S]$ denote the subgraph induced by $S$. For simplicity, the induced subgraph $G[V(G)\setminus S]$ is denoted by $G-S$. For two disjoint subsets $X, Y\subset V(G)$, we use $e(X, Y)$ to denote the number of edges with one end in $X$ and the other end in $Y$. The Cartesian product $G\Box H$ of two graphs $G$ and $H$ is the graph with vertex set $V(G\Box H) = V(G)\times V(H)$, and edge $(u_{1}, v_{1})(u_{2}, v_{2})\in E(G\Box H)$ if and only if either $u_{1} = u_{2}$ and $v_{1}v_{2}\in E(H)$ or $v_{1} = v_{2}$ and $u_{1}u_{2}\in E(G)$. In general, let $P_n$, $C_n$ denote a path, a cycle of order $n$, respectively.

A total dominating set of $G$ is a subset $S\subseteq V(G)$ such that each vertex in $V(G)$ has a neighbor in $S$. The total domination number $\gamma_{t}(G)$ is the cardinality of a minimum total dominating set of $G$. The notion of total domination in graphs was first introduced by Cockayne et al. ^[8]. Numerous results on this object have been obtained over the years. Reader may refer to an excellent total domination book ^[12] and a survey ^[9]. A problem on total domination appeared as Question 3 of the 40th International Mathematical Olympiad, which is equivalent to determining the total domination number of the Cartesian product of two path graphs with same even order, i.e. $\gamma_t(P_{2n}\Box P_{2n})$. And further, several authors have studied the total domination number on product of graphs such as Cartesian, strong and lexicographic products (see ^{[2,6,13,14,16,19]}).

Except the classical total domination problem, there are many different ways to generalize the total dominating set. One of them is introduced by Henning and Kazemi in ^[10,11]: Given an integer $k$, a subset $S\subseteq V(G)$ is a $k$-tuple total dominating set (kTDS in short) of $G$ if every vertex $v\in V(G)$ has $|N(v)\cap S|\geq k$, this is, every vertex of $G$ has at least $k$ neighbors in $S$. The $k$-tuple total domination number $\gamma_{\times k, t}(G)$ is the cardinality of a minimum kTDS of $G$. Henning and Kazemi ^[10] first studied the $k$-tuple total domination number, and obtained some results of the $k$-tuple total domination number of complete multipartite graphs. They also gave a useful observation.

Observation 1.1. ^[10] Let $G$ be graph of order $n$ with $\delta(G)\geq k$. Then,

$(a)$ $\gamma_{\times k, t}(G)\leq n$;

$(b)$ if $G$ is a spanning subgraph of graph $H$, then $\gamma_{\times k, t}(H) \leq \gamma_{\times k, t}(G)$;

$(c)$ if $v$ is a vertex with degree $k$ in $G$ and $S$ is a kTDS in $G$, then $N_{G}(x)\subseteq S$.

We remark that $1$-tuple total domination is the well-known total domination. When $k = 2$, a $k$-tuple total dominating set is called a double total dominating set, abbreviated to DTDS, and the 2-tuple total domination number is also called the double total domination number, denoted by $\gamma_{\times 2, t}(G)$. This parameter was studied in ^{[1,3,5,7,15,17,18]}. Especially, Kazemi et al. ^[15] determined the value of the double total domination number of Cartesian product of some complete graphs. Bermudo et al. ^[3] gave the following result on the double total domination number.

Theorem 1.2. ^[3] Let $j\geq 2, n\geq 3$ be two integers. Then,

$(a)$ when $j$ is odd, $\gamma_{\times 2, t}(P_j\Box C_n) = \frac{(j+1)n}{2}$;

$(b)$ when $j$ is even, $\gamma_{\times 2, t}(C_j\Box C_n) = \frac{jn}{2}$.

Naturally, we may ask the following problem: What are the values of the double total domination numbers of Cartesian products of paths? In order to answer the problem, we make a step in this paper. In the next section, we give the values of $\gamma_{\times 2, t}(P_i\square P_n)$ for $i = 2, 3$, and the lower and upper bounds for $\gamma_{\times 2, t}(P_i\square P_n)$ when $i \geq 4$.

2.   Double total domination number of Cartesian product of paths

In this section, we simplify the notation for $V(P_{m}\Box P_{n})$. For example, when $m = 4$, if $P_{4} = abcd$, $P_{n} = v_{1}v_{2}\ldots v_{n}$, we denote simply the vertices $(a, v_{i})$ as $a_{i}$, $(b, v_i)$ as $b_i$, $(c, v_i)$ as $c_i$, $(d, v_i)$ as $d_i$, respectively. Moreover, set $X_{i} = \{a_{i}, b_{i}, c_{i}, d_{i}\}$ for $1\leq i \leq n$.

First, we give a lower bound for the double total domination number of $P_{2}\Box P_{n}$.

Lemma 2.1. Let $n\geq 2$ be an integer. Then

Proof. Let $P_{2} = ab$, $P_{n} = v_{1}v_{2}\ldots v_{n}$, and $X_{i} = \{a_{i}, b_{i}\}$ for $1\leq i \leq n$. Denote $G = P_{2}\Box P_{n}$. Pick a minimum DTDS $D$ of $G$. Since $\delta(G) = 2$ and $\Delta(G) = 3$, then $D = D_2 \cup D_3$, where $D_{i} = \{v\in D: |N(v)\cap D| = i\}$ for $i\in \{2, 3\}$. Note that $X_i\subseteq D\ (i = 1, 2, n-1, n)$ by Observation 1.1 (c). Then, when $n\leq 4$, we have $|D| = |V(G)| = 2n$, as desired. Next, we consider the case that $n\geq 5$.

Let $\overline{D} = V(G)\setminus D$. First, we claim that

The first inequality holds because every vertex in $\overline{D}$ is adjacent to at least two vertices in $D$, and the second one holds because $e(X_1\cup X_{n}, \overline{D}) = 0$ and each of the remaining $|D|-4$ vertices has at most $\Delta-2$ neighbors in $\overline{D}$. Therefore

Since $\gamma_{\times 2, t}(G)$ is an integer, the result holds when $n\equiv 0\; (mod\; 3)$ or $n\equiv 2\; (mod\; 3)$.

The remaining case is $n = 3k+1$, where $k\geq 1$ is an integer. We apply induction on $k$. For $k = 1$, $G = P_2 \Box P_4$. As discussed above, $\gamma_{\times 2, t}(G) = 2n = \frac{4\times 4+8}{3}$. Suppose that the result holds for $k-1$, where $k\geq 2$. Our goal is to prove that it is also valid for $k$. Recall that $X_i\subseteq D\ (i = 1, 2, n-1, n)$. If $D$ contains at least two vertices in $X_{3}\cup X_{n-2}$, then there are at least two vertices in $X_{2}\cup X_{n-1}$ that are not adjacent to any vertex in $\overline{D}$. Furthermore, there are at least six vertices in $X_1\cup X_{2}\cup X_{n-1}\cup X_n$ which are in $D$ and not adjacent to any vertex in $\overline{D}$. Therefore, we have $e(D, \overline{D}) \leq (|D|-6)(\Delta-2) = |D|-6$. On the other hand, $e(D, \overline{D}) \geq 2|\overline{D}| = 2(|V(G)|-|D|)$. Then $|D|\geq \frac{4n+6}{3} = \frac{12k+10}{3}$. So $|D|\geq \frac{12k+12}{3} = \frac{4n+8}{3}$ because $|D|$ is an integer. If $D$ contains at most one vertex in $X_{3}\cup X_{n-2}$, without loss of generality, we may assume $X_{3}\cap D = \emptyset$. By definition of the double total dominating set, we know $X_{4}\subseteq D$ and then $X_{5}\subseteq D$. Note that, when $n = 7$, $X_5 = X_{n-2}$. This belongs to the preceding case. When $n\geq 10$, set $X = X_{1}\cup X_{2} \cup X_{3}$ and $G' = G-X$. Let $D' = D\setminus X = D\setminus (X_{1}\cup X_{2})$. It is easy to see that $D'$ is a DTDS of $G'$. By induction,

Thus we have $|D| = |D'|+4 \geq \frac{4n+8}{3}$.

Next we determine the value of $\gamma_{\times 2, t}(P_{2}\Box P_{n})$.

Theorem 2.2. Let $n\geq 2$ be an integer. Then

Proof. Let $X_{i}$ be defined as earlier in the proof of Lemma $\ref{lem2.1}$, where $1\leq i \leq n$. Let $G = P_{2}\Box P_{n}$. When $n\leq 4$, it is as desired. Next we assume that $n \geq 5$.

We will show the upper bound through constructing a DTDS $S$ of $G$. Let

By Observation 1.1 (c), $X'$ is contained in every DTDS of $G$. When $n = 3k$, set $S = X'\cup (\cup_{i = 1}^{k-1}X_{3i+1}) \cup (\cup_{i = 1}^{k-2}X_{3i+2}).$ Then $|S| = 8+2(k-1)+2(k-2) = \frac{4n+6}{3}$. Therefore $\gamma_{\times 2, t}(G) \leq |S| = \frac{4n+6}{3}$. When $n = 3k+1$, set $S = X'\cup (\cup_{i = 1}^{k-1}X_{3i+1}) \cup (\cup_{i = 1}^{k-1}X_{3i+2}).$ Then,

Finally, when $n = 3k+2$, set $S = X'\cup (\cup_{i = 1}^{k-1}X_{3i+1}) \cup (\cup_{i = 1}^{k-1}X_{3i+2}).$ Clearly,

Also, by Lemma 2.1, the proof is completed.

For $\gamma_{\times 2, t}(P_{3}\Box P_{n})$, we give a lower bound firstly. Before that, we need an observation.

Observation 2.3. Let $G = P_{m}\Box P_{n}$, $X = \cup_{i = 1}^{h}X_{i}$ and $G' = G-X$, where $h$ is a positive integer and $h < n$. If $D$ is a DTDS of $G$, then we can obtain a "nearly" DTDS, $D\setminus X$, of $G'$ by confining $D$ on $G'$. $($Each of $V(G')\setminus X_{h+1}$ has at least two neighbors in $D\setminus X$.$)$ Extend some vertices to $D\setminus X$, and denote the resulting set by $D'$. If each vertex in $X_{h+1}$ has at least two neighbors in $D'$, then $D'$ is a DTDS of $G'$.

Lemma 2.4. Let $n\geq 2$ be an integer. Then

Proof. Let $G = P_3 \Box P_n$ with $P_{3} = abc$ and $P_{n} = v_{1}v_{2}\dots v_{n}$, and $D$ be a minimum DTDS of $G$. Set $X_{i} = \{a_{i}, b_{i}, c_{i}\}$ for $1\leq i \leq n$.

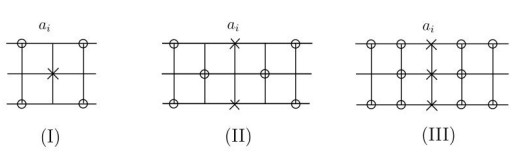
First, we introduce three constructions in Figure 1. (In the remaining, for the figures of the paper, a hollow dot denotes a vertex in $D$, a cross dot denotes a vertex not in $D$.) If $b_i\notin D$ ($2\leq i\leq n-1$), then $\{a_{i-1}, a_{i+1}, c_{i-1}, c_{i+1}\}\subseteq D$ because either of $a_i$ and $c_i$ must have at least two neighbors in $D$ (see construction (Ⅰ)). If $\{a_{i}, c_{i}\}\cap D = \emptyset$ ($3\leq i\leq n-2$), then $\{a_{i-2}, a_{i+2}, b_{i-1}, b_{i+1}, c_{i-2}, c_{i+2}\}\subseteq D$ because each of $\{a_{i-1}$, $a_{i+1}$, $c_{i-1}$, $c_{i+1}\}$ has at least two neighbors in $D$ (see construction (Ⅱ)). If $X_{i}\cap D = \emptyset$ ($3\leq i\leq n-2$), then $X_{i-1}\cup X_{i+1}\cup \{a_{i-2}, a_{i+2}, c_{i-2}, c_{i+2}\}\subseteq D$ by the definition of DTDS (see construction (Ⅲ)).

We prove the lemma by induction on $n$. When $n = 2$, the result holds by Theorem 2.2. According to Observation 1.1(c), we have the following conclusions for $3\leq n\leq 5$. When $n = 3$, we have $\{b_1, a_{2}, c_{2}, b_3\}\subseteq D$. Focusing on vertices $b_1, b_3$, at least two of $a_1, b_2, c_1$ and at least two of $a_3, b_2, c_3$ are in $D$. It implies that $\gamma_{\times 2, t}(P_3\Box P_3)\geq 7$. We give a DTDS with 7 vertices in Figure 2(a). When $n = 4$, we have $\{a_{2}, a_3, b_{1}, b_4, c_{2}, c_3\}\subseteq D$ (see Figure 2(b)). On each dash curve, there are at least two vertices contained in $D$ by the definition of DTDS. Thus, $\gamma_{\times 2, t}(P_3\Box P_4)\geq 10$. When $n = 5$, we know that $\{b_1, a_{2}, c_{2}, a_4, c_4, b_5\}\subseteq D$. Furthermore, on each dash curve, there are at least two vertices contained in $D$ (see Figure 2(c)). Thus $|D|\geq 10$. If $\{a_3, c_3\}\cap D = \emptyset$, then $D$ would contain all vertices of $\cup_{i = 1, 2, 4, 5}X_i$ by construction (Ⅱ), which means that $|D|\geq 12$. If $\{a_3, c_3\}\cap D\neq\emptyset$, then $|D|\geq 11$. Thus $\gamma_{\times 2, t}(P_3\Box P_5)\geq 11$ in either of these cases. (We give a minimum DTDS of $G$ with 11 vertices in Figure 2(d) when $n = 5$.)

When $n = 6$, $\{a_{2}, a_5, b_{1}, b_6, c_{2}, c_5\}\subseteq D$, at least 2 vertices of $N_G(b_1)$, $N_G(b_6)$ are contained in $D$, respectively. If $|(X_3\cup X_4)\cap D|\geq 4$, we are done. Consider the cases that $|(X_3\cup X_4)\cap D|\leq 3$. Without loss of generality, we may assume $|X_3\cap D|\leq 1$. If $X_3\cap D = \emptyset$, then $X_1\cup X_2\cup X_4\subseteq D$ by construction (Ⅲ), so $\gamma_{\times 2, t}(P_3\Box P_6)\geq 14$ (see Figure 2(e)). If $X_3\cap D = \{c_3\}$ (similarly, for $X_3\cap D = \{a_3\}$), then $\{a_2, a_4, c_2, c_4\}\subseteq D$ by construction (Ⅰ). Furthermore, $\{a_1, b_2, b_4\}\subseteq D$ because $a_3\notin D$. Thus $\gamma_{\times 2, t}(P_3\Box P_6)\geq 14$ (see Figure 2(f)). If $X_3\cap D = \{b_3\}$, then $\{a_1, a_5, b_2, b_4, c_1, c_5\}\subseteq D$ by construction (Ⅱ) (see Figure 2(g)). If $b_5\notin D$, then $\{a_4, a_6, c_4, c_6\}\subseteq D$ by construction (Ⅰ). If $b_5\in D$, noting that $a_5$ ($c_5$) has at least two neighbors in $D$, at least one of $a_4$ and $a_6$ ($c_4$ and $c_6$) is in $D$. In either of these cases, $\gamma_{\times 2, t}(P_3\Box P_6)\geq 14$.

Next, we only discuss the case $n\equiv 0\; (mod\; 2)$, and the argument of case $n\equiv 1\; (mod\; 2)$ is similar by replacing $2n+2$ with $2n+1$. Assume that the result holds for $n-2$ where $n\geq 8$. Suppose, to the contrary, $\gamma_{\times 2, t}(G) < 2n+2$. Next, we will choose a vertex subset $X$. Let $G' = G-X$. Then, basing on a DTDS $D$ of $G$, we obtain a DTDS $D'$ of $G'$. Finally, we deduce contradictions according to the relation between $|D|$ and $|D'|$ and induction on index $n$.

By Observation 1.1 (c), we have $\{a_{2}, b_{1}, c_{2}\}\subseteq D$. Focusing on $b_1$, it is clear that at least two of $a_1, c_1, b_2$ are contained in $D$. This means that $|D\cap (X_1\cup X_2)|\geq 5$. If $|D\cap (X_1\cup X_2)| = 6$ and $|D\cap (X_3\cup X_4)|\geq 4$, then we can extend the missing vertices of $X_3\cup X_4$ (with at most two) to $D\setminus (X_1\cup X_2)$ and obtain a vertex set $D' = (D\setminus (X_1\cup X_2))\cup (X_3\cup X_4)$. Then $|D'|\leq |D|-6+2 < 2n-2$. By Observation 2.3, $D'$ is a DTDS of $G' = G-(X_1\cup X_2)$. By induction, $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-2)+2 = 2n-2$, a contradiction. Similarly, if $|D\cap (X_1\cup X_2)| = 5$ and $|D\cap (X_3\cup X_4)|\geq 5$, then we also can obtain a contradiction. Since either of $a_3$, $c_4$ has at least two neighbors in $D$, we know that at least one of $a_4$ and $b_3$ ($c_3$ and $b_4$, respectively) in $D$. That is to say, $|D\cap (X_3\cup X_4)|\geq 2$. Therefore, we only need discuss the following two cases to complete the proof.

Case 1. $|D\cap (X_1\cup X_2)| = 6$ and $2\leq |D\cap (X_3\cup X_4)|\leq 3.$

Case 1.1. If $|D\cap (X_3\cup X_4)| = 3$, we claim that either $D' = (D\setminus \cup_{i = 1} ^4 X_i)\cup \{a_3, b_3, a_4, b_4, c_4\}$ or $D' = (D\setminus \cup_{i = 1} ^4 X_i)\cup \{b_3, c_3, a_4, b_4, c_4\}$ is a DTDS of $G' = G-(X_1\cup X_2)$. (For otherwise, focusing on vertices $a_4, c_4$, there would be $\{a_3, c_3, b_4\}\subseteq D$ and $a_5, c_5\notin D$. Also, $|D\cap (X_3\cup X_4)| = 3$ means that $b_3\notin D$. By construction (Ⅰ), $a_4, c_4\in D$, then $|D\cap (X_3\cup X_4)|\geq 5$, a contradiction.) There is $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-2)+2 = 2n-2$. On the other hand, $|D'| = |D|-9+5 < 2n-2$, a contradiction.

Case 1.2. If $|D\cap (X_3\cup X_4)| = 2$, then at least one of pairs $\{a_3, a_4\}, \{b_3, b_4\}, \{c_3, c_4\}$ does not intersect with $D$. If $\{b_3, b_4\}\cap D = \emptyset$, then $\{a_3, c_3, a_4, c_4\}\subseteq D$ by construction (Ⅰ), a contradiction. By symmetry, we discuss the case that $\{a_3, a_4\}\cap D = \emptyset$. Then there is $\{a_2, b_3, b_4, a_5\}\subseteq D$. The condition $|D\cap (X_3\cup X_4)| = 2$ implies that $\{c_3, c_4\}\cap D = \emptyset$ and furthermore $c_5\in D$. Focusing on vertices $a_5, c_5$, we know that $\{b_5, a_6, c_6\}\subseteq D$ (see Figure 3(a)). Set $X = \cup_{i = 1}^4 X_i$. Then $D' = D\setminus X$ is a DTDS of $G' = G-X$. Clearly, $|D'| = |D|-8 < 2n-6$. By induction, $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-4)+2 = 2n-6$, a contradiction.

Case 2. $|D\cap (X_1\cup X_2)| = 5$ and $2\leq |D\cap (X_3\cup X_4)|\leq 4.$

Case 2.1. If $|D\cap (X_3\cup X_4)| = 4$, then $D' = (D\setminus \cup_{i = 1} ^4 X_i)\cup \{a_3, b_3, a_4, b_4, c_4\}$ or $D' = (D\setminus \cup_{i = 1} ^4 X_i)\cup \{b_3, c_3, a_4, b_4, c_4\}$ is a DTDS of $G' = G-(X_1\cup X_2)$. There is $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-2)+2 = 2n-2$. On the other hand, $|D'| = |D|-9+5 < 2n-2$, a contradiction.

Case 2.2. If $|D\cap (X_3\cup X_4)| = 3$, we consider two subcases according to $b_2\in D$ or not.

(1) $b_2\notin D$. By construction (Ⅰ), $\{a_3, c_3\}\subseteq D$. We claim that $b_3\in D$. (For otherwise, there would be $\{a_4, c_4\}\subseteq D$ by construction (Ⅰ), then $|D\cap (X_3\cup X_4)|\geq 4$, a contradiction.) $|D\cap (X_3\cup X_4)| = 3$ means that $X_4\cap D = \emptyset$. By construction (Ⅲ), $X_5\cup \{a_6, c_6\}\subseteq D$ (see Figure 3(b)). Set $X = \cup_{i = 1}^4 X_i$. Then $D' = D\setminus X$ is a DTDS of $G' = G-X$. Clearly, $|D'| = |D|-8 < 2n-6$. By induction, $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-4)+2 = 2n-6$, a contradiction.

(2) $b_2\in D$. By symmetry, we may assume that $a_1\notin D$. First, we establish a claim.

Claim. $\{a_3, b_3\}\subseteq D$.

Since $a_2$ has at least two neighbors in $D$, clearly $a_3\in D$. Focusing on vertices $a_3, c_4$, we know that at least one of $b_3$ and $a_4$ ($c_3$ and $b_4$, respectively) in $D$ ($*$). If $b_3\notin D$, then $\{a_4, c_4\}\subseteq D$ by construction (Ⅰ). It implies that $|D\cap (X_3\cup X_4)|\geq 4$, a contradiction. The claim is done.

Recall that one of $c_3, b_4$ is in $D$ (see ($*$)). If $c_3 \in D$, then $X_4\cap D = \emptyset$. By construction (Ⅲ), $X_5\cup \{a_6, c_6\}\subseteq D$ (see Figure 3(c)). Similar to (1), we can deduce a contradiction. If $b_4\in D$, then $\{c_3, a_4, c_4\}\cap D = \emptyset$. By construction (Ⅱ), there is $\{b_5, a_6, c_6\}\subseteq D$. Also, focusing on $c_4$, we know that $c_5\in D$. Furthermore, focusing on $a_6$, we deduce that $a_5$ or $b_6$ in $D$ (see Figure 3(d)). No matter which one of $a_5$, $b_6$ being in $D$, $D' = D\setminus \cup_{i = 1}^4 X_i$ is a DTDS of $G' = G-\cup_{i = 1}^4 X_i$. However, there are $|D'| = |D|-8 < 2n-6$ and $|D'|\geq \gamma_{\times 2, t}(G')\geq 2(n-4)+2 = 2n-6$, a contradiction.

Case 2.3. If $|D\cap (X_3\cup X_4)| = 2$, then at least one of pairs $\{a_3, a_4\}, \{b_3, b_4\}, \{c_3, c_4\}$ does not intersect with $D$. Similar to the proof of Case 1.2, the unique possibility is $\{a_3, a_4, c_3, c_4\}\cap D = \emptyset$. Focusing on the vertices $a_2, c_2$, there is $\{a_1, b_2, c_1\}\subseteq D$. This means that $|D\cap (X_1\cup X_2)| = 6$, a contradiction.

In each of these cases, we deduce a contradiction. Therefore, we draw a conclusion that $\gamma_{\times 2, t}(P_{3}\Box P_{n}) \geq 2n+2$ when $n\equiv 0\; (mod\; 2)$. It is analogous to verify that $\gamma_{\times 2, t}(P_{3}\Box P_{n}) \geq 2n+1$ when $n\equiv 1\; (mod\; 2)$ by replacing $2n+2$ with $2n+1$ in the above proof.

We are ready to prove our second result.

Theorem 2.5. Let $n\geq 2$ be an integer. Then

Proof. When $n\equiv 0\; (mod\; 2)$, set $S = (\cup_{i = 1}^{n}\{a_i, c_i\})\cup \{b_{1}, b_{n}\}.$ It is clear that $S$ is a DTDS of graph $G$. Hence $\gamma_{\times 2, t}(G)\leq 2n+2$.

When $n\equiv 3\; (mod\; 4)$, i.e. $n = 4k+3$ for some nonnegative integer $k$, set

(see Figure 4(a) for the case $n = 7$), then $|S| = n+4(k+1) = 2n+1$. When $n\equiv 1\; (mod\; 4)$, i.e. $n = 4k+1$ for some positive integer $k$, set

(see Figure 4(b) for the case that $n = 9$), then $|S| = n-1+4k+3 = 2n+1$. In these two cases, it is easy to check that $S$ is a DTDS of $G$. Thus, $\gamma_{\times 2, t}(G) \leq |S| = 2n+1$ when $n\equiv 1\; (mod\; 2)$.

By Lemma 2.4, the proof is completed.

Let $G = P_m \Box P_n$ with $P_{m} = u_{1}u_{2}\dots u_{m}$, $P_{n} = v_{1}v_{2}\dots v_{n}$, where integers $m\geq 2$, $n\geq 2$. For the vertex $u_{i}\in V(P_{m})$ and $v_{j}\in V(P_{n})$, we denote simply the vertex $(u_{i}, v_{j})$ by $x_{ij}$, $1\leq i\leq m$, $1\leq j\leq n$. For each $1\leq i\leq m$ and $1\leq j\leq n$, we denote $X_j = \cup_{i = 1}^m x_{ij}$, $Y_{i} = \cup_{j = 1}^n x_{ij}$. Before moving forward, we give a useful lemma.

Lemma 2.6. Let $G = P_m \Box P_n$, where integers $n\geq 4, m\geq 4$, and $D$ be a minimum DTDS of $G$. Then

Proof. For any vertex set $W\in \{X_1, X_n, Y_1, Y_n\}$, we will show at least $\frac{|W|}{2}$ vertices of $W$ in $D$. W.l.o.g., we pick $W = Y_1 = \{x_{11}, x_{12}, \cdots, x_{1n}\}$. Set $D' = V(G)\setminus D$. Since each vertex of $Y_1\setminus\{x_{11}, x_{1n}\}$ has degree 3 and either of $x_{11}, x_{1n}$ has degree 2, it is impossible to appear three consecutive vertices in $Y_1 \cap D'$. (For otherwise, the interior vertex is adjacent to at most one vertex in $D$, a contradiction.) Moreover, if $x\in Y_1\cap D$, then $x$ has at least one neighbor in $Y_1\cap D$. By the above discussion and Observation 1.1 (c), we can establish the following four facts.

$({\rm{F1}})$ The length of any sequence of consecutive vertices is at most two in $Y_1 \cap D'$.

$({\rm{F2}})$ The length of any sequence of consecutive vertices is at least two in $Y_1 \cap D$.

$({\rm{F3}})$ For every four consecutive vertices in $Y_1$, at least two of them in $D$.

$({\rm{F4}})$ $\{x_{12}, x_{1(n-1)}\}\subset D$.

Concretely, we discuss the following three cases according to $x_{11}, x_{1n}$ in $D$ or not.

Case 1. $\{x_{11}, x_{1n}\}\cap D = \emptyset$. By (F2) and (F4), $\{x_{12}, x_{13}, x_{1(n-2)}, x_{1(n-1)}\}\subset D$. By virtue of (F3), we consider four subcases.

$(1.1)$ $n\equiv 0$ (mod 4).

Since $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1n}\})\cap D|\geq \frac{n-4}{2}$, $|Y_1\cap D|\geq \frac{n-4}{2}+2 = \frac{n}{2}$.

$(1.2)$ $n\equiv 1$ (mod 4).

Since $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-5}{2}$, $|Y_1\cap D|\geq \frac{n-5}{2}+3 = \frac{n+1}{2}$.

$(1.3)$ $n\equiv 2$ (mod 4).

Since $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-2)}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-6}{2},$ $|Y_1\cap D|\geq \frac{n-6}{2}+4 = \frac{n+2}{2}$.

$(1.4)$ $n\equiv 3$ (mod 4).

Since $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{14}, x_{1(n-2)}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-7}{2},$ $|Y_1\cap D|\geq \frac{n-7}{2}+4 = \frac{n+1}{2}$.

Case 2. $|\{x_{11}, x_{1n}\}\cap D| = 1$. We may assume that $x_{11}\notin D, x_{1n}\in D$. By (F2) and (F4), $\{x_{12}, x_{13}, x_{1(n-1)}, x_{1n}\}\subset D$. Then we have the following conclusions by (F3).

$(1.1)$ $n\equiv 0$ (mod 4).

$|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1n}\})\cap D|\geq \frac{n-4}{2}$, so $|Y_1\cap D|\geq \frac{n-4}{2}+3 = \frac{n+2}{2}$.

$(1.2)$ $n\equiv 1$ (mod 4).

$|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-5}{2}$, so $|Y_1\cap D|\geq \frac{n-5}{2}+4 = \frac{n+3}{2}$.

$(1.3)$ $n\equiv 2$ (mod 4).

$|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-2)}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-6}{2},$ then $|Y_1\cap D|\geq \frac{n-6}{2}+4 = \frac{n+2}{2}$.

$(1.4)$ $n\equiv 3$ (mod 4).

$|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{14}, x_{1(n-2)}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-7}{2},$ so $|Y_1\cap D|\geq \frac{n-7}{2}+4 = \frac{n+1}{2}$.

Case 3. $\{x_{11}, x_{1n}\}\subset D$. By (F2) and (F4), $\{x_{11}, x_{12}, x_{1(n-1)}, x_{1n}\}\subset D$. By (F3), the following are established.

$(1.1)$ $n\equiv 0$ (mod 4).

By $|(Y_1\setminus\{x_{11}, x_{12}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-4}{2}$, $|Y_1\cap D|\geq \frac{n-4}{2}+4 = \frac{n+4}{2}$.

$(1.2)$ $n\equiv 1$ (mod 4).

By $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-5}{2}$, $|Y_1\cap D|\geq \frac{n-5}{2}+4 = \frac{n+3}{2}$.

$(1.3)$ $n\equiv 2$ (mod 4).

By $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{1(n-2)}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-6}{2},$ $|Y_1\cap D|\geq \frac{n-6}{2}+4 = \frac{n+2}{2}$.

$(1.4)$ $n\equiv 3$ (mod 4).

Recall that $\{x_{11}, x_{12}, x_{1(n-1)}, x_{1n}\}\subset D$. Furthermore, by (F1), $|\{x_{13}, x_{14}, x_{15}\}\cap D|\geq 1$. By (F3), $|(Y_1\setminus\{x_{11}, x_{12}, x_{13}, x_{14}, x_{15}, x_{1(n-1)}, x_{1n}\})\cap D|\geq \frac{n-7}{2}.$ Thus $|Y_1\cap D|\geq \frac{n-7}{2}+5 = \frac{n+3}{2}$.

We will complete the proof by considering all cases dependent on $x_{11}, x_{1n}, x_{m1}, x_{mn}$ in $D$ or not.

$(1)$ If $\{x_{11}, x_{1n}, x_{m1}, x_{mn}\}\cap D = \emptyset,$ then

according to Case 1.

$(2)$ If $|\{x_{11}, x_{1n}, x_{m1}, x_{mn}\}\cap D| = 1,$ w.l.o.g., assuming that $x_{m1}\in D$, then

according to Cases 1 and 2. Similarly, $|D\cap (X_1\cup X_n)|\geq m+1$. Since $x_{m1}$ is counted twice, we have $|D\cap (X_1\cup X_n\cup Y_1\cup Y_m)|\geq m+n+1.$

$(3)$ If $|\{x_{11}, x_{1n}, x_{m1}, x_{mn}\}\cap D| = 2,$ then there are two possible subcases to be considered up to isomorphism. If $\{x_{m1}, x_{mn}\}\subset D$, then

according to Cases 1 and 3, and $|D\cap (X_1\cup X_n)|\geq m+1$ by Case 2. Noting that either of $x_{m1}, x_{mn}$ is counted twice, $|D\cap (X_1\cup X_n\cup Y_1\cup Y_m)|\geq m+n+1.$ If $\{x_{m1}, x_{1n}\}\subset D$, then

according to Case 2. Since either of $x_{m1}, x_{1n}$ is counted twice, $|D\cap (X_1\cup X_n\cup Y_1\cup Y_m)|\geq m+n.$

$(4)$ If $|\{x_{11}, x_{1n}, x_{m1}, x_{mn}\}\cap D| = 3,$ then we may assume that $x_{11}\notin D$ by symmetry. By Cases 2 and 3,

and similarly $|D\cap (X_1\cup X_n)|\geq m+2$. Noting that each of $x_{1n}, x_{m1}, x_{mn}$ is counted twice, we have $|D\cap (X_1\cup X_n\cup Y_1\cup Y_m)|\geq m+n+1.$

$(5)$ If $\{x_{11}, x_{1n}, x_{m1}, x_{mn}\}\subset D,$ then

by Case 3. Since each of $x_{11}, x_{1n}, x_{m1}, x_{mn}$ is counted twice, $|D\cap (X_1\cup X_n\cup Y_1\cup Y_m)|\geq m+n$.

Next, we will give bounds for $\gamma_{\times 2, t}(P_{m}\Box P_{n})$ when $m \geq 4$. When $m = 4$, it is stated as the following theorem.

Theorem 2.7. Let $n\geq 2$ be an integer. Then

Proof. Let $G = P_4 \Box P_n$ with $P_{4} = abcd$ and $P_{n} = v_{1}v_{2}\ldots v_{n}$, where $n\geq 2$. Set $X_{i} = \{a_{i}, b_{i}, c_{i}, d_{i}\}$ for $1\leq i \leq n$, $Y_1 = \cup_{i = 1}^n a_i$ and $Y_4 = \cup_{i = 1}^n d_i$.

We firstly prove the upper bound by constructing a DTDS of $G$. For integer $k\geq 0$, set

Clearly, $|X| = 12k$. Next, we give a DTDS, denoted by $S$, of $G$ according to the value of $n$.

When $n = 5k$, set $S = X\cup \{b_{5k}, c_{5k}\}.$ Thus $|S| = 12k+2 = \frac{12n}{5}+2$. Therefore $\gamma_{\times 2, t}(G) \leq |S| = \frac{12n}{5}+2$.

When $n = 5k+1$, set $S = X\cup X_{5k+1} \cup \{a_{5k}, d_{5k}\}.$ Then $\gamma_{\times 2, t}(G) \leq |S| = 12k+6 = \frac{12n+18}{5}$.

When $n = 5k+2$, set $S = X\cup X_{5k+1} \cup X_{5k+2}.$ So $\gamma_{\times 2, t}(G) \leq |S| = 12k+8 = \frac{12n+16}{5}$.

When $n = 5k+3$, set $S = X\cup X_{5k+1} \cup X_{5k+3} \cup\{a_{5k+2}, d_{5k+2}\}.$ Then $\gamma_{\times 2, t}(G) \leq |S| = 12k+10 = \frac{12n+14}{5}$.

Finally, when $n = 5k+4$, set

Hence

Next, let $D$ be a minimum DTDS in $G$ and $D' = V(G)\setminus D$. We will prove the lower bound by counting the edges between $D$ and $D'$. Set $W = X_1\cup X_n\cup Y_1\cup Y_4$. By Lemma 2.6, $|D\cap W|\geq n+4$. Note that each vertex in $D\cap W$ has at most one neighbor in $D'$, and each one in $D\setminus W$ has at most two neighbors in $D'$. So

Then

Hence we have $|D|\geq \frac{9n}{4}+1$.

Now, we consider the bounds of $\gamma_{\times 2, t}(P_{m}\Box P_{n})$ for $m\geq 5$ and $n\geq 5$.

Theorem 2.8. For integers $m\geq 5$, $n\geq 5$,

Proof. Let $G = P_m \Box P_n$ with $P_{m} = u_{1}u_{2}\dots u_{m}$, $P_{n} = v_{1}v_{2}\dots v_{n}$, where $m\geq 5$, $n\geq 5$. For the vertex $u_{i}\in V(P_{m})$ and $v_{j}\in V(P_{n})$, we denote simply the vertex $(u_{i}, v_{j})$ by $x_{ij}$, $1\leq i\leq m$, $1\leq j\leq n$. For each $1\leq i\leq m$ and $1\leq j\leq n$, we denote $X_j = \cup_{i = 1}^m x_{ij}$, $Y_{i} = \cup_{j = 1}^n x_{ij}$. Let $D$ be a minimum DTDS of $G$, and $D' = V(G)\setminus D$.

Let $W = X_1\cup X_n\cup Y_1\cup Y_m$. By Lemma 2.6, $|D\cap W|\geq m+n$. Counting the edges between $D$ and $D'$, we have $2(mn-|D|) = 2|D'|\leq e(D, D') = e(D\cap W, D')+e(D\setminus W, D')\leq |D\cap W|+2|D\setminus W| = 2|D|-|D\cap W|\leq 2|D|-(m+n)$. Then $\gamma_{\times 2, t}(P_{m}\Box P_{n}) = |D|\geq \frac{mn}{2}+\frac{m+n}{4}$.

To prove the upper bounds, for integer $k\geq 1$, set

Then $|X| = 2mk+2k$. Next, we give a DTDS of $G$ for each of the possible cases to complete the proof.

Case 1. $n = 4k$.

Let

set $S = X\cup A\cup \{x_{(m-2)4k}, x_{(m-1)4k}\}.$ When $m\equiv0\; (mod\; 4)$, $\{x_{(m-2)4k}, x_{(m-1)4k}\}\subseteq A$, so $|A\cup \{x_{(m-1)4k}, x_{(m-2)4k}\}| = \frac{m}{2}$. When $m\equiv1\; (mod\; 4)$, $x_{(m-2)4k}\in A$, so $|A\cup \{x_{(m-1)4k}, x_{(m-2)4k}\}| = \frac{m+1}{2}$. When $m\equiv2\; (mod\; 4)$, $|A\cup \{x_{(m-1)4k}, x_{(m-2)4k}\}| = \frac{m+2}{2}$. When $m\equiv3\; (mod\; 4)$, $|A\cup \{x_{(m-1)4k}, x_{(m-2)4k}\}| = \frac{m+1}{2}$. Hence, $|A\cup \{x_{(m-1)4k}, x_{(m-2)4k}\}|\leq \frac{m+2}{2}$. Clearly, each vertex in $V(G)\setminus X_{4k}$ has at least two neighbors in $S$. For any vertex $x\in X_{4k}$, $x$ has at least one neighbor in $S\cap X_{4k}$. Noting that $X_{4k-1}\subset S$, each vertex in $X_{4k}$ has at least two neighbors in $S$. That is to say, $S$ is a DTDS of $G$. Thus

Case 2. $n = 4k+1$.

Set $S = X \cup X_{4k+1} \cup \{x_{1(4k)}, x_{m(4k)}\}.$ Then $S$ is a DTDS of $G$. So $\gamma_{\times 2, t}(G) \leq |S| = 2mk+2k+m+2 = \frac{mn}{2}+\frac{m+n+3}{2}$.

Case 3. $n = 4k+2$.

Let

When $m\equiv 0\; (mod\; 4)$, set $S = X \cup B \cup \{x_{(m-1)(4k+2)}, x_{m(4k+2)}\}$. Then $|S|\leq |X|+ m+\frac{m}{2}+2 = |X|+\frac{3m+4}{2}$.

When $m\equiv 1\; (mod\; 4)$, set $S = X \cup B \cup \{x_{(m-1)(4k+2)}, x_{m(4k+2)}\}$. Then $|S|\leq |X|+ m+\frac{m-1}{2}+2 = |X|+\frac{3m+3}{2}$.

When $m\equiv 2\; (mod\; 4)$, set $S = X \cup B \cup \{x_{(m-1)(4k+2)}, x_{m(4k+2)}\}$. Then $|S|\leq |X|+m+\frac{m-2}{2}+2 = |X|+\frac{3m+2}{2}$.

When $m\equiv 3\; (mod\; 4)$, set $S = X \cup B \cup(\cup_{i = m-2}^{m}\{ x_{i(4k+2)}\})$. Then $|S|\leq |X|+m+\frac{m-3}{2} +3 = |X|+ \frac{3m+3}{2}$. In each of these cases, we have

Next, we show that $S$ is a DTDS of $G$. Clearly, for each vertex $x\in V(G)\setminus (X_{4k+1}\cup X_{4k+2})$, $x$ has at least two neighbors in $S$. Noting that $X_{4k+1}\subseteq S$, each vertex in $X_{4k+1}$ has two neighbors in $X_{4k+1}$ except $x_{1(4k+1)}$ and $x_{m(4k+1)}$. Also, $x_{1(4k+1)}$ ($x_{m(4k+1)}$) has another neighbor $x_{1(4k+2)}$ ($x_{m(4k+2)}$) in $S$. For any vertex $x\in X_{4k+2}$, $x$ has one neighbor in $X_{4k+1}$ and at least one neighbor in $S\cap X_{4k+2}$. Then each vertex in $X_{4k+1}\cup X_{4k+2}$ has at least two neighbors in $S$. Therefore, $S$ is a DTDS of $G$. Then

Case 4. $n = 4k+3$.

Set $S = X \cup X_{4k+1} \cup X_{4k+3} \cup\{x_{1(4k+2)}, x_{m(4k+2)}\}.$ Clearly, $S$ is a DTDS of $G$. Thus

3.   Conclusions

In the paper, the values of $\gamma_{\times 2, t}(P_i\square P_n)$ for $i = 2, 3$ are determined. For $\gamma_{\times 2, t}(P_4\square P_n)$, we give lower and upper bounds with a gap no more than $\frac{3}{20}n+\frac{13}{5}$ and, for $\gamma_{\times 2, t}(P_m\square P_n)$ with $m, n \geq 5$, we give lower and upper bounds with a gap at most $\frac{m+n}{4}+\frac{3}{2}$.

The lower bounds in Theorem 2.7 and Theorem 2.8 could be improved if one may analyze the adjacent structures of DTDSs of $P_m\square P_n$ more carefully according to definition of the double total domination. For example, it is easy to verify that $\gamma_{\times 2, t}(P_4\square P_4) = 12$, that attains the upper bound in Theorem 2.7 for the case $n = 4$. Moreover, Figure 5(a) demonstrates that the lower bound of $\gamma_{\times 2, t}(P_5\square P_5)$ could be improved to 18. (For an arbitrary DTDS $D$ of $P_5\square P_5$, each of the solid circle and the dash curves in Figure 5(a) covers at least two vertices of $D$.) In Figure 5(b), we give a DTDS to show that the value of $\gamma_{\times 2, t}(P_5\square P_5)$ is exactly 18, that is greater than the lower bound in Theorem 2.8 for the case $m = n = 5$.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (No. 12071265) and the Shandong Provincial Natural Science Foundation (No. ZR2019MA032).

Conflict of interest

The authors declare no conflicts of interest.