The generalized 4-connectivity of folded Petersen cube networks

1.   Introduction

As usual, the topological structure of an interconnection network is regarded as a graph $G = (V, E)$, in which vertices correspond to processors and edges represent communication links between processors. The fault tolerance is one of the most important factors in the design and analysis of an interconnection network and it can be measured by the connectivity of a graph. If the connectivity of a network is larger, then its fault tolerance is higher. The traditional connectivity $\kappa(G)$ of a graph $G$ is defined as the minimum number of vertices whose deletion results in a disconnected graph. An excellent theorem of Whitney ^[32] provided an equivalent statement about the definition of the connectivity. That is, for any 2-subset $S = \{u, v\} \subseteq V(G)$, if $\kappa(S)$ denotes the maximum number of internally disjoint paths between $u$ and $v$ in $G$, then $\kappa(G) = \min\{\kappa(S)\colon S \subseteq V(G), |S| = 2\}$. Clearly, $\kappa(G)$ reflects the connectivity between any two processors. To measure the connectivity capability of more processors, Chartrand et al. ^[6] and Hager et al. ^[11] introduced independently the concept of the generalized connectivity of a graph by generalizing the equivalent definition of connectivity.

Let $G$ be a connected graph with order $n$ and $\ell$ be an integer such that $2 \leq \ell \leq n$. For $S \subseteq V(G)$, a tree $T$ in $G$ is called an $S$-tree if $S \subseteq V(T)$. Let $\kappa(S)$ denote the maximum number $r$ of edge-disjoint $S$-trees $T_1, \dots, T_r$ satisfying $V(T_{i}) \cap V(T_{j}) = S$ for any two distinct integers $i, j \in \{1, \dots, r\}$. The generalized $\ell$-connectivity $\kappa_{\ell}(G)$ of $G$ is defined as $\min\{\kappa(S)\colon S \subseteq V(G), |S| = \ell\}$. Actually, $\kappa_{2}(G)$ is exactly $\kappa(G)$.

Though there are numerous results about the generalized $\ell$-connectivity over the past years, for general integer $\ell$, the exact values of $\kappa_{\ell}(G)$ are known for only a small class of graphs: complete graph ^[7], complete bipartite graph ^[16] and complete equipartition 3-partite graph ^[18]. Meanwhile, for a given graph $G$, any fixed integer $k \geq 2$ and a subset $S$ of $V(G)$, the decision problem whether $\kappa(S) \geq k$ is $NP$-complete ^[19]. The upper and lower bounds of the generalized 3-connectivity of a graph ^[21,25] and of Cartesian (Lexicographic) product of two graphs ^[13,14,26] were investigated, and extremal problems were studied in ^[17,22]. The generalized 3-connectivity of some graph classes are known, including Cayley graphs ^[20,31], star graphs and bubble-sort graphs ^[23], alternating group graphs and $(n, k)$-star graphs ^[34], $k$-ary $n$-cubes, split-star graphs and bubble-sort star graphs ^[37], $(n, k)$-bubble sort graphs ^[38], etc. We refer the readers to ^[15,27] for more details.

Unfortunately, the results of the generalized $4$-connectivity are less known. Only hypercubes ^[24], dual cubes ^[35], exchanged hypercubes ^[33], $(n, k)$-star graphs ^[12], hierarchical cubic networks ^[36] have been studied.

The main focus of this paper is to determine the generalized 4-connectivity of the folded Petersen cube networks $FPQ_{n, k}$. The following result is obtained.

Theorem 1.1. Let $k, n$ be two integers. Then $\kappa_{4}(FPQ_{n, k}) = n+3k-1$.

Theorem 1.1 implies that if $k = 0$, then $\kappa_{4}(FPQ_{n, 0}) = n-1$, which coincides the value of $\kappa_{4}(Q_{n})$. The key to prove Theorem 1.1 is Theorem 1.2.

Theorem 1.2. Let $FP_k$ be a $k$-dimensional folded Petersen graph. Then $\kappa_{4}(FP_k) = 3k-1$.

For a regular graph, the following lemma is useful.

Lemma 1.1. ^[24] Let $G$ be an $r$-regular graph. If $\kappa_{k}(G) = r-1$, then $\kappa_{k-1}(G) = r-1$, where $k \geq 4$.

Combining Theorem 1.1 and Lemma 1.1, the following corollary is an immediate consequence.

Corollary 1.1. Let $k, n$ be two integers. Then $\kappa_{3}(FPQ_{n, k}) = n+3k-1$.

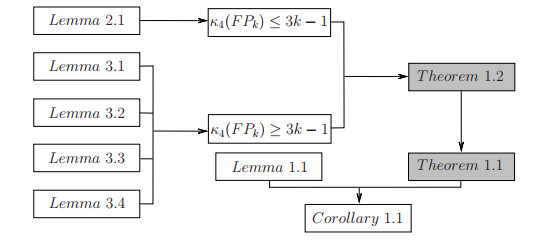
For helping readers to understand the proof process, a flow chart in Figure 1 is presented to illustrate the relationship between different lemmas, theorems and corollaries.

2.   Preliminaries

This section introduces some basic notations and results that will be used throughout the paper. All graphs considered in this paper are connected, simple, undirected, finite and for the notation and terminology not defined refer to ^[5].

2.1.   Basic notations and lemmas

Let $G = (V, E)$ be a graph with vertex set $V(G)$ and edge set $E(G)$. For a vertex $v$ of $G$, we use $N_{G}(v)$ to denote the set of neighbors of $v$ in $G$, and the degree of $v$ is $d_{G}(v) = |N_{G}(v)|$. The minimum degree and the maximum degree of $G$ are denoted by $\delta(G)$ and $\Delta(G)$, respectively. A graph $G$ is $r$-regular if $\delta(G) = \Delta(G) = r$. For two vertices $u, v\in V(G)$, a $(u, v)$-path is denoted by $P_{uv}$ and the length of a shortest $(u, v)$-path is called the distance between $u$ and $v$, denoted by $d_{G}(u, v)$. A subgraph of $G$ is a graph $H = (V', E')$ such that $V'(H)\subseteq V(G)$ and $E'(H)\subseteq E(G)$. If $V'(H) = V(G)$, then $H$ is called a spanning subgraph of $G$. The subgraph of $G$ induced by $V'$ is denoted by $G[V']$. Let $[b] = \{1, \dots, b\}$ for a given integer $b$.

Lemma 2.1. ^[21] If there are two adjacent vertices of degree $\delta$, then $\kappa_{\ell}(G) \leq \delta-1$ for $3 \leq \ell \leq |V(G)|$.

Theorem 2.1. (Menger's theorem ^[5]) A graph $G$ is $r$-connected if and only if any two distinct vertices of $G$ are connected by at least $r$ internally disjoint paths.

Lemma 2.2. (Fan Lemma ^[5]) Let $G$ be an $r$-connected graph, $x$ be a vertex of $G$, and let $Y \subseteq V(G) \setminus \{x\}$ be a set of at least $r$ vertices of $G$. Then there exists an $r$-fan in $G$ from $x$ to $Y$, that is, there exists a family of $r$ internally disjoint $(x, Y)$-paths whose terminal vertices are distinct in $Y$.

2.2.   The folded Petersen cube networks

The Cartesian product of graphs is an important tool to construct a bigger network. Recall that the Cartesian product of two graphs $G$ and $H$, denoted by $G \Box H$, is a graph with the vertex set $V(G) \times V(H)$ such that $(g, h)$ and $(g', h')$ are adjacent if and only if either $g = g'$ and $hh '\in E(H)$, or $h = h'$ and $gg '\in E(G)$.

The Petersen graph $\bf{P}$ with a vertex set $\{\bf{0, 1, 2, \dots, 9}\}$ has an outer $5$-cycle and an inner $5$-cycle are joined by a perfect matching (Figure 2$(a)$ depicts $\bf{P}$ with decimal vertex-labeling). It is a $3$-regular $3$-connected graph with diameter 2. The $k$-dimensional folded Petersen graph $FP_k$ is constructed by the $k$-th iteration of Cartesian product on Petersen graph $\bf{P}$, defined as $FP_k = \bf{P} \Box \cdots \Box \bf{P} = (V, E)$, where $V = \{x_1 \cdots x_k \colon x_i \in \{0, 1, ..., 9\}, 1 \leq i \leq k\}$ and $E = \{(x_1 \cdots x_{i-1} x_i x_{i+1} \cdots x_k, x_1 \cdots x_{i-1} y x_{i+1} \cdots x_k) \colon y \in \{0, 1, \ldots, 9\}$, $d_{\bf{P}}(y, x_i) = 1$ and $1\leq i \leq k\}$. As depicted in Figure 1$(b)$, $FP_2$ is obtained from $\bf{P}$ by replacing each of its vertices by $\bf{P}$, denoted by $\bf{P}^0, \bf{P}^1, \dots, \bf{P}^9$, respectively, moreover, between $\bf{P}^i$ and $\bf{P}^j$ have a perfect matching for $d_{\bf{P}}(i, j) = 1$. In fact, for $k\geq 2$, $FP_k$ is obtained from $\bf{P}$ by replacing each of its vertices by $FP_{k-1}$, and we denote the $10$ connected subgraphs by $FP_{k}^{i:0}, FP_{k}^{i:1}, \ldots, FP_{k}^{i:9}$, respectively, where $FP_{k}^{i:j} = FP_k[\{x_1 \cdots x_k \in V(FP_{k}), x_i = j\}]$. Clearly, $FP_{k}^{i:j} \cong FP_{k-1}$. For convenience, $FP^{j}$ denotes $FP_{k}^{1:j}$ for $j\in \{0, 1, \ldots, 9\}$ in the rest of this paper. It is easy to see that the subgraph induced by $V(FP^{i}) \cup V(FP^{j})$ is isomorphic to $FP_{k-1} \Box K_2$ for $d_{\bf{P}}(i, j) = 1$, and the edges between $V(FP^{i})$ and $V(FP^{j})$ are called the crossed edges.

For any $x\in V(FP^i)$, we call that $x^{i_j}$ is a corresponding vertex of $x$ in $FP^{i_j}$ if $x$ and $x^{i_j}$ differ in exactly the first digit. In particular, a corresponding vertex $x^{i_j}$ of $x$ is an outside neighbor of $x$ if $d_{\bf{P}}(i, i_j) = 1$. Apparently, there are exactly three outside neighbors of $x$. Two graphs $G'$ and $G''$ are corresponding if their vertices correspond one to one and $G'\cong G''$. Furthermore, $FP_k$ is a $3k$-regular $3k$-connected graph with diameter $2k$ and order $10^k$, also vertex and edge symmetric. More details see ^[8,10].

The folded Petersen cube network $FPQ_{n, k} = FP_k \Box Q_{n}$ with $10^{k} \times 2^{n}$ vertices is introduced by Öhring and Das ^[28], where $Q_n$ is an $n$-dimensional hypercube and it can be regarded as $n$-th iteration of Cartesian product on $K_2$. In particular, $FPQ_{0, k} = FP_{k}$ and $FPQ_{n, 0} = Q_{n}$. There are a lot of topological structures like linear arrays, rings, meshes, hypercubes can be embedded into it. Some research findings on the folded Petersen cube networks have been published for the past several years, see ^[9,28,30].

The following result will be used to prove Theorem 1.2.

Lemma 2.3. Let $S$ be a vertex subset of the Petersen graph $\bf{P}$ with $|S| = 4$. Then there exist two internally disjoint $S$-trees in $\bf{P}$.

Proof. Let $\bf{P}$ be a Petersen graph, $S = \{x, y, z, w\}\subseteq V(\bf{P})$ and $G = \bf{P}[S]$. Then $d_{G}(v)\leq 3$ for arbitrary $v \in V(G)$. Since $\bf{P}$ is vertex symmetric, assume that $d_{G}(x) = \Delta(G)$. If $d_G(x) = 3$, then $N_{G}(x) = \{y, z, w\}$. Two internally disjoint $S$-trees are demonstrated in Figure 3$(a)$. If $d_G(x) = 2$, without loss of generality, let $N_{G}(x) = \{y, z\}$. It suffices to consider two cases and the required $S$-trees are demonstrated in Figure 3$(b)$ and Figure 3$(c)$, respectively. If $d_G(x) = 1$, assume that $N_{G}(x) = \{y\}$, it suffices to consider two cases and the required $S$-trees are demonstrated in Figure 3$(d)$ and Figure 3$(e)$, respectively. If $d_G(x) = 0$, Figure 2$(f)$ demonstrates two internally disjoint $S$-trees.

3.   Main results

In this section, we mainly determine $\kappa_4(FP_k)$. First, propose the general idea of the proof $\kappa_4(FP_k) \geq 3k-1$. From the definition of $\kappa_4(FP_k)$, it suffices to show that $\kappa_{FP_k}(S) \geq 3k-1$ for arbitrary $S \subseteq V(FP_k)$ with $|S| = 4$. Furthermore, according to the definition of $\kappa_{FP_k}(S)$, find out $3k-1$ internally disjoint $S$-trees in $FP_k$. Let $S$ be a set of arbitrary four distinct vertices in $FP_k$. Recall that $FP_k$ can be decomposed into $10$ disjoint sub-folded Petersen graphs $FP^{0}, FP^{1}, \dots, FP^{9}$, each of which is isomorphic to $FP_{k-1}$ by removing all crossed edges.

For arbitrary four vertices $v_0, v_1, v_2, v_3$ in $\bf{P}$, by Lemma 2.3, there are two internally disjoint $\{v_0, v_1$, $v_2$, $v_3\}$-trees $T_1^*$ and $T_2^*$ in $\bf{P}$. At least one of the trees $T_1^*$ and $T_2^*$ contains a vertex $u$ different from $v_0, v_1, v_2, v_3$. Without loss of generality, let $T_2^*$ be such a tree. Clearly, $(T_1^* \cup T_2^*) \Box FP_{k-1}$ is a subgraph of $FP_k$. If we can prove that $\kappa_{T_1^* \Box FP_{k-1}}(S) \geq 3k-2$ and find out an $S$-tree in $T_2^* \Box FP_{k-1}$, then $\kappa_{FP_k}(S) \geq \kappa_{T_1^* \Box FP_{k-1}}(S) + 1 \geq 3k-1$. In this case, the problem is converted into finding out $3k-2$ internally disjoint $S$-trees in $T_1^* \Box FP_{k-1}$ and an $S$-tree in $T_2^* \Box FP_{k-1}$ such that all of the $S$-trees are internally disjoint.

Observation 3.1. For arbitrary three vertices $v_0, v_1, v_2$ in $\bf{P}$, one of the following holds.

(i) If $\{v_0, v_1, v_2\}$ is an isolated set, then there are three internally disjoint $\{v_0, v_1, v_2\}$-trees $T_1^*, T_2^*, T_3^*$ in $\bf{P}$. Moreover, there exists a vertex $u_i$ with degree 3 different from $v_0, v_1, v_2$ in $T_i^*$ for $i = 1, 2, 3$.

(ii) If $\{v_0, v_1, v_2\}$ is not an isolated set, then there are a $C_5$ and a $\{v_0, v_1, v_2\}$-tree $T_3^*$ in $\bf{P}$ such that $v_0, v_1, v_2 \in V(C_5)$ and $V(C_5)\cap V(T_3^*) = \{v_0, v_1, v_2\}$. Moreover, there exists a vertex $u$ with degree 3 different from $v_0, v_1, v_2$ in $T_3^*$.

For Observation 3.1$(i)$, it is easy to see that $(\bigcup_{i = 1}^3 T_i^*) \Box FP_{k-1}$ is a subgraph of $FP_k$ (see Figure 4). Notice that $T_1^*, T_2^*$ and $T_3^*$ are internally disjoint in $\bf{P}$, if we can prove that $\kappa_{T_1^* \Box FP_{k-1}}(S) \geq 3k-3$, find out an $S$-tree in $T_2^* \Box FP_{k-1}$ and another $S$-tree in $T_3^* \Box FP_{k-1}$, then $\kappa_{FP_k}(S) \geq \kappa_{T_1^* \Box FP_{k-1}}(S)+2 \geq 3k-1$. In this case, the problem is converted into finding out $3k-3$ internally disjoint $S$-trees in $T_1^* \Box FP_{k-1}$, an $S$-tree in $T_2^* \Box FP_{k-1}$ and another $S$-tree in $T_3^* \Box FP_{k-1}$ such that all of the $S$-trees are internally disjoint.

For Observation 3.1$(ii)$, let $C = C_5$, it can be seen that $(C \cup T_3^*) \Box FP_{k-1}$ is a subgraph of $FP_k$ (see Figure 5). If we can prove that $\kappa_{C \Box FP_{k-1}}(S) \geq 3k-2$, and find out an $S$-tree in $T_3^* \Box FP_{k-1}$, then $\kappa_{FP_k}(S) \geq \kappa_{C \Box FP_{k-1}}(S)+1 \geq 3k-1$. In this case, the problem is converted into finding out $3k-2$ internally disjoint $S$-trees in $C \Box FP_{k-1}$ and an $S$-tree in $T_3^* \Box FP_{k-1}$ such that all of the $S$-trees are internally disjoint.

For arbitrary two vertices $v_0, v_1$ in $\bf{P}$, by Theorem 2.1, there are three internally disjoint $(v_0, v_1)$-paths $L_1^*$, $L_2^*$ and $L_3^*$ in $\bf{P}$ because the Petersen graph $\bf{P}$ is 3-connected. Note that $\bigcup_{i = 1}^3 L_i^*$ is a subgraph of $\bf{P}$ and $(\bigcup_{i = 1}^3 L_i^*) \Box FP_{k-1}$ is a subgraph of $FP_k$ (see Figure 6). If we can prove that $\kappa_{L_1^* \Box FP_{k-1}}(S) \geq 3k-3$, find out an $S$-tree in $L_2^* \Box FP_{k-1}$ and another $S$-tree in $L_3^* \Box FP_{k-1}$, then $\kappa_{FP_k}(S) \geq \kappa_{(\cup_{i = 1}^3 L_i^*) \Box FP_{k-1}}(S) \geq \kappa_{L_1^* \Box FP_{k-1}}(S)+2 \geq 3k-1$. In this case, the problem is converted into finding out $3k-3$ internally disjoint $S$-trees in $L_1^* \Box FP_{k-1}$, an $S$-tree in $L_2^* \Box FP_{k-1}$ and another $S$-tree in $L_3^* \Box FP_{k-1}$ such that all of the $S$-trees are internally disjoint.

The following four lemmas will be helpful to main result.

Lemma 3.1. Let $FP_k$ be a $k$-dimensional folded Petersen graph and $S = \{x, y, z, w\}$ be a set of arbitrary four distinct vertices in $FP_k$ for $k \geq 2$. If the vertices in $S$ belong to four sub-folded Petersen graphs of $FP_k$, then there are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Proof. Let $FP^0, FP^1, \ldots, FP^9$ be 10 disjoint sub-folded Petersen graphs of $FP_{k}$. Since the vertices in $S$ belong to four sub-folded Petersen graphs of $FP_k$, there exist $v_0, v_1, v_2, v_3 \in \{0, 1, \dots, 9\}$ such that they are mutual distinct and $x \in V(FP^{v_0})$, $y \in V(FP^{v_1})$, $z \in V(FP^{v_2})$ and $w \in V(FP^{v_3})$.

For $v_0, v_1, v_2, v_3 \in V(\bf{P})$, there exist two internally disjoint $\{v_0, v_1, v_2, v_3\}$-trees $T_1^*$ and $T_2^*$ in $\bf{P}$ by Lemma 2.3. At least one of the trees $T_1^*$ and $T_2^*$ contains a vertex $c$ different from $v_0, v_1, v_2, v_3$, say $T_2^*$ is such a tree. Since $FP^c$ is connected, there exists an $\{x^c, y^c, z^c, w^c\}$-tree $T_{3k-2}'$ in $FP^c$. There is a unique path to connect arbitrary two vertices in $T_2^*$. That is, we can find the corresponding path to connect arbitrary two vertices in $T_2^* \Box FP_{k-1}$. Let $T_{3k-2} = T_{3k-2}' \cup P_{xx^c} \cup P_{yy^c} \cup P_{zz^c} \cup P_{ww^c}$.

Let $x_0 = x$. Choose $3k-2$ distinct vertices $x_0, x_1, x_2, \ldots, x_{3k-3}$ from $FP^{v_0}$ being $X$ such that $y^{v_0}, z^{v_0}$ and $w^{v_0}$ belong to $X$ and $|X| = 3k-2$. Without loss of generality, assume that $x_r = y^{v_0}, x_s = z^{v_0}, x_t = w^{v_0}$ for $r, s, t \in \{0, 1, \ldots, 3k-3\}$. Let $Y = \bigcup_{i = 0}^{3k-3}y_i$, $Z = \bigcup_{i = 0}^{3k-3}z_i$ and $W = \bigcup_{i = 0}^{3k-3}w_i$ be the corresponding vertices of vertices of $X$ in $FP^{v_1}, FP^{v_2}$ and $FP^{v_3}$, respectively, where $y_i = x_i^{v_1}$, $z_i = x_i^{v_2}$ and $w_i = x_i^{v_3}$ for each $i \in \{0, 1, \ldots, 3k-3\}$. Then $|Y| = |Z| = |W| = 3k-2$. By Lemma 2.2 and $\kappa(FP_{k-1}) = 3k-3$, there are $3k-3$ internally disjoint paths $A_1, A_2, \ldots, A_{3k-3}$ from $a$ to $A \setminus \{a\}$ in $FP^{v_j}$ for $(a, A, j) = (x, X, 0), (y, Y, 1), (z, Z, 2), (w, W, 3)$, respectively. Since there is a unique path to connect arbitrary two vertices in $T_1^*$, we can find the corresponding path to connect corresponding vertices in $T_1^* \Box FP_{k-1}$. Construct $3k-2$ internally disjoint $S$-trees in $T_1^* \Box FP_{k-1}$ as follows: $T_{i} = X_i \cup P_{x_iy_i} \cup Y_i \cup P_{y_iz_i} \cup Z_i \cup P_{z_iw_i} \cup W_i$ for $i\in\{0, 1, \ldots, 3k-3\}$, where $X_0 = \{x_0\} = \{x\}$, $Y_r = \{y_r\} = \{y\}$, $Z_s = \{z_s\} = \{z\}$ and $W_t = \{w_t\} = \{w\}$. Then, $T_0, T_1, \ldots, T_{3k-2}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$. See Figure 7.

Lemma 3.2. Let $FP_k$ be a $k$-dimensional folded Petersen graph and $S = \{x, y, z, w\}$ be a set of arbitrary four distinct vertices in $FP_k$ for $k \geq 2$. If the vertices in $S$ belong to three sub-folded Petersen graphs of $FP_k$, then there are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Proof. Let $FP^0, FP^1, \ldots, FP^9$ be 10 disjoint sub-folded Petersen graphs of $FP_{k}$. Since the vertices in $S$ belong to three sub-folded Petersen graphs of $FP_k$, there exist $v_0, v_1, v_2 \in \{0, 1, \dots, 9\}$ such that $x, y \in V(FP^{v_0})$, $z \in V(FP^{v_1})$ and $w \in V(FP^{v_2})$ by the symmetry of $FP_k$.

Since $FP_{k-1}$ is $(3k-3)$-connected, there exist $3k-3$ internally disjoint $(x, y)$-paths $P_1, P_2, \ldots, P_{3k-3}$ in $FP^{v_0}$. Choose $x_i \in V(P_i)$ such that $x_i \neq x$. Let $z_i = x_i^{v_1}$ and $w_i = x_i^{v_2}$ for $i\in [3k-3]$. By Lemma 2.2, there are $3k-3$ paths $P_{zz_1}, \ldots, P_{zz_{3k-3}}$ and $3k-3$ paths $P_{ww_1}, \ldots, P_{ww_{3k-3}}$ in $FP^{v_1}$ and $FP^{v_2}$, respectively. It is possible that one of the paths $P_{zz_i}$ (resp. $P_{ww_i})$ is a single vertex.

Case 1. $\{v_0, v_1, v_2\}$ is an isolated set.

By Observation 3.1$(i)$, there exists a $\{v_0, v_1, v_2\}$-tree $T_1^*$ which contains a vertex $a$ with degree 3 different from $v_0, v_1, v_2$ in $\bf{P}$. Moreover, there are a unique $(v_0, a)$-path $P_{v_0a}$, a unique $(v_1, a)$-path $P_{v_1a}$ and a unique $(v_2, a)$-path $P_{v_2a}$ in $T_1^*$. It is not hard to find $3k-3$ internally disjoint $S$-trees in $T_1^* \Box FP_{k-1}$, that is, $T_i = P_i \cup P_{x_ix_i^a} \cup P_{zz_i} \cup P_{z_ix_i^a} \cup P_{ww_i} \cup P_{w_ix_i^a}$ for $i\in [3k-3]$, where $P_{x_ix_i^a} \cong P_{v_0a}$, $P_{z_ix_i^a} \cong P_{v_1a}$ and $P_{w_ix_i^a} \cong P_{v_2a}$.

Except $T_1^*$, there are two internally disjoint $\{v_0, v_1, v_2\}$-trees $T_2^{*}$ and $T_3^{*}$ in $\bf{P}$, $T_2^{*}$ and $T_3^{*}$ contains a vertex with degree 3 different from $v_0, v_1$ and $v_2$, denoted by $b$ and $c$, respectively. Since $FP^b$ is connected, there exists an $\{x^b, y^b, z^b, w^b\}$-tree $T_{3k-2}'$ in $FP^b$ (resp. $\{x^c, y^c, z^c, w^c\}$-tree $T_{3k-1}'$ in $FP^c$). By the definition of $FP_k$, there exist the paths $P_{xx^b}, P_{yy^b}, P_{zz^b}, P_{ww^b}$ (resp. $P_{xx^c}, P_{yy^c}, P_{zz^c}, P_{ww^c}$) in $FP_k$ such that $P_{xx^b} \cong P_{yy^b} \cong P_{v_0b}, P_{zz^b} \cong P_{v_1b}, P_{ww^b} \cong P_{v_2b}$ (resp. $P_{xx^c} \cong P_{yy^c} \cong P_{v_0c}, P_{zz^c} \cong P_{v_1c}, P_{ww^c} \cong P_{v_2c}$) where $P_{v_0b}, P_{v_1b}, P_{v_2b}$ belong to $T_2^*$ (resp. $P_{v_0c}, P_{v_1c}, P_{v_2c}$ belong to $T_3^*$). Let $T_{3k-2} = T_{3k-2}' \cup P_{xx^b} \cup P_{yy^b} \cup P_{zz^b} \cup P_{ww^b}$ (resp. $T_{3k-1} = T_{3k-1}' \cup P_{xx^c} \cup P_{yy^c} \cup P_{zz^c} \cup P_{ww^c}$). Then, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$. See Figure 8.

Case 2. $\{v_0, v_1, v_2\}$ is not an isolated set.

By Observation 3.1$(ii)$, there exists a cycle $C$ for $C = C_5$ and a $\{v_0, v_1, v_2\}$-tree $T_3^*$ in $\bf{P}$ such that $V(C) \cap V(T_3^*) = \{v_0, v_1, v_2\}$. Let $R$ be a shorter path containing vertices $v_0, v_1, v_2$ in $C$, say $(v_0, v_2)$-path being such a path. Then $R = P_{v_0v_1}\cup P_{v_1v_2}$. Let $T_i = P_i \cup P_{x_iz_i} \cup P_{zz_i} \cup P_{z_iw_i} \cup P_{ww_i}$ for $i\in [3k-3]$, where $P_{x_iz_i} \cong P_{v_0v_1}$ and $P_{z_iw_i} \cong P_{v_1v_2}$.

Clearly, $R$ is a $\{v_0, v_1, v_2\}$-tree with $|V(R)| \leq 4$ and there exists another $(v_0, v_2)$-path $R'$ containing a non-end vertex $d$, then $R' = P_{v_0d} \cup P_{v_2d}$. Since $FP^d$ is connected, there exists an $\{x^d, y^d, z^d, w^d\}$-tree $T_{3k-2}'$ in $FP^d$. If $z^{v_0} \notin \bigcup_{i = 1}^{3k-3}V(P_i)$ (see Figure 9$(a)$), then $z^{v_0} \in P_{zz^d}$, where $P_{zz^d} \cong P_{v_0v_1} \cup P_{v_0d}$. Let $T_{3k-2} = T_{3k-2}' \cup P_{xx^d} \cup P_{yy^d} \cup P_{zz^d} \cup P_{ww^d}$, where $P_{xx^d} \cong P_{yy^d} \cong P_{v_0d}$ and $P_{ww^d} \cong P_{v_2d}$. If $z^{v_0} \in \bigcup_{i = 1}^{3k-3}V(P_i)$ (see Figure 9$(b)$), without loss of generality, assume that $z^{v_0} \in P_1$ and $x_1 = z^{v_0}$, then the path $P_{zz_1}$ is a single vertex. Let $z_{3k-2} = y^{v_1}$. Then there exists a path $P_{zz_{3k-2}}$ in $FP^{v_1}$. Let $T_{3k-2} = T_{3k-2}' \cup P_{xx^d} \cup P_{yy^d} \cup P_{yz_{3k-2}} \cup P_{zz_{3k-2}} \cup P_{ww^d}$, where $P_{xx^d} \cong P_{yy^d} \cong P_{v_0d}$, $P_{yz_{3k-2}} \cong P_{v_0v_1}$ and $P_{ww^d} \cong P_{v_2d}$. The $S$-tree $T_{3k-1}$ can be similarly constructed as $T_{3k-1}$ of Case 1. Then, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Lemma 3.3. Let $FP_k$ be a $k$-dimensional folded Petersen graph and $S = \{x, y, z, w\}$ be a set of arbitrary four distinct vertices in $FP_k$ for $k \geq 2$. If the vertices in $S$ belong to the same sub-folded Petersen graphs of $FP_k$, then there are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Proof. Let $FP^0, FP^1, \ldots, FP^9$ be 10 disjoint sub-folded Petersen graphs of $FP_{k}$. The vertices in $S$ belong to the same sub-folded Petersen graph, without loss of generality, suppose that $x, y, z, w \in V(FP^0)$. Since $FP^0 \cong FP_{k-1}$, by induction hypothesis, we have $\kappa_{4}(FP_{k-1})\geq 3k-4$. Hence, there exist $3k-4$ internally disjoint $S$-trees $T_1, T_2, \ldots, T_{3k-4}$ in $FP^0$. Clearly, there exists an $\{x^1, y^1, z^1, w^1\}$-tree $T_{3k-3}'$ in $FP^1$, an $\{x^4, y^4, z^4, w^4\}$-tree $T_{3k-2}'$ in $FP^4$ and an $\{x^5, y^5, z^5, w^5\}$-tree $T_{3k-1}'$ in $FP^5$. Let $T_{3k-3} = T_{3k-3}'\cup xx^1 \cup yy^1 \cup zz^1 \cup ww^1$, $T_{3k-2} = T_{3k-2}'\cup xx^4 \cup yy^4 \cup zz^4 \cup ww^4$ and $T_{3k-1} = T_{3k-1}'\cup xx^5 \cup yy^5 \cup zz^5 \cup ww^5$. Then, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Lemma 3.4. Let $FP_k$ be a $k$-dimensional folded Petersen graph and $S = \{x, y, z, w\}$ be a set of arbitrary four distinct vertices in $FP_k$ for $k \geq 2$. If the vertices in $S$ belong to two sub-folded Petersen graphs of $FP_k$, then there are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Proof. Let $FP^0, FP^1, \ldots, FP^9$ be 10 disjoint sub-folded Petersen graphs of $FP_{k}$. Suppose that the vertices in $S$ belong to two distinct sub-folded Petersen graphs $FP^{v_0}$ and $FP^{v_1}$, where $v_0, v_1 \in \{0, 1, \dots, 9\}$. For $v_0, v_1 \in V(\bf{P})$, since the Petersen graph $\bf{P}$ is 3-connected, by Theorem 2.1, there are three internally disjoint $(v_0, v_1)$-paths $L_1^*$, $L_2^*$ and $L_3^*$ in $\bf{P}$. For convenience, let $|V(L_1^*)| \leq |V(L_2^*)| \leq |V(L_3^*)|$. It implies that $2 \leq |V(L_1^*)|\leq 3$. We just consider $|V(L_1^*)| = 2$ as the discussion for $|V(L_1^*)| = 3$ is similar. Without loss of generality, suppose that $v_0 = \bf{0}$ and $v_1 = \bf{1}$. By the symmetry of $FP_k$, the following cases be considered.

Case 1. $x, y, z \in V(FP^{0})$ and $w \in V(FP^{1})$.

Case 1.1. $w^0 \in \{x, y, z\}$.

Without loss of generality, suppose that $w^0 = z$. By induction hypothesis and Lemma 1.1, we can find $3k-4$ internally disjoint $\{x, y, z\}$-trees $T_1', T_2', \ldots, T_{3k-4}'$ in $FP^0$. Let $\mathcal{T'} = \bigcup_{i = 1}^{3k-4} T_i'$.

Case 1.1.1. $|N_{\mathcal{T'}}(z) \cap \{x, y\}| \leq 1$.

First, construct two internally disjoint $S$-trees $T_{3k-2}$ and $T_{3k-1}$ in $L_2^* \Box FP_{k-1}$ and $L_3^* \Box FP_{k-1}$, respectively. Since $FP^4$ and $FP^5$ are connected, there exist an $\{x^4, y^4, z^4\}$-tree $T_{3k-2}'$ in $FP^4$ and an $\{x^5, y^5, z^5\}$-tree $T_{3k-1}'$ in $FP^5$, respectively. By the definition of $FP_k$, there exist two paths $P_{wz^4}$ and $P_{wz^5}$ such that $P_{wz^4} \cong L_2^* \setminus \{\bf{0}\}$ and $P_{wz^5} \cong L_3^* \setminus\{\bf{0}\}$. Let $T_{3k-2} = T_{3k-2}'\cup xx^4 \cup yy^4 \cup zz^4 \cup P_{wz^4}$ and $T_{3k-1} = T_{3k-1}'\cup xx^5 \cup yy^5 \cup zz^5 \cup P_{wz^5}$. Then $T_{3k-2}$ and $T_{3k-1}$ are internally disjoint $S$-trees in $FP_k$.

Next, construct $3k-3$ internally disjoint $S$-trees $T_1, T_2, \ldots, T_{3k-3}$ in $L_1^* \Box FP_{k-1}$ such that $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Since $|N_{\mathcal{T'}}(z) \cap \{x, y\}| \leq 1$, without loss of generality, assume that $|N_{T_i'}(z) \cap \{x, y\}| = 0$ and $d_{T_i'}(z) = 1$ for $i = 1, 2, \ldots, 3k-6$. Let $T_i = T_i' \cup z_iw_i \cup w_iw$, where $i \in [3k-6]$, $z_i$ is the neighbor of $z$ in $T_i'$ and $w_i = z_i^{1}$. Note that if $|N_{\mathcal{T'}}(z) \cap \{x, y\}| = 1$, say $y \in N_{\mathcal{T'}}(z)$. By symmetry, consider the following two cases.

Case 1.1.1.1. $d_{T_{3k-5}'}(z) = d_{T_{3k-4}'}(z) = 1$.

If $y \notin N_{\mathcal{T'}}(z)$, let $T_{i} = T_{i}' \cup z_{i}w_{i} \cup w_{i}w$ for $i = 3k-5$ and $3k-4$, where $z_i$ is the neighbor of $z$ in $T_i'$ and $w_i = z_i^{1}$. Otherwise, assume that $y \in N_{T_{3k-5}'}(z)$. Let $T_{3k-5} = T_{3k-5}' \cup zw$ and $T_{3k-4} = T_{3k-4}'\cup z_{3k-4}w_{3k-4} \cup w_{3k-4}w$. It is clear that $|N_{\mathcal{T'}}(z) \cap V(FP^0)| \leq 3k-4$, so there is a neighbor $z_{3k-3}$ of $z$ in $FP^0$. Let $\mathcal{T} = \bigcup_{i = 1}^{3k-4}T_i$ and $W = N_{\mathcal{T}}(w)$. Then $|W \cap V(FP^1)|\leq 3k-4$. Since $FP^1$ is $(3k-3)$-connected, $FP^1-W$ is still connected, thus we can find an $\{x^1, y^1, w, w_{3k-3}\}$-tree $T_{3k-3}'$ in $FP^1-W$, where $w_{3k-3} = z_{3k-3}^{1}$. Let $T_{3k-3} = T_{3k-3}' \cup xx^1 \cup yy^1 \cup zz_{3k-3} \cup z_{3k-3}w_{3k-3}$.

Case 1.1.1.2. $d_{T_{3k-5}'}(z) = 1$ and $d_{T_{3k-4}'}(z) = 2$.

If $y \notin N_{\mathcal{T'}}(z)$, let $T_{i} = T_{i}' \cup z_iw_i \cup w_iw$ for $i = 3k-5$ and $3k-4$, where $z_{i}$ is one of the neighbors of $z$ in $T_{i}'$ and $w_i = z_i^{1}$. Let $\mathcal{T} = \bigcup_{i = 1}^{3k-4}T_i$ and $W = N_{\mathcal{T}}(w)$. Then $|W \cap V(FP^1)| = 3k-4$. Since $FP^1$ is $(3k-3)$-connected, $FP^1-W$ is still connected, thus there exists an $\{x^1, y^1, w\}$-tree $T_{3k-3}'$ in $FP^1-W$. Let $T_{3k-3} = T_{3k-3}' \cup xx^1 \cup yy^1 \cup zw$.

Suppose that $y \in N_{\mathcal{T'}}(z)$. Without loss of generality, assume that $y \in N_{T_{3k-5}'}(z)$. Clearly, $T_{3k-5}'$ is an $(x, z)$-path containing $y$ and $T_{3k-4}'$ is an $(x, y)$-path containing $z$. That is, $T_{3k-5}' = P_{xy} \cup yz$ and $T_{3k-4}' = P_{xz} \cup P_{zy}$, where the lengths of $P_{xz}$ and $P_{zy}$ are least 2, see Figure 10$(a)$. Let $T_{3k-5}'' = P_{xy} \cup P_{zy}$ and $T_{3k-4}'' = P_{xz} \cup yz$, see Figure 10$(b)$. Actually, $T_{3k-5}'$ and $T_{3k-4}'$ in the case $y \in N_{T_{3k-4}'}(z)$ are $T_{3k-5}''$ and $T_{3k-4}''$, respectively. Let $T_{i} = T_{i}'' \cup z_{i}w_{i} \cup w_{i}w$ for $i = 3k-5, 3k-4$, where $z_{i} \neq y$ and $z_i$ is the neighbor of $z$ in $T_{i}''$. Let $\mathcal{T} = \bigcup_{i = 1}^{3k-4}T_i$ and $W = N_{\mathcal{T}}(w)$, then $|W \cap V(FP^1)| = 3k-4$ and $FP^1-W$ is still connected, thus there exists an $\{x^1, y^1, w\}$-tree $T_{3k-3}'$ in $FP^1-W$. Let $T_{3k-3} = T_{3k-3}'\cup xx^1 \cup yy^1 \cup zw$, see Figure 10$(c)$.

Then, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Case 1.1.2. $|N_{\mathcal{T'}}(z) \cap \{x, y\}| = 2$.

Recall the decimal vertex-labeling of the $FP_k$. Without loss of generality, assume that $w^0 = z = 000\ldots00$. Then $w = 100\ldots00$. Notice that $x, y, z$ are either in a subgraph of $FP_k$ isomorphic to $C_5$ or $C_4$ when $k \geq 2$.

Case 1.1.2.1. $x, y, z$ are in a subgraph of $FP_k$ isomorphic to $C_5$.

By symmetry, assume that $x = 000\ldots01$, $y = 000\ldots04$. If $k \geq 3$, then $x, y, z, w \in FP_{k}^{j:0}$ for $j \in \{2, \dots, k-1\}$ when dividing $FP_k$ along the $j$th dimension. Thus, the desired trees can be found similarly to Lemma 3.3. Suppose that $k = 2$. Then $x = 01$, $y = 04$, $z = 00$ and $w = 10$. The desired trees can be found similarly to Lemma 3.2 when dividing $FP_k$ along the $2$th dimension.

Case 1.1.2.2. $x, y, z$ are in a subgraph of $FP_k$ isomorphic to $C_4$.

In this case, $k \geq 3$. Without loss of generality, assume that $x = 000\ldots01$ and $y = 000\ldots10$. If $k \geq 4$, then $x, y, z, w \in FP^{j:0}$ for $j \in \{2, \dots, k-2\}$ when dividing $FP_k$ along the $j$th dimension. Thus, we can find out desired trees similarly to Lemma 3.3. Suppose that $k = 3$. Then $x = 001$, $y = 010$, $z = 000$ and $w = 110$. The desired trees are shown in Figure. 11.

Case 1.2. $w^0 \notin \{x, y, z\}$.

Case 1.2.1. $|N_{FP^0}(w^0) \cap \{x, y, z\}| \leq 1$.

First, construct $3k-3$ internally disjoint $S$-trees $T_1, T_2, \ldots, T_{3k-3}$ in $L_1^* \Box FP_{k-1}$ such that $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_k$.

Let $S' = \{x, y, z, w^0\}$. Since $FP^0 \cong FP_{k-1}$, by induction hypothesis, there exist $3k-4$ internally disjoint $S'$-trees $T_1', T_2', \ldots, T_{3k-4}'$ in $FP^0$. Since $|N_{FP^0}(w^0) \cap \{x, y, z\}| \leq 1$, without loss of generality, assume that $|N_{T_i'}(w^0) \cap \{x, y, z\}| = 0$ for $i\in [3k-4]$ and $i \neq 1$. Let $T_1 = T_1' \cup ww^0$. Since $d_{FP^0}(w^0) = 3k-3$, we have $1\leq d_{T_i'}(w^0) \leq 2$ for $i \in [3k-4]$. For $i = 2, \ldots, 3k-4$, let $T_i = (T_i'\setminus w^0) \cup w_iw_i^1 \cup w_i^1w$ if $N_{T_i'}(w^0) = \{w_i\}$ and let $T_i = (T_i'\setminus w^0) \cup w_iw_i^1 \cup w_i^1w \cup w_jw_j^1 \cup w_j^1w$ if $N_{T_i'}(w^0) = \{w_i, w_j\}$.

Let $\mathcal{T} = \bigcup_{i = 1}^{3k-4}T_i$ and $W = N_{\mathcal{T}}(w)$. Then $|W \cap V(FP^1)| = 3k-4$. Since $FP^1$ is $(3k-3)$-connected, $FP^1-W$ is still connected, thus there exists an $\{x^1, y^1, z^1, w\}$-tree $T_{3k-3}'$ in $FP^1-W$. Let $T_{3k-3} = T_{3k-3}' \cup xx^1 \cup yy^1 \cup zz^1$.

Next, construct two internally disjoint $S$-trees $T_{3k-2}$ and $T_{3k-1}$ in $L_2^* \Box FP_{k-1}$ and $L_3^* \Box FP_{k-1}$, respectively. Since $\bf{P}$ is a simple graph, there exist two non-end vertices $\bf{4}$ and $\bf{5}$ in $L_2^*$ and $L_3^*$, respectively. Clearly, $FP^4$ is connected and there exists an $\{x^4, y^4, z^4, w^4\}$-tree $T_{3k-2}'$ in $FP^4$. Let $T_{3k-2} = T_{3k-2}' \cup xx^4 \cup yy^4 \cup zz^4 \cup P_{ww^4}$, where $P_{ww^4} \cong L_2^* \setminus \{\bf{0}\}$. Similarly, construct $T_{3k-1} = T_{3k-1}' \cup xx^5 \cup yy^5 \cup zz^5 \cup P_{ww^5}$. Then, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_{k}$.

Case 1.2.2. $|N_{FP^0}(w^0) \cap \{x, y, z\}| \geq 2$.

Without loss of generality, suppose that $\{x, y\} \subseteq N_{FP^0}(w^0)$ and $w^0 = 000\cdots00$. Clearly, $w = 100\cdots00$. Note that $x, y, w^0$ are either in a subgraph of $FP_k$ isomorphic to $C_5$ or $C_4$ when $k \geq 2$.

Case 1.2.2.1. $x, y, w^0$ are in a subgraph of $FP_k$ isomorphic to $C_5$.

Without loss of generality, assume that $x = 000\cdots01$ and $y = 000\cdots04$. Let $z = 0z_2z_3\cdots z_{k-1}z_k$. If there exists $j \in \{2, \ldots, k-1\}$ such that $z_j = 0$, then $x, y, z, w \in FP_{k}^{j:0}$ when dividing $FP_k$ along the $j$th dimension. Thus, we can find out desired trees similarly to Lemma 3.3. It suffices to consider the case $z_j \neq 0$ for $j = 2, \ldots, k-1$.

If $k \geq 3$, then $x, y, w \in V(FP_{k}^{2:0})$, $z \in V(FP_{k}^{2:z_2})$, $z^0 = 00z_3\cdots z_{k-1}z_k \notin \{x, y, w\}$ and $|N(z^0) \cap \{x, y, w\}| \leq 1$ when dividing $FP_k$ along the $2$th dimension. Thus, we can find out desired trees Similarly to case 1.2.1.

Suppose that $k = 2$, there are $x = 01$, $y = 04$, $w = 10$, $z = 0z_2$ and $z_2 \notin \{0, 1, 4\}$. We can find out desired trees similarly to Lemma 3.1 when dividing $FP_k$ along the $2$th dimension.

Case 1.2.2.2. $x, y, w^0$ are in a subgraph of $FP_k$ isomorphic to $C_4$.

In this case, $k \geq 3$. Without loss of generality, assume that $x = 000\cdots01$ and $y = 000\cdots40$. Let $z = 0z_2z_3\ldots z_{k-2}z_{k-1}z_k$. If there exists $j \in \{2, \ldots, k-2\}$ such that $z_j = 0$, then $x, y, z, w \in FP_{k}^{j:0}$ when dividing $FP_k$ along the $j$th dimension. Thus, we can find out desired trees similarly to Lemma 3.3. It suffices to consider the case $z_2, z_3, \dots, z_{k-2} \neq 0$.

If $k \geq 4$, we divide $FP_k$ along the $2$th dimension. Then $x, y, w \in V(FP_{k}^{2:0})$, $z \in V(FP_{k}^{2:z_2})$, $z^0 = 00z_3 \cdots z_{k-1}z_k \notin \{x, y, w\}$ and $|N(z^0) \cap \{x, y, w\}| \leq 1$ except $z^0 = 0041$. Similarly to case 1.2.1, we can find $3k-3$ internally disjoint $S$-trees. When $z^0 = 0041$, $x = 0001$, $y = 0040$, $w = 1000$, assume that $z = 0141$ (for $z = 0z_241$ and $z_2 \neq 0$ is similar). Clearly, $|N(z^0) \cap \{x, y, w\}| = 2$. The desired trees are shown in Figure 12.

Suppose that $k = 3$, we have $x = 001$, $y = 040$, $w = 100$, $z = 0z_2z_3 \notin \{x, y, w^0\}$. If $z_2 \notin \{0, 4\}$, then $x, w \in FP_{3}^{2:0}, y \in FP_{3}^{2:4}$ and $z \in FP_{3}^{2:z_2}$ when dividing $FP_3$ along the $2$th dimension. Thus, we can find out desired trees similarly to Lemma 3.2. If $z_3 \notin \{0, 1\}$, then $x \in FP_{3}^{3:1}, y, w \in FP_{3}^{3:0}$ and $z \in FP_{3}^{3:z_3}$ when dividing $FP_3$ along the $3$th dimension. Thus, we can find out desired trees similarly to Lemma 3.2. Suppose $z_2 \in \{0, 4\}$ and $z_3 \in \{0, 1\}$. Since $z \neq x, y, w$, then $z = 041$. The desired trees are shown in Figure 13.

Case 2. $x, y \in V(FP^{0})$ and $z, w \in V(FP^{1})$.

Notice that $|V(L_2^*)| \geq 3$ and $|V(L_3^*)| \geq 3$. Without loss of generality, let $\bf{4} \in V(L_2^*)$ and $\bf{5} \in V(L_3^*)$. Since $FP^4$ is connected, there exists an $\{x^4, y^4, z^4, w^4\}$-tree $T_{3k-2}'$ in $FP^4$, similarly, there exists an $\{x^5, y^5, z^5, w^5\}$-tree $T_{3k-1}'$ in $FP^5$. By the definition of $FP_k$, there exist four paths $P_{zz^4}$, $P_{ww^4}$, $P_{zz^5}$ and $P_{ww^5}$ such that $P_{zz^4} \cong P_{ww^4} \cong L_2^* \setminus \{\bf{0}\}$ and $P_{zz^5} \cong P_{ww^5} \cong L_3^* \setminus\{\bf{0}\}$. Let $T_{3k-2} = T_{3k-2}'\cup xx^4 \cup yy^4 \cup P_{zz^4}\cup P_{ww^4}$ and $T_{3k-1} = T_{3k-1}'\cup xx^5 \cup yy^5 \cup P_{zz^5} \cup P_{ww^5}$. Then $T_{3k-2}$ and $T_{3k-1}$ are internally disjoint $S$-trees in $FP_k$. Main goal is to find out $3k-3$ internally disjoint $S$-trees in $L_1^*\Box FP_{k-1}$. Let $S'$ be a set of $x, y, z^0$ and $w^0$. Without loss of generality, assume that $d(x, z^0) = \min d(u, v)$ for $u, v \in S'$.

Case 2.1. $|S'| \leq 3$.

In this case, $d(x, z^0) = 0$, that is, $z^0 = x$. Since $FP_{k-1}$ is $(3k-3)$-connected, by Theorem 2.1, there exist $3k-3$ internally disjoint $(x, y)$-paths $P_1, P_2, \ldots, P_{3k-3}$ in $FP^0$ and $3k-3$ internally disjoint $(z, w)$-paths $P_1', P_2', \ldots, P_{3k-3}'$ in $FP^1$. Let $x_i \in N_{P_i}(x)$ and $z_i \in N_{P_i'}(z)$. Then there exists $z_i \in V(P_i')$ such that $z_i$ is a corresponding vertex of $x_j$ in $FP^1$ for $i, j \in [3k-3]$, suppose that $i = j$. Hence, $x_iz_i \in E(FP_k)$. Let $T_i = P_i \cup x_iz_i \cup P_i'$ for $i\in [3k-3]$. Then, $T_1, T_2, \ldots, T_{3k-3}$ are $3k-3$ internally disjoint $S$-trees in $L_1^*\Box FP_{k-1}$. See Figure 14$(a)$.

Case 2.2. $|S'| = 4$.

In this case, $d(x, z^0) \geq 1$. It implies that $d(x, z) \geq 2$. If $d(x, z) = 2$. Without loss of generality, assume that $x = 000\cdots00$. Then $z = 1c_2\cdots c_k$ such that there exist an $i \in \{2, \dots, k\}$ satisfying $d_{\bf{P}(0, c_i)} = 1$ and others $c_i = 0$, say $z = 110\cdots00$. If there exist a dimension $j$ such that $|S \cap FP^{j:i}| \neq 2$ for $j \in [k]$ and $i\in \{0, 1, \dots, 9\}$ when dividing $FP_k$ along the $j$th dimension, then we can find out the desired $S$-trees by the above discussion. Hence, suppose that $|S \cap FP^{j:i}| = 2$ for arbitrary $j$ when dividing $FP_k$ along the $j$th dimension. Thus, $y = 01 b_3\cdots b_k$ and $w = 10 b_3\cdots b_k$, where $b_i \neq 0$ for $i \in \{3, \dots, k\}$.

Let $FP^{ij} = FP_k[{d_1d_2d_3 \cdots d_k \in V(FP_k)} \colon d_1 = i, d_2 = j]$. Then $FP^{ij} \cong FP_{k-2}$. Let $x_1$ be corresponding vertex of $y$ in $FP^{00}$. Then $x_1 \neq x$. Choose $3k-7$ vertices $x_2, \dots, x_{3k-6}$ from $N_{FP^{00}}(x)$, denote $X = \{x_1, \dots, x_{3k-6}\}$. For $i = 1, \dots, 3k-6$, let $z_i$ be corresponding vertices of $x_i$ in $FP^{11}$, denote $Z = \{z_1, \dots, z_{3k-6}\}$. For $i = 2, \dots, 3k-6$, let $y_i$ and $w_i$ be corresponding vertices of $x_i$ in $FP^{01}$ and $FP^{10}$, respectively. Denote $Y = \{y_1, \dots, y_{3k-7}\}$ and $W = \{w_1, \dots, w_{3k-7}\}$, where $y_1$ and $w_1$ are be corresponding vertices of $x$ in $FP^{01}$ and $FP^{10}$, respectively. Since $FP_{k-2}$ is $(3k-6)$-connected, there exist $3k-6$ internally disjoint $(a, A)$-paths $A_1, \dots, A_{3k-6}$ in $FP^{ij}$ for $(a, A, ij) = (x, X, 00), (y, Y, 01), (z, Z, 10), (w, W, 11)$, respectively. Let $T_0 = X_1 \cup x_1y \cup yz_1 \cup Z_1 \cup z_1w$, $T_1 = xy_1 \cup Y_1 \cup y_1z \cup xw_1 \cup W_1$ and $T_i = X_i \cup x_iy_i \cup Y_i \cup Z_i \cup z_iw_i \cup W_i \cup x_iw_i$ for $i = 2, \dots, 3k-6$.

Let $B^0$ be a subgraph induced by $V(FP^0-FP^{00}-FP^{01})$ and $B^1$ be a subgraph induced by $V(FP^1- FP^{10}-FP^{11})$. Then there exist two internally disjoint paths $P_{3k-5}, P_{3k-4}$ to connect $x$ and $y$ in $FP_k[V(B^0) \cup \{x, y\}]$ and two internally disjoint paths $P_{3k-5}', P_{3k-4}'$ to connect $z$ and $w$ in $FP_k[V(B^1) \cup \{z, w\}]$. Let $T_j = P_{j} \cup x_jz_j \cup P_{j}'$ for $j = 3k-5$ and $3k-4$, where $xx_j \in E(P_j)$ and $z_j$ is corresponding vertex of $x_j$ in $P_{i}'$. Then, $T_0, T_1, \ldots, T_{3k-4}$ are $3k-3$ internally disjoint $S$-trees in $L_1^*\Box FP_{k-1}$. See Figure 14$(b)$.

Suppose that $d(x, z) \geq 3$. There are $3k-4$ internally disjoint $S'$-trees $T_1', T_2', \ldots, T_{3k-4}'$ in $FP^0$ because of the induction hypothesis. Notice that $|N_{FP_k}(z^0) \cap N_{FP_k}(w^0)| \leq 2$. Let $T_1'$ be a tree such that $|N_{T_1'}(z^0) \cap N_{T_1'}(w^0)| = 0$. Let $z_1 \in N_{T_1'}(z^0)$ and $w_1 \in N_{T_1'}(w^0)$. Then $z_1 \neq w_1$. Let $T_1 = T_1' \cup \{zz^0, ww^0\}$.

Let $S'' = \{x, y, z, w^0\}$. Since $d_{FP^0}(z^0) = 3k-3$, there are $1\leq d_{T_i'}(z^0) \leq 2$ for $i \in [3k-4]$. Construct $3k-5$ internally disjoint $S''$-trees as follows: $T_i'' = (T_i'\setminus z^0) \cup z_iz_i^1 \cup z_i^1z$ if $N_{T_i'}(z^0) = \{z_i\}$ and $T_i'' = (T_i'\setminus z^0) \cup z_iz_i^1 \cup z_i^1z \cup z_jz_j^1 \cup z_j^1z$ if $N_{T_i'}(z^0) = \{z_i, z_j\}$, where $i = 2, \ldots, 3k-4$. Similarly, construct $3k-5$ internally disjoint $S$-trees as follows: $T_i = (T_i'\setminus w^0) \cup w_iw_i^1 \cup w_i^1w$ if $N_{T_i''}(w^0) = \{w_i\}$ and $T_i = (T_i''\setminus w^0) \cup w_iw_i^1 \cup w_i^1w \cup w_jw_j^1 \cup w_j^1w$ if $N_{T_i''}(w^0) = \{w_i, w_j\}$, where $i = 2, \ldots, 3k-4$.

Let $\mathcal{T} = \bigcup_{i = 1}^{3k-4}T_i$, $W = N_{\mathcal{T}}(z) \cup N_{\mathcal{T}}(w)$ and $T_1''$ be a corresponding tree of $T_1'$ in $FP^1$. Then, $T_1''$ is a tree in $FP^1-W$. Let $T_{3k-3} = T_1'' \cup xx^1 \cup yy^1$. Then, $T_1, T_2, \ldots, T_{3k-3}$ are $3k-3$ internally disjoint $S$-trees in $L_1^*\Box FP_{k-1}$.

Therefore, $T_1, T_2, \ldots, T_{3k-1}$ are $3k-1$ internally disjoint $S$-trees in $FP_{k}$.

Giving an algorithm to find out $3k-1$ internally disjoint $S$-trees in $FP_k$ for any $S \subseteq V(FP_k)$ with $|S| = 4$, it means that $\kappa_{4}(FP_k) \geq 3k-1$.

Now we give the proof of the main result.

Proof of Theorem 1.2. Since $FP_k$ is a $3k$-regular graph, there are $\kappa_{4}(FP_k) \leq 3k-1$ as Lemma 2.1. Next we will show that $\kappa_{4}(FP_k) \geq 3k-1$. Let $S = \{x, y, z, w\}$ be a set of arbitrary four distinct vertices in $FP_k$. It suffices to show that there exist $3k-1$ internally disjoint $S$-trees. The proof of this result by induction on $k$. By Lemma 2.3, the statement holds for $k = 1$. Suppose that the statement holds in $FP_{k-1}$ for $k \geq 2$. Now consider $FP_{k}$. Decompose $FP_{k}$ into 10 disjoint sub-folded Petersen graphs $FP^0, \ldots, FP^9$, each of which is isomorphic to $FP_{k-1}$, by removing all crossed edges. We only need to take into account the following cases because of symmetry.

Case 1. $x, y, z$ and $w$ belong to four distinct sub-folded Petersen graphs.

By Lemma 3.1, the desired $3k-1$ internally disjoint $S$-trees can be obtained in $FP_k$.

Case 2. $x, y, z$ and $w$ belong to three distinct sub-folded Petersen graphs.

By Lemma 3.2, the desired $3k-1$ internally disjoint $S$-trees can be obtained in $FP_k$.

Case 3. $x, y, z$ and $w$ belong to two distinct sub-folded Petersen graphs.

By Lemma 3.4, the desired $3k-1$ internally disjoint $S$-trees can be obtained in $FP_k$.

Case 4. $x, y, z$ and $w$ belong to the same sub-folded Petersen graph.

By Lemma 3.3, the desired $3k-1$ internally disjoint $S$-trees can be obtained in $FP_k$.

Hence, $\kappa_4(FP_k) \geq 3k-1$ and the proof is completed.

Proof of Theorem 1.1. Remember that $FPQ_{n, k}$ can be regarded as replacing every vertex of $Q_n$ by $FP_k$. Take the Figure 15 as an example. Since $FPQ_{n, k}$ is $(n+3k)$-regular, we have $\kappa_4(FPQ_{n, k}) \leq n+3k-1$ by Lemma 2.1. In order to prove $\kappa_4(FPQ_{n, k}) \geq n+3k-1$, it needs to show that there are $n+3k-1$ internally disjoint $S$-trees in $FPQ_{n, k}$ for arbitrary $S \subseteq V(FPQ_{n, k})$ with $|S| = 4$.

If $n = 1$. According to Lemma 3.3 and 3.4, it is not hard to see that there exist $3k-3$ internally disjoint $S$-trees in $K_2 \Box FP_{k-1}$. That is, $\kappa_4(FPQ_{1, k-1}) \geq 3k-3$. Hence, $\kappa_4(FPQ_{1, k}) \geq 3k$.

Suppose that $n \geq 2$. When the vertices of $S$ distribute among one copy of $FP_k$. Similar to Lemma 3.3, the desired $n+3k-1$ internally disjoint $S$-trees can be found in $FPQ_{n, k}$.

When the vertices of $S$ distribute among two copies of $FP_k$. Since $\kappa(Q_n) = n$, there are $n$ internally disjoint paths $L_1^*, L_2^*, \dots, L_{n}^*$ connecting arbitrary two vertices of $Q_n$. Similar to Lemma 3.4, we can find $3k$ $S$-trees in $L_1^* \Box FP_{k}$ and $n-1$ $S$-trees in $(\bigcup_{i = 2}^{n}L_i^*) \Box FP_{k}$ such that these $n+3k-1$ $S$-trees are internally disjoint.

When the vertices of $S$ distribute among three copies of $FP_k$. Since $\kappa_3(Q_n) = n-1$, there are $n-1$ internally disjoint path $T_1^*, T_2^*, \dots, T_{n-1}^*$ connecting arbitrary three vertices of $Q_n$. Similar to Lemma 3.2, we can find $3k+1$ $S$-trees in $T_1^* \Box FP_{k}$ and $n-2$ $S$-trees in $(\bigcup_{i = 2}^{n-1}T_i^*) \Box FP_{k}$ such that these $n+3k-1$ $S$-trees are internally disjoint.

When the vertices of $S$ distribute among four copies of $FP_k$. Since $\kappa_4(Q_n) = n-1$, there are $n-1$ internally disjoint path $H_1^*, H_2^*, \dots, H_{n-1}^*$ connecting arbitrary four vertices of $Q_n$. Similar to Lemma 3.1, we can find $3k+1$ $S$-trees in $H_1^* \Box FP_{k}$ and $n-2$ $S$-trees in $(\bigcup_{i = 2}^{n-1}H_i^*) \Box FP_{k}$ such that these $n+3k-1$ $S$-trees are internally disjoint.

Therefore, $\kappa_4(FPQ_{n, k}) = n+3k-1$.

4.   Conclusions

The generalized $\ell$-connectivity is a natural generalization of the traditional connectivity and can serve for measuring the fault tolerance capability of a network. This paper centers on the generalized 4-connectivity of the folded Petersen cube network $FPQ_{n, k}$ and shows that $\kappa_{4}(FPQ_{n, k}) = n+3k-1$. As a corollary, $\kappa_{3}(FPQ_{n, k}) = n+3k-1$ is obtained easily. Furthermore, the results $\kappa_{4}(Q_{n}) = \kappa_{4}(FPQ_{n, 0}) = n-1$ and $\kappa_4(FP_k) = \kappa_{4}(FPQ_{0, k}) = 3k-1$ can be verified. Sabidussi ^[29] discussed the classical connectivity of Cartesian product graphs, in the next work, we would like to research the generalized $4$-connectivity of Cartesian product graphs.

Besides, fault tolerance or connectivity is mainly to provide a data to measure the reliability of a network, but in practical, when a system failure, it is worth considering how to compensate the impact of the fault and to recover the performance of the system before the failure as far as possible such that the system runs stably and reliably. Motivated by Alhasnawi et al. ^[1,2,3,4], it needs to design fault tolerance control to ensure steady-state operation, enhance network' fault resilience, improve network' robust and efficient operation. In future work, we would like to apply graph theory to solve practical problems.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 11971054, 11731002, 11661068) and the Science Found of Qinghai Province (No. 2021-ZJ-703). The authors would like to express their thanks to the referees for their helpful comments and suggestions which improve the presentation of this paper.

Conflict of interest

The authors declare that they have no competing interests.