1 Introduction

In a West Nile Virus (WNV) infection, there is a substantial self damage component and this is probably due to the way that the virus infects two cell populations differently. This difference, which involves an larger upregulation of MHC-1 sites on the surface of non-dividing infected cells over dividing infected cells, is critical in establishing a self damage or collateral damage response. In ^[1], we develop a macro level model of the nonlinear interactions between two critical signaling agents that mediate the interaction between these two sets of cell populations. In the case of WNV infection, the two signals are the MHC-1 upregulation level of the cell and the free WNV antigen level. This macro model allowed us to predict a hosts health response to varying levels of initial virus dose. Hence, we could begin to understand the oscillations in collateral damage and host health that lead to the survival data we see in WNV infections. In this work, we examine more general immunopathological interactions and develop a self affinity threshold model based on a first principles analysis of the immunosynapse. This model can then be used to gain insight into inappropriate autoimmunity events. In addition, this work serves as the background for two additional investigations: a general cytokine signal model and how this influences the self affinity threshold equation and a discussion of how the immunosynapse network model implied manifold structure allows us to interpret self damage as a topological defect.

---

2 Materials and method

The methods used here are quantitative and based on extensions of the Cubic Ternary Complex Model (CTC) model as discussed in ^[2,3] and ^[4]. The modifications are used to develop a simple model of an immunosynapse and how an autoimmune interaction can occur.

---

2.1 The cubic ternary complex model

The CTC model is quite involved and to use it and also to modify it requires a good understanding of all of its details. Therefore, we will begin with a tutorial on how the CTC model works and afterwords, when we can discuss alterations and extensions, they will make more sense. The general assumptions of the CTC model are:

1. The receptor has two distinct binding sites: an external site accessible to agonists and antagonists and an internal site accessible to G-proteins.

2. External ligands ( agonists and antagonists ) and G-proteins exist in separate phases and do not encounter each other.

3. Receptors exist in two states with respect to their ability to activate G-proteins and initiate biological responses: active and inactive.

4. The interactions of external ligands, G-proteins, and receptor activation states are assumed to be governed by the laws of mass action.

5. All possible two-way and three-way interactions between external ligands, G-proteins, and receptor activation states (subject to assumption two) are potentially significant and are represented by coefficients in the model.

Letting A denote the ligand, G, the G-protein and R the receptor, we have 8 possible receptor species: R_i, R_a, AR_i, AR_a, R_iG, R_aG, AR_iG and AR_aG where the subscripts i and a indicate inactive and active, respectively.

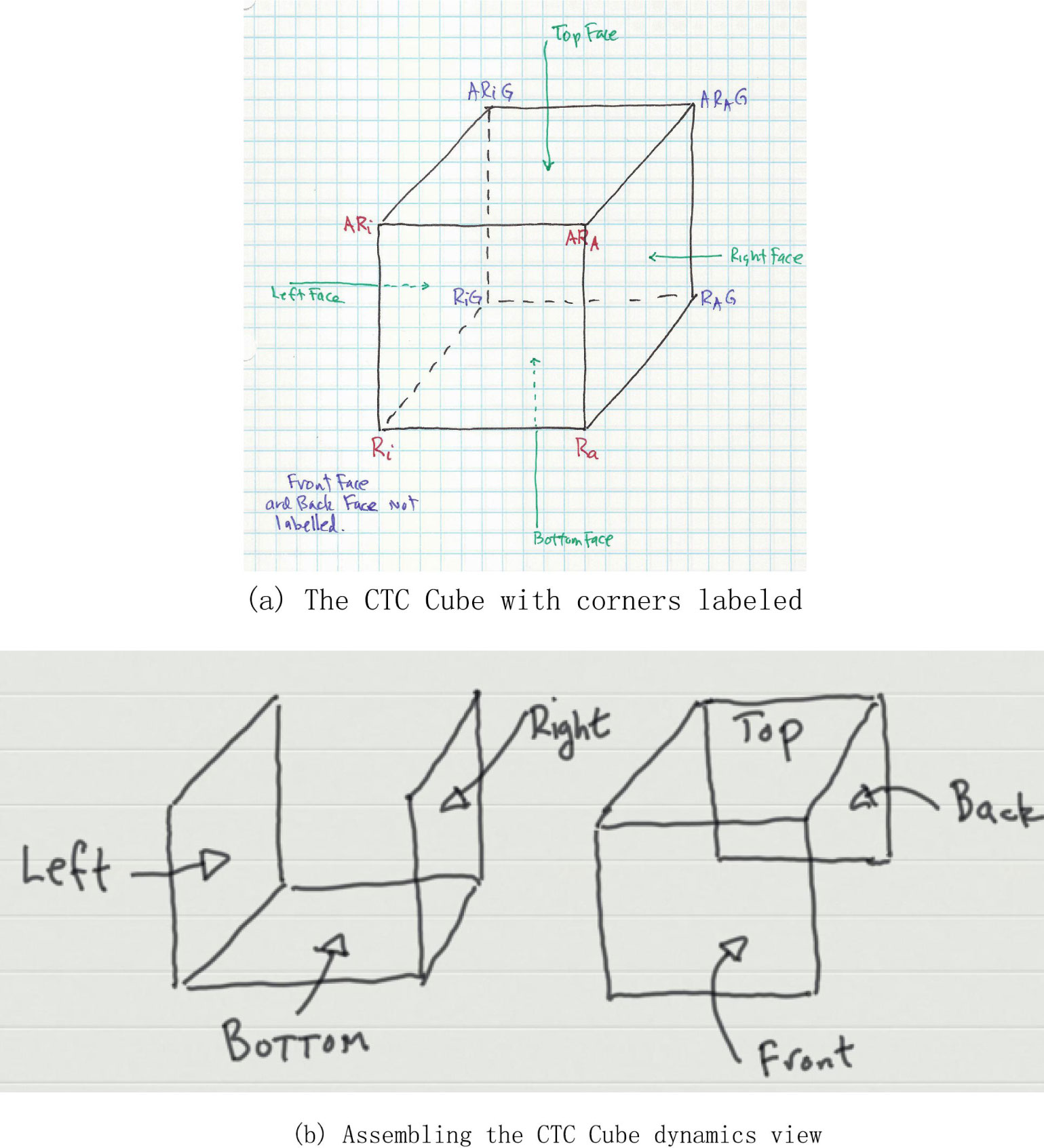
These eight possibilities define six sets of interactions which, in this case can be drawn as a cube. See ^[2] for much better figures! We have shown the faces of this cube in the equations below. It helps to think of a sugar cube. If you hold it in your hand you can touch its six faces. Drawing the cube and labeling all the necessary equations makes for a very cluttered image. But we can draw the cube and label the corners as in

Each face of this cube has four corners which you can read off from Figure 1a but it is easier to see what is going on by drawing the cube in an exploded view and explicitly writing out all the interactions for each face.

---

The six faces with interaction pathways are shown in the equations below.

$\left[\begin{array}{ccc}A{R}_i& \to & A{R}_a\\ \uparrow & & \uparrow \\ R_i& \to & R_a\\ & FrontFace\text{:}GFree& \end{array}\right]\left[\begin{array}{ccc}A{R}_{i}G& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ R_{i}G& \to & R_{A}G\\ & BackFace:GInvolved& \end{array}\right]$

$\left[\begin{array}{ccc}{R}_{i}G& \to & R_{a}G\\ \uparrow & & \uparrow \\ R_i& \to & R_a\\ & BottomFace:AFree& \end{array}\right]\left[\begin{array}{ccc}A{R}_{i}G& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ A{R}_i& \to & A{R}_a\\ & TopFace:AInvolved& \end{array}\right]$

$\left[\begin{array}{ccc}A{R}_i& \to & A{R}_{i}G\\ \uparrow & & \uparrow \\ R_i& \to & R_{i}G\\ & LeftFace:R_{i}Involved& \end{array}\right]\left[\begin{array}{ccc}A{R}_a& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ R_a& \to & R_{a}G\\ & RightFace:R_{a}Involved& \end{array}\right]$

Note these faces then define 12 interaction edges:

$\begin{array}{l}{R}_i\leftrightarrow R_a\mathrm{,}{R}_i\leftrightarrow A{R}_i\mathrm{,}\text{\ }{R}_a\leftrightarrow A{R}_a\mathrm{,}\text{\ }A{R}_i\leftrightarrow A{R}_a\\ R_a\leftrightarrow R_{a}G\mathrm{,}\text{\ }{R}_i\leftrightarrow R_{i}G\mathrm{,}\text{\ }A{R}_i\leftrightarrow A{R}_{i}G\mathrm{,}\text{\ }A{R}_a\leftrightarrow A{R}_{a}G\\ R_{A}G\leftrightarrow A{R}_{a}G\mathrm{,}\text{\ }{R}_{i}G\leftrightarrow A{R}_{i}G\mathrm{,}\text{\ }{R}_{i}G\leftrightarrow R_{a}G\mathrm{,}\text{\ }A{R}_{i}G\leftrightarrow A{R}_{a}G\end{array}$

where the double edged arrows indicate these reactions are reversible. An easy way to see this as a cube is to write all the equations as follows. We place the Back, Top and Front face above the Left, Bottom and Right faces for convenience of exposition.

$\begin{array}{ccc}\left[\begin{array}{ccc}A{R}_{i}G& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ R_{i}G& \to & R_{a}G\\ & Back& \end{array}\right]& \left[\begin{array}{ccc}A{R}_{i}G& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ A{R}_i& \to & A{R}_a\\ & Top& \end{array}\right]& \left[\begin{array}{ccc}A{R}_i& \to & A{R}_a\\ \uparrow & & \uparrow \\ R_i& \to & R_a\\ & Front& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}A{R}_i& \to & A{R}_{i}G\\ \uparrow & & \uparrow \\ R_i& \to & R_{i}G\\ & Left& \end{array}\right]& \left[\begin{array}{ccc}{R}_{i}G& \to & R_{a}G\\ \uparrow & & \uparrow \\ R_i& \to & R_a\\ & Bottom& \end{array}\right]& \left[\begin{array}{ccc}A{R}_a& \to & A{R}_{a}G\\ \uparrow & & \uparrow \\ R_a& \to & R_{a}G\\ & Right& \end{array}\right]\end{array}$

You can see this visually by taking the information in the columns above and assembling a cube as shown in Figure 1b. We want to make this notation more compact. The faces can be organized using mnemonics.

•   The right face is R_a, A, G interactions.

•   The left face is R_i, A, G interactions.

•   The back face is R_i, R_a, A, G interactions, i.e. interactions with the G-protein.

•   The front face is R_i, R_a, A interactions; i.e. no G-protein present

•   The bottom face is R_i, R_a, G interactions; i.e. no ligand present

•   The top face is R_i, R_a, A, G interactions; i.e. ligand is present

Let's organize this in column form with four systems: the R, A, G, the R, A, H, the R, B, G and the R, B, H for two G-proteins, G and H and two ligands A and B. Here we let Front = F, Back = Bk, Left = L, Right = R, Top = T and Bottom = Bo.

$\left[\begin{array}{cc}\text{R}& R_a,B,H\\ \text{L}& R_i,B,H\\ \text{Bk}& R_i,R_a,B,H\\ \text{F}& R_i,R_a,B\\ \text{Bo}& R_i,R_a,H\\ \text{T}& R_i,R_a,B,H\\ & B,H\end{array}\right]\begin{array}{c}\mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\\ \leftrightarrow \\ \mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\end{array}\left[\begin{array}{cc}\text{R}& R_a,B,G\\ \text{L}& R_i,B,G\\ \text{Bk}& R_i,R_a,B,G\\ \text{F}& R_i,R_a,B\\ \text{Bo}& R_i,R_a,G\\ \text{T}& R_i,R_a,B,G\\ & B,G\end{array}\right]\begin{array}{c}\mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\\ \leftrightarrow \\ \mathrm{.}\\ \mathrm{.}\end{array}\left[\begin{array}{cc}\text{R}& R_a,A,G\\ \text{L}& R_i,A,G\\ \text{Bk}& R_i,R_a,A,G\\ \text{F}& R_i,R_a,A\\ \text{Bo}& R_i,R_a,G\\ \text{T}& R_i,R_a,A,G\\ & A,G\end{array}\right]\begin{array}{c}\mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\\ \leftrightarrow \\ \mathrm{.}\\ \mathrm{.}\\ \mathrm{.}\end{array}\left[\begin{array}{cc}\text{R}& R_a,A,H\\ \text{L}& R_i,A,H\\ \text{Bk}& R_i,R_a,A,H\\ \text{F}& R_i,R_a,A\\ \text{Bo}& R_i,R_a,H\\ \text{T}& R_i,R_a,A,H\\ & A,H\end{array}\right]$

Connections between these subsystems are made with the ↔ markers. The R, B, H system connects to the R, B, G along the face with no G-protein interaction, the R, B, G then connects to the R, A, G system on the face with no ligand interaction and the R, A, G system interacts with the R, A, H system on the face with no G-protein interaction.

Activation is approached this way. Each face of these interaction cubes can be thought of as providing two paths to a given goal state. We assume thermodynamic closure so that the reaction rate constants for the reactions on the cube face are compatible. Here, K_act is association constant for the conversion of the inactive receptor R_i to the active form R_a; K_G is the constant for the conversion of the inactivated form R_i to R_iG and thermodynamic closure refers to the fact that the corresponding constant for the conversion of the activated form R_a to R_aG corresponds to a scaling by β. Similarly, the conversion of the inactivated receptor R_i to the activated receptor R_a is scaled by α when ligand is present. The ligand pathway for A is also shown below and the comments about association constants are similar. Hence, the discussed pathways are as follows:

$\left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\leftrightarrow }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\leftrightarrow }& R_a\end{array}\right]\text{\ }\left[\begin{array}{ccc}A{R}_i& \stackrel{\alpha K_{act}}{\leftrightarrow }& A{R}_a\\ \uparrow K_A& & \uparrow \alpha K_A\\ R_i& \stackrel{K_{act}}{\leftrightarrow }& R_a\end{array}\right]$

For the inactive pathway γ denotes how the ligand A binding alters the equilibrium constant for the R_i to R_iG pathway. We once again use thermodynamic closure to close the top pathway.

$\left[\begin{array}{ccc}{R}_{i}G& \stackrel{\gamma K_A}{\leftrightarrow }& A{R}_{i}G\\ \uparrow K_G& & \uparrow \gamma K_G\\ R_i& \stackrel{K_A}{\leftrightarrow }& A{R}_i\end{array}\right]$

How do we interpret γ? It measures how ligand binding effects the R_iG to AR_iG pathway-i.e. how ligand binding effects the G-protein coupling and also it measures how the addition of the G-protein effects the other pathway, AR_i to AR_iG. Now, at this point, the association constants that connect the three remaining pathways to AR_aG have not been specified. The left, front and bottom faces of the interaction cube have been totally specified, but the right, the top and the back each have two edges free. We have

$\begin{array}{ccc}\left[\begin{array}{ccc}A{R}_{i}G& \stackrel{?}{\to }& A{R}_{a}G\\ \uparrow \gamma K_A& & \uparrow ?\\ R_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ & \text{Back}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_{i}G& \stackrel{?}{\to }& A{R}_{a}G\\ \uparrow \gamma K_G& & \uparrow ?\\ A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ & \text{Top}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ \uparrow K_A& & \uparrow \alpha K_A\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Front}& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}A{R}_i& \stackrel{\gamma K_A}{\to }& A{R}_{i}G\\ \uparrow K_G& & \uparrow \gamma K_G\\ R_i& \stackrel{K_A}{\to }& R_{i}G\\ & \text{Left}& \end{array}\right]& \left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Bottom}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_a& \stackrel{?}{\to }& A{R}_{a}G\\ \uparrow \alpha K_A& & \uparrow ?\\ R_a& \stackrel{\beta K_G}{\to }& R_{a}G\\ & \text{Right}& \end{array}\right]\end{array}$

On the back, right and top face, there are two edges each unspecified. Note thermodynamic closure tells us that if we fix one edge on one of these faces, closure will fill in other edges. For example, specifying the R_aG to AR_aG path will fill in the rest of the right face and the rest of the back face. That will fill in the AR_iG to AR_aG path in the top face too and then closure fills in the rest of the top face. So specifying one edge, fills in the full cube of interactions. Hence, there are just the three free edges R_aG to AR_aG, AR_a to AR_aG and AR_iG to AR_aG; these are the three edges that lead to AR_aG. For example, if we set R_aG ↔ AR_aG to have constant αγK_A, by closure we fill in all pathways to find

$\begin{array}{ccc}\left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_A& & \uparrow \alpha \gamma K_A\\ R_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ & \text{Back}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_G& & \uparrow \gamma \beta K_G\\ A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ & \text{Top}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ \uparrow K_A& & \uparrow \alpha K_A\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Front}& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}A{R}_i& \stackrel{\gamma K_A}{\to }& A{R}_{i}G\\ \uparrow K_G& & \uparrow \gamma K_G\\ R_i& \stackrel{K_A}{\to }& R_{i}G\\ & \text{Left}& \end{array}\right]& \left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Bottom}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_a& \stackrel{\gamma \beta K_G}{\to }& A{R}_{a}G\\ \uparrow \alpha K_A& & \uparrow \alpha \gamma K_A\\ R_a& \stackrel{\beta K_G}{\to }& R_{a}G\\ & \text{Right}& \end{array}\right]\end{array}$

This gives the pathways

$\left[\begin{array}{ccc}& & R_{a}G\\ & & 0.6in\uparrow \text{\ }\alpha \gamma K_A\\ A{R}_{i}G& \stackrel{\alpha \beta K_{act}}{\to }& A{R}_{a}G\\ & & 0.6in\uparrow \text{\ }\beta \gamma K_G\\ & & A{R}_a\end{array}\right]$

To make things as general as possible, add an additional reaction parameter δ to these pathways:

$\left[\begin{array}{ccc}& & R_{a}G\\ & & 0.6in\uparrow \text{\ }\delta \alpha \gamma K_A\\ A{R}_{i}G& \stackrel{\delta \alpha \beta K_{act}}{\to }& A{R}_{a}G\\ & & 0.6in\uparrow \text{\ }\delta \beta \gamma K_G\\ & & A{R}_a\end{array}\right]$

Normally, the reactions R_a + G ↔ R_aG (constant βK_G) and AR_a + G ↔ AR_aG (constant γβK_G) differ by a factor γ. If the addition of the ligand enhances the G-protein coupling, then we can model that by changing the factor to δγ where δ > 1. If the G-protein coupling is diminished by the ligand, we can use δ < 1 to indicate that. Finally, if δ = 1, there is no advantage or disadvantage to the G - protein coupling due to using the ligand. This moves us to the following diagram

$\begin{array}{ccc}\left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\delta \alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_A& & \uparrow \delta \alpha \gamma K_A\\ R_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ & \text{Back}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\delta \alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_G& & \uparrow \gamma \delta \beta K_G\\ A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ & \text{Top}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ \uparrow K_A& & \uparrow \alpha K_A\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Front}& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}A{R}_i& \stackrel{\gamma K_A}{\to }& A{R}_{i}G\\ \uparrow K_G& & \uparrow \gamma K_G\\ R_i& \stackrel{K_A}{\to }& R_{i}G\\ & \text{Left}& \end{array}\right]& \left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Bottom}& \end{array}\right]& \left[\begin{array}{ccc}A{R}_a& \stackrel{\delta \gamma \beta K_G}{\to }& A{R}_{a}G\\ \uparrow \alpha K_A& & \uparrow \delta \alpha \gamma K_A\\ R_a& \stackrel{\beta K_G}{\to }& R_{a}G\\ & \text{Right}& \end{array}\right]\end{array}$

and in it, we can see how the factor δ shapes the interactions.

---

2.2 CTC affinity and efficacy

Now let's look at how to model affinity in these sorts of interactions.

We say the unbound receptor cloud here is the ensemble consisting of the four members R_i, R_a, R_iG and R_aG. There is then the ligand bound receptor cloud having members AR_i, AR_a, AR_iG and AR_aG. Thus, in the cubic ternary complex model, there are four ligand bound types in the ligand cloud. The total concentration of bound species is then R_B

$\left[R_B\right]=\left[A{R}_i\right]+\left[A{R}_a\right]+\left[A{R}_{i}G\right]+\left[A{R}_{i}G\right]\mathrm{.}$

The total concentration of unbound ligand is then denoted by R_U and we know the total amount of ligand R_T satisfies R_T = R_B + R_U. Let K_LA be the association constant for the reaction

$A+R_U\stackrel{K_{LA}}{\to }{R}_B\mathrm{.}$

In other words, K_LA is the equilibrium association constant for the overall conversion of unbound species into bound species. Standard equilibrium kinetics then says KLA=[RB][RU][A] which implies [R_B] = K_LA [A][R_U]. Now, consider the following interaction between the clouds: the arrow represents an intralayer interaction whereas on the right and left, we see interlayer relationships. The right side represents the ligand cloud with bound concentration R_B and the left side is the unbound receptor cloud with unbound concentration [R_U]. The transformation law between the clouds is then the equation K_LA [A] [R_U]. We show this diagrammatically as

$\left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{Receptors}\left[R_U\right]& \end{array}\right]\stackrel{K_{LA}\times \left[A\right]\times \left[R_U\right]=\left[R_B\right]}{\Rightarrow }\left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\delta \alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_G& & \uparrow \delta \gamma \beta K_G\\ A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ & \text{Ligands}\left[R_B\right]& \end{array}\right]$

There are four separate association constants here: K_A, αK_A, γK_A and δαγK_A. In ^[3], we find

$K_{LA}=w_1{K}_A+w_2\left(\alpha K_A\right)+w_3\left(\gamma K_A\right)+w_4\left(\delta \alpha \gamma K_A\right)$

where w₁, w₂, w₃ and w₄ are the relative frequencies of the various receptor species. Thus,

$\begin{array}{l}{w}_1=\frac{\left[R_i\right]}{\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]}\mathrm{,}\text{\ }{w}_2=\frac{\left[R_a\right]}{\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]}\\ w_3=\frac{\left[R_{i}G\right]}{\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]}\mathrm{,}\text{\ }{w}_4=\frac{\left[R_{a}G\right]}{\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]}\end{array}$

Using these weights, we find

$K_{LA}=\frac{K_A\left(\left[R_i\right]+\alpha \left[R_a\right]+\gamma \left[R_{i}G\right]+\delta \alpha \gamma \left[R_{a}G\right]\right)}{\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]}$

But R_a = K_actR_i, R_iG = K_GR_iG, R_aG = βK_GK_actR_iG and so after rearranging we have

$\begin{array}{l}{K}_{LA}=\frac{K_A\left[R_i\right]\left(1+\alpha K_{act}+\gamma K_G\left[G\right]+\delta \alpha \beta \gamma K_G{K}_{act}\left[R_i\right]\left[G\right]\right)}{\left[R_i\right]\left(1+K_{act}+K_G\left[G\right]+K_G{K}_{act}\left[G\right]\right)}\\ =K_A\frac{1+\alpha K_{act}+\gamma K_G\left[G\right]+\delta \alpha \beta \gamma K_G{K}_{act}\left[G\right]}{1+K_{act}+K_G\left[G\right]+\beta K_G{K}_{act}\left[G\right]}\end{array}$

We call K_LA the apparent affinity to distinguish it from the association constant K_A which governs the addition of ligand from the receptor cloud. Note if there is no G-protein, we have KLA≈KA1+αKact1+Kact which can be rewritten as a weighted sum of K_A and αK_A: KLA≈11+αKactKA+Kact1+Kact(αKA). Note the apparent affinity increases over K_A if α > 1 and decreases in α < 1. If the dominant terms involve the G-protein, the approximations become

$\begin{array}{l}{K}_{LA}=\frac{K_A\left[R_i\right]\left(1+\alpha K_{act}+\gamma K_G\left[G\right]+\delta \alpha \beta \gamma K_G{K}_{act}\left[R_i\right]\left[G\right]\right)}{\left[R_i\right]\left(1+K_{act}+K_G\left[G\right]+K_G{K}_{act}\left[G\right]\right)}\\ =K_A\frac{1+\alpha K_{act}+\gamma K_G\left[G\right]+\delta \alpha \beta \gamma K_G{K}_{act}\left[G\right]}{1+K_{act}+K_G\left[G\right]+\beta K_G{K}_{act}\left[G\right]}\end{array}$

Note the apparent affinity now is a weighted sum of the constants for the R_iG → AR_iG and R_aG → AR_aG pathways in the ligand cloud. However, it is important to note that the weights themselves depend only on receptor cloud constants.

Eventually, we want to define avidity in an immunological setting, but let's start with a notion of efficacy. We will follow the exposition in ^[4] with some modifications. In general, a compound that binds to a receptor and after being bound induces a physiological response is called an agonist. The ability of a ligand to bind to a receptor is quantified by its apparent affinity which we have just discussed. The efficacy of the ligand is the measure of how effective it is at eliciting a physiological response. We know there are antagonists which bind to receptors but generate no physiological response and so we suspect that affinity and efficacy are independent parameters. Of course, the agent must be able to bind the receptor in order to talk about efficacy, but as long as the affinity is not zero, the affinity and efficacy of a ligand - receptor pair is not correlated.

Before the ligand A is introduced to the CTC model system, there is only one active species present; R_aG. Following ^[4], we denote its concentration by [r_ag]. After the ligand is introduced, there are two active species, AR_aG and R_aG. The generation of active species can be thought of as a stimulus, S and so efficacy should be somehow related to the net stimulus ΔS = [AR_aG] + [R_aG] - [r_ag]. This means we call a ligand efficacious only if it changes the production of active species beyond what is observed in the absence of ligand. This kind of efficacy is called internal efficacy because it arises from the internal connections of the model. There is an additional source of efficacy we call external efficacy which comes from external connections. A useful diagram for this is as follows:

$\begin{array}{l}\left[\begin{array}{ccc}{R}_{i}G& \stackrel{\beta K_{act}}{\to }& R_{a}G\\ \uparrow K_G& & \uparrow \beta K_G\\ R_i& \stackrel{K_{act}}{\to }& R_a\\ & \text{ReceptorCloud}& \end{array}\right]\stackrel{K_{LA}}{\Rightarrow }\\ \left[\begin{array}{ccc}A{R}_{i}G& \stackrel{\delta \alpha \beta K_{act}}{\to }& A{R}_{a}G\\ \uparrow \gamma K_G& \text{InternalEfficacy}& \uparrow \delta \gamma \beta K_G\\ A{R}_i& \stackrel{\alpha K_{act}}{\to }& A{R}_a\\ & \text{LigandCloud}& \end{array}\right]\stackrel{\text{ExternalEfficacy}}{\Rightarrow }\end{array}$

We can derive an expression for internal efficacy in the CTC model. Recall an efficacious response for a ligand requires

$\frac{\left[A{R}_{a}G\right]+\left[R_{a}G\right]}{\text{TotalReceptorPostLigand}}-\frac{\left[r_{a}g\right]}{\text{TotalReceptorPriorLigand}}>0$

The total receptor concentration before the ligand is introduced is

$\begin{array}{l}{R}_T^{before}=\left[r_i\right]+\left[r_a\right]+\left[r_{i}g\right]+\left[r_{a}g\right]=\left[r_i\right]+K_{act}\left[r_i\right]+K_G\left[g\right]\left[r_i\right]+K_{act}\beta K_G\left[g\right]\left[r_i\right]\\ =\left[r_i\right]\left(1+K_{act}+K_G\left[g\right]+K_{act}\beta K_G\left[g\right]\right)=\left[r_i\right]a\end{array}$

where a is the long term in the parenthesis. After the ligand is introduced, we have

$\begin{array}{l}{R}_T^{after}=\left[R_i\right]+\left[R_a\right]+\left[R_{i}G\right]+\left[R_{a}G\right]\left[A{R}_i\right]+\left[A{R}_a\right]+\left[A{R}_{i}G\right]+\left[A{R}_{a}G\right]\\ =\left[R_i\right]+K_{act}\left[R_i\right]+K_G\left[G\right]\left[R_i\right]+K_{act}\beta K_G\left[G\right]\left[R_i\right]+\\ K_A\left[A\right]\left[R_i\right]+\alpha K_A\left[A\right]K_{act}\left[R_i\right]\gamma K_A\left[A\right]K_G\left[G\right]\left[R_i\right]+\alpha \gamma \delta K_A\left[A\right]K_{act}\beta K_G\left[G\right]\left[R_i\right]\\ =\left[R_i\right]\left(1+K_{act}+K_G\left[G\right]+K_{act}\beta K_G\left[G\right]+\right)\\ \left[R_i\right]\left(K_A\left[A\right]+\alpha K_A\left[A\right]K_{act}+\gamma K_A\left[A\right]K_G\left[G\right]+\alpha \gamma \delta K_A\left[A\right]K_{act}\beta K_G\left[G\right]\right)\\ =\left[R_i\right]\left(a^{*}+b\right)\end{array}$

where a* = 1 + K_act + K_G[G] + K_actβK_G[G] and b is the other term. Next, we note

$\begin{array}{l}\left[A{R}_{a}G\right]+\left[R_{a}G\right]=\alpha \gamma \delta K_{act}\beta \left[G\right]K_A\left[A\right]\left[R_i\right]+K_{act}\beta K_G\left[G\right]\left[R_i\right]\\ =K_{act}\beta K_G\left[G\right]\left[R_i\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)\end{array}$

and [r_ag] = K_actβK_G[g][r_i]. Thus,

$\begin{array}{l}\Delta S=\frac{K_{act}\beta K_G\left[G\right]\left[R_i\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)}{R_T^{after}}-\frac{K_{act}\beta K_G\left[g\right]\left[r_i\right]}{R_T^{before}}\\ =\frac{K_{act}\beta K_G\left[G\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)}{a^{*}+b}-\frac{K_{act}\beta K_G\left[g\right]}{a}\\ =\beta K_{act}{K}_G\left(\frac{\left[G\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)}{a^{*}+b}-\frac{\left[g\right]}{a}\right)=\beta K_{act}{K}_G\frac{\left[G\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)a-\left[g\right]\left(a^{*}+b\right)}{\left(a^{*}+b\right)a}\end{array}$

We want to find out when the efficacy is positive, so we only need look at the numerator of this large fraction. Plugging in for a*, a and b, and letting the numerator be N, we find

$\begin{array}{l}N=\left[G\right]\left(\alpha \gamma \delta K_A\left[A\right]+1\right)\left(1+K_{act}+K_G\left[g\right]+K_{act}\beta K_G\left[g\right]\right)\\ -\left[g\right]\left(1+K_{act}+K_G\left[G\right]+K_{act}\beta K_G\left[G\right]\right)\\ -\left[g\right]\left(K_A\left[A\right]+\alpha K_A\left[A\right]K_{act}+\gamma K_A\left[A\right]K_G\left[G\right]+\alpha \gamma \delta K_A\left[A\right]K_{act}\beta K_G\left[G\right]\right)\end{array}$

We can make a lot more sense out of this equation by starting to use vectors and dot products. We can rewrite N as

$\begin{array}{l}N=\left(\alpha \gamma \delta K_A\left[A\right]+1\right)\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[G\right]\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ \beta K_{act}{K}_G\left[g\right]\end{array}\right]-\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[g\right]\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[G\right]\\ \beta K_{act}{K}_G\left[G\right]\end{array}\right]\\ -\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[A\right]K_A\left[g\right]\left[\begin{array}{c}1\\ \alpha K_{act}\\ \gamma K_G\left[G\right]\\ \alpha \gamma \beta \delta K_{act}{K}_G\left[G\right]\end{array}\right]\end{array}$

Let

$\begin{array}{l}{Z}_g={\left[\begin{array}{cccc}\mathrm{1,}& K_{act}\mathrm{,}& K_G\left[g\right]\mathrm{,}& \beta K_{act}{K}_G\left[g\right]\end{array}\right]}^{\text{'}}\mathrm{,}\text{\ }{Z}_G={\left[\begin{array}{cccc}\mathrm{1,}& K_{act}\mathrm{,}& K_G\left[G\right]\mathrm{,}& \beta K_{act}{K}_G\left[G\right]\end{array}\right]}^{\text{'}}\\ X={\left[\begin{array}{cccc}\mathrm{1,}& \alpha \mathrm{,}& \gamma \mathrm{,}& \alpha \gamma \delta \end{array}\right]}^{\text{'}}\end{array}$

and then letting I be <1,1,1,1>', we can rewrite N as

$\begin{array}{l}N=\left(\alpha \gamma \delta K_A\left[A\right]+1\right)\left[G\right]\langle I\mathrm{,}{Z}_g\rangle -\left[g\right]\langle I\mathrm{,}{Z}_G\rangle -K_A\left[A\right]\left[g\right]\langle X\mathrm{,}{Z}_G\rangle \\ =\left(\alpha \gamma \delta K_A\left[A\right]\right)\left[G\right]\langle I\mathrm{,}{Z}_g\rangle +\left[G\right]\langle I\mathrm{,}{Z}_g\rangle -\left[g\right]\langle I\mathrm{,}{Z}_G\rangle -K_A\left[A\right]\left[g\right]\langle X\mathrm{,}{Z}_G\rangle \end{array}$

This simplifies to

$\begin{array}{l}N=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[\begin{array}{c}\left[G\right]-\left[g\right]\\ K_{act}\left(\left[G\right]-\left[g\right]\right)\\ 0\\ 0\end{array}\right]+K_A\left[A\right]\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[\begin{array}{c}\alpha \gamma \delta \left[G\right]-\left[g\right]\\ \alpha \gamma \delta K_{act}\left[G\right]-\alpha K_{act}\left[g\right]\\ \alpha \gamma \delta K_G\left[g\right]\left[G\right]-\gamma K_G\left[g\right]\left[G\right]\\ \alpha \beta \gamma \delta K_{act}{K}_G\left[g\right]\left[G\right]-\alpha \beta \gamma \delta K_{act}{K}_G\left[g\right]\left[G\right]\end{array}\right]\\ =\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[\begin{array}{c}\left[G\right]-\left[g\right]\\ K_{act}\left(\left[G\right]-\left[g\right]\right)\\ 0\\ 0\end{array}\right]+K_A\left[A\right]\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[\begin{array}{c}\alpha \gamma \delta \left[G\right]-\left[g\right]\\ \alpha \gamma \delta K_{act}\left[G\right]-\alpha K_{act}\left[g\right]\\ \alpha \gamma \delta K_G\left[g\right]\left[G\right]-\gamma K_G\left[g\right]\left[G\right]\\ 0\end{array}\right]\\ =\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[\begin{array}{c}\left[G\right]-\left[g\right]\\ K_{act}\left(\left[G\right]-\left[g\right]\right)\\ 0\\ 0\end{array}\right]+K_A\left[A\right]\left(\alpha \gamma \delta \left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\left[G\right]\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ 0\end{array}\right]-\left[\begin{array}{c}1\\ \alpha \\ \gamma \\ 0\end{array}\right]·\left[g\right]\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[G\right]\\ 0\end{array}\right]\right)\end{array}$

Now define the vectors ΔG, U and V as

$\Delta G={\left[\begin{array}{cccc}\left[G\right]-\left[g\right]& K_{act}\left(\left[G\right]-\left[g\right]\right)\mathrm{,}& \mathrm{0,}& \mathrm{0,}\end{array}\right]}^{\text{'}}\mathrm{,}\text{\ }U=\alpha \gamma \delta {\left[\begin{array}{cccc}\mathrm{1,}& \mathrm{1,}& \mathrm{1,}& 0\end{array}\right]}^{\text{'}}\mathrm{,}\text{\ }V={\left[\begin{array}{cccc}\mathrm{1,}& \alpha \mathrm{,}& \gamma \mathrm{,}& 0\end{array}\right]}^{\text{'}}$

Then, N has the form

$N=\langle I\mathrm{,}\Delta G\rangle +K_A\left[A\right]\left(\left[G\right]\langle U\mathrm{,}{Z}_g\rangle -\left[g\right]\langle V\mathrm{,}{Z}_G\rangle \right)$

In ^[4], to simplify the analysis, it is assumed [G] = [g]. In that case, Z_g = Z_G and we have ΔG = 0 giving N = K_A[A][G] < U - V, Z_G >. The equation we derive is a slight extension of the one in ^[4] as we want to apply this more general form to our discussion of the immunosynapse. Since we want N > 0, we can take the more general equation and break it apart some. Look at the top two components of each vector dot product and the bottom two components separately and assume [G] = ξ[g]. Then, we have

$\begin{array}{l}N=\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\left[g\right]\left(\xi \left[\begin{array}{c}\alpha \gamma \delta \\ \alpha \gamma \delta \end{array}\right]-\left[\begin{array}{c}1\\ \alpha \end{array}\right]\right)·\left[\begin{array}{c}1\\ K_{act}\end{array}\right]\\ +K_A\left[A\right]\left[g\right]\left(\xi \left[\begin{array}{c}\alpha \gamma \delta \\ \alpha \beta \delta \end{array}\right]·\left[\begin{array}{c}{K}_G\left[g\right]\\ 0\end{array}\right]-\left[\begin{array}{c}\gamma \\ 0\end{array}\right]·\left[\begin{array}{c}\xi K_G\left[g\right]\\ 0\end{array}\right]\right)\end{array}$

Thus, we have

$\begin{array}{l}N=\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\left[g\right]\left(\left(\xi \alpha \gamma \delta -1\right)+\alpha K_{act}\left(\xi \gamma \delta -1\right)\right)\\ +K_G\left[A\right]{\left[g\right]}^2\gamma K_A\xi \left(\alpha \delta -1\right)\end{array}$

Note if ξ = 1, we want (cancelling out the common [g]),

$N=K_A\left[A\right]\left(\left(\alpha \gamma \delta -1\right)+\alpha K_{act}\left(\gamma \delta -1\right)\right)+K_G\left[A\right]\left[g\right]\gamma K_A\left(\alpha \delta -1\right)>0.$

We can write this in dot product form as N = K_A[A][αγδ - 1, αγδ - α, αγδ - γ, 0]' · [1, K_act, K_G[g], 0]' which is the form used in ^[4]. We can put our modified equation into this form as well. Again, we let [G] = ξ[g]. Then, we have

$\begin{array}{l}N=\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\left[g\right]\langle \left[\begin{array}{c}\xi \alpha \gamma \delta \\ \xi \alpha \gamma \delta \\ \xi \alpha \gamma \delta \\ 0\end{array}\right]\mathrm{,}\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ 0\end{array}\right]\rangle -K_A\left[A\right]\left[g\right]\langle \left[\begin{array}{c}1\\ \alpha \\ \xi \gamma \\ 0\end{array}\right]\mathrm{,}\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ 0\end{array}\right]\rangle \\ =\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\xi \left[g\right]\left(\langle \left[\begin{array}{c}\alpha \gamma \delta \\ \alpha \gamma \delta \\ \alpha \gamma \delta \\ 0\end{array}\right]\mathrm{,}\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ 0\end{array}\right]\rangle -\langle \left[\begin{array}{c}{\xi }^{-1}\\ {\xi }^{-1}\alpha \\ \gamma \\ 0\end{array}\right]\mathrm{,}\left[\begin{array}{c}1\\ K_{act}\\ K_G\left[g\right]\\ 0\end{array}\right]\rangle \right)\end{array}$

If we let U = αγδ[1,1,1,0]' (as defined before), W_G and W_g as W_G = [1, K_act, K_G[G], 0]' and W_g = [1, K_act, K_G[g], 0]', the new vector V_ξ = [ξ⁻¹, ξ⁻¹α, γ, 0]', we can rewrite this as

$N=\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\xi \left[g\right]\langle U-V_{\xi }\mathrm{,}{W}_g\rangle$

---

2.3 An immunosynapse model

We now use the cubic ternary complex model to model the immunosynapse which forms when a T Cell binds to a peptide and MHC-I complex, pMHCI. We define the vector U - V_ξ to be the internal efficacy vector, e_I. This is based on the components that determine interactions in the ligand cloud. Then, we define W_g to be the receptor cloud vector which is based on the interactions that determine the relationships between the receptor species. Then, the dot product < U - V_ξ, W_g > is called the realized efficacy value, e_R. Note, the Cauchy - Schwartz inequality tells us that

$e_R=\langle U-V_{\xi }\mathrm{,}{W}_g\rangle =\Vert U-V_{\xi }\Vert \Vert W_g\Vert cos\left(\phi \right)$

where φ is the angle between ligand space and receptor space. The external efficacy is then e_E given by

$\begin{array}{l}{e}_E=\text{G-ProteinChange}+\text{ExternalScalingFactor}\times \text{RealizedEfficacy}\\ =\left(\xi -1\right)\left(1+K_{act}\right)\left[g\right]+K_A\left[A\right]\xi \left[g\right]\Vert U-V_{\xi }\Vert \Vert W_g\Vert cos\left(\phi \right)\end{array}$

Note the concentration [g] can be factored out to give

$e_E=\left[g\right]\left(\left(\xi -1\right)\left(1+K_{act}\right)+K_A\left[A\right]\xi \Vert U-V_{\xi }\Vert \Vert W_g\Vert cos\left(\phi \right)\right)$

Since [g] is a scaling factor, the algebraic sign of the change in stimulus is determined by the sign of the discriminant 𝒟 given by

$𝒟=\left(\xi -1\right)\left(1+K_{act}\right)+K_A\left[A\right]\xi \Vert U-V_{\xi }\Vert \Vert W_g\Vert cos\left(\phi \right)$

Recall, previously we found N ( the numerator which determined algebraic sign ) was given by

$N=\left[g\right]\left(\left(\xi -1\right)\left(1+K_{act}\right)+K_A\left[A\right]\xi \langle U-V_{\xi }\mathrm{,}{W}_g\rangle \right)$

Hence, N is the same as the external efficacy.

However, to understand any of this, we need to fully understand the meaning the the parameters α, δ and γ; let's review the discussion of ^[2]. The term α is concerned with the effect the binding of the ligand A has on the activation of the receptor. Hence, α > 1 tells us that the ligand binding increases the production of the activated form on the receptor R_a. The term γ models the effect the binding of the ligand A has on the coupling of the G-protein G to the receptor. If γ > 1, then the binding of the ligand helps later coupling to the G-protein. Finally, the parameter δ is the most interesting. There are several cases to consider; in all of them, if δ > 1, this means that the coupling of G-protein is enhanced by the addition of the ligand, if δ = 1, the addition of the ligand did not effect the G-protein binding and if δ < 1, the coupling of G-protein is reduced.

We need to define our terms. Here the inactivated receptor R_i is TcR prior to adding the auxiliary proteins needed to prepare it for binding to the pMHC; the activated receptor R_a is the TcR after these preparations are completed. The ligand A is the pMHC and the G-protein G here is a collection of proteins that provide a scaffolding for the TcR-pMHC interaction.

•   The effect a bound ligand has on whether or not a receptor will couple with a G-protein can be different if the receptor is inactive or active. Hence, the pathways R_a + G ↔ R_aG and AR_a + G ↔ AR_aG can be independent from each other. Without the δ interaction, the association constants for these two pathways are βK_G versus γβK_G, but the δ option changes the second pathway's constant to δγβK_G. Hence, if δ goes up here, there is enhanced coupling of the activated TcR and the scaffolding.

•   We can also look at the pathways R_i + G ↔ R_iG ( association constant K_G) and AR_i + G ↔ AR_iG (association constant γK_G). The δ option changes the second pathway's constant to δγK_G. We interpret the δ choices the same way. If δ increases here, there is an enhancement of the coupling of the scaffolding between the inactivated TcR and the scaffolding.

•   The pathways R_iG + A ↔ AR_iG (association constant γK_A) and R_aG + A ↔ AR_aG (association constant αγK_A). The δ option changes the second pathway's constant to δαγK_A. Thus, the binding of pMHC to the inactivated TcR and scaffolding complex is enhanced.

•   The pathways R_iG ↔ R_aG (association constant βK_act) and AR_iG ↔ AR_aG (association constant αβK_act). The δ option changes the second pathway's constant to δαβK_act. This means that the coupling between the inactivated TcR and the activated TcR is enhanced if δ increases.

•   The pathways AR_i ↔ AR_a ( association constant αK_act) and AR_iG ↔ AR_aG (association constant αβK_act). The δ option changes the second pathway's constant to δαβK_act. Here, if δ increases, the activation of the receptor TcR enhances the binding of pMHC to the receptor.

•   The pathways AR_i + G ↔ AR_iG (association constant γK_G) and AR_a + G ↔ AR_aG (association constant γβK_G). The δ option changes the second pathway's constant to δαβK_act. Now, if δ increases, the interpretation is that the addition of the scaffolding to the inactive TcR binding with pMHC is enhanced.

In all cases, the parameter δ has to do with a synergism between the ligand and G-protein binding. Indeed, increasing δ in several cases can potentially encourage autoimmune interactions.

Now let's add a bit more detail for our model of TcR and pMHC binding in the context of the adaptive immune system. We assume the ligand A is the pMHC complex, the receptor R is the TcR complex and there are accessory proteins P₁ and P₂ to determine a scaffolding that is build up to facilitate the TcR and pMHC interaction that forms the immunosynapse. We have lumped this activity into the G-protein actions of the CTC model. We will therefore the G label with the new label Sc. To save space, we will let T be the TcR receptor and P, the pMHC complex. Let's redo our fundamental equations for this context.

$\begin{array}{ccc}\left[\begin{array}{ccc}P{T}_{i}Sc& \stackrel{\alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ \uparrow \gamma K_P& & \uparrow \alpha \gamma K_P\\ T_{i}Sc& \stackrel{\beta K_{act}}{\to }& T_{a}Sc\\ & \text{Back}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_{i}Sc& \stackrel{\alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ \uparrow \gamma K_{Sc}& & \uparrow \gamma \beta K_{Sc}\\ P{T}_i& \stackrel{\alpha K_{act}}{\to }& P{T}_a\\ & \text{Top}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_i& \stackrel{\alpha K_{act}}{\to }& P{T}_a\\ \uparrow K_P& & \uparrow \alpha K_P\\ T_i& \stackrel{K_{act}}{\to }& T_a\\ & \text{Front}& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}P{T}_i& \stackrel{\gamma K_P}{\to }& P{T}_{i}Sc\\ \uparrow K_{Sc}& & \uparrow \gamma K_{Sc}\\ T_i& \stackrel{K_P}{\to }& T_{i}Sc\\ & \text{Left}& \end{array}\right]& \left[\begin{array}{ccc}{T}_{i}Sc& \stackrel{\beta K_{act}}{\to }& T_{a}Sc\\ \uparrow K_{Sc}& & \uparrow \beta K_{Sc}\\ T_i& \stackrel{K_{act}}{\to }& T_a\\ & \text{Bottom}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_a& \stackrel{\gamma \beta K_{Sc}}{\to }& P{T}_{a}Sc\\ \uparrow \alpha K_P& & \uparrow \alpha \gamma K_P\\ T_a& \stackrel{\beta K_{Sc}}{\to }& T_{a}Sc\\ & \text{Right}& \end{array}\right]\end{array}$

This gives the pathways

$\left[\begin{array}{ccc}& & T_{a}Sc\\ & & \uparrow \alpha \gamma K_P\\ P{T}_{i}Sc& \stackrel{\alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ & & \uparrow \beta \gamma K_{Sc}\\ & & P{T}_a\end{array}\right]$

which we make as general as possible by adding the δ synergy parameter as before:

$\left[\begin{array}{ccc}& & T_{a}Sc\\ & & \uparrow \delta \alpha \gamma K_P\\ P{T}_{i}Sc& \stackrel{\delta \alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ & & \uparrow \delta \beta \gamma K_{Sc}\\ & & P{T}_a\end{array}\right]$

Normally, the reactions T_a + Sc ↔ T_aSc (constant βK_Sc) and PT_a + Sc ↔ PT_aSc (constant γβK_Sc) differ by a factor γ. If the pMHC binding enhances the scaffold formation, then we can model that by changing the factor to δγ where δ > 1. If the scaffold coupling is diminished by the ligand, we can use δ < 1 to indicate that. Finally, if δ = 1, there is no advantage or disadvantage to the scaffold coupling due to the pMHC binding. This moves us to the following diagram

$\begin{array}{ccc}\left[\begin{array}{ccc}P{T}_{i}Sc& \stackrel{\delta \alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ \uparrow \gamma K_P& & \uparrow \delta \alpha \gamma K_P\\ T_{i}Sc& \stackrel{\beta K_{act}}{\to }& T_{a}Sc\\ & \text{Back}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_{i}Sc& \stackrel{\delta \alpha \beta K_{act}}{\to }& P{T}_{a}Sc\\ \uparrow \gamma K_{Sc}& & \uparrow \delta \gamma \beta K_{Sc}\\ P{T}_i& \stackrel{\alpha K_{act}}{\to }& P{T}_a\\ & \text{Top}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_i& \stackrel{\alpha K_{act}}{\to }& P{T}_a\\ \uparrow K_P& & \uparrow \alpha K_P\\ T_i& \stackrel{K_{act}}{\to }& T_a\\ & \text{Front}& \end{array}\right]\\ & & \\ \left[\begin{array}{ccc}P{T}_i& \stackrel{\gamma K_P}{\to }& P{T}_{i}Sc\\ \uparrow K_{Sc}& & \uparrow \gamma K_{Sc}\\ T_i& \stackrel{K_P}{\to }& T_{i}Sc\\ & \text{Left}& \end{array}\right]& \left[\begin{array}{ccc}{T}_{i}Sc& \stackrel{\beta K_{act}}{\to }& T_{a}Sc\\ \uparrow K_{Sc}& & \uparrow \beta K_{Sc}\\ T_i& \stackrel{K_{act}}{\to }& T_a\\ & \text{Bottom}& \end{array}\right]& \left[\begin{array}{ccc}P{T}_a& \stackrel{\delta \gamma \beta K_{Sc}}{\to }& P{T}_{a}Sc\\ \uparrow \alpha K_P& & \uparrow \delta \alpha \gamma K_P\\ T_a& \stackrel{\beta K_{Sc}}{\to }& T_{a}Sc\\ & \text{Right}& \end{array}\right]\end{array}$

and in it, we can see how the factor δ shapes the interactions. The external efficacy e_E here is given by

$\begin{array}{l}{e}_E=\text{Sc-Change}+\text{ExternalScalingFactor}\times \text{RealizedEfficacy}\\ =\left(\xi -1\right)\left(1+K_{act}\right)\left[sc\right]+K_P\left[P\right]\xi \left[sc\right]\left[\begin{array}{c}\alpha \gamma \delta -{\xi }^{-1}\\ \alpha \gamma \delta -\alpha {\xi }^{-1}\\ \alpha \gamma \delta -\gamma \\ 0\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}\\ K_{Sc}\left[sc\right]\\ 0\end{array}\right]\\ =\left[sc\right]\left(\left(\xi -1\right)\left(1+K_{act}\right)+K_P\left[P\right]\xi \langle U-V_{\xi }\mathrm{,}{W}_{sc}\rangle \right)\end{array}$

where [sc] denotes the concentration of the scaffolding system Sc prior to the pMHC binding to the receptor cloud.

---

2.4 Directional change

We can calculate the rate of change of the external efficacy e_E with respect to a given parameter p in the usual way:

$\begin{array}{l}\frac{\partial e_E}{\partial p}=\frac{\partial }{\partial p}\left\{\left[sc\right]\left(\left(\xi -1\right)\left(1+K_{act}\right)+K_P\left[P\right]\xi \langle U-V_{\xi }\mathrm{,}{W}_{sc}\rangle \right)\right\}\\ =\frac{\partial \left[sc\right]}{\partial p}\left\{\left(\xi -1\right)\left(1+K_{act}\right)+K_P\left[P\right]\xi \langle U-V_{\xi }\mathrm{,}{W}_{sc}\rangle \right\}\\ +\left[sc\right]K_P\left[P\right]\xi \frac{\partial }{\partial p}\left(\langle U-V_{\xi }\mathrm{,}{W}_{sc}\rangle \right)\end{array}$

where p is any parameter that is interesting to us. Now if [sc] does not depend on the parameter p, this becomes

$\frac{\partial e_E}{\partial p}=\left[sc\right]K_A\left[P\right]\xi \langle \frac{\partial \left(U-V_{\xi }\right)}{\partial p}\mathrm{,}{W}_{sc}\rangle$

We can calculate these partials. Since,

$U-V_{\xi }={\left[\begin{array}{cccc}\alpha \gamma \delta -{\xi }^{-1}\mathrm{,}& \alpha \gamma \delta -\alpha {\xi }^{-1}\mathrm{,}& \alpha \gamma \delta -\gamma \mathrm{,}& 0\end{array}\right]}^{\text{'}}$

we find

$\begin{array}{l}{\left(U-V_{\xi }\right)}_{\alpha }={\left[\begin{array}{cccc}\gamma \delta \mathrm{,}& \gamma \delta -{\xi }^{-1}\mathrm{,}& \gamma \delta \mathrm{,}& 0\end{array}\right]}^{\text{'}}\mathrm{,}\text{\ }{\left(U-V_{\xi }\right)}_{\delta }={\left[\begin{array}{cccc}\alpha \gamma \mathrm{,}& \alpha \gamma \mathrm{,}& \alpha \gamma \mathrm{,}& 0\end{array}\right]}^{\text{'}}\\ {\left(U-V_{\xi }\right)}_{\gamma }={\left[\begin{array}{cccc}\alpha \delta \mathrm{,}& \alpha \delta \mathrm{,}& \alpha \delta -\mathrm{1,}& 0\end{array}\right]}^{\text{'}}\end{array}$

Thus,

$\begin{array}{l}\frac{\partial e_E}{\partial \alpha }=\left[sc\right]K_P\left[P\right]\xi \langle \frac{\partial \left(U-V_{\xi }\right)}{\partial \alpha }\mathrm{,}{W}_{sc}\rangle =\left[sc\right]K_P\left[P\right]\xi \left[\begin{array}{c}\gamma \delta \\ \gamma \delta -{\xi }^{-1}\\ \gamma \delta \\ 0\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}\\ K_{Sc}\left[g\right]\\ 0\end{array}\right]\\ =\left[sc\right]K_P\left[P\right]\xi \left(\gamma \delta +\left(\gamma \delta -{\xi }^{-1}\right)K_{act}+\gamma \delta K_{Sc}\left[sc\right]\right)\end{array}$

and

$\begin{array}{l}\frac{\partial e_E}{\partial \delta }=\left[sc\right]K_A\left[P\right]\xi \langle \frac{\partial \left(U-V_{\xi }\right)}{\partial \delta }\mathrm{,}{W}_{sc}\rangle =\left[sc\right]K_A\left[P\right]\xi \left[\begin{array}{c}\alpha \gamma \\ \alpha \gamma \\ \alpha \delta \\ 0\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}\\ K_{Sc}\left[g\right]\\ 0\end{array}\right]\\ =\left[sc\right]K_A\left[P\right]\xi \left(\alpha \gamma +\alpha \gamma K_{act}+\alpha \gamma K_G\left[sc\right]\right)\end{array}$

and

$\begin{array}{l}\frac{\partial e_E}{\partial \gamma }=\left[sc\right]K_P\left[P\right]\xi \langle \frac{\partial \left(U-V_{\xi }\right)}{\partial \gamma }\mathrm{,}{W}_{sc}\rangle =\left[sc\right]K_P\left[P\right]\xi \left[\begin{array}{c}\alpha \delta \\ \alpha \delta \\ \alpha \delta -1\\ 0\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}\\ K_{Sc}\left[sc\right]\\ 0\end{array}\right]\\ =\left[sc\right]K_P\left[P\right]\xi \left(\alpha \delta +\alpha \delta K_{act}+\left(\alpha \delta -1\right)K_{Sc}\left[sc\right]\right)\end{array}$

In the three dimensional ligand association constant space (α, δ, γ), we see

$\nabla e_E=\left[sc\right]K_P\left[P\right]\xi \left(1+K_{act}+K_{Sc}\left[sc\right]\right)\left[\begin{array}{c}\gamma \delta \\ \alpha \gamma \\ \alpha \delta \end{array}\right]-\left[sc\right]K_P\left[P\right]\left[\begin{array}{c}{K}_{act}\\ 0\\ \xi K_G\left[sc\right]\end{array}\right]$

which implies the <∇e_E, u> gives us the directional derivative D_u(e_E) in any unit vector direction: i.e. ||u|| = 1 and for u = < Δα, Δδ, Δγ >', this implies Δα² + Δδ² + Δγ² = 1. To get a sense of what this implies, look at a unit change in γ only and also assume αδ = 1. Then

•   Δγ = 1, Δα = 0 and Δδ = 0. We have

$\begin{array}{l}{D}_u\left(e_E\right)=\langle \left[sc\right]K_P\left[P\right]\xi \left(1+K_{act}+K_{Sc}\left[sc\right]\right)\left[\begin{array}{c}\gamma \delta \\ \alpha \gamma \\ \alpha \delta \end{array}\right]-\left[sc\right]K_P\left[P\right]\left[\begin{array}{c}{K}_{act}\\ 0\\ \xi K_{Sc}\left[sc\right]\end{array}\right]\mathrm{,}\left[\begin{array}{c}\mathrm{0,}\\ \mathrm{0,}\\ 1\end{array}\right]\rangle \\ =\left[sc\right]K_P\left[P\right]\xi \left(1+K_{act}\right)>0.\end{array}$

We know γ measures the change in the R_i → R_iG pathway or how the ligand A binding effects G-protein coupling. In the context of an immunosynapse model, the ligand A is the pMHC containing an epitope on the cell's surface and the receptor R_i is the inactivated TcR cell. Hence, a one dimensional alteration of γ only in the ligand association space induces an increase in the external efficacy e_E. The positive increase in γ thus represents an increase in G - protein coupling to the inactive receptor due to the presence of the ligand A or pMHC. We can think of this as saying that as the TcR approaches the pMHC, there is a positive feedback loop which induces structural proteins to enhance the binding of the TcR to the pMHC. A similar analysis works for the case of the activated TcR also. Then an increase in γ enhances the G-protein (scaffolding) coupling between the pMHC and the activated TcR via another positive feedback loop.

•   Δγ = -1, Δα = 0 and Δδ = 0. We have

$\begin{array}{l}{D}_u\left(e_E\right)=\langle \left[sc\right]K_P\left[P\right]\xi \left(1+K_{act}+K_{Sc}\left[sc\right]\right)\left[\begin{array}{c}\gamma \delta \\ \alpha \gamma \\ \alpha \delta \end{array}\right]-\left[sc\right]K_P\left[P\right]\left[\begin{array}{c}{K}_{act}\\ 0\\ \xi K_{Sc}\left[sc\right]\end{array}\right]\mathrm{,}\left[\begin{array}{c}\mathrm{0,}\\ \mathrm{0,}\\ -1\end{array}\right]\rangle \\ =-\left[sc\right]K_P\left[P\right]\xi \left(1+K_{act}\right)<0.\end{array}$

implying a decrease in the external efficacy e_E.

In general, if the directional derivative in ligand associative space gives rise to an increase in external efficacy there is an increased probability of a successful TCR and pMHC binding to create the full immunological synapse.

---

3 Results

The modifications of the CTC model above now give us the tools to discuss how autoimmune events might occur.

---

3.1 Self versus non-self computations

There is much that is not known about T cell recognition algorithms in vivo. A current review of salient issues can be found in ^[5] and we will rely heavily on what is said in that review in what follows. Huppa et. al. distinguish three levels of complexity in the TcR-pMHC interaction: the kinetics and a structural basis for TcR-pMHC engagement, the TcR interactions with the structural protein scaffolding we have mentioned. His paper focuses on the TcR-CD3 complex and antigen recognition and the immunological synapse. New techniques have surfaced to help answer these questions. There has been a lot more crystallographic analysis of various TcR-pMHC complexes which has helped. Surface Plasmon Resonance (SPR) has allowed us to study these engagements in solution. The problem, of course, is that these bindings are constrained to be essentially 2D due to the ligand cloud and receptor cloud interaction at a planar interface. So there is a significant change in how many degrees of freedom are available which alters the measurement of what we call external efficacy. Other tools are total internal reflection (TIRF) microscopy, Förster resonance energy transfer (FRET) microscopy, superresolution fluorescence and so on. All have their problems and so there is no simple analytical tool to resolve our questions. However, these tools are letting us make a lot of progress.

---

3.2 Kinetics and TcR interactions

It is now clear the external affinity between the TcR and a pMHC is very low ( 1-100 μM) which is caused by a slow association and a fast disassociation rate. Also, peptides in the MHC groove which differ by only a slight amount in peptide composition from an antigen can produce very different T cell responses. This is very strange and hard to explain; yet, that is our job! There is evidence that TcR engagement of pMHC binding occurs in two stages: the first involves MHC binding and the second handles peptide scanning and binding. In the CDR 1-3 regions within the TcR, it seems to work this way: the CDR 1 and CDR 2 loops bind mostly to the MHC while the more diverse and flexible CDR 3 loop engages the MHC embedded peptide. TcRs engage the MHC primarily on a diagonal. V_α fits with the MHC helix α2 for class I and the β1 for class 2 and the peptide N-terminus where as V_β contacts the MHC α1 helix and the peptide C-terminus. Hence, the germline encoded CDR 1 and CDR 2 contact the α helices of the MHC and the CDR 3 regions bind to the central and most diverse part of the peptide in the MHC groove. There is a wide range of docking angles ( our φ in the external efficacy equation comes to mind!) of ±100 deg. But, it appears, there is a restricted range of angles that promote signaling.

Hence, there appears to be a germline bias for TcR recognition which suggest evolutionary pressures shape V-gene segments within the TcRα and TcRβ gene loci that allow them to bind to MHC regardless of the peptide cargo. The codon hypothesis posits that a given TcR equipped with a set of CDR 1 and CDR 2 loops can bind more than one MHC molecule. Binding can be achieved at a wide range of docking angles for MHC molecules specifically. The cost of this ability is probably a lack of binding strength which fits well with the generally low external affinity measured. Thus, there is significant TcR cross-reactivity. In more detail, each V_α and V_β interacts with diverse MHC surface residues on top of the helices of different MHC molecules. Suppose this happens for three MHC molecules called MA, MB and MC. Our TcR has two keys: the CDR 1 and CDR 2 loops. Let MA have two structural regions or locks, CA1 and CA2, MB have locks CB1 and CB2 and finally MC have CC1 and CC2. Then we can get the bindings CDR 1 + CA1 and CDR 2 + CA2, CDR 1 + CB1 and CDR 2 + CB2 and CDR 1 + CC1 and CDR 2 + CC2. These interactions are then influenced by the more flexible CDR 3 interaction with the peptide in the MHC groove. One of these interactions is the low binding energy solution. Also, these interactions are influenced by the binding angle ( our φ). The TcR-MHC interaction is very short lived and if this reaction had high affinity, then it would not be very helpful in helping discriminate between subtle differences in peptide structure. The human TcR repertoire is about 10⁸ TcRs at any given time and without cross-reactivity would not be enough to cover enough peptide variability for our protection. However, there is a price. If each TcR can interact profitably with multiple peptide loaded MHC cradles, there is a distinct possibility that a TcR could interact with a self MHC leading to autoimmunity issues.

As discussed in ^[6], it is now understood that α, β T cells have a broadly sensory role in detecting perturbations from self and normalcy.

Because the T cells must not only detect foreign antigens but also act on that information very rapidly, another important issue is what the threshold for an irreversible action will be.

The models for TcR mediated T cell activation have evolved over the years. First there was the monomer/ co-receptor model in which a single pMHC engages a TcR and also almost simultaneously engages CD4 or CD8 co-receptors. However, in general even high concentrations of monomeric pMHC fail to stimulate most T cells. Hence, the dimer of dimers model was developed. It was suggested that MHC dimerization could promote TcR dimerization and a following activation. But there is data that shows that even single pMHC complexes can trigger some T cells, so the pseudodimer model was developed. Here, a single pMHC could join up with an equivalent pMHC and with cross linking by CD4 or CD8 would provide the base unit for the T cell activation. The linking up with the CD4 or CD8 is why the model is called a pseudodimer, of course, as it is not really a dimer at all. Observations have shown that self or endogenous pMHC is strongly recruited to the immunological synapse by interactions with the TcR. The pseudodimer model was then modified in ^[6] to give a model of serial engagement. If an α or β TcR receptor on a CD4 T cell, TCR1, interacts with a pMHC having a foreign peptide or agonist pMHC complex, this interaction allows the recruitment of a second TcR, TCR2, through its associated CD4 molecule. TcR2 then interacts with a self pMHC. So the chain is TCR1 + agonist + TCR2 + self at this point. It is postulated the second TcR2 + self pMHC is very short lived. One possibility is that this short lived second complex stabilizes the first TCR1 + agonist interaction and allows the phosphorylation of TcR1's CD3 molecules. The second possibility is that the TcR1 + agonist acts like a catalyst and facilitates the addition of multiple short lived TcR + self complexes. Each additional TcR + self complex would be short lived but would cause additional CD3 phosphorylations on the T Cell. Hence, the chain would be

$TcR1+\text{agonist}+TcR2+\text{self A}+TcR3+\text{self B}+\dots$

where the additional TcRs need not recruit the same self pMHC and so we call them self A and self B here. Hence, T cells can use endogenous pMHC-TcR interactions to augment T cell responsiveness. In ^[6], this discussion of serial engagement is restricted to CD4 T cell which works with MHC class II and it is said there is less evidence for such a recruitment of endogenous pMHC for the CD8 T cells. However, this could well be that the experimental means to see this recruitment is currently not known. As is said in ^[6], there is every reason to believe the activation sequence for CD4 and CD8 T cells is similar, so from now on, we will assume we can model the TcR and pMHC activation sequence in this way for both a CD4 and a CD8 T cell.

We characterize the recruited endogenous pMHC recruited in this process as follows. The initial foreign peptide TcR pMHC interaction event causes a movement of self pMHCs, possibly similar by some measure, to the foreign one on the cell surface to the binding site. It is hard to say what we mean by similar at this point. Does it mean the peptides lying in the MHC cradles are similar in some fashion so that the binding of the CDR 3 flexible loop to the peptide in the cradle is similar? Or is it possible for quite dissimilar peptides to initiate similar external affinity values? Or can any self pMHC be recruited to help strength the original TcR and agonist pMHC?

---

3.3 Antigen recognition details

Following ^[5], we note that T cell antigen recognition and the formation of the immunological synapse (IS) are intimately connected.

The term “synapse” is now applied to any bimembranous junction between T cells and APCs...The common denominator of all immunological synapses is probably that they promote, with varying complexity, one -on-one conversations between two conjugated cells through engagement of cell-specific receptor-ligand pairs and in most cases, also through the directed secretion of cytokines and perforins.

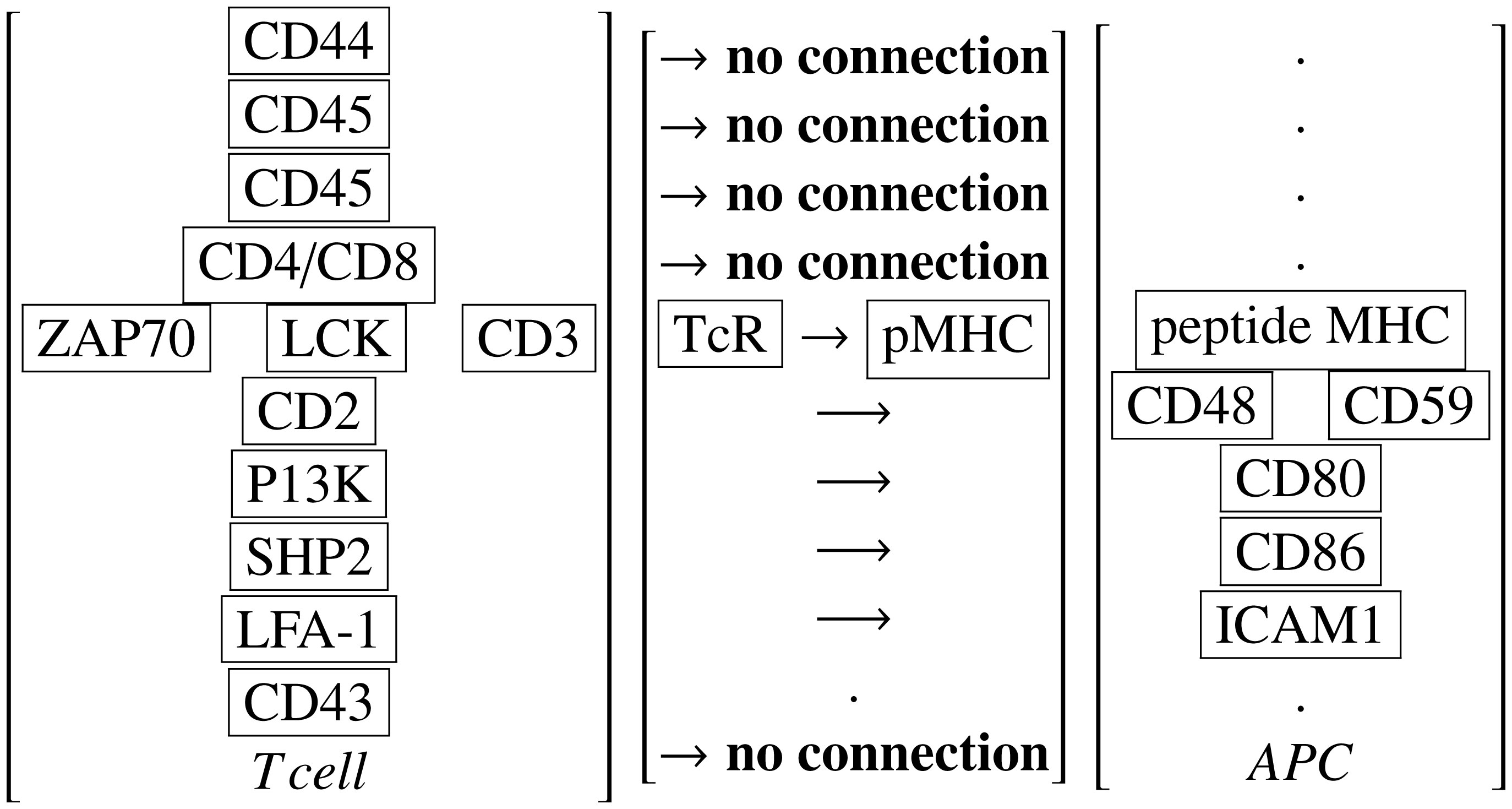
It is known the formation and maintenance of the IS is dependent on the TcR and APC engagement and the TcR mediated signaling. The typical look of this interaction in terms of what we have been calling the scaffolding is shown in Figure 2.

---

There are many proteins that are involved in the construction of what we call the scaffolding Sc. These scaffolding proteins accumulate in the mature IS in a nested sequence of proteins which is called the bulls eye as shown in Figure 3. As the serial interactions we have listed as

$TcR1+\text{agonist}+TcR2+\text{self A}+TcR3+\text{self B}+\dots$

continue, the bulls eye forms in the maturing IS. It must be noted though that this kind of synaptic binding is very different from binding in solution as the system is open instead of closed with energy moving in and out all the time. As ^[5] says

Molecular partners are preoriented and tied to flexible membrane surfaces, which can adjust their morphology in response to cell stimuli and acting forces. This should ... increase the on - rate of binding ... however, only if the two participating membranes are properly aligned. Moreover, molecular size could ... affect binding within the crowded confines of the immunological synapse.

---

For example, the protein CD45 is rather large and becomes pushed out of the central bulls eye because of its size. That is why CD45 is shown in the outer most rectangle in our bulls eye drawing. So it can not access the central part of the IS and so the equilibrium shifts towards the TcR-CD3 complex and its phosphorylation. During the IS formation, there is a huge flow of actin which imposes shear forces on the IS which destabilized weaker TcR-pMHC interactions. Hence, a more stable TcR-pMHC interaction is more probable if it followed the serial or chain interaction scheme which uses a stream of frequent bindings. It is theorized that these forces are an important part of the IS formation. Experiments have shown that the TcR-pMHC chains have a more vigorous response once it is attached to a glass supported lipid bilayer. Before such an attachment, TcR movement is in all three dimensions, but once there is an attachment, one degree of freedom in the movement is lost with a subsequent increase in the external affinity. Still, much is not known for sure. It is possible that LFA-1 when it binds to ICAM1 protects it from the shear stresses we mentioned earlier. And the CD2-CD48 interaction might help setup the T cell and APC membranes for an optimal TcR-pMHC interaction.

Also we should remember the T cell is like a large bag whose surface is studded with many protein complexes. The distribution of TcRs on the surface of a T cell appears to be organized as clusters. From ^[5], we have

a single quantum-dot labeled pMHC within the T cell APC interface caused the formation of TcR microclusters, in which hundreds of TcRs surrounded the antigenic pMHC.

---

4 Discussion

We can now begin to use the affinity model developed above to do quantitative experiments.

---

4.1 A simple self vs. nonself recognition model

It is illuminating to look at what happens during a binding event chain. In our model, the original TcR1 + agonist interaction has an external efficacy of

$\begin{array}{c}{e}_E^1=\left({\xi }_1-1\right)\left(1+K_{act}^1\right)\left[{\left(sc\right)}^1\right]+K_P^1\left[P^1\right]{\xi }_1\left[{\left(sc\right)}^1\right]\left[\begin{array}{c}{\alpha }^1{\gamma }^1{\delta }^1-{\xi }_1^{-1}\\ {\alpha }^1{\gamma }^1{\delta }^1-{\alpha }^1{\xi }_1^{-1}\\ {\alpha }^1{\gamma }^1{\delta }^1-{\gamma }^1\\ 0\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}^1\\ K_{Sc}^1\left[{\left(sc\right)}^1\right]\\ 0\end{array}\right]\\ =\left({\xi }_1-1\right)\left(1+K_{act}^1\right)\left[{\left(sc\right)}^1\right]+K_P^1\left[P^1\right]{\xi }_1\left[{\left(sc\right)}^1\right]<U^1-V_{{\xi }_1}^1\mathrm{,}{W}_{\left(s{c}^1\right)}>\end{array}$

We would then have similar expressions for the external efficacy of the TcR2, TcR3 and so forth additional complexes that are being recruited catalytically. This suggests the external efficacy of this growing T cell activation due to a chain of N recruitments should be

$𝒜=e_E^1+e_E^2+e_E^3+...+e_E^N$

where 𝒜 is the avidity of the interaction. The original $e_E^1$, although low, is enough to begin this complicated recruitment chain. The self pMHCs brought into this process could even be part of the thymus clonal expansion that results in a huge increase in the T cell population that targets the agonist.

Next, note this definition of avidity does not take into account time issues though, so next we will talk about that a bit. Let's assume a pMHC corresponding to an antigen binds to a TcR. There is a critical external efficacy which must be exceeded in order to the pMHC and TcR connection to take hold. Call this threshold $e_E^{1*}$ where the superscript 1 refers to the fact that this peptide anchors the chain of additional pMHC interactions we have talked about already. Hence, for a valid interaction, we must have $e_E^1>e_E^{1*}$ and moreover, the binding of the pMHC much last longer than a critical time interval we will label Δ^1*t. If the time interval that this interaction occurs is denoted by Δ¹t, we must have Δ¹t > Δ^1*t for a successful interaction. Each additional pMHC has an associated critical external efficacy level, $e_E^{j*}$, a critical time interval for interaction Δ^j*t and an actual time interval of contact Δ^jt. Hence, a better way to define avidity is

$𝒜=e_E^1{\Delta }^{1}t+e_E^2{\Delta }^{2}t+e_E^3{\Delta }^{3}t+...+e_E^N{\Delta }^{N}t$

The developing T cell-pMHC interface we call the immunological synapse sends out signals to its surroundings that enhance these interactions. Eventually, if the foreign peptide initiated first interaction exceeds the threshold affinity level needed for a sustained reaction, the resulting avidity increase causes a clonal expansion of the T cells that bind with the foreign antigen. It may also cause a clonal expansion of the pMHCs that are sufficiently similar to the foreign peptide. Hence, in addition to a greatly increased concentration of the T cells needed to remove the cells exhibiting the foreign peptide in an pMHC complex, there may also be a vast increase in the T cells bearing pMHCs that are similar to the pMHC with the foreign peptide. Now the foreign peptide bearing cells are lysed and within a short time removed. So how does this kind of event trigger autoimmunity in some circumstances?

If something did happen, there would be a catalyzing event of the form

${𝒜}_s=e_E^1{\Delta }^{1}t+e_E^2{\Delta }^{2}t+e_E^3{\Delta }^{3}t+...+e_E^N{\Delta }^{N}t$

where 𝒜_s is large enough to begin an interaction chain culminating in the construction of the full immunosynapse and a corresponding lysis event. If we let $e_E^{*}$ be the small avidity usually seen with a TcR-pMHC interaction of a T cell with a self protein, to start this chain we want a foreign peptide catalyst event whose avidity exceeds $e_E^{*}$. Hence, we need

$\begin{array}{l}{e}_E^1=\left({\xi }_1-1\right)\left(1+K_{act}^1\right)\left[{\left(sc\right)}^1\right]+K_P^1\left[P^1\right]{\xi }_1\left[{\left(sc\right)}^1\right]\left[\begin{array}{c}{\alpha }^1{\gamma }^1{\delta }^1-{\xi }_1^{-1}\\ {\alpha }^1{\gamma }^1{\delta }^1-{\alpha }^1{\xi }_1^{-1}\\ {\alpha }^1{\gamma }^1{\delta }^1-{\gamma }^1\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}^1\\ K_{Sc}^1\left[{\left(sc\right)}^1\right]\end{array}\right]\\ >e_E^{*}=\left({\xi }_{*}-1\right)\left(1+K_{act}^{*}\right)\left[{\left(sc\right)}^{*}\right]+K_P^{*}\left[P^{*}\right]{\xi }_{*}\left[{\left(sc\right)}^{*}\right]\left[\begin{array}{c}{\alpha }^{*}{\gamma }^{*}{\delta }^{*}-{\xi }_{*}^{-1}\\ {\alpha }^{*}{\gamma }^{*}{\delta }^{*}-{\alpha }^{*}{\xi }_{*}^{-1}\\ {\alpha }^{*}{\gamma }^{*}{\delta }^{*}-{\gamma }^{*}\end{array}\right]·\left[\begin{array}{c}1\\ K_{act}^{*}\\ K_{Sc}^{*}\left[{\left(sc\right)}^{*}\right]\end{array}\right]\end{array}$

(4.1)

The response $e_E^1$ may be less than the value required for an immunosynaptic event. If this case $e_E^1<e_E^{*}$. The directional derivative is largest if we move from the current point in ligand space to the new one determined by moving in the direction of D_u where $u={\nabla }_{e_E}/\Vert {\nabla }_{e_E}\Vert$. In general, any unit vector u which leads to a positive directional derivative is acceptable. This implies the directional derivative value at the base point must satisfy

$\begin{array}{l}\langle {\nabla }^{*}{e}_E\mathrm{,}\left[\begin{array}{c}\Delta \alpha \\ \Delta \delta \\ \Delta \gamma \end{array}\right]\rangle =\langle \left[{\left(sc\right)}^{*}\right]K_{P^{*}}\left[P^{*}\right]{\xi }^{*}\left(1+K_{act}^{*}\right)+K_{Sc}^{*}\left[s{c}^{*}\right]\left[\begin{array}{c}{\gamma }^{*}{\delta }^{*}\\ {\alpha }^{*}{\gamma }^{*}\\ {\alpha }^{*}{\delta }^{*}\end{array}\right]\mathrm{,}\left[\begin{array}{c}\Delta \alpha \\ \Delta \delta \\ \Delta \gamma \end{array}\right]\rangle \\ -\langle \left[s{c}^{*}\right]K_P^{*}\left[P^{*}\right]\left[\begin{array}{c}{K}_{act}^{*}\\ 0\\ {\xi }^{*}{K}_{Sc}^{*}\left[s{c}^{*}\right]\end{array}\right]\mathrm{,}\left[\begin{array}{c}\Delta \alpha \\ \Delta \delta \\ \Delta \gamma \end{array}\right]\rangle >0.\end{array}$

(4.2)

Looking at Equation 4.2, we see there are many ways for this inequality to be satisfied as the avidity is dependent on α, δ, γ and ξ assuming the other rate constants such as K_act are fixed. Another way to look at this is that

$\begin{array}{l}\left({\xi }_1-1\right)\left(1+K_{act}^1\right)\left[{\left(sc\right)}^1\right]+K_P^1\left[P^1\right]{\xi }_1\left[{\left(sc\right)}^1\right]<U^1-V_{{\xi }_1}^1\mathrm{,}{W}_{{\left(sc\right)}^1}>\\ >\left({\xi }_{*}-1\right)\left(1+K_{act}^{*}\right)\left[{\left(sc\right)}^{*}\right]+K_P^{*}\left[P^{*}\right]{\xi }_{*}\left[{\left(sc\right)}^{*}\right]<U^{*}-V_{{\xi }_{*}}^{*}\mathrm{,}{W}_{{\left(sc\right)}^{*}}>\end{array}$

(4.3)

or

$\begin{array}{l}\left({\xi }_1-1\right)\left(1+K_{act}^1\right)\left[{\left(sc\right)}^1\right]+K_P^1\left[P^1\right]{\xi }_1\left[{\left(sc\right)}^1\right]\Vert U^1-V_{{\xi }_1}^1\Vert \Vert W_{{\left(sc\right)}^1}\Vert cos\left(\phi \right)\\ >\left({\xi }_{*}-1\right)\left(1+K_{act}^{*}\right)\left[{\left(sc\right)}^{*}\right]+K_P^{*}\left[P^{*}\right]{\xi }_{*}\left[{\left(sc\right)}^{*}\right]\Vert U^{*}-V_{{\xi }_{*}}^{*}\Vert \Vert W_{{\left(sc\right)}^{*}}\Vert cos\left({\phi }^{*}\right)\end{array}$

(4.4)

Hence, if the parameter changes resulted in a decrease in φ from φ*, the avidity would increase. Evidently, under normal circumstances this does not occur, but perhaps if there are underlying genetic abnormalities in T cell generation and so on, this avidity increase is possible and there is an autoimmune effect.

---

4.2 Parameter analysis

Since this is so busy, let's try a thought experiment. First, let's assume the only parameters that matter are δ and ξ. Also, redefine all the units here so that all the other parameters have value 1. Then, we can write Equation 4.1 as

$e_E^1=\left({\xi }_1-1\right)\left(2\right)+{\xi }_1\left[\begin{array}{c}{\delta }^1-{\xi }_1^{-1}\\ {\delta }^1-{\xi }_1^{-1}\\ {\delta }^1-1\\ 0\end{array}\right]·\left[\begin{array}{c}1\\ 1\\ 1\\ 0\end{array}\right]>e_E^{*}=\left({\xi }_{*}-1\right)\left(2\right)+{\xi }_{*}\left[\begin{array}{c}{\delta }^{*}-{\xi }_{*}^{-1}\\ {\delta }^{*}-{\xi }_{*}^{-1}\\ {\delta }^{*}-1\\ 0\end{array}\right]·\left[\begin{array}{c}1\\ 1\\ 1\\ 0\end{array}\right]$

or

${\xi }_1-3+3{\xi }_1{\delta }^1>{\xi }_{*}-3+3{\xi }_{*}{\delta }^{*}$

Thus, to get over the threshold, we need

${\xi }_1\left(1+3{\delta }^1\right)>{\xi }_{*}\left(1+3{\delta }^{*}\right)\mathrm{.}$

(4.5)

Clearly, this occurs if ξ¹ > ξ* and δ¹ > δ* which is the easiest possibility. Now ξ¹ is the multiplier for the concentration of the scaffolding proteins we have prior to the binding of the ligand-i.e. the pMHC. The term δ¹ is related to the coupling of the ligand pMHC and the scaffolding. If δ¹ > 1, this means the coupling of the pMHC enhances the scaffolding protein complexes we lump together as Sc. So these two terms are related. Since we assume ξ¹ > ξ*, we know this means the concentration of the scaffolding complex is upregulated due to the pMHC binding over the threshold value for the self pMHC. Further, since δ¹ > δ*, we know the binding of the this self pMHC enhances the coupling between the scaffolding a bit over the threshold amount for this self pMHC. How could this happen? Here is a possible scenario. There is an initial viral infection creates an inflammatory response which upregulates the scaffolding protein complexes around a self pMHC. This pushes both ξ¹ and δ¹ up and allows the the serial method of T cell activation to create a mature IS. Although simplified enormously, this thought experiment allows us to focus on what we think is really important here. What is the mechanism or process that allows the self pMHC and TcR interaction to exceed the putative threshold value? Once this happens, the formation of the IS is essentially assured and self damage ensues. This clearly does not happen except in people who are susceptible.

We can do better if we do a numerical analysis of this model. If we assume all of the rate constants are set to one by either convenience or a suitable relabeling of units, we have the prototypical affinity equation

$\begin{array}{l}{e}_E=\left(\xi -1\right)\left(1+K_{act}\right)\left[\left(sc\right)\right]+K_P\left[P\right]\xi \left[\left(sc\right)\right]\left[\begin{array}{c}\alpha \gamma \delta -{\xi }^{-1}\\ \alpha \gamma \delta -\alpha {\xi }^{-1}\\ \alpha \gamma \delta -\gamma \end{array}\right]·\left[\begin{array}{c}1\\ K_{act}\\ K_{Sc}\left[\left(sc\right)\right]\end{array}\right]\\ =\left(\xi -1\right)\left(1+K_{act}\right)\left[\left(sc\right)\right]+K_P\left[P\right]\left[\left(sc\right)\right]\left(\alpha \gamma \delta \xi \left(1+K_{act}+K_{Sc}\left[\left(sc\right)\right]\right)\right)\\ -1-\alpha -\gamma K_{Sc}\left[\left(sc\right)\right]\xi \end{array}$

Let 1 + K_act = 2 and K_P[p][sc] = 1, K_Sc[(sc)] = 1 and so 1 + K_act + K_Sc[(sc)] = 3. Then we have

$e_E=2\left(\xi -1\right)+3\alpha \gamma \delta \xi -1-\alpha -\gamma \xi$

Finally, let A = αδγξ. Then we have

$e_E=2\left(\xi -1\right)+3A-1-\alpha -\gamma \xi$

We can perform some simulation studies with this equation and use it to describe a model of autoimmunity. Consider the function FindAffinities as shown in Appendix A.1. Our simulations calculate all the affinities associated with a fixed value of A = αδξγ. These parameters control scaffolding, TcR - pMHC binding, cytokine mediated positive feedback to strengthen the binding and so forth. For such a constant A, the affinities could be negative corresponding to no interaction between the TcR and the pMHC at all. The code is self explanatory. First, we compute all the affinities to find the minimum and maximum values, A_m and A_M, for this choice of A. Then scale the affinities into [0,1] using the transformation y ∈ [A_m, A_M] → (y - A_m)/(A_M - A_m). Then for the choice Nbin divide [0,1] into Nbin-1 uniform pieces and count how many affinities land in each bin. From this, we can then calculate frequencies and the original affinity values associated with each bin.

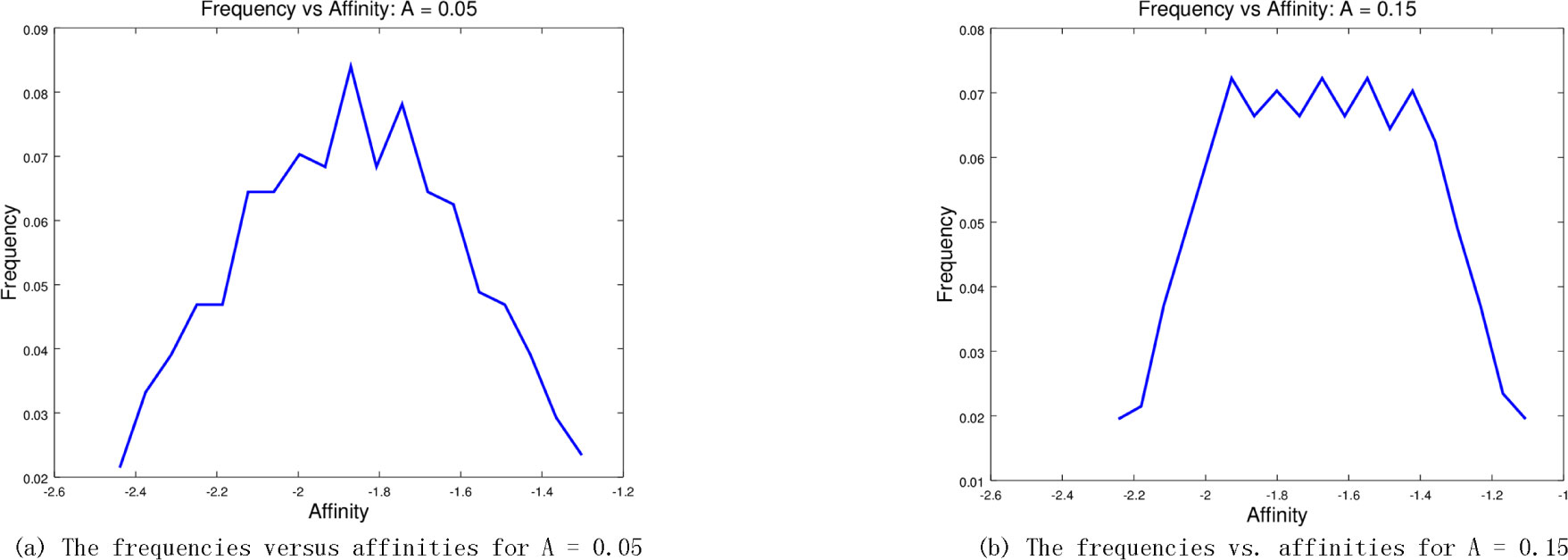
It is easy to see that as A increases A_M increases also. So a small A is equivalent to a low affinity for binding. In Figure 4a we see the affinity vs. frequency curve for A = .05. This is generated with

Note, the affinities range from −2.5 to −1.3 so for A = 0.05 so there is no binding event. If we increase A to A = .15, we see a slightly different graph in Figure 4b. Note the affinity spread has increased from [−2.5, −1.3] to [−2.3, −1.1] which shows the affinities are increasing although well below what is needed for binding event. If we increase to A = .75, we see the affinity range has now included some positive possibilities: the affinities belong to [−1.3, 0.07] so there is a small probability of a positive affinity with a very small probability of a binding event. We show this in Figure 5a.

---

---

Increasing to A = 1.5, the affinity range increase to [−0.04, 166] which means the probability of a binding event is greatly enhanced. We show this in Figure 5b. In a real situation, there will be a pool of T cells whose binding possibilities are modeled by a range of the parameters α, δ, ξ and γ determined from a distribution of A choices. The DrawSummedAffinities shown in Appendix A.2 allows us to draw affinity results from multiple families of P distributions. We can use this code to sum the affinities for A values in various ranges. Here we use A in [0.15, 0.35], [1.15, 1.35], [3.15, 5.35] and [7.15, 10.35].

---

This code generates the plot we see in Figure 6a. In Figure 6a, we see how the affinity families has affinities that increase from families with no possibility of a binding event to families with affinities as high as 15. If the formation on an immunosynapse requires affinities of say 60 or so, this can be achieved by positive feedback from earlier binding events to slowly increase the affinity. To see this graphically, consider another plot of affinity families as shown in Figure 6b. The probability of immunosynapse formation is quite high now.

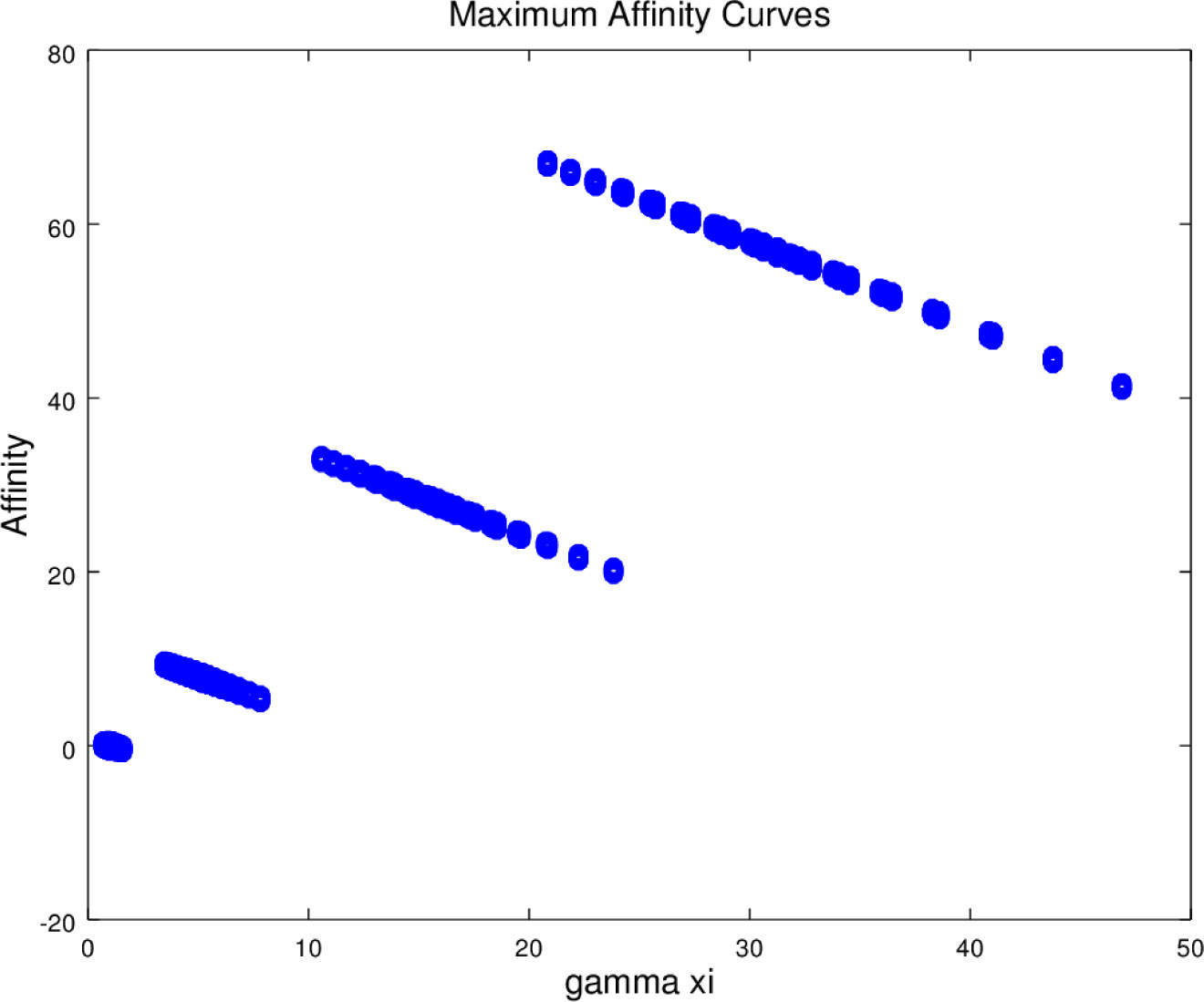
We will denote the αδγξ Ligand - Receptor interaction model by LR_αδγξ. The affinity/avidity obtained in this binding depends on many factors: this parameter space is actually nine dimensional and is comprised of realistic biological values of α, δ, γ, ξ, K_act, K_p, K_Sc, [P] and [sc]. The corresponding point cloud of data values lives in a topological space which whose structure is determined by the data. We suspect that once we move in parameter space from the maximum affinity value for a given A, that the remaining parameter values show a decrease in affinity which will look like part of a standard normal distribution. We can show this by looking at some computational results. The code in the function MaxAffinityCurve shown in Appendix A.3 computes the affinities for a select collection of parameter values for a given A and then returns two vectors: one is the set of all γξ values and other is the affinities. To find the maximum affinity curves for A = 1.0, 5.0, 10.0 and A = 30, we use the code below. In Figure 7, we show the results. Note as A increases, we see the right half of a typical normal distribution curve for the maximum affinity. As γxi moves away for the maximum, the affinities decrease. The LR_αδγξ makes it clear that the maximum affinity value depends on much more that the epitope T cell binding achieved in the pMHC groove.

From Figure 7, we see that the probability of an effective immunosynapse creation increases as A increases. The affinities for the lower A values, by themselves, as not enough to initiate such an event. We can also see that for an autoimmune event to occur there must be a chain of T Cell and pMHC interactions that push diagonally upward in the γξ - affinity positive quadrant.

---

---

4.3 A pathway to viral mediated autoimmune events

There are a number of very interesting papers that are relevant to a study of viral infections in the CNS and their possible involvement in autoimmune disease. For example, Multiple Sclerosis (MS) ( see the review ^[7]). may be due to a reaction against a virus and some believe the virus takes part in the immunopathology of the disease. There are other diseases which are similar such as Devic's disease, Marburg's variant, tumefactive MS, Balos's concentric sclerosis and acute disseminated encephalomyletis (ADEM) which all have interesting differences. From ^[7],

The most common hypothesis describes MS as an autoimmune disease induced by autoreactive T and B cells, which recognize myelin autoantigens and trigger inflammation in the CNS. The latter leads to the loss of myelin sheaths and CNS nervous conductivity and subsequently to the death of neurons.

It is known that autoreactive lymphocytes are present in all healthy people but it is not known why these autoreactive cells are triggered in MS patients. Again, from ^[7],

One possibility is that specific major histocompatibility complex (MHC) haplotype/autogen combinations together with specific genetic traits mainly of the immune system and additional triggering by infectious diseases initiates disease in MS patients.

There are a number of possibilities, We know there is a group of patients for which the primary problem is some sort of oligodendrocyte (ODC) degeneration which then triggers a subsequent inflammation that targets the mylenin sheathing. Four patterns of MS lesions were described.

1. Pattern I is primarily T cell based inflammatory type with few B cells and their complement.

2. Pattern II has a major antibody component so in addition to T cells there are also B cells, antibodies and complement.

3. Pattern III is dominated by apoptotic ODCs.

4. Pattern IV is characterized by a non apoptotic death of the ODCs.

Pattern I and II are associated with all forms of MS, Pattern III dominated in acute early MS. There is evidence that the ODC degenerative process could precede inflammation as well from a study of patients who died soon after a relapse. In a majority of them, Type III lesions were found but no leukocytes and mylenin degradation. So it is possible that in some cases of MS, the autoreactive lymphocyte scenario is secondary following an ODC problem. Of course, which of these scenarios is right determines the course of treatment. If the disease is primarily autoreactive then we would do one thing, but if the disease is primarily ODC related, we would need another approach. Hence, the animal model chosen to test the efficacy of new drugs depends on which of these scenarios is being followed. The primary animal model now being used is the Experimental autoimmune encephalomyletis (EAE) which is induced in mice. We know people who have been immunized against mylenin basic protein for rabies using material purified from rabbit brains have developed ADEM which resembles EAE. So the EAE mice model makes a lot of sense to pursue. EAE is induced in mice a variety of ways and generates Type I lesions and sometimes Type II. The methods at first involved injections of various mylenin proteins such as mylenin oligodendrocyte glycoprotein (MOG). However, new techniques have arisen using transgenesis. These used TcR transgenic models established in various mouse lines. These models showed spontaneous EAE and allowed new discoveries about tolerogenic mechanisms due to peripheral tolerance to T regulatory cells. A breakthrough occurred when the variant MOG_35-55 peptide was discovered to by autoantigenic and an efficient EAE inducing peptide.

An unresolved question in MS is that the number of CD8 T cells might outnumber the number of CD4 T cells in the MS lesions. There are questions about whether the mylenin damage is primarily due to CD4 T cells or whether it can be due to CD8 T cells. A number of experiments have been performed which show CD8 T cells can cause mylenin damage without the CD4 T cells being involved, but there remain questions and as of the year of the review in ^[7], it has not been resolved. Nevertheless, we are taking the view that the CD8 T cell involvement is possible along with the CD4 T cell pathway. Experiments in the 1980's showed conclusively that T cells are critical for the induction of EAE. However, mysteries remained. At first, EAE was thought of as a Th1 autoimmune disease where Th1 was an influential line of T helper cells. The amount of IFN-γ released from periphery of these cells and the lesions seemed very important. But then it was found that mice lacking IFN-γ were not resistant to EAE and instead were hyper susceptible. Further, when mice lacked the materials to develop Th1, such as IL-12,they were also hyper susceptible to EAE. Eventually it was shown that IL-23 is essential for the development of EAE. It was then shown that IL-23 is needed to develop T helper cells that produce IL-17. These cells are now named TH17s and have been accepted as a new T helper population. Further work has shown that IL-23 may not be needed for the development of the TH17 sub population but actually helps stabilize them.

Recently, there have been a number of illuminating reviews. There is a good summary discussion of how immunomodulation might effect MS in ^[8]. The genetics of multiple sclerosis is explored in ^[9]. The creation of the correct pools of B and T Cells from naive ones is determined by the individual's genetics to some extent. Hence, it is possible there is a genetic component to the self affinity model equations. Further information about the interplay between bacteria and viral vectors for possible MS causal analysis can be found in examining how therapies to find infections helps ameliorate MS progression ^[10]. Further, the role of viruses in the onset of MS is not well understood and in ^[11], there is a careful review of what we think we know. There are also new tools on the horizon: engineered T Cells can be used to both probe immune response and potentially help with disease. A review of the use of synthetic biology tools used to expand T Cell capability is in ^[12]. Some of the engineered T Cells are called CAR-T Cells and their design and implementation are outlined in ^[13]. The models we have presented may be useful in delineating how to find the right engineered T Cell design for therapeutic use. Finally, a most interesting connection between the intestinal biome and autoimmunity in the brain is presented in ^[14]. The model discussed shows how such gut interactions might enable immune interactions to cross the blood brain barrier surrounding the brain. It is notable that a healthy gut biome probably includes hundreds if not thousands of coexisting bacterial species whose presence in the gut influences immune response. It is essential that we study abstract models of these systems as the number of independent components is beyond our ability to simulate in detail. The models we present here are a small step in this direction.

---

5 Conclusions

So the question is why does a T cell become pathogenic? A T cell type produces many different factors and cytokines. Further experiments have shown that the Th17 sub population is very plastic and these cells tend to lose their cytokines and transcription factors both in vitro and in vivo. They readily express IFN-γ under appropriate conditions.

Our model gives us some insight into a pathway to an autoimmune event in the case of a long term viral infection as described above. If a viral agent has an epitope similar to a self protein--for example, simple to a protein carried by a mylenin sheath cell--then a large pool of T Cells is maintained whose affinity for this self protein is close to a binding event. From the graphs of frequencies above, we can see if this pool is large enough, even a small probability of a positive binding can lead to a successful binding event.

If the initial binding event between the TcR and the pMHC holds for T seconds before the scaffolding proteins break bonds, there is a window of T seconds for another virally generated T Cell to bind with the pMHC containing the self protein peptide. The probability of another binding is much enhanced by having a large pool of T cells that bind weakly to the self protein pMHC. If this binding occurs before T seconds elapses, additional positive feedback occurs.

Each binding event which leads to positive feedback is effectively increasing A and from Figure 6b, we see the increase in A moves us to the right on the Figure. This increases the probability of immunosynapse formation and a subsequent lysis event. The avidity chain

$𝒜=e_E^1{\Delta }^{1}t+e_E^2{\Delta }^{2}t+e_E^3{\Delta }^{3}t+...+e_E^N{\Delta }^{N}t$

thus effectively is a chain for increasing A values leading to affinity spreads which are better at initiating immunosynapse formation. It is easy, however, for this chain to break. All it takes is one Δ_i to be too large and scaffolding proteins and other positive feedback events based on cytokine signalling will move backwards and the movement forward to immunosynapse formation will be compromised.

Effectively, a successful autoimmune event requires a smooth continuous path through α, δ, ξ and γ space to be successful. As a mathematical aside, this will not be possible in general in the end state desired lies in a separate component of the topological space which the α, δ, ξ and γ reside in.

Note our model of an affinity threshold computation depends on a wide variety of factors including geometry of the interaction between the T cell and the pMHC via the angle φ and ligand interactions of various sorts. The affinity threshold equation in conjunction with serial chains of T cell-pMHC bindings sheds insight into some autoimmune events by helping us think about the rise of a weakly bound T cell-pMHC affinity to the level of lysis. The affinity threshold equation is just the first step however, As discussed above, we also need a general model of cytokine signalling and a way to organize the immunosynapse responses in a network setting. To organize the immunosynapse responses, we also need to look at the cytokine signal data modeling in terms of manifolds and to apply ideas from topology.

---

Acknowledgements

This research has been supported by grant W911NF-17-1-0455 from the Army Research Office.

The FindA_nities Code

A.2 The DrawSummedA_nities Code

---

A.3 MaxA_nityCurve

---

Conflict of interest

The author has no conflicts of interest in this paper.

---