Stability implies constancy for fully autonomous reaction-diffusion-equations on finite metric graphs

1.   Introduction

In a fundamental paper of 1979 H. Matano [18] showed that autonomous reaction-diffusion equations involving the Laplacian under Neumann boundary conditions in a convex $\mathcal{C}^3$-domain cannot possess stable (spatially) nonconstant stationary solutions. The present paper deals with the non existence of stable nonconstant stationary solutions of reaction-diffusion-equations on the edges of a metric graph and natural transition conditions at the vertices. The parabolic problem in question reads

where $\left\{k_j| 1\leq j\leq N\right\}$ denotes the edge set of the metric graph $G$ and where the subscript $K$ stands for the validity of the Kirchhoff condition

at each vertex $v_i$ of the graph. Note that we do not require the coefficients in (2) to be consistent with the diffusion coefficient, i.e. we do not impose $c_{ij} = 1$, but only the dissipativity assuring condition that all $ c_{ij}>0$. At the ramification nodes we impose the continuity condition

that clearly is contained in the condition $u\in \mathcal{C}(G)$. Throughout, the constant coefficients and nonlinearities are assumed to satisfy

Now we can state the

Main Theorem 1. On any finite connected metric graph all stable stationary solutions of Problem (1) are constant.

In 2001 E. Yanagida [21] published a list of five exceptional graphs that do not allow stable nonconstant stationary solutions in the consistent case of (1), see Section 5. Moreover, he established some fundamental instability tools, as the instability criterion in the presence of two different critical points in one edge. In 2015 the authors [9] showed that the assertion of the Main Theorem holds for any metric graph with sufficiently small edge lengths, as well as for any metric graph for the cubic balanced case $f(u) = u-u^3$, for $f(u) = \eta\ \sin(u)$ and for some other nonlinearities. Other recent instability criteria, also for dynamical Kirchhoff conditions, can be found in [11].

At first glance, the main result might seem to be surprising in view of the existence of stable nonconstant stationary solutions on non convex domains in higher dimensions, see [13,18] and the references therein. But, as it stands, with respect to the autonomous semilinear parabolic flows defined by (1), finite metric graphs behave like one-dimensional objects, i.e. like intervals of the real line. Clearly, Problem (1) can be regarded as an abstract interaction problem on a suitable interval in the sense of Gramsch and Ali Mehmeti, see e.g. [3,7], where the node transition conditions can be read as equivalent Cauchy conditions of order $0$ and $1$ and identifying conditions at interior points and on the boundary of the interval. However, tame deviations from the autonomous character of the differential equations as different diffusion coefficients or edge dependent nonlinearities can lead to the existence of nonconstant stable stationary solutions, see Section 8.

The present paper is organized as follows. After some stability prerequisites and graph theoretical preliminaries in Section 2, Section 3 presents the exclusion of stable nonconstant stationary solutions on paths and circuits. The basic cutting technique that is a crucial tool in showing the main theorem, is established in Section 4 for more general reaction-diffusion-problems and states, for short, that if the metric graph $G$ allows the stationary solution $u$ and if it is cut at some point $p = \pi_j(x_j)$ with $\partial_ju_{j}(x_j) = 0$, then stability of the corresponding solution on the resulting graph $\tilde{G}$ is equivalent with the one of $u$ on $G$. As another extension technique the edge doubling is presented at the end of this section. In Section 5 we present some elementary cases of graphs that exclude stable nonconstant stationary solutions. In Section 6 the proof of the main theorem will be given, first for trees and then for a general finite metric graph where the first case is a key tool of a recurrence procedure using the corank of the graph. In Section 7 some energy and localization results for stationary solutions in the consistent case are treated, based on the Hamiltonian system associated to the edge differential equations. Finally, Section 8 presents some examples of stable nonconstant stationary solutions of non autonomous problems as edge dependent diffusion coefficients or edge dependent nonlinearities, as well as under different node transition conditions.

2.   Metric graphs and stability

For any graph $\Gamma = (V, E, \in)$, the vertex set is denoted by $V = V(\Gamma)$, the edge set by $E = E(\Gamma)$ and the incidence relation by $\in \subset V\times E$. The valency of each vertex $v$ is denoted by $\gamma(v) = \#\{k\in E| v\in k\}$ counting incident loops twice. Unless otherwise stated, all graphs considered in this paper are assumed to be nonempty, connected and finite with

The vertices will be numbered by $v_1, \ldots, v_n$, the respective valencies by $\gamma_1, \ldots, \gamma_n$, and the edges by $k_1, \ldots, k_N$. The boundary vertices $V_{\rm b} = \{v_i\in V| \gamma_i = 1\}$ will be distinguished from the ramification nodes $V_{\rm r} = \{v_i\in V|\gamma_i\geq 2\}$ and the essential ramification nodes $V_\text{ ess} = \{v_i\in V|\gamma_i\geq 3\}$. By definition, a circuit is a connected and regular graph of valency $2$. A path is a connected graph with two distinct vertices of valency $1$ while the other vertices are all of valency $2$. By definition, a viaduct $\pi$ in $\Gamma $ is a path in $\Gamma $ joining two distinct vertices $v$ and $\tilde{v}$ such that there is no other walk in $\Gamma $ joining $v$ and $\tilde{v}$ having a vertex in the set $V(\pi)\backslash\{v, \tilde{v}\}$. For further graph theoretical terminology we refer to [12,20].

Moreover, we consider each graph as a topological graph in $\mathbb{R} ^m$, i.e. $V(\Gamma )\subset \mathbb{R} ^m$ and the edge set consists in a collection of Jordan curves

with the following properties: Each support $k_j = \pi_j\left([0, \ell_j]\right)$ has its endpoints in the set $V(\Gamma )$, any two vertices in $V(\Gamma )$ can be connected by a path with arcs in $E(\Gamma )$, and any two edges $k_j\not = k_h$ satisfy $k_j\cap k_h\subset V(\Gamma )$ and $\#(k_j\cap k_h)\leq 2.$ The arc length parameter of an edge $k_j$ is denoted by $x_j$. Unless otherwise stated, we identify the graph $\Gamma = (V, E, \in)$ with its associated metric graph, network or quantum graph

especially each edge $\pi_j$ with its support $k_j$. Throughout it will be assumed that all $\pi_j\in\mathcal{C}^2 ([0, \ell_j], \mathbb{R} ^m)$. Thus, endowed with the induced topology $G$ is a connected and compact space in $\mathbb{R} ^m$. Throughout, we shall denote the total graph length by

The orientation of the graph $\Gamma$ is given by the incidence matrix $ \mathcal{D}(\Gamma) = \left(d_{ik}\right)_{n\times N}$ with

For a function $u:G \to \mathbb{C} $ we set $u_j: = u\circ\pi_j:[0, \ell_j]\to\mathbb{C} $ and use the abbreviations

Endowed with a usual product norm we set

for $p\in[1, \infty]$ and $k\in\mathbb{N} $, respectively. The validity of the Kirchhoff law (2) in a function space will be indicated by the subscript $K$. In particular, for $m\in\mathbb{N} ^*, r\in\mathbb{N} $ we set

and for functions depending also on a time variable that ranges in an interval $I$, $\mathcal{C}_{K}^{m, r}(G\times I)$ denotes the vector space of all the functions $u\in \mathcal{C}(G\times I)$ satisfying (2) and

Closing this section we recall Lyapunov's notion of stability associated to the following reaction - diffusion - problem

under the hypotheses

A stationary solution $w$ of Problem (5) is called stable if for each $\epsilon>0$, there exists a $\delta>0$ such that, for each initial data $u_0\in \mathcal{C}(G)$ with $\left\| u_0-w \right\|_{\infty, G}<\delta$ the solution $u$ of (5) exists in $[0, \infty)$ and satisfies

Several instability criteria have been established in [9], among which we cite the following.

Lemma 2.1. If a stationary solution $u\in\mathcal{C}_K^2(G)$ of (5) under consistent Kirchhoff conditions satisfies either

then $u$ is unstable.

Moreover, let us cite the following elementary result from [9].

Lemma 2.2. A stationary solution $u\in\mathcal{C}_K^2(G)$ of (5) with consistent Kirchhoff conditions satisfies

for all $k\in\mathbb{N} $. If, in addition, $u$ is nonconstant, then the last inequality is strict.

On all finite metric graphs it can happen that there are no stationary solutions at all. E.g. for $f\equiv 1$, there is no such solution $u\in \mathcal{C}_K^2(G)$ of (1) with a consistent Kirchhoff law, since such a solution would have to fulfill $\int_G \partial^2 u\ dx = 0$ by the Kirchhoff flow condition (2).

3.   Paths and circuits

In this section we establish the exclusion of stable nonconstant stationary solutions on paths and circuits. Let $u\in \mathcal{C}^{2}_{K}(G)$ be a stationary solution of the autonomous and consistent problem

Recall that the Rayleigh quotient of the linearized elliptic operator at $u$ for (7) is given by

and that its admissible functions $\varphi$ are just given by the elements of $\mathcal{C}(G)\cap H^1(G)$. Set $\psi_j = \partial_ju_{j}$. On each edge $k_j$, $\psi_j$ satisfies the linearized equation

by standard regularity arguments. Now let $\Pi$ be a path with $N$ edges and vertices numbered by $1, \ldots, N+1$ such that $v_i$ and $v_{i+1}$ are adjacent, and such that $V_\textrm{b} = \left\{v_1, v_{N+1}\right\}$ forms the set of boundary vertices. The incidence matrix is given by

Lemma 3.1. Suppose that $u\in\mathcal{C}_K^2(\Pi)$ is a nonconstant stationary solution of (7) on the path $\Pi$. Then $u$ is unstable, more precisely

Proof. Here, in fact, $\psi = \left(\psi_j\right)_{N\times 1}$ defines an admissible function for the Rayleigh quotient since $\psi$ constitutes a function belonging to $\mathcal{C}^1 \left[0, L\right] $ by the consistent Kirchhoff condition in (7), by (3) and by the edge differential equations. Thus, denoting the numerator of $R(\varphi ;u)$ by $\mathcal{N}(\varphi )$, we obtain by (8)

since (3) and $f(u(v_i)) = -\partial_j \psi_{j} (v_i)$ imply

Thus, $R(\psi;u) = 0$ and, in turn, $\lambda_0(u)\leq 0$. If $\lambda_0(u)<0$, the instability follows from [9,21]. It remains to exclude the case $\lambda_0(u) = 0$. But, in that case, $\psi$ is not only admissible, but an eigenfunction belonging to the simple eigenvalue $\lambda_0 = 0$ and has a sign, say $\psi_j(x_j)>0$ at every point of $\Pi \backslash \left\{v_1, v_{N+1}\right\} $. By a well-known property of unrestricted minimizers of $R$ in $\mathcal{C}(\Pi)\cap H^1(\Pi) = H^1[0, L]$, see e.g. [1,2,7,18,19], the function $\psi$ satisfies the Kirchhoff condition in (7), in particular

But as a solution of the second order linear ODE $\partial_j^2 \psi_{j}+f'(u_j)\psi_j = 0$ on each edge $k_j$, $\psi_1$ vanishes identically by uniqueness, as well as all the other $\psi_j$ do by connectedness of $\Pi$, by the Kirchhoff condition and by (3). Thus, by continuity, $u$ must be constant, which leads to a contradiction.

Now we consider the general Kirchhoff law (2) on the path. As on all trees due to its homogeneous character, it can be written in the form

with positive constants $c_{j}$ on each edge, that leads to a self-adjoint resolvent by using a suitable scalar product and to the Rayleigh quotient

with $c = (c_j)_{N\times 1}$. Note that (11) is also the Kirchhoff law considered by Yanagida [21], as well as in [8] in order to reduce the eigenvalue asymptotics on trees to a consistent case. In fact, on the path $\Pi$, the form (11) is readily achieved by setting

The same technique applies on arbitrary trees and shows that for equilibria the linearized stability under (2) and (11) are equivalent. Set

As $0$ is the minimal eigenvalue of the Laplacian $- \left(\partial_j^2\right)_{N\times 1}$, and as the only harmonic functions on a finite metric graph are the constant ones, an equilibrium $u_0$ of (1) on a tree leads to

for all positive coefficients $c$.

Theorem 3.2. Let $\Pi$ be a path. Then any stationary nonconstant solution $u\in\mathcal{C}_{K}^2(\Pi)$ of the problem

is unstable.

Proof. The assertion is true on an interval by Matano's result [18,21]. Thus, we can assume that $N\geq 2$. Suppose that $u\in\mathcal{C}_K^2(\Pi)$ is a stable nonconstant stationary solution of (14) on $\Pi$. Distinguish the following three cases.

If $\partial_j u_j(x_j) = 0$ for some $x_j\in [0, \ell_j] $ with $\pi_j(x_j)\not\in V_b$ and $k_j\cap V_b\ne\emptyset$, then $u$ would be unstable by [9,Lemma 4.4] or Yanagida's Two Points Lemma [21], which is impossible.

If $\partial_j u_j(x_j) = 0$ for some $x_j\in [0, \ell_j] $ with $k_j\cap V_b = \emptyset$, then $\Pi$ splits up at $\pi_j(x_j)$ into two paths having less than $N$ edges and on which the restrictions of $u$ would be unstable by recurrence, which is impossible.

Thus, we are lead to the final case

Write $(K)$ in the form (11) and set $\psi_j = c_j\partial_j u_j$ on each edge, where it solves $\partial_j^2 \psi_{j}+f'(u_j) \psi_{j} = 0$. By (11), the $\psi_j$ define a function

If $\partial_1\psi_1(0) = 0$, then $\psi_1$ vanishes identically on $k_1$, and $u$ has to be constant on $k_1$. Omitting this edge, the restriction of $u$ to the remaining edges has to be unstable by recurrence, which is impossible. The same argument applies to $\partial_N\psi_N(\ell_N) = 0$. Thus, we can assume that

Denoting the numerator of $ R\left(\psi;u; \left({c_j}^{-1}\right)\right)$ by $\mathcal{N}\left(\psi;u; \left({c_j}^{-1}\right)\right)$ we get

since (3) and $c_jf(u(v_i)) = -\partial_j \psi_{j} (v_i)$ imply

Thus,

We conclude that the edge Schrödinger operators $\partial_j^2 +f'(u_j) $ in $H^1(\Pi)\cap \mathcal{C}(\Pi)$ under the Kirchhoff condition

lead to a Rayleigh quotient satisfying

Clearly, $\psi$ does not fulfill (16). But, if $\lambda_0 = 0$, then $\psi$ is a minimizer of $R\left(\cdot;u; \left({c_j}^{-1}\right)\right)$ and fulfills (16), in particular the Neumann condition at $v_1$ and $v_{N+1}$, which is impossible by (15). Thus, we can assume that there is $\eta\in\mathcal{C}^2(\Pi)$ satisfying (16) such that

This means that the zero solution is unstable for the edge operators $\partial_j^2 +f'(u_j) $ in $H^1(\Pi)\cap \mathcal{C}(\Pi)$ under (16). But all the norms

are equivalent in $ \mathcal{C}(\Pi)$, which implies that the zero solution is unstable for $\partial_j^2 +f'(u_j) $ in $H^1(\Pi)\cap \mathcal{C}(\Pi)$ under any dissipative Kirchhoff law too, in particular under $(K)$. Using the same argument as in [21,Lemma 2.3] in order to show that negative values of the Rayleigh quotient lead to instability, we conclude that $u$ is unstable.

On a circuit $\zeta$ the derivatives of a nonconstant stationary solution $u\in \mathcal{C}^{2}_{K}(\zeta)$ have to vanish at least twice. By cutting $\zeta$ at one of these points, we are led to a path to which the foregoing results can be applied. Thus we can state the

Corollary 1. Let $\zeta$ be a circuit and $u\in \mathcal{C}^{2}_{K}(\zeta)$ be a nonconstant stationary solution of the problem

Then $u$ is unstable.

Proof. Suppose that $u$ is stable on $\zeta$. By compactness, there is $\pi_j(x_j) = p\in\zeta$ such that

Cut the circuit at $p$ into two boundary vertices $\tilde{v}_1$ and $\tilde{v}_{N+1}$ and get a path $\tilde{\Pi}$ whose quantities stemming from $\zeta$ will be denoted by a tilde. In particular, $\tilde{u}\in \mathcal{C}^{2}_{K}(\tilde{\Pi})$ defines a nonconstant stationary solution of (19) on $\tilde{\Pi}$ with the distinguished property

Clearly, $ \mathcal{C}(\zeta)$ can be identified with $\mathcal{F}$. By Theorem 3.2, $\tilde{u}$ is unstable on $\tilde{\Pi}$. Thus, there is some $\widetilde{\varepsilon } _0>0$ such that for each $\delta>0$ there is an initial data $\tilde{w}_0\in \mathcal{C}(\tilde{\Pi})$ with $ \left\| \tilde{w}_0-\tilde{u}\right\|_{\infty, \tilde{\Pi}}< \delta $ and

for some $t_0>0$ where $\tilde{w}$ denotes the solution of (19) with initial condition $\tilde{w}_0$ on $\tilde{\Pi}$.

For each $0<\varepsilon < \widetilde{\varepsilon } _0$ there is some $\delta>0$ such that the solution $z\in\mathcal{C}(\zeta\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(\zeta\times(0, \infty))$ of (19) with initial condition $ \left\| {z}_0-{u}\right\|_{\infty, {\zeta}}< \delta $ satisfies

But for each $t> 0$, $\widetilde{z(\cdot, t)}$ belongs to $\mathcal{F}$, and $\tilde{z}$ is the solution of (19) on $\tilde{\Gamma}$ with initial condition $\tilde{z}_0 = \widetilde{z(\cdot, 0)}$. This leads to the contradiction

4.   Stability surgery

In this section we establish some basic facts and results about stationary stable or unstable classical solutions of the more general reaction - diffusion - problem

under the hypotheses (6). In particular we compare the stability on a metric graph $\Gamma$ with the one on a modified graph $\tilde{\Gamma}$ obtained by cutting an edge at a zero of the derivative of a stationary solution. In [6,7], a general Osgood type $L^\infty$-estimate for nonlinear parabolic problems on metric graphs has been shown. For the reader's convenience and for the proofs of Theorems 4.2 and 6.1, we cite it here in the setting of the special case (5).

Theorem 4.1. [6,7] Suppose $T\geq 0$ and let $u\in \mathcal{C}(G\times[0, T]\cap \mathcal{C}^{2, 1}_{K}(G\times(0, T])$ be a solution of Problem (5) subject to the Osgood condition

Then, the following estimate holds:

The basic reduction tool for establishing instability is the following surgery technique.

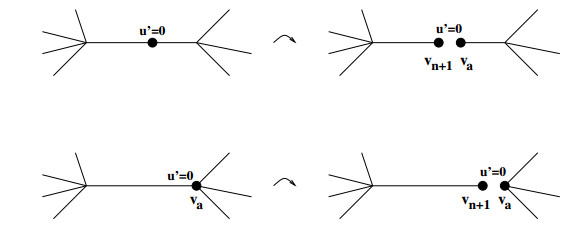
Theorem 4.2. Suppose that $u\in\mathcal{C}_K^2(G)$ is a stationary solution of (5) such that $\partial_ju_{j} (x_j) $ vanishes at $p = \pi_j(x_j)$ on some edge $k_j$. Cut the graph $\Gamma$ at $p$ and get a new possibly non connected graph $\tilde{\Gamma}$ on which $u$ defines a stationary solution $\tilde{u}$ of (5) on $\tilde{\Gamma}$ that belongs to $\mathcal{C}_{\tilde{K}}^2(\tilde{G})$. Here the Kirchhoff conditions $\tilde{K}$ extend the old one $(K)$ by adding the Neumann condition at the new vertex or at the two new vertices. In the first case note that $p = v_i$ leads to $\tilde{d}_{ij} = 0$.

Then $\tilde{u}$ is stable on $\tilde{\Gamma}$ if and only if $u$ is stable on $\Gamma$.

Proof. First, we consider the case where there is some constant $b_1\geq 0$ such that

The cutting of the edge $k_j$ defines one or two new vertices in $\tilde{\Gamma}$ that will be denoted by $v_{a} \in \left(V_{\rm b}(\tilde{\Gamma}) \backslash V({\Gamma})\right)\ \dot{\cup}\ \left(V(\tilde{\Gamma}) \cap V({\Gamma})\right)$ and $v_{n+1} \in V_{\rm b}(\tilde{\Gamma})\backslash V({\Gamma})$. Note that $v_{a} \in \left(V_{\rm b}(\tilde{\Gamma}) \backslash V({\Gamma})\right)$ corresponds to $x_j\in (0, \ell_j)$ and to a new boundary vertex, while $v_{a} \in \left(V(\tilde{\Gamma}) \cap V({\Gamma})\right)$ means that $p\in V({\Gamma})$. Set

and for $\varphi \in\mathcal{C}(G)$ and identifying $ G\backslash \{v_{n+1}, v_a\}$ with $\tilde{G}\backslash \{v_{n+1}, v_a\}$,

Then

is an isometric isomorphism with respect to both $L^\infty$-norms between $\mathcal{C}(G) $ and $ \tilde{C} = \iota \left(\mathcal{C}(G)\right)$. Moreover, $ \overline{\iota(F)} = \iota \left(\mathcal{C}(G)\right) $, since $\overline{F} = \mathcal{C}(G) $ by the Stone-Weierstrass-Theorem. This shows immediately that if $u$ is unstable on $\Gamma$, then $\tilde{u}$ is unstable on $\tilde{\Gamma}$.

Now, suppose that $\tilde{u}$ is unstable on $\tilde{G}$. Thus, there is some $\widetilde{\varepsilon } _0>0$ such that for each $\delta>0$ there is an initial data $\tilde{w}_0\in \mathcal{C}(\tilde{G})$ with $ \left\| \tilde{w}_0-\tilde{u}\right\|_{\infty, \tilde{G}}< \delta $ and $ \left\| \tilde{w}(\cdot, t_0)-\tilde{u}\right\|_{\infty, \tilde{G}}\geq \widetilde{\varepsilon } _0 $ for some $t_0>0$ where $\tilde{w}$ denotes the solution of (5) with initial condition $\tilde{w}_0$ on $\tilde{G}$. Set $\varepsilon _0 = \frac12 \widetilde{\varepsilon } _0$, and choose $\delta$ such that

If $\tilde{w}_0\in \overline{\iota(F)} = \tilde{C}$, then, by uniqueness, $w: = \iota^{-1}(\tilde{w})$ is the solution of (5) with initial condition $w_0$ on $G$ that satisfies $ \left\| {w}_0-u\right\|_{\infty, G}< \delta $ and $ \left\| w(\cdot, t_0)-u\right\|_{\infty, G}\geq \widetilde{\varepsilon } _0 >e_0 $.

Next, suppose that $\tilde{w}_0\not\in \overline{\iota(F)}$. As $\tilde{u}$ belongs to $\iota(F)$, and as $ \left\| \tilde{w}_0-\tilde{u}\right\|_{\infty, \tilde{G}}< \delta $, we can nevertheless choose $\tilde{z}_0\in \mathcal{C}(\tilde{G})\cap \overline{\iota(F)}$ with $|\text{supp}(\tilde{w}_0-\tilde{z}_0)|$ sufficiently small such that $ \left\| \tilde{z}_0-\tilde{w}_0\right\|_{\infty, \tilde{G}}<\delta$. Let $\tilde{z}$ denote the solution of (5) on $\tilde{G}$ with initial condition $\tilde{z}_0$ and $z$ be the solution of (5) on $G$ with initial condition $z_0 = \iota^{-1}(\tilde{z_0})$. Again, by uniqueness, $z = \iota^{-1}(\tilde{z})$.

Now we claim

Proof. $(\ast)$ The difference $d = z-w\in \mathcal{C}(G\times[0, t_0])\cap \mathcal{C}^{2, 1}_{K}(G\times(0, t_0])$ satisfies on each edge $k_j$ the equation

with a function $\lambda:\mathbb{R} \to [0, 1]$. Since the coefficient of the linear term $d_j$ is bounded from above by $b_1$, the Osgood type a priori estimate in Theorem 4.1 with $b_2 = 0 $ yields

This shows the claim $(\ast)$. Finally, we conclude

Thus, $u$ is unstable on $G$.

Finally, in order to get rid of (20), i.e. for arbitrary nonlinearities $f_j\in\mathcal{C}^1(\mathbb{R} )$, we modify them for the given stationary nonconstant solution $u\in\mathcal{C}_{K}^2(G)$ of (5) outside $[-2M, 2M]$ with $M: = \left\| u\right\|_{\infty, G}$ as follows

Thus, $u$ would be a stable nonconstant solution of (28) with the nonlinearities $\widetilde{f}_j$ iff $\tilde{u}$ would be a stable by the results shown first. This concludes the proof of the theorem.

As a first application of the surgery theorem 4.2 we generalize Yanagida's Two Points Lemma [9,21] known in the constant coefficients case under consistent Kirchhoff conditions to the more general problem (5).

Lemma 4.3. Suppose that $u\in\mathcal{C}_K^2(G)$ is a stationary solution of (5) that is nonconstant on some edge $k_j$. If there are two points on $k_j$ with $0\leq z_1<z_2\leq \ell_j$ such that $ \partial_ju_{j}(z_1) = \partial_ju_{j}(z_2) = 0$, then $u$ is unstable. If, in addition, the nonlinearity $f_j$ is an odd function, then the same conclusion holds, if there are two points on $k_j$ with $0\leq z_1<z_2\leq \ell_j$ such that $ u_{j}(z_1)\partial_j u_{j}(z_1) = 0 = u_{j}(z_2)\partial_j u_{j}(z_2).$

Proof. In the first case, we cut the edge $k_j$ twice and obtain instability on the resulting sole edge as a stationary solution of a Neumann problem by a result by Matano [18]. Then Theorem 4.2 permits to conclude. In the second case, the assertion can be shown exactly in the same way as in the consistent and constant coefficient case shown in [9,Lemma 4.5].

As already pointed out in [9], the hereditary properties of the stability notion with respect to subgraphs are very bad. However, the edge doubling is a simple extension technique that permits to conclude for stability from a graph containing the original one. Choose any edge $k_j$ incident to $v_i$ and $v_h$ in $\Gamma$ and copy all quantities and functions associated to $k_j$ on a new edge $k_{N+1}$ incident to $v_i$ and $v_h$ as well in the new graph $\tilde{\Gamma}$ with $E(\tilde{\Gamma}) = E(\Gamma)\cup \left\{k_{N+1}\right\}$ and $V(\tilde{\Gamma}) = V(\Gamma)$ except for the conductivities that are defined by

and lead to the Kirchhoff conditions denoted by $(\tilde{K})$. Then we can state the following

Lemma 4.4. Suppose that $u\in\mathcal{C}_K^2(G)$ is a stationary solution of (5). Let $\tilde{\Gamma}$ be the graph resulting from an edge doubling described above and $\tilde{u}\in \mathcal{C}_{\tilde{K}}^2(\tilde{G})$ be the corresponding extension of $u$ to $\tilde{G}$ by setting $\tilde{u}_{N+1} = \tilde{u}_j = u_j$. Then $\tilde{u}$ is stable on $\tilde{\Gamma}$ if and only if $u$ is stable on $\Gamma$.

Proof. Each $w\in\mathcal{C}_K^1(G)$ defines uniquely $\tilde{w}\in \mathcal{C}_{\tilde{K}}^1(\tilde{G})$. This leads to the continuous embedding

Thus, identifying $\mathcal{C}(G)$ with $\mathcal{F}: = \left\{\tilde{w}\in \mathcal{C}(\tilde{G})| \tilde{w}_{N+1} = \tilde{w}_j\right\}$, the stability of $\tilde{u}$ in $\mathcal{C}(\tilde{G})$ implies its stability in the closed subspace $\mathcal{F}$ and thereby, the stability of $u$ in $\mathcal{C}(G)$.

Conversely, suppose that $\tilde{u}$ is unstable on $\tilde{\Gamma}$, but that $u$ is stable in $\mathcal{C}(G)$. In fact, we can proceed as in the proof of Corollary 1. Thus, there is some $\widetilde{\varepsilon } _0>0$ such that for each $\delta>0$ there is an initial data $\tilde{w}_0\in \mathcal{C}(\tilde{G})$ with $ \left\| \tilde{w}_0-\tilde{u}\right\|_{\infty, \tilde{G}}< \delta $ and

for some $t_0>0$ where $\tilde{w}$ denotes the solution of (5) with initial condition $\tilde{w}_0$ on $\tilde{G}$. For each $0<\varepsilon < \widetilde{\varepsilon } _0$ there is some $\delta>0$ such that the solution $z$ of (5) with initial condition $ \left\| {z}_0-{u}\right\|_{\infty, {G}}< \delta $ satisfies

But for each $t> 0$, $z(\cdot, t)$ belongs to $\mathcal{F}$, and $\tilde{z}$ is the solution of (5) on $\tilde{\Gamma}$ with initial condition $\tilde{z}_0 = \tilde{z}(\cdot, 0)$. By construction, this leads to the contradiction

A non trivial application of the edge doubling is given by the following example.

Example 4.1. Suppose that $N = 2 = n$, and that $\Gamma$ consists in a loop $\zeta$ of length $\ell$ with ramification node $\left\{v_1\right\} = V(\zeta)$ and in an edge $k_3$ joining $v_1$ and the boundary vertex $v_2$. Then there is no stable nonconstant stationary solution of (5) on $\Gamma$. This will be shown as follows.

Suppose that $u\in\mathcal{C}_K^2(G)$ is a stable nonconstant stationary solution of (5). If $u$ vanishes on the whole $\zeta$ or on the whole $k_3$, then the problem is reduced to an interval under Neumann boundary conditions that admits only constant stable stationary solutions.

If $v_1$ is an extremum of $u$, then the problem on $\Gamma$ splits into two interval problems. Thus, by Lemma 4.3 and compactness, the derivative $\partial_j u_j$ vanishes exactly once outside the ramification node $v_1$ on $\zeta$ in $\Gamma$, say at $p\in\zeta$, since it cannot vanish in the interior of the edge $k_3$. The point $p$ cuts $\zeta$ into two edges, say $k_1$ and $k_2$, on which $u_1$ and $u_2$ respectively are strictly monotone by Lemma 4.3. Moreover, $u_1$ and $u_2$ fulfill

By unique solvability of the corresponding Cauchy problems, $u_1$ and $u_2$ coincide for $0\leq x_j\leq \min \left\{\ell_1, \ell_2\right\} $, where we have chosen $d_{11} = d_{12} = 1$. But, by continuity at $v_1$

Thus, if $k_1$ and $k_2$ were of different length, Rolle's Theorem and Lemma 4.3 would lead to instability of $u$. We conclude that $k_1$ and $k_2$ are of the same length

and that

Choose $ d_{13} = -1$ and denote the boundary vertex by $v_2$. Note that the conductivities on the loop at $v_1$ are identical, and the original Kirchhoff condition at $v_1$ reads

Cutting $\zeta$ at $p$ and omitting $k_2$ leads to a path $\Pi$ of two edges given by $k_1$ and $k_3$. It turns out that $\Gamma$ is just the graph $\tilde{\Pi}$ with $k_1$ doubled with $k_2$. Moreover, the restriction of $u$ to $\Pi$, say $w\in\mathcal{C}_{K_c}^2(\Pi)$ and $u = \tilde{w}$, constitutes a stable stationary solution on $\Pi$ and belongs to $\mathcal{C}_{K_c}^2(\Pi)$, where $K_c$ stands for the validity of the inconsistent Kirchhoff law (22) at $v_1$ and of the Neumann boundary condition at $p$ and $v_1$. Thus, by Theorem 3.2, $w$ and $u$ have to be constant, which leads to the desired contradiction.

5.   Yanagida graphs

Recall the following result by E. Yanagida from 2001.

Theorem 5.1. ([21]) If $\Gamma$ is one of the five graphs in Figure 5, then the reaction-diffusion problem

has no stable stationary nonconstant solution on $G$. This includes paths and circuits of arbitrary lengths of the same width $d_j>0$ on all their edges.

An important ingredient of Yanagida's proof was the self-adjoint character of the associated eigenvalue problem of the linearized problem. Note that Example 4.1 restricted to Problem (23), but without restriction on the $d_j$, yields another exceptional graph on which no stable stationary nonconstant solution can exist. In this argument only Theorem 3.2, Example 4.1 and the classical Two Points Lemma [9,21] interfere. As for paths and circuits in Section 3, we can add the following exceptional graphs.

does not admit any stable stationary nonconstant solution, if the graph $\Gamma$ is a generalized Yanagida graph with arbitrary edge lengths of Type 3, 4, or 5, i.e.

(3) either $\Gamma$ contains exactly one boundary vertex and exactly one essential ramification node, the latter being of valency $3$,

(4) or $V_\text{ b} = \emptyset$ and $ V_\text{ ess} = \left\{v_1\right\}$ and $\gamma_1 = 4$,

(5) or $V_\text{ b} = \emptyset$ and $ \Gamma$ contains exactly two essential ramification nodes, the latter being both of valency $3$ and being joined by an edge or a viaduct.

Proof. Throughout, let us suppose that $u\in\mathcal{C}_K^2(G)$ is a stable nonconstant stationary solution of (24). If $u$ is constant on some edge $k_j$ with $d_{ij}\ne 0\ne d_{hj}$, then we can identify $v_i$ and $v_h$ and omit $k_j$. Thus, we can assume that $u$ is nonconstant on each edge of $\Gamma$.

By hypothesis, $\Gamma$ is unicyclic. If some $\partial_j u_j$ vanishes at $v_1$, the graph reduces to a sole path or splits into a circuit and a path. Working with $\mathcal{C}^1$-solutions, in particular at nodes of valency $2$, we can assume w.l.o.g. that the circuit $\zeta$ is a loop of length $\ell$ and that the path joining $v_1$ and the boundary vertex $v_2$ is just an edge, say $k_3$.

Exactly as in Example 4.1 and using the notations given there, cut $\zeta$ at $p\in\zeta\backslash \left\{v_1\right\}$ into two edges $k_1$ and $k_2$ with

and $\ell_1 = \ell_2 = \frac{\ell}{2}$. Then the Kirchhoff law (22) at $v_1$ reads

Cutting $\zeta$ at $p$ and omitting $k_2$ leads to a path $\Pi$ of two edges given by $k_1$ and $k_3$. Then the restriction $\tilde{u}$ of $u$ to $\Pi$ is a stationary solution of the differential equations on the edges of $\Pi$ and belonging to $\mathcal{C}_{K_c}^2(\Pi)$, where $K_c$ stands for the validity of the inconsistent Kirchhoff law (25) at $v_1$ and of the Neumann boundary condition at $p$ and $v_1$. Denoting by $\Sigma$ the star formed by $k_1$, $k_2$ and $k_3$, respective identifying leads to the embeddings

since each $\varphi\in\mathcal{C}_{K_c}^1(\Pi)$ extends uniquely to $ \mathcal{C}_K^1(\Sigma)$ and $ \mathcal{C}_K^1(\Gamma )$ by even extension with respect to $\pi_1 \left(0\right) = p = \pi_2 \left(0\right)$ onto the remaining edge $k_2$. This leads to stability of the restriction $\tilde{u}$ of $u$ to $\Pi$ as follows. First, note that if $w\in \mathcal{C}_{K_c}^{2, 1}(\Pi\times [0, \infty))$ is the solution on $\Pi$ with initial condition $w_0\in \mathcal{C}(\Pi)$, and if $\bar{w}\in\mathcal{C}_K ^{2, 1}(\Gamma\times [0, \infty))$ is the solution on $\Gamma$ with initial condition $\bar{w}_0\in \mathcal{C}(G)$ such that $\bar{w}_0 = \iota(w_0)$, then these solutions coincide by uniqueness of the corresponding flow, i.e.

Secondly, for $\varepsilon>0$ and $\delta>0$ such that $\left\|u-z_0\right\|_{\infty, \Gamma}<\delta $ implies $\left\|u-z(\cdot, t)\right\|_{\infty, \Gamma}<\varepsilon $ for all $t>0$, we conclude for an initial condition $w_0\in \mathcal{C}(\Pi)$ with $\left\|\tilde{u}-w_0\right\|_{\infty, \Pi}<\delta $ that

Thus, the restriction of $u$ to $\Pi$ is stable there, which is impossible by Theorem 3.2. This achieves the proof in Case (3).

By Lemma 4.3, on each loop or circuit in $\Gamma$ the derivative $\partial_j u_j$ vanishes exactly once outside the ramification node $v_1$. As in Case (3), this allows the reduction to two pairs of edges of identical lengths that, in turn, lead to a restriction to a path of two edges even under a consistent Kirchhoff condition at the ramification node. As above, the two evolution flows are compatible with the extension-restriction procedure and permit to conclude with Lemma 3.1, or even with Matano's classical result on an interval.

Again, dealing with $\mathcal{C}^1$-solutions, we can assume w.l.o.g. that the two circuits $\zeta_1$ and $\zeta_2$ are loops of length $\ell_1$ and $\ell_2$, respectively, and that the viaduct between the nodes $v_1$ and $v_2$ of $\Gamma$ is just an edge denoted by $k_3$. Assume that $v_i\in V(\zeta_i)$.

If $\partial_j u_j$ vanishes at some point on $k_3$, then we are led to two graphs of Case 3, or one of this type and a loop. Thus, it remains to consider the case where the derivative $\partial_j u_j$ vanishes exactly once on each $\zeta_i$ outside $v_i$. As in Case (3), this allows the reduction to two pairs of edges of identical lengths that, in turn, lead to a restriction to a path of 3 edges under an inconsistent Kirchhoff condition at $v_1$ and $v_2$ as in (25). As above, the two evolution flows are compatible and permit to conclude with Theorem 3.2.

Figure 5 presents some graphs fulfilling the conditions of Theorem 5.2, that are not in Yanagida's list. Note that the embedding (26) yields compatibility of solutions for the extension-reduction-procedure related to appropriate subgraphs. However, in general graphs, such embeddings compatible with the different involved flows do not seem to be available. They would strongly simplify subgraph reduction techniques in showing instability. Therefore, the surgery techniques from Section 4 will be applied for the general case, rather than the ones above.

6.   Proof of the main result

In this section we shall use the notation

for the outer normal derivative of a function $u$ on the edge $k_j$ at the vertex $v_i\in k_j$. First, we consider Problem (1) on a tree $T$, i.e.

under Condition (4). Theorem 3.2 settles the case of a tree without essential ramification nodes and forms part of the following

Theorem 6.1. On any finite metric tree $T$ there is no stable stationary nonconstant solution of Problem (28).

Proof. Let $u\in\mathcal{C}_{K}^2(T)$ be a stable stationary nonconstant solution of (28). For a sole edge or a path this is impossible due to Theorem 3.2. Thus we can suppose that $N>2$ and that $\# V_\text{ ess}\geq 1$, and reason by recurrence on $N$. Modifying $f$ for the given solution $u\in\mathcal{C}_{K}^2(T)$ of (28) outside $[-2M, 2M]$ with $M: = \left\| u\right\|_{\infty, {T}}$ as in (21) for the proof of Theorem 4.2, we can assume w.l.o.g. that

with some constant $b_1\geq 0$. Moreover, recall that under a dissipative Kirchhoff condition, i.e. all $c_{ij}>0$, as the third condition in (28), differentiable functions at an extremum in a vertex behave like at an interior point, and all incident derivatives have to vanish there.

If $\partial_j u_j(x_j) = 0$ for some $x_j\in [0, \ell_j] $ with $\pi_j(x_j)\not\in V_b$ and $k_j\cap V_b\ne\emptyset$, then $u$ is unstable by Lemma 4.3.

If $\partial_j u_j(x_j) = 0$ for some $x_j\in [0, \ell_j] $ with $k_j\cap V_b = \emptyset$, then $T$ splits up at $\pi_j(x_j)$ into two trees having less than $N$ edges and on which the restrictions of $u$ are stable. This is impossible by recurrence.

Thus, we conclude that $\partial_j u_j(x_j)\ne0$ except at the boundary vertices $V_{\rm b}$ at which clearly $\partial_j u_j(v_i) = 0$. It follows that on each edge $k_j$, the function $u_j$ is strictly monotone.

Choose any essential ramification node $v_i$. Then there are at least two incident edges, say $k_1$ and $k_2$, satisfying

Remove $k_1$ from $T$ and get two disjoint subtrees of $T$. Let $\tilde{T}$ denote the one containing $v_i$ and set

Then the restriction of $u$ to $\tilde{T}$ belongs to $\mathcal{C}_{\widetilde{K}}^2(\tilde{T})$ with the dissipative Kirchhoff law

and constitutes a stationary nonconstant solution of (28) on $\tilde{T}$ that has to be unstable by recurrence. Thus, there is some $\varepsilon _0>0$ such that for each $\delta>0$ there is an initial data $\tilde{w}_0\in \mathcal{C}(\tilde{T})$ with $ \left\| \tilde{w}_0-u\right\|_{\infty, \tilde{T}}< \delta $ and $ \left\| \tilde{w}(\cdot, t_0)-u\right\|_{\infty, \tilde{T}}\geq \varepsilon _0 $ for some $t_0>0$ where $\tilde{w}$ denotes the solution of (28) with initial condition $\tilde{w}_0$ on $\tilde{T}$.

Next, we modify and extend $\tilde{w}_0$ to a function $w_0$ on $T$ as follows. Choose $\delta_0$ sufficiently small such that for all $0<\delta\leq \delta_0 \leq \frac{\varepsilon _0}{4}e^{-b_1t_0}$, there exists ${w}_0\in \mathcal{C}(\tilde{T})$ that coincides with $u$ in a small neighborhood of $v_i$ and fulfills the constraints

Then define $w_0$ outside $\tilde{T}$ on $T$ simply by $u$. Evidently,

Moreover, for the solution $w$ of (28) with the initial data $w_0$ on $T$ we claim

Proof. $(\ast)$ The difference $z = w-\tilde{w}\in \mathcal{C}(\tilde{T}\times[0, t_0])\cap \mathcal{C}^{2, 1}_{\widetilde{K}}(\tilde{T}\times(0, t_0])$ satisfies on each edge $k_j$ the equation

with a function $\lambda:\mathbb{R} \to [0, 1]$. Since the coefficient of the linear term $z_j$ is bounded from above by $b_1$, the Osgood type a priori estimate in Theorem 4.1 with $b_2 = 0 $ yields

This shows the claim $(\ast)$.

By stability of $u$ on $T$, there is a $\delta\in(0, \delta_0]$ such that the initial data $w_0$ from above with $\left\| {w}_0-u\right\|_{\infty, \tilde{T}} = \left\| {w}_0-u\right\|_{\infty, {T}}< \delta$ leads to the solution satisfying

for all $t>0$. On $\tilde{T}$ evaluated at $t_0>0$, this leads to

which is absurd.

In order to achieve the proof of the general case we need a technical combinatorial lemma for graphs with circuits.

Lemma 6.2. Let $\Gamma$ be a finite graph that contains circuits of lengths at least $2$. Let the set of real numbers $\left\{\Delta_{ij}| 1\leq i \leq n, 1\leq j\leq N\right\} $ satisfy the following properties:

(a) $\forall v_i\in V_{\rm r}\ \forall j\in \left\{1, \ldots, N\right\}:\, \left(d_{ij}\ne 0 \iff\Delta_{ij} \ne 0\right)$.

(b) $\forall v_i\in V_{\rm r}:\, \sum_{j = 1}^N \Delta_{ij} = 0$.

(c) $\forall j\in \left\{1, \ldots, N\right\}\ \forall v_i, v_h\in V_{\rm r}:\, \left(v_i, v_h\in k_j\, \Longrightarrow\, \Delta_{ij} \Delta_{hj}<0\right).$

(d) Each circuit $\zeta$ in $\Gamma$ contains a pair of edges $k_j, k_s$ incident to $v_i\in V(\zeta)$ such that

Then there exists an edge $k_j$ with ramification nodes $v_i, v_h\in k_j$ or a viaduct $\pi$ with endpoints $v_i, v_h$ such that there are two edges $k_r$ and $k_s$ with

Proof. Note first that, by (c) and (d), each circuit $\zeta$ in $\Gamma$ contains a pair of edges $k_j, k_s$ incident to $v_i\in V(\zeta)$ such that $\Delta_{ij}>0$ and $ \Delta_{is}>0$ or a pair of edges $k_l, k_t$ incident to $v_m\in V(\zeta)$ such that $\Delta_{ml}<0$ and $ \Delta_{mt}<0$.

Let $\zeta$ be a circuit of length $m$ with $V(\zeta) = \left\{v_1, \ldots, v_m\right\}$ ordered by the relations $ d_{ii} = -1$ and $ d_{i+1, i} = 1$ with indices to be taken $\text{mod }m$. Suppose that

W.l.o.g. assume that $\Delta_{11}>0$ and $ \Delta_{1 m}>0$ and that each viaduct is replaced by an edge of corresponding length. Then each

By (c), $\Delta_{21}<0$. If $\Delta_{22}<0$ or $\Delta_{2j}<0$ for some incident edge outside $\zeta$, then the assertion is shown. Thus, we can assume

It follows recursively, that for $\Delta_{i, i-1}<0$, if $\Delta_{ii}<0$ or $\Delta_{ij}<0$ for some incident edge outside $\zeta$, then the assertion is shown with $v_i$ and $v_{i-1}$. Thus, we can assume

with some incident edge $k_j$ outside $\zeta$. If no pair $v_i$ and $v_{i-1}$ for $i\leq m-1$ has been found yet as asserted, then, finally, $v_{m-1}$ and $v_m$ (as well as $v_m$ and $v_{1}$) will fulfill the requirements since then

with some incident edge $k_j$ outside $\zeta$. This permits to conclude.

Note that the assertion of Lemma 6.2 does not hold on trees as simple examples readily display. Now, we can show the exclusion result in the general case.

Theorem 6.3. There are no stable nonconstant stationary solutions of Problem (1) on any finite connected metric graph $G$.

Proof. W.l.o.g. by introducing artificial nodes with Kirchhoff conditions leading to continuous differentiability, we can assume that $\Gamma$ is simple, i.e. $\Gamma$ has neither loops, nor multiple edges. We shall reason by recurrence on $d: = \text{corank}(\Gamma)$. Recall that the circuit space ${\bf{\Pi }}(\Gamma)$ of the graph $\Gamma$ is defined by

and satisfies ${\bf{\Pi }}(\Gamma) = \ker\mathcal{D}(\Gamma)$, see e.g. [12]. Moreover

that amounts to $N-n+1$ for connected graphs. For $d = 0$, the assertion is true by Theorem 6.1. Thus, we can suppose

Let $u\in\mathcal{C}_{K}^2(G)$ be a stable stationary nonconstant solution of (1). Let $k_j$ be an edge such that $\partial_j u_j(x_j) = 0$ for some $x_j\in [0, \ell_j]$ and set $p = \pi_j(x_j)$. First, consider the case that

1. If $k_j$ is incident to a boundary vertex, then Lemma 4.3 permits to conclude.

2. If $k_j$ is a bridge that is not incident to $V_{\rm b}$, then cutting at $p$ leads to two disjoint metric subgraphs $\tilde{\Gamma}_1$ and $\tilde{\Gamma}_2$ of $G$. If one of them, say $\tilde{\Gamma}_1$, were a tree, then $u$ would have to be unstable by Theorem 4.2 and Theorem 6.1. If both of them contain circuits, then clearly

By recurrence, the restrictions of $u$ to $\tilde{\Gamma}_1$ and $\tilde{\Gamma}_2$ are unstable, and so is $u$ by Theorem 4.2.

3. If $k_j$ belongs to a circuit, then cutting at $p$ leads to a graph $\tilde{\Gamma}$ of corank $d-1$. By recurrence the restriction of $u$ to $\tilde{\Gamma}$ must be unstable, and so does $u$ by Theorem 4.2.

Thus, it remains to show the assertion in the case

Use notation (27). At the endpoints $v_i, v_h\not\in V_{\rm b}$ of an edge $k_j$ or of a viaduct with $d_{ij} d_{hl}\ne 0$ we have

or $\Delta_{ij} \Delta_{hl}<0$, respectively. Thus, w.l.o.g. we can consider any viaduct as an edge in the remaining reasoning. The set of $\Delta_{ij}$ clearly satisfies the hypotheses (a)-(c) of Lemma 6.2, while Condition (d) is fulfilled by (6), by the continuity requirement at the nodes and by the strictly monotone character of each $u_j$. Thus, Lemma 6.2 guarantees the existence of an edge $k_1$ with ramification nodes $v_i, v_h\in k_1$ such that there are two edges $k_r$ and $k_s$ with

respectively. Then introduce the modified conductivities by

Finally, omit the edge $k_1$ in $\Gamma$ and proceed on the resulting and possibly non connected graph $\tilde{\Gamma}$ as in the proof of Theorem 6.1. This is possible by the local character of the modifications applied there in the vicinity of $k_1$.

7.   Common Hamiltonian edge system

The stationary case of the fully autonomous consistent parabolic problem

leads to the same first order system (33) defined by $f$ and $' = \partial_j$ on each edge, i.e.

On each edge (33) is Hamiltonian with respect to the function

Thus, a stationary solution of (32) corresponds to $N$ parts of trajectories in the phase plane of (33) related to each other by the continuity condition (3) and by the Kirchhoff law $(K)$. Let us recall from [9] some properties of stationary solutions of (32).

Proposition 1. Let $u\in\mathcal{C}_K^2(G)$ be a stationary solution of (32). Then

Moreover, if $H_j$ denotes the Hamiltonian constant of the trajectory belonging to the edge $k_j$, then for incident edges $k_j, k_s$ at $v_i$ it holds

Formula (34) applies e.g. in order to exclude stationary nonconstant solutions between $-1$ and $1$ for nonlinearities of the form $f(u) = u^{2k+1}-u^{2m-1}$ with $1\leq m\leq k$ or of the form $f(u) = -\sin(\pi u)$. Again, by Lemma 2.2, $\int_G f(u)\, dx = 0$. Thus, $f$ must have zeros and must change sign in $u(G)$. Set $z_{\min} = \min\left\{z| f(z) = 0\right\}$ and $z_{\max} = \max\left\{z| f(z) = 0\right\}$.

Lemma 7.1. Let $u\in\mathcal{C}_K^2(G)$ be a stationary solution of (32) and suppose that

Then

If, in addition, $u$ is nonconstant, then

In particular, $ \left\|u\right\|_{L^\infty(G)} \geq \max \left\{\left|z_{\min}\right|, \left|z_{\max}\right|\right\}$ implies that $u$ is one of the equilibria $z_{\min}$ or $z_{\max}$.

Proof. At a point $x_j\in[0, \ell_j]$ where $\pm\left\|u\right\|_{L^\infty(G)}$ is attained, we conclude $v_j(x_j) = 0$. But, if $u$ is nonconstant in a neighborhood of $x_j$, for $u>z_{\max}$ or $u<z_{\min}$, and $v = 0$, it holds $v'>0$ and $v'<0$ respectively, i.e. there can never be a maximum or a minimum at $(u, 0)$ respectively. Moreover, if $u$ attains $z_{\max}$ on some edge, then $z_{\max} = \max_G u$. But, by flow uniqueness, there cannot be a nonconstant trajectory arriving at the equilibrium $\left(z_{\max}, 0\right)$ on a finite interval in the phase plane. By connectedness, $u$ has to be the constant $z_{\max}$ on $G$, which is absurd. In the case that $u$ attains $z_{\min}$ on some edge, $z_{\min} = \min_G u$ which shows that $u$ has to be the constant $z_{\min}$ on $G$ with an analogous argument as above.

The lemma applies in particular to the case of the balanced cubic $f(u) = u-u^3$ treated in [9].

Remark 7.1. Without (35) the assertion of the lemma is no longer true. Clearly, for $f(z)>0$ in $(-\infty, z_{\min})$ we have $z_{\min}\leq u$, while in the case $f(z)<0$ in $(z_{\max}, \infty)$, we have $u \leq z_{\max}$. But in the general case, both conclusions are invalid. E.g. for $f(u) = u^3-u$, there are nonconstant stationary solutions $u$ defined on a suitable interval corresponding to periodic solutions surrounding the equilibria $(-1, 0)$ and $(1, 0)$ that satisfy $ \left\|u\right\|_{L^\infty(G)} > 1$. But in all the cases, by Lemma 2.2, a nonconstant stationary solution $u$ satisfies

For a Lyapunov-energy-calculus we introduce

Lemma 7.2. Let $u\in \mathcal{C}(G\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(G\times(0, \infty))$ be a solution of (1).

(a) Along $u$ the energy decreases:

(b) If $u\in\mathcal{C}_K^2(G)$ is a stationary solution of (1) , then $\mathcal{E}(u)+\mathcal{H}(u) = \left\|u\right\|_{H_0^1(G)}^2 $ and

In particular, if $u$ is an equilibrium $A$, then $ \mathcal{E}(u) = -L H(u, 0)$.

Proof. As for (a), we can follow a standard density argument using the Kirchhoff and the continuity condition:

As for (b), both assertions follow readily with the definitions and from Proposition 1.

In order to apply Lasalle's principle, we have to impose an additional condition to $f$. E.g. under the hypothesis

we obtain with $M: = \max_\mathbb{R} F^+<\infty $ that

This enables the application of Lasalle's Principle [4] in order to conclude the following

Corollary 2. Under Condition (36) the solutions $u\in \mathcal{C}(G\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(G\times(0, \infty))$ of (32) tend to stationary solutions as $t\to\infty$ with respect to $\left\|\cdot\right\|_{L^\infty(G)}$, since their $\omega$-limits belong to the set of functions satisfying $\dot{\mathcal{E}}(u) = 0$.

We apply the preceding results to the attractivity properties of the equilibria for a nonlinearity $f$ subject to the following conditions.

They clearly include the case of a cubic $f(x) = \alpha (A-x) (B-x)(C-x)$ with $\alpha >0$. Moreover, Condition (36) is satisfied with

and Corollary 2 applies. Now we can state the following results about the flow defined by Problem (32) subject to Condition (37).

Theorem 7.3. (a) The equilibrium $A$ is a local attractor, whose domain of attraction satisfies

(b) The equilibrium $C$ is a local attractor, whose domain of attraction satisfies

(c) Any nonconstant stationary solution $w\in\mathcal{C}_K^2(G)$ satisfies $A<w<C$ and $\mathcal{E}(w)\geq - M L$ and takes values in $(A, B)$ and values in $(B, C)$.

(d) A stationary solution $w\in\mathcal{C}_K^2(G)$ satisfies $ \mathcal{E}(w) = -L M $ iff $w$ is an equilibrium of minimal energy.

Proof. The claimed inclusions in (a) and (b) follow with [9,Theorem 4.1]. By continuity, Corollary 2 ensures that the solutions $u\in \mathcal{C}(G\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(G\times(0, \infty))$ of (32) with initial data $u_0$ belonging to $\mathcal{D}(A)$ or to $\mathcal{D}(C)$ satisfy $\lim_{t\to\infty} \int_G u(\cdot, t)dx = A \int_G dx = LA$ and $\lim_{t\to\infty} \int_G u(\cdot, t)dx = LC$, respectively. It follows that $\mathcal{D}(A)$ and $\mathcal{D}(C)$ belong to the sets in the middle. But according to Lemma 7.1, a nonconstant stationary solution $w$ satisfies

Thus, for $u_0$ belonging to one of the sets in the middle, its solution has to be attracted by the equilibrium $A$ or $C$, respectively.

The assertion (c) follows readily by Lemma 7.1 and (a) and (b). As for (d), $ \mathcal{E}(w) = -L M $ implies that $\left\|w\right\|_{H_0^1(G)}^2 \leq \int_G \left(F(w)-M\right)\, dx\leq 0$, which permits to conclude.

For the balanced cubic $f(u) = u^3-u$ the equilibrium $0$ is a global attractor, see [9,p.180], while for $f(u) = u-u^3$ it is not a repeller, since its basin of attraction is given by the set of continuous initial conditions $u_0$, whose solutions satisfy

see [9,Prop. 6.9]. Theorem 7.3 applies in particular to the balanced cubic $f(u) = \alpha u(A-u) (u-A) $ that defines the nonlinearity of the Schlögl system. For the latter one it has been shown in [15] that the equilibrium $0$ for the Schlögl system on a sufficiently small interval can by $L^2$-stabilized exponentially fast by a suitable Robin boundary feedback condition. The open question arises whether an analogous result holds on general metric graphs too.

8.   The non autonomous case and other transition conditions

The smallest example of the existence of a stable nonconstant stationary solution in presence of reaction terms depending on the edges is the following one.

Example 8.1. Let $\Gamma$ be the path of length $2$ with $\ell_1 = \ell_2 = 1$ and the orientation and labeling given by (9). Define $w\in\mathcal{C}^2_K(G)$ by

Then $\partial^2_1 w_1 +1 = 0$ and $\partial^2_2 w_2 -1 = 0$ in $[0, 1]$, and $u$ is stable with respect to the flow generated by the edge evolution equations $\partial_t u_j = \partial_j^2u_{j}-(-1)^j$ in $\mathcal{C}^0(G)$ (or $L^2(G)$). This follows from the fact that for any solution $u\in \mathcal{C}(G\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(G\times(0, \infty))$, the difference $\delta = u-w$ solves the heat equation $ \partial_t \delta_j = \partial_j^2\delta_j$ on each edge $k_j$. But the minimal eigenvalue of the Laplacian $- \left(\partial_j^2\right)_{N\times 1}$ under (2) and (3) is $0$. Thus, eigenfunction expansion and Dirichlet's Theorem yield

Example 8.2. If we admit homogeneous Dirichlet boundary conditions at some vertices, stable nonconstant stationary solution occur already on an interval. On $[0, \ell]$ consider the parabolic problem

Then

defines a global attractor for the solutions of (38) in $\mathcal{C}^0[0, \ell]$ (or $L^2(0, \ell)$), since for any solution $u\in \mathcal{C}([0, \ell]\times[0, \infty))\cap \mathcal{C}^{2, 1}([0, \ell]\times(0, \infty))$, the difference $\delta = u-w$ solves again the heat equation on $[0, \ell]$. But the minimal eigenvalue of the Laplacian on $[0, \ell]$ under $u(0) = 0 = u'(\ell)$ amounts to

and leads via eigenfunction expansion and Dirichlet's Theorem to the conclusion

Example 8.3. If the nonlinearity depends on the edges and on $x_j$, but not on $u$, then either there is no stationary solution or there is a unique stable one, that can be nonconstant. In detail and generalizing Example 8.1, for given $f_j\in\mathcal{C}[0, \ell_j]$ we consider the inhomogeneous heat flow problem

If $\int_G f(x)\ dx \ne 0$, then there is no stationary solution $w\in \mathcal{C}^{2}_{K}(G)$ of (39), since this would lead to

But if $f$ fulfills $ \int_G f(x)\ dx = 0$, then a unique stationary solution $w\in \mathcal{C}^{2}_{K}(G)$ of (39) can be obtained as follows. Introduce

Using $ (3)$ and $(K)$, it readily follows as in [5,7,10,16,17], that there exist unique coefficients $b_j$ and $c_j$ for $1\leq j \leq N$ such that $w\in \mathcal{C}^{2}_{K}(G)$ defined by

is the unique stationary solution of (39). As in Example 8.1, $w$ is seen to be stable, since for every solution $u$ of (39), the difference $u-w $ solves the heat equation in $\mathcal{C}(G\times[0, \infty))\cap \mathcal{C}^{2, 1}_{K}(G\times(0, \infty))$.

Example 8.4. If the diffusion coefficients are allowed to be different, then again stable nonconstant stationary solutions can occur. The example follows a refinement of Matano's type of counterexamples for non convex domains established by Cónsul and Solá-Morales [13]. Consider the path $\Pi$ with $3$ edges using the numbering (9) and choosing the edge lengths and diffusion coefficients $a_j$ to be

with $\delta$ and $\varepsilon$ sufficiently small to be determined later. As common nonlinearity we choose $f(u) = u-u^3$. Using the double well potential $G(u) = \frac{1}{4} (1-u^2)^2$ and the modified energy

it can be shown that for $\varepsilon = \delta^2$, there exists a minimizer $w$ of $E$ in

that is close to $-1$ on $k_1$ and close to $1$ on $k_3$. Moreover, $w$ is stable.

Remark 8.1. The anti-Kirchhoff condition: If we replace the transition conditions (2) and (3) by their orthogonal condition, the famous anti-Kirchhoff condition

then the stability results change dramatically. E.g., there are no exceptional graphs, since for any finite metric graph, there is a suitable nonlinearity $f$ such that there is a stable nonconstant stationary solution $ \left(u_j \right)_{N\times 1}$ governed by the edge equations $\partial_j^2 u_j+f(u_j) = 0$. We refer to [10] for the details.

Remark 8.2. As already pointed out above, node transition conditions different from the ones given by (2) and (3) can allow stable nonconstant stationary solutions. In particular, consider the limit problem of a parabolic problem on $\Gamma$ depending on a parameter and allowing only constant stable stationary solutions. If the limit problem changes the type of its transition conditions or even the type of its edge differential equations, then stable nonconstant stationary solutions can occur in the limit. An example is given by Problem (1) with (2) replaced by the dynamical Kirchhoff condition

see [11]. Letting $\sigma$ tend to $\infty$ leads to a parabolic problem with a certain Dirichlet condition at the nodes, that can allow stable nonconstant stationary solutions using a similar argument as in 8.2.

As the stationary solutions of the parabolic and the corresponding hyperbolic problem are the same when keeping the same node transition conditions, the interesting question arises, whether stability properties can be carried over from one case to the other. More generally, if the hyperbolic problem is approximated by parabolic ones with established stability criteria, e.g. by relaxation, is it possible to conclude stability criteria for the hyperbolic case from those in the parabolic case? A precise answer to this question is certainly of big interest and could apply e.g. to gas networks considered in [14], where the existence of nonconstant stationary solutions has been established for certain metric graphs.

Acknowledgments

Joachim von Below is grateful for several invitations to the UPC Barcelona between 2014 and 2016 within the research group GREDPA. José A. Lubary is grateful for the stays as invited professor to ULCO in Calais between 2014 and 2017 within the LMPA Joseph Liouville. The authors are indebted to Professor Xavier Cabré for pointing out Example 8.4 and to the anonymous referee for valuable remarks.