Spectral distribution and semigroup properties of a queueing model with exceptional service time

1.   Introduction

The M/G/1 queueing model with exceptional service time for the first customer in each busy period can be described by the following system of integro-differential equations ^[1,2]:

here, $x, t\in[0, \infty)$; $p_0(t)$ is the probability that at time $t$, the system is idle and there are no customers in the system; $p_k(x, t)dx (\; k\geq 1)$ is the probability that at time $t$, there are $k$ customers in the system, the server is busy, and the remaining service time between $[x, x+dx)$; $Q_n(x, t)dx (\; n\geq1)$ is the probability that at time $t$, there are $n$ customers in the system, the server is busy, and the elapsed service time of the first service between $[x, x+dx)$; $\lambda$ is the arrival rate of customers; $\mu(x)$ is the ordinary service rate of server at time $x$; and $\eta(x)$ is the exceptional service rate of server at time $x$. In this system, the first customer during each busy period will receive exceptional services, while customers in other situations will receive regular services.

Queueing system with exceptional service time have been applied to many issues in service systems, manufacturing systems, production managing, communication networks, etc.; see ^[1,3,4,5,6]. For example, in a customer service call center, during periods of high call volume (busy periods), the first caller could be given priority in being connected to a senior or highly experienced agent. This could enhance the initial resolution rate and improve customer satisfaction. In a retail setting, such as a supermarket checkout during rush hours, the first customer in each busy period might be offered a discount or a quicker checkout lane to create a positive impression and encourage future patronage. In transportation systems like a bus terminal or an airport check-in counter, this model could ensure that the first passenger in a busy period gets faster processing or additional assistance, improving the efficiency and passenger experience. Welch ^[6] studied an M/G/1 queueing system, where the first customer to arrive in the system receives different services from other customers. Takagi ^[1] first obtained the system (1.1) by applying the supplementary variable technique. Second, he investigated the time-dependent solution (TDS) and the Laplace-Stieltjes of the probability generating functions of the system (1.1).

Semigroup theory is an important tool for studying the properties of integral differential equations, functional differential equations, or infinite dimensional control theory ^[7,8,9]. The method of semigroup theory has also been successfully applied to specific equations, such as population dynamical systems ^[10,11], queueing systems ^[12,13,14], reliability systems ^[15,16], neural networks ^[17], diffusion-advection dynamics ^[18], blow-up analysis ^[19], and so on. Gupur ^[20] first rewrote the system (1.1) as an abstract Cauchy problem in a Banach space and then showed that the Cauchy problem admits a unique positive TDS by applying the $C_0-$semigroup theory in functional analysis.

To study the asymptotic behavior of the TDS of system (1.1), we should understand the operator spectra of the corresponding system operator ^[14,15]. If the service rate $\mu(\cdot)$ and the exceptional service rate $\eta(\cdot)$ are constants, then the M/G/1 queueing model ^[1,2] is called the M/M/1 queueing model with exceptional service time for the first customer in each busy period. Gupur ^[21] determined the resolvent set of the adjoint operator of the system operator. Then, he proved that all points on the imaginary axis, except for the zero point, are regular points of the system operator; zero point is the spectral point of the system operator and its adjoint operator, with a geometric multiplicity of one. This means the TDS of the system (1.1) strongly converges to its nonzero steady-state solution (SSS) [13, Theorem 14]. When the service rate and the exceptional service rate of the server are bounded functions, Gupur and Ehmet ^[2] obtained the same results as ^[21]. In ^[22,23,24], the authors found that the system operator has an infinitely number of point spectra on the left real axis. This shows that the strong convergence of the TDS of system (1.1) obtained in Gupur ^[2,21] is the best result on the convergence of the TDS.

In this article, we attempt to further study the spectral distribution of the system (1.1) and investigate the semigroup properties of the system (1.1). First, when $\mu(\cdot) = \mu, \eta(\cdot) = \eta$ are positive constants, $0 < \lambda < \mu$ and $\eta > 0$, we prove that the following set

is in the point spectrum set of the system operator, and the geometric multiplicity of each point in this set is one, where $\Re z$ is the real part of $z$. Consequently, our result includes the main results of ^[22,23,24]. We also prove that all points of a set on the left-half complex plane are not point spectra of the system operator. Second, we obtain that the SDG condition holds true and the $C_0$-semigroup generated by the system operator is not asymptotically stable, compact, eventually compact, or even quasi-compact. Furthermore, we prove that the growth bound and the essential growth bound of this semigroup are equal to one. These properties are essentially different from the queueing model ^[14], reliability model ^[16], and population models ^[10,11].

The remaining of this article is arranged as follows. In the next Section, we rewrite the system (1.1) as a Cauchy problem in a Banach space and list the results obtained regarding the system. Section 3 is devoted to the spectral distribution of the system operator of system (1.1) on the left-half complex plane. The stability and compactness of the corresponding semigroup of the system (1.1) are developed in Section 4. In Section 5, in order to clarify the results of spectral distribution, some numerical analysis will be conducted. We conclude this article and raise some further research questions in Section 6.

2.   Abstract Cauchy problem and previous results

The abstract Cauchy problem is a fundamental concept in mathematics, especially in the field of differential equations. It helps us formulate and solve such questions precisely and provides a framework to determine the future behavior of a system based on its initial conditions. In a more general sense, the abstract Cauchy problem is essential in many areas of science and engineering where we need to understand and predict the evolution of a system based on its starting state ^{[10,12,14,17,19,25]}. Now, to rewrite the system (1.1) into an abstract Cauchy problem, we first select an appropriate state space and define the system operators.

We consider the following state space (see ^[2]):

It is not difficult to verify that $\mathcal{X}$ is a Banach space and also a Banach lattice.

Next, we define the system operator (underlying operator) of system (1.1):

where

We refer to $\mathcal{A+U+E} = \Theta$ as the system operator of system (1.1). Then, the system (1.1) can be written as a Cauchy problem in $\mathcal{X}$:

The following theorem can be found in ^[20,21].

Theorem 2.1. The system operator $\Theta$ generates a positive $C_0$-semigroup $e^{\Theta t}$ of contractions on $\mathcal{X}$. Hence, the problem (2.1) admits a unique positive TDS $(p, Q)$ satisfying

If $\mu(\cdot) = \mu, \eta(\cdot) = \eta$ are positive constants and $0 < \lambda < \mu$, then zero is an eigenvalue of $\Theta$ and its adjoint operator $\Theta^*$ with geometric multiplicity of 1. Moreover, the set

is in the resolvent set $\rho(\Theta)^*$. Especially, except for the zero point, each point on the imaginary axis belongs to $\rho(\Theta)$.

When the service rates $\mu(\cdot)$ and $\eta(\cdot)$ are bounded functions, Gupur and Ehmet ^[2] studied the strong convergence of the TDS:

Theorem 2.2. Let $\mu(x), \eta(x):[0, \infty)\to[0, \infty)$ be measurable functions and

Then, the TDS of the system (2.1) converges strongly to its SSS. In other words,

here, $(p^*, Q^*)$ and $(p, Q)$ satisfy the equations $\Theta^*(p^*, Q^*) = 0$ and $\Theta(p, Q) = 0$, respectively.

For the exponential convergence of the TDS of system (1.1), in ^[22,23,24], the authors have obtained the following result:

Theorem 2.3. Let $\mu(\cdot) = \mu$ and $\eta(\cdot) = \eta$ be positive constants. Then, the following results hold:

(1) If $\sqrt{\mathstrut\lambda} < \sqrt{\mathstrut\mu} < \sqrt{\mathstrut\lambda}+\sqrt{\mathstrut\eta},$ then each point in the set $\left[2\sqrt{\mathstrut\lambda\mu}-\lambda-\mu, 0\right)$ is a point spectrum of $\Theta$ with geometric multiplicity of 1.

(2) If $\lambda < \mu < \lambda+\eta,$ then $\lambda-\mu$ is a point spectrum of $\Theta$ with geometric multiplicity of 1.

We provide a brief outline or reference to the proof of the above three Theorems in the appendix.

3.   Spectrum of the system operator

In this section, we further investigate the point spectrum $\sigma_p(\Theta)$ of system operator $\Theta$ on the left-half complex plane. Specifically, we will discuss the real spectrum of $\Theta$, pointing out the exponential convergence of TDS and the differences between our results and existing ones. We have the following result:

Theorem 3.1. Let $\mu(\cdot) = \mu$ and $\eta(\cdot) = \eta$ be positive constants, $0 < \lambda < \mu$ and $\eta > 0$. Then,

and the geometric multiplicity of each point in this set is 1. In particular,

Proof. We consider $(z I-\Theta)(p, Q) = 0$ for unknown $(p, Q)$. This is equivalent to

By Eqs (3.1b)–(3.1e), we have

By repeatedly using (3.2a)–(3.2d) to obtain

Combining the boundary condition (3.1g) with the Eq (3.3b), it follows that

This together with the formula

for $k\ge 1$ and $\Re z+\lambda+\eta > 0$, we have

If $\; \Re z+\eta > 0,$ then the inequality (3.5) gives

Using the Eqs (3.1f), (3.3a), (3.3b) and the formula

for $k\ge 1$ and $\Re z+\lambda+\mu > 0$, we obtain

This implies that

Multiplying the two sides of the Eq (3.8) by $\frac{\lambda}{z+\lambda+\mu}$ and subtracting the Eq (3.7), it yields

If we set

then the above equation is equivalent to

observing the Eqs (3.9) and (3.10), we find that $a, b$, and $c_k$ satisfy the following relationship

By the first two equations in (3.11) it follows that

It is not difficult to see that the Eq (3.10) contains the following recursive equation

From the above Eq (3.13), we can further conclude that the following relationship holds

By adding the second equation from each of the above Eqs (3.14a)–(3.14f), we obtain

If $\; a = b$, then using the Eq (3.15) and the Cauchy product of series, we have

If $\; a\ne b$, then use the Eq (3.15) again to obtain

Using the third equation of Eq (3.11) and methods similar to the Eqs (3.14a)–(3.14f), we conclude that

Then, by adding the second equation from each of the above Eqs (3.18a)–(3.18d) and using Eqs (3.11) and (3.1g), we obtain

If $\Re z+\mu > 0$, then using Eq (3.3a), the Cauchy product and the formula

we have

When $\Re z+\min\{\mu, \eta\} > 0$, by inserting Eqs (3.2a), (3.2c), (3.1g) into (3.1a), we obtain

By combining the Eqs (3.7) and (3.21), it is easy to calculate that

Now, we introduce $\Lambda$ as

Then, from the Eqs (3.12a) and (3.12b) it is easy to show that

Therefore, if $z\in\Lambda$, then by Eqs (3.6), (3.16), (3.17), and (3.19)–(3.23), we obtain

The inequality (3.24) means $(p, Q)\in \mathcal{X}$ when $z\in\Lambda$. Therefore, this together with Theorem 2.1 means that each $z\in\Lambda\cup\{0\}$ is a eigenvalue of $\Theta$. In addition, since Eqs (3.21), (3.22), (3.3a), (3.4), (3.15) and Theorem 2.1, it is clear to verify that the geometric multiplicity of each $z\in\Lambda\cup\{0\}$ is 1.

Next, we will discuss the real spectral distribution of $\Theta$. Theorems 2.1 and 2.2 imply that every $z\in(0, \infty)$ belongs to $\rho(\Theta)$. Therefore, the real spectrum of $\Theta$ can only be in $(-\infty, 0]$. Now, we will discuss $\sigma(\Theta)$ in the following three cases:

Case Ⅰ: $(z+\lambda+\mu)^2 > 4\lambda\mu$ if and only if $|z+\lambda+\mu| > 2\sqrt{\lambda\mu}$. Since $z+\mu > 0$, we obtain $z > 2\sqrt{\lambda\mu}-\lambda-\mu$. Moreover, using the conditions $\lambda > 0, \mu > 0$ and $z < 0$, we calculate that

Since $\lambda < \mu$ and $-z > 0$, the last of the above inequalities is equivalent to

That is, $z+\lambda+\mu+\sqrt{(z+\lambda+\mu)^2-4\lambda\mu} < 2\mu$. Therefore, from this inequality, we obtain that $a$ and $b$ given in the Eqs (3.12a) and (3.12b) satisfy

In addition, by the inequality $\lambda < \mu$, it is easy to deduce that $2\sqrt{\lambda\mu}-\lambda > 0$, that is, $2\sqrt{\lambda\mu}-\lambda-\mu > -\mu$. Hence, this together with $z+\eta > 0$ and the inequality (3.25), leads to

Theorem 2.1 shows that if $\lambda < \mu$, then $0\in\sigma_p(\Theta)$. Therefore, we have

In particular, if $\sqrt{\mu} < \sqrt{\lambda}+\sqrt{\eta}$, that is, $\sqrt{\mu} -\sqrt{\lambda} < \sqrt{\eta}$, it is easy to see that $\mu+\lambda-2\sqrt{\lambda\mu} < \eta$. This means that $-\eta < 2\sqrt{\lambda\mu}-\lambda-\mu$. Hence, under this condition it follows that

This means our result includes the main result of ^[22].

Case Ⅱ: $(z+\lambda+\mu)^2 = 4\lambda\mu$ if and only if $|z+\lambda+\mu| = 2\sqrt{\lambda\mu}$. In this case, using the inequality $z+\mu > 0$, we have $z = 2\sqrt{\lambda\mu}-\lambda-\mu$. Moreover, if $\lambda < \mu,$ then we have

That is, the point $2\sqrt{\lambda\mu}-\lambda-\mu\in\sigma_p(\Theta)$.

In particular, if $\sqrt{\mu} < \sqrt{\lambda}+\sqrt{\eta}$, then the inequality $-\eta < 2\sqrt{\lambda\mu}-\lambda-\mu$ holds true. This implies $z+\mu > 0$ and $z+\eta > 0$. Hence, by the inequality (3.26), we obtain $2\sqrt{\lambda\mu}-\lambda-\mu\in\sigma_p(\Theta)$. This shows that our result implies the main result of ^[24].

Case Ⅲ: $(z+\lambda+\mu)^2 < 4\lambda\mu$ if and only if $|z+\lambda+\mu| < 2\sqrt{\lambda\mu}$. In this case, the inequality $z+\mu > 0$ implies that $z < 2\sqrt{\lambda\mu}-\lambda-\mu$. When $\lambda < \mu$, we have

Therefore, we have

This means

In particular, if $\lambda < \mu < \lambda+\eta$, then using the inequalities $\lambda-\mu > -\mu, \lambda-\mu > -\eta$ and discussions similar to the above, we obtain $[\lambda-\mu, 0]\subset\sigma_p(\Theta)$. This implies that our result includes ^[23].

Theorem 3.1 means that our results include the main results of ^[22,23,24]. Moreover, Theorem 3.1 shows that the TDS of the system (1.1) is not exponentially convergent to its SSS. That is, strong convergence is the best result in terms of the convergence of TDS.

Theorem 3.2. Let $\lambda > 0$ and $\mu = \eta > 0$. Then, we have

Proof. Consider the equation $(z I-\Theta)(p, Q) = 0$ of unknown $(p, Q)$. Then, this is equivalent to Eqs (3.1a)–(3.1g). When $\mu = \eta$, by Eqs (3.9) and (3.15), we obtain

here, $a$ and $b$ are given by Eqs (3.12a) and (3.12b). If $z\in\Lambda_1$, then it is easy to see that $|b| < 1 < |a|$. This means that when $z\in\Lambda_1$, we have $\sum_{k = 1}^{\infty} p_{k+2}(0) = \infty$. Hence, using the Eqs (3.3a) and (3.28), we obtain $\|(p, Q)\| = \infty$. This means that if $z\in\Lambda_1$, then $z\notin\sigma_p(\Theta)$.

4.   Stability and compactness of the semigroup

In this section, based on the Theorem 3.1, we will investigate the stability and compactness of the $C_0$-semigroup $e^{\Theta t}$, from which we obtain that the SDG condition holds true, and we further investigate the asymptotic properties of the TDS of system (2.1).

Theorem 4.1. The SDG condition holds for $e^{\Theta t}$ and $\omega_0(\Theta) = s(\Theta) = 0$, where $\omega_0(\Theta) = \{\omega\mid \exists\; \mathbb M\; \mathit{\text{such that}}\; \|e^{\Theta t}\|\le \mathbb M e^{\omega t}\}$ is the growth bound of $e^{\Theta t}$ and $s(\Theta) = \{\Re z\mid z\in\sigma(\Theta)\}$ is the spectral bound of $\Theta$. Moreover, the semigroup $e^{\Theta t}$ is not asymptotically stable.

Proof. Clearly, $\mathcal{X}$ is a Banach lattice and by Theorem 2.1 we know that $e^{\Theta t}$ is positive on $\mathcal{X}$. For $(p, Q)$, $(y, h)\in \mathcal{X}_+$, here $g = (g_0, g_1, g_2, \cdots), h = (h_1, h_2, \cdots)$, it is not difficult to calculate that

where

Thus, $\mathcal{X}$ is a AL-space. Since Theorems 3.1 and 2.2, it is clear that $0\in\sigma_p(\Theta)$ and $\sigma(\Theta)\subset\{z\in\mathbb{C}\mid \Re z < 0\}\cup\{0\}$. Then, using Corollary 12.9 of [7, p.188], we obtain $s(\Theta)\in\sigma(\Theta)$ and $s(\Theta) = 0$. Therefore, since [7, Theorem 12.17, p.193], we derive that the SDG condition holds and $\omega_0(\Theta) = s(\Theta) = 0$. This shows the semigroup $e^{\Theta t}$ is not exponentially stable, see [8, Theorem Ⅵ.1.14, p.357]. In addition, due to $e^{\Theta t}$ being uniformly bounded (Theorem 2.1), Theorems 3.1 and 2.2 show that $\sigma(\Theta)\cap i\mathbb{R}\subset\sigma_p(\Theta)$. Then, $e^{\Theta t}$ is not asymptotically stable from Theorem 3.26 of [26, p.130]. It implies that the semigroup $e^{\Theta t}$ does not tend to a stable equilibrium state as time progresses to infinity. This is different from the recent results ^{[14,18,19,25]}.

Theorem 4.2. The semigroup $e^{\Theta t}$ is not compact, eventually compact, or even quasi-compact. Furthermore, the spectral radius and essential spectral radius of $e^{\Theta t}$ are equal to one.

Proof. Due to Theorem 3.1 and Theorem Ⅳ. 3.7 of [8, p.277]:

we see that $e^{\Theta t}$ has an uncountable infinite number of eigenvalues and therefore it is not compact. It means that $e^{\Theta t}$ does not map bounded sets into relatively compact sets. Hence, this could make the analysis of solutions and the approximation of the system (1.1) more challenging (see, e.g., ^[27,28]). Moreover, by Corollary Ⅴ.3.2 of [8, p.330], we know that the semigroup $e^{\Theta t}$ is not even eventually compact.

In addition, since $e^{\Theta t}$ is a $C_0-$semigroup on the Banach space $\mathcal{X}$, by Corollary Ⅳ.2.11 of [8, p.258] we have the following results:

(1) $\omega_0(\Theta) = \max\{\omega_{ess}, s(\Theta)\}$, here $\omega_{ess}$ is the essential growth bound of the semigroup $e^{\Theta) t}$.

(2) The intersection of $\sigma(\Theta)$ and $\{z\in\mathbb{C}\; |\; \Re z\ge w\}$ is finite for all $w > \omega_{ess}$.

Theorem 4.1 means that $\omega_0(\Theta) = s(\Theta) = 0$. Then, we use the above results (1), (2) and Theorem 3.1 to obtain $\omega_{ess} = 0$. Hence, by Proposition 3.5 of [8, p.332], it is not difficult to see that the semigroup $e^{\Theta t}$ is not quasi-compact. It suggests that the spectral properties of $e^{\Theta t}$ are not conducive to establishing stability or convergence results easily. This result is significantly different from the results in population models ^[10,11], neural networks ^[17], the reliability model ^[16], and the retrial queueing model ^[14].

Furthermore, since $\omega_{ess} = \omega(\Theta) = 0$ and [29, p.74], we obtain that the spectral radius $r(e^{\Theta t})$ and the essential spectral radius $r_{ess}(e^{\Theta t})$ of $e^{\Theta t}$ satisfy

5.   Numerical analysis

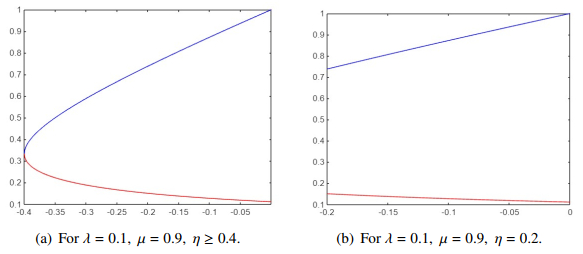
In order to clarify the conditions for certain spectral characteristics in Theorems 3.1 and 3.2, we conducted some numerical analyses, as shown in Figures 1–3. In Figures 1–3 we only consider the real spectrum of the system operator $\Theta$, where the blue curve refers to the characteristic root $a$ ($a$ is given in the Eq (3.12a)), and the red curve refers to the characteristic root $b$ ($b$ is given in the Eq (3.12b)). We used Matlab to draw these Figures.

In Figure 1a, we take $\lambda = 0.1, \; \mu = 0.9$, and $\eta\ge0.4$. Then, it is easy to see that $\frac{\lambda}{\mu} = \frac{0.1}{0.9} < 1$ and $2\sqrt{\lambda\mu}-\lambda-\mu = 2\sqrt{0.09}-0.1-0.9 = -0.4\ge-\eta$. That is, $\max\{2\sqrt{\lambda\mu}-\lambda-\mu, -\eta\} = 2\sqrt{\lambda\mu}-\lambda-\mu$. It is not difficult to prove that $0 < a < 1$ and $0 < b < 1$ under the above $\lambda, \mu$ and for any $z\in(-0.4, 0)$. Therefore, all $z\in(-0.4, 0)$ are the point spectra of the system operator $\Theta$.

In Figure 1b, if we choose $\lambda = 0.1, \; \mu = 0.9$ and $\eta = 0.2$. Then, it is not difficult to calculate that $\frac{\lambda}{\mu} < 1$ and $2\sqrt{\lambda\mu}-\lambda-\mu = -0.4 < -\eta = -0.2$. That is, $\max\{2\sqrt{\lambda\mu}-\lambda-\mu, -\eta\} = -\eta$. In addition, it is clear that for any $z\in(-0.2, 0)$ and the above conditions, $a$ and $b$ satisfy $0 < a < 1$ and $0 < b < 1$. Thus, every $z\in(-0.2, 0)$ is the point spectrum of $\Theta$. Figure 1 shows that the spectral results of the system operator $\Theta$ in Theorem 3.1 are correct.

It has been proven in references ^[22,24] that $[2\sqrt{\lambda\mu}-\lambda-\mu)\subset\sigma_p(\Theta)$ if $\sqrt{\mu} < \sqrt{\lambda}+\sqrt{\eta}$. Below, we point out that our results include ^[22,24]. In Figure 2a, if we take $\lambda = 0.04, \; \mu = 0.09$ and $\eta = 0.04$. Then, we have $\sqrt{0.09} < \sqrt{0.04}+\sqrt{0.04}$, that is, $\sqrt{\mu} < \sqrt{\lambda}+\sqrt{\eta}$. In addition, $2\sqrt{\lambda\mu}-\lambda-\mu = 2\sqrt{0.0036}-0.13 = -0.01$. It is not difficult to see that $0 < a < 1$ and $0 < b < 1$ under the above $\lambda, \mu$ and for all $z\in[-0.01, 0)$. Hence, all $z\in[-0.01, 0)$ are the point spectrum of $\Theta$. This means that the main result of ^[22] holds true.

In Figure 2b, if we choose $\lambda = 0.01, \; \mu = 0.09$ and $\eta = 0.01$. Then, it is easy to see that $\sqrt{0.09} > \sqrt{0.01}+\sqrt{0.01}$, that is, $\sqrt{\mu} > \sqrt{\lambda}+\sqrt{\eta}$. Hence, $2\sqrt{\lambda\mu}-\lambda-\mu = 2\sqrt{0.0009}-0.1 = -0.04$. In addition, for any $z\in(-0.04, 0)$ and the above conditions, $a$ and $b$ satisfy $0 < a < 1$ and $0 < b < 1$. Therefore, each $z\in(-0.04, 0)$ is the point spectrum of $\Theta$. This indicates that the condition of Theorem 3.1 is better than ^[22,24].

Firstly, we check whether the condition $\lambda < \mu$ in Theorem 3.1 is necessary. If we take $\lambda = 0.09,$ $\mu = 0, 01$ and $\eta > 0$, then we have $\lambda > \mu$. Figure 3a means that, if $z\in(-0.04, 0)$, then $a > 3$ and $b > 1$. Of course, we can choose a different $\lambda$ and $\mu$ to satisfy $\lambda > \mu$, and we can all come to the same conclusion. In this case, we cannot determine whether it is $z\in\sigma_p(\Theta)$, or even whether it is $z\in\sigma(\Theta)$, where $z\in(\max\{-\eta, 2\sqrt{\lambda\mu}-\lambda-\mu\}, 0)$. Therefore, in Theorem 3.1, we must consider the condition $\lambda < \mu$.

Next, we check whether there is a point spectrum on the right real axis to determine the correctness of the existing result ^[2,21]. In Figure 3b, if we take $\lambda = 0.01, \mu = 0.09$ and $\eta > 0$, then, $\lambda < \mu$. Moreover, $0 < a < 1$ and $0 < b < 1$ when $z\in(-0.04, 0)$, and $a > 1$ and $0 < b < 1$ when $z\in(0, 0.04)$. Hence, by Theorems 3.1 and 3.2, we deduce that $(-0.04, 0)\subset\sigma_p(\Theta)$ and $(0, 0.04)\nsubseteq\sigma_p(\Theta)$. This means that there is no point spectrum on the right real axis.

6.   Conclusions and future work

In this article, we study the spectral distribution and semigroup properties of the M/G/1 queueing model with exceptional service time for the first customer in each busy period. We prove that the system operator of the queueing system has an uncountable infinite number of point spectra on the left-half complex plane. This indicates that the TDS of the model cannot exponentially converge to its SSS. In addition, our result implies the main results of ^[22,23,24]. We also obtain that all points of a set on the left-half complex plane are not point spectra of the system operator. But we did not answer whether the set is a residual spectrum or a continuous spectrum. Recently, we have achieved results in continuous spectrum and residual spectrum in other queuing models ^[14,30]. This is our next research topic for this queueing model.

In addition, based on the positive $C_0-$semigroup properties and operator spectrum analysis, in this article, we prove that the SDG condition holds true and is equal to zero. However, the $C_0-$semigroup is not asymptotically stable, compact, eventually compact, or even quasi-compact. The methods and ideas presented in this article are applicable to some queuing models that are described by integro-differential equations ^[31,32,33].

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 12301150).

Conflict of interest

The authors declare there is no conflict of interest.

Appendix A

A.1.   Outline of the proof of Theorem 2.1

We only give a brief outline to the proof of Theorem 2.1.

Step 1: We show that $(z I-\mathcal{A})^{-1}$ exists and is bounded when $z > \max\{\overline\mu, \overline\eta\}$, where $\overline\mu = \sup_{x\in[0, \infty}\mu(x) < \infty$ and $\overline\eta = \sup_{x\in[0, \infty}\eta(x) < \infty$. For this purpose, for every $(y, h)\in \mathcal X$, we consider $(z I-\mathcal A)(p, Q)$ for unknown $(p, Q)$. Then, through a series of calculations, we obtain

where $\mathbb M: = \max\{\overline\mu, \overline\eta\}$. This means that $(z I-\mathcal A)^{-1}:\mathcal X\rightarrow D(\mathcal A)$ and

Step 2: We verify that $D(\mathcal{A})$ is dense in $\mathcal{X}$.

It is clear that for every $(p, Q)\in \mathcal X$ and $\varepsilon > 0$, $\exists\; K\in \mathbb N_+$, for every $n > K$ such that

We take the following two sets

and

Then, by corollary 2.30 of ^[34], we see that $S_1$ is dense in $X$, and $S_2$ is dense in $S_1$. Therefore, to obtain $\overline{D(\mathcal A)} = \mathcal X$, it is only needed to verify $S_2\subset\overline{D(\mathcal A)}$. As a matter of fact, when $S_2\subset\overline{D(\mathcal A)}$, we have $\overline{S_2}\subset \overline{\overline{D(\mathcal A)}} = \overline{D(\mathcal A)}$. Thus, using $D(\mathcal A)\subset \mathcal X$ and $\overline{S_2} = \overline{\overline{S_2}} = \overline{S_1} = X$ it follows that $\overline{D(\mathcal A)}\subset\overline{\mathcal X} = \mathcal X$. Hence, $\overline{D(\mathcal A)} = \mathcal X$.

Hence, due to the Steps 1 and 2 and the Hille-Yosida theorem (see, [15, Theorem 1.68]), we see that $\mathcal{A}$ generates a $C_0-$semigroup.

Step 3: We prove that $\mathcal{U}$ and $\mathcal{E}$ are linear bounded operators. Due to the definitions of $\mathcal{U}$ and $\mathcal{E}$, it is easy to prove this step.

Then, due to the perturbation theorem of semigroup (see, [15, Theoremm 1.80]), it is easy to obtain that $\Theta$ generates a $C_0-$semigroup $e^{\Theta t}$.

Step 4: We prove that $\Theta$ is a dispersive operator. For $(p, Q)\in \mathcal X$, we take $(p^+, Q^+)$ as

where

and

Then, through a series of calculations, we can conclude that

This means that $\Theta$ is dispersive.

Therefore, using the above four steps and the Phillips theorem (see, [15, Theorem 1.77], we obtain that $\Theta$ generates a positive $C_0$-semigroup $e^{\Theta t}$ of contractions on $X$.

Step 5: Verify that $\Theta$ is a conservative with respect to the set $J(\cdot)$, where

and the dual space $\mathcal{X}^*$ of $\mathcal{X}$ is:

Then, by [35, Theorem 3.6.1, p. 155], we obtain that if $\overline\mu < \infty, \overline\eta < \infty$ and $(p, Q)(\cdot, 0)\in D(\mathcal{A}^2)$, then

Step 6: Assume that $\overline\mu < \infty, \overline\eta < \infty$ and $(p, Q)(\cdot, 0)\in D(\mathcal{A}^2)$. Then, the problem (2.1) exists in a unique positive TDS $(p, Q)(\cdot, \cdot)$ satisfying

Using the above five Steps and Theorem 1.81 of ^[15], it is easy to verify that Step 6 holds true.

Step 7: If $\; \lambda < \mu,$ then $0$ is an eigenvalue of $\Theta$ and the adjoint operator $\Theta^*$ has geometric multiplicity of 1, where

and the operators $\mathcal{L, N}$ and $\mathcal{R}$ are defined by

If $\mu(\cdot) = \mu$ and $\eta(\cdot) = \eta$, then Step 7 is the special case of Lemmas 2.1 and 2.6 of ^[2].

Step 8: All points in the set

belong to the resolvent set $\rho(\Theta^*)$. Especially, we have $i\mathbb{R}\cap\sigma(\Theta) = \{0\}$.

To prove this step, we consider $(z I-\Theta^*)(p^*, Q^*) = 0$ for unknown $(p^*, Q^*)$. Then, we obtain $\sigma(\Theta^*)$ on $i\mathbb{R}$. Therefore, using the relationship between operator spectrum and its adjoint operator spectrum, we give $\sigma(\Theta)$ on $i\mathbb{R}$.

We suggest readers refer to references ^{[12,15,36,37]} to learn about other queuing models and reliability models that have similar proofs to this theorem.

A.2.   Outline of the proof of Theorem 2.2

Since this Theorem is the main result of ^[2], we suggest that interested readers refer to reference ^[2].

A.3.   Outline of the proof of Theorem 2.3

In order to show Theorem 2.3, we consider $(z I-\Theta)(p, Q) = 0$ for unknown $(p, Q)$. This is equivalent to the Eqs (3.1a)–(3.1g). We will discuss the cases where $z = (2\sqrt{\mathstrut\lambda\mu}-\lambda-\mu)\theta, \theta\in(0, 1]$ and $z = \lambda-\mu$, respectively. The remaining proofs of this Theorem are similar to Eqs (3.2a)–(3.22) and (3.24).