Theoretical analysis of unsteady squeezing nanofluid flow with physical properties

List of Nomenclature:

1.   Introduction

The processes widely used in engineering (mainly chemical, mechanical and other such fields) state ample utility of the fluid flow between stretching sheets in a rotating system. In a simpler word, be it papers' fabrication, material's insulation, or manufacturing of plastics or else the material goes through elongating, line stretching, and most importantly rotating phenomena. These processes follow four-square movement of products and the studying of viscous drags for gaining the desired faces. For further understanding, theoretical insight of the properties of the flow would be significant for the related setups.

In the long list of researchers, Stefan ^[1] pioneered his classical paper based on the lubrication approximation (highlighting squeezing flow). In tandem, Reynolds ^[2] focused on the solution of elliptic plates, while the rectangular plates were studied by Archibald ^[3]. All of these conducted studies supplement multiple examples of flow and its squeezing that are injection molding, compression, and polymer processing. Additionally, the lubrication system does regard this process of squeezing flows. Over the past and even now in the present era, new fields of studies have been uncovered which substantiate the implication of the concept of Nano fluids. Now nano fluid is named as the suspended solid sized nanometer ranging (1–100nm) in diameters. Although fluids have lower thermal conductivity than solid, the fluid's mixture and nano-particles can easily develop the heat transfer of fluid with valuable assistance of thermal conductivity.

Von Karman ^[4] is credited for the foot work of rotating discs. However wide ranged studies have been later conducted after him. He focused the rotating disc in fluid with constant angular velocity. When it comes to the introduction of transformation and reduction of Naviar stokes equation to ordinary differential equation of fourth grade with the help of approx. Cochran ^[5] fortuned a more simplified concept. He took to higher accuracy by analyzing the fluid's motion at rest and thus gave the solution of this state of fluid. Hamza and MaCDonald ^[6] tried finding the solution of the fluid flow between the two plates placed at the angle$\theta$. They explained that at time 't' a plate separation of ${\Omega }$ (1-$\alpha$ t)^-1/2 plates are permitted to rotate with rotational velocity that is proportional to ${\Omega }$(1-$\alpha$ t)^-1, (${\Omega }$ represents rotational velocity). By Ibrahim ^[7], we come to the study that studies the phenomena of unsteady flow plus heat transfer between two rotating flow. He established the finding that the temperature and heat transfer process observe a very small impact of rotation of two plates. He also added that the movement of the upper plate traces a prominent effect on both temperature and heat transfer. In a step ahead, Mustafa et al. ^[8] examined a squeezed and viscous fluid between the plates which are placed parallel by highlighting the characteristics (that are mass and heat transfer). They draw the conclusion that Nusselt number has been observed as an increasing function of Prandtland Eckert number. Another researcher named Turkyilmazogl ^[9] investigated laminar flow (three-dimensional stagnation point) that conducted electric charge in a fluid in a stretching rotation disk. In addition, in ^[10] formerly studied the transport of heat in nano-fluid flow of a rotating disk.

At some other point in his research, Hu et al. ^[11] examined, through disks that were rotated counter to each other, the thermo-capillary flow instability. The technique he used was Chebyshev technique (a pseudo spectral technique); the solutions obtained therein were of velocity and temperature. Hayat et al. ^[12] focused viscous flow by using non-fourier flux of heat between two rotating disks. His later research ^[13] was about the carbon nano-tubes allowing flow with dual conditions of slips in a rotating disk system. Along with this, Rashidi et al. ^[14] held incompressible flow under his study, in which the plates were moving or had the motion normal. However, two plates (a porous rotating one and a fixed impermeable one) laminar flow comes into account in the study done by Kavenuke ^[15]. Rashid et al. ^[16] looked for utility of the second law of thermodynamics for MHD flow of nano fluid over a porous disc that is rotating. They extracted that the magnetically driven rotating disc finds its utility in the systems of renewable energy occurring due to phenomena of transfer of heat. Analytical or numerical methods should be used with the help of governing equations regarding fluid's flow between two rotating discs, or plates.

Sheikholeslami et al. ^[17] observed the features of heat transfer and nanofluid flow between two plates which are parallel but are held horizontally in a system. He highlighted that the Nusselt number (Nu) is increased by increasing volume fraction of nano-particle; in the reciprocal way Nusselt number scale down with the enhanced in Eckert number, magnetic parameters and rotation. Sheikholeslami and Ganji ^[18] questioned MHD flow in nano-fluid in a penetrable channel. Their collective results underlined that the velocity of boundary layer thickness is enhanced by scaling Hartmann number. While velocity of boundary layer thickness goes down with enlarge in Reynold's number. Sheikholeslami and Ganji ^[19] numerically studied using fourth order Range-Kutta method the flow of nano-fluid and heat transfer. He focused the rotatory system. However, thermophoresis and the Brownian motion have been given ample consideration in this model of study. While the numerical evaluation and investigation is done by governing different parameters; Injection parameter, Reynolds number, Schmidt number, Rotation parameter, Brownian parameter and Thermophoresis.

Shankar et al. ^[20] has underlined the characteristics of mass and heat transfer of unsteady magnetohydrodynamic Casson nanofluid flow between plates held parallel due to the effects of viscous dissipation and first order chemical reaction of homogeneous in nature. This investigation suggests that the concentration-field serves as a function of thermophoresis parameter in a decreasing manner. Unlikely, Brownian motion parameter increases with an enhancement of concentration profile. Bhatta et al. ^[21] has studied the squeezing flow of nano fluid; an unsteady water based flow among two disks held parallel. Thus, the findings were (ⅰ) The velocity field has shown peculiar variations, by channel middle layer separated and (ⅱ) heat transfer coefficient enhances owing to the buoyancy parameter. Incompressible squeezing and time dependent flow of Casson and micropolar nanofluids confined throughout corresponding disks is also analyzed. He noted that an increase in squeezing Reynolds number pushes the radial velocity profile to the upper disk. Ramesh et al. ^[22] focuses that the micro-polar parameter attends to the rotation in conflicting way because of which micro-rotational field scale up and later down. The results specify that, for the flow of nano-fluid, the rate of heat and mass transfer is inversely co-relate to fraction of volume and its magnetic parameter. The rate of mass transfer also goes up with the increase in the values of squeeze number and Schmidt number. Gupta and Ray ^[23] cited a problem regarding unsteady flow of a squeezing nano-fluid between two parallel plates. The results highlight that when the plates come close together; the Nusselt number (Nu) shows a direct relationship with both Eckert number and nano-particle volume fraction while "Nu" shows opposite behaviour with the squeezing number.

The form influence of gold (Au) nanoparticles on squeezing nanofluid flow and heat transmission across parallel plates is investigated by Rashid et al. ^[24]. Water was used as the base fluid to investigate the varied shapes of nanoparticles, including column, sphere, hexahedron, tetrahedron, and lamina. The obtained results show that lamina shape nanoparticles have the highest rate of heat transfer, and the spherical shape of nanoparticles has played a significant role in temperature dispersion when compared to other shapes of nanoparticles. Bilal et al. investigate the CNT–Fe₃O₄/H₂ flow into a horizontal parallel channel with thermal radiation through squeezing and dilating porous walls in a hybrid magnetohydrodynamics (MHD) nanofluid (Carbon nanotubes and ferrous oxide–water). The thermal enhancement of hybrid nanofluid is shown to be more than that of plain nanofluid. Furthermore, single-wall carbon nanotubes have a greater temperature influence than multi-wall carbon nanotubes ^[25]. The unstable flow in rotating circular plates located at a finite distance filled with Reiner-Rivlin nanofluid is studied by Arain et al. ^[26]. It's worth noting that the DTM-Padé approach has been found to be both stable and accurate. These flows can be used to mimic problems in geophysics, oceanography, and a variety of commercial applications such as turbo machinery. To solve the fourth-order nonlinear ordinary differential equations emerging from squeezing unstable nanofluid flow. Nouar et al. ^[27] employed very efficient, intelligent approaches. Log-sigmoid, radial basis and tan-sigmoid activation functions were employed to create the three models. In contrast to the discrete form generated by the numerical method, the solutions found by using the neural network technique of our variables field (velocity and temperature) are continuous. Khan et al. ^[28] analyze the heat transmission behaviour of an ionized nano liquid motion between two parallel discs. The suggested model analyses the squeezing flow of Cu-water nanofluid with electrical potential force to evaluate the flow properties and applies a uniform magnetic field to that fluid by making the bottom disc porous. He also looked at the effects of various nanomaterials on heat transfer through nanofluids. Upreti et al. ^[29] studied the entropy generation and heat transfer of unsteady hybrid pressed magnetic nanofluid flows between parallel plates, taking into account heat sources/sinks and heat radiation. He observed that the contours of entropy generation accelerated with increasing magnetic field values as the hybrid nanofluid moved away from the surface. Li et al. ^[30] analyzed by axisymmetric transient squish flow of Newton non-conductive liquid through a porous system "circular plate".

This present study will serve as an extension of the article by ^[19] which will aim at investigating the unsteady squeezing of nano-fluid in a rotatory system. It would be furthered by applying two or multiple phase models for initiating nano-fluid and heat transfer in the system. All the mentioned parameters in ^[19] will be found out by keeping the variables of Viscosity and Thermal conductivity. These results will be a step forward towards several interpretations of the key concepts and would be a base for times to come for new researchers. There are different techniques to solve PDEs. Here I used to solve PDEs through Parametric Continuation Method and result is validated through BVP4c because my problem mostly consists of the parametrical behaviour, thus PCM is one of the best techniques to get the result.

2.   Mathematical modeling

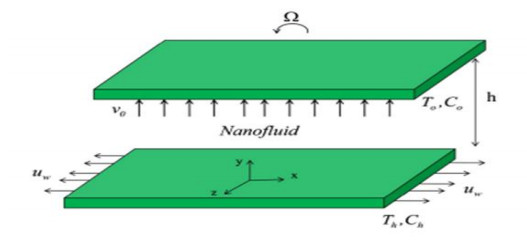
In the present study, unsteady squeezing nano fluid flow in center of between two plates held horizontally parallel is considered. The upper plate, as well as the fluid, is rotating with a certain rotational velocity around y-axis while plate at origin position is fixed. Considering the Cartesian coordinates for the system goes as follows: an x-axis is alongside the lower plate, and the y-axis is at 90° to it; while the axis which is normal to the xy plan is the z-axis as shown in below Figure 1.

Wall injection subjects the upper plate of the system to a constant velocity v₀. The location of the plates is as follows: the lower plate is just alongside the horizontal line i.e., y = 0 and the upper plate is placed at some specific height i.e., y = h. The placement of the points (0, 0, 0) is kept unchanged for lower plate. This balance is achieved through the Newton's third law (two opposite forces with equal magnitude). Thus, the equations for the said frame of references are as under.

2.1.   Governing equations for the stated problem with boundary conditions

The governing equations in a rotating frame of reference are:

Continuity equation:

Navier Stokes Equation:

Energy Equation:

Concentration Equation:

After transforming into Cartesian coordinates:

The following non-dimensional variables are introduced:

here differentiation with respect to $\eta$ is denoted by a prime. Substituting Eq (2.11) with Eqs (2.5)–(2.10),

Using the below boundary conditions for above equations,

For other non-dimensional quantities:

Nusselt number $(Nu$) and coefficient of skin friction (${C}_{f}$), are as under:

2.2.   Numerical solution by PCM

The basic idea of PCM application to non-liner Eqs (2.12)–(2.15) with the relative boundary condition (2.16) expressed in the steps which are following:

Step 1. Converting the system of BVPs to a system of ODEs of first order, the following procedure as adopted.

here $f$ is a function of $\eta$. By using the transformation, we get the following equations:

Step 2. Introducing the embedding parameter p.

Step 3. Differentiating by parameter "p".

By differentiating Eqs (2.23)–(2.26) with repect to "p" we get the result as follow.

here R represents remainder while A represent coefficient matrix.

where $i = \mathrm{1, 2}, \dots 13.$

Step 4. The two Cauchy problems given below have to solve.

here a- unknown blend coefficient ${U}_{1}and\;w$ are unknown vector function. For each component the two Cauchy problems are Solve.

Substituting the approximate solution Eq (2.29) into the original Eq (2.27), we obtain

Step 5. Solving the Cauchy problems.

In this work numerical implicit scheme is used which is presented as below.

From Eqs (2.30) and (2.31),

From above iterative form of the solution is obtained.

3.   Results

Mathematical formulation for the consecutive expressions of Newtonian flow for unsteady squeezing fluid is taken into account for modeling the flow between two rectangular plates in Eqs (2.1)–(2.18) which is subjected to the boundary conditions as per Eq (2.14) through PCM and BVP4c. The equations are thus analyzed, solved and equated for investigations numerically. Furthermore, the method of parametric-analysis for dimensionless physical parameters, i.e., Injection parameter, Squeezing Reynolds number (Sq), Prandtle number (Pr), Schmidt number (Sc), Brownian parameter (Nb) and Thermophoretic parameter (Nt), has been applied. The results of these parameters are shown in Figures 2–6.

4.   Discussion

Figure 2(a), (b) are represent the graph of velocity profile through horizontal direction f'($\eta$) and vertical direction $f(\eta)$ for the different value of injection $\lambda$ parameter. It shows that if the value of injection parameter ($\lambda$ = 1, 2, 3, 4) increases (which means injecting the fluid through upper plate into the system) while other quantities such that Sq = 0.5, Pr = 10, Kr = 0.5, Nt = 0.1, Nb = 0.1, Sc = 0.5 remain unchanged then the value of f'($\eta$) mean flow along horizontal direction and f($\eta$) which is the alongside of y-axis also increases. It is because of the existence of porosity in the plate, allows the fluid flow through the system and leads to increase the motion of the fluid. The effect of injection parameter ($\lambda$) on temperature profile in Figure 2(c) and concentration profile in Figure 2(d), are highlighted respectively. It is noted in Figure 2(c), (d) that due to increase in the value of injection parameter ($\lambda$ = 0.9, 1, 1.2, 3) for temperature and $\lambda$ = 0, 1, 2, 3 for concentration profile, while other quantities as Sq = 0.3, Pr = 5, Kr = 0.5, Nt = 0.1, Sc = 0.5, Nb = 0.1 is fixed, then temperature decreases while opposite in concentration profile is being observed. It is because when injection parameter increases then the thermal diffusivity decreases, which eventually mean that the thermal conductivity decreases or to say that density increases.

Figure 3(a) is exhibit the impact of squeeze Reynolds number (Sq) on the component along x-axis in the field of velocity while keeping Sc = 0.5, Kr = 0.5, Nt = 0.5, Nb = 0.5, Pr = 10 and $\lambda =$0.5 fixed. With a decrease in the velocity of the upper plate i.e., (Sq = 25, 15, 5, 0) moving towards the lower plate, as the value of Sq scale down which means that there is an increase within the kinematic viscosity i.e., decrease in the density of the fluid. Similarly, when the space or length between the plates is decreased, the velocity profile has increased. As a result, the fluid initiates to move along x-axis. Figure 3(b) shown the variation of temperature profile $\theta \left(\eta \right)$ for different value of Squeezing number i.e., (Sc = 0.5, Kr = 0.5, Nt = 0.5, Nb = 0.5, Pr = 10 and $\lambda =$1). Considerable increase in the profile of temperature field $\left(\theta \right(\eta \left)\right)$ is noted for diminutive worth of Sq as (Sq = 5, 3, 1, 0). It is very clear from Figure 3(b) that graph of temperature raises when plates move in directions opposite to each other. It is because when decrease in the value of squeezing number (Sq) can relate as kinematic viscosity scale up (i.e., internal resistance of fluid flow become increase) or decrease in the length through which the plates are separated. So we get increasing phenomena in temperature profile. In Figure 3(c) the findings of smaller values of Sq = 12, 7, 4, 1 on the concentration field is witnessed when such parameters Sc = 0.5, Kr = 0.1, Nt = 0.5, Nb = 0.5, Pr = 0.5, $\lambda =$5 are fixed. In Figure 3(c) opposite impact is being seen for the concentration profile, when it is compared to temperature field $\theta$. It is because of increasing kinematic viscosity (decrease in the density).

The impact of Prandtle number (Pr = 1, 3, 5, 7) on temperature field while such parameters Sc = 0.5, Kr = 0.1, Nt = 0.5, Nb = 0.5, Sq = 0.5, Pr = 5, $\lambda =$5) are fixed. As the Prandtle number is a quotient of momentum diffusivity to thermal diffusivity. So it is clear shown in Figure 4(a) that increases in Pr causes increase in temperature due to scaling down in thermal diffusion or can say that thermal conductivity raises or density of the fluid scale down. Figure 4(b) represent the impact of Prandtle number (Pr) on Concentration profile while keeping these parameters $\lambda =$3, Sc = 0.5, Kr = 0.1, Nt = 0.5, Nb = 0.5, Sq = 0.5 remain unchanged. Concentration profile behaviour as shown in Figure 4(b) which shows that increase in Pr = 1, 2, 3, 5 shows increase in Concentration because to increase in Momentum diffusivity i.e., momentum of the fluid particle increasing in the direction of the flow of fluid.

Thermophoretic (Nt) and Brownian parameter (Nb) impact on dimensionless temperature profile are shown in Figure 5(a). As thermophoresis and Brownian motion are two important sources of nano-particle migration in nano fluids, having considerable effects on the thermo physical traits of nano fluids. It is shown here that the smaller nano-particles are able to accumulate at the heated walls and enhances the heat exchange rate. We can see from Figure 5(a) temperature profile scale up as the value of Nt = Nb = 1, 2, 3, 4 increases while keeping Sc = 0.5, Kr = 0.1, Sq = 0.5, Pr = 5, $\lambda =$3 these parameter fixed. Increasing behavior of temperature is due to the specific factor that Nt and Nb has direct relation with the transformation of heat coefficient corresponding with the nanofluid particles. Figure 5(b) used to analyze the impact for different value of Thermophoretic (Nt) and Brownian parameter (Nb) on Concentration profile. Figure 5(b) showing the behavior of Concentration profile $\left(\phi \right(\eta \left)\right)$ by changing the value of Sc while Kr = 0.5, Nt = 0.5, Nb = 0.5, Sq = 0.5, Pr = 5, $\lambda =$2) are fixed. As it is being observed in Figure 5(b) that when the value of Nt = N_b = 0.1, 0.5, 0.9, 1.5 increases while other parameters such as Sc = 0.5, Kr = 0.5, Sq = 0.5, Pr = 5, $\lambda =$2 are kept constant then the similar impact of both parameter Nt and Nb scale down the Concentration profile. It is because of the random motion of the nanoparticle or dimensionless nanoparticle volume fraction profile.

It finds in Figure 6 that concentration profile graph decreases when the Schmidt number is increased. it is because Schmidt number is one of the numbers without dimension and it is stated as the co-relation between momentum diffusivity to mass diffusivity. So for high Schmidt numbers i.e., (Sc = 1, 3, 6, 10) momentum diffusion will dominate such as by increasing Schmidt number dynamic viscosity increases and density decreases.

The numerical comparison has also been presented for better understanding for both coefficient of skin friction (Cf) and Nusselt number (Nu) as a particular case for this study. Increasing Reynolds number, Prandtle number and injection parameter results into scale-up in the coefficient of skin friction with also Nusselt number. Also it is shown that Nusselt number increases due to the increase in injection parameter. Opposite trend follows when the value of Schmidt number is increased as seen in Tables 1–5.

5.   Conclusions

Theoretical analysis of physical characteristics of unsteady, squeezing nanofluid is studied. Nanofluid model includes the pivotal impact of thermophoresis and Brownian motion. By using the concept of similarity transformation PDEs morphed into combine scheme of ODEs. Parametric Continuation Method (PCM) used for the numerical evaluation of all the major parameters i.e., Schmidt number, squeezing number, Prandtle number, Brownian and Thermophoretic parameter. Tabulated findings analyzed for studying the effect of Nusselt number and Skin friction. The result indicates that:

● If we have to increase the value of injection parameter ($\lambda$) then the velocity profile f'($\eta$), f($\eta$) and concentration profile $\phi \left(\eta \right)$ increases while temperature profile $\theta \left(\eta \right)$ decreases.

● It is observed that when the squeezing number decreases (means that upper plate come close towards lower plate), as a result velocity and temperature profile increases and Concentration profile decreases.

● It is shown that increase in Prandtle number, temperature profile decreases and opposite behaviour is observed in Concentration profile.

● Similar implications of Thermophoresis and Brownian parameter on temperature profile and concentration profile is drawing out in which temperature increases and concentration decreases.

● It is shown that when Schmidt number (Sc) increases then profile of Concentration decreases.

● Also it originates that Skin friction and Nusselt number have direct affiliation with Squeezing Reynolds number, Prandtle number and also with injection parameter while it is observed that, it has an opposite relation with Schmidt number.

In future we have:

● The same problem may able to studied in this type of system in Partial differential equation.

● An advance numerical MATLAB program is required for the analysis of these system models.

Conflict of interest

The authors declare no conflict of interest in this paper.

Acknowledgment

The author extended their appreciation to Deanship of Scientific Research at King Khalid University for funding this work through research group program under grant number R.G.P.2/76/43. Also the work of U.F.G was supported by the government of the Basque Country for the ELKARTEK21/10 KK-2021/00014 and ELKARTEK22/85 research programs, respectively.