Citation: Zui-Cha Deng, Fan-Li Liu, Liu Yang. Numerical simulations for initial value inversion problem in a two-dimensional degenerate parabolic equation[J]. AIMS Mathematics, 2021, 6(4): 3080-3104. doi: 10.3934/math.2021187
| [1] | Yilihamujiang Yimamu, Zui-Cha Deng, Liu Yang . An inverse volatility problem in a degenerate parabolic equation in a bounded domain. AIMS Mathematics, 2022, 7(10): 19237-19266. doi: 10.3934/math.20221056 |
| [2] | Yu Xu, Youjun Deng, Dong Wei . Numerical solution of forward and inverse problems of heat conduction in multi-layered media. AIMS Mathematics, 2025, 10(3): 6144-6167. doi: 10.3934/math.2025280 |
| [3] | Andrey Muravnik . Wiener Tauberian theorem and half-space problems for parabolic and elliptic equations. AIMS Mathematics, 2024, 9(4): 8174-8191. doi: 10.3934/math.2024397 |
| [4] | Jia Li, Zhipeng Tong . Local Hölder continuity of inverse variation-inequality problem constructed by non-Newtonian polytropic operators in finance. AIMS Mathematics, 2023, 8(12): 28753-28765. doi: 10.3934/math.20231472 |
| [5] | Yashar Mehraliyev, Seriye Allahverdiyeva, Aysel Ramazanova . On one coefficient inverse boundary value problem for a linear pseudoparabolic equation of the fourth order. AIMS Mathematics, 2023, 8(2): 2622-2633. doi: 10.3934/math.2023136 |
| [6] | Abdulghani R. Alharbi . Numerical solutions to two-dimensional fourth order parabolic thin film equations using the Parabolic Monge-Ampere method. AIMS Mathematics, 2023, 8(7): 16463-16478. doi: 10.3934/math.2023841 |
| [7] | Taghread Ghannam Alharbi, Abdulghani Alharbi . Traveling-wave and numerical investigations to nonlinear equations via modern computational techniques. AIMS Mathematics, 2024, 9(5): 12188-12210. doi: 10.3934/math.2024595 |
| [8] | Varadharaj Dinakar, Natesan Barani Balan, Krishnan Balachandran . Identification of Source Terms in a Coupled Age-structured Population Model with Discontinuous Diffusion Coefficients. AIMS Mathematics, 2017, 2(1): 81-95. doi: 10.3934/Math.2017.1.81 |
| [9] | Ailing Zhu, Yixin Wang, Qiang Xu . A weak Galerkin finite element approximation of two-dimensional sub-diffusion equation with time-fractional derivative. AIMS Mathematics, 2020, 5(5): 4297-4310. doi: 10.3934/math.2020274 |
| [10] | Lin Fan, Shunchu Li, Dongfeng Shao, Xueqian Fu, Pan Liu, Qinmin Gui . Elastic transformation method for solving the initial value problem of variable coefficient nonlinear ordinary differential equations. AIMS Mathematics, 2022, 7(7): 11972-11991. doi: 10.3934/math.2022667 |
In this work, we consider an inverse problem of recovering the initial value in a two-dimensional degenerate parabolic equation from terminal observation. The problem can be stated in the following form:
● Problem P: Consider the following two-dimensional degenerate parabolic equation
| $\left\{ \begin{array}{l} {u_t} - \nabla \cdot ((a(X)\nabla u)) = 0, \quad (X, t) \in Q = \Omega \times (0, T], \\ u(X, 0) = \varphi (X), \quad \quad \quad \;X \in \Omega , \\ \end{array} \right.$ | (1.1) |
where $a(X)$ is a given smooth function satisfying
| $a(X){|_{\partial \Omega }} = 0, \quad a(X) \gt 0, X \in \Omega , $ |
and $\Omega {\rm{ = }}{(0, l)^2} \subset {R^2}$ is a two-dimensional bounded plane region. $\varphi (X)$ is an unknown initial function in (1.1). Assume that an additional condition is given as:
| $u{|_{t = T}} = \psi (X), \quad X \in \Omega , $ | (1.2) |
where $T > 0$ is a fixed time, and $\psi (X)$ is the observation data. In this paper, we use $X$ to denote the two-dimensional spatial variable $(x, y).$ The inverse problem is to determine the functions $u$ and $\varphi $ satisfying (1.1) and (1.2).
In recent years, many inverse problems of degenerate parabolic equations have been proposed to meet actual needs (see [2,6,16,29,33]), which often appear in many engineering and financial fields. It is noted that the degenerate parabolic equation has attracted the attention of many scholars and has been successfully applied to porous media (see [1,3,4,5,25,27]). These results have a profound impact on the development of related fields. Eq (1.1) also belongs to degenerate parabolic equations. Compared with the traditional parabolic equation, the degenerate one can get rid of the limitation of boundary conditions in some cases. According to the famous Fichera theory, whether or not the boundary conditions of the degenerate parabolic equation should be given is determined by the corresponding symbol of the Fichera function (see [23]). If the sign is nonnegative, the boundary condition is not necessary; otherwise, it is the opposite. Using the Fichera's theorem, we can easily calculate that the value of Fichera function of Eq (1.1) is zero at the corresponding degenerate boundary. Therefore, Eq (1.1) does not need to give boundary conditions.
For general heat conduction problems, the initial value function usually represents the initial temperature distribution field of the object. While for the inverse heat conduction problem, the main task is to reconstruct the initial temperature with some additional observation data. This is a kind of severly ill-posed problem, that is, the small change of observation data will lead to the big change of solution. This is easy to understand. In fact, most things in nature are irreversible. If we can easily reconstruct the past temperature by using the current measurement data, then we can easily obtain the temperature of the earth 65 million years ago. Maybe we can know how dinosaurs died out, but it's impossible. (The reason why dinosaurs died out has always been a mystery. One is that 65 million years ago, the earth's climate suddenly changed, the temperature dropped sharply, dinosaurs were frozen to death. Another view is that because of the eruption of volcanoes, a large amount of carbon dioxide spewed out, resulting in the earth's rapid greenhouse effect, making food death, and eventually the extinction of dinosaurs.) However, this is a problem that must be solved in some engineering fields. For example, in steel smelting, we need to obtain the ideal temperature distribution at a certain time, so how to accurately control the initial temperature is such a problem.
For the inverse initial value problems of nondegenerate parabolic equations, there have been a lot of research work, and abundant theoretical and numerical results have been obtained (see [9,10,11,12,13,14,15,17,18,19,20,31]). In [17], the data assimilation problem for the soil water movement model is analysed carefully, where the numerical computation is realized through searching the minimum of the cost function iteratively by a descent gradient method.
For the case of degeneration, the literatures are quite few. These works mostly discuss the coefficient inversion of degenerate parabolic equation from the angle of theoretical analysis, such as source term coefficient or zero-order term coefficient, etc. Documents [7,8,22] are earlier ones involving degenerate parabolic equations. In these papers, the authors establish the Carleman estimate in the case of boundary degradation, and discuss the null controllability of related equations. Since then, these works have been widely extended and successfully applied to the inverse coefficient(s) problem of degenerate parabolic equations (see [2,6,29]). In [26], the uniqueness of the inverse source problem of one-dimensional degenerate heat equation
| ${u_t} - {(a(x){u_x})_x} = f(x), \quad (x, t) \in Q, $ |
is proved by the extremum principle, and the numerical simulation is also given. In [29], the authors consider the inverse problem of determining the insolation function, where the underlying equation is the nonlinear Sellers climate model. The uniqueness and Lipschitz stability of the solution are also obtained. In [2], the inverse source problem for multidimensional parabolic operators of Grushin type
| ${u_t} - {\Delta _x}u - |x{|^{2r}}b(x){\Delta _y}u = g(x, y, t), {\rm{ }}(x, y, t) \in {\Omega _1} \times {\Omega _2} \times (0, \infty ), $ |
where ${\Omega _1}$ is a bounded open region that contains the origin and thus the principle coefficient is degenerate.
In [32], numerical inversion for an inverse initial value problem is studied carefully, where the mathematical model is governed by a one-dimensional degenerate parabolic equation. In [33], the authors consider an inverse problem of simultaneously reconstructing the initial value and source term in a degenerate parabolic equation. Uniqueness and stability of the solution are obtained by the Carleman estimate. It should be pointed out that the vast majority of literature in the previous work is about one-dimensional degenerate parabolic equation, and there are few relevant literature about higher-dimensional case. The main reason is that in the case of higher dimension, the degree and way of coefficient degeneration is much more complex than that in the case of one dimension. However, the application in high dimension is more extensive than that in one dimension. For example, in the field of computer signal processing, one-dimensional functions can only represent one-dimensional signals, but two dimensional functions can represent more complex information, such as digital images. If it is a color image or a video, the dimension of the function will be higher.
This work studies the inverse initial value problem for a two-dimensional degenerate diffusion equation. In a sense, this is an extension of the one-dimensional form, and its thermal conductivity is also extended from one-dimension to two-dimension. The change of thermal conductivity enables us to take into account both anisotropic diffusion and slow diffusion, but it also brought essential difficulty for theoretical analysis and numerical simulations. In particular, these results in the case of two-dimension can be easily applied to the field of digital image processing. The outline of the manuscript is as follows: In Section 2, based on the finite volume method, a difference scheme of the forward problem is proposed. The stability and convergence of the scheme are proved in Section 3. In Section 4, the Landweber iteration and conjugate gradient method (CGM) are used to solve the numerical solution for the inverse problem. Some typical numerical examples are presented in the last section to show the validity of the inversion method.
The main purpose of this paper is to study the problem P from the perspective of numerical analysis. The conclusions on the theoretical aspects are only briefly introduced, and those proofs can be found in the references (see [20,23]). Let
| ${\Omega _\varepsilon } = \{ {\rm{ }}X|{\rm{ }}d(X, \Omega ) \lt \varepsilon , {\rm{ }}X \in {R^2}{\rm{ }}\} , $ |
where $\varepsilon $ is an arbitrarily small positive constant. If $a$ and $\varphi $ satisfy
| $a(X) \in {W^{k + 1, \infty }}({\Omega _\varepsilon }), {\rm{ }}\varphi (X) \in {W^{k + 2, \infty }}({\Omega _\varepsilon });{\rm{ }}a(X) \geqslant 0, {\rm{ }}X \in {\Omega _\varepsilon }, $ |
then there exists a unique weak solution $u(X, t) \in {W^{k, \infty }}(\bar Q)$ to the Eq (1.1) (see [23]). In this paper, we always assume that the solution of the direct problem has sufficient regularity (at least belongs to ${C^{2 + \alpha, 1 + \alpha /2}}(\bar Q), {\rm{ 0 < }}\alpha < 1$). Considering the embedding property of space, it seems that $k \geqslant 5$ is enough. Moreover, the uniqueness and stability of the solution for problem P can be proved by the logarithmic convexity method (see [20]).
In this article, we use the finite difference method to obtain the numerical solution of Eq (1.1). For the sake of simplicity, we assume that the domain $\Omega $ is a square. For the case of rectangle, we can discuss it similarly, which is not the key of the problem.
Assumed that the domain $\Omega $ is divided into a mesh $J \times J$ with the spatial step size $h = {h_x} = {h_y} = \frac{l}{J}$ and the time step size $\tau = \frac{T}{N}, $ respectively.
Grid points $({x_i}, {y_j})$ of the layer ${t_n}({t_n} = n\tau, n = 0, 1, 2, \cdots, N)$ are defined by
| $\begin{array}{l} {x_i} = ih, \quad \quad i = 0, 1, 2, \cdots , J, \\ {y_j} = jh, \quad \quad j = 0, 1, 2, \cdots , J. \\ \end{array} $ |
The notation $u_{ij}^n$ is used for the finite difference approximation of $u(ih, jh, n\tau)$.
Remark: The region can be generalized to a general rectangular region where the spatial steps can be taken as
Using the finite volume method (see[21,28]), one can derive the following implicit difference scheme of (1.1).
| $\frac{{u_{ij}^{n + 1} - u_{ij}^n}}{\tau } - \frac{{{a_{i + \frac{1}{2}, j}}u_{i + 1, j}^{n + 1} - ({a_{i + \frac{1}{2}, j}} + {a_{i - \frac{1}{2}, j}})u_{ij}^{n + 1} + {a_{i - \frac{1}{2}, j}}u_{i - 1, j}^{n + 1}}}{{{h^2}}} - \frac{{{a_{i, j + \frac{1}{2}}}u_{i, j + 1}^{n + 1} - ({a_{i, j + \frac{1}{2}}} + {a_{i, j - \frac{1}{2}}})u_{ij}^{n + 1} + {a_{i, j - \frac{1}{2}}}u_{i, j - 1}^{n + 1}}}{{{h^2}}} = 0, $ | (2.1) |
for $1 \leqslant i$, $j \leqslant J - 1$ and $0 \leqslant n \leqslant N - 1$, where${a_{ij}} = a({x_i}, {y_i}).$
In this section, we always assume that $a(X)$ at least belongs to ${C^2}(\bar \Omega)$. Note that on the boundary of $\Omega $, Eq (1.1) is degenerated into the following first order hyperbolic equations
| $\begin{array}{l} {u_t} - {a_x}{u_x} = 0, \quad \quad x = 0, l, \\ {u_t} - {a_y}{u_y} = 0, \quad \quad y = 0, l. \\ \end{array} $ | (2.2) |
Therefore, the boundary conditions of (1.1) can be divided into three cases according to the value of $\nabla a(X)$.
Case 1. If ${a_x}\left| {_{x = 0, l}} \right. = {a_y}\left| {_{y = 0, l}} \right. = 0$, we get the follow boundary condition from (2.2) and (1.1)
| ${\left. u \right|_{\partial \Omega }} = {\left. \varphi \right|_{\partial \Omega }}.$ |
Case 2. If, the boundary conditions can be discretized as
| $\begin{array}{l} \frac{{u_{0, j}^{n + 1} - u_{0, j}^n}}{\tau } - {\left. {{a_x}} \right|_{x = 0}}\frac{{u_{1, j}^{n + 1} - u_{0, j}^{n + 1}}}{h} = 0, \;\quad \frac{{u_{i, 0}^{n + 1} - u_{i, 0}^n}}{\tau } - {\left. {{a_y}} \right|_{y = 0}}\frac{{u_{i, 1}^{n + 1} - u_{i, 0}^{n + 1}}}{h} = 0, \\ \frac{{u_{J, j}^{n + 1} - u_{J, j}^n}}{\tau } - {\left. {{a_x}} \right|_{x = l}}\frac{{u_{J, j}^{n + 1} - u_{J - 1, j}^{n + 1}}}{h} = 0, \;\quad \frac{{u_{i, J}^{n + 1} - u_{i, J}^n}}{\tau } - {\left. {{a_y}} \right|_{y = l}}\frac{{u_{i, J}^{n + 1} - u_{i, J - 1}^{n + 1}}}{h} = 0. \\ \end{array} $ | (2.3) |
Case 3. If at least one of the four values ${a_x}\left| {_{x = 0, l}} \right., {a_y}\left| {_{y = 0, l}} \right.$, is not zero, we can discuss it similarly.
The initial condition
| $u(x, y, 0) = \varphi (x, y), \quad (0 \leqslant x \leqslant l, 0 \leqslant y \leqslant l), $ |
can be discretized by
| $u_{ij}^0 = {\varphi _{ij}}, \quad i, j = 0, 1, 2, \cdots , J.$ | (2.4) |
Without loss of generality, in the following discussions, the boundary conditions are assumed to be Case 2.
In order to write the difference equation conveniently, we introduce the following symbol
| ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _j} = \left( {\begin{array}{*{20}{c}} \begin{array}{l} {u_{0, j}} \\ {u_{1, j}} \\ \end{array} \\ {{u_{2, j}}} \\ \vdots \\ {{u_{J, j}}} \end{array}} \right), \quad 0 \leqslant j \leqslant J.$ |
Setting
| $r = \tau /{h^2}, $ |
the difference scheme of (2.1) can be rewritten as
| $\begin{array}{l} - r{a_{i, j - \frac{1}{2}}}u_{i, j - 1}^{n + 1} - r{a_{i - \frac{1}{2}, j}}u_{i - 1, j}^{n + 1} + \left[ {1 + r\left( {{a_{i + \frac{1}{2}, j}} + {a_{i - \frac{1}{2}, j}} + {a_{i, j + \frac{1}{2}}} + {a_{i, j - \frac{1}{2}}}} \right)} \right]u_{i, j}^{n + 1} \\ - r{a_{i + \frac{1}{2}, j}}u_{i + 1, j}^{n + 1} - r{a_{i, j + \frac{1}{2}}}u_{i, j + 1}^{n + 1} = u_{i, j}^n, \quad 1 \leqslant i, j \leqslant J. \\ \end{array} $ | (2.5) |
Let
| ${A_j} = \left( {\begin{array}{*{20}{r}} {1 + r{a_{0, j}}}&{}&{}&{}&{} \\ {}&{1 + r{a_{1, j}}}&{}&{}&{} \\ {}&{}& \ddots &{}&{} \\ {}&{}&{}&{1 + r{a_{J - 1, j}}}&{} \\ {}&{}&{}&{}&{1 + r{a_{J, j}}} \end{array}} \right), $ |
| ${B_j} = \left( {\begin{array}{*{20}{r}} { - r{a_{0, j}}}&{}&{}&{}&{} \\ {}&{ - r{a_{1, j}}}&{}&{}&{} \\ {}&{}& \ddots &{}&{} \\ {}&{}&{}&{ - r{a_{J - 1, j}}}&{} \\ {}&{}&{}&{}&{ - r{a_{J, j}}} \end{array}} \right), $ |
| ${C_j} = \left( {\begin{array}{*{20}{c}} {1 + r{a_{1, j}}}&{ - r{a_{1, j}}}&{}&{}&{}&{}&{} \\ { - r{a_{\frac{1}{2}, j}}}&{1 + r({a_{\frac{3}{2}, j}} + {a_{\frac{1}{2}, j}} + {a_{1, j + \frac{1}{2}}} + {a_{1, j - \frac{1}{2}}})}&{ - r{a_{\frac{3}{2}, j}}}&{}&{}&{}&{} \\ {}&{ - r{a_{\frac{3}{2}, j}}}&{1 + r({a_{\frac{5}{2}, j}} + {a_{\frac{3}{2}, j}} + {a_{2, j + \frac{1}{2}}} + {a_{2, j - \frac{1}{2}}})}&{ - r{a_{\frac{5}{2}, j}}}&{}&{}&{} \\ {}&{}& \ddots & \ddots & \ddots &{}&{} \\ {}&{}&{}&{ - r{a_{J - \frac{5}{2}, j}}}&{1 + r({a_{J - \frac{3}{2}, j}} + {a_{J - \frac{5}{2}, j}} + {a_{J - 2, j + \frac{1}{2}}} + {a_{J - 2, j - \frac{1}{2}}})}&{ - r{a_{J - \frac{3}{2}, j}}}&{} \\ {}&{}&{}&{}&{ - r{a_{J - \frac{3}{2}, j}}}&{1 + r({a_{J - \frac{1}{2}, j}} + {a_{J - \frac{3}{2}, j}} + {a_{J - 1, j + \frac{1}{2}}} + {a_{J - 1, j - \frac{1}{2}}})}&{ - r{a_{J - \frac{1}{2}, j}}} \\ {}&{}&{}&{}&{}&{ - r{a_{J - 1, j}}}&{1 + r{a_{J - 1, j}}} \end{array}} \right), _\rm{and} $ |
| ${D_j} = \left( {\begin{array}{*{20}{c}} 0&0& \cdots &{}&{}&{}&0 \\ {}&{ - r{a_{1, j + \frac{1}{2}}}}&{}&{}&{}&{}&{} \\ {}&{}&{ - r{a_{2, j + \frac{1}{2}}}}&{}&{}&{}&{} \\ {}&{}&{}& \ddots &{}&{}&{} \\ {}&{}&{}&{}&{ - r{a_{J - 2, j + \frac{1}{2}}}}&{}&{} \\ {}&{}&{}&{}&{}&{ - r{a_{J - 1, j + \frac{1}{2}}}}&{} \\ 0& \cdots &{}&{}&{}&0&0 \end{array}} \right).$ |
Combining (2.3) and (2.5), the diference scheme can be further written as the following matrix equation:
| $\left( {\begin{array}{*{20}{r}} {{A_1}}&{{B_1}}&{}&{}&{}&{}&{} \\ {{D_0}}&{{C_1}}&{{D_1}}&{}&{}&{}&{} \\ {}&{{D_1}}&{{C_2}}&{{D_2}}&{}&{}&{} \\ {}&{}& \ddots & \ddots & \ddots &{}&{} \\ {}&{}&{}&{{D_{J - 3}}}&{{C_{J - 2}}}&{{D_{J - 2}}}&{} \\ {}&{}&{}&{}&{{D_{J - 2}}}&{{C_{J - 1}}}&{{D_{J - 1}}} \\ {}&{}&{}&{}&{}&{{B_{J - 1}}}&{{A_{J - 1}}} \end{array}} \right)\left( {\begin{array}{*{20}{r}} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _0^{n + 1}} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _1^{n + 1}} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _2^{n + 1}} \\ \vdots \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _{J - 2}^{n + 1}} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _{J - 1}^{n + 1}} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _J^{n + 1}} \end{array}} \right) = \left( {\begin{array}{*{20}{r}} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _0^n} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _1^n} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _2^n} \\ \vdots \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _{J - 2}^n} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _{J - 1}^n} \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} _J^n} \end{array}} \right).$ | (2.6) |
Solving Eq (2.6), we can obtain the numerical solution of the forward problem.
In order to obtain the stability and convergence of the difference equation, we introduce the following notations:
| $\begin{array}{l} {\delta _x}{u_{i + \frac{1}{2}, j}} = \frac{1}{h}({u_{i + 1, j}} - {u_{ij}}), \quad \delta _x^2{u_{ij}} = \frac{1}{h}({\delta _x}{u_{i + \frac{1}{2}, j}} - {\delta _x}{u_{i - \frac{1}{2}, j}}), \\ {\delta _y}{u_{i, j + \frac{1}{2}}} = \frac{1}{h}({u_{i, j + 1}} - {u_{ij}}), \quad \delta _y^2{u_{ij}} = \frac{1}{h}({\delta _y}{u_{i, j + \frac{1}{2}}} - {\delta _y}{u_{i, j - \frac{1}{2}}}), \\ {D_{{x^ + }}}{u_{ij}} = \frac{1}{h}({u_{i + 1, j}} - {u_{ij}}), \quad {D_{{x^ - }}}{u_{ij}} = \frac{1}{h}({u_{ij}} - {u_{i - 1, j}}), \\ {D_{{y^ + }}}{u_{ij}} = \frac{1}{h}({u_{i, j + 1}} - {u_{ij}}), \quad {D_{{y^ - }}}{u_{ij}} = \frac{1}{h}({u_{ij}} - {u_{i, j - 1}}), \\ {D_{\bar t}}u_{ij}^n = \frac{1}{\tau }(u_{ij}^n - u_{ij}^{n - 1}), \\ \end{array} $ |
and the norms
| $\left\| u \right\| = \sqrt {{h^2}\sum\limits_{i, j = 1}^{J - 1} {{\alpha _{ij}}u_{ij}^2} } , \quad \left| {\left[ u \right]} \right| = \sqrt {{h^2}\sum\limits_{i, j = 0}^J {{\alpha _{ij}}u_{ij}^2} } , $ |
where
| ${\alpha _{0, j}} = {\alpha _{J, j}} = {\alpha _{i, 0}} = {\alpha _{i, J}} = \frac{1}{2}, \quad i, j = 0, 1, 2, \cdots , J, $ |
| ${\alpha _{ij}} = 1, \quad i, j = 1, 2, \cdots , J - 1.$ |
Before proving the stability, we first introduce the following lemmas.
Lemma 3.1. (discrete Gronwall inequality). Let be a non-negative sequence which satisfies
| ${F^{k + 1}} \leqslant (1 + C\tau ) \cdot {F^k} + \tau G, \quad k = 0, 1, 2, \cdots , $ |
where $C > 0$ and $G \geqslant 0$ are two constants. Then we have the following estimate:
| ${F^{k + 1}} \leqslant {e^{Ck\tau }} \cdot ({F^0} + \frac{G}{C}), \quad k = 0, 1, 2, \cdots .$ |
The proof can be found in [28,lemma 3.8].
Lemma 3.2. Assuming that $\{ u_{ij}^n|0 \leqslant i, j \leqslant J, 0 \leqslant n \leqslant N\} $ be the solution of difference Eqs.(2.1), (2.3) and (2.4), then we have for relatively small $\tau $,
| ${\left| {\left[ {{u^n}} \right]} \right|^2} \leqslant \exp \left( {\frac{3}{2}AT} \right){\left| {\left[ \varphi \right]} \right|^2}, \quad n = 1, 2, 3, \cdots , N, $ |
where the constant $A$ is dependent on $a(X)$.
Proof. Using the above notations the difference equations (2.1), (2.3), (2.4) can be rewritten as the following system:
| ${D_{\bar t}}u_{ij}^{n + 1} - {\delta _x}({a_{ij}}{\delta _x}u_{ij}^{n + 1}) - {\delta _y}({a_{ij}}{\delta _y}u_{ij}^{n + 1}) = 0, \quad 1 \leqslant i, j \leqslant J - 1, \;0 \leqslant n \leqslant N - 1, $ | (3.1) |
| $u_{ij}^0 = {\varphi _{ij}}, \quad 0 \leqslant i, j \leqslant J, $ | (3.2) |
| ${D_{\bar t}}u_{0, j}^{n + 1} - {a_x}\left| {_{x = 0}} \right.{D_{{x^ + }}}u_{0, j}^{n + 1} = 0, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.3) |
| ${D_{\bar t}}u_{J, j}^{n + 1} - {a_x}\left| {_{x = l}} \right.{D_{{x^ - }}}u_{J, j}^{n + 1} = 0, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.4) |
| ${D_{\bar t}}u_{i, 0}^{n + 1} - {a_y}\left| {_{y = 0}} \right.{D_{{y^ + }}}u_{i, 0}^{n + 1} = 0, \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.5) |
| ${D_{\bar t}}u_{i, J}^{n + 1} - {a_y}\left| {_{y = l}} \right.{D_{{y^ - }}}u_{i, J}^{n + 1} = 0, \quad 0 \leqslant i \leqslant J, 0 \leqslant n \leqslant N - 1.$ | (3.6) |
Multiplying ${h^2}u_{ij}^{n + 1}$ on both sides of (3.1) and summing from $i$, $j = 1$ to $J - 1$, we have
| $\sum\limits_{i, j = 1}^{J - 1} {({D_{\bar t}}u_{ij}^{n + 1}) \cdot {h^2} \cdot u_{ij}^{n + 1}} - \sum\limits_{i, j = 1}^{J - 1} {{\delta _x}({a_{ij}}{\delta _x}u_{ij}^{n + 1}) \cdot {h^2} \cdot u_{ij}^{n + 1}} - \sum\limits_{i, j = 1}^{J - 1} {{\delta _y}({a_{ij}}{\delta _y}u_{ij}^{n + 1})} \cdot {h^2} \cdot u_{ij}^{n + 1} = 0.$ | (3.7) |
For the first term of (3.7), we have
| $\begin{array}{l} \sum\limits_{i, j = 1}^{J - 1} {({D_{\bar t}}u_{ij}^{n + 1}) \cdot {h^2} \cdot u_{ij}^{n + 1}} = \frac{1}{\tau }\sum\limits_{i, j = 1}^{J - 1} {(u_{ij}^{n + 1} - u_{ij}^n)} \cdot {h^2} \cdot u_{ij}^{n + 1} \\ \quad \quad \quad \quad \quad \quad \;\; = \frac{{{h^2}}}{\tau }\sum\limits_{i, j = 1}^{J - 1} {\left[ {{{(u_{ij}^{n + 1})}^2} - u_{ij}^nu_{ij}^{n + 1}} \right]} \\ \quad \quad \quad \quad \quad \quad \;\; = \frac{1}{\tau }{\left\| {{u^{n + 1}}} \right\|^2} - \frac{{{h^2}}}{\tau }\sum\limits_{i, j = 1}^{J - 1} {(u_{ij}^nu_{ij}^{n + 1})} \\ \quad \quad \quad \quad \quad \quad \;\; \geqslant \frac{1}{\tau }{\left\| {{u^{n + 1}}} \right\|^2} - \frac{{{h^2}}}{{2\tau }}\sum\limits_{i, j = 1}^{J - 1} {\left[ {{{(u_{ij}^n)}^2} + {{(u_{ij}^{n + 1})}^2}} \right]} \\ \quad \quad \quad \quad \quad \quad \;\; = \frac{1}{\tau }{\left\| {{u^{n + 1}}} \right\|^2} - \frac{1}{{2\tau }}({\left\| {{u^n}} \right\|^2} + {\left\| {{u^{n + 1}}} \right\|^2}) \\ \end{array} $ |
| $ \; = \frac{1}{{2\tau }}({\left\| {{u^{n + 1}}} \right\|^2} - {\left\| {{u^n}} \right\|^2}), $ | (3.8) |
where we have used the following basic inequality:
| $ab \leqslant \frac{1}{2}({a^2} + {b^2}).$ |
From (3.7) and (3.8), we obtain
| $\frac{1}{{2\tau }}({\left\| {{u^{n + 1}}} \right\|^2} - {\left\| {{u^n}} \right\|^2}) - \sum\limits_{i, j = 1}^{J - 1} {{\delta _x}({a_{ij}}{\delta _x}u_{ij}^{n + 1}) \cdot {h^2} \cdot u_{ij}^{n + 1}} - \sum\limits_{i, j = 1}^{J - 1} {{\delta _y}({a_{ij}}{\delta _y}u_{ij}^{n + 1})} \cdot {h^2} \cdot u_{ij}^{n + 1} \leqslant 0.$ | (3.9) |
For the second term of (3.7), we have
| $ - {h^2}\sum\limits_{i, j = 1}^{J - 1} {{\delta _x}({a_{ij}}{\delta _x}u_{ij}^{n + 1}) \cdot u_{ij}^{n + 1}} \\ = - {h^2}\sum\limits_{i, j = 1}^{J - 1} {\left[ {\frac{{{a_{i + \frac{1}{2}, j}}{\delta _x}u_{i + \frac{1}{2}, j}^{n + 1}}}{h} - \frac{{{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1}}}{h}} \right] \cdot u_{ij}^{n + 1}} \\ = h\sum\limits_{i, j = 1}^{J - 1} {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1} \cdot u_{ij}^{n + 1} - } h\sum\limits_{i, j = 1}^{J - 1} {{a_{i + \frac{1}{2}, j}}{\delta _x}u_{i + \frac{1}{2}, j}^{n + 1} \cdot u_{ij}^{n + 1}} \\ = h\sum\limits_{i, j = 1}^{J - 1} {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1} \cdot u_{ij}^{n + 1} - } h\sum\limits_{i, j = 2}^J {{a_{i - \frac{1}{2}, j - 1}}{\delta _x}u_{i - \frac{1}{2}, j - 1}^{n + 1} \cdot u_{i - 1, j - 1}^{n + 1}} \\ = h\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1} \cdot u_{ij}^{n + 1} - } h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}{\delta _x}u_{J - \frac{1}{2}, j}^{n + 1} \cdot u_{J, j}^{n + 1} - h\sum\limits_{i = 1}^J {{a_{i - \frac{1}{2}, J}}{\delta _x}u_{i - \frac{1}{2}, J}^{n + 1} \cdot u_{i, J}^{n + 1}} } \\ \quad - h\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j - 1}}{\delta _x}u_{i - \frac{1}{2}, j - 1}^{n + 1} \cdot u_{i - 1, j - 1}^{n + 1}} + h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j - 1}}{\delta _x}u_{\frac{1}{2}, j - 1}^{n + 1} \cdot u_{0, j - 1}^{n + 1}} + h\sum\limits_{i = 1}^J {{a_{i - \frac{1}{2}, 0}}{\delta _x}u_{i - \frac{1}{2}, 0}^{n + 1} \cdot u_{i - 1, 0}^{n + 1}} \\ = h\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1} \cdot u_{ij}^{n + 1} - } h\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1} \cdot u_{i - 1, j}^{n + 1}} - h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} + h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j}}({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1} \\ = h\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1}(u_{ij}^{n + 1} - u_{i - 1, j}^{n + 1}) - h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} + h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j}}({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1}} \\ $ |
| $ = {h^2}\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{{\left| {{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1}} \right|}^2} - h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} + h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j}}({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } } u_{0, j}^{n + 1}.$ | (3.10) |
Similarly, for the third part of (3.7), we have
| $ - \sum\limits_{i, j = 1}^{J - 1} {{\delta _y}({a_{ij}}{\delta _y}u_{ij}^{n + 1})} \cdot {h^2} \cdot u_{ij}^{n + 1}$ |
| $ = {h^2}\sum\limits_{i, j = 1}^J {{a_{i, j - \frac{1}{2}}}{{\left| {{\delta _y}u_{i, j - \frac{1}{2}}^{n + 1}} \right|}^2} - h\sum\limits_{i = 1}^J {{a_{i, J - \frac{1}{2}}}({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot } u_{i, J}^{n + 1} + h\sum\limits_{i = 1}^J {{a_{i, \frac{1}{2}}}({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot } } u_{i, 0}^{n + 1}, $ | (3.11) |
where we have used the boundary informations of $a(X).$
Combining (3.8)-(3.11), we obtain
| $\begin{array}{l} \frac{1}{{2\tau }}({\left\| {{u^{n + 1}}} \right\|^2} - {\left\| {{u^n}} \right\|^2}) + {h^2}\sum\limits_{i, j = 1}^J {{a_{i - \frac{1}{2}, j}}{{\left| {{\delta _x}u_{i - \frac{1}{2}, j}^{n + 1}} \right|}^2}} + {h^2}\sum\limits_{i, j = 1}^J {{a_{i, j - \frac{1}{2}}}{{\left| {{\delta _y}u_{i, j - \frac{1}{2}}^{n + 1}} \right|}^2}} \\ \leqslant h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} - h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j}}({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1} \\ \end{array} $ |
| $\quad + h\sum\limits_{i = 1}^J {{a_{i, J - \frac{1}{2}}}({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot } u_{i, J}^{n + 1} - h\sum\limits_{i = 1}^J {{a_{i, \frac{1}{2}}}({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot } u_{i, 0}^{n + 1}.$ | (3.12) |
Multiplying $\frac{1}{2}{h^2}u_{0, j}^{n + 1}$ on both sides of Eq (3.3) and summing from $j = 0$ to $J$, and using the Cauchy inequality, we get
| $\frac{{{h^2}}}{{2\tau }}\sum\limits_{j = 0}^J {{{(u_{0, j}^{n + 1})}^2} \leqslant \frac{{{h^2}}}{{4\tau }}\sum\limits_{j = 0}^J {{{(u_{0, j}^n)}^2}} + \frac{{{h^2}}}{{4\tau }}\sum\limits_{j = 0}^J {{{(u_{0, j}^{n + 1})}^2}} + \frac{{{h^2}}}{2}\sum\limits_{j = 0}^J {{a_x}\left| {_{x = 0}} \right.({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1}} , $ |
which implies
| $\begin{array}{l} \frac{{{h^2}}}{{4\tau }}\sum\limits_{j = 0}^J {[{{(u_{0, j}^{n + 1})}^2} - {{(u_{0, j}^n)}^2}] \leqslant \frac{{{h^2}}}{2}\sum\limits_{j = 0}^J {{a_x}\left| {_{x = 0}} \right.({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1}} \\ \quad \quad \quad \quad \quad \quad \quad = \frac{{{h^2}}}{2}\sum\limits_{j = 1}^J {{a_x}\left| {_{x = 0}} \right.({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1}. \\ \end{array} $ | (3.13) |
Likewise, for (3.4), (3.5) and (3.6), we have
| $\frac{{{h^2}}}{{4\tau }}\sum\limits_{j = 0}^J {[{{(u_{J, j}^{n + 1})}^2} - {{(u_{J, j}^n)}^2}] \leqslant \frac{{{h^2}}}{2}\sum\limits_{j = 1}^J {{a_x}\left| {_{x = l}} \right.({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1}} , $ | (3.14) |
| $\frac{{{h^2}}}{{4\tau }}\sum\limits_{i = 0}^J {[{{(u_{i, 0}^{n + 1})}^2} - {{(u_{i, 0}^n)}^2}] \leqslant \frac{{{h^2}}}{2}\sum\limits_{i = 1}^J {{a_y}\left| {_{y = 0}} \right.({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot } u_{i, 0}^{n + 1}} , $ | (3.15) |
| $\frac{{{h^2}}}{{4\tau }}\sum\limits_{i = 0}^J {[{{(u_{i, J}^{n + 1})}^2} - {{(u_{i, J}^n)}^2}] \leqslant \frac{{{h^2}}}{2}\sum\limits_{i = 1}^J {{a_y}\left| {_{y = l}} \right.({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot } u_{i, J}^{n + 1}} .$ | (3.16) |
From (3.12) to (3.16), we obtain
| $\begin{array}{l} {\rm{ }}\frac{1}{{2\tau }}({\left| {\left[ {{u^{n + 1}}} \right]} \right|^2} - {\left| {\left[ {{u^n}} \right]} \right|^2}) \\ \leqslant h\sum\limits_{j = 1}^J {{a_{J - \frac{1}{2}, j}}({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} - h\sum\limits_{j = 1}^J {{a_{\frac{1}{2}, j}}({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1} \\ {\rm{ }} + h\sum\limits_{i = 1}^J {{a_{i, J - \frac{1}{2}}}({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot } u_{i, J}^{n + 1} - h\sum\limits_{i = 1}^J {{a_{i, \frac{1}{2}}}({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot } u_{i, 0}^{n + 1} \\ {\rm{ }} + \frac{{{h^2}}}{2}\sum\limits_{j = 1}^J {{a_x}\left| {_{x = 0}} \right.({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot } u_{0, j}^{n + 1} + \frac{{{h^2}}}{2}\sum\limits_{j = 1}^J {{a_x}\left| {_{x = l}} \right.({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot } u_{J, j}^{n + 1} \\ \end{array} $ |
| $ + \frac{{{h^2}}}{2}\sum\limits_{i = 1}^J {{a_y}\left| {_{y = 0}} \right.({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot } u_{i, 0}^{n + 1} + \frac{{{h^2}}}{2}\sum\limits_{i = 1}^J {{a_y}\left| {_{y = l}} \right.({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot } u_{i, J}^{n + 1}.$ | (3.17) |
Noticing the smoothness of $a(X)$, we have from the Taylor's formulation (Because in the expansion, only one variable is expanded, and the other keeps unchanged. For the sake of simplicity, another variable is omitted when we take the value in the expansion.)
| ${a_{\frac{1}{2}, j}} = a(\frac{h}{2}, jh) = a(0, jh) + {a_x}\left| {_{x = 0}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{xx}}\left| {_{x = {\theta _1}}} \right. \cdot \frac{{{h^2}}}{4}$ |
| $\quad = {a_x}\left| {_{x = 0}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{xx}}\left| {_{x = {\theta _1}}} \right. \cdot \frac{{{h^2}}}{4}, \quad (0 \leqslant {\theta _1} \leqslant \frac{h}{2}), $ | (3.18) |
| ${a_{J - \frac{1}{2}, j}} = a(Jh - \frac{1}{2}h, jh) = a(l, jh) - {a_x}\left| {_{x = l}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{xx}}\left| {_{x = {\theta _2}}} \right. \cdot \frac{{{h^2}}}{4}$ |
| $ = - {a_x}\left| {_{x = l}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{xx}}\left| {_{x = {\theta _2}}} \right. \cdot \frac{{{h^2}}}{4}, \quad ((J - \frac{1}{2}h) \leqslant {\theta _2} \leqslant Jh).$ | (3.19) |
Similarly
| ${a_{i, \frac{1}{2}}} = {a_y}\left| {_{y = 0}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{yy}}\left| {_{y = {\theta _3}}} \right. \cdot \frac{{{h^2}}}{4}, \quad 0 \leqslant {\theta _3} \leqslant \frac{h}{2}, $ | (3.20) |
| ${a_{i, J - \frac{1}{2}}} = - {a_y}\left| {_{y = l}} \right. \cdot \frac{h}{2} + \frac{1}{2}{a_{yy}}\left| {_{y = {\theta _4}}} \right. \cdot \frac{{{h^2}}}{4}, \quad (J - \frac{1}{2}h) \leqslant {\theta _4} \leqslant Jh.$ | (3.21) |
From (3.17) -(3.21), we can get
| $\begin{array}{l} \frac{1}{{2\tau }}({\left| {\left[ {{u^{n + 1}}} \right]} \right|^2} - {\left| {\left[ {{u^n}} \right]} \right|^2}) \leqslant \frac{{{h^3}}}{8}\sum\limits_{j = 1}^J {{a_{xx}}\left| {_{x = {\theta _2}}} \right.({D_{{x^ - }}}u_{J, j}^{n + 1}) \cdot u_{J, j}^{n + 1} - } \frac{{{h^3}}}{8}\sum\limits_{j = 1}^J {{a_{xx}}\left| {_{x = {\theta _1}}} \right.({D_{{x^ + }}}u_{0, j}^{n + 1}) \cdot u_{0, j}^{n + 1}} \\ \quad \quad \quad \quad \quad \quad \quad + \frac{{{h^3}}}{8}\sum\limits_{i = 1}^J {{a_{yy}}\left| {_{y = {\theta _4}}} \right.({D_{{y^ - }}}u_{i, J}^{n + 1}) \cdot u_{i, J}^{n + 1}} \\ \end{array} $ |
| $ - \frac{{{h^3}}}{8}\sum\limits_{i = 1}^J {{a_{yy}}\left| {_{y = {\theta _3}}} \right.({D_{{y^ + }}}u_{i, 0}^{n + 1}) \cdot u_{i, 0}^{n + 1}} .$ | (3.22) |
By the smoothness of $a(X)$, we may assume
| $A = \max \left\{ {{{\left| {{a_{xx}}} \right|}_{x = {\theta _1}}}, {\rm{ }}{{\left| {{a_{xx}}} \right|}_{x = {\theta _2}}}, {\rm{ }}{{\left| {{a_{yy}}} \right|}_{y = {\theta _3}}}, {\rm{ }}{{\left| {{a_{yy}}} \right|}_{y = {\theta _4}}}} \right\}.$ | (3.23) |
Using (3.22) and (3.23), we have
| $\begin{array}{l} \frac{1}{{2\tau }}({\left| {\left[ {{u^{n + 1}}} \right]} \right|^2} - {\left| {\left[ {{u^n}} \right]} \right|^2}) \leqslant \frac{{{h^3}}}{8}A\sum\limits_{j = 1}^J {[\left| {{D_{{x^ - }}}u_{J, j}^{n + 1} \cdot u_{J, j}^{n + 1}} \right| - } \left| {{D_{{x^ + }}}u_{0, j}^{n + 1} \cdot u_{0, j}^{n + 1}} \right|] \\ \quad \quad \quad \quad \quad \quad \quad + \frac{{{h^3}}}{8}A\sum\limits_{i = 1}^J {[\left| {{D_{{y^ - }}}u_{i, J}^{n + 1} \cdot u_{i, J}^{n + 1}} \right|} - \left| {{D_{{y^ + }}}u_{i, 0}^{n + 1} \cdot u_{i, 0}^{n + 1}} \right|] \\ \quad \quad \quad \quad \quad \quad \quad \leqslant \frac{{{h^3}}}{8}A\sum\limits_{j = 1}^J {[\left| {(u_{J, j}^{n + 1} - u_{J - 1, j}^{n + 1}) \cdot u_{J, j}^{n + 1}} \right|\frac{1}{h} + } \left| {(u_{1, j}^{n + 1} - u_{0, j}^{n + 1}) \cdot u_{0, j}^{n + 1}} \right|\frac{1}{h}] \\ \quad \quad \quad \quad \quad \quad \quad + \frac{{{h^3}}}{8}A\sum\limits_{i = 1}^J {[\left| {(u_{i, J}^{n + 1} - u_{i, J - 1}^{n + 1}) \cdot u_{i, J}^{n + 1}} \right|} \frac{1}{h} + \left| {(u_{i, 1}^{n + 1} - u_{i, 0}^{n + 1}) \cdot u_{i, 0}^{n + 1}} \right|\frac{1}{h}] \\ \end{array} $ |
| $ \leqslant \frac{3}{{16}}A{\left| {[{u^{n + 1}}]} \right|^2}, $ | (3.24) |
which implies
| ${\left| {[{u^{n + 1}}]} \right|^2} \leqslant \frac{1}{{2\tau }}{(\frac{1}{{2\tau }} - \frac{3}{{16}}A)^{ - 1}}{\left| {[{u^n}]} \right|^2}.$ | (3.25) |
So, if we choose $ \mathrm{\tau } $ small enough such that
| $\frac{1}{{2\tau }} \gt \frac{3}{8}A, $ |
then we have
| $\begin{array}{l} \frac{1}{{2\tau }}{(\frac{1}{{2\tau }} - \frac{3}{{16}}A)^{ - 1}} = \frac{1}{{1 - \frac{3}{{16}}A \cdot 2\tau }} \\ \quad \quad \quad \quad \quad = 1 + \frac{3}{{16}}A \cdot 2\tau {(1 - \frac{3}{{16}}A \cdot 2\tau )^{ - 1}} \\ \end{array} $ |
| $ \lt 1 + \frac{3}{4}A\tau .$ | (3.26) |
From (3.25) and (3.26), we get
| ${\left| {\left[ {{u^{n + 1}}} \right]} \right|^2} \leqslant (1 + \frac{3}{4}A\tau ){\left| {\left[ {{u^n}} \right]} \right|^2}, \quad n = 0, 1, 2, \cdots , N - 1.$ | (3.27) |
By the Lemma 3.1 and (3.27), we get
| ${\left| {\left[ {{u^n}} \right]} \right|^2} \leqslant \exp (\frac{3}{4}An\tau ){\left| {\left[ {{u^0}} \right]} \right|^2}{\rm{ = }}\exp (\frac{3}{4}AT){\left| {\left[ \varphi \right]} \right|^2}, \quad n = 1, 2, 3, \cdots , N.$ |
This completes the proof of Lemma 3.2.
The stability of the scheme is the direct consequence of Lemma 3.2.
Remark: For a more general case:
| ${D_{\bar t}}u_{ij}^{n + 1} - {\delta _x}({a_{ij}}{\delta _x}u_{ij}^{n + 1}) - {\delta _y}({a_{ij}}{\delta _y}u_{ij}^{n + 1}) = g_{ij}^{n + 1}, \quad 1 \leqslant i, j \leqslant J - 1, \;0 \leqslant n \leqslant N - 1, $ |
| $u_{ij}^0 = {\varphi _{ij}}, \quad 0 \leqslant i, j \leqslant J, $ |
| ${D_{\bar t}}u_{0, j}^{n + 1} - {a_x}\left| {_{x = 0}} \right.{D_{{x^ + }}}u_{0, j}^{n + 1} = g_{0, j}^{n + 1}, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ |
| ${D_{\bar t}}u_{J, j}^{n + 1} - {a_x}\left| {_{x = l}} \right.{D_{{x^ - }}}u_{J, j}^{n + 1} = g_{J, j}^{n + 1}, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ |
| ${D_{\bar t}}u_{i, 0}^{n + 1} - {a_y}\left| {_{y = 0}} \right.{D_{{y^ + }}}u_{i, 0}^{n + 1} = g_{i, 0}^{n + 1}, \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1, $ |
| ${D_{\bar t}}u_{i, J}^{n + 1} - {a_y}\left| {_{y = l}} \right.{D_{{y^ - }}}u_{i, J}^{n + 1} = g_{i, J}^{n + 1}, \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1, $ |
we may have
| ${\left| {\left[ {{u^n}} \right]} \right|^2} \leqslant C \cdot \exp (CT)({\left| {\left[ \varphi \right]} \right|^2} + \mathop {\max }\limits_{1 \leqslant k \leqslant n} {\left| {\left[ {{g^k}} \right]} \right|^2}), \quad n = 1, 2, 3, \cdots , N, $ | (3.28) |
where $C$ is dependent on $a(X)$.
The proof is similar to that of Lemma 3.2.
Theorem 3.3. Assume that the initial data $\varphi (X) \in {C^2}(\Omega)$ in (1.1), $\{ u({x_{ij}}, {y_{ij}}, {t_n})|0 \le i, j \le J, 0 \le n \le N\} $ is the solution of (1.1), and $\{ u_{ij}^n|0 \le i, j \le J, 0 \le n \le N\} $ is the solution of (3.1)-(3.6). Then, as $\tau \to 0$ and $h \to 0$, the approximate solution $u_{ij}^n$ unconditionally converges to the real solution and the convergence rate is $O\left({\tau + {h^{\frac{3}{2}}}} \right)$, that is
| ${\left| {\left[ {u( \cdot , {t_n}) - {u^n}} \right]} \right|^2} \leqslant O(\tau ) + O\left( {{h^{\frac{3}{2}}}} \right), \quad 0 \leqslant n \leqslant N.$ |
Proof. Let
| $e_{ij}^n = u({x_{ij}}, {y_{ij}}, {t_n}) - u_{ij}^n, \quad 0 \leqslant i, j \leqslant J, 0 \leqslant n \leqslant N.$ |
Subtracting (1.1) from (3.1) to (3.6), we get the error equation:
| ${D_{\bar t}}e_{ij}^{n + 1} - {\delta _x}({a_{ij}}{\delta _x}e_{ij}^{n + 1}) - {\delta _y}({a_{ij}}{\delta _y}e_{ij}^{n + 1}) = R_{ij}^{n + 1}, \quad 1 \leqslant i, j \leqslant J - 1, \;0 \leqslant n \leqslant N - 1, $ | (3.29) |
| $e_{ij}^0 = 0, \quad 0 \leqslant i, j \leqslant J, $ | (3.30) |
| ${D_{\bar t}}e_{0, j}^{n + 1} - {a_x}\left| {_{x = 0}} \right.{D_{{x^ - }}}e_{0, j}^{n + 1} = R_{0, j}^{n + 1}, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.31) |
| ${D_{\bar t}}e_{J, j}^{n + 1} - {a_x}\left| {_{x = l}} \right.{D_{{x^ - }}}e_{J, j}^{n + 1} = R_{J, j}^{n + 1}, \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.32) |
| ${D_{\bar t}}e_{i, 0}^{n + 1} - {a_y}\left| {_{y = 0}} \right.{D_{{y^ + }}}e_{i, 0}^{n + 1} = R_{i, 0}^{n + 1}, \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.33) |
| ${D_{\bar t}}e_{i, J}^{n + 1} - {a_y}\left| {_{y = l}} \right.{D_{{y^ - }}}e_{i, J}^{n + 1} = R_{i, J}^{n + 1}, \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1.$ | (3.34) |
Using the regularity of the exact solution $u(X, t) \in {C^{2 + \alpha, 1 + \alpha /2}}(\bar Q), {\rm{ 0 < }}\alpha < 1, $ it can be easily seen that
| $R_{ij}^{n + 1} = O(\tau + {h^2}), \quad 1 \leqslant i, j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.35) |
| $R_{0, j}^{n + 1} = O(\tau + h), \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.36) |
| $R_{J, j}^{n + 1} = O(\tau + h), \quad 0 \leqslant j \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.37) |
| $R_{i, 0}^{n + 1} = O(\tau + h), \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1, $ | (3.38) |
| $R_{i, J}^{n + 1} = O(\tau + h), \quad 0 \leqslant i \leqslant J, \;0 \leqslant n \leqslant N - 1.$ | (3.39) |
Combining (3.29-3.39) and using (3.28), one can easily get the conclusion.
It can be easily seen that the Problem P is a linear problem. Let $K$ be the parameter-to-data mapping, that is
| $K:\quad {L^2}(\Omega ) \to {L^2}(\Omega ), $ |
| $K\varphi = u( \cdot , T) = \psi , $ | (4.1) |
where $u$ is the weak solution of (1.1). In this article, we would like to use the Landweber iteration method to solve the operator Eq (4.1).
Lemma 4.1.1. The mapping defined in (4.1) is a linear bounded operator from to and it has the following bound
| ${\left\| K \right\|_{{L^2}}} \leqslant 1.$ |
Proof. From (1.1), we have
| $\frac{1}{2}\int_\Omega {{u^2}dX\left| {_{t = T} + \int_0^T {\int_\Omega {a{{\left| {\nabla u} \right|}^2}dXdt = \frac{1}{2}} } \int_\Omega {{{\left| {\varphi (X)} \right|}^2}dX.} } \right.} $ |
That is
| $\left\| {K\varphi } \right\|_{{L^2}}^2 = \int_\Omega {{u^2}(x, y, T;\varphi )dX \leqslant \left\| \varphi \right\|_{{L^2}}^2.} $ |
This completes the proof of Lemma 4.1.
Note that (4.1) can be rewritten as
| $\varphi = (I - \alpha {K^ * }K)\varphi + \alpha {K^ * }\psi , $ | (4.2) |
for some $\alpha > 0$, where ${K^ * }$ is the adjoint operator of $K$. Then, we use the iteration method to solve (4.2), that is, computing
| ${\varphi _0} = 0, $ |
| ${\varphi _m} = (I - \alpha {K^ * }K){\varphi _{m - 1}} + \alpha {K^ * }\psi , \quad m = 1, 2, \cdots .$ | (4.3) |
From (4.3) and the definition of the operator $K$, we have
| $\begin{array}{l} {\varphi _m} = {\varphi _{m - 1}} - \alpha {K^ * }(K{\varphi _{m - 1}} - \psi ) \\ {\rm{ }} = {\varphi _{m - 1}} - \alpha {K^ * }({u_{m - 1}}( \cdot , T) - \psi ), \\ \end{array} $ | (4.4) |
where ${u_{m - 1}}$ is the solution of (1.1) with $\varphi = {\varphi _{m - 1}}$.
The following Lemma (4.2) illustrates the specific form of the adjoint operator${K^ * }$.
Lemma 4.1.2. For any given $\phi (X)$, let ${K^ * }\phi = v(\bullet, 0).$Then $v$ satisfies the following backward parabolic equation:
| $ \left\{ \begin{array}{l} - {v_t} - \nabla \cdot (a\nabla v) = 0, \quad \quad \quad (X, t) \in Q, \\ v(X, T) = \phi (X), \quad \quad \quad \quad \;X \in \Omega . \\ \end{array} \right. $ | (4.5) |
Proof. From (1.1) and (4.5) and using the Green's theorem, we have
| $\begin{array}{l} 0 = \int_0^T {\int_\Omega {\{ v[{u_t} - \nabla (a(X) \cdot \nabla u)] - u} } [ - {v_t} - \nabla (a(X) \cdot \nabla v)]\} dXdt \\ \;\; = \int_0^T {\int_\Omega {(v{u_t} + u} } {v_t})dXdt \\ \quad + \int_0^T {\int_\Omega {[u\nabla \cdot (a(X)\nabla v) - v\nabla \cdot (a(X)\nabla u)} } ]dXdt \\ \;\; = \int_\Omega {uv\left| {_{t = 0}^{t = T}dX} \right.} + \int_0^T {\int_\Omega {[\nabla \cdot (a(X)u\nabla v) - \nabla \cdot (a(X)v\nabla u)} dXdt} \\ \;\; = \int_\Omega {uv\left| {_{t = 0}^{t = T}dX} \right.} + \int_0^T {{{\left. {a(X)(u\nabla v) - v\nabla u) \cdot \vec n} \right|}_{\partial \Omega }}dt} \\ \end{array} $ |
| $\;\; = \int_\Omega {u(X, T)v(X, T)dX} - \int_\Omega {u(X, 0)v(X, 0)dX} , $ | (4.6) |
that is
| $\int_\Omega {u(X, T)v(X, T)dX} = \int_\Omega {u(X, 0)v(X, 0)dX} .$ | (4.7) |
By the definition of $K$, we have
| ${\left\langle {K\varphi , \phi } \right\rangle _{{L^2}(\Omega )}} = {\left\langle {\varphi , v(X, 0)} \right\rangle _{{L^2}(\Omega )}}, $ |
that is
| $v(x, 0) = {K^ * }\phi .$ |
This completes the proof of Lemma 4.1.2.
Based on (4.3), (4.4) and Lemma 4.1.2, the procedure of the iterative algorithm can be stated as follows:
Step 1. Choose an initial value of iteration For simplicity, we can choose
Step 2. Solve the degenerate parabolic problem (1.1) to obtain the solution, where
Step 3. Solve the adjoint problem of (1.1)
| $\left\{ \begin{array}{l} - {v_t} - \nabla \cdot (a\nabla v) = 0, \quad \quad \quad (X, t) \in Q, \\ v(X, T) = {u_0}(X, T) - \psi (X), \;\;\;X \in \Omega , \\ \end{array} \right.$ |
to get the solution $v(X, t)$ which is denoted by ${v_0}(X, t).$
Step 4. Let
| ${\varphi _1}(X) = {\varphi _0}(X) - \alpha {v_0}(X, 0), $ |
where $\alpha > 0$, and let ${u_1}(X, t)$ be the solution of (1.1) with $\varphi = {\varphi _1}(X)$.
Step 5. Select an arbitrarily small positive constant as error bound. Compute
| ${\left\| {{u_1}(X, T) - \psi (X)} \right\|_{{L^2}(\Omega )}}$ |
and compare it with $\varepsilon $.
If
| ${\left\| {{u_1}(X, T) - \psi (X)} \right\|_{{L^2}(\Omega )}} \lt \varepsilon , $ |
then stop the iteration scheme and take $\varphi (X) = {\varphi _1}(X).$
Otherwise go to Step 3. Let ${\varphi _1}(X)$ be a new initial value of iteration and go on computing by the induction principle.
The proof of convergence for the Landweber iterative method can be found in [18,19].
Remark 4.1.1: The paramter is called acceleration factor, and is usually required. The iterative algorithm (including the CGM below) is also applicable to the observation data with noise, i.e., can be replaced by, where satisifes
| $\left\| {{\psi ^\delta }(X){\rm{ - }}\psi (X)} \right\| \leqslant \delta , $ |
and $\delta > 0$ is the noise level.
In this part, we introduce the CGM iteration to solve the inverse problem of (1.1). Generally speaking, the convergence rate of CGM is much faster than that of Landweber iterative method. But at the same time, the iterative procedure of conjugate gradient method is more complex than that of Landweber iterative method. Both methods have advantages and disadvantages.
The CGM iteration algorithm can be stated as follows:
Step 1. Set and choose an initial value of iteration. For simplicity, we can choose
Step2. Solve the initial value problem (1.1) to obtain the solution${u_k}(X, t)$, where$\varphi (X, t) = {\varphi _k}(X, t)$.
Step3. Solve the following conjugate equation
| $\left\{ \begin{array}{l} - {V_t} - \nabla \cdot (a(X)\nabla V) = 0, \quad \quad (X, t) \in Q, \\ V\left| {_{t = T} = {r_k}(X): = \psi (X) - {u_k}(X, T), } \right. \\ \end{array} \right.$ |
to obtain the solution ${V_k}(X, t)$, where ${r_k}(X): = \psi (X) - {u_k}(X, T)$ is the residual.
Step4. Calculate
| ${s_k}( \bullet ) = {V_k}( \bullet , 0) + {\alpha _{k - 1}}{s_{k - 1}}( \bullet ), $ |
where
| ${\alpha _{k - 1}} = \left\{ \begin{array}{l} 0, \quad \quad \quad k = 0, \\ \frac{{\left\| {{V_k}( \bullet , 0)} \right\|_{{L^2}(\Omega )}^2}}{{\left\| {{V_{k - 1}}( \bullet , 0)} \right\|_{{L^2}(\Omega )}^2}}, \;k \geqslant 1. \\ \end{array} \right.$ |
Step5. Solve the following equation
| $\left\{ \begin{array}{l} {u_t} - \nabla \cdot (a(X)\nabla u) = 0, \quad (X, t) \in Q, \\ u\left| {_{t = 0} = {s_k}, } \right. \\ \end{array} \right.$ |
to obtain the solution $u(\bullet, T) = {u_k}(\bullet, T): = {q_k}.$ Set
| ${\beta _k} = \frac{{\left\| {{V_k}( \bullet , 0)} \right\|_{{L^2}(\Omega )}^2}}{{\left\| {{q_k}} \right\|_{{L^2}(\Omega )}^2}}, $ |
and let
| ${\varphi _{k + 1}} = {\varphi _k} + {\beta _k}{s_k}.$ |
Step6. Increase and go to (Step2). The stopping rule is taken as follows: Let be a fixed number. Then we stop the algorithm at the first occurrence of such that ${\left\| {{r_k}} \right\|_{{L^2}(\Omega )}} \le \lambda \delta .$
The proof of stability and convergence for the CGM can be found in [24].
In this section, we try to reconstruct the initial temperature field through the terminal observation data of $t = T$, which is a serious ill-posed problem. For a given initial condition, the change of temperature will decrease exponentially with the increase of time. So the terminal moment $T$ cannot be too large. We take $T = 0.5$ in the process of numerical simulation. The other basic parameters are
| $\Omega = [0, 1] \times [0, 1], \quad \alpha = 0.7, $ |
and the diffusion coefficient $a(X)$ is taken as
| $a(X) = \sin (\pi x) \cdot \sin (\pi y), \quad (x, y) \in [0, 1] \times [0, 1].$ |
The direct problem is numerically solved by the finite difference method. In the process of numerical computations, the spatial step size $h$ and the time step size $\tau $ are taken as:
| $ h = 0.01, \tau = 0.01. $ |
Example 1. In the first numerical experiment, we take
| $\varphi (X) = 1 + \sin (\pi x) \cdot \sin (\pi y), \;{\rm{ }}(x, y) \in [0, 1] \times [0, 1], $ |
the additional condition $\psi (X)$ is given by
| $\psi (X) = u(x, y, T;\varphi (X)), \quad (x, y) \in [0, 1] \times [0, 1], $ |
where $u(x, y, T; \varphi (X))$ is the numerical solution of (1.1) with the given initial value $\varphi (X)$.
The noisy data is also considered in the numerical experiment and generated in the following form
| ${\psi ^\delta } = {u^\delta }(X, T) = u(X, T)[1 + \delta \times random(X)].$ |
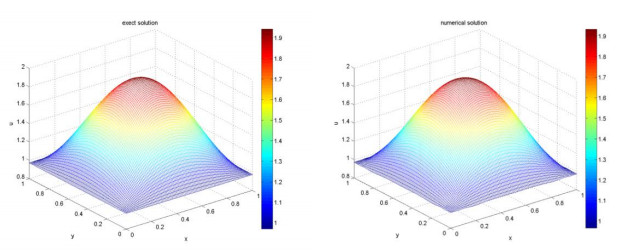
As can be seen from the above Figures 1, 2, when the number of iterations reaches 1000, the reconstruction effect is remarkably good. The initial guess is taken as zero. Obviously, this initial guess is not good at all, but the convergence of the iterative algorithm is very stable and the error order is about ${10^{ - 2}}$. After adding noise, the reconstruction effect is also very good (see the Figures 3, 4).
When the number of CGM iterations reaches 300, the error reaches ${10^{ - 3}}$, which shows that the reconstruction effect is satisfactory (see the Figures 5, 6). Furthermore, it shows that the convergence speed of CGM is faster than that of the Landweber iterative method. For the case of adding noise, it can be seen from the figure that the reconstruction effect is also satisfactory (see the Figures 7, 8).
Example 2. In the second numerical experiment, we consider a digital image deblurring problem. We chose two gray images as examples. For the convenience of calculation, the pixels of these two images are $ 128\times 128 $. The diffusion coefficient is taken as
| $a(X) = \sin (\frac{{\pi x}}{{128}}) \cdot \sin (\frac{{\pi y}}{{128}}), \quad (x, y) \in [0,128] \times [0,128], $ |
and the observation time is taken as $T = 0.5$. The initial value $\varphi (X)$ is the original clear image, while the blur image $\psi (X)$ is obtained from the clear image through the above diffusion process. Our task is to restore the original clear image from the blur image. We have tested the two algorithms, and the results are similar. The convergence speed of CGM algorithm is faster than that of Landweber iterative algorithm. The Landweber iterative algorithm needs 100 iterations, while CGM only needs about 50 iterations. The reconstruction effect of the two images is shown in Figures 9-12 (since the reconstructed results are similar, we only use the results obtained by the Landweber iterative algorithm).
From these four groups of pictures, we can see that the image restoration effect is very good. Because the fuzzy part is mainly concentrated in the middle of the image (this is true of most images in reality (see [30])), our diffusion function can describe the evolution process quite well. After a period of iterations, the middle blurred part of the image is almost completely restored, and the edge part of the image is also well preserved.
In this paper, the inverse initial value problem for a two-dimensional degenerate parabolic equation is discussed. The finite volume method is used to construct the difference scheme for the forward problem, and the stability and convergence of the difference scheme is also proved. Then, we use the Landweber iteration and CGM to construct the calculation process of the inverse problem and do numerical experiments. Numerical results show that our algorithm is stable and converges quickly. These methods and results can be widely applied in engineering heat conduction problems and computer graphics and image processing.
We would like to thank the anonymous referees for their valuable comments and helpful suggestions to improve the earlier version of the paper. The work is partially supported by the National Natural Science Foundation of China (Grant Nos. 61663018, 11961042), Foundation of A Hundred Youth Talents Training Program of Lanzhou Jiaotong University, and NSF of Gansu Province of China (No. 18JR3RA122).
The authors declare no conflict of interest in this paper.
| [1] | G. Albuja, A.I. Ávila, A family of new globally convergent linearization schemes for solving Richards' equation, Appl. Numer. Math., 159 (2021), 281-296. |
| [2] |
K. Beauchard, P. Cannarsa, M. Yamamoto, Inverse source problem and null controllability for multidimensional parabolic operators of Grushin type, Inverse Problems, 30 (2014), 025006. doi: 10.1088/0266-5611/30/2/025006

|
| [3] | M. Berardi, F. Difonzo, F. Notarnicola, M. Vurro, A transversal method of lines for the numerical modeling of vertical infiltration into the vadose zone, Appl. Numer. Math., 135 (2019) 264-275. |
| [4] |
M. Berardi, F. Difonzo, L. Lopez, A mixed MoL-TMoL for the numerical solution of the 2D Richards' equation in layered soils, Comput. Math. Appl., 79 (2020), 1990-2001. doi: 10.1016/j.camwa.2019.07.026

|
| [5] |
N. Brandhorst, D. Erdal, I. Neuweiler, Soil moisture prediction with the ensemble Kalman filter: Handling uncertainty of soil hydraulic parameters, Adv. Water Res., 110 (2017), 360-370. doi: 10.1016/j.advwatres.2017.10.022

|
| [6] |
P. Cannarsa, J. Tort, M. Yamamoto, Determination of source terms in a degenerate parabolic equation, Inverse Problems, 26 (2010), 105003. doi: 10.1088/0266-5611/26/10/105003

|
| [7] |
P. Cannarsa, P. Martinez, J. Vancostenoble, Carleman estimates for a class of degenerate parabolic operators, SIAM J Control Optim, 47 (2008), 1-19. doi: 10.1137/04062062X

|
| [8] | P. Cannarsa, P. Martinez, J. Vancostenoble, Null controllability of degenerate heat equations, Adv. Differ. Equ., 10 (2005), 153-190. |
| [9] | J. R. Cannon, The One-Dimensional Heat Equation, Addison-Wesley, 1984. |
| [10] | J. R. Cannon, Y. Lin, S. Xu, Numerical procedure for the determination of an unknown coefficient in semilinear parabolic partial differential equations, Inverse Problems, 10 (1994), 227-243. |
| [11] |
J. Cheng, J. J. Liu, A quasi Tikhonov regularization for a two-dimensional backward heat problem by a fundamental solution, Inverse Problems, 24 (2008), 065012. doi: 10.1088/0266-5611/24/6/065012

|
| [12] |
M. Dehghan, Identification of a time-dependent coefficient in a partial differential equation subject to an extra measurement, Numer. Meth. Part. Diff. Equ., 21 (2005), 611-622. doi: 10.1002/num.20055

|
| [13] |
M. Dehghan, Determination of a control function in three-dimensional parabolic equations, Math. Comput. Simul., 61 (2003), 89-100. doi: 10.1016/S0378-4754(01)00434-7

|
| [14] |
M. Dehghan, M. Tatari, Determination of a control parameter in a one-dimensional parabolicequation using the method of radial basis functions, Math. Comput. Model., 44 (2006), 1160-1168. doi: 10.1016/j.mcm.2006.04.003

|
| [15] |
M. Dehghan, An inverse problems of finding a source parameter in a semilinear parabolic equation, Appl. Math. Model., 25 (2001), 743-754. doi: 10.1016/S0307-904X(01)00010-5

|
| [16] |
Z. C. Deng, K. Qian, X. B. Rao, L. Yang, G. W. Luo, An inverse problem of identifying the source coefficient in a degenerate heat equation, Inverse Probl. Sci. Eng., 23 (2015), 498-517. doi: 10.1080/17415977.2014.922079

|
| [17] |
F. L. Dimet, V. Shutyaev, J. Wang, M. Mu, The problem of data assimilation for soil water movement, ESAIM: Control, Optimisation and Calculus of Variations, 10 (2004), 331-345. doi: 10.1051/cocv:2004009

|
| [18] | A. Kirsch, An introduction to the mathematical theory of inverse problem, Springer, New York, 1999. |
| [19] | H. W. Engl, M. Hanke, A. Neubauer, Regularization of inverse problems, Dordrecht: Kluwer Academic Publishers, 1996. |
| [20] | V. Isakov, Inverse Problems for Partial Differential Equations, Springer, New York, 1998. |
| [21] | J. F. Lu, Z. Guan, Numerical Solution of Partial Differential Equations, Tsinghua University Press, Beijing, 2004. |
| [22] |
P. Martinez, J. Vancostenoble, Carleman estimates for one-dimensional degenerate heat equations, J. Evol. Equ., 6 (2006), 325-362. doi: 10.1007/s00028-006-0214-6

|
| [23] | O. A. Oleinik, E. V. Radkevic, Second order differential equations with non-negative characteristic form, Rhode Island and Plenum Press, New York: American Mathematical Society, 1973. |
| [24] | M. Hanke, Conjugate Gradient Type Methods for Ill-Posed Problems, Harlow, Longman Scientific and Technical, Essex, 1995. |
| [25] | I. S. Pop, Regularization Methods in the Numerical Analysis of Some Degenerate Parabolic Equations, IWR, University of Heidelberg, 1998. |
| [26] |
X. B. Rao, Y. X. Wang, K. Qian, Z. C. Deng, L. Yang, Numerical simulation for an inverse source problem in a degenerate parabolic equation, Appl. Math. Model., 39 (2015), 7537-7553. doi: 10.1016/j.apm.2015.03.016

|
| [27] | R. B. Ricardo, Numerical Methods and Analysis for Degenerate Parabolic Equations and Reaction-Diffusion Systems, 2008. |
| [28] | Z. Z. Sun, Numerical Solution of Partial Differential Equations, Science Press, Beijing, 2005. |
| [29] |
J. Tort, J. Vancostenoble, Determination of the insolation function in the nonlinear Sellers climate model, Ann. I. H. Poincare-AN, 29 (2012), 683-713. doi: 10.1016/j.anihpc.2012.03.003

|
| [30] | D. K. Wang, Y. Q. Hou, J. Y. Peng, Partial Differential Equation Method for Image Processing, Science Press, Beijing, 2008. |
| [31] |
L. Yang, Z. C. Deng, J. N. Yu, G. W. Luo, Optimization method for the inverse problem of reconstructing the source term in a parabolic equation, Math. Comput. Simul., 80 (2009), 314-326. doi: 10.1016/j.matcom.2009.06.031

|
| [32] |
L. Yang, Z. C. Deng, An inverse backward problem for degenerate parabolic equations, Numer. Meth. Part. Differ. Equ., 33 (2017), 1900-1923. doi: 10.1002/num.22165

|
| [33] |
L. Yang, Y. Liu, Z. C. Deng, Multi-parameters identification problem for a degenerate parabolic equation, J. Comput. Appl. Math., 366 (2020), 112422. doi: 10.1016/j.cam.2019.112422

|
| 1. | Batirkhan Turmetov, Valery Karachik, On solvability of some inverse problems for a nonlocal fourth-order parabolic equation with multiple involution, 2024, 9, 2473-6988, 6832, 10.3934/math.2024333 |