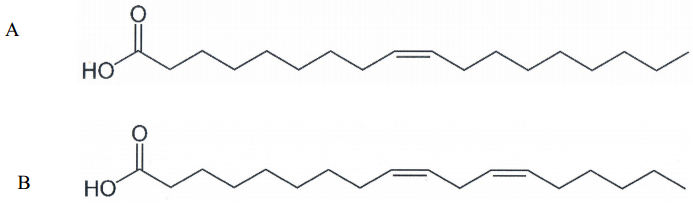
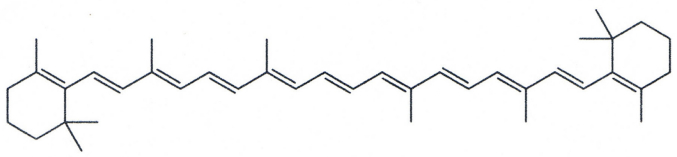
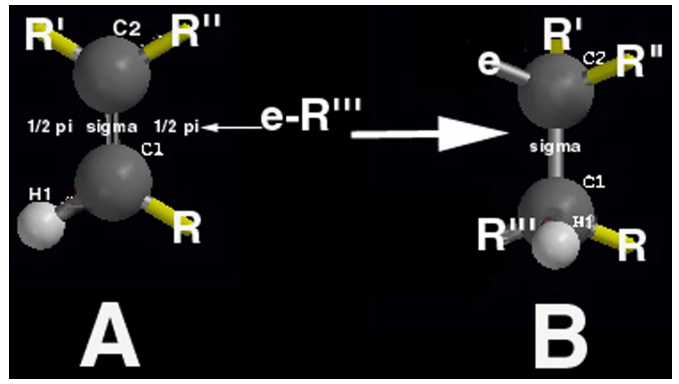
|
[1]
|
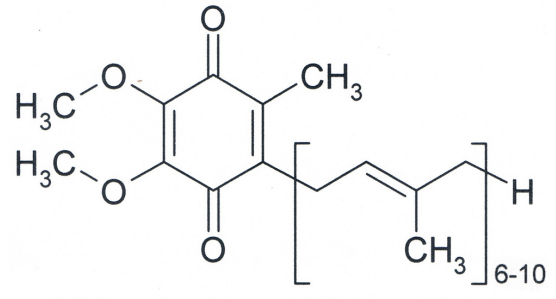
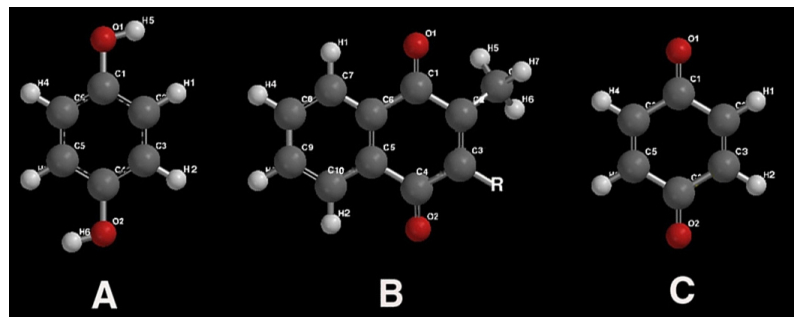
Petersen R (2012) Reactive secondary sequence oxidative pathology polymer model and antioxidant tests, Int Res J Pure Appl Chem 2: 247–285.
|
|
[2]
|
Singer S, Nicolson G (1972) The fluid mosaic model of the structure of cell membranes. Science 175: 720–731. doi: 10.1126/science.175.4023.720

|
|
[3]
|
Nicolson G (2014) The fluid-mosaic model of membrane structure: still relevant to understanding the structure, function and dynamics of biological membranes after more than 40 years. Biochim Biophys Acta 1838: 1451–1466. doi: 10.1016/j.bbamem.2013.10.019

|
|
[4]
|
Michael J, Sircar S, (2011) The Cell Membrane, In: Fundamentals of Medical Physiology, New York: Thieme Medical Publishers, 9–16.
|
|
[5]
|
Jeong M, Kang J (2008) Acrolein, the toxic endogenous aldehyde, induces neurofilament-L aggregation. BMB Rep 41: 635–639. doi: 10.5483/BMBRep.2008.41.9.635

|
|
[6]
|
Torosantucci R, Mozziconacci O, Sharov V, et al. (2012) Chemical modifications in aggregates of recombinant human insulin induced by metal-catalyzed oxidation: covalent crosslinking via Michael addition to tyrosine oxidation products. Pharm Res 29: 2276–2293. doi: 10.1007/s11095-012-0755-z

|
|
[7]
|
Rubenstein M, Leibler L, Bastide J (1992) Giant fluctuations of crosslink positions in gels. Phys Rev Lett 68: 405–407. doi: 10.1103/PhysRevLett.68.405

|
|
[8]
|
Nossal R (1996) Mechanical properties of biological gels. Physica A 231: 265–276. doi: 10.1016/0378-4371(95)00455-6

|
|
[9]
|
Barsky S, Plischke M, Joos B, et al. (1996) Elastic properties of randomly cross-linked polymers Phys Rev E 54: 5370–5376.
|
|
[10]
|
Ulrich S, Zippelius A, Benetatos P (2010) Random networks of cross-linked directed polymers. Phys Rev E 81: 021802.
|
|
[11]
|
Rodriquez F, (1996) 11.3 Polymer degradation, In: Principles of Polymer Systems, 4 Eds., Washington D.C.: Taylor and Francis, 398–399.
|
|
[12]
|
Dröge W (2002) Free radicals in the physiological control of cell function. Physiol Rev 82: 47–95.
|
|
[13]
|
Valko M, Leibfritz D, Moncol J, et al. (2007) Free radicals and antioxidants in normal physiological functions and human disease. Int J Biochem Cell Biol 39: 44–84. doi: 10.1016/j.biocel.2006.07.001

|
|
[14]
|
Floyd R, Towner R, He T, et al. (2011) Translational research involving oxidative stress diseases of aging. Free Radic Biol Med 51: 931–941. doi: 10.1016/j.freeradbiomed.2011.04.014

|
|
[15]
|
Sena L, Chandel N ( 2012) Physiological roles of mitochondrial reactive oxygen species. Mol Cell 48: 158–167.
|
|
[16]
|
Labunskyy V, Gladyschev V (2013) Role of reactive oxygen species-mediated signaling in aging. Antioxid Redox Signal 19: 1362–1372. doi: 10.1089/ars.2012.4891

|
|
[17]
|
Hill S, Remmen H (2014) Mitochondrial stress signaling in longevity: a new role for mitochondrial function in aging. Redox Biol 2: 936–944. doi: 10.1016/j.redox.2014.07.005

|
|
[18]
|
Schieber M, Chandel N (2014) ROS function in redox signaling and oxidative stress. Curr Biol 24: R453–R462. doi: 10.1016/j.cub.2014.03.034

|
|
[19]
|
Girotti A (1998) Lipid hydroperoxide generation, turnover, and effector action in biological systems. J Lipid Res 39: 1529–1542.
|
|
[20]
|
Beckman K, Ames B (1998) The free radical theory of aging matures. Physiol Rev 78: 547–581.
|
|
[21]
|
Valko M, Rhodes C, Moncol, et al. (2006) Free radicals, metals and antioxidants in oxidative stress-induced cancer. Chem Biol Interac 160: 1–40. doi: 10.1016/j.cbi.2005.12.009

|
|
[22]
|
Silva J, Coutinho O (2010) Free radicals in the regulation of damage and cell death-basic mechanisms and prevention. Drug Discov Ther 4: 144–167.
|
|
[23]
|
Jacob K, Hooten N, Trzeciak A, et al. (2013) Markers of oxidant stress that are clinically relevant in aging and age-related disease. Mech Ageing Dev 134: 139–157. doi: 10.1016/j.mad.2013.02.008

|
|
[24]
|
Phaniendra A, Jestadi D, Periyasamy L (2015) Free radicals: properties, sources, targets, and their implication in various diseases. Ind J Clin Biochem 30: 11–26.
|
|
[25]
|
Harman D (1956) Aging: a theory based on free radical and radiation chemistry. J Gerontol Soc 11: 298–300. doi: 10.1093/geronj/11.3.298

|
|
[26]
|
Shigenaga M, Hagen T, Ames B (1994) Oxidative damage and mitochondrial decay in aging. Proc Natl Acad Sci USA 91: 10771–10778. doi: 10.1073/pnas.91.23.10771

|
|
[27]
|
Balaban R, Nemoto S, Finkel T (2005) Mitochondria, oxidants, and aging. Cell 120: 483–495.
|
|
[28]
|
Harman D (2006) Free radical theory of aging: an update. Ann NY Acad Sci 1067: 10–21. doi: 10.1196/annals.1354.003

|
|
[29]
|
Colavitti R, Finkel T (2005) Reactive oxygen species as mediators of cellular senescence. IUBMB Life 57: 277–281. doi: 10.1080/15216540500091890

|
|
[30]
|
Ziegler D, Wiley C, Velarde M (2015) Mitochondrial effectors of cellular senescence: beyond the free radical theory of aging. Aging Cell 14: 1–7. doi: 10.1111/acel.12287

|
|
[31]
|
Eichenberger K, Böhni P, Wintehalter K, et al. (1982) Microsomal lipid peroxidation causes an increase in the order of the membrane lipid domain. FEBS Letters 142: 59–62. doi: 10.1016/0014-5793(82)80219-6

|
|
[32]
|
Kaplán P, Doval M, Majerová Z, et al. (2000) Iron-induced lipid peroxidation and protein modification in endoplasmic reticulum membranes. Protection by stobadine. Int J Biochem Cell Biol 32: 539–547. doi: 10.1016/S1357-2725(99)00147-8

|
|
[33]
|
Solans R, Motta C, Solá R, et al. (2000) Abnormalities of erythrocyte membrane fluidity, lipid composition, and lipid peroxidation in systemic sclerosis. Arthritis Rheum 43: 894–900. doi: 10.1002/1529-0131(200004)43:4<894::AID-ANR22>3.0.CO;2-4

|
|
[34]
|
Pretorius E, Plooy J, Soma P, et al. (2013) Smoking and fluidity of erythrocyte membranes: a high resolution scanning electron and atomic force microscopy investigation. Nitric Oxide 35: 42–46. doi: 10.1016/j.niox.2013.08.003

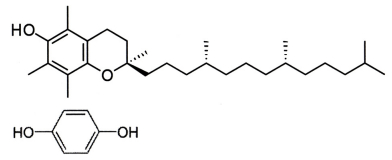
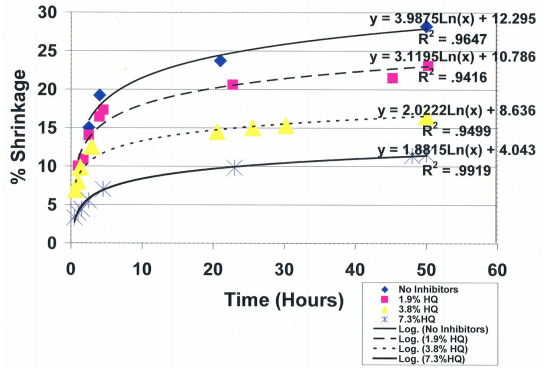
|
|
[35]
|
de la Haba C, Palacio J, Martínez P, et al. (2013) Effect of oxidative stress on plasma membrane fluidity of THP-1 induced macrophages. Biochim Biophys Acta 1828: 357–364. doi: 10.1016/j.bbamem.2012.08.013

|
|
[36]
|
Alberts B, Johnson A, Lewis J, et al. (2002) The Lipid Bilayer, In: Molecular Biology of the Cell, 4 Eds., New York: Garland Science.
|
|
[37]
|
Weijers R (2012) Lipid composition of cell membranes and its relevance in type 2 diabetes mellitus. Curr Diabetes Rev 8: 390–400. doi: 10.2174/157339912802083531

|
|
[38]
|
Benderitter M, Vincent-Genod L, Pouget J, et al. (2003) The cell membrane as a biosensor of oxidative stress induced by radiation exposure: a multiparameter investigation. Radiat Res 159: 471–483. doi: 10.1667/0033-7587(2003)159[0471:TCMAAB]2.0.CO;2

|
|
[39]
|
Zimniak P (2011) Relationship of electrophilic stress to aging. Free Radic Biol Med 51: 1087–1105. doi: 10.1016/j.freeradbiomed.2011.05.039

|
|
[40]
|
Wang S., Von Meerwall E, Wang SQ, et al. (2004). Diffusion and rheology of binary polymer mixtures. Macromolecules 37: 1641–1651. doi: 10.1021/ma034835g

|
|
[41]
|
Williams R (1989) NMR studies of mobility within protein structure. Euro J Biochem 183: 479–497.
|
|
[42]
|
Sapienza, P, Lee A (2010) Using NMR to study fast dynamics in proteins: methods and applications. Curr Opin Pharmacol 10: 723–730.
|
|
[43]
|
Petersen R (2014) Computational conformational antimicrobial analysis developing mechanomolecular theory for polymer biomaterials in materials science and engineering. Int J Comput Mater Sci Eng 3: 145003.
|
|
[44]
|
Goldstein D, (1990) Chapter 143 Serum Calcium, In: Walker H, Hall W, Hurst J, Editors, Clinical Methods: The History, Physical, and Laboratory Examinations, 3 Eds., Boston: Butterworths.
|
|
[45]
|
Tung IC (1991) Application of factorial design to SMC viscosity build-up. Polym Bull 25: 603–610.
|
|
[46]
|
Peters S, (1998) Particulate Fillers, In: Handbook of Composites, 2 Eds., New York: Chapman & Hall, 242–243.
|
|
[47]
|
Gaucheron F (2005) The minerals of milk. Reprod Nutr Dev 45: 473–483. doi: 10.1051/rnd:2005030

|
|
[48]
|
Komabayashi T, Zhu Q, Eberhart R, et al. (2016) Current status of direct pulp-capping materials for permanent teeth. Dent Mater J 35: 1–12.
|
|
[49]
|
Petersen R, Vaidya U, (2011) Chapter 16 Free Radical Reactive Secondary Sequence Lipid Chain-Lengthening Pathologies, In: Micromechanics/Electron Interactions for Advanced Biomedical Research, Saarbrücken: LAP LAMBERT Academic Publishing Gmbh & Co. KG., 233–287.
|
|
[50]
|
McMurry J, (2004) Organic Chemistry 6 Eds, Belmont, CA: Thompson Brooks/Cole., 136–138.
|
|
[51]
|
Esterbauer H, Schaur R, Zollner H (1991) Chemistry and biochemistry of 4-hydroxynonenal, malonaldehyde and related aldehydes. Free Radic Biol Med 11: 81–128. doi: 10.1016/0891-5849(91)90192-6

|
|
[52]
|
Lovell M, Xie C, Markesbery W (2000) Acrolein, a product of lipid peroxidation, inhibits glucose and glutamate uptake in primary neuronal cultures. Free Radic Biol Med 29: 714–720. doi: 10.1016/S0891-5849(00)00346-4

|
|
[53]
|
Shi R, Rickett T, Sun W (2011) Acrolein-mediated injury in nervous system trauma and diseases. Mol Nutr Food Res 55: 1320–1331. doi: 10.1002/mnfr.201100217

|
|
[54]
|
Uchida K (1999) Current status of acrolein as a lipid peroxidation product. Trends Cardiovasc Med 9: 109–113. doi: 10.1016/S1050-1738(99)00016-X

|
|
[55]
|
Minko I, Kozekov I, Harris T, et al. (2009) Chemistry and biology of DNA containing 1,N2-deoxyguanosine adducts of the α,β-unsaturated aldehydes acrolein, crotonaldehyde, and 4-hydroxynonenal. Chem Res Toxicol 22: 759–778. doi: 10.1021/tx9000489

|
|
[56]
|
Singh M, Kapoor A, Bhatnagar A (2014) Oxidative and reductive metabolism of lipid-peroxidation derived carbonyls. Chem Biol Interact 234: 261–273.
|
|
[57]
|
Ishii T, Yamada T, Mori T, et al. (2007) Characterization of acrolein-induced protein cross-links. Free Radic Res 41: 1253–1260. doi: 10.1080/10715760701678652

|
|
[58]
|
Michael J, Sircar S, (2011) Electrophysiology of Ion Channels, In: Fundamentals of Medical Physiology, New York: Thieme Medical Publishers, 43–46.
|
|
[59]
|
Han P, Trinidad B, Shi J (2015) Hypocalcemia-induced seizure: demystifying the calcium paradox. ASN Neuro 7: 1–9.
|
|
[60]
|
Parekh A, Putney J (2005) Store-operated calcium channels. Physiol Rev 85: 757–810. doi: 10.1152/physrev.00057.2003

|
|
[61]
|
Sherwood L, (2004) Endocrine Control of Calcium Metabolism, In: Human Physiology, 5 Eds., Belmont, CA: Thomson-Brooks/Cole, 733–742.
|
|
[62]
|
Michael J, Sircar S, (2011) Mechanisms to Regulate Whole Body pH, In: Fundamentals of Medical Physiology, New York: Thieme Medical Publishers, 399–400.
|
|
[63]
|
Lide D, (1996) Electrical Resistivity of Pure Metals, In: Handbook of Chemistry and Physics, 77 Eds., New York: CRC Press, 12-40–12-41.
|
|
[64]
|
Jendrasiak G, Smith R (2004) The interaction of water with the phospholipid head group and its relationship to the lipid electrical conductivity. Chem Phys Lipids 131: 183–195. doi: 10.1016/j.chemphyslip.2004.05.003

|
|
[65]
|
Petersen R (2011) Bisphenyl-polymer/carbon-fiber-reinforced composite compared to titanium alloy bone implant. Int J Polym Sci 2011: 2341–2348.
|
|
[66]
|
Callister W, (1997) Room Temperature Electrical Resistivity Values for Various Engineering Materials Table C.9, In: Materials Science and Engineering, New York: John Wiley & Sons, 796–798.
|
|
[67]
|
Park B, Lakes R, (1992) Characterization of Materials II Table 4.1, In: Biomaterials, 2 Eds., New York: Plenum Press, 64.
|
|
[68]
|
Halliday D, Resnick R, Walker J, (1993) 46-2 Electrical Conductivity, In: Fundamentals of Physics, 4 Eds., New York: JohnWiley & Son, 1210.
|
|
[69]
|
Periodic Table of the Elements (2016) Sulfur-Electrical Properties accessed November 10, 2016. Available from: http://www.periodictable.com/Elements/016/data.html.
|
|
[70]
|
Clandinin M, Cheema S, Field C, et al. (1991) Dietary fat: exogenous determination of membrane structure and cell function. FASEB J 5: 2761–2769.
|
|
[71]
|
McMurry J, (2004) Biomolecules: Lipids, In: Organic Chemistry, 6 Eds., Belmont, CA: Thompson Brooks/Cole, 1027–1033.
|
|
[72]
|
Sherwood L, (2004) Lipids, In: Human Physiology, 5 Eds., Belmont, CA: Thomson-Brooks/Cole, A12–A13.
|
|
[73]
|
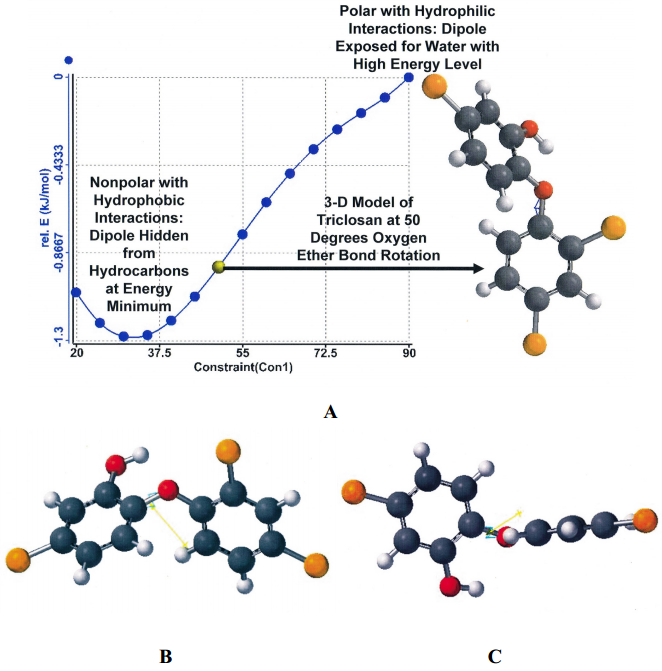
Villaláın J, Mateo C, Aranda F, et al. (2001) Membranotropic effects of the antibacterial agent triclosan. Arch Biochem Biophys 390: 128–136.
|
|
[74]
|
Guillén J, Bernabeu A, Shapiro S, et al. (2004) Location and orientation of Triclosan in phospholipid model membranes. Eur Biophys J 33: 448–453.
|
|
[75]
|
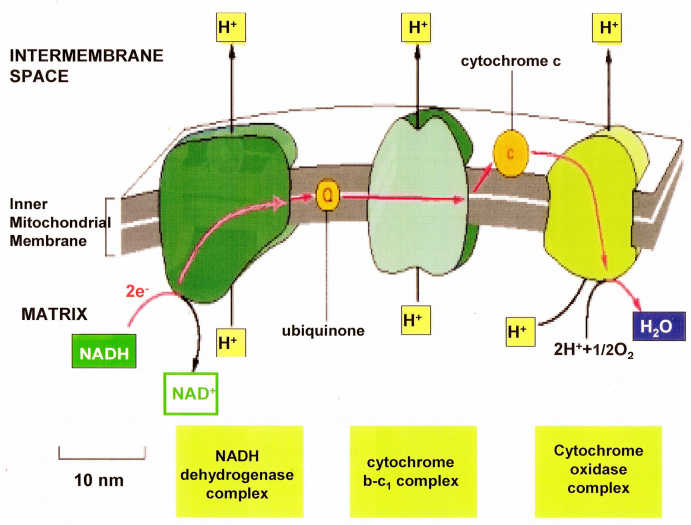
Alberts B, Johnson A, Lewis J, et al. (2002) Electron-Transport Chains and Their Proton Pumps, In: Molecular Biology of the Cell, 4 Eds., New York: Garland Science.
|
|
[76]
|
Sherwood L, (2004) Acid-Base Balance, In: Human Physiology, 5 Eds., Belmont, CA: Thomson-Brooks/Cole, 571–577.
|
|
[77]
|
Hüttemann M, Lee I, Grossman L, et al. (2012) Chapter X. phosphoylation of mammalian cytochrome c and cytochrome c oxidase in the regulation of cell destiny: respieration, apoptosis, and human disease. Adv Exp Med Biol 748: 237–264.
|
|
[78]
|
Srinivasan S, Avadhani N (2012) Cytochrome c oxidase dysfunction in oxidative stress. Free Radic Biol Med 53: 1252–1263. doi: 10.1016/j.freeradbiomed.2012.07.021

|
|
[79]
|
Finkel T, Holbrook N (2000) Oxidants, oxidative stress and the biology of ageing. Nature 408: 239–247. doi: 10.1038/35041687

|
|
[80]
|
Brand M, Affourtit C, Esteves T, et al. (2004) Serial review: the powerhouse takes control of the cell: the role of mitochondria in signal transduction. Free Radic Biol Med 37: 755–767. doi: 10.1016/j.freeradbiomed.2004.05.034

|
|
[81]
|
Tosato M, Zamboni V, Ferrini A, et al (2007) The aging process and potential interventions to extend life expectancy. Clinical Interv Aging 2: 401–412.
|
|
[82]
|
Murphy M (2009) How mitochondria produce reactive oxygen species. Biochem J 417:1–13. doi: 10.1042/BJ20081386

|
|
[83]
|
Kagan V, Wipf P, Stoyanovsky D, et al. (2009) Mitochondrial targeting of electron scavenging antioxidants: regulation of selective oxidation vs random chain reactions. Adv Drug Deliv Rev 61: 1375–1385. doi: 10.1016/j.addr.2009.06.008

|
|
[84]
|
Niizuma K, Yoshioka H, Chen H, et al. (2010) Mitochondrial and apoptotoc neuronal death signaling pathways in cerebral ischemia. Biochim Biophys Acta 1802: 92–99. doi: 10.1016/j.bbadis.2009.09.002

|
|
[85]
|
Michael J, Sircar S, (2011) Metabolic Pathways, In: Fundamentals of Medical Physiology, New York: Thieme Medical Publishers, 467–468.
|
|
[86]
|
Halliwell B (1987) Oxidants and human disease: some new concepts. FASEB J 1: 358–364.
|
|
[87]
|
Petersen R (2013) Free-radical polymer science structural cancer model: a review. Scientifica 2013: 143589.
|
|
[88]
|
Alberts B, Johnson A, Lewis J, et al. (2002) Proteins Function, In: Molecular Biology of the Cell, 4 Eds., New York: Garland Science.
|
|
[89]
|
Reineri S, Bertoni A, Sanna E, et al. (2007) Membrane lipid rafts coordinate estrogen-dependent signaling in human platelets. Biochim Biophys Acta 1773: 273–278. doi: 10.1016/j.bbamcr.2006.12.001

|
|
[90]
|
Pamplona R, Portero-Otin M, Requena J, et al. (1999) A low degree of fatty acid unsaturation leads to lower lipid peroxidation and lipoxidation-derived protein modification in heart mitochondria of the longevous pigeon than in the short-lived rat. Mech Ageing Dev 106: 283–286. doi: 10.1016/S0047-6374(98)00121-3

|
|
[91]
|
Wang Y, Cui P (2015) Reactive carbonyl species derived from omega-3 and omega-6 fatty acids. J Agric Food Chem 63: 6293–6296. doi: 10.1021/acs.jafc.5b02376

|
|
[92]
|
National Cancer Institute/National Institutes of Health/Department of Health and Human Services (2006) What You Need To Know About Cancer Bethesda, MD: NIH.
|
|
[93]
|
Weinhouse S, Warburg O, Burk D, et al. (1956) On respiratory impairment in cancer cells. Science 124: 269–270.
|
|
[94]
|
Gillies R, (2001) The Tumour Microenvironment: Causes and Consequences of Hypoxia and Acidity, Novartis Foundation Symposium 240, New York: JohnWiley & Sons.
|
|
[95]
|
Stavridis J, (2008) Oxidation: the Cornerstone of Carcinogenesis, New York: Springer.
|
|
[96]
|
Grek C, Tew K (2010) Redox metabolism and malignancy. Current Opin Pharmacol 10: 362–368. doi: 10.1016/j.coph.2010.05.003

|
|
[97]
|
Fogg V, Lanning N, MacKeigan J (2011) Mitochondria in cancer: at the crossroads of life and death. Chin J Cancer 30: 526–539. doi: 10.5732/cjc.011.10018

|
|
[98]
|
Hielscher A, Gerecht S (2015) Hypoxia and free radicals: role in tumor progression and the use of engineering-based platforms to address these relationships. Free Radic Biol Med 79: 281–291. doi: 10.1016/j.freeradbiomed.2014.09.015

|
|
[99]
|
Görlach A, Dimova E, Petry A, et al. (2015) Reactive oxygen species, nutrition, hypoxia and diseases: problems solved? Redox Biol 6: 372–385. doi: 10.1016/j.redox.2015.08.016

|
|
[100]
|
Tafani M, Sansone L, Limana F, et al. (2016) The interplay of reactive oxygen species, hypoxia, inflammation, and sirtuins in caner initiation and progression. Oxid Med Cell Longev 2016: 1–18.
|
|
[101]
|
Peacock J, Calhoun A, (2006) Polymer Chemistry Properties and Applications, Munich, Germany: Hanser.
|
|
[102]
|
Mironi-Harpaz I, Narkis M, Siegmann A (2007) Peroxide crosslinking of a styrene-free unsaturated polyester. J Appl Polym Sci 105: 885–892. doi: 10.1002/app.25385

|
|
[103]
|
Wang Y, Woodworth L, Han B (2011) Simultaneous measurement of effective chemical shrinkage and modulus evolutions during polymerization. Exp Mech 51: 1155–1169. doi: 10.1007/s11340-010-9410-y

|
|
[104]
|
Jansen K, Vreugd de J, Ernst L (2012) Analytical estimate for curing-induced stress and warpage in coating layers. J Appl Polym Sci 126: 1623–1630. doi: 10.1002/app.36776

|
|
[105]
|
Weinberg R, (2007) 14.3 The epithelial-mesenchymal transition and associated loss of E-cadherin expression enable carcinoma cells to become invasive, In: The Biology of Cancer, New York: Garland Science, 597–624.
|
|
[106]
|
Wenger J, Chun S, Dang D, et al. (2011) Combination therapy targeting cancer metabolism. Med Hypotheses 76: 169–172. doi: 10.1016/j.mehy.2010.09.008

|
|
[107]
|
Vinogradova T, Miller P, Kaverina I (2009) Microtubule network asymmetry in motile cells: role of Golgi-derived array. Cell Cycle 8: 2168–2174. doi: 10.4161/cc.8.14.9074

|
|
[108]
|
Lindberg U, Karlsson R, Lassing I, et al. (2008) The microfilament system and malignancy. Semin Cancer Biol 18: 2–11. doi: 10.1016/j.semcancer.2007.10.002

|
|
[109]
|
San Martín A, Griendling K (2010) Redox control of vascular smooth muscle migration. Antioxid Redox Signal 12: 625–640. doi: 10.1089/ars.2009.2852

|
|
[110]
|
Copstead LE, Banasik J, (2005) Pathophysiology, 6 Eds., St. Louis, MO: Elsevier Saunders, 221.
|
|
[111]
|
Li Z, Hannigan M, Mo Z, et al. (2003) Directional Sensing Requires Gβγ-Mediated PAK1 and PIXα-Dependent Activation of Cdc42. Cell 114: 215–227. doi: 10.1016/S0092-8674(03)00559-2

|
|
[112]
|
Hattori H, Subramanian K, Sakai J, et al. (2010) Small-molecule screen identifies reactive oxygen species as key regulators of neutrophile chemotaxis. PNAS 107: 3546–3551. doi: 10.1073/pnas.0914351107

|
|
[113]
|
Parisi F, Vidal M (2011) Epithelial delamination and migration: lessons from Drosophila. Cell Adh Migr 5: 366–372. doi: 10.4161/cam.5.4.17524

|
|
[114]
|
Barth A, Caro-Gonzalez H, et al. (2008) Role of adenomatous polyposis coli (APC) and microtubules in directional cell migration and neuronal polarization. Semin Cell Dev Biol 19: 245–251. doi: 10.1016/j.semcdb.2008.02.003

|
|
[115]
|
Dent E, Gupton S, et al. (2010) The growth cone cytoskeleton in axon outgrowth and guidance. Cold Spring Harb Perspect Biol 3: a001800.
|
|
[116]
|
Saraswathy S, Wu G, et al. (2006) Retinal microglial activation and chemotaxis by docosahexaenoic acid hydroperoxide. Invest Ophthalmol Vis Sci 47: 3656–3663. doi: 10.1167/iovs.06-0221

|
|
[117]
|
Dunlop R, Dean R, Rodgers K (2008) The impact of specific oxidized amino acids on protein turnover in J774 cells. Biochem J 410: 131–140. doi: 10.1042/BJ20070161

|
|
[118]
|
Darling E, Zauscher S, Block J (2007) A thin-layer model for viscoelastic, stress-relaxation testing of cells using atomic force microscopy: do cell properties reflect metastatic potential. Biophys J 92: 1784–1791. doi: 10.1529/biophysj.106.083097

|
|
[119]
|
Fleischer F, Ananthakrishnan R, (2007) Actin network architecture and elasticity in lamellipodia of melanoma cells. New J Phys 9: 420. doi: 10.1088/1367-2630/9/11/420

|
|
[120]
|
Pokorný J, Jandový A, Nedbalová (2012) Mitochondrial metabolism-neglected link of cancer transformation and treatment. Prague Med Rep 113: 81–94.
|
|
[121]
|
Qian Y, Luo J, Leonard S, et al. (2003) Hydrogen peroxide formation and actin filament reorganization by Cdc42 are essential for ethanol-induced in vitro angiogenesis. J Biol Chem 278: 16189–16197. doi: 10.1074/jbc.M207517200

|
|
[122]
|
Gawdzik B, Księzopolski J, Matynia T (2003) Synthesis of new free-radical initiators for polymerization. J Appl Polym Sci 87: 2238–2243. doi: 10.1002/app.11585

|
|
[123]
|
Miller Y, Worrall D, Funk C, et al. (2003) Actin polymerization in macrophages in response to oxidized LDL and apoptotic cells: role of 12/15-lipoxygenase and phosphoinositide 3-kinase. Mol Biol Cell 14: 4196–4206. doi: 10.1091/mbc.E03-02-0063

|
|
[124]
|
Ushio-Fukai M, Nakamura Y (2008) Reactive oxygen species and angiogenesis: NADPH oxidase as target for cancer therapy. Cancer Lett 266: 37–52. doi: 10.1016/j.canlet.2008.02.044

|
|
[125]
|
Taparowsky E, Suard Y, Fasano O (1982) Activation of the T24 bladder carcinoma transforming gene is linked to a single amino acid change. Nature 300: 762–765. doi: 10.1038/300762a0

|
|
[126]
|
Swaminathan V, Mythreye K, Tim O'Brien E, et al. (2011) Mechanical Stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res 71: 5075–5080. doi: 10.1158/0008-5472.CAN-11-0247

|
|
[127]
|
Xu W, Mezencev R, Kim B, et al. (2012) Cell stiffness is a biomarker of the metastatic potential of ovarian cancer cells. PLoS ONE 7: e46609. doi: 10.1371/journal.pone.0046609

|
|
[128]
|
Hoyt K, Castaneda B, Zhang M, et al. (2008) Tissue elasticity properties as biomarkers for prostate cancer. Cancer Biomark 4: 213–225. doi: 10.3233/CBM-2008-44-505

|
|
[129]
|
Ghosh S, Kang T, Wang H, et al. (2011) Mechanical phenotype is important for stromal aromatase expression. Steroids 76: 797–801. doi: 10.1016/j.steroids.2011.02.039

|
|
[130]
|
Kraning-Rush C, Califano J, Reinhart-King C (2012) Cellular traction stresses increase with increasing metastatic potential. PLoS ONE 7: e32572. doi: 10.1371/journal.pone.0032572

|
|
[131]
|
Trichet L, Le Digabel J, Hawkins R, et al. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc Natl Acad Sci U.S.A. 109: 6933–6938.
|
|
[132]
|
Peto R, Doll R, Buckley J (1981) Can dietary beta-carotene materially reduce human cancer rates? Nature 290: 201–208. doi: 10.1038/290201a0

|
|
[133]
|
Shike M, Winawer S, Greenwald P, et al. (1990) Primary prevention of colorectal cancer. Bull World Health Organ 68: 337–385.
|
|
[134]
|
Dorgan J, Schatzkin A (1991) Antioxidant micronutrients in cancer prevention. Hematol Oncol Clin North Am 5: 43–68.
|
|
[135]
|
Chlebowski R, Grosvenor M (1994) The scope of nutrition intervention trials with cancer-related endpoints. Cancer 74: 2734–2738. doi: 10.1002/1097-0142(19941101)74:9+<2734::AID-CNCR2820741824>3.0.CO;2-U

|
|
[136]
|
Ziegler R, Mayne S, Swanson C (1996) Nutrition and lung cancer. Cancer Causes Control 7: 157–177. doi: 10.1007/BF00115646

|
|
[137]
|
Levander O (1997) Symposium: newly emerging viral diseases: what role for nutrition? J Nutr 127: 948S–950S.
|
|
[138]
|
Willett W (1999) Convergence of philosophy and science: the Third International Congress on Vegetarian Nutrition. Am J Clin Nutr 70(suppl): 434S–438S.
|
|
[139]
|
Meydani M (2000) Effect of functional food ingredients: vitamin E modulation of cardiovascular diseases and immune status in the elderly. Am J Clin Nutr 71(suppl): 1665S–1668S.
|
|
[140]
|
Simopoulos A (2001) The Mediterranean diets: what is so special about the diet of Greece? The scientific experience. J Nutr 131: 3065S–3073S.
|
|
[141]
|
Rock C, Demark-Wahnefried W (2002) Nutrition and survival after the diagnosis of breast cancer: a review of the evidence. J Clin Oncol 20: 3302–3316. doi: 10.1200/JCO.2002.03.008

|
|
[142]
|
Seifried H, McDonald S, Anderson D, et al. (2003) The antioxidant conundrum in cancer. Cancer Res 63: 4295–4298.
|
|
[143]
|
Männistö S, Smith-Warner S, Spiegelman D, et al. (2004) Dietary carotenoids and risk of lung cancer in a pooled analysis of seven cohort studies. Cancer Epidemiol Biomarkers Prev 13: 40–48. doi: 10.1158/1055-9965.EPI-038-3

|
|
[144]
|
Fraga C (2007) Plant polyphenols: how to translate their in vitro antioxidant actions to in vivo conditions. Life 59: 308–315.
|
|
[145]
|
Kushi L, Doyle C, McCullough M, et al. (2012) American cancer society guidelines on nutrition and physical activity for cancer prevention. CA Cancer J Clin 62: 30–67. doi: 10.3322/caac.20140

|
|
[146]
|
Heinonen O, Albanes D, Huttunen J, et al. (1994) The effect of vitamin E and beta carotene on the incidence of lung cancer and other cancers in male smokers. N Engl J Med 330: 1029–1035. doi: 10.1056/NEJM199404143301501

|
|
[147]
|
Hennekens C, Buring J, Manson J, et al. (1996) Lack of effect of long-term supplementation with beta carotene on the incidence of malignant neoplasms and cardiovascular disease. N Engl J Med 334: 1145–1149. doi: 10.1056/NEJM199605023341801

|
|
[148]
|
Omenn G, Goodman G, Thornquist M, et al. (1996) Effects of a combination of beta carotene and vitamin A on lung cancer and cardiovascular disease. N Engl J Med 334: 1150–1155. doi: 10.1056/NEJM199605023341802

|
|
[149]
|
Albanes D (1999) β-carotene and lung cancer: a case study. Am J Clin Nutr 69(suppl): 1345S–1350S.
|
|
[150]
|
Virtamo J, Albanes D, Huttunen J, et al. (2003) Incidence of cancer and mortality following α-tocopherol and β-carotene supplementation. JAMA 290: 476–485. doi: 10.1001/jama.290.4.476

|
|
[151]
|
Sommer A, Vyas K (2012) A global clilnical view on vitamin A and carotenoids. Am J Clin Nutr 96(suppl): 1204–1206.
|
|
[152]
|
Thompson I, Kristal A, Platz E (2014) Prevention of prostate cancer: outcomes of clinical trails and future opportunities. Am Soc Clin Oncol Educ Book 2014: e76–e80.
|
|
[153]
|
Virtamo J, Taylor P, Kontto J, et al (2014) Effects of α-tocopherol and β-carotene supplementation on cancer incidence and mortality: 18-year post-intervention follow-up of the alpha-tocopherol, beta-carotene cancer prevention (ATBC) study. Int J Cancer 135: 178–185. doi: 10.1002/ijc.28641

|
|
[154]
|
Yusuf S, Phil D, Dagenais G, et al. (2000) Vitamin E supplementation and cardiovascular events in high-risk patients. N Engl J Med 342: 154–160. doi: 10.1056/NEJM200001203420302

|
|
[155]
|
Devaraj S, Tang R, Adams-Huet B, et al. (2007) Effect of high-dose α-tocopherol supplementation on biomarkers of oxidative stress and inflammation and carotid atherosclerosis in patients with coronary artery disease. Am J Clin Nutr 86: 1392–1398.
|
|
[156]
|
Sesso H, Buring J, Christen W, et al (2008) Vitamins E and C in the prevention of cardiovascular disease in men. JAMA 300: 2123–2133.
|
|
[157]
|
Brigelius-Flohe R, Galli F (2010) Vitamin E: a vitamin still awaiting the detection of its biological function. Mol Nutr Food Res 54: 583–587. doi: 10.1002/mnfr.201000091

|
|
[158]
|
Schultz M, Leist M, Petrzika M, et al. (1995) Novel urinary metabolite of α-tocopherol, 2,5,7,8-tetramethyl-2(2'-carboxyethyl)-6-hydroxychroman, as an indicator of an adequate vitamin E supply. Am J Clin Nutr 62(suppl): 1527S–1534S.
|
|
[159]
|
Azzi A (2007) Molecular mechanism of α-tocopherol action. Free Radic Biol Med 43: 16–21. doi: 10.1016/j.freeradbiomed.2007.03.013

|
|
[160]
|
Boddupalli S, Mein J, Lakkanna S, et al. (2012) Induction of phase 2 antioxidant enzymes by broccoli sulforaphane: perspectives in maintaining the antioxidant activity of vitamins A, C, and E. Front Genet 3: 1–15.
|
|
[161]
|
Lü JM, Lin P, Yao Q, et al. (2010) Chemical and molecular mechanisms of antioxidants: experimental approaches and model systems. J Cell Mol Med 14: 840–860. doi: 10.1111/j.1582-4934.2009.00897.x

|
|
[162]
|
Apak R, Güçlü K, Özyürek M, et al. (2008) Mechanism of antioxidant capacity assays and the CUPRAC (cupric ion reducing antioxidant capacity) assay. Microch Acta 160: 413–419.
|
|
[163]
|
Özyürek M, Bektaşoğlu B, Güçlü K, et al. (2008) Simultaneous total antioxidant capacity assay of lipohilic and hydrophilic antioxidants in the same acetone-water solution containing 2% methyl-β-cyclodextrin using the cupric reducing antioxidant capacity (CUPRAC) method. Anal Chim ACTA 630: 28–39. doi: 10.1016/j.aca.2008.09.057

|
|
[164]
|
McMurry J, (2004) Organic Chemistry, 6 Eds., Belmont, CA: Thompson Brooks/Cole, 403–405, 482–483, 486–487.
|
|
[165]
|
Dumas D, Muller S, Gouin F, et al. (1997) Membrane fluidity and oxygen diffusion in cholesterol enriched erythrocyte membrane. Arch Biochem Biophys 341: 34–39. doi: 10.1006/abbi.1997.9936

|
|
[166]
|
Cazzola R, Rondanelli M, Russo-Volpe S, et al. (2004) Decreased membrane fluidity and altered susceptibility to peroxidation and lipid composition in overweight and obese female erythrocytes. J Lipid Res 45: 1846–1851. doi: 10.1194/jlr.M300509-JLR200

|
|
[167]
|
Madmani M, Yusaf S, Tamr A, et al. (2014) Coenzyme Q10 for heart failure (Review). Cochrane Database Syst Rev 2014.
|
|
[168]
|
Watts G, Playford D, Croft K, et al. (2002). Coenzyme Q10 improves endothelial dysfunction of brachial artery in type II diabetes mellitus. Diabetologia 45:420–426.
|
|
[169]
|
DeCaprio A (1999) The toxicology of hydroquinone-relevance to occupational and environmental exposure. Crit Rev Toxicol 29: 283–330. doi: 10.1080/10408449991349221

|
|
[170]
|
McMurry J, (2004) 17.11 Reactions of Phenols, In: Organic Chemistry, 6 Eds., Belmont, CA: Thompson Brooks/Cole, 618–619.
|
|
[171]
|
Takata J, Matsunage K, Karube Y (2002) Delivery systems for antioxidant nutrients. Toxicology 180: 183–193. doi: 10.1016/S0300-483X(02)00390-6

|
|
[172]
|
Pifer, J, Hearne F, Friedlander B, et al. (1986) Mortality study of men employed at a large chemical plant, 1972 through 1982. J Occup Med 28: 438–444. doi: 10.1097/00043764-198606000-00011

|
|
[173]
|
Pifer J, Hearne F, Swanson F (1995) Mortality study of employees engaged in the manufacture and use of hydroquinone. Int Arch Occup Environ Health 67: 267–280. doi: 10.1007/BF00409409

|
|
[174]
|
Sterner J, Oglesby F, Anderson B (1947) Quinone vapors and their harmful effects. I Corneal and conjunctival injury. J Ind Hyg Toxicol 29: 60–73.
|
|
[175]
|
Carlson A, Brewer N (1953) Toxicity studies on hydroquinone. Proc Soc Exp Biol Med 84: 684–688. doi: 10.3181/00379727-84-20751

|
|
[176]
|
O'Donoghue J (2006) Hydroquinone and its analogues in dermatology-a risk-benefit viewpoint. J Cosmet Dermatol 5: 196–203. doi: 10.1111/j.1473-2165.2006.00253.x

|
|
[177]
|
Nordlund J, Grimes P, Ortonne J (2006) The safety of hydroquinone. JEADV 20: 781–787.
|
|
[178]
|
Arndt K, Fitzpatrick T (1965) Topical use of hydroquinone as a depigmenting agent. JAMA 194: 965–967. doi: 10.1001/jama.1965.03090220021006

|
|
[179]
|
Deisinger P, Hill T, English C (1996) Human exposure to naturally occurring hydroquinone. J Toxicol Env Health 47: 31–46.
|
|
[180]
|
Levitt J (2007) The safety of hydroquinone: a dermatologist's response to the 2006 Federal Register. J Am Acad Dermatol 57: 854–872. doi: 10.1016/j.jaad.2007.02.020

|
|
[181]
|
Marcus R, Sutin N (1985) Electron transfers in chemistry and biology. Biochim Biophys Acta 811: 265–322. doi: 10.1016/0304-4173(85)90014-X

|
|
[182]
|
Dumas D, Latger V, Viriot M-L, et al. (1999) Membrane fluidity and oxygen diffusion in cholesterol-enriched endothelial cells. Clin Hemorheol Microcirc 21: 255–261.
|
|
[183]
|
National Toxicology Program (1989) Toxicology and carcinogenesis studies of hydroquinone in F-344/N rats and B6C3F mice. NIH Publication : 90–2821.
|
|
[184]
|
Shibata MA, Hirose M, Tanaka H, et al. (1991) Induction of renal cell tumors in rats and mice, and enhancement of hepatocellular tumor development in mice after long-term hydroquinone treatment. Jap J Can Res 82: 1211–1219. doi: 10.1111/j.1349-7006.1991.tb01783.x

|
|
[185]
|
Poet T, Wu H, English J, et al (2004) Metabolic rate constants for hydroquinone in F344 rat and human liver isolated hepatocytes: application to a PBPK model. Toxicol Sci 82: 9–25. doi: 10.1093/toxsci/kfh229

|
|
[186]
|
MacDonald J (2004) Human carcinogenic risk evaluation, part IV: assessment of human risk of cancer from chemical exposure using a global weight-of-evidence approach. Toxicol Sci 82: 3–8. doi: 10.1093/toxsci/kfh189

|
|
[187]
|
Food and Drug Administration (2015) Hydroquinone studies under the national toxicology program (NTP). 11/27/2015. Accessed 11/2016, Available from: http://www.fda/gov/About FDA/CentersOffices/OfficeofMedicalProductsandTobacco/CDER/ucm203112.htm.
|









 DownLoad:
DownLoad: