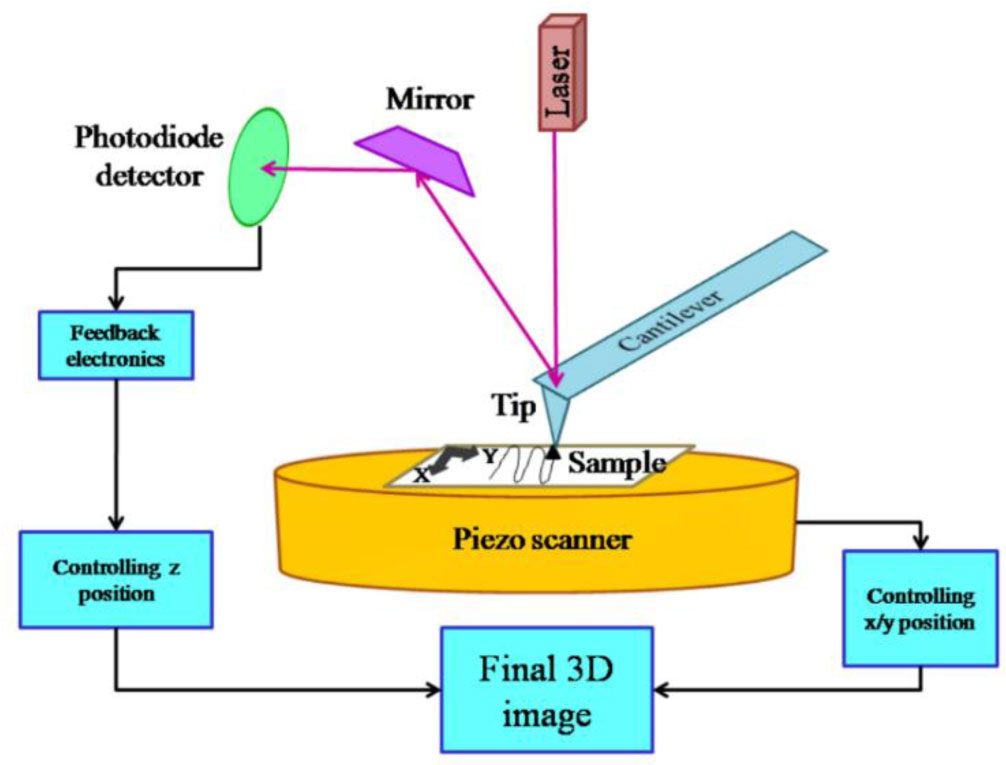
1. AFM technology
Nanotechnology is an evolving field of research that has presented wide applications to the sectors of basic research and engineering. One of the extraordinary outcomes of this development is atomic force microscopy (AFM) [1], a member of the scanning probe microscopy family. It scans the surface of the material under examination using a fine probe at the end of a cantilever and reconstructs a 3D topography image of the sample (Figure 1).
The AFM probe (or AFM tip) interacts with the surface of the sample via the whole spectrum of non-covalent forces, such as electrostatic interactions, attractive van-der-Waals forces, and Pauli repulsion. Attractive interactions deflect the cantilever arm towards the sample surface; repulsive interaction forces deflect it away from the surface. The deflection of the cantilever is most commonly detected by an optical system, with a laser beam that is reflected from the cantilever onto a position sensitive photodetector (Figure 1) [2]. A feedback system restrains the interaction forces between tip and sample surface by up- or down-regulating the tip-sample distance. The feedback loop signal also simultaneously indicates the sample height at each pixel position and serves as the basis for a topography map of the sample (see also Figure 1).
AFM offers high spatial (typically nm range) and force (pN-µN) resolution, limited by the AFM tip end diameter and the cantilever stiffness, respectively. In addition to its high resolution, AFM further involves relatively simple and fast sample preparation. Furthermore, experiments can be carried out on samples in their native hydrated states in liquid environment. These properties make AFM a highly attractive technique for the investigation of biological systems ranging from whole cells to individual bio-molecules. In particular, in the past thirty years, AFM has been applied to a wide diversity of proteins. For instance, imaging of highly ordered protein systems in 2D crystals has enabled sub-nanometer resolution structures of membrane protein complexes by AFM [3,4]. Also for more heterogenic samples, the high, sub-molecular resolution of AFM imaging has provided direct visualization of dynamic conformational transitions of proteins [5,6,7]. In addition, protein conformational changes induced by interactions with diverse ligands such as ATP [8], RNA [9], DNA [10], or other proteins [11] have been demonstrated by AFM. Exemplary for the versatile information obtainable by AFM, in this review, we will discuss AFM applications to the study of protein-DNA interactions.
Its high sensitivity allows the resolution of individual molecules and their interactions by AFM, the qualifying property of a single molecule technique. Single molecule resolution is provided either visually or in terms of the forces involved in the structural stabilization or functional interactions of individual molecules. These different types of information can be accessed by two different AFM application modes, imaging and force spectroscopy.
For AFM imaging, the sample is deposited onto a flat, clean, and smooth substrate. Imaging can be carried out either in air on dried samples or in solution. For imaging of protein-DNA samples in air, the deposition buffer typically contains ≥ 5 mM divalent cations such as Mg2+. The ions serve to chelate the negatively charged DNA to the mica surface, which is also negatively charged under neutral (or close to neutral) pH condition. The samples are rinsed with deionized water and dried, typically in a stream of nitrogen. During the rinsing step, the surrounding solution is depleted of all buffer solution ions, leaving the negatively charged DNA stably chelated to the mica surface via the divalent cations. Imaging in solution mostly requires a more stable attachment of sample molecules to the substrate surface than imaging in air. This can be achieved by functionalizing the surface with reactive chemical groups. For example, aminopropyl triethoxy silane (APTES) or silatrane functionalization provides a positively charged surface instead of the negatively charged bare mica surface at neutral pH [12], leading to stable anchoring of the highly negatively charged DNA backbone for imaging of protein-DNA complexes. Silicon or highly oriented pyrolytic graphite (HOPG) are alternative substrates that provide (locally) flat, atomically smooth surfaces [13,14]. HOPG is widely used in AFM imaging applications on 2D protein crystals, especially of membrane proteins within lipid membranes due to the hydrophobic nature of its surface [13,14], but has also been applied for DNA samples [15,16]. In particular for imaging applications in liquid, DNA attachment strength on HOPG can be conveniently controlled by the ionic strength of the buffer solution.
There are three prominent modes of operation in AFM imaging [17,18]—contact mode, non-contact mode, and tapping or intermittent contact mode. In contact mode, the tip of the probe is in direct contact with the sample as it scans the surface. In non-contact mode, the tip is oscillated above the surface of the sample without directly contacting the sample, and attractive tip-sample interactions are detected at each pixel position during the scanning process. In tapping mode/intermittent mode, the tip is also oscillated above the sample surface, directly touching (tapping) the surface of the sample at the bottom amplitude of each oscillation cycle. In this operational mode, the degree of cutting of the oscillation amplitude due to tip-sample interactions is detected. Tapping mode imaging is popular for studies of proteins since it completely eliminates lateral forces between tip and sample during scanning and strongly reduces the force on the sample particles (as well as on the tip) compared to typical contact mode application [19].
For AFM force spectroscopy, biological molecules have to be attached stably between the AFM tip and the substrate surface. Attachment is achieved by functionalizing tip and substrate surface with functional groups that will interact with groups in the molecule. Popular bio-conjugation systems are, for example, streptavidin coating for immobilization of biotinylated molecules such as DNA or proteins or Ni2+-NTA functionalization for attachment of His-tagged proteins [2,20,21,22]. The force response of a biomolecule that is tethered between tip and surface upon stretching and relaxing by moving the tip up and down can be measured. The basis of force measurements are the detected cantilever deflections, which are directly related via the cantilever stiffness or spring constant, as described by Hooke's law. Commercial systems conveniently determine the spring constant of a cantilever from its thermal noise spectrum based on the equipartition theorem. The resulting force-extension curves have provided interesting insight into the mechanical properties of DNA [22,23], direct protein-DNA interaction strengths [22], and structural properties as well as energy landscapes of proteins from unfolding/re-folding [24,25,26]. Comprehensive reviews covering AFM force spectroscopy applications to protein-DNA systems have been published by several laboratories [22,26,27]. Within the vast scope of and wealth of available data on protein-DNA interaction studies by AFM, we will focus here exclusively on AFM imaging applications to protein-DNA systems. Previous reviews have also elegantly covered AFM imaging studies of protein-DNA interactions [28,29,30]. Here, we describe a broad spectrum of DNA processing systems and the parameters accessible by AFM. We provide instructive examples from a range of biologically essential pathways that will serve to demonstrate the versatility and power of AFM for obtaining unique insights into protein-DNA interactions by AFM imaging.
2. Protein-DNA interactions
A varied number of pivotal biological processes demand the binding of proteins to nucleic acids [31]. Pathways involving protein-DNA interactions include DNA packing, DNA replication, transcription, recombination and repair. These different systems are typically composed of a number of proteins that work together to achieve their specific, complex task. For instance, heteromeric complexes of histones organise DNA in eukaryotic DNA packing [32]. DNA replication requires the concerted actions of topoisomerases, proteins for origin recognition, helicases, single stranded DNA binding proteins (SSBs), primase, DNA polymerases, and DNA ligase. Transcription factors bind to promoter or enhancer sequences in DNA to initiate gene transcription by RNA polymerase [33]. Finally, DNA maintenance by repair of faulty DNA bases or DNA strand breaks requires the removal of either whole stretches of DNA, a single damaged base, or a single offending chemical group from a modified base via nucleophilic attack by transferases or nucleases. Most DNA repair systems also involve intricate interactions of many protein factors to achieve efficient and specific recognition and removal of their particular target lesions. Furthermore, enzymes that modify different amino acid residues in proteins, such as kinases or methyltransferases, can regulate the function of DNA processing proteins by enabling or suppressing protein interactions [34].
Traditional biochemical and biophysical bulk assays are still invaluable assets in the analyses of protein-DNA interactions. Examples are the electrophoretic mobility shift assay (EMSA), filter binding assay, surface plasmon resonance (SPR), bio-layer interferometry (BLI), DNase I footprinting, and fluorescence anisotropy. However, many of these methods measure binding indirectly. For instance, BLI measures molecular adhesion as a shift in laser wavelength through a layer of molecules bound to a surface attached interaction partner. Such wavelength changes due to changes in a bound bio-layer may be difficult to interpret and/or disentangle from interfering contributions. Importantly, these measurements provide only ensemble properties and fail to resolve heterogeneity in a system such as, for instance, different conformational states that may contribute to the ensemble [35,36,37,38].
A major advantage of AFM imaging for the study of protein-DNA samples is the direct resolution of individual molecules and molecular assemblies with nanometric scale. Its single molecule resolution places AFM right at the interface between the atomic resolution achievable by crystallography and the comparably poor spatial resolution of optical microscopy that is limited by diffraction to several hundred nanometers. In fact, these methods ideally complement each other.
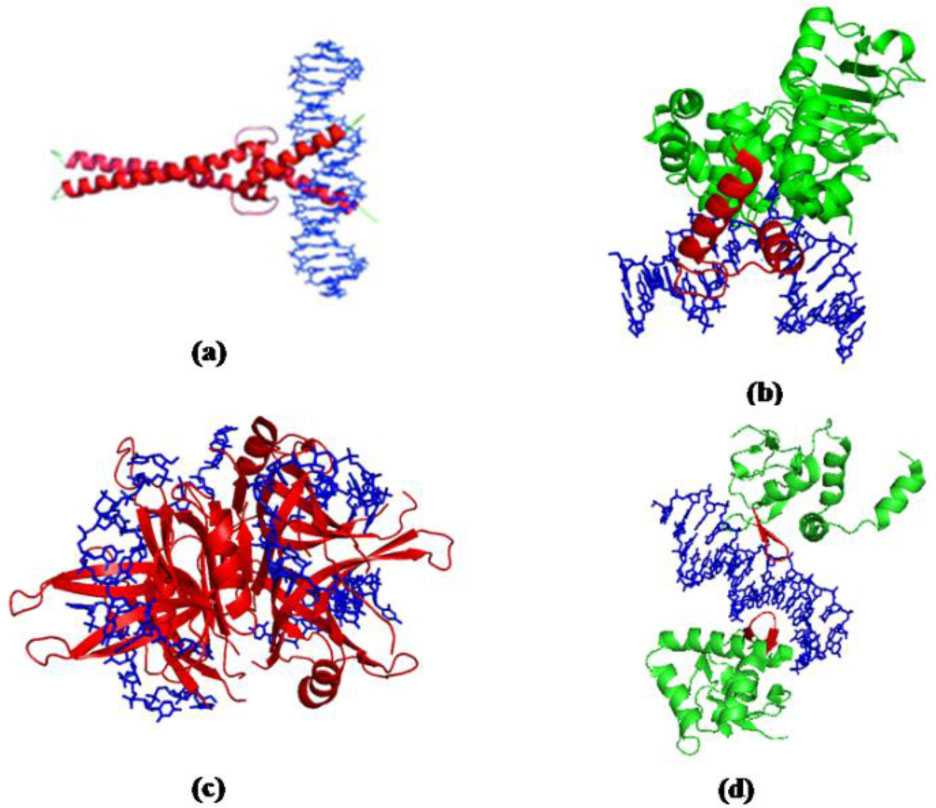
Crystallographic studies have provided us with a wealth of information on the structural details of protein-DNA interactions that form the foundation of the molecular mechanisms of DNA processing systems. These data revealed that DNA binding proteins predominantly possess a multi-domain structure. DNA processing interactions are specific to the function of the particular protein and can be hosted within the DNA binding domain (DBD) directly or on a separate, functional domain [39,40]. From crystal structures, we know a variety of protein motifs in these DBDs and how they mediate DNA interactions by the proteins (Figure 2) [39,41,42]. Structural proteins like histones famously employ non-specific, electrostatic interactions with the DNA backbone [43]. Compensation of positive charges in a protein's DNA binding surface with the negatively charged DNA can stabilize protein-DNA complexes. In contrast, many proteins require selective recognition of and interactions with specific DNA sequences or structures. Sequence specific interactions can be achieved by several structural motifs such as helix turn helix (HTH), helix loop helix (HLH), winged helix, or zinc finger that interact with the major groove of the DNA (Figure 2a). Prominent examples of proteins that recognize and bind specific sequences of DNA are transcription factors or DNA endonucleases [44,45,46]. Recent advances in structural studies have provided detailed insight into sequence recognition and binding strategies, for example, by E2F [47] and STAT [48] transcription factors. E2Fs interact with the DNA major groove via winged helix motifs [47], while STATs use immunoglobulin-like domains for sequence specific DNA interactions [48,49]. Both classes of transcription factors additionally employ dimerization to modulate DNA binding affinities [47,48]. Binding in the DNA minor groove, such as by the helix hairpin helix (HhH) motif (Figure 2b), involves no direct read out of DNA bases [50]. These protein-DNA interactions are therefore non-specific for the DNA sequence; instead they are sensitive to DNA superstructure. Other examples of structure specific interactions are the binding to replication forks by DNA polymerases [51]. Single stranded DNA (ssDNA) is also specifically recognized and bound by the ssDNA binding (SSB) proteins via one or multiple OB-fold(s) consisting of a five-stranded β-barrel (Figure 2c) [52]. Further structural motifs have evolved that play roles in protein-DNA interactions. For example, a β-hairpin probe can be inserted into the DNA double helix to investigate the DNA for the presence of specific target sites, for example in the nucleotide excision repair (NER) helicase UvrB or the growth factor signaling protein Smad5 (Figure 2d) [53,54,55]. Finally, features such as an arginine finger can be exploited by proteins that flip a base into an active site pocket for further processing, to replace the vacated position of the base in the DNA double helix and thus stabilize the protein-DNA complex [56].
In contrast to AFM imaging experiments, optical microscopy requires fluorescent labeling of sample molecules for their detection. Furthermore, optical microscopy offers only low spatial resolution. However, one of the major advantages of optical microscopy versus AFM is that it can resolve dynamic processes with fluorescently labeled particles at high time resolution in the order of microseconds. For AFM imaging, on the other hand, the relatively low time resolution governed by the scan speed is a major limitation for the study of dynamic processes in protein-DNA interactions. Conventional AFM systems require imaging times in the order of minutes for surface areas of approximately 1 × 1 µm2. Reducing scan size and pixel resolution can bring scan times down to ∼30 seconds per image area. Nevertheless, most biological processes occur at much higher rates. Significantly enhanced time resolutions have been made possible relatively recently for AFM with the development of high speed AFM (HS-AFM) by Toshio Ando and colleagues [58,59], as will be discussed below.
Electron microscopy (EM) also offers single molecule resolution imaging of protein-DNA assemblies. However, standard EM requires more aggressive substrate functionalization than AFM that can affect conformations of sample particles, for instance DNA bending. In addition, samples are mostly coated by negative staining for suitable contrast, which can introduce artifacts in the images. In contrast, cryo-EM is performed on samples frozen in ice and recent advances in EM technology have enabled resolutions approaching those of crystallographic structures. However, for sub-nanometer resolution, averaging is applied to the data, which requires ordered structures and is hence not ideally applicable to non-specific protein-DNA interactions. Details on EM of protein-DNA complexes have been discussed elsewhere [60,61]. Compared to AFM, EM applications are considerably more expensive and involve more elaborate sample preparations.
While AFM does not provide atomic resolution structures of protein-DNA complexes, it allows the direct visualization of protein-DNA complexes at the level of the individual molecules in the context of their specific DNA target sites and under different conditions. AFM images further uniquely offer structural information on transient complexes of proteins bound to non-specific DNA sites, which are not accessible by crystallographic studies or other techniques based on the detection of ensemble properties. Structural information from crystallography or nuclear magnetic resonance (NMR) can add important information for the interpretation of the AFM molecular resolution protein-DNA complex structures. Similarly, high time resolution kinetics and dynamics of protein-DNA interactions can often be contributed by methods orthogonal to AFM imaging such as fluorescence imaging or anisotropy measurements. Here, we will discuss different examples of AFM applications to diverse protein-DNA interactions that highlight the power of AFM for the structural and functional analysis of protein-DNA interactions. In these examples, we will also demonstrate the complementarity of AFM and atomic resolution crystallographic structures, as well as biochemical and biophysical bulk interaction assays.
3. Resolving effects of protein binding on DNA structure by AFM
Protein binding can induce structural changes in DNA. The compaction of DNA is, for instance, regulated by proteins such as topoisomerases that affect the state of supercoiling of the bacterial genome. Different superstructural DNA states can be distinguished in AFM images due to their different twists and linking numbers. Figure 3a shows distinct changes in DNA superstructure that indicate DNA condensation induced by protein binding likely mediated via protein-protein interactions [62]. In the context of eukaryotic DNA chromatin, AFM imaging has been applied to investigate the effects of different solution conditions on nucleosome remodeling [63].
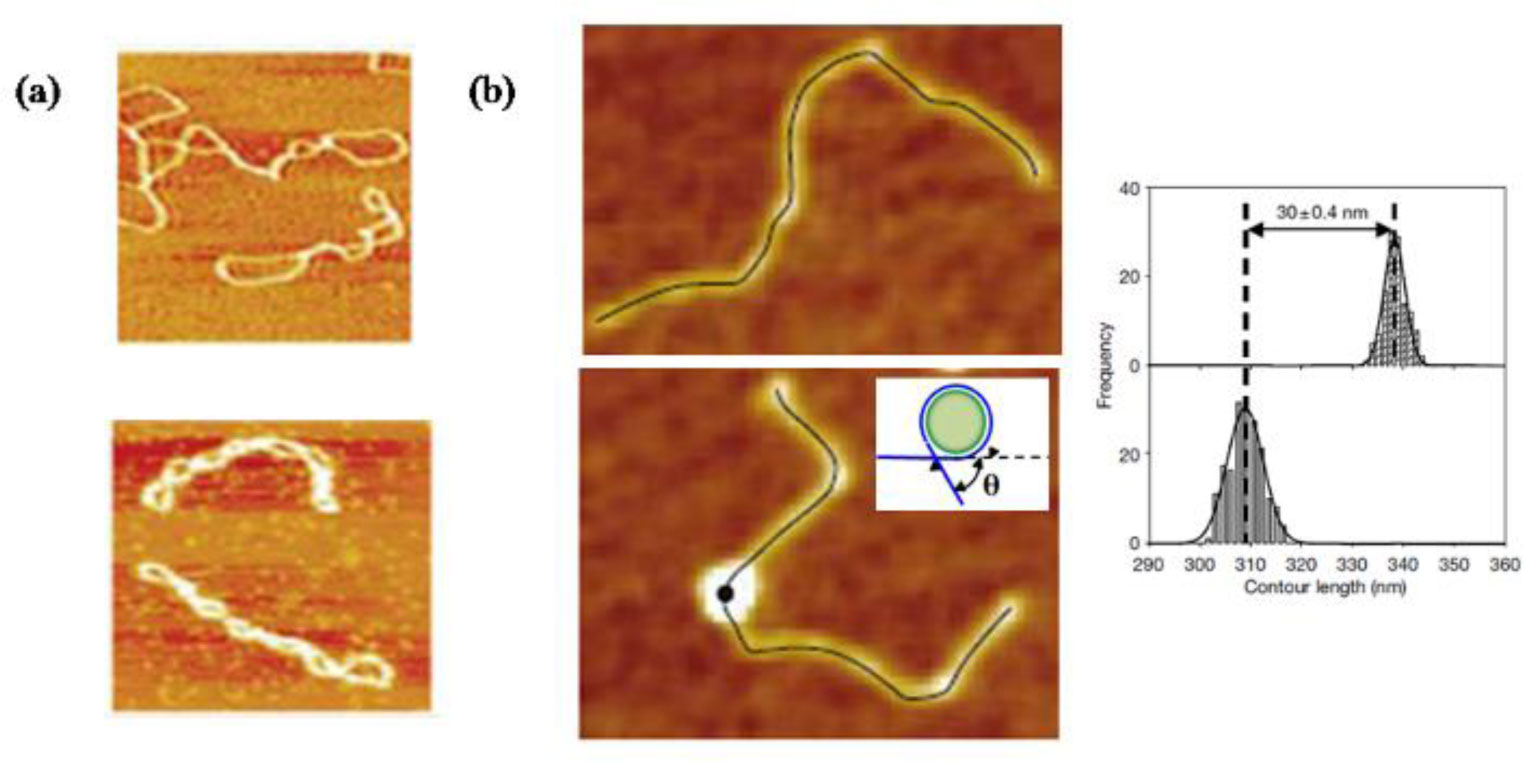
DNA looping or wrapping around proteins can serve to destabilize the DNA double helix to allow easier access for the protein. Extrusions of dsDNA and ssDNA loops from protein-DNA complexes, which result in a shortening of the overall DNA substrate length, have been observed and characterized by AFM imaging for the MCM replication initiation complex and for a restriction enzyme, respectively [64,65]. Examples for proteins that have been shown by AFM imaging to wrap DNA around themselves are RNA polymerase or the DNA repair helicase UvrB [66,67,68]. Such wrapping can be detected from AFM images by measuring the DNA contour lengths of protein bound DNA versus those of free DNA fragments (Figure 3b).
4. Direct AFM visualization of cooperative protein-DNA interactions
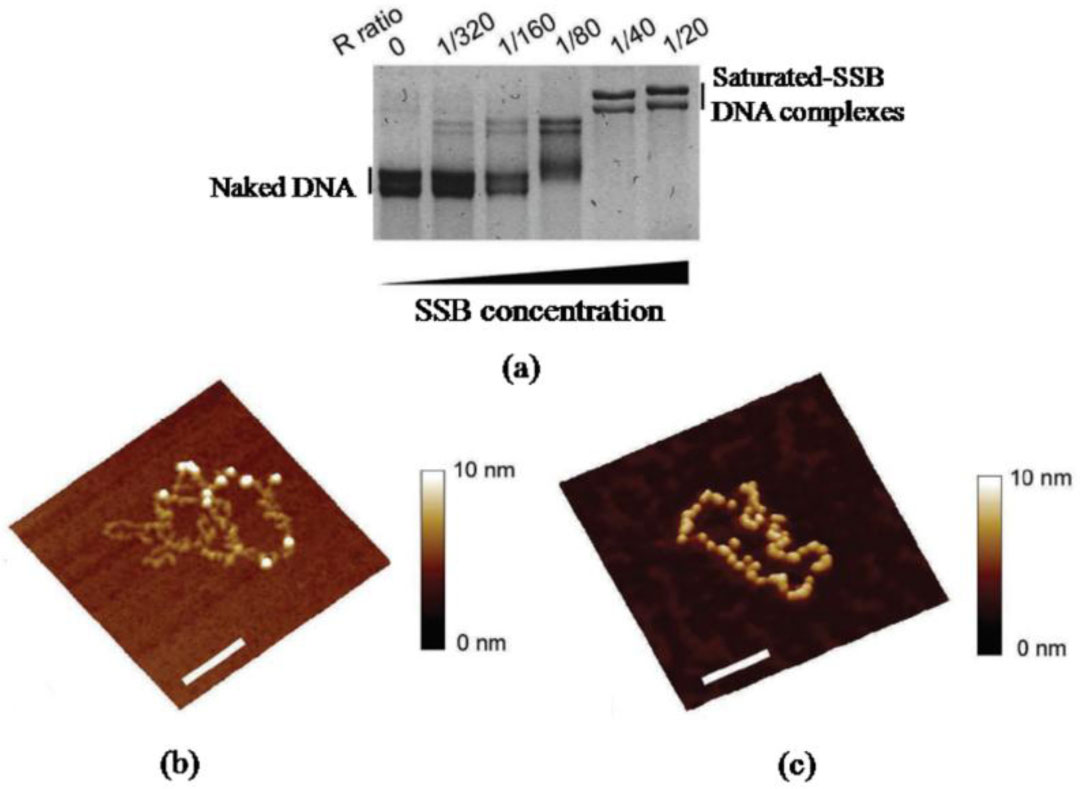
Many proteins apply cooperative interactions in DNA binding. Cooperativity can be based either on modifications in the protein, or in the DNA upon protein-DNA interaction, which favour the binding of additional protein molecules to the existing protein-DNA complex. Atomic force microscopy can directly visualize protein-DNA assemblies and thus reveal protein concentration dependent coverage of the DNA as well as changes in the conformational or stoichiometric properties of the complexes. Examples of cooperative DNA binding protein systems studied by AFM imaging include SSB and RecA on ssDNA, and RecA and the alkylguanine DNA alkyltransferase (AGT) with dsDNA [69,70,71,72,73]. For instance, increasing degrees of saturation of ssDNA with nucleoprotein filaments of E coli SSB were visualized at high resolution by Hamon and coworkers for increasing protein concentrations, as also corroborated by EMSA [70]. In the AFM images, fast conversion from single binding events of SSB tetramers that likely serve as nucleation sites to complete coverage of the DNA substrate was indicative of a cooperative binding process (Figure 4).
5. Following dynamic DNA target site search by HS-AFM
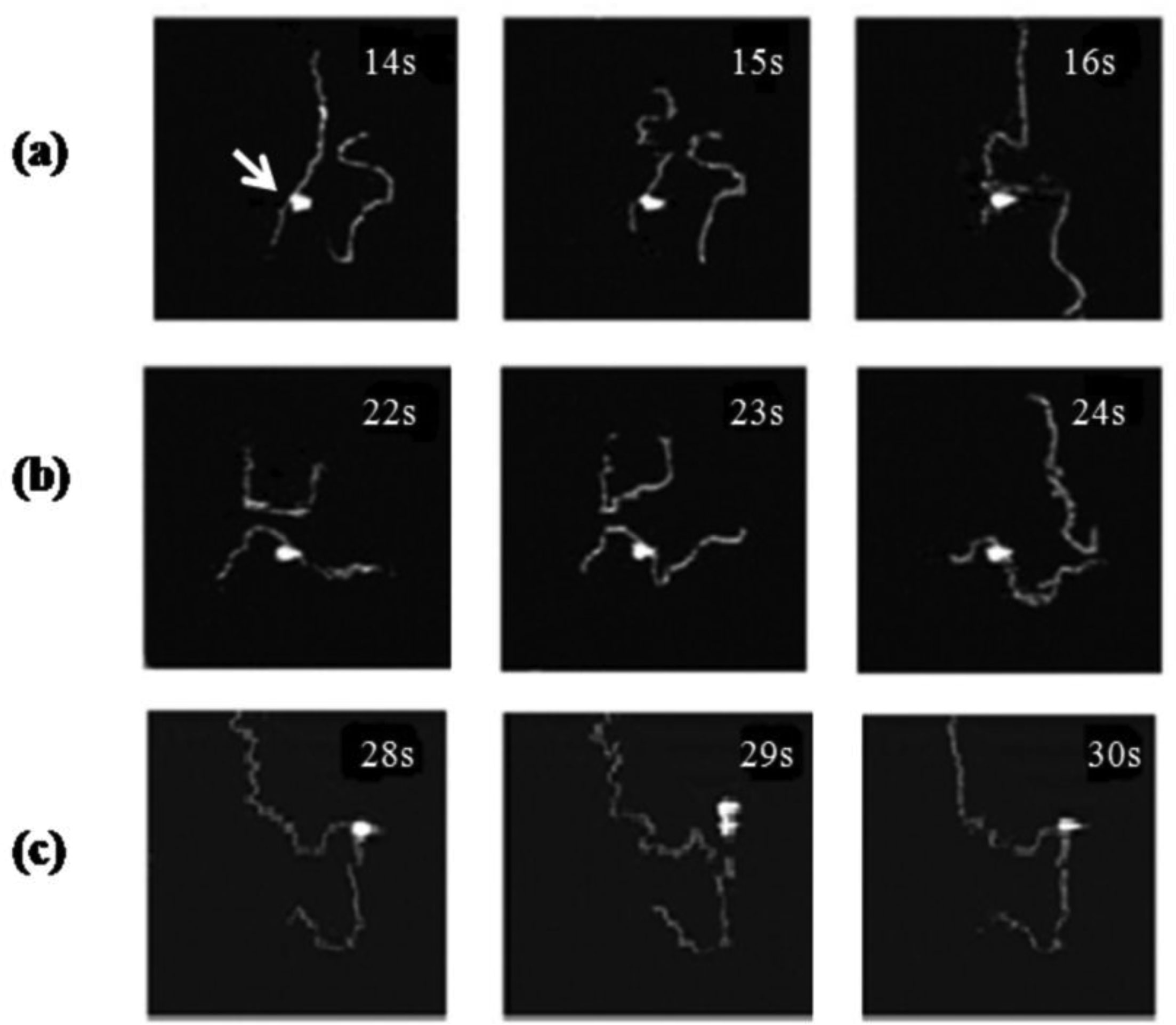
High-speed (HS) AFMs have recently become commercially available. HS-AFM technology is based on faster, advanced electronics and mechanics [59]. A key step towards the realization of HS-AFM have also been advancements in AFM cantilever manufacturing technology, leading to the ability to produce significantly smaller cantilevers. Smaller cantilevers result in less background noise and higher oscillation rates allowing for higher scan speeds at better signal to noise ratio. High time resolution by HS-AFM on the order of seconds to sub-seconds has been demonstrated in AFM movies on various protein systems [74,75,76,77]. For instance, Lyubchenko and co-workers used HS-AFM to follow nucleosome dynamics to gain a better understanding of chromatin organization [74]. In the context of recombinational repair, Wyman and co-workers demonstrated ATP independent hopping and sliding modes of RAD54 monomers by HS-AFM [75] and Waelti and colleagues resolved target site search and recognition by RecA and structurally characterized the DNA bound protein filaments at the molecular level [77]. Sliding, hopping, and intersegmental transfer modes of DNA translocation have also been visualized for RNA polymerase during its target site search by Suzuki and co-workers using HS-AFM (Figure 5) [78].
6. Studying target site recognition by AFM positional analyses
On linear DNA fragments, specific binding site preferences of a protein system can be determined from AFM images by measuring the distance of the protein peaks from the DNA fragment ends. The DNA fragments can be prepared to contain specific target sites such as DNA lesions or structural elements, for instance a DNA flap or unpaired region (bubble) at a well defined position [79]. Specificity S of a protein for a particular target can then be calculated from a Gaussian fit to the position distribution using Eq 1:
Where S is the binding specificity of the protein, N is the total number of binding sites in the given DNA substrate, and Asp/Ansp is the ratio of specific (at the target site of interest) to non-specific binding events [80]. Asp is the area under the Gaussian fit curve, and Ansp the area of the background binding events, which is described by the product of the length of the substrate (in % of DNA length) and the background height in the distribution (see schematic in Figure 6d).
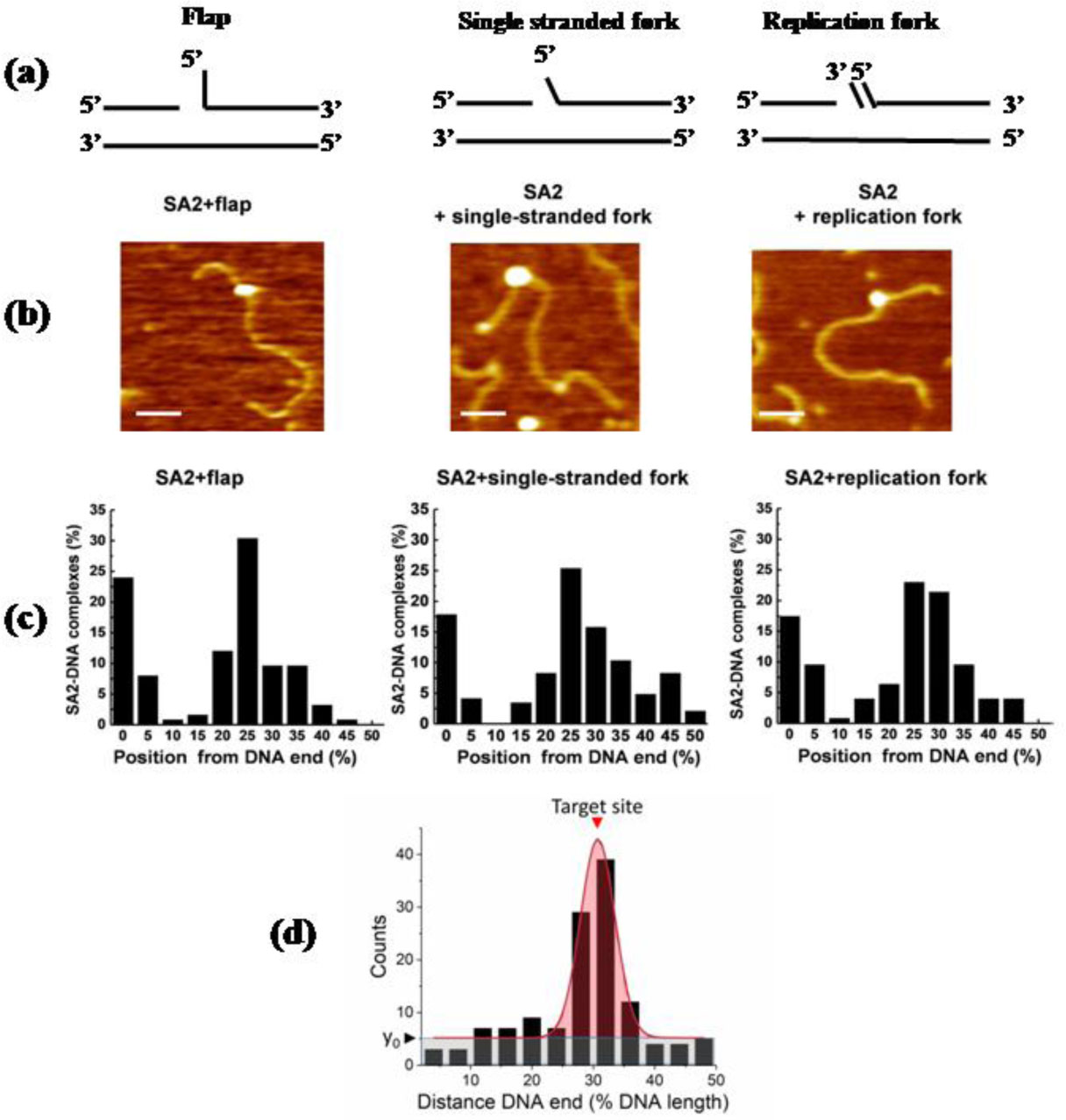
AFM analysis of protein binding specificities has been applied to multiple protein systems, such as DNA repair proteins, proteins involved in transcription, and sequence specific endonucleases. Examples of DNA repair proteins include PARP proteins from recombinational repair or the prokaryotic and eukaryotic nucleotide excision repair helicases UvrB and XPD (see also below) [81,82,83]. AFM analyses of binding specificity of the transcription machinery include studies on RNA polymerase (RNAP) and different transcription factors binding to their respective target sequences in DNA [84,85,86]. For instance, Timofeeva and colleagues have investigated DNA binding by the transcription factor STAT3 [86]. STAT3 is involved in gene expression and can be constitutively phosphorylated in cancers. Using AFM, the authors found unphosphorylated STAT3 to bind specifically not only at its interferon activated recognition sequence, but also at different types of DNA structures such as DNA nodes in negatively supercoiled DNA, suggesting potential roles in chromatin organization. AFM imaging also provides an expanded toolbox for a better understanding of the genetics of transcription factor DNA-binding variations. We envision powerful applications of AFM single molecule visualisation of target site recognition and conformational properties of different transcription factor complexes, to complement recent elegant studies of disease-associated genetic variations, for instance by single nucleotide polymorphisms sequencing, EMSA, or cell proliferation assays [87,88,89]. AFM single molecule imaging of protein positions on DNA has also directly revealed collision, stalling and back-tracking of RNAP on two convergent promoters that would result in different transcriptional outcomes in vivo [90]. Last not least, Wang and colleagues investigated binding of the protein SA2 to different targets in DNA [91]. SA2 is part of the cohesion complex that organizes chromosome alignment and segregation during mitosis. Interestingly, their AFM studies clearly showed preferential binding to various DNA structures that form during DNA recombination, repair, or replication (Figure 6) suggesting potential unknown roles of SA2 in these processes.
Importantly, the single molecule character of AFM allows further to separately characterize specifically (target site) bound and non-specific protein complexes on DNA. Resolving their potentially different conformational or stoichiometric properties (see sections below) gives important insight into mechanistic functions of a protein system.
7. Determining stoichiometries of protein-DNA complexes from AFM volumes
Atomic force microscopy produces three-dimensional topological images. Measuring the height and base areas of protein peaks in the images provides their volumes, for example as the volumes of a spherical cap given by Eq 2.
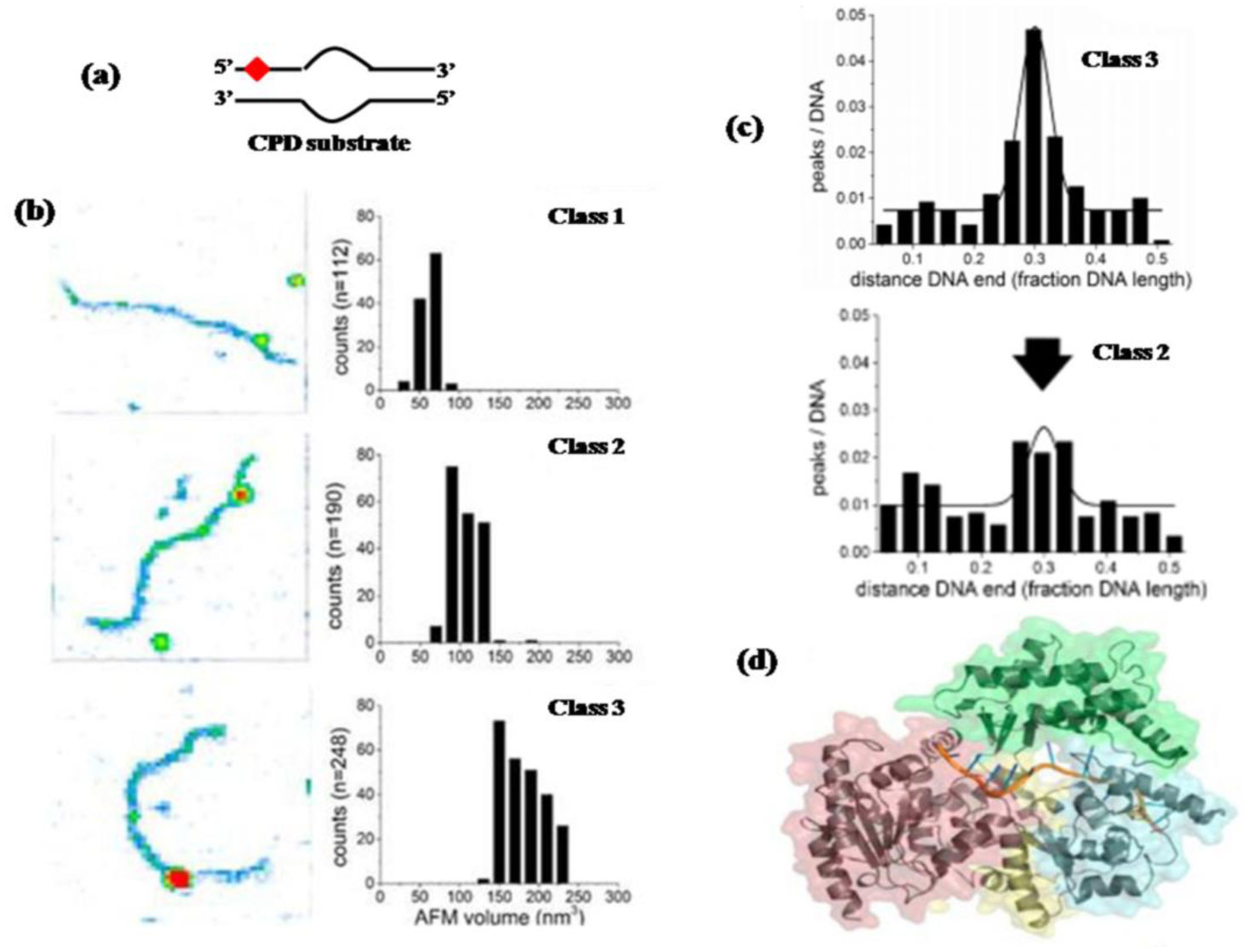
Where h is the height of the complex, d is its diameter. These volumes can be calibrated using a range of proteins with known molecular mass [92,93,94,95]. From the measured volumes, approximate molecular weights of the protein molecules and protein complexes in the images can thus be calculated, which provide information on their oligomeric state or stoichiometry. This approach has been applied to a range of protein samples [6,93,94,95,96], as well as proteins complexed with DNA [83,95,97]. For instance, in our own laboratory we applied AFM volume analysis to complexes of the eukaryotic NER helicase xeroderma pigmentosum group D protein (XPD) bound to DNA. The DNA substrates in these studies contained a cyclobutane pyrimidine dimer (CPD), a prominent UV lesion that is repaired by the NER system [83], at a well-defined position (at 30% of the DNA fragment length). In humans, NER is the only DNA repair pathway that targets UV lesions in DNA. Dysfunctional NER hence leads to severe diseases such as Xeroderma pigmentosum (XP) that involve UV hypersensitivity and a high predisposition for cancer development. The 5′ to 3′ helicase activity of XPD requires activation by the protein co-factor p44. Volume analysis was able to distinguish between DNA bound XPD and XPD/p44 complexes and thus confirm that CPD lesion recognition by XPD requires interaction with and helicase activation by p44 when protein loading occurred at a short distance from the actual lesion site (Figure 7). In the protein position distributions on DNA, stalling at the lesion due to target site recognition by XPD shows as enhanced binding occurances at the lesion position (at 30% DNA length). By placing the loading site for XPD in DNA, an unpaired DNA bubble, either 3′ or 5′ to the lesion, these studies could delineate strand preferences for lesion recognition from the obtained binding specificities due to the directionality of XPD (see above). Interestingly, CPD was preferentially recognized by XPD on the non-translocated strand (Figure 7c), and even more intriguingly the strand preference depended on the type of lesion [83].
8. Structural characterization of protein-DNA complexes via bend angle measurements
Intrinsic DNA bending can play important roles in recognition and binding by a protein [38,97]. Different curvature in linear DNA deposited on an AFM substrate correlates with different distances R between the DNA fragment ends, and reflects its elasticity or flexibility. The two dimensional (2D) worm like chain (WLC) model can be used to describe DNA polymer strands characterized by their measured end-to-end distances R. WLC fits thus provide intrinsic DNA curvature and flexibility from the mean square end-to-end distances R2 of the DNA fragments (Eq 3).
| R2=4LpLc(1−2LpLc(1−e−Lc2Lp)) |
(3) |
Where Lp and Lc are the persistence length and contour length of DNA, respectively [98]. This method has been employed, for instance, in AFM investigations on effects of cytosine methylation on DNA elasticity [99]. Extended models have been employed to describe the sequence dependence of DNA curvature [100,101]. End-to-end distance measurements have also been applied to the analysis of flexibility in protein structures from AFM images, for instance of Rad50-Mre11 coiled coil structures [102].
In addition, proteins can introduce distortion, bending, or kinking in DNA. DNA bending induced by protein interactions often reflects and forms an intricate part of mechanistic functions [38,64,65,103]. Proteins can bend DNA by adopting the DNA curvature to that of the binding interface in the protein [97] or by actively pushing or pulling at different positions in the DNA backbone or bases. For example, interactions from amino acid side chains of structural elements such as a β-hairpin or an arginine finger that insert themselves into the DNA double helix can result in DNA kinks [38,104]. DNA bending can be directly measured in AFM images using manual tangent overlay, which implies laying two short lines through the DNA backbone on either side of a DNA bound protein peak and measuring the angle between them (φ) (see schematic in Figure 8). The DNA bend angle (θ) is defined as the deviation from a straight DNA backbone and is hence given by Eq 4.
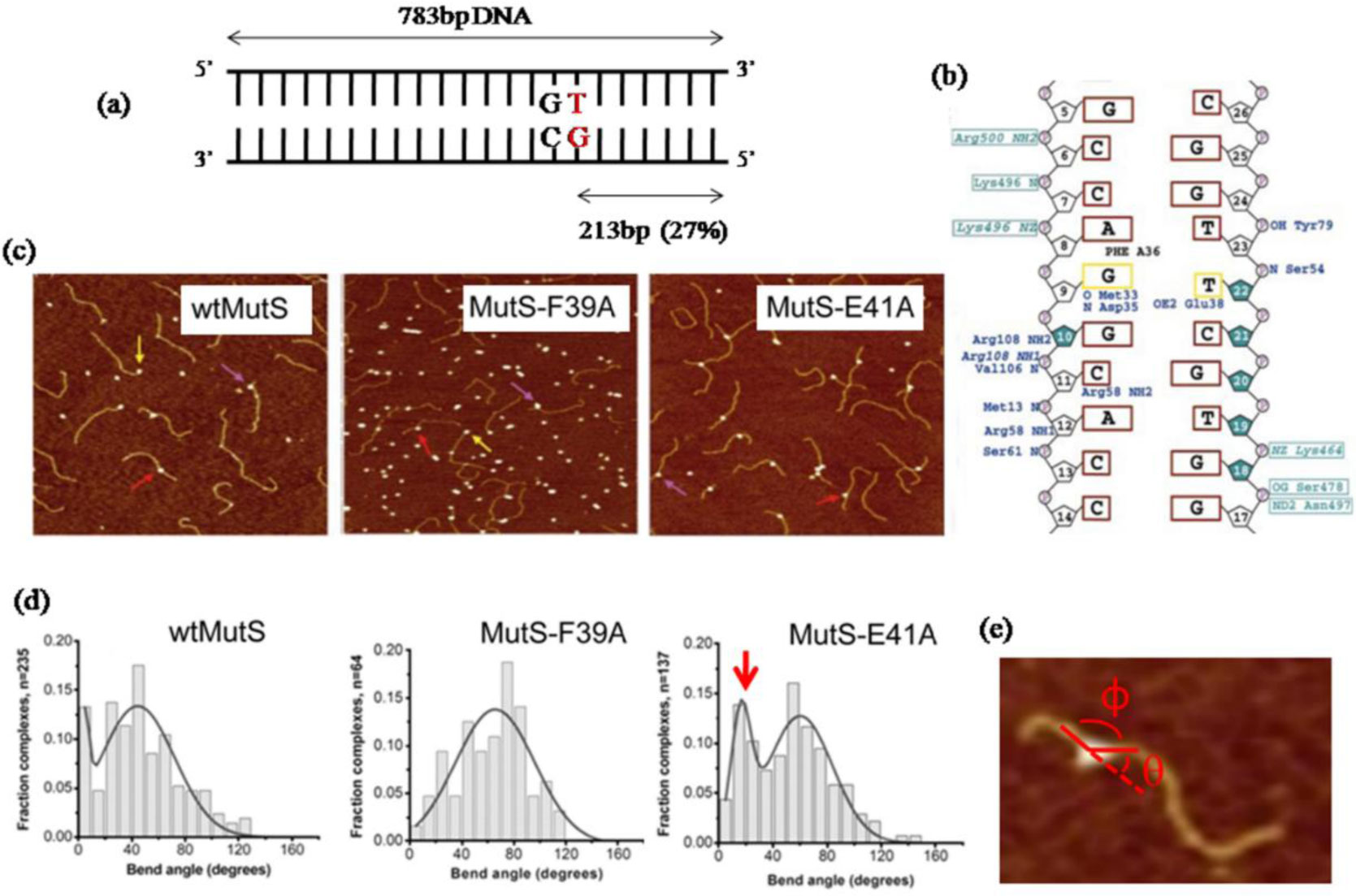
Several protein-DNA complexes have been characterized by AFM in terms of DNA bending [38,103,105,106,107]. For instance, specific recognition by the base excision repair glycosylases 8-oxoguanine DNA glycosylase (OGG1) and thymine DNA glycosylase (TDG) of their respective target lesions, 8-oxoguanine and U/T:G mismatches, was directly demonstrated and the characteristics of recognition (lesion specific) and search (non-specific) complexes were compared by AFM [38,107]. AFM studies of the DNA interactions by the DNA mismatch repair protein MutS were able to compare conformational properties of mismatch bound and non-specific complexes with DNA by measuring DNA bending at the different binding positions [103,106]. Combination of AFM with mutational studies further elucidated the mechanistic role in mismatch specific pathway initiation of two conserved amino acid residues that directly interact with the mismatch as known from crystal structures [103,108] (Figure 8). Finally, AFM experiments were carried out on RNAP molecules bound to two convergent promoters with a range of spacings integrated in a supercoiled, circular plasmid. Open promoter complexes could be identified from the bending introduced into the DNA. In combination with transcription assays, a model of transcriptional interference could thus be developed from the frequencies of open promoter complexes on the differently spaced promoters [109].
9. Future perspectives
Here, we reviewed current applications and capabilities of AFM imaging in protein-DNA interaction studies. In summary, protein induced changes in DNA structure such as DNA compaction or looping can be detected by AFM directly by visual analysis as well as quantitatively by statistical analysis, for instance of DNA contour lengths. The single molecule 3D resolution of AFM enables us to uncover stoichiometries and conformational properties in protein-DNA complexes.
To conclude, we briefly want to address future perspectives of AFM. Advances in the technique include combination with other technologies and developments towards enhanced lateral as well as time resolution. AFM integration with fluorescence microscopy is nowadays readily available in commercial AFM systems. Applications of combined super-resolution fluorescence microscopy and AFM to the study of protein-DNA interactions have been reported by several laboratories including our own [110,111,112]. These studies require fluorescent markers (e.g. nanoscale fluorescent polystyrene spheres) in the sample for registration of fluorescence and AFM images, careful preparation (and functionalization) of the mica substrate, and specific site labeling of the proteins with (organic) fluorophores. Although somewhat labor intensive, this approach has returned localization accuracies in the order of 10 nm for fluorescent signals within nucleoprotein complexes [110,112]. In the resulting hybrid images, the fluorescence signals serve to locate and identify specific, fluorescently labeled proteins within heteromeric assemblies, allowing the specific identification of proteins and quantification of complex stoichiometries.
Enhancement of AFM lateral resolution can reveal greater detail in protein molecules and protein-DNA complexes. AFM image resolution is limited by the finite size of the imaging probe, the AFM tip. Commercially available tips typically have end radii of 1-10 nm. It is possible to further improve the sharpness of the AFM tip, by chemical etching or by modifying them with atoms or small organic molecules that then serve as the imaging probe, producing sub-nanometer resolution [113,114,115,116]. Furthermore, labeling the AFM tip with a ligand molecule that interacts with protein molecules on the surface allows for the specific identification of the binding partner in heteromeric assemblies on the substrate surface. This approach is referred to as simultaneous topography and recognition (TREC) imaging AFM and recent developments in this field have been reviewed elsewhere (e.g. [116]). Furthermore, enhanced image resolution has been achieved using more complex detection schemes, such as frequency modulation or multifrequency force microscopy [117,118]. Recently, Wang and Erie and colleagues presented multifrequency imaging with conductive AFM tips that were able to resolve the path of DNA within protein complexes based on different electrostatic properties [119].
Advanced time resolutions in AFM imaging have been enabled by the development of high speed AFM (HS-AFM) [58,59]. Currently, this technology offers time resolutions in the order of one second to sub-second, and has been applied to the study of various protein-DNA systems [76,77]. Typically, these studies also exploit another recent nanotechnological development, DNA origami. DNA tethers are anchored into DNA origami frames to slightly lift the DNA off the substrate surface and thus enable easier translocation along the DNA by proteins as the protein-DNA system is scanned by the AFM tip. Recently, HS-AFM with high time resolution (approximately 1 s) at simultaneously reasonable spatial resolution (approximately 5 nm) has been applied to characterize nucleoprotein filaments of RecA at molecular resolution and to distinguish different DNA translocation modes during homology search on DNA [77]. High speed AFM technology is based on advancements in AFM cantilever fabrication leading to smaller cantilevers with higher resonant frequencies that in turn allow for faster scan speeds. Currently, the smallest AFM cantilevers produced are only 90 nm thick and 7 µm long. Ultimately, theoretical limits in AFM time resolution result from limitations in piezo scanners and AFM cantilevers and promise maximum time resolutions of down to 6 ms in the future [59].
These developments further have improved and still further advance AFM as a versatile and powerful tool for the investigation of protein-DNA interactions.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: