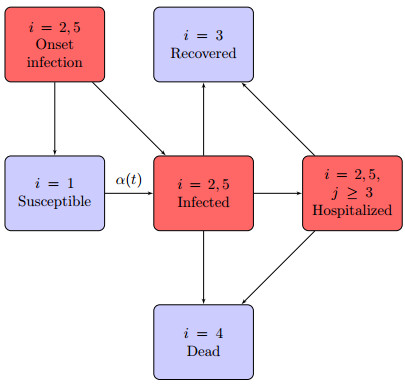
Transfer diagram of the model. Boxes represent functional subsystems and arrows indicate transition of individuals
.This paper focuses on the multiscale modeling of the COVID-19 pandemic and presents further developments of the model [
Citation: Nicola Bellomo, Diletta Burini, Nisrine Outada. Multiscale models of Covid-19 with mutations and variants[J]. Networks and Heterogeneous Media, 2022, 17(3): 293-310. doi: 10.3934/nhm.2022008
| [1] | Nicola Bellomo, Francesca Colasuonno, Damián Knopoff, Juan Soler . From a systems theory of sociology to modeling the onset and evolution of criminality. Networks and Heterogeneous Media, 2015, 10(3): 421-441. doi: 10.3934/nhm.2015.10.421 |
| [2] | Nicola Bellomo, Raluca Eftimie, Guido Forni . What is the in-host dynamics of the SARS-CoV-2 virus? A challenge within a multiscale vision of living systems. Networks and Heterogeneous Media, 2024, 19(2): 655-681. doi: 10.3934/nhm.2024029 |
| [3] | Pierre-Emmanuel Jabin . Small populations corrections for selection-mutation models. Networks and Heterogeneous Media, 2012, 7(4): 805-836. doi: 10.3934/nhm.2012.7.805 |
| [4] | Xiaoqian Gong, Benedetto Piccoli . A measure model for the spread of viral infections with mutations. Networks and Heterogeneous Media, 2022, 17(3): 427-442. doi: 10.3934/nhm.2022015 |
| [5] | Pierre Degond, Gadi Fibich, Benedetto Piccoli, Eitan Tadmor . Special issue on modeling and control in social dynamics. Networks and Heterogeneous Media, 2015, 10(3): i-ii. doi: 10.3934/nhm.2015.10.3i |
| [6] | Xavier Blanc, Claude Le Bris, Frédéric Legoll, Tony Lelièvre . Beyond multiscale and multiphysics: Multimaths for model coupling. Networks and Heterogeneous Media, 2010, 5(3): 423-460. doi: 10.3934/nhm.2010.5.423 |
| [7] | Qi Luo, Ryan Weightman, Sean T. McQuade, Mateo Díaz, Emmanuel Trélat, William Barbour, Dan Work, Samitha Samaranayake, Benedetto Piccoli . Optimization of vaccination for COVID-19 in the midst of a pandemic. Networks and Heterogeneous Media, 2022, 17(3): 443-466. doi: 10.3934/nhm.2022016 |
| [8] | Henri Berestycki, Jean-Pierre Nadal, Nancy Rodíguez . A model of riots dynamics: Shocks, diffusion and thresholds. Networks and Heterogeneous Media, 2015, 10(3): 443-475. doi: 10.3934/nhm.2015.10.443 |
| [9] | Fabio Camilli, Italo Capuzzo Dolcetta, Maurizio Falcone . Preface. Networks and Heterogeneous Media, 2012, 7(2): i-ii. doi: 10.3934/nhm.2012.7.2i |
| [10] | Giulia Bertaglia, Liu Liu, Lorenzo Pareschi, Xueyu Zhu . Bi-fidelity stochastic collocation methods for epidemic transport models with uncertainties. Networks and Heterogeneous Media, 2022, 17(3): 401-425. doi: 10.3934/nhm.2022013 |
This paper focuses on the multiscale modeling of the COVID-19 pandemic and presents further developments of the model [
The onset of SARS–CoV–2, responsible for the initial COVID-19 outbreak, has generated a subsequent pandemic all over the globe and societies. A multiscale modeling approach has been developed in [7] that involves many disciplines. In addition to applied mathematicians, also immunologists, economists and virologists contribute to the new approach. We refer to [26] which, in addition to a detailed description of the biology of the virus dynamics, provides useful indications on the world spread of a pandemic which has induced huge problems affecting not only health and well being in general, but also complex economical problems and has modified collective behaviors and social life. A concise quotation extracted from [7] summarizes the aforementioned concepts:
SARS–CoV–2 is mainly transmitted via respiratory droplets that an infected person expels. If the viral charge is high, the carrier is more infective. The large spike protein forms a sort of crown on the surface of the viral particles and acts as an anchor allowing the virus to bind to the Angiotensin-Converting Enzyme 2 (ACE2) receptors on the host cell. After binding, the host cell transmembrane proteases cut the Spike proteins, allowing the virus surface to approach the cell membrane, fuse with it and the viral RNA enter the cell. The virus hijacks the cell machinery and the cell dies releasing millions of new viruses thus generating a virus infection.
The interested reader is referred to [1,38,44,49] for the origin and mutations of the virus and to [46] for the RNA virus evolution. Modifications of the so-called SIR models [33], for instance SEIR models, have been proposed to consider the specificity of COVID-19 [31]. An interesting alternative is developed in [27] based on individual-based Markov models. Space propagation on networks of nodes have been developed in [14], where the dynamics within each node are modeled by SEIR structures, while transport dynamics are modeled with a kinetic theory approach. The general framework is the multiscale systems approach proposed in [7].
Various aspects of the immune competition are treated in [40,49], a topic somehow related to the search for vaccines [16,29,45]. Additional topics on the biology of the virus are reported in [17,21,36,41,47]. Various aspects of contagion dynamics have been studied in [30]. In addition, the impact on the economy of nations is treated in various research contributions, e.g. [3,5,23,24,32]. These citations do not claim to be exhaustive. Indeed, the research activity in the field keeps growing, motivated by the impact that the virus spread is exerting on our society and a huge flow of new results reaches daily the literature in the field.
A key indication from the literature in biology, is that infectivity is not a constant parameter, but it depends on the viral charge. In addition, it is necessary to account for the dynamics of the in-host immune competition which develops as the presence of virus particles releases danger signals which activate the reaction of the host's innate immunity. Coronaviruses are successful at suppressing various mechanisms, but not all of them, in the immune response.
Accordingly, the modeling approach should refer to general issues of the immune response [42], specifically, of the activation of the system from the innate to the activated immunity [18,20]. Pioneering contributions on the mathematical modeling of the immune competition are known in the literature, for instance [11] on the interaction of immune and tumor cells, while [22] specifically focuses on virus epidemics in the presence of mutations and selection.
Recently published articles have shown a rapidly growing interest towards a systems approach to social dynamics and behavioral economy, where the mathematical sciences are charged with capturing the complex features of these systems under the influence of individual and collective human behaviors. The objective of our paper specifically focuses on this topic by further developing the model [7] with the aim of depicting, firstly how relaxations of the confinement rules can generate sequential waves, and subsequently of describing how this specific action can modify the dynamics of the pandemics. These objectives can show how mathematics may provide to crisis managers simulations describing the possible scenarios generated by mathematical models and how external actions modify them thus contributing to planning strategy of the aforementioned actions.
We do not naively claim that mathematics can solve problems of epidemiology and virology as we are aware that the modeling approach cannot be developed by standalone mathematicians, an interdisciplinary approach is necessary as shown in [7]. Bearing all above in mind a detailed description of the contents of our paper is given in the following.
Section 2 presents the derivation of a multiscale mathematical model which describes the onset and diffusion of a COVID-19 epidemic as a natural development of the model proposed in [7]. The new model includes a detailed description of the confinement strategy on the epidemic dynamics and considers mutations into new variants. A multiscale approach is developed to model these dynamics which is followed by a in-host competition between virus and immune cells.
Section 3 presents first a set of simulations which aims at describing the scenarios of onset of the virus diffusion and of the subsequent waves related to locking and de-locking dynamics modeled by the parameters
Section 4 presents a second set of simulations which includes the dynamics of mutations and Darwinist selection. The objective consists in studying how this dynamic modifies the progression of the pathology with respect to that delivered in Section 3.
Section 5 develops a critical analysis on the use of simulations and related interpretation as a support to crisis managing and, out of this analysis, looks ahead to research perspectives.
A new class of mathematical models is derived in this section within the framework of the rationale proposed in [7]. Accordingly, we go beyond the approach of deterministic population dynamics by considering various aspects of the heterogeneity of individuals and of their reaction to the infection. The modeling is developed by a multiscale approach which refers both to dynamics of contagion and to the in-host competition between virus particles and the immune system. The two scales constantly interact, as the contagion at the macro scale depends of the viral load of each individual which in turn depends on the dynamics at the micro-scale. After contagion, the in-host dynamics include the immune competition within each individual.
We consider also a detailed description of confinement rules, as well as virus mutations and selection up to new variants. The contents are presented through a sequence of subsections focused on a phenomenological description of the biological system and its mathematical representation, derivation of a general mathematical structure suitable to capture the main features of the system, followed by derivation of models by implementing into said structure the mathematical description of multiscale interactions. The modeling is grounded on mathematical tools of the so-called kinetic theory of active particles [8] which provides mathematical structures suitable to model systems of interacting living entities. Applications of kinetic theory methods to living systems are critically analyzed in [2], where the main focus refers to dynamics far from equilibrium.
The following qualitative description of the biological dynamics is proposed to be transferred into mathematical models.
1.
2.
3.
4.
5.
We consider a population of
| u={uj=j−1m−1}andw={wk=k−1m−1},withj,k=1,…,m, |
where the same number of nodes has been selected for both dynamics.
Remark 2.1. If birth events are not considered, the normalization, with respect to
| m∑k=1f1,k1(t)+m∑k=1m−1∑j=2fj,k2(t)+f3(t)+f4(t)+m∑k=1m−1∑j=2fj,k5(t)=1. | (1) |
Remark 2.2. It is useful introducing the density of each FS defined as the number of individuals denoted, for each
| n1(t)=m∑k=1f1,k1(t),n2(t)=m∑k=1m−1∑j=2fj,k2(t),n5(t)=m∑k=1m−1∑j=2fj,k5(t), | (2) |
while
The dynamics of transition across FSs is shown in the flow chart of Fig. 1, where each block identifies the specific FS.
Let us now transfer the aforementioned qualitative assumptions into a differential system according to detailed assumptions on the interactions involving a-particles of all FSs. Interactions modify the internal activity variables and, in addition, promote transition across FSs.
The kinetic theory of active particle with discrete states provides mathematical tools to model the dynamics of the dependent variables
The formal structure that provides the conceptual framework to derive models that can be obtained by the superposition of kinetic type model, where the interaction rate and the transition probability determine the dynamics of the dependent variable, and a source term modeling transition across FSs and external actions, for instance vaccines:
| ∂tfj,ki=Gj,ki[f]−Lj,ki[f]+Sj,ki[f], | (3) |
where
The kinetic theory of active particles provides the following expressions gain and loss terms:
| Gj,ki[f]=5∑y,z=1m∑r,s=1m∑p,q=1ηqspr(y,z)Aqszpry(y→i,pr→jk)fp,ryfq,sz, | (4) |
and
| Lj,ki[f]=fj,ki5∑z=1m∑s=1m∑q=1ηqsjk(i,z)fq,sz, | (5) |
while the modeling of the source term
1.
2.
3.
4.
5.
The description in Items 1–5 can be transferred into a mathematical framework by a detailed modeling of interactions which inserted them into the general structure (3) leading to models of virus dynamics. In more details, we consider the following models of interactions:
| ∂tf1,k1(t)=−Lk1[f](t)=−m∑s=1m−1∑j=2αujf1,k1(t)fj,s2(t), | (6) |
for
The dynamics refers to
| ∂tfj,k2(t)=Gj,k2[f](t)−Lj,k2[f](t). | (7) |
Two positive defined parameters
| Gj,k2[f](t)=δ2jLk1[f](t)+βuj−1fj−1,k2(t)+γkwkfj+1,k2(t), | (8) |
and
| Lj,k2[f](t)=βujfj,k2(t)+γkwkfj,k2(t) | (9) |
for
| fj,k5=fj,k5(t)β5=β(1+λ), |
where
| ∂tf3(t)=m∑k=1wkγkf2,k2(t)+m∑k=1wkγkf2,k5(t). | (10) |
| nj2(t)=m∑k=1fj,k2(t)andnj5(t)=m∑k=1fj,k5(t), |
for high values of the level of progression of the virus, i.e. increasing values of
| ∂tf4(t)=βum−1m∑k=1fm−1,k2(t)+β(1+λ)um−1m∑k=1fm−1,k5(t). | (11) |
Collecting all equations into a differential system yields:
| {∂tf1,k1(t)=−α(t)m∑s=1m−1∑j=2ujf1,k1(t)fj,s2(t)−α(t)m∑s=1m−1∑j=2ujf1,k1(t)fj,s5(t),∂tfj,k2(t)=α(t)m∑s=1m−1∑r=2urf1,k1(t)fr,s2(t)δ2j+βuj−1fj−1,k2(t)+γkwkfj+1,k2(t)−βujfj,k2(t)−γkwkfj,k2(t),∂tf3(t)=∂tn3=m∑k=1γkwkf2,k2(t)+m∑k=1wkγkf2,k5(t),∂tf4(t)=∂tn4=βum−1m∑k=1fm−1,k2(t)+β(1+λ)um−1m∑k=1fm−1,k5(t),∂tfj,k5(t)=α(t)m∑s=1m−1∑r=2urf1,k1(t)fr,s5(t)δ2j+β(1+λ)uj−1fj−1,k5(t)+γkwkfj+1,k5(t)−β(1+λ)ujfj,k5(t)−γkwkfj,k5(t), | (12) |
where
The mathematical model (12) accounts for mutations and selection into variants, which act an important role in the spread and control of the pandemics. We are interested in understanding how these two events modify the dynamics in absence of them which is as follows:
| {∂tf1,k1(t)=−α(t)m∑s=1m−1∑j=2ujf1,k1(t)fj,s2(t),∂tfj,k2(t)=α(t)m∑s=1m−1∑r=2urf1,k1(t)fr,s2(t)δ2j+βuj−1fj−1,k2(t)+γkwkfj+1,k2(t)−βujfj,k2(t)−γkwkfj,k2(t),∂tn3(t)=m∑k=1γkwkf2,k2(t),∂tn4(t)=βum−1m∑k=1fm−1,k2(t). | (13) |
Remark 2.3. Equations
Remark 2.4. In absence of virus infection or total lack of awareness of the risk of infection, the locking parameter, which may also be called social distancing, is taken
This section presents some simulations selected with the aim of understanding how the dynamics of the epidemics develops after a locking action. We consider the dynamics in absence of mutations corresponding to model (13). In more details, we consider, for different values of the locking parameter
All simulations are developed for
| f1,k1=1−εm,f2,k2=εm,k=1,…,m,ε=0.001. | (14) |
Figure 2 studies the influence of
| α(t)=αℓ=0.1,fort∈[0,Td]andα(t)=αdfort>Td, | (15) |
while different values of
Sample simulation are reported in Figs. 4, 5 which report the dynamic of
These simulations show an emergent behavior that has been effectively observed in the real situation, namely that although a locking is applied and the virus is brought to very low levels, apparently it has disappeared, but it remains at a latent state ready to start again once the social confinement is relaxed. This emergent behavior is confirmed by the onset of subsequent waves which always appear when a de-locking action is applied. Therefore, an important indication to crisis managers is that the locking parameter can be brought to a value
This section presents a selection of simulations which aim at understanding how the dynamics of the epidemics develops in the presence of mutations. These generate the onset of variants, whose dynamic is described by model (12), that modifies the dynamics of the primary virus described by model (13). Simulations are referred to the locking strategy with the objective of showing, by quantitative results, how the more aggressive variants end up with replacing the primary virus. As in Section 3, simulations are developed for
Empirical evidence shows that mutations can generate aggressive variants that show an ability to infect greater than that of the primary virus. This general trend can be explained by the model proposed in our paper as it is based on the assumption that a virus with high proliferative ability produces a high viral charge which increases the infectivity ability. Simulations show how far the variant increases the number of infected people, as well as the death of those who do not succeed in recovering.
Simulations presented in this section do not claim that an exhaustive description has been given. Indeed, further simulations accounting for a detailed parameters sensitivity analysis should be developed. However, all simulations clearly show that the onset of a new variant, more aggressive than the primary virus, generates a progressive prevalence of the variant over the firstly appeared virus. This overcoming appears by different types of dynamics, but ultimately confirming the aforementioned trend. This is an important piece of information, as it contributes to the amount of information necessary to design strategies to fight the virus. Further reasonings follow in the critical analysis proposed in the next section.
The mathematical model proposed in this paper considers the multiscale dynamics of the virus from the infection of individuals to the within-host competition which may lead to recovery, but also to hospitalization, or even death. In more details, our model includes virus mutations that generate, by selection, new more aggressive variants and a multiscale modeling of the in-host vaccination dynamics related to strategies to mitigate the damage of pandemics [37].
Without repeating concepts already stated in the first sections, we stress that a multiscale approach is necessary to consider the aforementioned mutations and selections. Indeed, more aggressive variants of the virus exhibit higher proliferative ability which increases the infectivity properties of the virus. These dynamics are related to the fact that increasing the number of virus particles in the lung, namely the so-called viral load, makes the individual more infective when in contact with other individuals. Unfortunately, these dynamics end up with increasing the number of infected humans who need hospitalization or even die.
Comparing the present simulations to those developed for the simpler model [7], we have used a higher number of collocation nodes to account in a more precise way for the in-host dynamics and, specifically, the progression of the pathological state. Computing the number of individuals that need hospitalization is an important information to be delivered to crisis managers as in the pandemic time hospitals have been obliged to face crisis situations related to lack of space for patients affected by pathologies different from that of Covid19. Hence a higher number of internal states can refine the indications by referring the number of people who need hospitalization to their level of pathology.
The computational study has also allowed the study of emerging behaviors such as the onset of new waves and their shape depending on the parameters of the model. In addition, hospitalization dynamics can be related to different levels of progression of the pathology.
Therefore, the model appears to be able to provide a panorama of emerging behaviors which may contribute to the activity of crisis managers. The main focus of our simulations has been referring to the role of variants on the overall response of the system. In particular, the following specific features of the model, as well as of the plan of simulations, can be selected as appropriate to contribute to support crisis management:
However, we do not naively claim that the sample simulations we have presented in our paper do cover an exhaustive parameter sensitivity analysis. Simply, we have shown that the model can provide a rich description of different scenarios that might hopefully contribute to strategies that make lighter crisis situations related to the pandemics. A program to develop a systematic sensitivity analysis is in progress in order to design a database, where the broad variety of scenarios of dynamics of the complex system can be tested.
Hopefully, new studies might take advantage of the indications given above and contribute to further developing the model. The following specific modeling perspectives are selected among various possible ones:
(i) Heterogeneity referred not only to the ability of the immune defence, that can be somehow referred to age, but also to the role of individuals in society. This means accounting for both levels of contagion risk during work and of the economical impact on society.
(ii) Contagion in crowds starting from the pioneering contributions [12,34,35] towards development of models of crowd dynamics which include social awareness [4,9,43], where one of the key problem consists of modeling the contagion parameter [25]. Contagion in crowds described by a macroscopic equation derived from the underlying description delivered by kinetic theory [6].
(iii) Modeling vaccination to improve the ability of immune defence and medical actions to weaken the proliferative and invasive ability of the virus. The modeling approach should start from a knowledge of vaccine actions, for instance from [16,29,37,45] to the mathematical description of the dynamics within vaccinated individuals and viruses.
(iv) Modeling in-host space dynamics by reaction-diffusion equations [10], based on micro-macro derivation [15].
(v) Calibration of models based on empirical data referred to well defined regional areas. Indeed, empirical data have reached a sufficient level of precision and, thanks to this increase of reliability, an effective toning of SEIR appeared related to control problems [39].
Further developments of the model proposed in our paper can contribute to tackle the research perspectives that have been indicated above. These, as mentioned, represent a selection based on our personal ideas and research past experience. A common aspect of these perspectives is that a key dynamics, which is present in all of them, is the dynamics of the immune competition which has been included in our approach at a very primitive level. This topic definitely deserves further developments and improvements.
Nicola Bellomo acknowledges the support of the University of Granada, Project Modeling in Nature MNat from micro to macro. This paper has been partially supported by the Consejeria de Economia, Conocimiento, Empresas y Universidad and European Regional Development Fund (ERDF), ref. SOMM17/6109/UGR. https://www.modelingnature.org.
| [1] |
The proximal origin of SARS-CoV-2. Nature Medicine (2020) 26: 450-452. 
|
| [2] |
Biological systems as nonequilibrium structures described by kinetic methods. Results in Physics (2019) 13: 102232. 
|
| [3] |
B. Avishai, The pandemic isn't a black swan but a portent of a more fragile global system, The New Yorker, (2020), https://www.newyorker.com/news/daily-comment/the-pandemic-isnt-a-black-swan-but-a-portent-of-a-more-fragile-global-system. |
| [4] |
On a unified multiscale vision of behavioral crowds. Math. Models Methods Appl. Sci. (2020) 30: 1-22. 
|
| [5] |
P. Baldwin and B. W. Di Mauro, Economics in the Time of COVID-19, VoxEU.org Book, (2020). |
| [6] |
On multiscale models of pedestrian crowds from mesoscopic to macroscopic. Commun. Math. Sci. (2015) 13: 1649-1664. 
|
| [7] |
A multi-scale model of virus pandemic: Heterogeneous interactive entities in a globally connected world. Math. Models Methods Appl. Sci. (2020) 30: 1591-1651. 
|
| [8] |
What is life? A perspective of the mathematical kinetic theory of active particles. Math. Models Methods Appl. Sci. (2021) 31: 1821-1866. 
|
| [9] |
On the interplay between behavioral dynamics and social interactions in human crowds. Kinet. Relat. Models (2019) 12: 397-409. 
|
| [10] |
Occurrence vs. absence of txis-driven instabilities in a May–Nowak Model for virus infection. SIAM J. Appl. Math. (2019) 79: 1990-2010. 
|
| [11] |
A. Bellouquid and M. Delitala, Modelling Complex Biological Systems - A Kinetic Theory Approach, Modeling and Simulation in Science, Engineering and Technology. Birkhäuser Boston, Inc., Boston, MA, 2006. |
| [12] |
Contagion shocks in one dimension. J. Stat. Phys. (2015) 158: 647-664. 
|
| [13] |
RNA virus evolution via a quasispecies-based model reveals a drug target with a high barrier to resistance. Viruses (2017) 9: 347. 
|
| [14] |
Modeling and simulating the spatial spread of an epidemic through multiscale kinetic transport equations. Math. Models Methods Appl. Sci. (2021) 31: 1059-1097. 
|
| [15] |
A Multiscale view of nonlinear diffusion in biology: From cells to tissues. Math. Models Methods Appl. Sci. (2019) 29: 791-823. 
|
| [16] |
Coronavirus vaccines: Five key questions as trials begin. Nature (2021) 592: 670-671. 
|
| [17] |
M. Cecconi, G. Forni and A. Mantovani, COVID-19: An executive report April 2020 update, Accademia Nazionale dei Lincei, Commissione Salute, (2020), https://www.lincei.it/sites/default/files/documenti/Commissioni. |
| [18] |
M. Cecconi, G. Forni and A. Mantovani, COVID-19: An executive report Summer 2020 update, Accademia Nazionale dei Lincei, Commissione Salute, (2002), https://www.lincei.it/sites/default/files/documenti/Commissioni. |
| [19] |
Ten things we learned about COVID-19. Intensive Care Medicine (2020) 46: 1590-1593. 
|
| [20] |
Evolution of immune system from self/not self to danger to artificial immune system. Physics of Life Review (2010) 7: 55-78. 
|
| [21] |
Profile of a killer: The complex biology powering the coronavirus pandemic. Nature (2020) 22-26. 
|
| [22] |
Modelling epidemics and virus mutations by methods of the mathematical kinetic theory for active particles. Math. Models Methods Appl. Sci. (2009) 19: 1405-1425. 
|
| [23] |
G. Dimarco, L. Pareschi and G. Toscani, et al., Wealth distribution under the spread of infectious diseases, Phys. Rev. E, 102 (2020), Article 022303, 14 pp. |
| [24] |
Unequal societies in usual times, unjust societies in pandemic ones. Journal of Industrial and Business Economics (2020) 47: 371-389. 
|
| [25] |
Estimating density limits for walking pedestrians keeping a safe interpersonal distancing. Scientific Reports (2021) 11: 1534. 
|
| [26] |
COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep. (2020) 869: 1-51. 
|
| [27] |
Individual-based Markov model of virus diffusion: Comparison with COVID-19 incubation period, serial interval and regional time series. Math. Models Methods Appl. Sci. (2021) 31: 907-939. 
|
| [28] |
J. F. Fontanari, A stochastic model for the influence of social distancing on loneliness, Phys. A, 584 (2021), Paper No. 126367, 10 pp. |
| [29] |
COVID-19 vaccines: Where we stand and challenges ahead. Cell Death & Differentiation (2021) 28: 626-639. 
|
| [30] |
Transmission dynamics and quarantine control of COVID-19 in cluster community: A new transmission-quarantine model with case study for diamond princess. Math. Models Methods Appl. Sci. (2021) 31: 619-648. 
|
| [31] |
Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proceedings of the National Academy of Sciences (2020) 117: 10484-10491. 
|
| [32] |
The paradox of productivity during quarantine: An agent-based simulation. European Physical Journal B (2021) 94: 40. 
|
| [33] |
The mathematics of infectious diseases. SIAM Rev. (2000) 42: 599-653. 
|
| [34] |
A kinetic theory approach to model pedestrian dynamics in bounded domains with obstacles. Kinet. Relat. Models (2019) 12: 1273-1296. 
|
| [35] |
Coupling kinetic theory approaches for pedestrian dynamics and disease contagion in a confined environment. Math. Models Methods Appl. Sci. (2020) 30: 1893-1915. 
|
| [36] |
Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science (2020) 368: 860-868. 
|
| [37] |
W. Lee, S. Liu, W. Li and S. Osher, Mean field control problems for vaccine distribution, arXiv preprint, arXiv: 2104.11887, (2021). |
| [38] |
No evidence for distinct types in the evolution of SARS-CoV-2. Virus Evolution (2020) 6:. 
|
| [39] |
Control of COVID-19 outbreack using an extended SEIR model. Math. Models Methods Appl. Sci. (2021) 31: 2399-2424. 
|
| [40] |
The first, holistic immunological model of COVID-19: Implications for prevention, diagnosis, and public health measures. Pediatric Allergy Imunology (2020) 31: 454-470. 
|
| [41] |
Cytokine release syndrome in severe COVID-19. Science (2020) 368: 473-474. 
|
| [42] |
P. Musiani, and G. Forni, Basic Immunology, Piccin, Padua, 2018. |
| [43] |
Disease contagion models coupled to crowd motion and mesh-free simulation. Math. Models Methods Appl. Sci. (2021) 31: 1277-1295. 
|
| [44] | Mechanisms of viral mutation. Cellular and Molecular Life Sciences (2016) 73: 4433-4448. |
| [45] | Preliminary identification of potential vaccine targets for the COVID-19 coronavirus (SARS-CoV-2) based on SARS-CoV immunological studies. Viruses (2020) 12: 254. |
| [46] |
A modelling paradigm for RNA virus assembly. Current Opinion in Virology (2018) 31: 74-81. 
|
| [47] |
Hamiltonian path analysis of viral genomes. Nature Communications (2018) 9:. 
|
| [48] |
Immunology of COVID-19: Current state of the science. Immunity 2020 (2020) 52: 910-941. 
|
| [49] |
Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV. N. Engl. J. Med. (2020) 382: 1564-1567. 
|
| 1. | A.M. Elaiw, A.J. Alsaedi, A.D. Hobiny, S. Aly, Stability of a delayed SARS-CoV-2 reactivation model with logistic growth and adaptive immune response, 2023, 616, 03784371, 128604, 10.1016/j.physa.2023.128604 | |
| 2. | D. Burini, N. Chouhad, Virus models in complex frameworks: Towards modeling space patterns of SARS-CoV-2 epidemics, 2022, 32, 0218-2025, 2017, 10.1142/S0218202522500476 | |
| 3. | N. Bellomo, F. Brezzi, M. A. J. Chaplain, New trends of mathematical sciences towards modeling virus pandemics in a globally connected world, 2022, 32, 0218-2025, 1923, 10.1142/S0218202522010011 | |
| 4. | A. M. Elaiw, A. S. Shflot, A. D. Hobiny, Stability analysis of SARS-CoV-2/HTLV-I coinfection dynamics model, 2022, 8, 2473-6988, 6136, 10.3934/math.2023310 | |
| 5. | A. M. Elaiw, N. H. AlShamrani, E. Dahy, A. A. Abdellatif, Aeshah A. Raezah, Effect of Macrophages and Latent Reservoirs on the Dynamics of HTLV-I and HIV-1 Coinfection, 2023, 11, 2227-7390, 592, 10.3390/math11030592 | |
| 6. | Ahmed M. Elaiw, Abdullah J. Alsaedi, Afnan Diyab Al Agha, Aatef D. Hobiny, Global Stability of a Humoral Immunity COVID-19 Model with Logistic Growth and Delays, 2022, 10, 2227-7390, 1857, 10.3390/math10111857 | |
| 7. | Giulia Bertaglia, Chuan Lu, Lorenzo Pareschi, Xueyu Zhu, Asymptotic-Preserving Neural Networks for multiscale hyperbolic models of epidemic spread, 2022, 32, 0218-2025, 1949, 10.1142/S0218202522500452 | |
| 8. | Ahmed M. Elaiw, Raghad S. Alsulami, Aatef D. Hobiny, Modeling and Stability Analysis of Within-Host IAV/SARS-CoV-2 Coinfection with Antibody Immunity, 2022, 10, 2227-7390, 4382, 10.3390/math10224382 | |
| 9. | Ryan Weightman, Anthony Sbarra, Benedetto Piccoli, Coupling compartmental models with Markov chains and measure evolution equations to capture virus mutability, 2022, 32, 0218-2025, 2099, 10.1142/S0218202522500506 | |
| 10. | Jiying Ma, Shasha Ma, Dynamics of a stochastic hepatitis B virus transmission model with media coverage and a case study of China, 2022, 20, 1551-0018, 3070, 10.3934/mbe.2023145 | |
| 11. | Marcelo Bongarti, Luke Diego Galvan, Lawford Hatcher, Michael R. Lindstrom, Christian Parkinson, Chuntian Wang, Andrea L. Bertozzi, Alternative SIAR models for infectious diseases and applications in the study of non-compliance, 2022, 32, 0218-2025, 1987, 10.1142/S0218202522500464 | |
| 12. | N. Bellomo, M. Esfahanian, V. Secchini, P. Terna, What is life? Active particles tools towards behavioral dynamics in social-biology and economics, 2022, 43, 15710645, 189, 10.1016/j.plrev.2022.10.001 | |
| 13. | Ahmed M. Elaiw, Abdulsalam S. Shflot, Aatef D. Hobiny, Global Stability of Delayed SARS-CoV-2 and HTLV-I Coinfection Models within a Host, 2022, 10, 2227-7390, 4756, 10.3390/math10244756 | |
| 14. | Henrique A. Tórtura, José F. Fontanari, The synergy between two threats: Disinformation and COVID-19, 2022, 32, 0218-2025, 2077, 10.1142/S021820252250049X | |
| 15. | Juan Pablo Agnelli, Bruno Buffa, Damián Knopoff, Germán Torres, A Spatial Kinetic Model of Crowd Evacuation Dynamics with Infectious Disease Contagion, 2023, 85, 0092-8240, 10.1007/s11538-023-01127-6 | |
| 16. | A.M. Elaiw, A.J. Alsaedi, A.D. Hobiny, Global stability of a delayed SARS-CoV-2 reactivation model with logistic growth, antibody immunity and general incidence rate, 2022, 61, 11100168, 12475, 10.1016/j.aej.2022.05.034 | |
| 17. | A. D. Al Agha, A. M. Elaiw, Global dynamics of SARS-CoV-2/malaria model with antibody immune response, 2022, 19, 1551-0018, 8380, 10.3934/mbe.2022390 | |
| 18. | Diletta Burini, Nadia Chouhad, Nicola Bellomo, Waiting for a Mathematical Theory of Living Systems from a Critical Review to Research Perspectives, 2023, 15, 2073-8994, 351, 10.3390/sym15020351 | |
| 19. | Ahmed M. Elaiw, Afnan D. Al Agha, Global Stability of a Reaction–Diffusion Malaria/COVID-19 Coinfection Dynamics Model, 2022, 10, 2227-7390, 4390, 10.3390/math10224390 | |
| 20. | A. M. Elaiw, Raghad S. Alsulami, A. D. Hobiny, Global dynamics of IAV/SARS-CoV-2 coinfection model with eclipse phase and antibody immunity, 2022, 20, 1551-0018, 3873, 10.3934/mbe.2023182 | |
| 21. | Ali Algarni, Afnan D. Al Agha, Aisha Fayomi, Hakim Al Garalleh, Kinetics of a Reaction-Diffusion Mtb/SARS-CoV-2 Coinfection Model with Immunity, 2023, 11, 2227-7390, 1715, 10.3390/math11071715 | |
| 22. | Matthew O. Adewole, Farah A. Abdullah, Majid K. M. Ali, 2024, 3203, 0094-243X, 030007, 10.1063/5.0225272 | |
| 23. | Elsayed Dahy, Ahmed M. Elaiw, Aeshah A. Raezah, Hamdy Z. Zidan, Abd Elsattar A. Abdellatif, Global Properties of Cytokine-Enhanced HIV-1 Dynamics Model with Adaptive Immunity and Distributed Delays, 2023, 11, 2079-3197, 217, 10.3390/computation11110217 | |
| 24. | Nicola Bellomo, Jie Liao, Annalisa Quaini, Lucia Russo, Constantinos Siettos, Human behavioral crowds review, critical analysis and research perspectives, 2023, 33, 0218-2025, 1611, 10.1142/S0218202523500379 | |
| 25. | Diletta Burini, Damian A. Knopoff, Epidemics and society — A multiscale vision from the small world to the globally interconnected world, 2024, 34, 0218-2025, 1567, 10.1142/S0218202524500295 | |
| 26. | Ahmed M. Elaiw, Aeshah A. Raezah, Matuka A. Alshaikh, Global Dynamics of Viral Infection with Two Distinct Populations of Antibodies, 2023, 11, 2227-7390, 3138, 10.3390/math11143138 | |
| 27. | Nicola Bellomo, Massimo Egidi, From Herbert A. Simon’s legacy to the evolutionary artificial world with heterogeneous collective behaviors, 2024, 34, 0218-2025, 145, 10.1142/S0218202524400049 | |
| 28. | Ryan Weightman, Benedetto Piccoli, 2024, Chapter 7, 978-3-031-56793-3, 157, 10.1007/978-3-031-56794-0_7 | |
| 29. | Luca Serena, 2023, Methodological Aspects of Multilevel Modeling and Simulation, 979-8-3503-3784-6, 111, 10.1109/DS-RT58998.2023.00025 | |
| 30. | Aeshah A. Raezah, A.M. Elaiw, M.A. Alshaikh, Global stability of secondary DENV infection models with non-specific and strain-specific CTLs, 2024, 10, 24058440, e25391, 10.1016/j.heliyon.2024.e25391 | |
| 31. | Nicola Bellomo, Raluca Eftimie, Guido Forni, What is the in-host dynamics of the SARS-CoV-2 virus? A challenge within a multiscale vision of living systems, 2024, 19, 1556-1801, 655, 10.3934/nhm.2024029 | |
| 32. | A. M. Elaiw, E. A. Almohaimeed, A. D. Hobiny, Stability of HHV-8 and HIV-1 co-infection model with latent reservoirs and multiple distributed delays, 2024, 9, 2473-6988, 19195, 10.3934/math.2024936 | |
| 33. | Yunfeng Xiong, Chuntian Wang, Yuan Zhang, Tom Britton, Interacting particle models on the impact of spatially heterogeneous human behavioral factors on dynamics of infectious diseases, 2024, 20, 1553-7358, e1012345, 10.1371/journal.pcbi.1012345 | |
| 34. | Ahmed M. Elaiw, Ghadeer S. Alsaadi, Aatef D. Hobiny, Global co-dynamics of viral infections with saturated incidence, 2024, 9, 2473-6988, 13770, 10.3934/math.2024671 | |
| 35. | Matthew O. Adewole, Taye Samuel Faniran, Farah A. Abdullah, Majid K.M. Ali, COVID-19 dynamics and immune response: Linking within-host and between-host dynamics, 2023, 173, 09600779, 113722, 10.1016/j.chaos.2023.113722 | |
| 36. | Giulia Bertaglia, Andrea Bondesan, Diletta Burini, Raluca Eftimie, Lorenzo Pareschi, Giuseppe Toscani, New trends on the systems approach to modeling SARS-CoV-2 pandemics in a globally connected planet, 2024, 34, 0218-2025, 1995, 10.1142/S0218202524500301 | |
| 37. | Nicola Bellomo, Seung-Yeal Ha, Jie Liao, Wook Yoon, Behavioral swarms: A mathematical theory toward swarm intelligence, 2024, 34, 0218-2025, 2305, 10.1142/S0218202524500490 | |
| 38. | Mohamed Zagour, 2024, Chapter 6, 978-3-031-56793-3, 127, 10.1007/978-3-031-56794-0_6 | |
| 39. | Nisrine Outada, A forward look to perspectives, 2023, 47, 15710645, 133, 10.1016/j.plrev.2023.10.011 | |
| 40. | Luca Serena, Moreno Marzolla, Gabriele D’Angelo, Stefano Ferretti, A review of multilevel modeling and simulation for human mobility and behavior, 2023, 127, 1569190X, 102780, 10.1016/j.simpat.2023.102780 | |
| 41. | Christian Parkinson, Weinan Wang, Analysis of a Reaction-Diffusion SIR Epidemic Model with Noncompliant Behavior, 2023, 83, 0036-1399, 1969, 10.1137/23M1556691 | |
| 42. | D. Burini, N. Chouhad, Cross-diffusion models in complex frameworks from microscopic to macroscopic, 2023, 33, 0218-2025, 1909, 10.1142/S0218202523500458 | |
| 43. | Ahmed M. Elaiw, Raghad S. Alsulami, Aatef D. Hobiny, Global properties of SARS‐CoV‐2 and IAV coinfection model with distributed‐time delays and humoral immunity, 2024, 47, 0170-4214, 9340, 10.1002/mma.10074 | |
| 44. | B. Bellomo, M. Esfahanian, V. Secchini, P. Terna, From a mathematical science of living systems to biology and economics, 2023, 47, 15710645, 264, 10.1016/j.plrev.2023.11.002 | |
| 45. | Ahmed M. Elaiw, Amani S. Alsulami, Aatef D. Hobiny, Global properties of delayed models for SARS-CoV-2 infection mediated by ACE2 receptor with humoral immunity, 2024, 9, 2473-6988, 1046, 10.3934/math.2024052 | |
| 46. | Bishal Chhetri, Krishna Kiran Vamsi Dasu, Stability and bifurcation analysis of a nested multi-scale model for COVID-19 viral infection, 2024, 12, 2544-7297, 10.1515/cmb-2024-0006 | |
| 47. | Vinicius V. L. Albani, Jorge P. Zubelli, Stochastic transmission in epidemiological models, 2024, 88, 0303-6812, 10.1007/s00285-023-02042-z | |
| 48. | Hyeong-Ohk Bae, Seung Yeon Cho, Jane Yoo, Seok-Bae Yun, Mathematical modeling of trend cycle: Fad, fashion and classic, 2024, 01672789, 134500, 10.1016/j.physd.2024.134500 | |
| 49. | Juan Pablo Agnelli, Claudio Armas, Damián A. Knopoff, Spatial Kinetic Modeling of Crowd Evacuation: Coupling Social Behavior and Infectious Disease Contagion, 2025, 17, 2073-8994, 123, 10.3390/sym17010123 | |
| 50. | Gabriel Benedetti, Ryan Weightman, Benedetto Piccoli, Optimizing overlapping non-pharmaceutical interventions with a socio-demographic model, 2025, 1972-6724, 10.1007/s40574-025-00477-4 |
Transfer diagram of the model. Boxes represent functional subsystems and arrows indicate transition of individuals
Infected population
Infected population
Infected population
Infected population
Infected population
Infected population
Infected population
Death in the case of absence of mutations:
Death in the case of mutations: