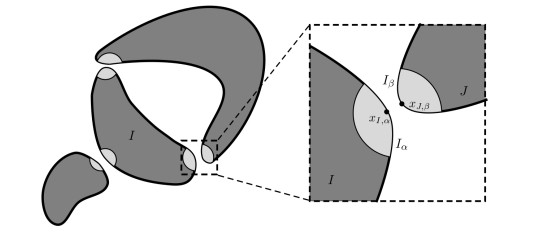
Geometry of the inclusions with a close-up on a gap
.We investigate the homogenization of inclusions of infinite conductivity, randomly stationary distributed inside a homogeneous conducting medium. A now classical result by Zhikov shows that, under a logarithmic moment bound on the minimal distance between the inclusions, an effective model with finite homogeneous conductivity exists. Relying on ideas from network approximation, we provide a relaxed criterion ensuring homogenization. Several examples not covered by the previous theory are discussed.
Citation: David Gérard-Varet, Alexandre Girodroux-Lavigne. Homogenization of stiff inclusions through network approximation[J]. Networks and Heterogeneous Media, 2022, 17(2): 163-202. doi: 10.3934/nhm.2022002
| [1] | Mohamed Belhadj, Eric Cancès, Jean-Frédéric Gerbeau, Andro Mikelić . Homogenization approach to filtration through a fibrous medium. Networks and Heterogeneous Media, 2007, 2(3): 529-550. doi: 10.3934/nhm.2007.2.529 |
| [2] | Xiangdong Du, Martin Ostoja-Starzewski . On the scaling from statistical to representative volume element in thermoelasticity of random materials. Networks and Heterogeneous Media, 2006, 1(2): 259-274. doi: 10.3934/nhm.2006.1.259 |
| [3] | Marc Briane, David Manceau . Duality results in the homogenization of two-dimensional high-contrast conductivities. Networks and Heterogeneous Media, 2008, 3(3): 509-522. doi: 10.3934/nhm.2008.3.509 |
| [4] | Mario Ohlberger, Ben Schweizer, Maik Urban, Barbara Verfürth . Mathematical analysis of transmission properties of electromagnetic meta-materials. Networks and Heterogeneous Media, 2020, 15(1): 29-56. doi: 10.3934/nhm.2020002 |
| [5] | Mohamed Camar-Eddine, Laurent Pater . Homogenization of high-contrast and non symmetric conductivities for non periodic columnar structures. Networks and Heterogeneous Media, 2013, 8(4): 913-941. doi: 10.3934/nhm.2013.8.913 |
| [6] | Paolo Luzzini, Paolo Musolino . Perturbation analysis of the effective conductivity of a periodic composite. Networks and Heterogeneous Media, 2020, 15(4): 581-603. doi: 10.3934/nhm.2020015 |
| [7] | Natalia O. Babych, Ilia V. Kamotski, Valery P. Smyshlyaev . Homogenization of spectral problems in bounded domains with doubly high contrasts. Networks and Heterogeneous Media, 2008, 3(3): 413-436. doi: 10.3934/nhm.2008.3.413 |
| [8] | Patrick Henning . Convergence of MsFEM approximations for elliptic, non-periodic homogenization problems. Networks and Heterogeneous Media, 2012, 7(3): 503-524. doi: 10.3934/nhm.2012.7.503 |
| [9] | Giovanni Scilla . Motion of discrete interfaces in low-contrast periodic media. Networks and Heterogeneous Media, 2014, 9(1): 169-189. doi: 10.3934/nhm.2014.9.169 |
| [10] | Martin Heida, Benedikt Jahnel, Anh Duc Vu . Regularized homogenization on irregularly perforated domains. Networks and Heterogeneous Media, 2025, 20(1): 165-212. doi: 10.3934/nhm.2025010 |
We investigate the homogenization of inclusions of infinite conductivity, randomly stationary distributed inside a homogeneous conducting medium. A now classical result by Zhikov shows that, under a logarithmic moment bound on the minimal distance between the inclusions, an effective model with finite homogeneous conductivity exists. Relying on ideas from network approximation, we provide a relaxed criterion ensuring homogenization. Several examples not covered by the previous theory are discussed.
The classical theory of homogenization deals with conductivity matrices
| {−Δuε=fin U∖Fε,uε|∂U=0,∂νuε|∂Fε=0. | (1) |
Here,
| {−div (A0∇u0)=(1−λ)fin U,u0|∂U=0, | (2) |
for some non-degenerate effective conductivity matrix
| div (1Fε∇uε)=1Fεf in U |
meaning that the divergence of the flux
As regards the opposite case of inclusions with infinite conductivity, the theory of homogenization is less complete. The analogue of 1 reads:
| {−Δuε=fin U∖Fε,∇uε=0in Fε,uε|∂U=0,∫∂Iε∂νuε=0,∀Iε∈CC(Fε). | (3) |
Here, we denote
Again, the point is to show convergence to the effective system 2. However, contrary to the case of soft inclusions 1, the case of stiff inclusions (in the terminology of [27]) requires more than the connectedness of
Up to our knowledge, homogenization was so far only established by Zhikov for a random spherical structure
| lim supN→+∞1N3∑Bi⊂(−N,N)3μi<+∞, where μi:=|ln(d(Bi,F∖Bi))|. | (4) |
See Theorem 2.6 below, or [27,chapter 8] for more. Obviously, in the case where there is a minimal distance
In the opposite very dense setting where for all
| {−Δuε=0in U∖Fε,∇uε=0in Fε,uε|∂U=φ,∫∂Iε∂νuε=0,∀Iε∈CC(Fε) | (5) |
for which
| lim infε→0∫U|∇uε|2=+∞. |
Such negative results for dense settings rely notably on the so-called network approximation method, as described in the monograph [7]. The idea behind this method is that when the spheres get close to one another, the analysis of systems of type 5 can be simplified: the asymptotic behaviour of the system (notably of its energy), can be deduced from the properties of an underlying weighted graph where:
● nodes of the graph are the spheres of infinite conductivity
● edges are pairs of spheres close to one another, in the sense that they belong to adjacent Voronoi cells
● each edge
For instance, the energy of the system can be approximated as the parameter
The goal of this paper is to investigate some intermediate situations, in which the condition on the distance between the inclusions 4 is not necessarily satisfied, but homogenization is still possible. To identify situations of this kind, we will rely on two notions:
● the notion of multigraph of inclusions, reminiscent of the network approximation just mentioned
● the notion of short of inclusions, reminiscent of the study of electrical circuits.
Thanks to these notions, we will formulate two assumptions H1-H2. The weaker one, H1, allows to define the homogenized matrix
The outline of the paper is as follows. In Section 2, after a brief reminder on stationary closed sets, we describe the class of inclusions under consideration. For such class, we define multigraphs and shorts of inclusions. We conclude the section by the statement of our homogenization results. In Section 3, we show certain extension properties for potential and solenoidal vector fields, crucial to the proof of homogenization. This proof is then given in Section 4. Eventually, Section 5 provides complements on our main hypothesis H1-H2.
We follow here the definition in the lecture notes [11,chapter 13]. A random closed set is a random variable
| CL={F⊂R3,Fclosed} |
equipped with the borelian
Note that there is a trick to turn a
| ˜F:(CL×(0,1)3,PF⊗Leb)→CL,(ω,x)→ω−x. |
Then, one considers on
| P˜F∘τ−1x(A)=PF×Leb({(ω,y),ω−y∈A+x})=∫(0,1)3∫CL1A+x(ω−y)dPF(ω)dy=∫(0,1)3PF(τ−x−y(A))dy. |
By
| P˜F(A)=∫(0,1)3PF(τ−y(A))dy=PF(A)∈{0,1}. |
Note that a property that is almost sure with respect to
More generally, let
A convenient unified description, that we adopt from now on, is the following. We consider a probability space
i)
ii)
iii)
iv)
Under this description, an (ergodic) stationary closed set is then a r. v.
| F(τx(ω))=F(ω)−x,∀ω∈Ω,∀x∈R3. |
Introducing the subset
| F={ω∈Ω,0∈F(ω)} | (6) |
one can notice that
| F(ω)={x,τx(ω)∈F}. |
This is the point of view taken in [27].
Our homogenization results apply to a class of ergodic stationary closed sets
(G1) Regularity of the inclusions : there exists
(G2) Geometry of the gaps : there exists
| I∩{d(x,F∖I)≤δ} |
has a finite number of connected components
| Iα⊂{z≥d(Iα,Iβ)/2+ar2},Iβ⊂{z≤−d(Iα,Iβ)/2−ar2}, | (7) |
that is
Remark 1. By 7, there is a unique couple of points
| |xI,α−xJ,β|=d(Iα,Jβ). |
See Figure 1.
Definition 2.1. (Admissible set of inclusions)
We say that an ergodic stationary closed set
Remark 2. At this stage, we do not assume anything on the diameter of the inclusions.
We now associate to a closed set satisfying (G1)-(G2) an unoriented multigraph that we call multigraph of inclusions. Roughly, the nodes of the multigraph are the connected components of the closed set, and we link pieces of these connected components that are
Definition 2.2. (Multigraph of inclusions)
Let
| e=[xI,α,xJ,β], with I≠J∈CC(F),1≤α≤NI,1≤β≤NJ,d(Iα,Jβ)≤δ. |
We say that an edge
| μe:=|ln|e||=|lnd(Iα,Jβ)| for e=[xI,α,xJ,β],|e|=|xJ,β−xI,α|. | (8) |
As explained in the introduction, there is a strong analogy between our multigraph of inclusions and the network approximation of [7].
For later use, we further define
Definition 2.3. (Cluster of inclusions)
Let
Remark 3. For
●
●
In the case
| Iy,F(ω)=I0,F(τy(ω)),Cy,F(ω)=C0,F(τy(ω)). |
This implies that
A last notion we need to explain before stating our main results is the notion of short of inclusions. It is directly inspired from the study of electrical networks and their associated multigraphs:
Definition 2.4. (Short of a multigraph)
Let
We say that
For electrical circuits, it is well-known that nodes with the same potential can be shorted, without changing the values of the currents through the remaining edges. This is a useful fact, as one can short the multigraph of an electrical circuit to simplify calculations. In other words, shorting two nodes is the same as imposing the same potential on each of the node, which can be interpreted as having zero resistance between those nodes. We refer to [12,chapter 2] for more.
At the level of the inclusions, an analogue of a short between two nodes consists in bridging the gap between two inclusions, so as to obtain one single connected component out of the two, with a single potential. We introduce the following
Definition 2.5. (Short of inclusions)
Let
●
●
● there exists
| {d(x,e)<η}⊂F′⊂F∪∪e∈Ed(F)∖Ed(F′){d(x,e)<2η}. |
Furthermore, if
As explained above, a short of
We now turn to the homogenization problem described roughly in the introduction. For the rest of this section, we assume that
| Iε:=εI∀I∈CC(F),Fε:=⋃Iε⊂U,d(Iε,∂U)>εδ0Iε. | (9) |
Let
| ‖∇uε‖L2(U)≤C‖f‖L6/5(U). |
In particular,
As mentioned in the introduction, Zhikov has tackled the homogenization problem, for a collection of random spheres of unit radius, under a logarithmic moment bound on the minimal distance between the spheres. The result extends easily to admissible sets of inclusions, under a uniform bound on their diameter. It can further be expressed in terms of multigraphs of inclusions. Namely, for all
| QN:=(−N,N)3,FN:=⋃I∈CC(F),I⊂QNI. | (10) |
Then the homogenization theorem of Zhikov reads
Theorem 2.6. (Zhikov, [27]) Let
| lim supN→+∞1|QN|∑e∈Ed(FN)μe<+∞. | (11) |
Then, almost surely, the whole sequence
Remark 4. As pointed out to us by A. Gloria, it can be seen from the ergodic theorem that:
As usual in stochastic homogenization, the effective conductivity matrix
| ∀ξ∈R3,B0ξ⋅ξ:=infzE∫Q1∖F|ξ+z|2, |
where the infimum is taken over the set of vector fields
i)
ii)
iii)
Then, part of the proof of Theorem 2.6 is to show that
| A0=(B0)−1. | (12) |
Our goal is to relax the assumption in the previous theorem, notably to identify configurations for which no condition on the minimal distance is needed. Our criterion for homogenization will be expressed again through multigraphs of inclusions. A key role will be played by the following discrete energy functional: for
| E(F,{uI},{bIJe})=∑I,J∈CC(F)∑e∈Ed(F),Ie↔Jμe|bIJe−bJIe+uI−uJ|2+∑I∈CC(F)|I||uI|2. | (13) |
We start with the definition of the homogenized matrix. We remind the notation
Proposition 1. (Existence of the homogenized matrix)
Let
| lim supN→+∞inf{uI}1|QN|E(FN,{uI},{bIJe=ξ⋅xI})<+∞ | (H1) |
where
Compared to the assumptions in Theorem 2.6, those of Proposition 1 are better in two regards.
a) The uniform bound on the diameter of the inclusions (see Remark 4) is replaced by a moment bound. This possibility of considering inclusions of arbitrary large size, interesting in its own, will turn very useful when combined to our homogenization result involving shorts, cf. Theorem 2.7.
b) As mentioned in the introduction, H1 is weaker than 11. Indeed, for inclusions satisfying
| lim supN→+∞1|QN|E(FN,{0},{ξ⋅xI})<+∞. |
In other words, Zhikov's condition 11 corresponds to the simplest choice
| Ediam(C0,F)2<+∞ |
where
We now turn to the homogenization of 3. It is an interesting open problem to be able to perform homogenization under the mere assumption H1. We must here strengthen it a little.
Theorem 2.7. (Homogenization of stiff inclusions)
Let
| lim supN→+∞1|QN|sup{bIJe}inf{uI}E(F′N,{uI},{bIJe})/‖(bIJe)‖2s<+∞ | (H2) |
where
| ‖(bIJe)‖s=(1|QN|∑I,J∈CC(F′N)∑e∈Ed(F′N),Ie↔J|bIJe|s)1s. |
Then, there exists
| Ediam(I0,F′)p<+∞, | (14) |
the solution
Here are a few remarks, to be complemented in Section 5.
i) Of course, in previous statements, it is enough that all assumptions involving the
ii) In practice, the following reformulation of H2 will be used:
One can find almost surely an
| E(FN,{uI},{bIJe})≤M|QN|(1|QN|∑I,J∈CC(FN)∑e∈Ed(FN),Ie↔J|bIJe|s)2/s. |
iii) Let
| Ediam(I0,F′)s<+∞ |
then H2 implies H1. See Lemma 5.5. In particular, by Proposition 1, the matrix
iv) H2 is implied by the following logarithmic moment bound, see Lemma 5.4:
| lim supN→+∞1|QN|∑e∈Ed(FN)μke<+∞,k=(s2)′=ss−2. | (15) |
In the case where
iv) A corollary of Theorem 2.7, to be established in Section 5 and illustrated in Figure 4, is the following:
Corollary 1. Let
| E(♯C0,F)p<+∞,for somep>2, |
where
v) Another important corollary of Theorem 2.7 is:
Corollary 2. Let
| Ediam(C0,F)p<+∞ |
then homogenization holds.
Indeed, if we simply bridge all pairs of nodes
Let us point out that the sharper bound
| Eexp(diam(C0,F)γ)<+∞, for one γ>1 |
has been shown to hold for several examples of admissible sets of inclusions, satisfying strong mixing assumptions, below the critical percolation threshold. We refer to the recent article [18] for details, where, moreover, the homogenization of both Laplace and Stokes equation is obtained in this special case by a different method.
vi) The local blow-up of the energy between two close inclusions
vii) In this work, the dimension
In this whole section,
The two main results of this paragraph are
Proposition 2. Let
| ∇ϕε=ξinFε,ε−1‖ϕε‖L2(U)+‖∇ϕε‖L2(U)≤C|ξ|. |
Proposition 3. Assume H2 with
| Ediam(I0,F)p<+∞, |
one can find almost surely
| ∇ϕε=∇φεinFε,ε−1‖ϕε‖L2(U)+‖∇ϕε‖L2(U)≤C‖∇φε‖L˜s(Fε). |
We will focus on the proof of the latter proposition, as the former requires only minor modifications.
Proof. In all the proof, the realization
| ∀I∈CC(F),∀u∈W1,t(I),‖u−(u)I‖Lt(I)≤Cdiam(I)r‖∇u‖Lt(I), | (16) |
with
| N:=ε−1,˜FN:=NFε=⋃I⊂F∩NU,d(I,N∂U)>δ0I |
the set of all the connected components of
| ∇ϕN=∇φ in ˜FN,‖ϕN‖H1(NU)≤CN3˜s−62˜s‖∇φ‖L˜s(˜FN). | (17) |
Let
| ϕe|I=φI−−∫IφI+uI,ϕe|J=φJ−−∫JφJ+uJ | (18) |
and
| ‖ϕe‖2H1(Ve)≤Cμe|φI(xI,α)−−∫IφI−φJ(xJ,β)+−∫JφJ+uI−uJ|2+C(|uI|2+|uJ|2)+C(diam(I)2r‖∇φI‖2L2(I)+diam(J)2r‖∇φJ‖2L2(J))+C(diam(I)2r‖∇φI‖2Ls(I)+diam(J)2r‖∇φJ‖2Ls(J)) | (19) |
Step 1. Let
| −∫IφI=0∀I, so that, for all t≥2,‖φI‖W1,t(I)≤Cdiam(I)r‖∇φI‖Lt(I) |
thanks to 16. Let now
| Pα={z≥|e|2+ar2},Pβ={z≤−|e|2−ar2}. |
By Lemma A.1, given
| Fe(d):={r2≤d2,ar2+|e|2≥z≥−|e|2−ar2} |
and where
| 0≤we≤1,we|Pα=1,we|Pβ=0,∫Fe(d)|∇we|2dx≤Cμe,∫Fe(d)|∇we|2|x−xI,α|2γdx≤Cγ∀γ>0. |
We take
Now, using the Stein extension operator from
| ‖˜φI‖W1,t(R3)≤c‖φI‖W1,t(I)≤c′diam(I)r‖∇φI‖Lt(I) ∀I∈CC(F) |
We remark that the analysis in [31,Chapter 6] provides constants
| ϕe:=we(˜φI+uI)+(1−we)(˜φJ+uJ) |
that we consider as a function of
| Ve:=Pα∪Pβ∪Fe(d)∩{|z|≤R} | (20) |
where
| ∫Fe(d)|∇ϕe|2dx≤∫Fe(d)|∇we(˜φI+uI−˜φJ−uJ)+we∇˜φI+(1−we)∇˜φJ|2dx. |
Hence,
| ∫Fe(d)|∇ϕe|2dx≤C(∫Fe(d)|∇we|2|˜φI+uI−˜φJ−uJ|2dx+∫Fe(d)|∇˜φI|2+|∇˜φJ|2dx)≤C′(∫Fe(d)|∇we|2|φI(xI,α)+uI−φJ(xJ,β)−uJ|2dx+∫Fe(d)|∇we|2|˜φI−φI(xI,α)+φJ(xJ,β)−˜φJ|2dx+diam(I)2r‖∇φI‖2L2(I)+diam(J)2r‖∇φJ‖2L2(J)). |
Thanks to Morrey's inequality
| |˜φI(x)−φI(xI,α)|≤C|x−xI,α|γ‖∇˜φI‖Ls(R3)≤C′|x−xI,α|γdiam(I)r‖∇φI‖Ls(I) |
for any
| ∫Fe(d)|∇we|2|˜φI−φI(xI,α)+φJ(xJ,β)−˜φJ|2dx≤Cdiam(I)2r‖∇φI‖2Ls(I)∫Fe(d)|∇we|2|x−xI,α|2γdx+Cdiam(J)2r‖∇φJ‖2Ls(J)∫Fe(d)|∇we|2|x−xJ,β|2γdx≤C′(diam(I)2r‖∇φI‖2Ls(I)+diam(J)2r‖∇φJ‖2Ls(J)). |
Finally, combining the previous inequalities entails
| ∫Fe(d)|∇ϕe|2dx≤C(μe|φI(xI,α)+uI−φJ(xJ,β)−uJ|2+diam(I)2r‖∇φI‖2L2(I)+diam(J)2r‖∇φJ‖2L2(J)+diam(I)2r‖∇φI‖2Ls(I)+diam(J)2r‖∇φJ‖2Ls(J)). |
It is even simpler to show that
| ∫Ve∖Fe(d)|∇ϕe|2dx+∫Ve|ϕe|2dx≤C(|uI|2+|uJ|2+diam(I)2r‖∇φI‖2L2(I)+diam(J)2r‖∇φJ‖2L2(J)) |
which concludes the derivation of 19, and the first step.
Step 2. We now explain how to construct a global extension
| ϕN|I=φI−−∫IφI+uI,∀I∈CC(˜FN). | (21) |
For all
●
●
●
● the supports of
●
Existence of such functions is easily deduced from our geometric assumptions (G1)-(G2). We now set
| ϕN,1:=∑e∈Ed(˜FN)χeϕe. |
By our choice of functions
| ϕN,1|Iα=φI−−∫IφI+uI,∀I∈CC(˜FN),∀α=1,…,NI. | (22) |
Moreover, by estimate 19,
| ‖ϕN,1‖2H1(NU)≤C∑e=[xI,α,xJ,β]∈Ed(˜FN)(μe|φI(xI,α)−−∫IφI−φJ(xJ,β)+−∫JφJ+uI−uJ|2+|uI|2+|uJ|2diam(I)2r‖∇φI‖2L2(I)+diam(J)2r‖∇φJ‖2L2(J)+diam(I)2r‖∇φI‖2Ls(I)+diam(J)2r‖∇φJ‖2Ls(J)) |
It remains to construct some
| ϕN,2|I=ψI,ψI:=φI−−∫IφI+uI−ϕN,1,∀I∈CC(˜FN), | (23) |
in order for
| ˜ψI|I=ψI,‖˜ψI‖H1(R3)≤C‖ψI‖H1(I) |
and for all
| ˜ψI=0on Jβ,ν:=Jβ∩{|z|≤ν}. |
Now, for each
| Supp(χJ)∩I⊂∪1≤α≤NIIα,ν. |
We finally set
| ϕN,2=∑I∈CC(˜FN)χI˜ψI. |
The keypoint in the definition of
| ‖ϕN,2‖2H1(NU)≤C(‖ϕN,1‖2H1(NU)+∑I∈CC(˜FN)(diam(I)2r‖∇φI‖2rL2(I)+|I||uI|2)) |
so that eventually
| ‖ϕN‖2H1(NU)≤C∑e=[xI,α,xJ,β]∈Ed(˜FN)(μe|φI(xI,α)−−∫IφI−φJ(xJ,β)+−∫JφJ+uI−uJ|2+C∑I∈CC(˜FN|I||uI|2+∑I∈CC(˜FN)diam(I)2r(‖∇φI‖2L2(I)+‖∇φI‖2Ls(I)). |
The final step of the proof is to show that for a proper choice of the family
| ‖ϕN‖2H1(NU)≤CE(˜FN,{uI},{bIJe})+C∑I∈CC(˜FN)diam(I)2r(‖∇φI‖2L2(I)+‖∇φI‖2Ls(I))≤CE(˜FN,{uI},{bIJe})+C∑I∈CC(˜FN)diam(I)2r(|I|˜s−2˜s+|I|2(˜s−s)s˜s)‖∇φI‖2L˜s(I)≤CE(˜FN,{uI},{bIJe})+C′(∑I∈CC(˜FN)diam(I)2r˜s˜s−2|I|)˜s−2˜s‖∇φ‖2L˜s(˜FN). |
Now, taking
| E(˜FN,{uI},{bIJe})≤E(FN′,{ˉuI},{ˉbIJe}) |
for any extensions
| E(FN′,{ˉuI},{¯bIJe})≤M|QN′|(1|QN′|∑I,J∈CC(FN′)∑e∈Ed(FN′),Ie↔J|ˉbIJe|s)2/s≤M′|QN|(1|QN|∑I,J∈CC(˜FN)∑e∈Ed(˜FN),Ie↔J|bIJe|s)2/s. |
Using one last time the Morrey injection yields
| |bIJe|s=|φI(xI,α)−φI(xI)|s≤|xI−xI,α|s−3‖∇˜φI‖sLs(R3)≤Cdiam(I)s−3+rs‖∇φI‖sLs(I). |
Setting
| ‖ϕN‖2H1(NU)≤M′|QN|(1|QN|∑I,J∈CC(˜FN)diam(I)s−3+rs‖∇φI‖sLs(I))2s+C′(∑I∈CC(˜FN)diam(I)2r˜s˜s−2|I|)˜s−2˜s‖∇φ‖2L˜s(˜FN)≤C″N3˜s−6˜s(1|QN′|∑I∈CC(˜FN)diam(I)p|I|)˜s−2˜s‖∇φ‖2L˜s(˜FN) |
where
| 1|QN′|∑I∈CC(˜FN)diam(I)p|I|≤1|QN′|∫QN′diam(Iy,F)pdy |
we find by the ergodic theorem that
| lim supN→+∞1|QN′|∑I∈CC(˜FN)diam(I)p|I|≤Ediam(I0,F)p<+∞ |
which concludes the proof.
Our proof of homogenization, based on the div-curl lemma, will require proper extensions of solenoidal vector fields, or of fields with given divergence, inside the inclusions. This is the purpose of
Proposition 4. Assume that H2 holds with
| ∫∂Iεpε⋅ν=∫Iεfε,∀Iε∈CC(Fε). |
Then, there exists a field
| ‖Pε‖Lt(U)≤Ct(‖pε‖L2(U∖Fε)+‖fε‖L6/5(U)). |
Proof. Let
| Δw=fε on U,w|∂U=0. |
It satisfies the estimate
| ‖∇w‖Lq(U)≤Cq‖fε‖W−1,q(U)≤C′q‖fε‖L3q/(3+q)(U)∀q∈(1,2]. |
Denoting
| ‖Sε‖Lt(U)≤Ct‖sε‖L2(U∖Fε). |
Then
| {Δvε=0in ˚Iε,∂νvε=sε⋅νin ∂Iε. |
This Neumann problem is well-posed thanks to the compatibility condition
| ∫∂Iεsε⋅ν=∫∂Iεpε⋅ν−∫∂Iε∂νw=∫Iεfε−∫˚IεΔw=0,∀Iε∈CC(Fε). |
We then define the random field
| Φ|Iε:=P˚IεΦ+∇φε,∀Iε∈CC(Fε) |
where for any open set
| ‖P˚IεΦ‖L˜s(Iε)+‖∇φε‖L˜s(Iε)≤C˜sdiam(I)R‖Φ‖L˜s(Iε), for some R>0. |
Indeed, by scaling, it is enough to show this inequality for
| Δuf=div f on ˚I,∂νu|∂I=f⋅ν. |
One must then look carefully at the proof of the inequality
We now introduce the function
| ∫Fε∇vε⋅Φ=∑Iε∈CC(Fε)∫Iε∇vε⋅∇φε−∫Iεvεdiv P˚IεΦ+∫∂IεvεP˚IεΦ⋅ν⏟=0=∑Iε∈CC(Fε)∫∂Isε⋅νφε using the equation on vε=∑Iε∈CC(Fε)∫∂Isε⋅νϕε using that ∫∂Isε⋅ν=0=∫U∖Fεsε⋅∇ϕε≤‖sε‖L2(U∖Fε)‖∇ϕε‖L2(U∖Fε)≤C‖sε‖L2(U∖Fε)‖∇φε‖L˜s(Fε) |
where the last inequality comes from Proposition 3. Now,
| ‖∇φε‖˜sL˜s(Fε)=∑Iε∈CC(Fε)‖∇φε‖˜sL˜s(Iε)≤C∑Iε∈CC(Fε)diam(I)R˜s‖Φ‖˜sL˜s(Iε)≤C(∑Iε∈CC(Fε)|Iε|diam(I)p)t′−˜st′‖Φ‖˜sLt′(Fε),p=R˜st′t′−˜s. |
Again,
| ∑Iε∈CC(Fε)|Iε|diam(I)p≤C∫Udiam(Ix/ε,F)p→ε→0C|U|Ediam(Ip0,F)<+∞ |
so that we end up with
| ∫USε⋅Φ=∫U∖Fεsε⋅Φ+∫Fε∇vε⋅Φ≤C‖sε‖L2(U∖Fε)(‖Φ‖L2(U∖Fε)+‖Φ‖Lt′(Fε))≤C′‖sε‖L2(U∖Fε)‖Φ‖Lt′(U). |
This concludes the proof.
Here, again,
The goal of this section is to define properly the matrix
| ∀ξ∈R3,B0ξ⋅ξ:=infzE∫Q1∖F|ξ+z|2, |
where the infimum is taken over vector fields
| ∀ξ∈R3,B0ξ⋅ξ:=infZ∈V2sol(Ω)∫Ω∖F|ξ+Z|2, | (24) |
where:
●
●
We remind that introducing the other subspace of vector fields
| L2pot(Ω)={U∈L2(Ω),y→U(τy(ω))potential vector field} |
one has the orthogonal decomposition
Still following [27,chapter 8], if we now denote
| X : the closure in L2(Ω∖F) of the space {Z|Ω∖F,Z∈V2sol(Ω)} | (25) |
then there exists a unique minimizer
| ∫Ω∖F(ξ+Z)⋅Z′=0,∀Z′∈V2sol(Ω). |
In particular,
The last step of proof of Proposition 1 is showing that the matrix
Lemma 4.1. [27,Lemma 8.7] Assume that for any
| vε|Fε(ω)=0,vε→ξweakly in L^2(U) ,lim supε→0‖vε‖L2≤C|ξ| for some C > 0 . |
Then,
The keypoint is that under H1, the assumptions of the lemma are granted by Proposition 2: one can take
We prove in this section part of Theorem 2.7. Namely, we focus on the case where H2 is satisfied with
First, by Remark iii) after Theorem 2.7, H2 implies H1. Hence, we can apply Proposition 1, so that
Let now
| ˉz(y,ω)=ˉZ(τy(ω)),ˉzν(y,ω)=ˉZν(τy(ω)),zν(y,ω)=Zν(τy(ω)). |
Let
| Pε|U∖Fε=pε,div Pε=f1U∖Fε in U,‖Pε‖Lt(U)≤Ct. |
The last bound implies weak convergence of (a subsequence of)
| ∫Uφ(x)∇uε(x)⋅(ξ+ˉz(x/ε))dx→∫Uφ(x)∇u0(x)⋅ξdx | (26) |
as well as
| ∫Uφ(x)∇uε(x)⋅(ξ+ˉz(x/ε))dx→∫Uφ(x)P0⋅B0ξdx. | (27) |
Identifying the limits, it follows that
The proof of 26-27 is an adaptation of the one in [27], so that we indicate only the main elements and the changes that are needed. As regards 26, we write
| ∫Uφ(x)∇uε(x)⋅(ξ+ˉz(x/ε))dx=∫Uφ(x)∇uε(x)⋅(ˉz(x/ε)−ˉzν(x/ε))dx+∫Uφ(x)∇uε(x)⋅(ˉzν(x/ε)−zν(x/ε))dx+∫Uφ(x)∇uε(x)⋅(ξ+zν(x/ε))dx. | (28) |
The first term at the r.h.s. satisfies
| |∫Uφ(x)∇uε(x)⋅(ˉz(x/ε)−ˉzν(x/ε))dx|≤‖φ‖∞‖∇uε‖L2(U)‖ˉz(x/ε)−ˉzν(x/ε)‖L2(U) |
so that, by the uniform
| |lim supε∫Uφ(x)∇uε(x)⋅(ˉz(x/ε)−ˉzν(x/ε))dx|≤C‖ˉZ−ˉZν‖L2(Ω)=C‖Z−Zν‖L2(Ω∖F) |
and finally
| lim supνlim supε|∫Uφ(x)∇uε(x)⋅(ˉz(x/ε)−zν(x/ε))dx|=0. |
For the second term at the r.h.s. of 28, we notice that
| Uη:={x∈U,d(x,∂U)≤η},η>0. |
A crucial point is that, under the moment condition
| sup{diam(Iε),Iε∈CC(εF),Iε∩Uδ0ε≠∅}=o(1) as ε→0. |
Hence, for any
| |∫Uφ(x)∇uε(x)⋅(ˉzν(x/ε)−zν(x/ε))dx|=|∫(εF∩U)∖Fεφ(x)∇uε(x)⋅(ξ+zν(x/ε))dx|≤‖φ‖L∞‖∇uε‖L2(Uη)‖ξ+zν(⋅/ε)‖L2(Uη)≤C‖ξ+zν(⋅/ε)‖L2(Uη) |
and by the ergodic theorem
| lim supε|∫Uφ(x)∇uε(x)⋅(ˉzν(x/ε)−zν(x/ε))dx|≤C‖1Uη‖L2‖ξ+Zν‖L2(Ω)≤C′η1/2. |
As
| lim supε|∫Uφ(x)∇uε(x)⋅(ˉzν(x/ε)−zν(x/ε))dx|=0. |
Finally, as regards the third term at the r.h.s. of 28, by the div-curl lemma and the ergodic theorem, for any given
| limε∫Uφ(x)∇uε(x)⋅(ξ+zν(x/ε))dx=∫Uφ(x)∇u0(x)⋅(ξ+EZν)dx=∫Uφ(x)∇u0(x)⋅ξdx |
where the last equality comes from the property
As regards 27, we want again to rely on the div-curl lemma but switching the potential and solenoidal vector fields. Therefore, we write
| ∫Uφ(x)∇uε(x)⋅(ξ+ˉz(x/ε))dx=∫Uφ(x)Pε(x)⋅∇wεdx |
taking into account that
| ∇wε→E(ξ+ˉZ)=B0ξweakly in L2(U), almost surely. |
If
| wε,l(x)=wε(x)if |wε(x)|≤l,wε,l(x)=lif wε(x)≥l,wε,l(x)=−lif wε(x)≤−l. |
We refer to [27,chapter 8,page 286] for implementation of this argument.
We tackle the proof of Theorem 2.7 in the general case where
First, we introduce the sequence of admissible shorts
| Ed(Fκ)=Ed(F′)∪{e∈Ed(F)∖Ed(F′),|e|≥κ}. |
In other words,
Lemma 4.2. If
Proof. We will first show that,
| almost surely, ∀κ∈Q∩(0,1],supI∈CC(Fκ),I∩QN≠∅diam(I)=o(N). | (29) |
Indeed, let
| AN={ω,there exists I∈CC(Fκ(ω)),I∩QN≠∅,I∩QcN(1+η)≠∅}. |
We recall that all inclusions satisfy an inner sphere condition with uniform deterministic radius. Hence, there exists a (deterministic) set of points
| P(AN)≤KN∑i=1P(diam(Ixi,Fκ)≥ηN)≤CN2P(diam(I0,Fκ)≥ηN). |
The moment bound implies that
| supI∈CC(Fκ),I∩QN≠∅diam(I)≤ηN. |
By taking a countable subset of
| almost surely, supI′∈CC(F′),I′∩QN≠∅diam(I′)=o(N). | (30) |
We now turn to the proof of the lemma. Let
● if
● if
● if
We introduce the family
| E(F′2N,{u′I′},{b′I′J′e})=inf{t′I′}E(F′2N,{t′I′},{b′I′J′e}). |
We then define a family
| uI=u′I′ for I′ the single c.c. of F′2N containing I. |
With this choice, we have
| ∑I′,J′∈CC(F′2N)∑e∈Ed(F′2N),I′e↔J′|bI′J′e|s≤∑I,J∈CC(FκN)∑e∈Ed(FκN),Ie↔J|bIJe|s |
and
| ∑I∈CC(FκN)|I||uI|2≤C∑I′∈CC(F′2N)|I′||u′I′|2 |
and
| E(FκN,{uI},{bIJe})≤CE(F′2N,{u′I′},{b′I′J′e})+∑I′∈CC(F′2N)∑I,J∈CC(FκN),I,J⊂I′.∑e∈Ed(FκN),Ie↔J|bIJe−bJIe|2μe. |
Now, by definition of
| C|lnκ|∑I,J∈CC(FκN)∑e∈Ed(FκN),Ie↔J|bIJe|2≤C′|lnκ||QN|(1|QN|∑I,J∈CC(FκN)∑e∈Ed(FκN),Ie↔J|bIJe|s)2s. |
The result follows easily from assumption H2 for
We have now all ingredients to perform the proof of our main Theorem 2.7, for a general admissible short
Similarly, we introduce
| Iκ,ε:=εIκ∀Iκ∈CC(Fκ),Fκ,ε=⋃Iκ,ε⊂U,d(Iκ,ε,∂U)≥δ02εIκ,ε. |
We would like to extend the function
| div Pκ,ε=f1U∖Fεin U, |
relying on Proposition 4 and the fact that
| ∫∂Iκ,ε∂νuε=∑Iε∈CC(Fε),Iε⊂Iκ,ε∫∂Iε∂νuε+∫∂(Iκ,ε∖F)∂νuε=∫∂(Iκ,ε∖Fε)∂νuε=∫Iκ,ε∖FεΔuε=∫Iκ,ε∖Fεf=∫Iκ,εf1U∖Fε. |
But there is a little technicality here, due to the fact that
Eventually, by applying Proposition 4, we obtain a field
Moreover, for all
By diagonal extraction, there exists a subsequence in
Let
| (31) |
The novel difficulty lies in the adaptation of the proof of 27. We shall prove that
| (32) |
Comparing 31 and 32, we get
which shows that
so that sending
and finally, sending
It remains to show 31. We take into account that
The first integral can be treated as in Section 4.2, resulting in
The second integral is bounded by
where we have used the uniform bound on
The integral at the right-hand side converges to zero as
Hence,
| (33) |
We still have to control
where
Note that for the last equality, we have used that
resulting in
By using the uniform
as seen above. It remains to treat
using the ergodic theorem to bound the factor
| (34) |
Indeed, following the proof of Proposition 4, we see that inside each inclusion
so that in particular
while
A crucial point is that
Indeed, by a scaling argument, it is enough to consider the case
applied in the domain
Summing over all
As
Again, the power of
Using Hölder inequality, we find for any
where
Back to
which goes to zero taking
We start here an extended discussion of the assumptions H1-H2. We remind the definition of
It follows from this definition that for closed sets
| (35) |
for any extensions
Indeed, the sum in the right-hand side of 35 has more (positive) terms than the one at the left-hand side.
H1 for a short implies H1. An important property of the discrete energy above concerns closed sets
| (36) |
We remind that for any set
| (37) |
Indeed, introducing
where
For the third inequality, we have used the fact that
Moreover,
which yields 37. We are now ready to show
Lemma 5.1. Let
as well as H1. Then,
Remark 5. In the case where
see the proof of 30.
Proof. One must realize once again that for
Let now
We associate to
Furthermore, by using 35, we have
so that combining everything we find
As
Clusters with a moment bound on the diameter. We prove here
Lemma 5.2. Let
where
Proof. We want to consider the discrete energy
Sending
which shows that
Link with the graph Laplacian. Another interesting result starts with the following observation. Assumption H1 is verified by
Writing the Euler equations of the minimization problem at the left-hand side leads to the following linear system
where we remind that
where
This kind of matrix arises in the graph literature as the weighted Laplacian matrix for the pondered unoriented graph
The energy of this problem is a superadditive quantity over sets and one can expect our discrete minimization problem to verify a similar property. We state
Lemma 5.3. Let
The quantity
Proof. It is enough to prove the results for a simple decomposition
where
Let
which ends the argument.
We can then use the superadditive ergodic theorem (cf. [1,14]), which yields a sufficient condition for H1 to hold :
Proposition 5. Assume that
then the admissible set
Logarithmic moment bound.
Lemma 5.4. Let
| (38) |
then
Proof. Let
for a suitable choice of
Using Hölder inequality with
which together with the bound 38 gives the expected result.
H2 implies H1.
Lemma 5.5. Let
and if H2 is satisfied by
Proof. By Lemma 5.1 and Remark 5, it is enough to show that
Clearly, from assumptions (G1)-(G2), one has
and
Thanks to the ergodic theorem, we end up with
Cycle-free graphs. The previous lemma comes from a trivial choice of the family
Proof of Corollary 1. Let
Note that in particular,
Using that
we find
We get, for any
Thanks to the cycle-free hypothesis, we get that
Finally, we notice that
This concludes the proof.
The object of this appendix is the following
Lemma A.1. Let
Furthermore we note
(see the picture below).Then there exists
where
Proof. For
that we extend by
by direct computation of the integral. The other bounds can be computed similarly. Note that functions of the type of
We explain here how to obtain inequality (16) with
Our starting point is the following statement: given an open set
one has
where
| (39) |
and then
| (40) |
where
To prove (16), we first introduce a covering
i) for each
ii) The cardinal
There are of course many possible choices to satisfy such properties. As regards i), our assumption (G1) ensures that we can cover a vicinity of the boundary by such type of open sets, while the remaining part of
then the cardinal
Then, given this covering, we write
where we used property ii) and the fact that
●
●
● The cardinal
We finally write: for all
where we used (39)-(40) for the second inequality.
The authors acknowledge the support of the SingFlows project, grant ANR-18-CE40-0027 of the French National Research Agency (ANR). David Gérard-Varet acknowledges the support of the Institut Universitaire de France. Alexandre Girodroux-Lavigne acknowledges the support of the DIM Math Innov de la Région Ile-de-France.
| 1. | Mitia Duerinckx, Antoine Gloria, Continuum Percolation in Stochastic Homogenization and the Effective Viscosity Problem, 2023, 247, 0003-9527, 10.1007/s00205-023-01857-w | |
| 2. | Azdine Nait-Ali, Sami Ben Elhaj Salah, Variational modeling adapted to the medium with gradient properties, 2024, 352, 1873-7234, 159, 10.5802/crmeca.254 | |
| 3. | Thuyen Dang, Yuliya Gorb, Silvia Jiménez Bolaños, Homogenization of High-Contrast Dielectric Elastomer Composites, 2025, 23, 1540-3459, 668, 10.1137/24M1631420 |
Geometry of the inclusions with a close-up on a gap
Spherical set up. The graph obtained with the whites lines is isomorphic to the multigraph of inclusions
Two inclusions configuration, shorted on the right
Cycle-free configuration set up
On the left, all clusters are far away from the others. On the right, groups of inclusions joined by a grey line form a short
Separation of the domain
Geometry of the gap