$\Gamma$-convergence of quadratic functionals with non uniformly elliptic conductivity matrices

1.   Introduction

In this paper, we consider the following two-dimensional multi-term time fractional diffusion equation:

where $f\in C(\bar{Q})$, $\Omega \subset \mathbb{R}^{2}$. In Eq(1.1a), ${D}_{t}^{\mathit{\boldsymbol{\alpha}}} u$ denotes the multi-term fractional derivative, which is defined by

where $J$ is a positive integer, $b_m \geq 0$, $\mathit{\boldsymbol{\alpha}}: = (\alpha_1, \cdots, \alpha_J)$ with $0 < \alpha_J < \cdots < \alpha_1 < 1$, and the fractional Caputo derivative $D_{t}^{\alpha} u (0 < \alpha < 1)$ in Eq (1.2) is defined by

For existence and uniqueness of the exact solution for problem (1.1), one can refer to ^[15,17]. The initial weak singularity of the solution for problem (1.1) is given in ^[9]. In recent years, many authors have investigated single-term time-fractional diffusion equations, see, e.g., ^[16,28,30]. At the same time, multi-term fractional equations ^[12,22,26] which have been successfully used in application of real life have attracted more and more attention. Among many types of fractional derivatives, some researchers have used Riemann-Liouville derivative ^[7,25], while others, including this article, choose to use Caputo derivative ^[13,27,30]. However, most of the previous work assumes that the exact solutions in temporal direction are smooth enough, whereas the solutions typically exhibit some weak singularities at initial time. Alternating direction implicit (ADI) method was first introduced in ^[18], the advantage of the ADI method is that it can reduce the computational cost by transforming a multi-dimensional problem into sets of 1D problems. Nowadays, there are many researchers using ADI method to solve various types of fractional derivative problems, such as ^{[2,6,14,19,20,21,23,31]}. Recently, Huang et al. ^[11] have presented an ADI scheme for 2D multi-term time-space fractional nonlinear diffusion-wave equations under reasonable solution regularity assumption. Cao and Chen ^[1] have used ADI difference method on uniform mesh to solve a 2D multi-term time-fractional subdiffusion equation with initial singularity. However, the global accuracy in time direction of ^[1] is low. It is only $O(\tau^\alpha)$. So, our current work is on graded mesh to improve the temporal accuracy. More precisely, we investigate a fully discrete ADI method for solving the problem (1.1) with weakly singular solution, where the temporal discretization is based L1 approximation on graded mesh, and finite difference method is used for spatial discretization. We establish the stability and convergence of the fully discrete L1-ADI scheme, both $L^2$-norm and $H^1$-norm error estimates are obtained, and the final error bounds do not blow up when $\alpha_1 \to 1^-$.

The rest of the paper is organized as follows. In Section 2, we construct a fully discrete L1-ADI scheme for problem (1.1). In Section 3, we establish the stability and convergence L1-ADI scheme in discrete $L^2$-norm. Then, the sharp $H^{1}$-norm convergence of L1-ADI scheme is presented in Section 4. Some numerical experiments are given in Section 5. The final part is the conclusion.

Notation. Throughout the paper, we denote by $C$ a generic positive constant, which may change its value at different occurrences, but is always independent of the mesh sizes. We call a constant $C$ $\alpha$-robust, if it doesn't blow up when $\alpha_1 \to 1^-$.

2.   Fully discrete L1-ADI scheme

In the whole paper, to simplify the analysis, let us choose $\Omega = (0, L)\times(0, L)$, where $L > 0$ is constant. We use positive integers $N_{1}$, $N_{2}$ and $M$ respectively to define the spatial and temporal partition parameters. Consider the graded temporal grid in $[0, T]: t_{j} = T(j/M)^r$, $j = 0, 1, \ldots, M$ and $r\geq1$. Denote time step $\tau_n: = t_n-t_{n-1}$ for $n = 1, \cdots, M$. Then, we use $x_{m} = mh_{1}$ for $m = 0, 1, \ldots, N_{1}$ and $y_{n} = nh_{2}$ for $n = 0, 1, \ldots, N_{2}$ to denote the spatial grids, where $h_{1} = L/N_{1}$, $h_{2} = L/N_{2}$. Set $\Omega^{\ast}_{h} = \{(x_{m}, y_{n})\lvert0\leq m \leq N_{1}, 0\leq n \leq N_{2}\}$, $\Omega_{h} = \Omega^{\ast}_{h}\cap \Omega$, and $\partial\Omega_{h} = \Omega^{\ast}_{h}\cap \partial\Omega$.

We approximate the Caputo fractional derivative $D_{t}^{\alpha_{m}} u\left(\cdot, \cdot, t_{n}\right)$ with $0 < \alpha_{m} < 1$ and $1 \leq n \leq M$ on graded mesh by using well-known L1 scheme as follows:

where

Then, we denote

Thus one can approximate the multi-term fractional derivative $D_t^{\mathit{\boldsymbol{\alpha}}} u$ in Eq (1.2) by

Given a mesh function$\{v^j\}_{j = 0}^M$, and for $0\leq n\leq M$, we define

The notations $\delta_{y}v^n_{i, j-\frac{1}{2}}$, $\delta_{y}^{2}v^n_{i, j}$ and $\delta_{x}\delta_{y}v^n_{i-\frac{1}{2}, j-\frac{1}{2}}$ can be defined similarly. We define the discrete Laplace operator $\Delta_{h}: = \delta_{x}^{2}+\delta_{y}^{2}$ which is a second-order approximation of $\Delta$. Let $u_{i, j}^{n}$ be the numerical approximation of the exact solution $u(x_{i}, y_{j}, t_{n})$, so the discrete problem of (1.1) is as follows

To solve 2D problem, we want to solve 1D problem at first, after that we solve another 1D problem. If a small term $\gamma_{n}^{2}\delta_{x}^{2}\delta_{y}^{2}\delta_{t}^{\mathit{\boldsymbol{\alpha}}} u_{i, j}^{n}$ for $n = 1, \ldots, M$, where $\gamma_{n} = z_{n, 1}^{-1}$, is added to the left side of Eq (2.5a), one gets

Thus the purpose is achieved as Eq (2.6) can be rewritten by

We set $u_{i, j}^{*} = (1-\gamma_{n}\delta_{y}^{2})u_{i, j}$. Then, the first 1D problem we need to solve is, for $1\leq j\leq N_2-1$,

and the second 1D problem we need to solve is, for $1\leq i\leq N_1-1$,

Thus, we have the following fully discrete ADI scheme for the problem (1.1):

3.   Analysis of stability and convergence

We define the convolution multipliers $\sigma_{n, j}$, which is positive for $n = 1, 2, \ldots, M$ and $j = 1, 2, \ldots, n-1$ by

We have the following two lemmas on the properties of the convolution multipliers $\sigma_{n, j}$.

Lemma 1. ([10, Corollary 1]) One has

Lemma 2. ([10, Corollary 2]) Set $l_M = 1/\ln M$. Assume that $M\ge 3$ so $0 < l_M < 1$. Then

To investigate the stability and convergence of the fully discrete L1-ADI scheme (2.9), we need the following fractional discrete Gronwall inequality.

Lemma 3. [8, Lemma 5.3] Suppose that the sequences $\left\{\varepsilon^n\right\}_{n = 1}^{\infty}, \left\{\eta^n\right\}_{n = 1}^{\infty}$ are nonnegative and assume the grid function $\left\{V^n: n = 0, 1, \ldots, M\right\}$ satisfies $V_0 \geq 0$ and

Then,

Set

For any mesh functions $u, v \in \mathcal{V}_h$, define the discrete $L^2$ inner product $(u, v) = h_1h_2\sum_{i = 1}^{N_1-1}\sum_{j = 1}^{N_2-1}u_{i, j}v_{i, j}$, and the norm $\Vert v \Vert = \sqrt{(v, v)}$. We also define a new inner product $(u, v)_{\gamma_{n}}: = (u, v)+$ $\gamma_{n}^2(u, v)_{xy}$, where

and set $\|u\|_{\gamma_{n}} = \sqrt{(u, u)_{\gamma_{n}}}$.

Lemma 4. [1, Lemma 3] The inner product $(u, v)_{\gamma_{n}}$ satisfies

Lemma 5. For $n = 1, 2, \ldots, M$, the solution of ADI scheme (2.9) satisfies

Proof. On both sides of Eq (2.9a), we take the discrete inner product with $u^n$. Then, one has

Then, by linear property of the inner product and discrete Green formula, the Eq (3.2) becomes

Using Lemma 4, one has

which is equivalent to

Then, setting all $\eta^n = 0$ in Lemma 3, and applying it to Eq (3.3), the result is proved. □

From [3, Lemmas 2.2 and 2.3], one can easily get that

Lemma 6. Set $\sigma \in(0, 1)$. Suppose that $\left|u^{(k)}(t)\right| \leq C\left(1+t^{\sigma-k}\right)$ where $k = 0, 1, 2$. Then, for $1\leq n\leq M$, one has

Now we come to the convergence of the fully discrete ADI scheme (2.9).

Theorem 1. Suppose that {$\left|u^{(l)}(t)\right| \leq C\left(1+t^{\sigma-l}\right)$} for $l = 0, 1, 2$ with $\sigma \in(0, 1)$. Then the computed solution errors $e_{i, j}^n: = u\left(x_i, y_j, t_n\right)-u_{i, j}^n$ satisfy:

where C is $\alpha$-robust.

Proof. From Eqs (2.9a) and (1.1a), we get the following error equation:

where $\phi_{i, j}^n$ is the truncation error. By the well-known simple bound $|\Delta u-\Delta_h u|\leq C(h_1^{2}+h_2^2)$, $|\gamma_{n}^2| \leq C M^{-2\alpha_1}$, and Lemma $6$, the truncation error $\phi_{i, j}^n$ satisfies

From Lemma 5, and noting that $e^0 = 0$, we have

Then, using Lemmas 1 and 2, we can get

where $C$ is $\alpha$-robust. Finally, according to the definition of the norm $\left\|\cdot\right\|_{\gamma_{n}}$, the proof is completed. □

4.   $H^1$-norm convergence of L1-ADI scheme

In order to prove the stability and convergence of the fully discrete ADI scheme (2.9) in $H^1$-norm sense in this section, we first define some norms. For any grid functions $U, V \in \mathcal{V}_h$, define

The corresponding seminorms are

For any function $V \in \mathcal{V}_h$, define

According to the definition of $\left\|\nabla_h V^n\right\|$ and $\|V^n\|_A$, we can see that $\left\|\nabla_h V^n\right\| \leq \|V^n\|_A$. From [31, Lemma 2.2], one has $\|V^n\| \leq C\left\|\nabla_h V^n\right\|$ for all functions $V \in \mathcal{V}_h$, then, we have $\|V^n\|_{H^1} \leq C\left\|\nabla_h V^n\right\|$, hence, $\|V^n\|_{H^1} \leq C\|V^n\|_A$.

Lemma 7. [29, Lemma 3.2] For any grid functions $U, V \in \mathcal{V}_h$, one has

where the equality holds when $U = V$.

Next, we denote $R_t u_{i, j}^n = \left(1+\gamma_{n}^2 \delta_x^2 \delta_y^2\right) \delta_t^{\mathit{\boldsymbol{\alpha}}} u\left(x_i, y_j, t_n\right)-D_t^{\mathit{\boldsymbol{\alpha}}} u\left(x_i, y_j, t_n\right)$, $R_s u_{i, j}^n = \Delta u\left(x_i, y_j, t_n\right)-\Delta_h u\left(x_i, y_j, t_n\right)$. Then the error equation (3.4) can be written as

Besides, we have

and

Theorem 2. Suppose that $\left|u^{(l)}(t) \right|\leq C\left(1+t^{\sigma-l}\right)$ for $l = 0, 1, 2$ with $\sigma \in(0, 1)$. Then, the computed solution error $e_{i, j}^n: = u\left(x_i, y_j, t_n\right)-u_{i, j}^n$ satisfy:

where C is $\alpha$-robust.

Proof. Taking discrete $L^2$ inner product with $-\Delta_h e^n$ on both sides of Eq (4.1) and noting that $e^0 = 0$, we get

Using Lemma 7, one has

From Eqs (4.2) and (4.3), we obtain

that is

Thus, by Lemma 3, from Eq (4.5) we have

Then, using Lemmas 1 and 2, we come to the conclusion

by noting that

and

Finally, the results follow from $\left\|e^n\right\|_{H^1} \leq C\left\|e^n\right\|_A$ for $n = 1, 2, \ldots, M$. The proof is completed. □

5.   Numerical experiments

In this section, some numerical examples are reported to support our theoretical analysis. In this section, we present some 2D numerical examples to illustrate the result of our error analysis and convergence order on the temporal graded mesh. We define $\max\limits_{1 \leq n \leq M} \left\|u\left(t_n\right)-u^n\right\|$ as temporal global $L^2$-norm error and global $H^1$-norm error is defined similarly.

Example 1. In Eq (1.1) take $\Omega = [0, \pi]\times[0, \pi]$, $T = 1$, $J = 2$, $b_1 = b_2 = 1$. Choose $u(x, y, t) = t^{\alpha_{1}}\sin x\sin y$ as an exact solution. The force term $f(x, y, t) = b_1\Gamma(1+\alpha_{1})+b_2\Gamma(1+\alpha_{1})\frac{t^{\alpha_{1}-\alpha_{2}}}{\Gamma(1-\alpha_{2}+\alpha_{1})}\sin x\sin y+2t^{\alpha_{1}}\sin x\sin y$.

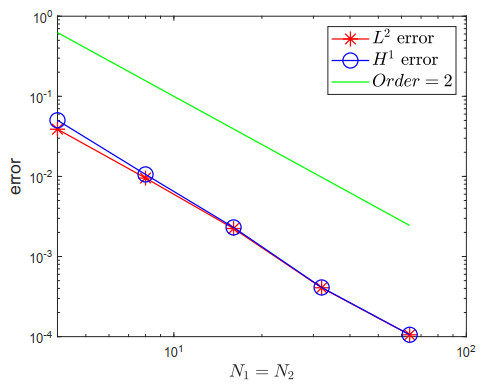
For this example, the regularity parameter $\sigma$ in Lemma 6 is $\sigma = \alpha_{1}$. Thus, both the temporal convergence orders in Theorems 1 and 2 are $O(M^{-\min \left\{ 2\alpha_{1}, r\alpha_1, 2-\alpha_1\right\}})$. We take $N_1 = N_2 = 1000$ to eliminate the contamination of spatial errors. Tables 1–3 present $L^2$-norm errors and orders of convergence for Example 1 with different $\alpha_1$, $\alpha_{2}$ and $r$. And Tables 4, 6 and 8 present $H^1$-norm errors and convergence orders. From these tables, we find that the temporal convergence orders are consistent with our theoretical results. As in ^[1], we also present the local $H^1$-norm errors and orders of convergence at $t = 1$ for Example 1 in Tables 5, 7 and 9, which have better convergence rates than the global errors. We next test the spatial accuracy of the fully discrete ADI scheme (2.9). Take $M = 1000$ such that the spatial errors are dominant. We using $\alpha_{1} = 0.6$, $\alpha_{2} = 0.4$ and $r = 2$ as an example and the results are presented in Figure 1. The results show that the spatial convergence orders are second order in $L^2$ and $H^1$-norm sense as is indicated in Theorems 1 and 2.

Example 2. In Eq (1.1) take $\Omega = [0, \pi]\times[0, \pi]$, $T = 1$, $J = 2$, $b_1 = b_2 = 1$. Let $u_0(x, y) = \sin x\sin y$, the force term $f(x, y, t) = 0$.

The exact solution $u(x, y, t)$ of Example 2 is unknown. We use the two-mesh principle in [4, p107] to calculate the convergence order of the numerical solution. Let $u_{i, j}^{n}$ with $0 \leq i \leq N_1$, $0 \leq j \leq N_2$ and $0 \leq n \leq M$ be the solution computed by our L1-ADI Scheme 2.6. Then, consider a spatial mesh and the temporal mesh which is defined by $0 \leq i \leq N_1$, $0 \leq j \leq N_2$ and $t_{n} = T(n /(2M)) {\text { for }} 0 \leq n \leq 2M$. We denote $W_{h}^{n}$ with $0 \leq n \leq 2M$ as the computed solution on this mesh. Then, we define $D_{h}^{n} = \left\|u_{h}^{n}-W_{h}^{2 n}\right\|_{H^1}$ as the $H^1$-norm of the two-mesh differences and the estimated rate of convergence is computed by $\log _{2} (D_{h}^{n}/D_{h}^{2n})$.

To test the temporal convergence of our scheme we set spatial partition parameters $N_1 = N_2 = 1000$. Tables 10, 12 and 14 present $H^1$-norm errors and convergence orders for Example 2 in the case of $\alpha_{1} = 0.4, 0.6, 0.8$ with $\alpha_{2} = 0.2, 0.4, 0.6$. The results show that the temporal convergence rates are $O(M^{-\min \left\{ 2\alpha_{1}, r\alpha_1, 2-\alpha_1\right\}})$, which, once again, confirm the sharpness of our theoretical analysis. We have also present the local $H^1$-norm errors and convergence orders at $t = 1$ for Example 2 in Tables 11, 13 and 15, which have better convergence rates than global errors.

6.   Conclusion

A fully discrete L1-ADI scheme is investigated for the initial-boundary problem of a multi-term time-fractional diffusion equation. Stability and convergence of the fully discrete L1-ADI scheme are rigorously established. Both $L^2$-norm and $H^1$-norm error estimates of the fully discrete L1-ADI scheme are obtained, and they are $\alpha$-robust. Numerical experiments are given to illustrate the sharpness of the theoretical analysis. It should be noted that since the computational cost of numerical methods for time-fractional PDEs will be very time-consuming. One can also use the fast and parallel numerical methods such as ^[5,24,32] for accelerating the proposed method, which will be the focus of our future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The research is supported in part by the National Natural Science Foundation of China under Grant 11801026, and Fundamental Research Funds for the Central Universities (No. 202264006).

Conflict of interest

The authors declare there is no conflict of interest.