1.
Introduction
In this study, we consider a mathematical model for a particular component of the nephron, the functional unit of kidney [1]. It describes the ionic exchanges through the nephron tubules in the Henle's loop. The main function of kidneys is to filtrate the blood. Through filtration, secretion and excretion of filtered metabolic wastes and toxins, the kidneys are able to maintain a certain homeostatic balance within cells. The first models of nephrons and kidneys were developed in the 1950s with the purpose of explaining the concentration gradient, [10] (or [16] in Chap.3). In their attempt, the authors describe for the first time the urinary concentration mechanism as a consequence of countercurrent transport in the tubules. At a later time the point of view starts to change and a simple mathematical model for a single nephron has been introduced and described, [17]. Furthermore, thanks to the work of J.L. Stephenson [26] it turns out that the formation of a large axial concentration gradient in the kidney depends mainly on the different permeabilities in the tubules and on their counterflow arrangement. Most mathematical models were stationary systems of coupled differential equations. It is possible to find an historical excursus and how these types of models have been developed, referring to [26]. Sophisticated models have been developed to describe the transport of water and electrolyte in the kidney in the recent literature. At the microscopic level of description, cell-based models have been proposed in [23,30,14,31,4] to model small populations of nephrons at equilibrium. Macroscopic models have been also considered in [28,27,21,5,2,9] without accounting for cell-specific transport mechanisms. Despite the development of such sophisticated models, some aspects of the fundamental functions of the kidney remain yet to be fully explained [15]. For example, how a concentrated urine can be produced by the mammalian kidney when the animal is deprived of water remains not entirely clear.
The loop of Henle and its architecture play an important role in the concentrated or diluted urine formation. In order to explain the regulation of urine's concentration, we analyse the counter-current transport in the 'ascending' and 'descending' tubules. There the ionic exchanges between the cell membrane and the environment where tubules are immersed, take place.
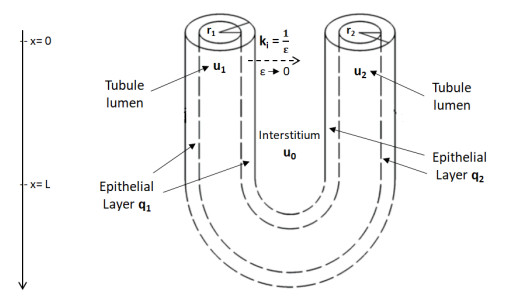
We consider a simplified model for sodium exchange in the kidney nephron : the nephron is modelled by an ascending (resp. descending) tubule, of length denoted L. Ionic exchanges and transport occur at the interface between the lumen and the epithelial layer (cell membrane) and at the interface between the cells and the interstitium (the surrounding tissue between tubules and blood vessels) c.f. Figure 1. Denoting by t≥0 (resp. x∈(0,L)) the time (resp. space) variable, the dynamics of ionic concentrations is modelled by the semi-linear hyperbolic system [19,27,28,29] :
complemented with the boundary and initial conditions
In this model, we have used the following notations :
● ri: denote the radius for the lumen i ([m]).
● ri,e: denote the radius for the tubule i with epithelium layer.
● Sodium's concentrations ([mol/m3]) :
ui(t,x): in the lumen i,
qi(t,x): in the epithelial layer of lumen i,
u0(t,x): in the interstitium.
● Permeabilities ([m/s]):
Pi: between the lumen and the epithelium,
Pi,e: between the epithelium and the interstitium.
● Section areas ai ([m2]), i∈{0,…,4} are defined as
In this work we indicate as lumen the limb under consideration and as tubule the segment together with its epithelial layer. In physiological common language, the term 'tubule' refers to the cavity of lumen together with its related epithelial layer (membrane) as part of it, [16].
In the ascending tubule, the transport of solutes both by passive diffusion and active re-absorption uses Na+/K+-ATPases pumps, which exchange 3 Na+ ions for 2 K+ ions. This active transport is taken into account in (1) by a non-linear term given by Michaelis-Menten's kinetics :
where kM,2 and Vm,2 are real positive constants. In each tubule, the fluid (mostly water) is assumed to flow at constant rate α and we only consider one generic uncharged solute in two tubules as depicted in Figure 1.
In a recent paper [19], the authors have studied, from the modelling and biological perspective, the role of the epithelial layer in the ionic transport. The aim of this work is to clarify from the mathematical point of view the link between model (1) taking into account the epithelial layer and models neglecting it. In particular, when the permeability between the epithelium and the lumen is large it is expected that these two regions merge, allowing to reduce system (1) to a model with no epithelial layer. More precisely, as the permeabilities P1 and P2 grow large, we show rigorously that solutions of (1) with boundary conditions (2) relax to solutions of a reduced system with no epithelial layer. From a mathematical and numerical point of view, system (1) may be seen as a hyperbolic system with a stiff source term. The source term is in some sense a relaxation of another hyperbolic system of smaller dimension. Such an approach has been widely studied in the literature, see e.g. [13,22,12,25]. Since the initial data of the starting system for fixed ε has no reason to be compatible with the limit system, the mathematical analysis of this relaxation procedure should account for initial layers. For relaxed convection-diffusion systems, but in the Cauchy case, for ill-prepared data, (out of equilibrium with respect to the reduced manifold), the construction of initial layers and the corresponding error analysis in Sobolev spaces can be found in [6]. The proof of our convergence result is obtained thanks to a BV compactness argument in space and in time. This framework is better suited for purely hyperbolic problems. Another difficulty is due to the presence of the boundary, which must be carefully handled in the a priori estimates, in order to be uniform with respect to ε, the relaxation parameter depending on the permeabilities.
The outline of the paper is the following. In the next section, we provide the mathematical model and state our main result. Section 3 is devoted to the proof of existence of solution of our model. Then, we focus on the convergence of this solution when permeabilies go to infinity. To this aim, we first establish in section 4 a priori estimates. Using compactness results, we prove convergence in section 5. Numerical illustration of this convergence result is proposed in section 6. Finally an appendix is devoted to a formal computation of the convergence rate at stationary state.
2.
Main results
Before presenting our main result, we list some assumptions which will be used throughout this paper.
Assumption 2.1. We assume that the initial solute concentrations are non-negative and uniformly bounded in L∞(0,L) and with respect to the total variation :
For detailed definitions of the BV setting we refer to the standard text-books [7,32]. A more recent overview gives a global picture in an extensive way [11], it unifies also the diversity of definitions found in the literature dealing with the BV spaces in either the probabilistic or the deterministic context.
Assumption 2.2. Boundary conditions are such that
Assumption 2.3. Regularity and boundedness of G.
We assume that the non-linear function modelling active transport in the ascending limb is an odd and W2,∞(R) function :
We notice that the function G defined on R+ by the expression in (3) may be straightforwardly extended by symmetry on R by a function satisfying (6).
To simplify our notations in (1), we set 2πri,ePi,e=Ki, i=1,2 and 2πriPi=ki, i=1,2. The orders of magnitude of k1 and k2 are the same even if their values are not definitely equal, we may assume to further simplify the analysis that k1=k2. We consider the case where permeability between the lumen and the epithelium is large and we set, k1=k2=1ε for ε≪1. Then, we investigate the limit ε goes to zero of the solutions of the following system :
Formally, when ε→0, we expect the concentrations uε1 and qε1 to converge to the same function. The same happens for uε2 and qε2. We denote u1, respectively u2, these limits. Adding (7a) to (7c) and (7b) to (7d), we end up with the system
Passing formally to the limit when ε goes to 0, we arrive at
coupled to the equation for the concentration in the interstitium obtained by passing into the limit in equation (7e)
This system is complemented with the initial and boundary conditions
Finally, we recover a simplified system for only three unknowns. From a physical point of view this means fusing the epithelial layer with the lumen. It turns out to merge the lumen and the epithelium into a single domain when we consider the limit of infinite permeability. For ε fixed, the actual speed at which u1 (resp. u2) is convected in (7a) is α/a1 (resp −α/a2 in (7b)). When ε goes to zero, since the permeability increases, the lumen and the epithelium layer are merged. Thus, as q1 (resp. q2) are not transported, this results in a slower convection at speed αa1+a3 in the descending tubule (resp. αa2+a4 in the ascending tubule).
The aim of this paper is to make these formal computations rigorous. For this sake, we define weak solutions associated to the limit system (8)-(10) :
Definition 2.4. Let u01(x), u02(x), u00(x)∈L1(0,L)∩L∞(0,L) and ub(t)∈L1(0,T)∩L∞(0,T). We say that U(t,x)=(u1(t,x), u2(t,x), u0(t,x))⊤∈L∞((0,T);L1(0;L)∩L∞(0,L))3 is a weak solution of system (8)-(10) if for all ϕ∈S3, with
we have
More precisely, the main result reads
Theorem 2.5. Let T>0 and L>0. We assume that initial data and boundary conditions satisfy (4), (5), (6). Then, the weak solution (uε1,uε2,qε1,qε2,uε0) of system (7) with boundary and initial conditions (2) converges, as ε goes to zero, to the weak solution of reduced (or limit) problem (8)–(10) complemented with (11)–(13). More precisely,
where (u1,u2,u0) is the unique weak solution of the limit problem (8)–(10) in the sense of Definition 2.4.
The system (7) can be seen as a particular case of the model without epithelial layer introduced and studied in [28] and [27].
A priori estimates uniform with respect to the parameter ε (accounting for permeability) are obtained in Section 4. We emphasize that estimates on time derivatives are more subtle due to specific boundary conditions of system and because one has to take care of singular initial layers. Concerning existence and uniqueness of a solution, in previous works [28] and [27], authors proposed a semi-discrete scheme in space in order to show existence. In this work we propose a fixed point theorem giving the same result for any fixed ε>0 in Section 3. The advantage of our approach is that we directly work with weak solutions associated to (7). After recalling the definition of weak solution for problem (1), we report below the statement of Theorem 2.7, and we refer to Section 3 for the proof.
Definition 2.6. Let (u01(x), u02(x), q01(x), q02(x), u00(x))∈(L1(0,L)∩L∞(0,L))5 and ub(t)∈L1(0,T)∩L∞(0,T). Let ε>0 be fixed. We say that Uε(t,x)=(uε1(t,x), uε2(t,x), qε1(t,x), qε2(t,x), uε0(t,x))∈L∞((0,T);L1(0,L)∩L∞(0,L))5 is a weak solution of system (7) if for all ϕ=(ϕ1,ϕ2,ϕ3,ϕ4,ϕ5)∈S5, with
we have
Theorem 2.7. (Existence). Under assumptions (4), (5), (6) and for every fixed ε>0, there exists a unique weak solution Uε of the problem (7).
3.
Proof of the existence result
We define the Banach space B:=(L1(0,L)∩L∞(0,L))5. We prove existence using the Banach-Picard fixed point theorem (see e.g., [24] for various examples of its application). We consider a time T>0 (to be chosen later) and the map T:XT→XT with the Banach space XT=L∞([0,T];B), and we denote ‖⋅‖XT=supt∈(0,T)‖⋅‖B. For a given function ˜U∈XT, with ˜U=(˜u1,˜u2,˜q1,˜q2,˜u0), we define U:=T(˜U) solution to the problem :
with initial data u01, u02, q01, q02, u00 in L1(0,L)∩L∞(0,L) and with boundary conditions
where ub∈L1(0,T)∩L∞(0,T).
First we define the solutions of (16) using Duhamel's formula. Under these hypothesis, we may compute u1 and u2 with the method of characteristics
with u01(x), and ub(t) initial and boundary condition, respectively. We have a similar expression for u2(t,x) with u02 instead of u01 and the boundary condition u2(t,L)=u1(t,L) which is well-defined thanks to (17). It reads :
Then, for the other unknowns, one simply solves a system of uncoupled ordinary differential equations leading to :
Using Theorem B.1, the previous unknowns solve the weak formulation reading :
for any (φ1,φ2)∈C1([0,T]×[0,L])2. Using again Theorem B.1 with Φ=|⋅| show that the same holds true for |u1| (resp. |u2|) :
The same holds also for the other unknowns (qi)i∈{1,2} and u0, since for the ODE part of the system (19) provides directly similar results. In the rest of the paper, each time that we mention that we are multiplying formally by sgn each function of system (16) in order to get :
we actually mean that these inequalities hold in the previous sense, i.e. in the sense of (21). The reader should notice that the stronger regularity of the integrated forms (17), (18) and (19) allows to define these solutions on the boundaries of the domain ∂((0,T)×(0,L)). If these would only belong to L∞((0,T);L1(0,L)) they would not make sense. Now the meaning of the formal setting is well defined, we then can proceed by writing that one has :
We have used the fact that sgn(G(˜q2))=sgn(˜q2) from (6), which implies in particular −G(˜q2)⋅ sgn(˜q2)= −|G(˜q2)| and G(˜q2)⋅sgn(u0)≤|G(˜q2)|. In order to obtain inequalities in the weak formulation associated to the latter system it is enough to choose non-negative test functions in C1([0,T]×[0,L]).
Adding all equations and integrating on [0,L], we obtain formally
where we use the boundary condition u1(t,L)=u2(t,L) and (6). Let us define ‖U(t,⋅)‖L1(0,L)5:=∫L0(|u1|+|u2|+|q1|+|q2|+|u0|)(t,x)dx and integrating with respect to time, we obtain:
with η=1miniai(K1+K2+1ε)>0. Here the formal computations are to be understood in the following manner : in the weak formulation associated to (22) we choose the test function φ=(1,1,1,1,1), and the result (23) comes in a straightforward way when neglecting the out-coming characteristic at x=0.
On the other hand, using (17), (18) and (19), one quickly checks that
where the generic constant C depends only on (ai)i∈{0,…,4}, (Ki)i∈{1,2} and ‖G′‖L∞(R) but not on ˜U nor on the data U0. At this step, T maps XT into itself.
Let us now prove that T is a contraction. Let (˜U,˜W)∈X2T, we define U:=T(˜U), W:=T(˜W). Then, by the same token as obtaining (23), we have
Again similar computations as in (24), show that
Therefore, as soon as T<min(1/η,ε/C), T is a contraction in XT. It allows to construct a solution on [0,T] for T small enough. The fixed point solves (17) and (19) in an implicit way. Along characteristics solutions have enough regularity to satisfy (7) in a weak sense (20). Choosing then the test functions φ:=(φi)i∈{1,…,5} to belong to S5 shows that the fixed point is a weak solution in the sense of Definition 2.6. Since the solution U(t,x)=(u1(t,x),u2(t,x),q1(t,x),q2(t,x),u0(t,x)) is well defined as on {T}×(0,L) thanks to regularity arguments stated above, U(T,x) becomes the initial condition of a new initial boundary problem. Thus, we may iterate this process on [T,2T], [2T,3T], …, since the condition on T does not depend on the iteration.
As a result of above computations, we have also that if U1 (resp. U2) is a solution with initial data U1,0 (resp. U2,0) and boundary data u1b (resp. u2b). Then we have the comparison principle :
which shows and implies uniqueness as well.
4.
Uniform a priori estimates
In order to prove our convergence result, we first establish some uniform a priori estimates. The strategy of the proof of Theorem 2.5 relies on a compactness argument. In this Section we will omit the superscript ε in order to simplify the notation.
4.1. Non-negativity and L1∩L∞ estimates
The following lemma establishes that all concentrations of system are non-negative and this is consistent with the biological framework.
Lemma 4.1. (Non-negativity). Let U(t,x) be a weak solution of system (1) such that the assumptions (4), (5), (6) hold. Then for almost every (t,x)∈(0,T)×(0,L), U(t,x) is non-negative, i.e.: u1(t,x), u2(t,x), q1(t,x), q2(t,x), u0(t,x) ≥0.
Proof. We prove that the negative part of our functions vanishes. Using Stampacchia's method, we formally multiply each equation of system (7) by corresponding indicator function as follows:
Again as in the proof of existence in Section 3, these computations can be made rigorously using the extra regularity provided along characteristics in the spirit of Lemma 3.1, [20] summarized in Theorem B.1.
Using again Theorem B.1, one writes formally :
Adding the previous expressions, one recovers a single inequality reading
By Assumption 2.3, we have that sgn(G(q2))=sgn(q2). Thus G(q2)(1{q2<0}−1{u0<0})= G(q2) (1{G(q2)<0}−1{u0<0})≤0. Then integrating on the interval [0,L], we get :
Since u−1(t,L)=u−2(t,L) thanks to condition (5), it follows:
From Assumptions 2.2 and 2.1, the initial and boundary data are all non-negative. Thus u−1(0,x), q−1(0,x), q−2(0,x), u−2(0,x), u−0(0,x) are necessarily zero. This proves solutions' non-negativity and concludes the proof.
Lemma 4.2. (L∞ bound). Let (u1,u2,q1,q2,u0) be the unique weak solution of problem (7). Assume that (4), (5), (6) hold, then it is bounded i.e. for a.e. (t,x)∈(0,T)×(0,L),
where the constant κ≥max{‖G‖∞,‖ub‖∞,‖u00‖∞,‖u0i‖∞,‖q0i‖∞,i∈{1,2}}.
Proof. We use the same method as in the previous lemma for the functions
From system (7) and using the fact that
we get
Adding expressions above gives
Integrating with respect to x yields
where we use the fact that G(q2)≥0 from assumption (6) since q2≥0 thanks to the previous lemma. From the boundary conditions in (1), we have for all t≥0, w+2(t,L)=[u2(t,L)−κ(1+t)]+=[u1(t,L)−κ(1+t)]+=w+1(t,L). Then,
If we adjust the constant κ such that κ≥max{‖G‖∞,‖ub‖∞}, it implies that :
which shows the claim.
For the last estimate on u1(t,L), we sum the first and the third inequalities of the system (26) and integrate on (0,L),
Integrating on (0,T) and since we have proved above that w+0=0 and z+1=0, we arrive at
for κ≥‖ub‖∞.
Lemma 4.3. (L∞tL1x estimates). Let T>0 and let (u1,u2,q1,q2,u0) be a weak solution of system (1) in (L∞([0,T];(L1∩L∞)(0,L)))5. We define:
Then, under hypothesis (4), (5), (6) the following a priori estimate, uniform in ε>0, holds:
Moreover the following inequalities hold:
and
with C>0 constant.
Proof. Since from Lemma 4.1 all concentrations are non-negative, we may write from system (7)
Adding all equations and integrating on (0,L), we get, recalling the boundary condition u1(t,L)=u2(t,L),
Integrating now with respect to time, we obtain:
with H(t) previously defined. It gives the first two estimates of the Lemma. Finally, to obtain the last inequality, we add equations (7a) and (7c) and integrate on (0,L) to get
Since we have shown that ∫L0|u0|dx≤1a0H(t)<∞, we can conclude after integrating with respect to time.
4.2. Estimates on the derivatives
4.2.1. Data regularization
Here we detail the notion of regularization for BV functions. The C∞((0,L))-regularization denoted fδ for a BV(0,L) function f follows the steps below [32,Theorem 5.3.3], i.e.
where {ζk}∞k=1 is a sequence of regular cut-off functions s.t.
where
and there exists δk>0 such that
Although fδ converges strongly to f in L1(0,L), one has only that
where the right hand side is the total variation of the Radon measure associated to the derivative of f [32,Theorem 5.3.3]. This result comes partly form the estimates from above :
Then we set
where c is a given real constant and
χ∈C∞(R) being a positive monotone function.
Lemma 4.4. If f∈BV(0,L), c∈R and fδc defined as above, one has :
where the generic constant C(c,χ) is independent of δ.
Proof. Differentiating (31) and integrating in space gives :
where we used (30).
Definition 4.5. If (u01,u02,q01,q02,u00) and ub are respectively the initial and boundary data associated to the problem (7), under hypotheses 4 and 5, we define as regular data their regularization in the following manner : we set
where u01,δ is the approximation introduced above, the same notation holding for the rest of the initial data.
The matching is C∞ in the neighborhood of (0,0) in [0,L]×[0,T]. Indeed, u0,δ1(x)=c1 when x is close enough to 0 and in the same way uδb(t)=c1 when t is near 0, whereas for the derivatives (u0,δ1)(k)(x)=0 when x is close to zero for any derivative of order k, and the same holds for (uδb)(k)(t) when t is sufficiently small. The same holds true in the neighborhood of the point (t,x)=(L,0).
This regularization procedure allows then to obtain
Lemma 4.6. Assume hypotheses 2.3, and let Uδ be the solution associated to problem (7) with initial data U0,δ=(u0,δ1,u0,δ2,q0,δ1,q0,δ2,u0,δ0) and the boundary condition uδb. Then ∂tUδ belongs to XT:=L∞((0,T);(L1(0,L)∩L∞(0,L)))5. and solves the problem
where uδi,t=∂tuδi and so on.
Proof. The Duhamel's formula obtained by the fixed point method in the proof of Theorem 2.7 provides a solution Uδ∈XT. Deriving Uδ with respect to t, one can show that ∂tUδ solves (32) with initial and boundary conditions (33). Applying then the existence result again proves that actually ∂tUδ belongs to XT.
Remark 1. A priori estimates from previous sections, when applied to the problem (32) complemented with initial-boundary data (33), do not provide a control of ∂tUδ which is uniform with respect to ε.
This remark motivates next paragraphs.
4.2.2. The initial layer
At this step we introduce initial layer correctors. For this sake, on the microscopic scale we define for t∈R+, functions (˜u1,˜u2,˜q1,˜q2) solving
with initial conditions
Actually, this system may be solved explicitly and we obtain for i∈{1,2},
4.2.3. Uniform L1 bounds of the time derivatives
We introduce the following quantities on the macroscopic time scale t∈[0,T] :
Next, we prove uniform bounds on the time derivatives :
Proposition 1. Let T>0. If the data is regular in the sense of Definition 4.5, setting :
with functions v1,v2,sδ1,sδ2 defined in (36), one has :
where W1,1(0,L) denotes the vector-space W1,1(0,L)5.
Proof. From system (7) we deduce
with following initial and boundary conditions:
As G∈C2(R), thanks to Lemma 4.6, ∂tUδ∈L∞((0,T);(L1(0,T)∩L∞(0,L)))5, taking the derivative with respect to t in system (38), ∂tVδ=∂t(vδ1,vδ2,sδ1,sδ2,uδ0) solves
in the sense of Definition (2.6). Again formally, we multiply each equation respectively by sgn(vδi,t) with i=1,2, and sgn(sδj,t), for j=1,2, and by sgn(uδ0,t) in the sense explained in the proof of Theorem 2.7. It gives
Indeed, the right hand side of the 4th and 5th inequalities can be obtained as follows. On the one hand, we have
On the other hand
since G is non-decreasing by assumption (6). Summing all inequalities in (40) and integrating with respect to space on (0,L), we obtain formally
where
Integrating (41) in time, we get
Let us consider each term of the right hand side of (42) separately:
● F1: On the right boundary x=L, one has
where we used trace operator's continuity for W1,1(0,L) functions (using integration by parts, one shows as well that the constant C does not depend on δ).
● F2: On the other hand at x=0, the boundary condition can be estimated as
as above.
● F3: With the change of variable τ=tε, we have, using again (35),
which is uniformly bounded with respect to ε.
● F4: similarly, we have
thanks to the fact that ∂t˜qi(τ,x)=(q0i(x)−u0i(x))e−2τ with i=1,2.
It remains to estimate ˜Ht(0) in (42). Indeed, using (38) at t=0 in order to convert time derivatives into expressions involving only the data and its space derivatives, one obtains
So, for instance, for the first term of the sum, we use the first equation in (38) and we write
Recalling that sδ1(0,x)=q01(x) and vδ1(0,x)=q01(x) as defined in (39) we get: a1∂tvδ1(0,x)=α∂x(q01(x)−u01(x))−α∂xvδ1(0,x)=−α∂xu01(x), then
The rest follows exactly the same way. We conclude from (42) and the above calculations that
Finally, in order to recover (37), we add the first and third inequalities in (40) and integrate on (0,T)×(0,L), we get
We have already proved that the second term of the right hand side is bounded. We have also proved above that uδ0,t is uniformly bounded in L∞((0,T);L1(0,L)). From (39), we have vδ1,t(t,0)=u′b(t)+1ε˜u1,t(tε,0). As above, we use the expressions of ˜u1 and ˜q1 and a change of variable to bound each term of the right hand side.
As a consequence, we deduce the following estimates on the time derivatives of the original unknowns (uδ1,uδ2,qδ1,qδ2,uδ0) :
Corollary 1. Let T>0, under the same assumptions, there exists a constant CT>0 depending only on the W1,1 norm of the data but independent on ε, such that :
Proof. We recall the expressions
By the triangle inequality, we have for i∈{1,2},
The first terms of the latter right hand side are bounded from Proposition 1. For the second terms, we have, as above,
Furthermore, from (42), we get
By the triangle inequality, it implies the second estimate in (43) To recover the third claim in (43), we notice that by definition of vδ1 and a triangle inequality, we have
where again we use the continuity of the trace operator on W1,1(0,L) functions in order to recover the dependence between the values at x=L and the W1,1(0,L)-norm of the initial data. Integrating in time and using (37) allows to conclude.
4.2.4. Uniform bounds on the space derivatives
Lemma 4.7. Let T>0. If the data is regular in the sense of Definition 4.5, then, the space derivatives of functions uδ1, uδ2 satisfy the following estimates :
for some non-negative constant CT uniformly bounded with respect to ε.
Proof. Adding equation (7a) with (7c) and also (7b) with (7d) we get
Using Corollary 1 and (6), the right hand sides are uniformly bounded in L1((0,T)×(0,L)). Deriving the ODE part of (7) with respect to the space variable and using the latter estimates provides the results for uδ0, qδ1 and qδ2.
4.3. Extension to BV data
We show here how to use Corollary 1 and Lemma 4.7 in order to obtain BV compactness.
Theorem 4.8. Under hypotheses (2.1)-(2.3), there exists a uniform bound such that the ε-dependent solutions of system (7) satisfy
where the generic constant C is independent on ε.
Proof. Setting Uδ(t,x):=(uδ1(t,x),uδ2(t,x),qδ1(t,x),qδ2(t,x),uδ0(t,x)), one has from the previous estimates :
Now thanks to Lemma 4.4, one estimates the right hand side with respect to the BV norm of the data :
We are in the hypotheses of [32,Theorem 5.2.1. p. 222] : by L1-continuity, shown in Theorem 2.7, Uδ tends to U:=(u1,u2,q1,q2,u0) in L1((0,T)×(0,L)) strongly, when δ vanishes. Then for any open set V⊂(0,T)×(0,L) one has
and since the BV bound of the sequence (Uδ)δ is uniformly bounded with respect to δ, the result extends by [32,Remark 5.2.2. p. 223] to the whole set (0,T)×(0,L).
5.
Proof of the convergence result (Theorem 2.5)
It is divided into two steps.
1. Convergence : From Lemma 4.2, Lemma 4.3 and Corollary 1, sequences (uε1)ε and (uε2)ε are uniformly bounded in L∞∩BV((0,T)×(0,L)). Thanks to the Helly's theorem [3,18], we deduce that, up to extraction of a subsequence,
with limit function u1,u2∈L∞∩BV((0,T)×(0,L)).
By equations (7a), one shows by testing with the appropriate C1 compactly supported functions in (0,T)×(0,L) and using the definition of the BV norm (cf for instance, [32,p. 220-221]):
which tends to zero as ε goes to 0 thanks to the bounds in Corollary 1 and Lemma 4.7. Therefore, qε1u→ε→01 strongly in L1((0,T)×(0,L)). By the same argument, we show that qε2u→ε→02 strongly in L1((0,T)×(0,L)). Moreover, since G is Lipschitz-continuous, we have, when ε goes to zero,
For the convergence of uε0, let us first denote u0 a solution to the equation
Then, taking the last equation of system (7), subtracting by this latter equation and multiplying by sgn(uε0−u0), we get in a weak sense that
Using Grönwall's Lemma, we get, after an integration on [0,L],
Thus, one concludes that
2. The limit system :
We pass to the limit in (15), the weak formulation of system (7). Suppose that ϕ∈S5. Taking ϕ1=ϕ3 and ϕ2=ϕ4 in (15) we may pass to the limit ε→0 and we obtain
which is exactly (14) with initial data coming from system (7). Finally, since the solution of the limit system is unique, we deduce that the whole sequence converges. This concludes the proof of Theorem 2.5.
6.
Numerical validation
For the sake of simplicity, we assume, in what follows that ai=1, for i∈{0,4} when we discretise problems (7) and (8)-(10). We discretize the domain (0,L) with a uniform mesh in space of size Nx setting :
In order to avoid an ε-dependent CFL, we discretize the linear parts of the source term in (7) in an implicit way, while we keep the transport part explicit and use a MUSCL second order discretization in space [8]. This leads to write the scheme, for i∈{1,Nx−1}
where the time step is chosen s.t.
is less than 1, and the flux limiters are defined as
and the minmod function is defined in a Generalised minmod limiter [8] :
We complement the scheme with initial and boundary conditions :
and
Proposition 2. Under the CFL condition : λ5∈(0,1] which is independent of ε, the scheme (44) preserves positivity and the discrete version of the L∞((0,T);L∞∩L1((0,L)))-norm. Moreover, under the same condition, it is possible to prove that
For the first part, the proof uses at the discrete level similar ideas as in Lemmas 4.1 and 4.2. For the second part, one adds the initial layer (19) to the numerical solutions for each time step and proceeds as in Proposition 1 and Lemma 1. Since the ideas are very similar and the properties of the transport part are rather standard once it is written in a convex form [8,Harten's Lemma], the proof is left to the reader for the sake of concision.
For various values of ε, we compare the solutions provided by (44) with a similar discretisation of (8)-(10), reading :
where
We initialize the data setting :
and boundary conditions are similar to (45). We compare (uni,j)n,i,j and (vni,j)n,i,j using the discrete L1 norm in space and time. Indeed we compute
the results are displayed in Fig. 2.
Appendix A.
Stationary system
Although the study of the rate of convergence for the dynamical system is quite complicated, explicit computations may be performed for the stationary system. This system reads, for x∈(0,L),
completed with the boundary conditions
This system may be reduced by noticing that, after adding the equations in (46), we obtain
From the boundary condition at x=L, we deduce that ˉu1=ˉu2, we denote ˉu:=ˉu1=ˉu2. With (46a)–(46b), we get
From (46e), we deduce
Injecting this latter expression and (47) into (46c), we obtain
With (46e), we deduce
Using also (46a), we obtain the following Cauchy problem
Solving this system, we deduce ˉq2, then we compute ˉu, ˉq1, and ˉu0 thanks to relations (49), (47), and (48).
When, ε=0, system (50) reads
In order to have semi-explicit expression, we introduce an antiderivative of 1/G denoted G, i.e. G′=1G. Then, integrating (50) we get
By the same token on (51), we have
Subtracting the last two equalities, we obtain
Thanks to a Taylor expansion, there exist ζ2 between ˉq2 and ˉq2,0 and ζ02 between ˉq02 and ub such that
where we use (50) for the last equality. Hence we conclude that, formally, the convergence of ˉq2 towards ˉq02 is of order ε.
Appendix B.
Mild solutions of transport equations
We define the problem :
where the data (w,z,u0,v0,ub,vb) satisfy
and (α,ω)∈(R+)2. We define by Duhamel's formula
and v is similarly defined as a function of (v0,vb,z). Then one has, as in [20,Theorem 2.1,Lemma 2.1 and Lemma 3.1], that
Theorem B.1. Let (u,v) be solutions of (52) defined in the sense of characteristics through Duhamel's formula (53), then u (resp. v) satisfies (52) in the weak sense :
for all φ∈C∞([0,T]×[0,L]) and every Φ∈Lip(R).
Acknowledgments
The authors acknowledge the unkonwn referees for their comments and remarks which help in improving the paper.









 DownLoad:
DownLoad:



