A multiclass Lighthill-Whitham-Richards traffic model with a discontinuous velocity function

1.   Introduction

1.1.   Scope

The multiclass Lighthill-Whitham-Richards (MCLWR) model is a generalization of the well-known Lighthill-Whitham-Richards (LWR) model [25,28] to multiple classes of drivers and was formulated independently by Wong and Wong [31] and Benzoni-Gavage and Colombo [1]. The model is given by the following system of conservation laws in one space dimension, where the sought unknowns are the densities $\phi_i = \phi_i (x,t)$ of vehicles of class $i$, $i = 1, \dots, N$, as a function of distance $x$ and time $t$ [1,31]:

Here $\phi = \phi_1 + \dots + \phi_N$ denotes the total density of vehicles. The velocity function $v_i$ is assumed to depend on $\phi$, where we assume that

where $v_1^{\max} < v_2^{\max} < \dots < v_N^{\max}$ are the maximum velocities of the $N$ classes of vehicles and $V$ is a hindrance function that models the drivers' attitude to reduce speed in the presence of other cars. This function is usually assumed to be continuous and piecewise smooth on an interval $[0, \phi_{\max}]$, where $\phi_{\max}> 0$ denotes a maximum vehicle density, with

The simplest function having all these properties is the linear interpolation $V( \phi) = 1- \phi/ \phi_{\max}$. However, equation (1.1) is studied herein under the assumption that $V$ is piecewise continuous with one decreasing jump at a density value $\phi^* \in (0, \phi_{\max})$, that is

We consider (1.1) on the domain $\Pi_T: = (-L,L)\times (0,T)$, where $L>0$ and $T>0$, along with the initial and boundary conditions

Here and throughout the paper, we denote by a tilde the multivalued version of a given discontinuous function. The non-standard boundary condition (1.4b) on the total density is required in case that $s(t) = \phi^*,$ where $\smash{\boldsymbol{s}(t): = (s_{1}(t), \dots, s_{N}(t))^{\mathrm{T}}}$ and $s(t) = s_{1}(t)+\cdots+s_{N}(t).$ This implies that we assign values to $\boldsymbol{\mathcal{F}}(t)$ according to

This assumption is motivated in a wider sense by models of phase transitions between free and congested traffic flow regimes [13,14], and more specifically by treatments of the single-class scalar version of (1.1)–(1.4). In the scalar case the model can be formulated as the following initial-boundary value problem for a scalar conservation law defined on $\Pi_T$:

with a jump in $V$ or equivalently, in the flux $f$, see [29,30], where $\smash{\mathcal{F}(t)\in \tilde{f}(s(t))}$ represents the non-standard boundary condition of the flux discontinuity, see [29].

It is the purpose of the present contribution to introduce a numerical scheme for the MCLWR model with discontinuous flux (1.1)–(1.3) that is based on the available treatment [29] of the scalar model (1.6). The scalar version of the scheme slightly differs from that of [29] but we prove that it produces approximations that also converge to a weak solution. Numerical experiments provide evidence that it approximates the same solutions as the scheme of [29]. In the multiclass case we prove satisfaction of an invariant region principle, that is, numerical solutions assume values in

under corresponding assumptions on the initial and boundary data.

1.2.   Related work

The MCLWR model (1.1) has been studied intensively in recent years. The system (1.1), (1.2) has some interesting properties and in particular admits a separable entropy function for an arbitrary number of driver classes. We refer to [1,2,5,7,9,10,11,19,20,31,32,33,34,35,36,37] for numerical and analytical treatments and emphasize that to our knowledge, a velocity function discontinuous in the unknowns has not been considered so far for the MCLWR model.

Conservation laws with discontinuous flux function arise in many physical applications including flow in porous media [22], sedimentation [8,18], and the LWR traffic model [26,30]. Here we limit the discussion to analyses where the flux is a discontinuous function of the unknown (as opposed to the more widely studied discontinuous dependence on spatial position). This property implies that standard numerical methods cannot be applied directly due to the presence of waves that travel at infinite speed, namely so-called zero waves. These waves carry information about the flux but this value is transported instantaneously, which excludes applying explicit schemes due to the lack of regularity of the flux. Gimse [21] was the first to present a solution to this problem. He studied a conservation law where the flux function has a single jump. He discussed the existence of the zero wave, generalized the method of convex hull construction, and solved the Riemann problem using a front tracking algorithm.

Carrillo [12] studied conservation laws with a discontinuous flux function where the flux is allowed to have discontinuities on a finite subset of real numbers. The proof of existence of solutions is based on the comparison principle and an entropy inequality involving a version of semi-Kružkov entropies. Dias and Figueira [15] studied a related problem by using a mollification technique to smooth out discontinuities. They showed that solutions to a suitably regularized problem converge to solutions of the original problem in the limit. They also defined the notions of weak solution and weak entropy solution. The mollification technique was implemented in [16,17]. Moreover, Dias and Figueira [16] proposed a numerical scheme for Riemann problem. Specifically, they introduced a procedure to obtain a new Lipschitz continuous flux function with the same lower convex envelope of the original flux, and then a standard Lax-Friedrichs method is employed.

Martin and Vovelle [27] considered the problem of numerical approximation in the Cauchy-Dirichlet problem for a scalar conservation law with a flux function having finitely many discontinuities. The well-posedness of this problem had been proved by Carrillo. An implicit finite volume scheme is constructed in [27] and Newton's method is employed to solve the resulting system of nonlinear equations. Furthermore, convergence to the unique entropy solution is shown.

Lu et al. [26] explicitly constructed the entropy solutions for the LWR traffic flow model with a piecewise quadratic flow-density relationship. Their approach is based on constructions of entropy solutions to a sequence of approximate problems in which the flow-density relationship is continuous but tends to the discontinuous flux when a small parameter in this sequence tends to zero.

Bulí$\mathrm{\check{c}}$ek et al. [3] introduced new concepts of entropy weak and measure-valued solutions that are consistent with the standard ones if the flux is continuous. They identified a given discontinuous flux function with a continuous curve that consists of the graph of this flux and abscissae that fill the jumps. Consequently, instead of a discontinuous flux function of the unknown, they deal with an implicit relation that represents a curve. One has one degree of freedom to set up the "optimal" unknown (independent variable). These ideas are combined in [4], where the authors treat the case of a flux function discontinuous in spatial position and the unknown. Through appropriate estimates for entropy measure-valued solutions well-posedness is shown.

Wiens et al. [30] applied Dias and Figueira's mollification approach to solving a conservation law with a piecewise linear flux function in which there is a single discontinuity at a critical point. They introduced a mollified function and then the analytical solution to the corresponding Riemann problem is derived in the limit. Furthermore they constructed a Riemann solver that forms the basis for a high-resolution finite volume scheme of Godunov type and used an alternate approach that eliminates the severe $\mathrm{CFL}$ constraint by incorporating the effect of zero waves directly into the local Riemann solver.

Towers [29] presented a finite difference scheme that implements a splitting consistent with the decomposition the flux $f(u) = p(u)+g(u)$, where $p$ is a Lipschitz continuous function and $g$ is a function of Heaviside type that includes the jumps of $f$. The scheme has the form (see [29,Eq. (3.11)])

which can be written in conservation form as follows:

The first part of the scheme is implicit and consistent with $u_{t}+g(u)_{x} = 0$, but the resulting equations can be solved by evaluation of a piecewise linear function. Hence, an iterative solver like Newton's method is not required. The second part of the scheme is consistent with $u_{t}+p(u)_{x} = 0$ and is explicit, and can be solved by any scheme suitable for a scalar conservation law with Lipschitz continuous flux. Towers [29] focused on the Godunov flux for the explicit part but also presented a simple flux-limited Lax-Wendroff-type modification to the Godunov scheme.

1.3.   Outline of the paper

The remainder of the paper is organized as follows. In Section 2 we present a numerical scheme for the LWR traffic flow model. We first introduce some assumptions and the notion of weak solution in Section 2.1. Next, Section 2.2 is devoted to the presentation of our scheme for the scalar case ($N = 1$) and we imposed the appropriate $\mathrm{CFL}$ condition. Then, in Section 2.3, we prove that under the $\mathrm{CFL}$ condition it satisfies uniform $L^{\infty}$ and $\mathrm{TVD}$ properties. Moreover we prove some kind time continuity estimates and to the end this section we prove convergence of our numerical solutions to a weak solution. In Section 3 we extend the algorithm to the multiclass case ($N>1$) and prove that the scheme preserves the invariant region $\mathcal{D}$. In Section 4 we present several numerical examples to confirm all the results mentioned before. Section 5 collects some conclusions.

2.   Construction of the numerical scheme in the scalar case

Before describing the numerical scheme we introduce some assumptions and the definition of weak solutions proposed in [16], which is employed herein.

2.1.   Preliminaries

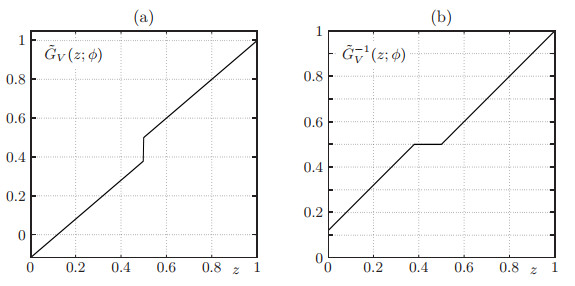
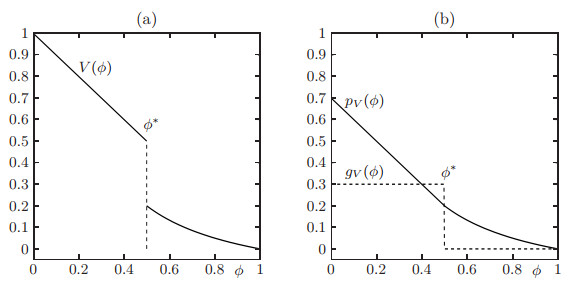
To outline the basic idea, and to make the comparison with [29] transparent, we define the functions

where $p_V$ is a Lipschitz continuous, piecewise smooth and decreasing function, while $g_V$ is a non-negative and decreasing function, see Figure 1. Furthermore, as in [29], we can equivalently specify

where we recall that $\tilde{g}_{V}$ denotes the multivalued version of $g_{V}$. Moreover, we assume that the initial density function $\phi_0$ satisfies

The boundary functions $r$ and $s$ are assumed to satisfy

We also assume that $\mathcal{G}(t)\in[0,\alpha_V]$ for all $t\in[0,T],$ and $\mathcal{G}\in BV([0,T]).$

Definition 2.1 (Weak solution [16]) A function $\phi\in L^{\infty}(\Pi_{T})$ is said to be a weak solution to the initial-boundary value problem (1.6) if there exists a function $q\in L^{\infty}(\Pi_{T})$ satisfying $q(x,t)\in\tilde{f}(\phi(x,t) )$ a.e. such that for all test functions $\psi\in C_{0}^{1}([-L,L]\times[0,T))$,

2.2.   Numerical scheme

The domain $\Pi_T$ is discretized as follows. We choose a partition $\smash{\{I_j\}_{j = 1}^M}$ of $[-L,L]$ composed of uniform cells $I_j = [x_{j-1/2},x_{j+1/2})$, where $x_{j+1/2} = x_{j}+\Delta x/2$, that are centered in $x_j$ and have length $|I_j| = \Delta x = 2L/M$. Then, for $\Delta t >0$, we let $t^n = n\Delta t$ for $n = 0, \dots, \mathcal{N}$, where $\mathcal{N}$ is an integer such that $T\in[t^\mathcal{N},t^\mathcal{N}+\Delta t)$. The unknowns $\smash{\phi_j^n}$ approximate the cell average of the exact solution $\phi(\cdot,t^n)$ in the cell $I_j$. The initial condition is discretized by

and the boundary conditions with $\smash{\mathcal{F}(t)\in\tilde{f}(s)}$ are discretized as follows:

Before proposing our scheme we recall that the basic idea of a splitting scheme consists in solving within each time step, first the PDE

followed by the solution of the conservation law with continuous flux

Note that in the scalar case the constant $v^{\max}$ is immaterial. For the remainder of the analysis of the scalar case we assume that $t$ or $x$ are rescaled so that $v^{\max} = 1$.

Based on the form of the flux function of equations (2.4) and (2.5) and the properties of the functions $g_V$ and $p_V$, we may write a numerical scheme for (1.6) that is motivated by Scheme 4 of [6] in the following form:

The first half-step in (2.6) is semi-implicit and is consistent with (2.4) whereas the second half-step is explicit and consistent with (2.5). Scheme 4 of [6] exploits the density times velocity structure of the flux by calculating the numerical flux by evaluating density on the left cell and velocity (if non-negative) on the right cell adjacent to a cell interface. This idea goes back to a discrete traffic model proposed by Hilliges and Weidlich [23].

In order to evaluate the first line in (2.6), we start by computing the values $\smash{g_{V,j}^{n+1/2}}$ from $j = M+1$ to $j = 1$ (in decreasing order). This is motivated by the following argument, where we start from the semi-implicit equation

along with a known value $\smash{\mathcal{G} (\phi_{M+1}^{n+1/2} )}$ arising from the boundary condition. Next, we write $\smash{g_V (\phi_{j+1}^{n+1/2} )}$ as $\smash{g_{V,j+1}^{n+1/2}}$ and then rearrange (2.7) as

Let us now define the function

along with its multivalued version (with respect to $z$) $\smash{\tilde{G}_V( \cdot; \phi) }$. Then $\tilde{G}_V$ is strictly increasing and has a unique inverse $z \mapsto \smash{\tilde{G}_V^{-1}(z; \phi)}$, see Figure 2. Explicitly, we get

Consequently, we may express (2.8) as

which allows us to obtain $\phi_j^{n+1/2}$ by applying $\smash{\tilde{G}_V^{-1}(z; \phi)}$ to both sides, that is

Now that $\phi_j^{n+1/2}$ is available, we solve for $g_{V, j}^{n+1/2}$ the equation

provided that $\phi_{j-1}^n>0$. If $\phi_{j-1}^n = 0$, we define directly

The numerical scheme can be summarized in Algorithm 2.1:

Algorithm 2.1 (BCOV scheme, scalar case).

Input: approximate solution vector $\{\phi_j^n\}_{j = 1}^M$ for $t = t^n$

$g_{V,M+1}^{n+1/2} \leftarrow \mathcal{G}(\phi_{M+1}^{n+1/2})$ (using (2.3))

do $j = M, M-1, \dots, 1$

      $\phi_j^{n+1/2} \leftarrow \tilde{G}_V^{-1} \bigl( \phi_j^n - \lambda \phi_{j}^n g_{V,j+1}^{n+1/2} ; \phi_{j-1}^n \bigr)$

      if $\phi_{j-1}^n\neq 0$ then

          $g_{V ,j}^{n+1/2} \leftarrow \frac{\phi_j^{n+1/2} - \phi_j^n + \lambda g_{V,j+1}^{n+1/2} \phi_j^n }{ \lambda \phi_{j-1}^n }$

      else

          $g_{V ,j}^{n+1/2} \leftarrow g_V(\phi_j^{n+1/2})$

      endif

enddo

do $j = 1,2, \dots, M$

      $\phi_{j}^{n+1} \leftarrow \phi_{j}^{n+1/2} - \lambda \bigl( \phi_{j}^{n+1/2} p_V \bigl(\phi_{j+1}^{n+1/2} \bigr) - \phi_{j-1}^{n+1/2} p_V \bigl( \phi_j^{n+1/2} \bigr) \bigr)$

enddo

Output: approximate solution vector $\{\phi_j^{n+1}\}_{j = 1}^M$ for $t = t^{n+1} = t^n+\Delta t$

Next, we demonstrate that the numerical scheme (2.11) is consistent with (2.4).

Lemma 2.1. Assume that $\smash{\phi_{j}^{n+1/2}\in[0,\phi_{\max}]}$ for all $j$. Then $\smash{g_{V,j}^{n+1/2}\in\tilde{g}_V(\phi_{j}^{n+1/2})}$ for all $j$. In particular $\smash{g_{V,j}^{n+1/2}\in[0,\alpha_V]}$ for all $j$.

Proof. Let us first assume that $\phi_{j-1} = 0$. Then the result follows from the definition of the function $g_V$ and the corresponding assignment to $\smash{g_{V ,j}^{n+1/2}}$ in Algorithm 2.1. If $\phi_{j-1}\neq 0$, then (2.10) and (2.9) imply that

Therefore, by a straightforward case-by-case study (of the cases arising in (2.9)) we conclude that $\smash{g_{V,j}^{n+1/2}\in \tilde{g}_V(\phi_{j}^{n+1/2})}$.

Now, to derive CFL conditions, we write the scheme (2.6) in incremental form

with the spatial difference operators $\Delta_{+}V_{j}: = V_{j+1}-V_{j}$ and $\Delta_{-}V_{j}: = V_{j}-V_{j-1}$ and the incremental coefficients

To have an $L^{\infty}$ estimate (Lemma 2.2 below) and the Total Variation Diminishing (TVD) property (Lemma 2.3 below) sufficient conditions are

First, we observe the following fact about $\tilde{g}_V.$ If $z_{1},z_{2}\in[0, \phi_{\max}]$ and $z_{1}\not = z_{2},$ then

This property and Lemma 2.1 imply that

Next, the properties of the function $p_V$ ensure that

Finally, to enforce the inequalities

we impose the CFL conditions

2.3.   Convergence of the scalar scheme

The goal is to prove convergence of approximate solution to a weak solution of (1.6). The discrete solutions $\smash{\{\phi_{j}^{n+1/2}\}}$ constructed via the scheme (2.6) are extended to the whole domain $\Pi_{T}$ by defining the piecewise constant function

where $\Delta = (\Delta x,\Delta t)$, and $\chi_{j}(x)$ and $\chi^{n}(t)$ are the characteristic functions of cell $I_{j}$ and the time interval $[t^{n},t^{n}+\Delta t)$, respectively. The ratio $\lambda = \Delta t / \Delta x$ is always kept constant, so the limits $\Delta t \to 0$, $\Delta x \to 0$, and $\Delta \to \boldsymbol{0}$ are equivalent.

We start by proving an $L^{\infty}$ estimate on $\phi^{\Delta}$. In the remainder of this section it is always assumed that the CFL condition (2.14) is in effect.

Lemma 2.2. If $\smash{\phi_{j}^{0}\in[0, \phi_{\max}]}$ for $j = 1,\ldots,M$, then

Proof. Taking $n = 0$ and $j = M$ in (2.10) yields

The boundary condition $g_{V,M+1}^{1/2} = \mathcal{G}(t^0)\subseteq[0,\alpha_V]$ together with the assumption implies that

Since $\smash{\tilde{G}_V^{-1}(\cdot ; \phi)}$ is a nondecreasing function and maps $[-\lambda\alpha_V \phi,\phi_{\max}]$ onto $[0,\phi_{\max}]$, (2.17) implies that $\smash{\phi_{M}^{1/2}\in[0,\phi_{\max}]}$. It follows from (2.1) that $\smash{g_{V,M}^{1/2}\in[0,\alpha_V]}$. Reasoning in this way for $j = M-1,M-2,\ldots,1$ yields $\smash{\phi_{j}^{1/2}\in[0, \phi_{\max}]}$ for $j = 1,\ldots,M$. Since $\smash{\phi_{0}^{1/2},\phi_{M+1}^{1/2}\in[0,\phi_{\max}]}$ by (2.3), and taking into account (2.12), we find that $\smash{\phi_{j}^{1}}$ is a convex combination of $\smash{\phi_{j-1}^{1/2}}$, $\smash{\phi_{j}^{1/2}}$ and $\smash{\phi_{j+1}^{1/2}}$. Thus, $\smash{\phi_{j}^{1}\in[0,\phi_{\max}]}$ for $j = 1, \dots, M$. Repeating this argument inductively for $n = 1,\ldots,\mathcal{N}$ we obtain (2.16).

Lemma 2.3. The discrete approximate solutions generated by the scheme (2.12) satisfy the following spatial variation bounds:

Proof. Applying the operator $\Delta_+$ to (2.12a) and rearranging yields

Taking absolute values, summing over $j = 1,\ldots,M-1$ and using (2.14) we get

Cancelling telescoping terms we obtain

The boundary condition implies

After taking absolute values in the two previous equations, we get

From (2.19) and (2.20)

Reasoning in the same way as the proof of Lemma 5.2 in [29] we find that

It follows by induction that

From (2.21) and (2.22) we get (2.18).

Now, we prove some time continuity estimates. The proof of the first of them is very similar to that of [29,Lemma 5.5], so we omit the details.

Lemma 2.4. The following discrete $L^1$ time continuity estimate holds for $n \geqslant0$:

Lemma 2.5. The following estimate holds:

Proof. We define $g_{V,j}^{0} = g_{V}(\phi_{j}^{0})$. The first equation in (2.6) with $n = 0$ implies

Thus

Taking absolute values in (2.24) and using (2.13) we find that

Summing over $j = 1,\ldots,M$ and cancelling telescoping terms yields

Applying the boundary condition in (2.25), Lemmas 2.1, 2.2, and the CFL condition (2.14) we get (2.23).

Lemma 2.6. There exists a constant $\Omega_3$ that is independent of $\Delta$ such that the following time continuity estimate holds:

Proof. For $n \geqslant2$ and subtracting from the first half-step of (2.6) the corresponding formula for $\smash{\phi_{j}^{n-1/2}}$ and rearranging terms we get

Taking absolute values and applying the CFL condition (2.14) yields

From (2.13) we get

Summing over $j$ and cancelling telescoping terms we obtain

The last inequality implies

We observe that

where

Herein $\varphi(\phi_{j+1},\phi_{j}) = \phi_{j}p_V(\phi_{j+1})$ and $\partial_i \varphi$ denotes the partial derivative of $\varphi$ with respect to the $i$-th argument ($i = 1,2$). Since $\phi,p_V(\phi) \geqslant0$ and $p_V'(\phi) \leqslant 0$, the function $\varphi(\phi_{j+1},\phi_{j})$ is nonincreasing with respect to $\phi_{j+1}$ and nondecreasing with respect to $\phi_{j}$. This implies (together with the CFL condition)

The remainder of the proof is similar to the proof of Lemma 5.6 in [29]. Details are omitted.

Now, we are ready to prove the convergence of $\phi^{\Delta}$ as $\Delta \to \boldsymbol{0}$.

Lemma 2.7. The functions $\phi^{\Delta}$ defined by (2.15) converge in $L^1(\Pi_{T})$ and boundedly a.e. a along subsequence to a limit function $\phi\in C([0,T], L^{1}(-L,L))\cap L^{\infty}(\Pi_{T}) )$.

Proof. The proof is a standard argument using the $L^\infty$ estimate (Lemma 2.2), the uniform spatial variation bound (Lemma 2.3), and the $L^1$ Lipschitz continuity in time estimate (Lemma 2.6).

In order to show that the limit function $\phi$ identified in Lemma 2.7 is a weak solution in the sense of Definition 2.1, we must also prove the convergence of the flux approximations. Instead of showing that the approximations $\smash{\{g_{V,j}^{n+1/2}\}}$ converge we show that the approximations $\smash{\{h_{j}^{n+1/2} \}}$ converge, where we define

and extend these quantities to functions defined on $\Pi_{T}$ by

Now, we require additional time continuity estimates, which is the contents of the following lemma. Its proof is very similar to that of Lemmas 5.8 and 5.9 in [29], and is therefore omitted.

Lemma 2.8. The following uniform estimates hold for $n \geqslant1$, where the constant $\Omega_{4}$ is independent of $\Delta$:

The following lemma is needed to establish a spatial variation bound on the approximations $\smash{h_{j}^{n+1/2}}$.

Lemma 2.9. There exists a constant $\Omega_{5}$ that is independent of $\Delta$ such that

Proof. From the first half-step of the scheme we get

which can be rerranged as

Taking absolute values and summing over $j = 1,\ldots,M$ we get

From Lemma 2.1 and the CFL condition (2.14) we have

The result is obtained from (2.31) in Lemma 2.8 and Lemma 2.3.

We are now ready to bound the spatial variation of the approximations $\smash{h_j^{n+1/2}}$.

Lemma 2.10. There exists a constant $\Omega_{6}$ that is independent of $\Delta$ such that

Proof. The first part of scheme (2.6) can be written as

Applying the spatial difference operator to the above equation we get

Thus

After taking absolute values and using $\smash{|\Delta_{+}g_{V,j}^{n+1/2}| \leqslant\alpha_V}$, Lemma 2.1 and the CFL condition (2.14) we get

Summing over $j = 1,\ldots,M$ we get

Finally, the result follows from Lemma 2.3, (2.31) in Lemma 2.8, and Lemma 2.9.

The following lemma is required to prove the $L^1$ Lipschitz continuity in time and spatial variation bounds on $\smash{ \{ h_{j}^{n+1/2}\} }$.

Lemma 2.11. There exists a constant $\Omega_{7}$ that is independent of $\Delta$ such that

Proof. From (2.27) we get

By induction we obtain

Recalling (2.28) we have

Cancelling telescoping terms and applying (2.29) yields

Then (2.34) becomes

Summing over $n \geqslant2$ and $j = 1,\ldots,M,$ cancelling telescoping terms and multiplying the result by $\Delta x$ we get

where we define

In view of the bounds established so far, there holds

These bounds in conjunction with $\smash{|g_{V,j}^{3/2}-g_{V,j}^{1/2}| \leqslant\alpha_V}$ imply that there exists a constant $\Omega_7$ such that (2.33) is valid.

Lemma 2.12. There exists a constant $\Omega_{8}$ that is independent of $\Delta$ such that

Proof. In light of the spatial variation bound (2.32) we find that

The first part of (2.6) implies

Consequently,

Taking absolute values and using the CFL condition (2.14) we get

Multiplying this inequality by $\Delta x$ and summing over $j$ and $n$ we get

where we define

From (2.18), (2.26), (2.30), (2.31) and (2.33) we have

Combining these bounds we see that there exists a constant $\Omega_8$ that is independent of $\Delta$ such that (2.35) is valid.

In the following lemma we state and prove convergence of the functions $h^{\Delta}$ as $\Delta \to \boldsymbol{0}$. To this end, we define $Q(\phi): = \phi g_{V}(\phi)$ and denote by $\tilde{Q}$ the multivalued version of $Q$.

Lemma 2.13. The functions $h^{\Delta}$ converge in $L^1(\Pi_{T})$ and boundedly a.e. along subsequence to some limit function $w\in L^{1}(\Pi_T)\cap L^{\infty}(\Pi_T)$. Moreover, by a suitable choice of a subsequence, we have $\smash{w(x,t)\in\tilde{Q}(\phi(x,t))}$ a.e. in $\Pi_{T}$, where $\phi(x,t)$ is the limit of Lemma 2.7.

Proof. We observe that $\smash{|h_{j}^{n+1/2}| \leqslant \phi_{\max}\alpha_V}$. Then by Helly's theorem [24] there exists a function $w\in L^{1}(\Pi_{T})$ such that $h^{\Delta}\rightarrow w$ along a subsequence in $L^{1}(\Pi_{T})$ and boundedly a.e. in $\Pi_{T}$. To prove the second assertion, we assume (by extracting further subsequences if necessary) that $\phi^{\Delta}\to \phi,\; h^{\Delta}\to w$ in $L^{1}(\Pi_{T})$ and fix a point $(x,t)\in\Pi_{T}$ where $\phi^{\Delta}(x,t)\to \phi(x,t)$ and $h^{\Delta}(x,t)\rightarrow w(x,t)$ as $\Delta \to \boldsymbol{0}$. First, we consider the case $\phi(x,t) = \phi^{*}$. Lemma 2.1 implies that $0 \leqslant h^{\Delta}(x,t) \leqslant\alpha_V\phi^{\Delta}(x,t)$. Then passing to the limit in the above inequality we obtain

In case $\phi(x,t)\not = \phi^{*}$ first we consider $\phi(x,t)<\phi^{*},$ then $\smash{\tilde{Q}(\phi(x,t)) = \alpha_V\phi(x,t)}$. For sufficiently small $\Delta$ the inequality $\phi^{\Delta}(x,t)<\phi^*$ implies that $\smash{\phi_{j}^{n+1/2} < \phi^*}$ and $\smash{\tilde{g}_{V}(\phi_{j}^{n+1/2}) = \{\alpha_V\}}$. Then, by Lemma 2.1 we get

Thus $w(x,t) = \lim h^{\Delta}(x,t) = \alpha_V\lim\phi^{\Delta}(x,t) = \alpha_V\phi(x,t) = \tilde{Q}(\phi(x,t)).$

In the case $\phi(x,t)>\phi^{*}$ there holds $\smash{\tilde{Q}(\phi(x,t)) = 0}$. In this case it is necessary extend $\smash{\{g_{V,j}^{n+1/2}\}}$ to functions defined on $\Pi_{T}$ by

and we need to utilize the following consequence of Lemma 2.1:

For sufficiently small $\Delta$, $\phi^{\Delta}(x,t)>\phi^*$ implies that $\tilde{g}_{V}(\phi^{\Delta}(x,t)) = \{0\}$, hence $g_{V}^{\Delta}(x,t) = 0$. Finally observe that $0 \leqslant h^{\Delta}(x,t) \leqslant\phi^{\Delta}(x,t) g_{V}^{\Delta}(x,t) = 0$ for sufficiently small $\Delta$. Hence $w(x,t) = \tilde{Q}(\phi(x,t)) = 0.$

Theorem 2.14 (Main result). The functions $\phi^{\Delta}$ converge in $L^1(\Pi_{T})$ and boundedly a.e. along subsequence to some $\phi\in C([0,T],L^{1}(-L,L))\cap L^{\infty}(\Pi_{T})$. The limit function $\phi(x,t)$ is a weak solution in sense of Definition 2.1.

Proof. The convergence is ensured by Lemma 2.7. It remains to prove that the limit $\phi$ is a weak solution. Let us fix a point $(x,t)\in\Pi_{T}$, then Lemma 2.13 implies that $\smash{w(x,t)\in\tilde{Q}(\phi(x,t))}$ a.e. in $\Pi_{T}$. If $\phi(x,t)\not = \phi^*$, then $\smash{\tilde{Q}(\phi(x,t)) = Q(\phi(x,t))}$. Thus $w(x,t) = Q(\phi(x,t)),$ then we define $q(x,t) = \phi p_V(\phi)+ Q(\phi(x,t)) = f(\phi(x,t))$. In the case where $\phi(x,t) = \phi^*$ we take $w(x,t)\in[0,\alpha_V\phi^*]$ and define

In either case $q(x,t)\in\tilde{f}(\phi(x,t))$.

We note that the two steps of (2.6) imply

We now choose a test function $\psi\in C_0^{1} ((-L,L)\times[0,T))$ and define $\psi_{j}^{n}: = \psi(x_j,t^n)$. Multiplying (2.36) by $\Delta x \psi_{j}^n$ and summing the result over $j$ and $n$ yields

A summation by parts yields

An application of (2.12) yields, as $\Delta x, \Delta t \to 0$,

This equation and Lemma 2.3 imply that the two first sums in (2.37) converge to

Concerning the last term in (2.37), we get

By properties of the function $p_V$ we get the estimate

Thus

which tends to zero as $\Delta x\rightarrow 0$. Therefore the last term in (2.37) converges to

as $\Delta x\rightarrow 0$. The second term in (2.37) can be written as

Using Lemmas 2.9, 2.1, and 2.8 we get

Consequently, as $\Delta x\rightarrow 0$,

Then substituting $\smash{g_V^{\Delta}(x_j,t^n) = g_{V,j}^{n+1/2}}$ and applying the dominated convergence theorem we obtain that the second term in (2.37) converges to

Collecting the previous results we get

so $\phi$ is a weak solution in sense of Definition 2.1.

3.   Extension to the MCLWR model

Algorithm 2.1 cannot be applied directly in a component-wise manner for each class $i$ in the multiclass case (1.1)–(1.4), but we can first solve for the total density $\phi$ and then update the densities $\phi_1, \dots, \phi_N$ for each class. The multiclass version of the scalar scheme (1.6) can be written as

where the following quantity is an approximate value of the total density $\phi$:

In order to solve (3.1), we need to impose the non-standard boundary condition (1.4b). Recalling that $V(\phi) = g_{V}(\phi)+p_V(\phi)$ we can equivalently specify for the multiclass case the condition (2.2). The correspondence when $s(t) = \phi^*$ is

Coming back to (3.1), we define $\smash{\Phi_j^n : = (\phi_{1,j}^n, \dots, \phi_{N,j}^n)^{\mathrm{T}}}$. Summing over $i$, assuming that $g_V$ is evaluated at the new time step, and replacing $\smash{g_{V} ( \phi_{j+1}^{n+1/2})}$ by $\smash{g_{V,j+1}^{n+1/2}}$ yields

This can be rearranged as

Let us now define the function $G_V ( z; \Phi ) : = z - \lambda ( \boldsymbol{v}^{\max})^{\mathrm{T}} \Phi g_V (z)$ and denote by $\smash{\tilde{G}_V( \cdot; \Phi)}$ its multivalued version (with respect to $z$). Then $\smash{\tilde{G}}$ is strictly increasing and has a unique inverse $z \mapsto \smash{\tilde{G}_V^{-1}(z; \Phi)}$. Expressing (3.4) as

which allows us to obtain $\smash{\phi_j^{n+1/2}}$ by applying $\smash{\tilde{G}_V^{-1}(\cdot; \Phi_{j-1}^n)}$ to both sides, that is

Now that $\phi_j^{n+1/2}$ is available, we solve for $\smash{g_{V, j}^{n+1/2}}$ the equation

(cf. (3.3)). This yields

provided that $\smash{ \Phi_{j-1}^n \neq \boldsymbol{0}}$. If $\smash{ \Phi_{j-1}^n = \boldsymbol{0}}$ then we set $\smash{ g_{V ,j}^{n+1/2} = g_V(\phi_j^{n+1/2}) }$. The numerical scheme for the multiclass model can be summarized in the following algorithm.

Algorithm 3.1 (BCOV scheme, multiclass case).

Input: approximate solution vector $\{\phi_{i,j}^n\}_{j = 1}^M$, $i = 1,\dots,N$ for $t = t^n$

$g_{V,M+1}^{n+1/2} \leftarrow \mathcal{G}(\phi_{M+1}^{n+1/2})$ (using (2.3) and (3.2))

do $j = M, M-1, \dots, 1$

      $\phi_j^{n+1/2} \leftarrow \tilde{G}_V^{-1} \bigl( \phi_j^n - \lambda g_{V,j+1}^{n+1/2} (\boldsymbol{v}^{\max})^{\mathrm{T}} \Phi_j^n ; \Phi_{j-1}^n \bigr)$

      if $\Phi_{j-1}^n\neq \boldsymbol{0}$ then

          $g_{V ,j}^{n+1/2} \leftarrow \frac{\phi_j^{n+1/2} - \phi_j^n + \lambda g_{V,j+1}^{n+1/2} (\boldsymbol{v}^{\max})^{\mathrm{T}} \Phi_j^n }{ \lambda (\boldsymbol{v}^{\max})^{\mathrm{T}}\Phi_{j-1}^n }$

      else

          $g_{V ,j}^{n+1/2} \leftarrow g_V(\phi_j^{n+1/2})$

      endif

enddo

do $j = 1, \dots, M$

      do $i = 1, \dots, N$

          $\phi_{i,j}^{n+1/2} \leftarrow \phi_{i,j}^n - \lambda v_i^{\max} \bigl( \phi_{i,j}^n g_{V,j+1}^{n+1/2} - \phi_{i,j-1}^n g_{V,j}^{n+1/2} \bigr)$

      enddo

enddo

do $j = 1, \dots, M$

      do $i = 1, \dots, N$

$\phi_{i,j}^{n+1} \leftarrow \phi_{i,j}^{n+1/2} - \lambda v_i^{\max} \bigl( \phi_{i,j}^{n+1/2} p_V \bigl(\phi_{j+1}^{n+1/2} \bigr) - \phi_{i,j-1}^{n+1/2} p_V \bigl( \phi_j^{n+1/2} \bigr) \bigr)$

      enddo

enddo

Output: approximate solution vectors $\{\phi_{i,j}^{n+1}\}_{j = 1}^M$, $i = 1,\dots,N$ for $t = t^{n+1} = t^n+\Delta t$

Remark 3.1 We recall that $\smash{g_{V,M+1}^{n+1/2} = \mathcal{G}(\phi_{M+1}^{n+1/2})}$, the boundary condition that appears in Algorithm 3.1, is defined using (2.3) for the total density $\smash{\phi_{M+1}^{n+1/2}}$. We illustrate this boundary condition in Section 4.5.

The problem of interest to us is to show that $\mathcal{D}$ is an invariant region of the scheme. To this end we first consider the evolution of the total density $\phi$. Summing over $i = 1,\ldots,N$ the second equation in (3.1) yields

The above equation can be written in incremental form as

where we define

Since $p_V(\phi)$ is a non-increasing positive function we have $\smash{C_{j+1/2}^{n+1/2},D_{j-1/2}^{n+1/2} \geqslant 0}$. To ensure that $\smash{|C_{j+1/2}^{n+1/2}| \leqslant 1/2}$ and $\smash{|D_{j-1/2}^{n+1/2}| \leqslant 1/2}$ we impose the CFL condition

Lemma 3.1. Assume that $\Phi_j^{0}\in\mathcal{D}$ for $j = 1,\dots,M$. Then $\smash{\Phi_j^{n},\Phi_j^{n+1/2}}\in\mathcal{D}$ for $j = 1,\dots,M$.

Proof. We claim that

In the case $\smash{\Phi_{j-1}^n} = \boldsymbol{0}$ the result follows from the definition of the function $g_V$ and (2.1). Suppose that $\smash{\Phi_{j-1}^n} \not = \boldsymbol{0},$ summing over $i = 1,\dots, N$ the first equation in (3.1) yields

Using (3.5) and (3.3) we find that

Thus, a straightforward case-by-case study and (3.5) prove that (3.8) is valid. The remainder of the proof is similar to the proof of Lemma 2.2.

4.   Numerical examples

We now present some numerical simulations to illustrate the behaviour of solutions to system (1.1) by using Algorithms 2.1 and 3.1 for the scalar and multiclass case, respectively. In the scalar case, we compare numerical approximations with those generated by the scheme (1.7) proposed by Towers in [29]. In all numerical examples for both the scalar ($N = 1$) and system ($N \geqslant 2$) cases we use the discontinuous velocity function

where $\phi^{\ast} = 0.5,$ $w_{\mathrm{f}} = 0.2$, $\phi_{\max} = 1$, and $\alpha_V = 0.3$.

In all numerical experiments computations are performed on a finite interval $[-1,1]$ that is subdivided into $M$ subintervals of length $\Delta x = 2/M$, and the time step is computed by $\Delta t = \Delta x / 2$ in the scalar case ($N = 1$) and $\Delta t = \Delta x / ( 2 \max \{ v_1^{\max}, \dots, v_N^{\max} \})$ in the multiclass case ($N \geqslant 2$). These choices ensure that the respective CFL conditions (2.14) and (3.7) are satisfied.

4.1.   Example 1: scalar Riemann problem ($N=1$).

We consider the Riemann problem for the scalar equation $\partial_t \phi + \partial_x (\phi V(\phi)) = 0$ with initial data

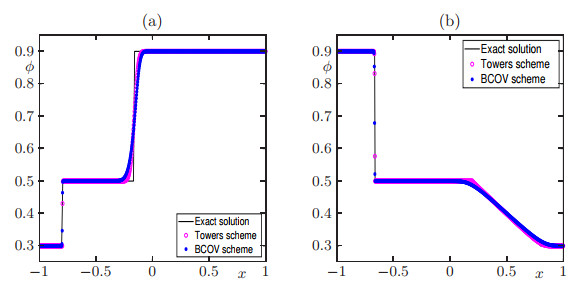
(no boundary conditions are involved). For $\phi_{\mathrm{L}} = 0.3$ and $\phi_{\mathrm{R}} = 0.9$, the solution consists of two shock waves with negative velocities of propagation, namely a shock wave connecting $\phi_{\mathrm{L}}$ with $\phi^*$ that travels at velocity $\sigma_1 = -0.55$ and another shock wave connecting $\phi^*$ with $\phi_{\mathrm{R}}$ with velocity $\sigma_2 = -0.2$. Figure 3(a) shows the numerical approximations to the solution of this problem computed with $M = 800$ for both schemes at simulated time $T = 1.8$.

For $\phi_{\mathrm{L}} = 0.9$ and $\phi_{\mathrm{R}} = 0.3$, the solution consists of a shock wave connecting $\phi_{\mathrm{L}}$ with $\phi^*$ that travels at velocity $\sigma_1 = -0.575$ and a rarefaction wave connecting $\phi^*$ with $\phi_{\mathrm{R}}$. In Figure 3(b) we display the numerical solutions computed with $M = 800$ for both schemes at simulated time $T = 1.5$. In both scenarios, all waves are approximated correctly by both schemes.

4.2.   Example 2: scalar problem ($N=1$), smooth initial datum

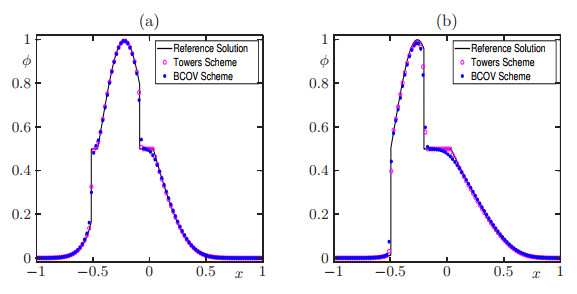
In this example we compare numerical approximations for equation (1.1) obtained by both schemes (Towers scheme (1.7) and Algorithm 2.1), starting from the initial function $\phi_0(x) = \exp(-(x+0.2)^2/(0.04))$ for $x\in[-1,1]$. Numerical approximations are computed at simulated times $T = 0.1$ and $T = 0.3$ with discretizations $M = 100\times 2^l$, $l = 0,1,\dots,4$. Table 1 displays the corresponding approximate $L^1$ errors obtained by utilizing a reference solution computed by the Towers scheme with $M_{\text{ref}} = 12800$. We observe that the approximate $L^{1}$ errors decrease as the grid is refined. In Figure 4 we display the numerical approximations for $M = 100$ and compare them with the reference solution.

4.3.   Example 3: scalar problem ($N=1$), non-standard boundary condition

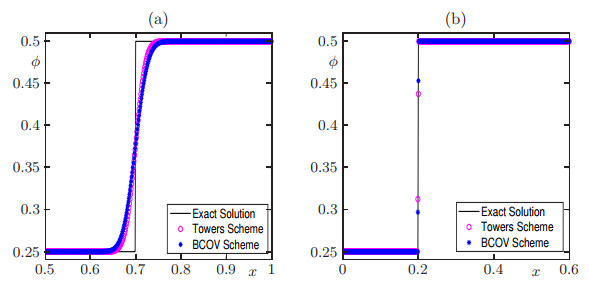
This example comes from [29,Example 6.2] and is designed to illustrate that when $s(t^n) = \phi^*$, the solutions depend on the boundary condition $\mathcal{F}(t)\in\smash{\tilde{f}}(\phi ^*)$. For this example we consider the Riemann problem with initial data (4.1) with $\phi_{\mathrm{L}} = 1/4$ and $\phi_{\mathrm{R}} = 1/2$. We compute the solution twice, once using $\mathcal{G}(t) = \alpha_V$ (equivalently, $\mathcal{F}(t) = 1/2$), and the second time using $\mathcal{G}(t) = 0$ (equivalently, $\mathcal{F}(t) = 1/4$). As shown in Figure 5, in the first case the solution corresponds to a shock wave connecting $\phi_{\mathrm{L}}$ with $\phi_{\mathrm{R}}$ with speed of propagation $\sigma = 1$, and in the second case the solution corresponds to a stationary shock ($\sigma = 0$) connecting $\phi_{\mathrm{L}}$ with $\phi_{\mathrm{R}}$.

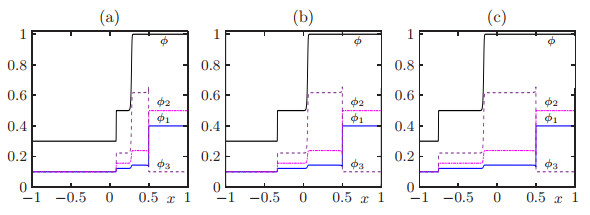
4.4.   Example 4: multiclass case ($N=3$), preservation of invariant region

To illustrate the invariant region property of the proposed scheme (Lemma 3.1), we consider the case $N = 3$ and the Riemann initial data

with velocities $\boldsymbol{v}^{\max} = (1,3,10)^{\mathrm{T}}$. The solution consists of a stationary shock plus two shock waves that travel with negative velocities. The numerical simulation at three simulated times is displayed in Figure 6. The profile for each class and the total density are displayed in this figure. Furthermore we can see that the profile of the total density in Figure 6 looks like the profile of Figure 3(a).

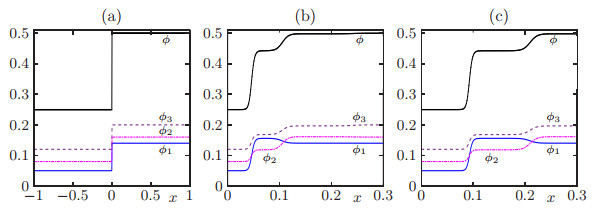
4.5.   Example 5: multiclass case ($N=3$), non-standard boundary condition

It is the purpose of this example to illustrate the boundary condition

where $\mathcal{G}( \cdot)$ is specified in (2.3), that appears within Algorithm 3.1. To this end consider $N = 3$ and the velocities and Riemann initial data

Observe that $\phi_{\mathrm{R}} = \phi^{*} = s(t)$, where $\phi_{\mathrm{R}}$ is the total density of the right state $\Phi_{\mathrm{R}}$.

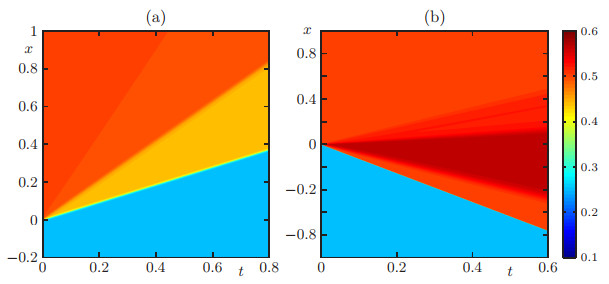
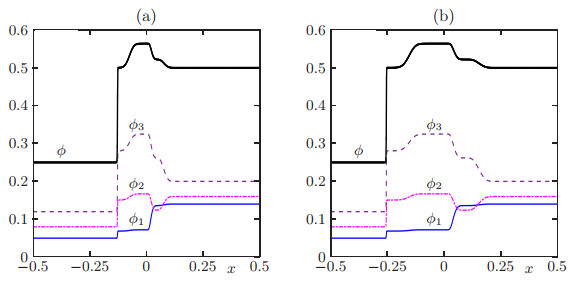
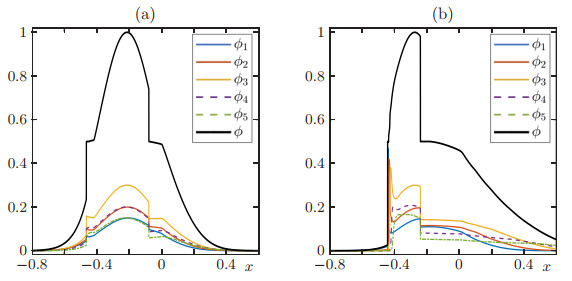
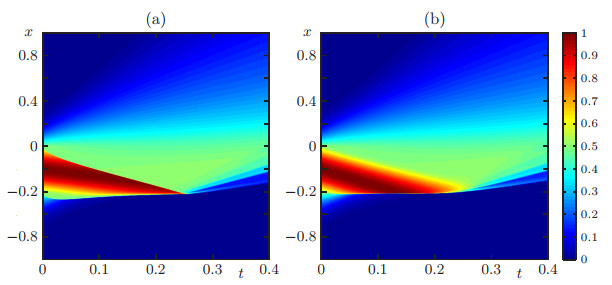
As in Example 3 we show that the solution depends on the boundary condition $\boldsymbol{\mathcal{F}}(t)\in(\boldsymbol{v}^{\max})^{\mathrm{T}}\boldsymbol{s}(t)\tilde{V}(s(t)).$ We start with the initial condition shown in Figure 7(a) and compute the solution twice, once using $\mathcal{G}(t) = \alpha_V,$ and the second time using $\mathcal{G}(t) = 0$. In Figures 7(b) and (c) we display the profile for each class and total density for the first case $\mathcal{G}(t) = \alpha_V$ at two different simulated times. We can see that in this case a free-flow regime is produced, which is verified in Figure 8(a). In Figure 9 we display the profiles for each class and total density for the second case $\mathcal{G}(t) = 0$ at two different simulated times. In contrast to the previous cases, a congested flow regime is produced, as is illustrated in Figure 8(b).

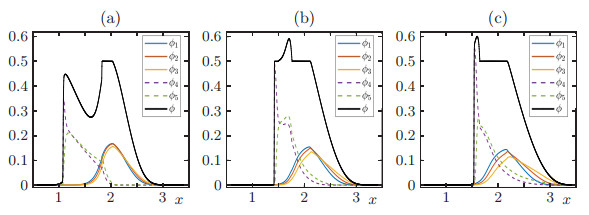
4.6.   Example 6: multiclass case ($N=5$), smooth initial condition

In this example we consider $N = 5$, the velocities $\boldsymbol{v}^{\max} = (1,2,3,4,5)^{\mathrm{T}}$, and the initial condition

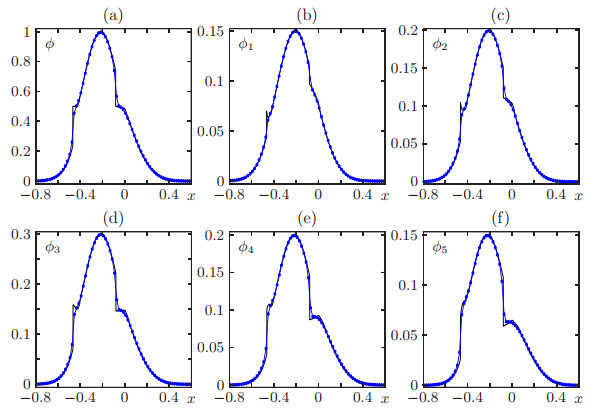
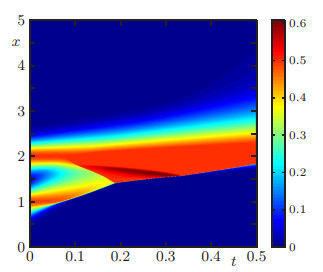
We display in Figure 10 numerical approximation computed with $M = 1600$ at simulation times $T = 0.02$ and $T = 0.12.$ We observe the dynamics of each individual densities $\phi_{i}$ and the total density $\phi$, which exhibits a shock wave due to the discontinuity in the flux. This behaviour is similar to that presented in Figure 4. In Figure 11 we display the evolution of $\phi^{\Delta}(\cdot,t)$ for $t\in[0,0.12],$ and we compare the solution with the approximation of the continuous problem (where $\alpha_V = 0$). For the discontinuous case the shock is more clearly observed than in the continuous case. In Figures 12 and 13 we compare the numerical approximation computed with $M = 100,$ with a reference solution at simulated times $T = 0.02$ and $T = 0.12$. In Table 2 we compute the approximate $L^1$ error based on a reference solution obtained by the BCOV scheme with $M_{\text{ref}} = 12800$. We observe that the approximate $L^{1}$ errors decrease as the grid is refined.

4.7.   Example 7: multiclass case ($N=5$), bimodal smooth initial condition

In this example we consider $N = 5$, the velocity vector $\boldsymbol{v}^{\max} = (1,1.5,2,6,7)^{\mathrm{T}}$, and the initial condition

where we define

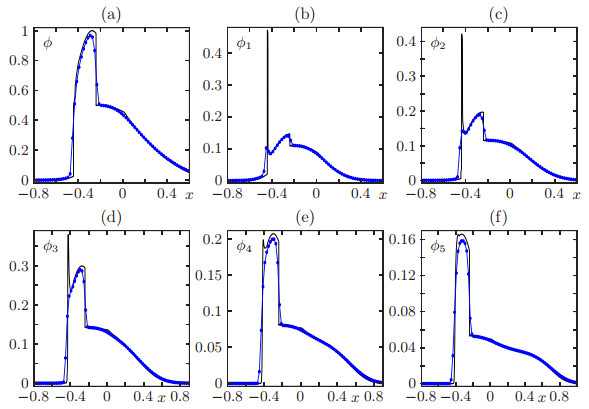
for $x\in[0,5]$. We compute numerical approximation at simulated times $T = 0.1$, $T = 0.2$ and $T = 0.3$ with different discretizations by using $M = 100\times 2^l$ and $l = 0,1,\dots,4.$ In Table 3 we compute the $L^1$ error comparing with respect to a reference solution computed by the BCOV scheme with $M_{\text{ref}} = 12800$. We observe that the approximate $L^{1}$ errors decrease as the grid is refined. Figure 14 shows results for $M = M_{\text{ref}} = 12800$. The numerical results of Figure 14 indicate that jumps in the total density $\phi$ only occur from smaller to higher values in an increasing $x$-direction. This phenomenon occurs because the speeds of the last two classes are greater than the first three. Furthermore, in Figure 15 we show the simulated total density computed by the BCOV scheme with $N = 5$ and $M = 1600$.

5.   Conclusions

We have proposed a numerical scheme for an MCLWR model with a velocity function that is discontinuous in the solution variable. The treatment is motivated and in part based on the numerical scheme proposed by Towers [29]. However, in contrast to that approach we assume that the discontinuity is present in the velocity function (not in the flux); this observation makes it possible to construct an alternative scheme based on Scheme 4 of [6]. Furthermore, we have seen that our scheme can easily be extended to the multiclass case. We have proved for the scalar case that the numerical approximations convergence to a weak solution and for the multiclass case that the scheme preserves an invariant region. Examples 1 to 3 indicate that the scheme converges to the same weak solution as that of [29], and all numerical examples indicate that our scheme converges in both the scalar and multiclass cases.

The present analysis and numerical method can be extended in several directions. Concerning the model itself, at the moment a certain shortcoming is the limitation to the initial-boundary value problem on a fixed road segment. This is due to the particular boundary condition (1.5). It seems desirable to obtain a formulation for a closed road with periodic boundary conditions (a configuration that is commonly studied in traffic modeling to analyze, say, the formation of stop-and-go waves; cf., e.g., [5,11]). However, it is not obvious whether the way the boundary condition is posed allows "gluing together" the ends of the computational domain to create a "seamless" closed circuit. Open issues also include the incorporation of discontinuities in spatial position (akin to the treatment in [9]), and the discussion of the notion of entropicity. In fact, the issue of convergence to an entropy solution is an open problem even in the scalar case for both the scheme advanced in [29] as well as the present approach. Likewise, we recall that for general $N$ the MCLWR model with a Lipschitz continuous function $V$ admits a separable entropy function (see [1,2]) that can be utilized, for instance, to construct entropy stable schemes [10]. It remains to be explored whether these concepts are meaningful for the MCLWR model with a discontinuous velocity function $V$. Finally, it is clear that the numerical method is formally first-order accurate and can possibly improved by known techniques (e.g., weighted essentially non-oscillatory (WENO) reconstructions in combination with higher-order time integrators).

Acknowledgments

The authors are supported by the INRIA Associated Team "Efficient numerical schemes for non-local transport phenomena" (NOLOCO; 2018–2020). RB, RO and LMV also acknowledge support by project CMM, ANID-/PIA/AFB170001. In addition, LMV is supported by Fondecyt project 1181511 and RB by projects Fondecyt 1170473 and CRHIAM, ANID/FONDAP/15130015.