Robot's finger and expansions in non-integer bases

1.   Introduction

Microwave and millimeter wave imaging (MMI) techniques are growing fast in a broad range of applications including but not limited to biomedical imaging ^[1], security screening ^[2,3], non-destructive testing ^[4,5], through-the-wall imaging ^[6], imaging of buried objects ^[7], etc. They offer significant advantages such as non-ionizing radiation, penetration inside optically opaque media, lower cost, and more compact systems compared to other competitive technologies in relevant applications.

Three-dimensional (3D) MMI imaging provides high resolution images of the interior of the inspected medium. In practice, fast and robust 3D MMI techniques have been developed based on the use of frequency-stepped holographic techniques for far-field ^[2] and near-field imaging applications ^[8]. In frequency-stepped techniques, the inspected medium is illuminated by high frequency electromagnetic waves at multiple (discrete) frequencies and the scattered fields due to the objects are acquired at those frequencies. Besides, the data acquisition process is based on the collection of the scattered fields over a two-dimensional (2D) surface referred to an "aperture" (e.g., see ^[9]) similar to the synthetic aperture radar (SAR) techniques ^[2].

Recently, the use of frequency-modulated continuous-wave (FMCW) radar technology along with data collection over a 2D aperture (similar to SAR imaging) has been employed in compact and cost-effective imaging systems. In FMCW radar, the frequency of the transmitted signal varies up and down over a fixed period of time by a modulating signal. Frequency difference between the received signal and the transmitted signal increases with delay, and hence with distance. Echoes from a target are then mixed with the transmitted signal to produce a beat signal which will give the distance of the target after demodulation ^[10]. Unlike pulse radars that operate with high peak transmission power, FMCW systems require low transmission power. This leads to lower cost and more compact systems which is desired for civilian and military applications.

In ^[11], a mm-wave imaging system has been proposed for detection of concealed weapons or contraband in luggage. It uses a FMCW radar along SAR technique and a polar format algorithm (PFA) has been employed for reconstructing 3D images. The drawback of this system is that only a limited region can be imaged well. Besides, it requires 2D interpolation, which is computationally expensive. Another near-field 3D imaging based on FMCW radar has been proposed in ^[12]. It offers a freehand scanner employing an optical tracking system to capture the position of the radar. Thus, the scanning time is reduced significantly compared to conventional SAR imaging due to the partial scanning of the 2D aperture. The imaging technique is inspired by the time-domain delay and sum (DAS) algorithm. In ^[13], yet another near-field 3D imaging has been proposed based on the combination of the FWCW radar and SAR imaging. The reconstruction technique is based on the back-propagation (BP) principle. To reduce the computational time, the principle of stationary phase (POSP) has been employed along with Stolt interpolation to derive the image reconstruction expressions. This modified BP technique is called range migration (RM) imaging. The focusing capability of this algorithm is better than the PFA algorithm in ^[11]. Besides, it only needs interpolation in the range dimension, and thus the processing is much faster than the method in ^[11].

In this paper, we show that the imaging techniques proposed based on the BP concept in ^[13] and DAS concept in ^[12] (when scanning the whole aperture) are equivalent within the context of FMCW radar. Then, for the first time, we compare the quality of the reconstructed images based on these methods along with those based on the RM method ^[13] by 3D image reconstruction examples and study the degradations due to the increased sampling step and reduced aperture size. For a quantitative comparison, we use the structural similarity (SSIM) index proposed in ^[14].

2.   Signal modeling and 3D imaging in FMCW radar

In FMCW radar, the complex time-domain transmitted signal is expressed as ^[15]:

where ${f_c}$ is the center frequency, ${T_s}$ is the chirp duration, and $\alpha $ is the frequency sweep rate which is equal to the ratio of the bandwidth B to the chirp duration ${T_s}$ as:

From (1), the instantaneous frequency ${f_{TX}}(t)$ can be obtained as:

After mixing the transmitted and received signals in a dechirp-on-receive system to reduce the required sampling rate ^[15], neglecting the amplitude variations in near-field imaging, and using Born approximation ^[16], the intermediate frequency (IF) also known as beat signal can be written as:

where $r = (x, y, z)$ and ${r_t} = ({x_t}, {y_t}, {z_t})$ denote the positions of the object and transceiver, respectively, O is the object's spatial domain, $c(r)$ is the object's reflectivity function (also known as the contrast function), and $\tau ({r_t}, r)$ is the time delay for the signal traveling the distance $R({r_t}, r)$ between the transceiver position and point object position and can be written as:

where ${v_0}$ is the velocity of light. The FMCW radar systems typically do not capture the complex signal as represented in (4) due to the lack of an IQ mixer. However, the complex data can be constructed analytically using Hilbert transform ^[17]. Furthermore, in near-field imaging, the phase term $ - 0.5\alpha {\tau ^2}({r_t}, r)$ in (4) can be neglected ^[12].

In the following, we prove that the imaging techniques based on the DAS ^[12] and BP ^[13] concepts, within the context of FMCW radar, are equivalent.

2.1.   Image reconstruction inspired by DAS concept in FMCW radar

Here, we consider the 3D image reconstruction that was originally presented in ^[12] inspired by the time-domain DAS imaging concept. First, for each pair of transceiver position ${r_t}$ and image position $r' = (x', y', z')$, the beat signal is compensated by ${e^{ - j2\pi {f_c}\tau ({r_t}, r')}}$ term and then the Fourier transform of that is written as:

If there is a point object at $r'$, we expect $\tilde s({r_t}, r', f)$ to have a peak in the so called beat frequency at $f = \alpha \tau ({r_t}, r')$ ^[15]. Thus, evaluating $\tilde s({r_t}, r', f)$ at the beat frequency, we obtain:

Then, the reconstructed image ${I^{{\rm{DAS}}}}$ is obtained by implementing this process for every pair of ${r_t}$ and $r'$ positions and integrating them over the scanned aperture A as:

Now, by substituting $s({r_t}, t)$ from (4) in (8) (neglecting the last phase term in (4) in near-field imaging), keeping the terms depending on time t inside the inner-most integral, and using (5), we obtain:

The inner-most integral can be considered as a Fourier transform integral and it can be written as

where ${\rm{sinc}}(\cdot)$ is the sinc function. Then, (9) is written as:

For an ideal scenario, when the chirp duration is very long ${T_s} \to \infty $, the reconstructed image can be written as:

where $\delta (\cdot)$ denotes the Dirac delta function. Eq (12) can be further simplified as:

2.2.   Image reconstruction based on the BP concept

Here, we consider the 3D image reconstruction based on the BP concept that was originally proposed in ^[13]. For this purpose, first, the range wavenumber is defined as:

Using (14), (4) can be written as (neglecting the last phase term in (4) in near-field imaging):

Then, the reconstructed image ${I^{{\rm{BP}}}}(r')$ can be obtained as:

Using (15) in (16) leads to:

If ${k_r}$ is substituted from (14) in (17), we obtain:

Now, by changing the variable for the inner-most integral from ${k_r}$ to $t$, keeping the terms depending on time t inside the inner-most integral, and using (5), we obtain:

Obviously, the reconstructed image in (19) is similar to the one in (9). Following similar discussions, it can be written as:

Thus, it is deduced that the image reconstruction expressions in (11) and (20) are equivalent (ignoring the coefficients that disappear after image normalization).

2.3.   Image reconstruction based on the RM concept

In ^[13], the original imaging based on the BP concept has been extended further to expedite the processing. There, an RM solution has been proposed based on the use of POSP along with Stolt interpolation along one dimension. For the sake of brevity, we only present the final expression here:

where $F{T_{x, y}}\{ \cdot \} $ denotes the Fourier transform with respect to x and y axes, and ${k_x}$, ${k_y}$, and ${k_z}$ are wavenumbers with respect to x, y, and z, respectively, with the following relation between them:

3.   Simulation results

In order to compare the performance of the discussed 3D imaging techniques, we conduct a simulation study where the values of the parameters are: ${T_s} = 1{\rm{ ms}}$, ${f_c} = 94{\rm{ GHz}}$ (wavelength $\lambda = 3.2{\rm{ mm}}$), and $B = 6{\rm{ GHz}}$. The beat signal is sampled with a frequency of 256 KHz. The above-mentioned bandwidth B leads to a range resolution $\delta z = {v_0}/(2B)$ = 25 mm.

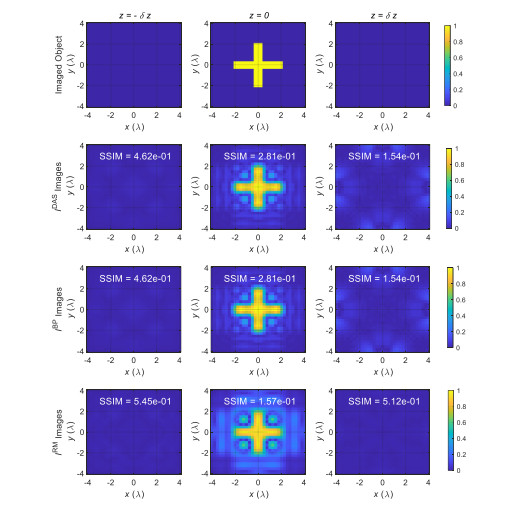
In the first example shown in Figure 1, an X-shape object is placed at $z = 0$ and 2D images are reconstructed over three planes with a distance of $\delta z$ between them. The transceiver is scanning an aperture with the length of ${L_x}$ and ${L_y}$ along the x and y directions, respectively. In this example, ${L_x} = {L_y} = 10\lambda $ and the spatial sampling steps are $\Delta x = \Delta y = \lambda /2$. The scanned aperture is at a range distance of $z = 2\delta z$. Figure 1 shows the imaging results for ${I^{{\rm{DAS}}}}$, ${I^{{\rm{BP}}}}$, and ${I^{{\rm{RM}}}}$.

To assess the quality of the reconstructed images, we employ the so called structural similarity (SSIM) index proposed in ^[14]. SSIM is based on the computation of three terms, namely the luminance term, the contrast term, and the structural term. Please refer to the Appendix for the details of computing SSIM. Here, SSIM is computed for each reconstructed 2D image when taking the true object's image as the reference. The true image has a value of 1 at the pixels overlapping the object and 0 elsewhere. A higher SSIM value indicates higher similarity to the true image.

As it is observed in Figure 1, the images obtain from ${I^{{\rm{BP}}}}$ and ${I^{{\rm{DAS}}}}$ imaging technique are exactly identical, while the one obtained from RM technique shows slightly lower SSIM for this example.

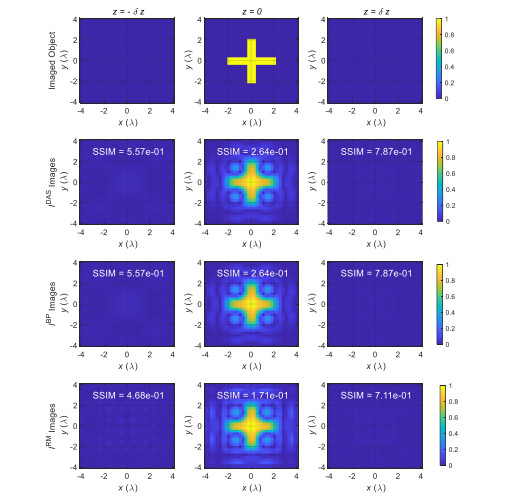
In the second example, the imaged object and the parameters are similar to those in the first example except that the spatial sampling steps are increased to $\Delta x = \Delta y = \lambda $. This is desired since it reduces the scanning time to one half. Figure 2 shows the imaging results for ${I^{{\rm{DAS}}}}$, ${I^{{\rm{BP}}}}$, and ${I^{{\rm{RM}}}}$. As expected the quality of the images obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$ is the same and slightly degrades compared to those in Figure 1. The object's image obtained from ${I^{{\rm{RM}}}}$ shows lower quality compared to those obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$. Also when comparing the degradation of SSIM values for the three techniques between first and second examples, the SSIM value corresponding to ${I^{{\rm{RM}}}}$ shows larger degradation when the spatial sampling step is increased.

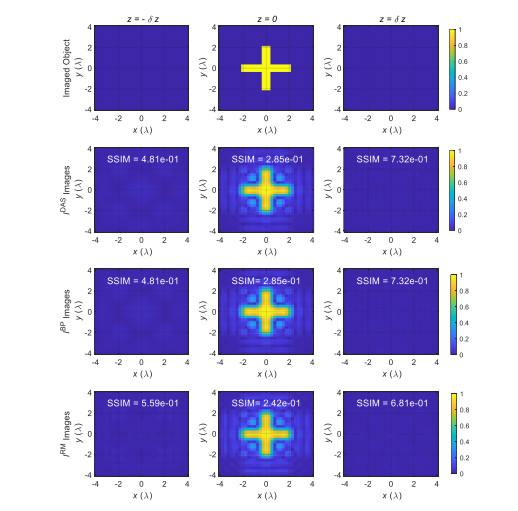
In the third example, again, the imaged object and the parameters are similar to those in the first example except that the size of the aperture is reduced to ${L_x} = {L_y} = 8\lambda $. This is also desired since it expedites the data acquisition process. Figure 3 shows the imaging results for ${I^{{\rm{DAS}}}}$, ${I^{{\rm{BP}}}}$, and ${I^{{\rm{RM}}}}$. As expected the quality of the images obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$ is the same and slightly degrades compared to those in Figure 1. The image obtained from ${I^{{\rm{RM}}}}$ shows lower quality compared to those obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$. Also, when comparing the degradation of SSIM values for the three techniques between first and third examples, the SSIM value corresponding to ${I^{{\rm{RM}}}}$ shows larger degradation when the length of the aperture is reduced.

To compare the performance of the imaging techniques for the above-mentioned three studied cases, Table 1 summarizes the obtained values for SSIM for the image of the object (at z = 0).

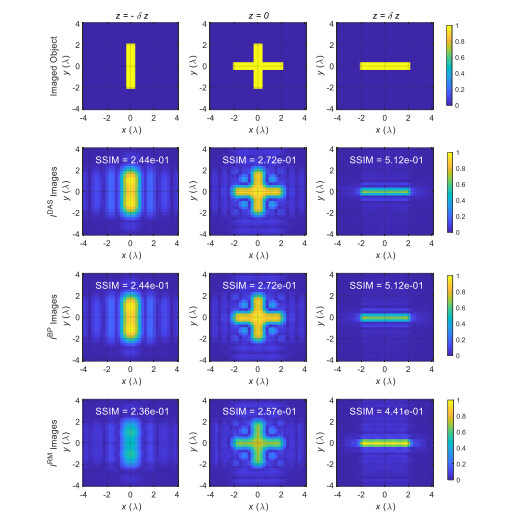
In the fourth example, the parameters are similar to those in the first example but in addition to the X-shape object at $z = 0$ a vertical bar and a horizontal bar are placed at range positions of $z = - \delta z$ and $z = \delta z$, respectively. Figure 4 shows the reconstructed images for ${I^{{\rm{DAS}}}}$, ${I^{{\rm{BP}}}}$, and ${I^{{\rm{RM}}}}$. Again, as expected the quality of the images obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$ is the same. The images obtained from ${I^{{\rm{RM}}}}$ show lower quality compared to those obtained from ${I^{{\rm{DAS}}}}$ and ${I^{{\rm{BP}}}}$.

4.   Conclusion

In this paper, we studied the 3D near-field imaging techniques based on BP and DAS concepts, within the context of FMCW radar, and we showed the equivalence of their normalized reconstructed images. We also compared the quality of the reconstructed images based on these techniques as well as those obtained from RM technique. Our study showed that the images obtained from BP and DAS concepts have exactly the same quality as expected while those obtained from RM technique have lower quality due to the involved approximations. Besides, the degradations of the image quality due to the increased sampling steps and reduced aperture size are more severe when using RM technique.

Please note that although the notations DAS, BP, and RM are used for the images obtained from the three studied techniques, we emphasize that these techniques are not the conventional DAS, BP, and RM techniques but rather borrow similar concepts from their conventional counterparts. For instance, the technique in ^[12] is not implemented in the time domain the way conventional DAS works. Furthermore, the equivalence of conventional DAS and BP techniques and the pros and cons of conventional RM technique have been already well-understood in the microwave imaging community (e.g., see ^[18,19,20]).

As a final note, in this work, the stack of 2D images at multiple range positions (z) provides 3D information. It is a common approach to present 3D images in microwave imaging works (e.g., see ^[8,21,22]).

Acknowledgments

This work was supported by the U.S. National Science Foundation (NSF) under Award 1920098 and the New York Institute of Technology's Institutional Support for Research and Creativity (ISRC) Grant.

Conflict of interests

The author declares that there is no conflict of interest in this paper.

Appendix

Suppose that x and y are two generic 2D images that we would like to assess their similarity. According to ^[14], the SSIM is computed using three terms, namely the luminance term $l(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}})$, the contrast term $c(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}})$, and the structural term $s(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}})$ as:

where ${\mu _x}$, ${\mu _y}$, ${\sigma _x}$, ${\sigma _y}$, and ${\sigma _{xy}}$ are the means, standard deviations, and cross-covariance for the images, respectively, ${C_1}$, ${C_2}$, and ${C_3}$ are constants determined based on the dynamic range of the pixel values 14, and $\alpha $, $\beta $, and $\gamma $ are used to adjust the importance of the terms (here, we use $\alpha = \beta = \gamma = 1$).