Nanoparticle-based organic polymer retinal prostheses: modeling, solution map and simulation

1.   Introduction

Ocular pathologies represent a serious danger for the health and life quality of million individuals worldwide because in extreme manifestations they may turn out into loss of eyesight. This is the case, for instance, with Retinitis Pigmentosa (RP), a hereditary degeneration characterized by a progressive dysfunction of rod and cone photoreceptors ^[31], and Age-related Macular Degeneration (AMD), a pathology of the macula, the small central area of the retina that controls vision acuity.

AMD is the main cause of blindness in subjects aged $\geq$55 years ^[7,21]. Currently, 67 million people are affected by AMD in the EU ^[15] and 11 million individuals are affected with AMD in the U.S. ^[21], with a global prevalence of 170 million. The prevalence of AMD in the U.S. is anticipated to increase to 22 million by the year 2050, and the global prevalence is expected to increase to 288 million by the year 2040 ^[7,21]. Existing noninvasive approaches for the cure of RP and AMD, such as gene therapy, neuroprotection and pharmacology ^[19], can be effectively applied at early stages of the disease, otherwise more invasive therapeutic interventions, such as injection of anti-VEGF drugs ^[11] and/or photodynamic laser treatment ^[26], must be employed to treat late disease stages.

A valid alternative to the above mentioned medical cure for RP and AMD has been suggested in recent years by the development of biocompatible implantable prostheses ^[8,22,32]. Retinal prostheses have been shown to successfully stimulate the inner retinal network, but severe technical difficulties and undesired side effects have strongly limited so far their efficacy in the application on individuals. These limitations may have been overcome by the advent of a second generation of prosthetics based on conjugated polymers ^[2] which has been translated into a functioning technology in ^[20] and ^[6] where conjugated polymer nanoparticles (P3HT NPs) are subretinally injected in a rat model of RP and shown to mediate light-evoked stimulation of retinal neurons and persistently rescue visual functions.

Despite P3HT NPs open up a wide potential in the application of retinal prosthetics to the cure of pathologies secondary to photoreceptor death, the physical mechanisms underlying their function are still poorly understood. For this reason, in this article we conduct a theoretical and numerical study of a mathematical model, developed from that proposed in ^[4,6], to describe the stationary function of a bio-hybrid system constituted by: (i) a P3HT NP; (ii) a retinal neuron; (iii) an aqueous extracellular region; and (iv) an interstitial cleft separating the NP from the retinal neuron. The theoretical model translates into mathematical relations the chain of physical events that transform an external supply of light stimulation into a depolarization of the retinal neuron upon mediation of the P3HT NP, and consists of the Drift-Diffusion (DD) system ^[12,30] to describe light photoconversion into free charged carriers in the NP bulk and the Poisson-Nernst-Planck (PNP) system ^{[13,14,23,27]} to describe ion electrodiffusion in the aqueous medium.

We solve the model in one spatial dimension with the Gummel Map, a functional iteration customarily employed in inorganic semiconductor device simulation ^[10], for which we are able to prove the existence of a fixed point, upon introducing suitable smallness limitations on model parameters and coefficients. The Gummel Map reduces the nonlinear coupling between the DD system and the PNP system into a sequence of spatially heterogenous, linearized balance equations for electric potential (in both NP and aqueous medium), ion molar densities (in the sole aqueous medium) and photogenerated carrier number densities (in the sole NP). For each considered balance equation, interdomain connection is dealt with through transmission conditions expressing: (a) electron-driven molecular oxygen reduction at the NP-solution interface; (b) electrostatic coupling between NP and surrounding aqueous environment; and (c) ion electrodiffusion between extracellular bath and interstitial cleft.

The sequence of linearized boundary value problems is discretized using the finite element method with proper stabilization terms to prevent spurious unphysical oscillations in the electric potential and ensure positivity of the carrier number densities and ion molar densities in their respective domains of definition [24, Chapters 22-23].

The above described computational model is then used to simulate the response of the bio-hybrid system to given input sources. Simulations provide a physical picture of the mechanisms occurring inside the NP when coupled with an electrolytic solution. In particular, model predictions seem to suggest that the coupling between the neuron and the NP may affect cleft polarization due to an electrostatic effect. Simulations also provide a quantitative estimate of the superoxide anion concentration that reaches the neuron membrane at different light intensities. This information may be biologically relevant because superoxide molecules may activate chemical pathways or induce oxidative distress at the neuron cellular membrane.

An outline of the article is as follows. In Section 2 we introduce the geometric scheme of the bio-hybrid system, the dependent variables of the problem and the scaling factors that are used to adimensionalize the equation system. In Section 3 we write the boundary value problems (in scaled form) which constitute the nonlinearly coupled differential model of the system. In Section 4 we describe the various steps of the Gummel Map that is used to iteratively solve the nonlinearly coupled model, while in Section 5 we describe the basic structure of the Gummel Map and state the theorem of existence of a fixed point of the proposed solution map also commenting on its uniqueness. The proof of the theorem is described in detail in Section 8. In Section 6 we illustrate the finite element approximation of the boundary value problems constituting the Gummel Map while in Section 7 we deal with the validation of the proposed model and algorithm and we illustrate the main results obtained from our numerical formulation. We close the article with Section 9, in which we draw the principal conclusions on the investigated bio-hybrid system and indicate future research directions.

2.   Preliminaries

In Section 2.1 we describe the geometric representation of the bio-hybrid system under investigation. Then, in Section 2.2 we introduce the dependent variables of the problem (electric potential, ion molar densities and carrier number densities) together with their respective domain of definition. Finally, in Section 2.3 we define the scaling factors which are used to write the model equations in adimensional form.

2.1.   Geometric representation of the bio-hybrid system

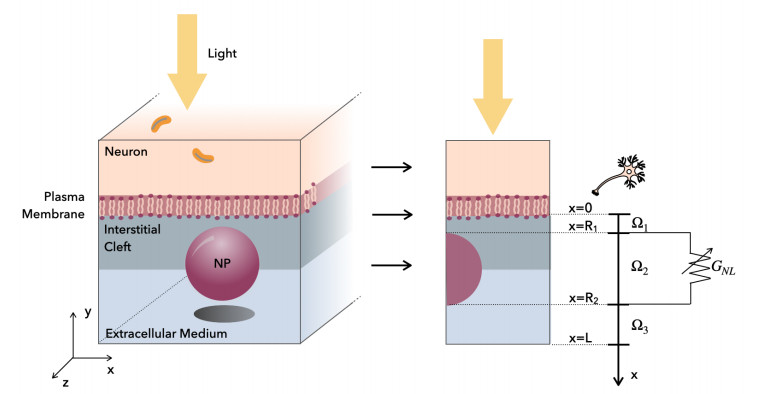
Figure 1 (left panel) shows a three-dimensional (3D) schematic representation of the bio-hybrid system studied in the present work. The system is composed of (i) the cytoplasm of a retinal neuron (indicated as "Neuron" in the left panel of Figure 1); (ii) the plasma membrane of the neuron (indicated as "Plasma Membrane" in the left panel of Figure 1); (iii) a P3HT NP (indicated as "NP" in the left panel of Figure 1); (iv) an aqueous extracellular region (indicated as "Extracellular Medium" in the left panel of Figure 1); and (v) a porous interstitial cleft separating the NP from the retinal neuron (indicated as "Interstitial Cleft" in the left panel of Figure 1). The yellow arrow represents the external input light source. The rotational invariance of the system with respect to the $z$ axis allows us to reduce the 3D structure (in the cartesian reference system $x$-$y$-$z$) into the two-dimensional (2D) axial symmetric structure depicted in the middle panel of Figure 1 (x-z axisymmetric coordinate system). To further reduce model complexity, we introduce the one-dimensional (1D) open interval $\Omega = (0, \, L)$ represented in the right panel of Figure 1. The origin $x = 0$ is set in correspondence of the interface between the cleft region and the neuron membrane. The cleft region is represented by the open interval $\Omega_1 = (0, \, R_1)$. The NP is represented by the open interval $\Omega_2 = (R_1, \, R_2)$. The extracellular region is represented by the open interval $\Omega_3 = (R_2, \, L)$. The computational domain for the nonlinear differential system is $\Omega = \Omega_1 \cup \Omega_2 \cup \Omega_3$. We also set $\Omega_{1, 3}: = \Omega_1 \cup \Omega_3$. The nonlinear conductance $G_{NL}$ which connects the points $x = R_1$ and $x = R_2$ is a lumped electric representation of ion motion from the extracellular medium into the cleft in the 2D scheme in the middle panel of Figure 1.

2.2.   Dependent variables

To describe in mathematical terms the physical mechanisms occurring in each subdomain $\Omega_i$, $i = 1, 2, 3$; at the interfaces $x = 0$, $x = R_1$, $x = R_2$ and $x = L$; and across the nonlinear conductance $G_{NL}$, we need:

● the electric potential $\psi$ (units: $\rm{V}$);

● the chemical variables $n$ and $p$ representing the carrier number densities of electrons and holes that are photogenerated in the NP (units: $\rm{m}^{-3}$);

● the chemical variables $c_\alpha$, $\alpha = \left\{ \rm{Na}^+, \, \rm{Cl}^-, \, \rm{K}^+\right\}$, representing the ion molar densities that passively flow in the cleft and extracellular regions (units: $\rm{mol \, m^{-3}} = \rm{mM}$), where $\rm{Na}^+$, $\rm{Cl}^-$ and $\rm{K}^+$ indicate sodium, chlorine and potassium, respectively;

● the chemical variable $c$ representing the ion molar density of superoxide $\rm{O}_2^-$ (units: $\rm{mM}$) that is generated at the interfaces $x = R_1$ and $x = R_2$ between NP and surrounding medium, and that subsequently flows by electrodiffusion in the extracellular medium and cleft.

We have:

From the above definitions we see that $n$, $p$, $c_\alpha$ and $c$ are positive quantities. This property is a consequence of the Maxwell-Boltzmann statistics:

where $\varphi_n$, $\varphi_p$, $\varphi_\alpha$ and $\varphi$ are the electrochemical potentials of electrons, holes and ions (units: $\rm{V}$), $V_{th}$ is the thermal voltage (units: $\rm{V}$), $n_{ref}$ is the reference number density (units: $\rm{m}^{-3}$), $c_{ref}$ is the reference molar density (units: $\rm{mM}$) and $z_\alpha$ is the chemical valence of each ion, with $z_\alpha = +1$ for $\rm{Na}^+$ and $\rm{K}^+$ and $z_\alpha = -1$ for $\rm{Cl}^-$ and $\rm{O}_2^-$.

For further elaboration, it is useful to introduce the following set of alternative depedent variables:

The above dependent variables will be referred to henceforth as Slotboom variables in analogy with the Drift-Diffusion model for semiconductor devices (see ^[29]). From (2.3), we see that $u_n$, $u_p$, $u_\alpha$ and $u$ are strictly positive quantities and

2.3.   Scaling

In the remainder of the article every quantity will be scaled by an appropriate positive constant referred to as "scaling factor". Precisely, let $\mathcal{U}$ denote a variable whose units are $\rm{U}$. Assume that $U^\ast$ is a quantity whose units are $\rm{U}$. Then, the scaled variable associated with $\mathcal{U}$ is defined as

Table 1 summarizes the expressions and the values of the scaling factors for the model variables and parameters. The symbol $t$ represents the time coordinate.

3.   The mathematical model of the bio-hybrid system

In this section we illustrate the boundary value problems (in scaled form) that constitute the nonlinearly coupled differential formulation of the bio-hybrid system. For reader's ease we denote each scaled variable with the same symbol used to represent the variable in its dimensional form. Throughout the text we use $(\cdot)^\prime$ as a shorthand notation for $\partial (\cdot)/\partial x$.

3.1.   The boundary value problem for the electric potential

The electric potential $\psi$ is governed by the nonlinear Poisson equation (NLP)

The piecewise constant function $\varepsilon$ is the dielectric permittivity defined as

$\varepsilon_{j}$ being the value of the relative dielectric permittivity in each subdomain $\Omega_j$, $j = 1, 2, 3$. The function $f$ is the space charge density defined as

The quantities $\rho _{j}$, $j = 1, 2, 3$, are given functions of $x$ and physically represent the doping profile in each region $\Omega_j$. The quantities $\gamma_1$ and $\gamma_2$ are dimensionless parameters defined as:

where $N_{Av} = 6.022 \cdot 10^{23}$ is the Avogadro's constant (units: $\rm{mol}^{-1}$). Based on the values of $c^\ast$ and $n^\ast$ (see Table 1), it turns out that $N^\ast = n_{ref} = c^\ast N_{Av}$, so that $\gamma_1 = 1$ and $\gamma_2 = 1.407 \cdot 10^{-14}$.

Finally, the quantity $\lambda$ has the following expression

$\lambda_D$ being the Debye length (units: $\rm{m}$) defined as

where $\varepsilon_0 = 8.854 \cdot 10^{-12}$ (units: $\rm{F \, m^{-1}}$) and $q = 1.602 \cdot 10^{-19}$ (units: $\rm{C}$) are the dielectric permittivity of vacuum and the electron charge, respectively.

Remark 3.1. The numerical value of $\lambda_D$ is $1.4394 \cdot 10^{-10}$ m and the value of the dimensionless parameter $\lambda^2$ is $1.1205 \cdot 10^{-7}$. Since $\lambda^2 \ll 1$, the NLP equation (3.1a) has a markedly singularly perturbed nature. We refer to ^[18] for a detailed analysis of the singular perturbation property of the NLP equation in the case of inorganic semiconductor devices.

The boundary conditions for (3.1a) are defined as follows.

The expressions (3.7a)–(3.7e) are linear transmission conditions that physically represent the capacitive coupling between neighbouring subdomains. $C_m^0$ and $C_m$ denote the specific capacitance of the neuron membrane and of the NP surface, respectively, and $\psi_N$ is the neuron resting potential. The expression (3.7f) is a Dirichlet boundary condition that fixes the electric potential to ground in correspondence of a position ($x = 1$) in the extracellular medium that is sufficiently far from the interface with the nanoparticle at $x = R_2$.

Remark 3.2. The electric potential $\psi$ is, in general, a discontinuous function over the domain $\Omega$. In particular, according to the transmission conditions(3.7a)–(3.7e), $\psi$ has a jump at $x = 0$, $x = R_1$ and $x = R_2$. We see that if $C_m^0 \rightarrow +\infty$ and $C_m \rightarrow +\infty$, then the capacitive coupling is so strong that the electric potential becomes a continuous function over $\overline{\Omega}$. Conversely, if $C_m^0 \rightarrow 0^+$ and $C_m \rightarrow 0^+$, then the capacitive coupling is so weak that the nanoparticle subdomain $\Omega_2$ becomes completely decoupled from $\Omega_1$ and $\Omega_3$. In this case, the electric potential turns out to be defined up to an arbitrary constant in both $\Omega_1$ and $\Omega_2$, and further compatibility conditions have to be enforced to determine the constant in both subdomains.

3.2.   The boundary value problems for the ions $u_{\alpha }, \alpha = {Na}^{+}, \, {Cl}^{-}, \, {K}^{+}$

The ion molar densities $u_\alpha$, $\alpha = \left\{ \rm{Na}^{+}, \, \rm{Cl}^{-}, \, \rm{K}^{+} \right\}$, are governed by the following continuity equation

where

We introduce the following quantities:

The boundary conditions for the restriction of $u_\alpha$ in $\Omega_1$ are:

The boundary conditions for the restriction of $u_\alpha$ in $\Omega_3$ are:

For the purpose of analysis, it is convenient to perform in $\Omega _{3}$ the following change of dependent variable

Inserting (3.11e) into (3.8a) yields

The boundary conditions for $v_\alpha$ are:

The quantity $u_{\alpha, N}$ is a positive constant denoting the value of the ion molar density $u_\alpha$ in the neuron. The quantity $\overline{u}_{\alpha }$ is a positive constant denoting the value of the ion molar density $u_\alpha$ in the extracellular medium, far from $x = R_2$. The quantities $P_\alpha$ denote the permeability to ion $u_\alpha$ of the neuron membrane. The quantities $P_{\alpha, i}$ denote the permeability to ion $u_\alpha$ of the nonlinear conductance $G_{NL}$ which represents with a lumped equivalent electric parameter the electrodiffusive flow of ions between cleft $\Omega_1$ and extracellular region $\Omega_3$.

The expressions (3.11a)–(3.11c) are transmission conditions that physically represent the electrodiffusive coupling between neighbouring subdomains according to the Goldman-Hodgkin-Katz model [24, Chapter 17]. The expression (3.11d) is a Dirichlet boundary condition that fixes the ion molar density to the equilibrium value in correspondence of a position ($x = 1$) in the extracellular medium that is sufficiently far from the interface with the nanoparticle at $x = R_2$.

3.3.   The boundary value problem for the superoxide ion $u=u_{O_{2}^{-}}$

The superoxide ion molar density $u = u_{O_{2}^{-}}$ is governed by the following continuity equation

where

The quantity $k_1$ is the rate of the kinetic reaction (3.22). The quantity $C^{EQ}$ is the superoxide ion equilibrium molar density of the kinetic reaction (3.22). The quantity $\tilde{C}$ is the molar density of molecular oxygen O$_2$ dissolved into the aqueous solution in which the NP is immersed.

We introduce the following quantities:

The boundary conditions for the restriction of $u$ in $\Omega _{1}$ are:

The boundary conditions for the restriction of $u$ in $\Omega _{3}$ are:

The expressions (3.15a) and (3.15d) are homogeneous Neumann boundary conditions which physically represent the fact that no superoxide ion flux density can flow out of the computational domain. The expressions (3.15b) and (3.15c) are nonlinear Robin boundary conditions which physically represent the net balance between the recombination and generation processes that regulate consumption and production of O$_2^{-}$ at the interfaces between the NP and the surrounding environment.

3.4.   The boundary value problems for the photogenerated carriers

The photogenerated carriers $u_n$ and $u_p$ are governed by the following continuity equations:

The quantity $G$ is a given function of $x$ and represents the light illumination rate. The dimensionless quantity $\eta$ is the photogeneration efficiency. The function $\mathcal{R}$ is defined as

and physically represents the net recombination rate due to two-particle interaction, according to the Shockley-Read-Hall theory ^[28], $\tau_n$ and $\tau_p$ being the electron and hole lifetimes, respectively. At thermodynamic equilibrium conditions (corresponding to switching illumination off, $G = 0$), $u_n u_p = 1$ so that $\mathcal{R} = 0$ and both $u_n$ and $u_p$ are constant. If $u_n u_p > 1$, then $\mathcal{R} > 0$ and both $u_n$ and $u_p$ tend to decrease due to the fact that recombination prevails over generation. Conversely, if $u_n u_p < 1$, then $\mathcal{R} < 0$ and both $u_n$ and $u_p$ tend to increase due to the fact that generation prevails over recombination.

We introduce the following quantities:

The boundary conditions for $u_{n}$ are:

The boundary conditions for $u_{p}$ are:

The expressions (3.19a)–(3.19b) are nonlinear Robin boundary conditions that physically represent the surface mechanisms of conversion of photogenerated electrons into superoxide ions according to the Marcus-Gerischer theory ^[17]. The expressions (3.19c)–(3.19d) are Robin boundary conditions that physically represent the surface mechanisms of recombination of photogenerated holes with the superoxide ions that are present at $x = R_1$ and $x = R_2$. The quantities $k_n$ and $k_p$ are the tunneling coefficient for electrons in the P3HT and the hole surface recombination probability, respectively. The function $g$ is defined as follows

where $A$ and $B$ are constants, $B > 0$, and $\tilde{C}$ is a positive constant such that

$C^{EQ}$ denoting the superoxide ion equilibrium molar density of the kinetic reaction which transforms molecular oxygen O$_2$ into superoxide O$_2^-$

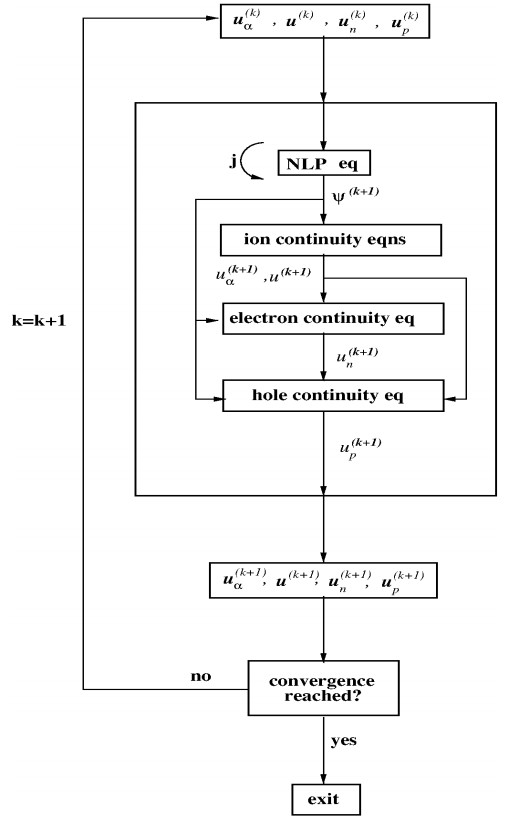
4.   The Gummel Map: solution algorithm

In this section we illustrate the Gummel Map for the decoupled solution of the nonlinear differential model constituted by the boundary value problems (3.1), (3.8), (3.12) and (3.16). The solution algorithm is inspired by the fixed-point iteration originally introduced in ^[10] and customarily adopted in the simulation of inorganic semiconductor devices with the DD model (see ^[12,18]).

For a given tolerance $\delta > 0$ and given $u_\alpha^{(k)}$, $u^{(k)}$, $u_n^{(k)}$ and $u_p^{(k)}$, $k\geq 0$, the fixed-point iteration proposed in this work consists of the successive execution of the following steps:

${\bf{S.1}}$ solve the nonlinear Poisson (NLP) equation for the electric potential:

with the following boundary conditions:

${\bf{S.2}}$ solve the linearized continuity equation for the ion molar density of Na$^+$, Cl$^-$ and K$^+$:

with the following boundary conditions:

${\bf{S.3}}$ solve the linearized continuity equation for the ion molar density of O$_2^-$:

with the following boundary conditions:

${\bf{S.4}}$ solve the linearized continuity equation for the photogenerated electrons:

where

with the following boundary conditions:

${\bf{S.5}}$ solve the linearized continuity equation for the photogenerated holes:

where

with the following boundary conditions:

${\bf{S.6}}$ compute the maximum absolute relative increment of the electron electrochemical potential

${\bf{S.7}}$ compute the maximum absolute relative increment of the hole electrochemical potential

${\bf{S.8 }}$ compute the maximum absolute relative increment of the electrochemical potentials of the Na$^+$, Cl$^-$ and K$^+$ ions:

${\bf{S.9}}$ update the electrochemical potential of the O$_2^-$ ion:

${\bf{S.10}}$ compute the maximum absolute relative increment:

${\bf{S.11}}$ check for convergence:

if $\delta^{(k+1)} < \delta$ then terminate the iteration, otherwise go back to step 1. and continue.

A flow-chart of the sequence of the above steps is illustrated in Figure 2.

Remark 4.1. From the algorithmic point of view, the solution map schematically represented in the flow-chart of Figure 2 consists of:

● the nonlinear step S.1 to solve the NLP equation. This step, performed by using the Newton Method, is described in 4.1 and gives rise to the successive solution of a sequence of linear diffusion-reaction equations, with a positive reaction term, to update the electric potential;

● the sequence of linear steps S.2–S.5 to solve the continuity equation for ions and carriers. Each step is a self-adjoint diffusion-reaction-production equation with nonnegative reaction and production terms.

4.1.   Iterative solution of the NLP equation

The NLP equation (4.1a) can be written in the following residual form

where

is the residual associated with the nonlinear operator $\mathcal{N}_\psi$. To iteratively solve (4.11a) through a linearization procedure, we use the Newton Method and denote by $j\geq 0$ the iteration counter. To initialize the Newton iteration we set $\psi^{(j = 0)} = \psi^{(k)}$, where $\psi^{(k)}$ is the electric potential distribution currently available from the Gummel Map. Then, each $j$-th iteration of the Newton Method consists of the following two steps:

${\bf{NM.1 }}$ compute the Newton increment $\delta \psi^{(j)}$ by solving

where

is the Frèchet derivative of the nonlinear operator $\mathcal{N}_\psi$ evaluated at $v$;

${\bf{NM.1}}$ update the Newton iterate through the relation

until convergence is reached.

Let $j^\ast \geq 0$ denote the value of the iteration counter $j$ in correspondence of which the sequence of steps NM.1–NM.2 has reached convergence. The final step of the procedure for the solution of the NLP equation consists of setting

Then, we are in the position to continue the Gummel Map from step S.2.

5.   The Gummel Map

In this section, we illustrate the structure of the solution map which is proposed to iteratively solve the fully nonlinear differential model described in Section 3. Then, we introduce an appropriate functional setting for the action of the fixed-point iteration, analyzing existence and uniqueness of a fixed-point.

5.1.   Abstract formulation

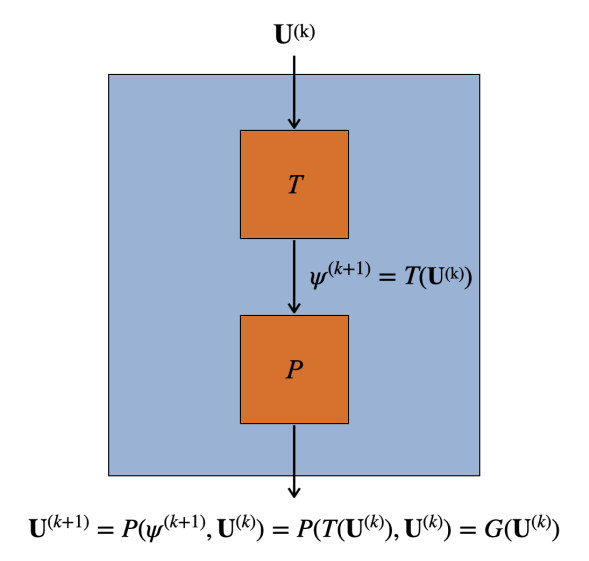
We denote by ${\bf U} = \left(u_n, \, u_p, \, u_\alpha, \, u \right)$ the vector of photogenerated carrier number densities and ion molar densities. Then, we introduce the fixed-point operator

where, for every $k\geq 0$,

represents the nonlinear step S.1 of Section 4 and

represents the sequence of linear steps S.2–S.5 of Section 4.

Given ${\bf U}^{(0)}$, the Gummel Map described in Section 4 can be written in the form of a fixed-point iteration as

The block structure of the Gummel Map (5.1d) is represented in the scheme of Figure 3.

5.2.   Functional setting

For any interval $\mathcal{S}$, in the following we denote $L^p(\mathcal{S})$, $p \in [1, \, \infty]$, the space of functions that are $p$-integrable over $\mathcal{S}$ and by $H^{k}(\mathcal{S})$, $k\geq 0$, the Sobolev space of functions that are square integrable over $\mathcal{S}$ with their first $k$ derivatives (see ^[16] for an extensive discussion of Sobolev spaces and their properties). We also denote by $H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right)$ the subset of $H^{1}\left(\Omega _{3}\right)$ of functions vanishing at $x = 1$ and we define:

Relations (5.2) allow us to define the dependent variables $u_\alpha$, $u$, $u_n$ and $u_p$ over all the computational domain $\Omega = \Omega_1 \cup \Omega_2 \cup \Omega_3$. In view of the subsequent theoretical analysis of the model, we introduce the broken $H^1$ spaces:

Then, we introduce the following function spaces (for the electric potential)

where

and having introduced the positive constants $C_I$ and $C_L$, and the following quantities:

We also introduce the following function spaces (for ions, electrons and holes), each one being a closed, bounded and convex set of $L^2(\Omega)$:

Consistent with (5.2), we have:

We set $N = G_{max} \tau_{max}$, where $G_{max} = \max_{x \in \Omega_2} G(x)$ and $\tau_{max} = \max\left\{\tau_{diff, n}, \, \tau_{diff, p}\right\}$, $\tau_{diff, n}$ and $\tau_{diff, p}$ being the diffusion times of electrons and holes, respectively. We define:

where:

Finally, to gather the nonreacting ions, the superoxide ion and the photogenerated carriers, we define the function space

Remark 5.1. It is worth noting that $u_\alpha(x) > 0$ and $u(x) > 0$ for $x \in \overline{\Omega}_{1, 3}$, while $u_{n, p}(x) > 0$ for $x \in \overline{\Omega}_{2}$. The reason why we have used the mathematical expression $0 \leq$, instead of $0 <$, in the definition of the spaces (5.6) is because of (5.2).

5.3.   Existence (and uniqueness) of a fixed point

The following theorem is the principal theoretical result of this article. For its proof, we refer to Section 8.

Theorem 5.1. The Gummel Map (5.1a) has the following properties:

a) $\mathbb{G}: {\bf X} \rightarrow {\bf X}$.

b) $\mathbb{G}$ is continuous and compact.

Then $\mathbb{G}$ has a fixed point ${\bf U}^\ast = \left(u_{\alpha }^\ast, \, u^\ast, \, u_{p}^\ast, \, u_{n}^\ast\right) \in {\bf X}$.

The electric potential associated with the fixed-point is $\psi^\ast = \mathcal{T}({\bf U}^\ast)$ such that $\psi^\ast \in \mathcal{V}$, $\mathcal{T}$ being the map defined in (5.1b).

Corollary 5.2. Setting

we see that $\mathbb{G}$ is endowed with the following invariant region

Remark 5.2. For the meaning of invariant region, cf. ^[12].

Remark 5.3. As it is common in these kinds of models (e.g., semiconductor devices), uniqueness of a solution is not expected in general. In the present case, uniqueness of a fixed point for the Gummel Map can be restored by modifying in a rather straightforward way the estimates in the proof of Theorem 5.1, under additional restrictions on the parameters in (5.5c) and $\mathcal{M}_\alpha$, $\mathcal{M}_u$ in (5.6a) and (5.6b), in order to make the Gummel Map a strict contraction.

Remark 5.4. Theorem 5.1 shows that the ion molar densities and the photogenerated carrier number densities are strictly positive in their domains of definition. This property agrees with physical expectation.

6.   Finite element approximation

This section is devoted to illustrate the numerical approximation of each linearized equation in the Gummel Map using the Galerkin Finite Element Method. To this purpose, it is immediate to verify that each linearized equation can be written in the general form of a diffusion-production-consumption equation for the dependent variable $\chi = \chi(x)$

where $\omega$ is an interval such that $\omega \subseteq \Omega$. The quantity $a = a(x)$ is the diffusion coefficient, such that

The quantity $s = s(x)$ is the consumption coefficient, such that

The quantity $p = p(x)$ is the production coefficient, whose sign is not predictable in the case of Eq (4.11c), whereas, in the case of the other equations in the Gummel Map, $p$ is such that

It is worth noticing that the diffusion coefficient $a = a(x)$ may be an exponential function of the electric potential. Therefore, $a$ may experience significant variations, especially close to the boundary of $\omega$ where interface phenomena take place. The same consideration holds for the consumption and production coefficients, $s$ and $p$. In such conditions, it is important to adopt a stable discretization scheme to prevent from spurious oscillations to arise in the numerical solution of (6.1a). Denoting by $\mathcal{T}_h$ a partition of $\omega$ into subintervals $K$ (elements) of size $h$, the approach taken in the present article is based on the following choices:

● piecewise linear continuous finite elements;

● harmonic average of $a$ over each $K \in \mathcal{T}_h$ (see ^[25]);

● mass lumping of the tridiagonal matrix corresponding to the consumption term;

● trapezoidal quadrature rule to evaluate the right-hand side of the linear system associated with the discrete form of (6.1a).

The benefits emanating from the above discretization strategy are:

● discretization error $e_h: = \chi - \chi_h$ of order $h$ and $h^2$ in the $H^1(\omega)$ and $L^2(\omega)$ norms, respectively;

● absence of unphysical oscillations in the spatial distributions of all the dependent variables over the interval $\omega$;

● nonnegative spatial distributions of ion molar densities and photogenerated carrier number densities;

● weak conservation of the computed electric displacement vector, molar flux density of ions and carrier current densities over $\mathcal{T}_h$.

We refer to [24, Chapter 23] for more details on the theoretical and computational properties of the above described discretization strategy of the diffusion-production-consumption equation (6.1a).

7.   Simulations

In this section we perform a series of simulation tests conducted by running a user-coded MatLab software which implements the algorithm illustrated in Section 4 and the finite element discretization scheme illustrated in Section 6. In Section 7.1 we analyze the convergence performance of the algorithm and verify the a priori bounds illustrated in Section 5. In Section 7.2 we investigate the role of each considered biophysical mechanism in the function of the bio-hybrid system studied in this article.

7.1.   Convergence of Gummel's Map and a priori estimates

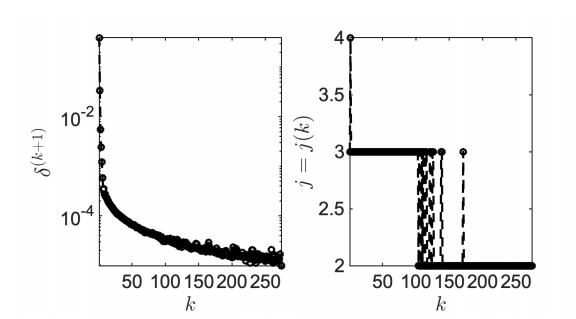
In Figure 4 (left panel) we represent the convergence history of the solution algorithm. On the $x$-axis, the quantity $k$, with $k \geq 0$, represents the number of Gummel's Map iterations and on the $y$-axis the quantity $\delta^{(k+1)}$ represents the maximum absolute relative increment on the electrochemical potentials computed using Eq (4.10). As customary in Numerical Analysis, $\delta^{(k+1)}$ is used as an estimator of the actual maximum absolute relative error. In the computations the tolerance $\delta$ was set equal to $10^{-5}$. Interestingly, the plotted curve shows that the error decreases fastly during the first $\simeq$25 iterations, and then starts decreasing more slowly and non monotonically. In Figure 4 (right panel) we represent the number of NLP iterations $j = j(k)$ needed to meet a tolerance equal to $10^{-10}$ on the absolute maximum relative error of the Newton increment at each Gummel's Map iteration $k$. Results show that $j(k) \leq 4$ and $j(k) = 2$ for $k \geq 100$.

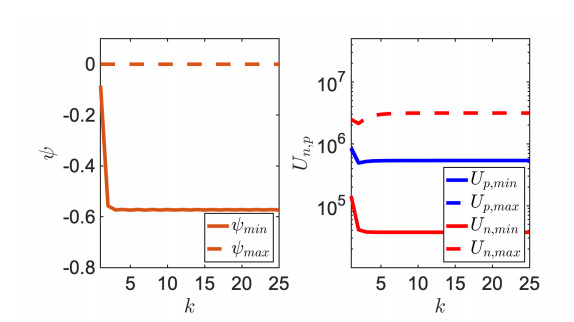
In Figure 5 (left panel) we represent the minimum and maximum values $\psi_{min}$ and $\psi_{max}$ of the electric potential $\psi$ as a function of $k$. Results show that $\psi_{max} = 0$, corresponding to the Dirichlet datum at $x = 1$, where the electrolyte is supposed to be electroneutral, and $\psi_{min} = -0.6$, in the vicinity of the neuron membrane (see Section 7.2). In Figure 5 (right panel) we represent the minimum and maximum values $U_{p, min}$ and $U_{p, max}$ of the hole number density (blue color) and the minimum and maximum values $U_{n, min}$ and $U_{n, max}$ of the electron number density (red color) as a function of $k$. It is interesting to notice that in the case of holes $U_{p, min}$ and $U_{p, max}$ are almost overlapped, whereas in the case of electrons $U_{n, min}$ and $U_{n, max}$ differ by almost two orders of magnitude. These results are consistent with the physical transport properties of the two charge carriers: while the holes are able to redistribute across the domain $\Omega_2$ due to their "elevated" mobility, the electrons are instead almost immobile, and spatially distribute themselves throughout $\Omega_2$ according to the Lambert-Beer profile of the light source $G$.

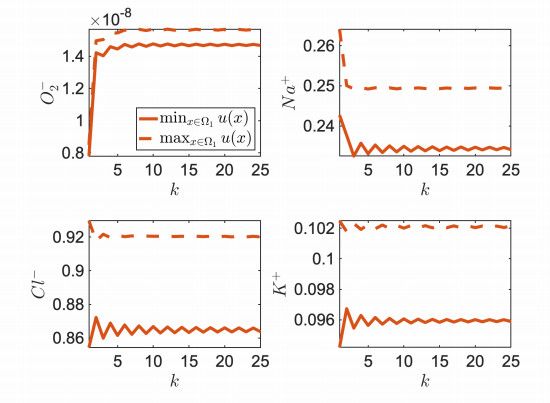
In Figure 6 we represent the minimum and maximum values of the ion molar densities as a function of $k$ in the subdomain $\Omega_1$. It is interesting to notice that the behaviour of the O$_2^-$ ion is markedly different from that of Na$^+$, Cl$^-$ and K$^+$: both minimum and maximum values of O$_2^-$ molar density increase monotonically to their corresponding limit values, whereas the minimum and maximum values of the other ions slowly converge with oscillations to their corresponding limit values.

7.2.   Physical analysis of model predictions

Throughout the section we abandon the dimensionless form of the variables and represent each quantity with its units. This allows us to provide a consistent physical interpretation to the simulation results.

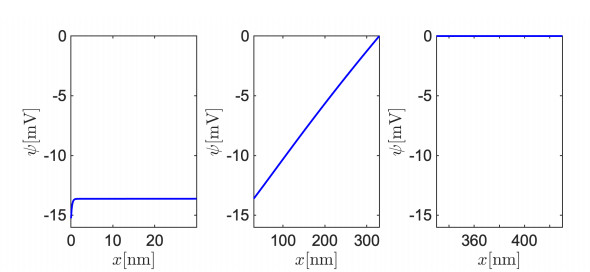
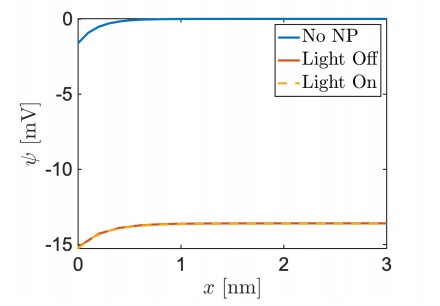
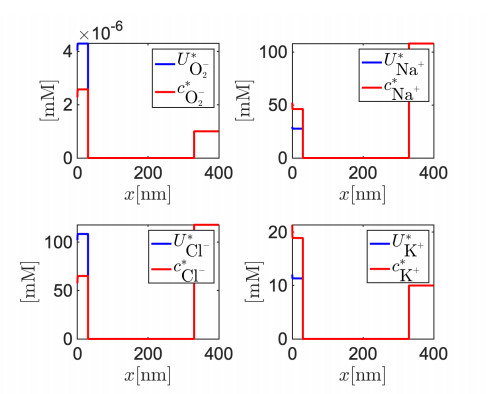
Table 2 provides a list of all the numerical values of model parameters used in the simulations. In Figure 7 we represent the piecewise spatial distribution of the electric potential over the computational domain $\Omega = (0, \, L)$, distinguishing the cleft region $\Omega_1$ (left panel), the NP region $\Omega_2$ (middle panel) and the electrolyte region $\Omega_3$ (right panel). Results indicate that in the proximity of the neuron the electric potential exhibits a steep boundary layer due to the capacitive coupling induced by the cellular membrane on the cleft region. Inside the NP the electric potential has a linear behavior. In the electrolyte side the electric potential is clamped to the boundary value of 0 V enforced at $x = L$ which represents the electroneutrality of the biological electrolytic solution far away from the NP-neuron interface. In Figure 8 we show a zoom of the boundary layer of the electric potential $\psi$ at the interface with the neuron in three different simulation conditions: (ⅰ) when no NP is present in the environment and the neuronal membrane is directly in contact with the bulk electrolyte (blue line); (ⅱ) when the NP is present and forms a cleft region but it is not photo-activated by light; (ⅲ) when the NP is present and is also activated by light. Results indicate that in case (ⅰ), the amplitude of the boundary layer is of $\simeq -1.5 \ \rm{mV}$. In both cases (ⅱ) and (iii), the qualitative behavior of the electric potential profile is the same as in case (ⅰ), but the amplitude of the electrostatic shift is of $\simeq -15 \ \rm{mV}$. This physical behavior is to be solely ascribed to the interface electrostatic coupling of neuron and NP with the cleft electrolytic solution, expressed by Eqs (3.7b), (3.7d) and (3.7e). Other electrostatic coupling effects, such as that induced by the polarization of the nanoparticle or by the electrostatic production and accumulation of superoxide anions in the cleft region are hindered by the presence of bulk ions in the cleft region, which are able to screen any polarizing effect in a few Debye lengths.

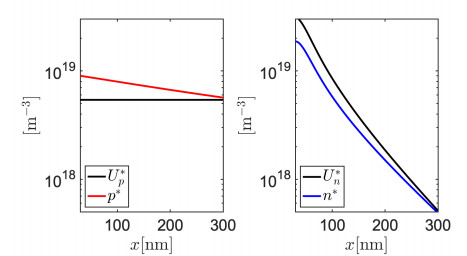
In Figure 9 we represent the spatial distribution in the NP region $\Omega_2$ of the number density of holes and electrons ($p$ and $n$) and of their corresponding Slotboom variables ($u_p$ and $u_n$). It is interesting to notice that holes are able to redistribute almost homogeneously across the NP domain (Figure 9 left) thanks to their high mobility. Electrons instead, due to the formation of $P3HT^+: \, ^3O_2^-$ with the molecular oxygen ^[3], are characterized by a mobility which is 4 orders of magnitude smaller than hole mobility, and, as a consequence, their spatial distribution closely resembles the Lambert-Beer profile of the input light $G$ (Figure 9 right), in agreement with the considerations already drawn in Section 7.1 and in ^[4]. The strong asymmetry in the mobilities of the two charge carriers leads to the formation of a dipole-like distribution of positive and negative charge across the NP domain, which is responsible of the NP polarization. The combination of the asymmetric transport properties of holes and electrons inside P3HT with the asymmetric Lambert-Beer light profile, is an instance of the so-called Dember Effect ^[5,9]. This effect leads to the formation of a dipole-like electric potential distribution, referred to as Dember photovoltage, and is caused by an asymmetric distribution of charge inside a semiconducting material due to a markedly different accumulation and redistribution of charges according to their transport properties and light incidence.

In Figure 10 we represent the spatial distribution of the ion molar density of the electrolytic ions across the whole domain $\Omega$. Consistent with definitions (5.2a), all the ion molar densities are set equal to zero in $\Omega_2$ since no ions are allowed to travel across the NP, a physical evidence of the high hydrophobicity of P3HT. Results indicate that O$_2^-$ molar density increases with respect to its bulk concentration in the cleft region, where it gets accumulated (top left panel). In the simulation, light comes from the left, from the neuron towards the NP, inducing, as clearly visible in Figure 9, an accumulation of electrons at the NP-cleft interface. This favors the production of O$_2^-$ compared to the bulk electrolyte side. It is also interesting to notice that a steep boundary layer shows up at the cellular membrane, due to the negative peak of the electric potential (see Figure 7, left panel). In the bulk electrolyte the O$_2^-$ molar density, as well as that of the other bulk electrolytic ions, does not depart significantly from its Dirichlet boundary value at $x = L$. Bulk ions, such as Na$^+$, Cl$^-$ and K$^+$, show in the cleft a different behaviour depending on their valence and their Nernst potential in contact with the neuron. In particular, Cl$^-$ and Na$^+$, whose concentration is low in the intracellular region, are reduced with respect to their bulk concentrations, whereas K$^+$ is accumulating. Depending on the valence of each ion, the formed boundary layer exhibits a different slope: cations tend to accumulate around a peak of negative potential, whereas anions tend to deplete the boundary layer in proximity of the cell membrane.

7.3.   The role of light intensity

In our model description of the bio-hybrid system, the presence of an electrolytic solution in the cleft screens the polarization and the Dember Effect of the NP very efficiently but does not affect the chemical role of O$_2^-$, which, as a Reactive Oxygen Species (ROS), may possibly trigger some signaling pathways at the neuron membrane.

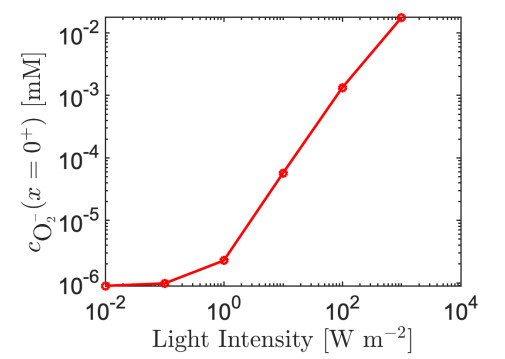
Figure 11 represents the predicted superoxide molar density at the neuron membrane, for different values of light intensity impinging onto the NP. As light intensity becomes higher than 1 $\rm{W \, m^{-2}}$, the dependence between the superoxide molar density at the neuron membrane and the light intensity becomes almost linear in the logarithmic scale. Below this threshold value, instead, the superoxide molar density tends to a plateu value, coinciding with the equilibrium concentration of O$_2^-$ in the aqueous solution, which is assumed to be around 1 nM. From the data reported in ^[1], the light intensity regime hitting the retinal layers under sunlight exposure is of 0.2 $\rm{W \, m^{-2}}$, which corresponds in Figure 11 to a value of superoxide molar density of a few nM, likely a too small molar density to trigger any photochemical effect at the neuron membrane.

The increase in light intensity not only affects the efficiency of the interface reactions leading to the production of O$_2^-$, but has also some numerical consequences. Figure 12 represents the number of Gummel's Map iterations that are required to meet a tolerance $\delta = 10^{-5}$ as a function of light intensity. When light intensity exceeds 10 $\rm{W \, m^{-2}}$ we observe that the convergence of the algorithm is significantly deteriorated and the number of iterations abruptly becomes three times larger than in the lower light intensity regime. This may be explained by the increased rate of nonlinear interface reactions, which, correspondingly, gives rise to an increase of the coupling between continuity equations and NLP equation, resulting into a reduced convergence rate of the Gummel Map. This behavior agrees favorably with similar conclusions drawn in ^[18] and ^[12] in the application of Gummel's Map to semiconductor device simulation.

8.   Proof of Theorem 5.1

In this section we provide the full details of the proof of Theorem 5.1.

The adopted notation is:

8.1.   Strategy for the existence of a solution: the Gummel Map

The strategy to prove the existence of a solution of the fully coupled nonlinear differential model constituted by the boundary value problems (3.1), (3.8), (3.12) and (3.16), consists in constructing a solution map, henceforth referred to as Gummel's Map in analogy to that used in the case of the Drift-Diffusion model for semiconductor devices ^[10], acting over some convex, closed subsets of suitable Sobolev spaces and showing that this map has a fixed point.

As illustrated in Section 5.1, the Gummel Map is a composition of two other maps: the first map, $\mathcal{T}$, determines the potential $\psi ^{(1)}$ once the other variables $u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}$ have been fixed. The differential problem for $\psi ^{(1)}$ is nonlinear (cf. (4.1a) with $k = 0$) and to solve it we shall use the Leray-Schauder Theorem. Once $\psi ^{(1)}$ has been uniquely determined, still keeping the same $u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}$, a second map, $\mathcal{P}$, computes a set of new variables $u_{\alpha }^{(1)}, u^{(1)}, u_{n}^{(1)}, u_{p}^{(1)}$. The problems for all these variables are all linear and the main tool will be the Lax-Milgram Theorem. The Gummel Map is precisely $\mathbb{G} = \mathcal{P} \circ \mathcal{T}$ and it turns out (Schauder Theorem) that it has a fixed point, which is a solution of the original nonlinear fully coupled problem constituted by the boundary value problems (3.1), (3.8), (3.12) and (3.16).

8.2.   The map $\mathcal{T}:$ $\left(u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}\right) \rightarrow \psi ^{(1)}$

In this section, we study the mathematical properties of the map that represents the step to update the electric potential in the Gummel Map. We assume that $u_{\alpha }^{(0)}$, $\alpha = Na^{+}, Cl^{-}, K^{+}$, and $u^{(0)}$ are given in $H^{1}\left(\Omega _{1, 3}\right)$, $u_{n}^{(0)}, u_{p}^{(0)}$ are given in $H^{1}\left(\Omega _{2}\right)$ and that they are all nonnegative. To solve the nonlinear Poisson equation (4.1a) for $\psi^{(1)}$ we will use a variational formulation and the Lax-Milgram Theorem. To this purpose, let us consider the space $V$ defined in (5.5a). In $V$ we introduce the following scalar product (see Lemma 8.1):

wih energy norm

Lemma 8.1. (8.1) is a scalar product in $V$ and the norm $\left\Vert v\right\Vert _{V}$ is equivalent to the norm

Moreover, $V$ is a Hilbert space with respect to the scalar product (8.1).

Proof. (8.1) is bilinear, symmetric and $\left(v, v\right) \geq 0.$ If $\left(v, v\right) = 0$ then $v$ is constant on every $\Omega _{j},$ and $v\left(0\right) = 0,$ $v\left(R_{1}^{+}\right) = v\left(R_{1}^{-}\right)$ $v\left(R_{2}^{+}\right) = v\left(R_{2}^{-}\right)$. Since $v\left(0\right) = v\left(1\right) = 0$, then $v = 0$ on $\Omega _{1}\cup \Omega _{3}.$ In particular $v\left(R_{2}^{+}\right) = 0$ so that also $v\left(R_{2}^{-}\right) = 0$ from which $v = 0$ on $\Omega _{2}$ too. Thus (8.1) is a scalar product. For the equivalence of the norms (8.2) and (8.3) it is enough to prove that there exists a constant $C_{L}$ such that

By contradiction, let $\left\{ v_{k}\right\} \subset V$ such that, for $k\geq 1,$

Normalizing, we can assume that $\left\Vert v_{k}\right\Vert _{L^{2}\left(\Omega \right) } = 1, \forall k\geq 1.$ Then, in particular $\left\{ v_{k}\right\}$ is bounded in $H^{1}\left(\Omega _{j}\right)$, $j = 1, 2, 3$ and

From Rellich theorem, there exists a sequence $\left\{ v_{k_{m}}\right\}$ such that

The weak lower semicontinuity of the norm gives

and hence $v$ is constant in $\Omega _{1}, \Omega _{2}, \Omega _{3}.$ In particular, $v = 0$ in $\Omega _{3}$, since $v\left(1\right) = 0$, and therefore $v_{k_{m}}\left(R_{2}^{+}\right) \rightarrow 0.$ From (8.5) we deduce that $v_{k_{m}}\left(R_{2}^{+}\right) -v_{k_{m}}\left(R_{2}^{-}\right) \rightarrow 0$ so that also $v_{k_{m}}\left(R_{2}^{-}\right) \rightarrow 0$ which implies $v = 0$ in $\Omega _{2}$. Finally, again from (8.5), $v_{k_{m}}\left(0\right) \rightarrow v\left(0\right) = 0$ and hence $v = 0$ in $\Omega _{1}.$ Thus $v = 0$ in $\Omega,$ while $\left\Vert v_{k}\right\Vert _{L^{2}\left(\Omega \right) } = 1\rightarrow \left\Vert v\right\Vert _{L^{2}\left(\Omega \right) }:$ contradiction.

Corollary 8.2. Let

with the norm

Then

with compact embedding $V\hookrightarrow C^{\ast }$.

In view of the weak formulation of the NLP equation, we introduce the bilinear form

It is easy to check that $B:V\times V\rightarrow \mathbb{R}\,$ is continuous. Moreover

whence

which shows the coercivity of $B$ on $V$.

For fixed, nonnegative, $u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}$, let us consider the nonlinear problem of finding $\psi \in V$ such that

where

Theorem 8.3. There exists a unique solution $\psi ^{(1)} = \mathcal{T}\left(u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}\right) \in V$ to (8.7) satisfying

where

We also have $\psi ^{(1)}\in H^{2}\left(\Omega _{j}\right), j = 1, 2, 3,$ and therefore $(\psi ^{(1)})^{\prime }\in C^{\ast }.$ In particular, $\mathcal{T}$ is compact in both the topologies of $V$ and $C^{\ast }$. An alternate estimate for $\psi^{(1)}$, possibly more convenient than (8.8a), is

where:

Proof. (Existence and regularity of a solution) We use the Leray-Schauder fixed point Theorem. Fix $\psi ^{\ast }\in C^{\ast };$ the linear problem

has a unique solution $\psi = S\left(\psi ^{\ast }\right) \in V\hookrightarrow C^{\ast }$, by Lax Milgram Theorem. The operator $S:C^{\ast }\rightarrow C^{\ast }$ is continuous, as it is easy to check, and compact (from Corollary 8.2).

To conclude, we need an apriori estimate for the solutions of the family of equations

that is of

of the type

with $M$ independent of $s$ and $\psi$.

First observe that, since the functions $u_{\alpha}^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)}$ are nonnegative, the map $\psi \longmapsto f^{0}\left(x, \psi \right) -f^{0}(x, 0)$ is decreasing and hence

Choosing $\varphi = \psi,$ we find

from which

and

The $H^{2}-$regularity follows directly from the differential equation.

Proof. (Uniqueness of the solution) Let $\eta, \psi$ be solutions to (8.7). Then $w = \psi -\eta$ solves the equation

Letting $\varphi = w$ we get,

from which $w = 0$. By the Leray-Schauder Theorem, the map $S$ has a unique fixed point $\psi ^{0}.$ This fixed point is the unique weak solution to problem (8.7) and satisfies the estimate (8.8a). This concludes the proof of Theorem 8.3.

8.3.   The map $\mathcal{P}:(\psi ^{1}, u_{\alpha }^{(0)}, u^{(0)}, u_{n}^{(0)}, u_{p}^{(0)})\rightarrow (u_{\alpha }^{(1)}, u^{(1)}, u_{n}^{(1)}, u_{p}^{(1)})$

In this section, we study the mathematical properties of the map that represents the step to update the ion molar densities and the carrier number densities in the Gummel Map.

8.3.1.   Determining $u_{\alpha }^{1},$ $\alpha =Na^{+}, Cl^{-}, K^{+}$

Given $\psi ^{(1)}$ as uniquely determined in Theorem 8.3, in this subsection we solve problem (3.8a)–(3.11g). For notational simplicity, we denote $u_{\alpha }^{(1)}$ by $u_{\alpha}$ and $\psi ^{(1)}$ by $\psi$.

Consider first the problem in $\Omega _{1}.$ In $H^{1}\left(\Omega _{1}\right)$ we use the norm (equivalent to the usual one)

The weak formulation of our problem is the following. To find $u_{\alpha }\in H^{1}\left(\Omega _{1}\right)$ such that, for every $v\in H^{1}\left(\Omega _{1}\right)$

It is immediate to see that the bilinear form $A_{1}:$ $H^{1}\left(\Omega _{1}\right) \times H^{1}\left(\Omega _{1}\right)$ is continuous. Moreover

Since $Be\left(2M\right) \leq Be\left(\pm \Psi _{\alpha }\right) \leq Be\left(-2M\right)$ we find

and therefore $A_{1}$ is coercive in $H^{1}\left(\Omega _{1}\right).$ Since

is an element of $H^{1}\left(\Omega _{1}\right) ^{\ast }$ (the dual of $H^{1}\left(\Omega _{1}\right)$), the following result holds.

Theorem 8.4. There exists a unique solution $u_{\alpha }^{1}\in H^{1}\left(\Omega _{1}\right)$ of problem (8.9) and

Moreover $u_{\alpha }^{1}\in H^{3}\left(\Omega _{1}\right),$ $u_{\alpha }^{1}$ takes its maximum and minimum at $x = 0$ or $x = R_{1}$ and

Proof. For notational simplicity, we denote $u_{\alpha }^{1}$ by $u_{\alpha}$. Existence, uniqueness and the stability estimate (8.10) follow from Lax-Milgram Theorem. The regularity follows directly from the differential equation that can be written in the form

Since $\psi^{\prime }$ is bounded and continuous, $u_{\alpha }$ attains maximum and minimum at the endpoints of $\Omega_1$, by the maximum principle.

If $u_{\alpha }\left(0\right) = \min u_{\alpha }\leq 0$, then, by the Hopf principle, $u_{\alpha }^{\prime }\left(0\right) > 0,$ while if $u_{\alpha }\left(R_{1}^{-}\right) = \min u_{\alpha }\leq 0,$ then $u^{\prime }\left(R_{1}^{-}\right) < 0.$ In both cases we get a contradiction with the Robin conditions. Thus $u_{\alpha } > 0.$

Let max $u_{\alpha } = u_{\alpha }\left(0\right).$ Then the Hopf principle gives $u_{\alpha }^{\prime }\left(0\right) < 0$ and from the Robin condition we find

since

On the other hand, if max $u_{\alpha } = u_{\alpha }\left(R_{1}^{-}\right),$ from the Hopf principle we deduce $u_{\alpha }^{\prime }\left(R_{1}^{-}\right) > 0$ and from the Robin condition we get

since

Consider now the problem in $\Omega _{3}$ for $v_{\alpha }$. Its weak formulation reads:

To find $v_{\alpha }\in H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right)$ such that, for every $\eta \in H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right),$

It is immediate to see that the bilinear form $A_{3}:$ $H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right) \times H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right) \rightarrow \mathbb{R}$ is continuous. Moreover

and $A_{3}$ is also coercive. The following result holds.

Theorem 8.5. There exists a unique solution $v_{\alpha }\in H_{0, \left\{ 1\right\} }^{1}\left(\Omega _{3}\right)$ of problem (8.12) and

As a consequence, there exists a unique solution $u_{\alpha }^{1} = v_{\alpha }+ \overline{u}_{\alpha }$ of the original problem. Moreover, $u_{\alpha }^{1}\in H^{3}\left(\Omega _{3}\right),$ $u_{\alpha }^{1}$ attains its maximum and minimum at $x = 0$ or $x = R_{2}$ and

Proof. The proof follows the same lines as the proof of Theorem 8.4.

Remark 8.1. From the definition (5.6a), $X_{\alpha }$ is a closed, convex and bounded subset of $C^{\ast \text{ }}$ and if $u_{\alpha }^{(0)}\in X_{\alpha} \,$ then

8.3.2.   Determining $u^{1}=u_{O_{2}^{-}}^{(1)}$

In this section we solve problem (3.12a)–(3.15d) where we denote $\psi ^{(1)}$ by $\psi$. With this aim, we introduce the bilinear form $E:H^{1}\left(\Omega _{1, 3} \right) \times H^{1}\left(\Omega_{1, 3} \right) \rightarrow \mathbb{R}$ defined as

where $D = D(x)$ is defined in (3.12b).

We want to find $u^{1}\in H^{1}\left(\Omega _{1, 3}\right)$ such that, for all $v\in H^{1}\left(\Omega _{1, 3} \right),$

The bilinear form $E$ is symmetric, continuous and coercive in $H^{1}\left(\Omega _{1, 3}\right)$ with coercivity constant $\delta e^{-M}$ where

The following result holds.

Theorem 8.6. There exists a unique solution $u^{1}\in H^{1}\left(\Omega_{1, 3}\right)$ of problem (8.15) and the following stability estimates hold:

where:

Moreover, $u^{1} > 0$ in $\Omega _{1, 3}$ and $u^{1}\in H^{^{3}}\left(\Omega _{1, 3}\right).$

Proof. The existence and uniqueness of the solution, as well as the stability estimates (8.17), (8.18), follow from Lax Milgram Theorem. The $H^{3}-$regularity follows directly from the differential equation. For notational simplicity set $u \equiv u^{1}.$ To show that $u > 0$, write the differential equation in the form.

If $x_{0}\in \Omega _{1, 3}$ is a point of minimum, then $u^{\prime \prime }\left(x_{0}\right) \geq 0, u^{\prime }\left(x_{0}\right) = 0.$ Thus it cannot be $u\left(x_{0}\right) \leq 0$. Also it cannot be $\min u = u\left(0\right) \leq 0,$ since then, by Hopf principle, $u^{\prime }\left(0\right) > 0$, while we have $u^{\prime }\left(0\right) = 0$. If $\min u = u\left(R_{1}^{-}\right) \leq 0$, Hopf principle gives $u^{\prime }\left(R_{1}^{-}\right) < 0$ in contradiction with the Robin condition. Thus $\min_{\overline{\Omega }_{1}}u > 0.$ Similarly, it cannot be $\min u = u\left(1\right) \leq 0$ since $u^{\prime }\left(1\right) = 0;$ finally, if $\min u = u\left(R_{2}^{-}\right) \leq 0,$ Hopf principle gives $u^{\prime }\left(R_{2}^{-}\right) > 0$ in contradiction with the Robin condition. Thus, also $\min_{\overline{\Omega _{3}}}u > 0.$

Remark 8.2. We assume that $u_{n}^{(0)}\leq N = G_{max} \tau_{max} \sim 10^9$, and that

is sufficiently small. Then, we have

where

and, for a suitable $K_{3}$ depending only on $\beta, N$ and $\lambda,$ (see the definition (8.8g))

To complete the analysis for the superoxide molar density, we need a bound from below for u. In this direction, the following result holds.

Lemma 8.7. Let $u^{1}(x_{\min }) = \min_{\overline{ \Omega }_{1}\cup \overline{\Omega }_{3}}u^{1}.$ If $a)$ $x_{\min }\in \Omega _{1}\cup \Omega _{3}$ or $b)$ $x_{\min } = 0$ or $x_{\min } = 1,$ then

Proof. a) If $x_{\min }\in \Omega _{1}\cup \Omega _{3}$, directly from the differential equation we get $u^{1}\left(x_{\min }\right) \geq C^{EQ}e^{\psi\left(x_{\min }\right)}\geq C^{EQ}e^{-M}$. b) If $x_{\min } = 0,$ since $(u^{1})^{\prime }\left(0\right) = 0$, upon integrating the differential equation over $\left(0, \varepsilon _{k}\right)$ yields

at least along a sequence $\varepsilon _{k}\rightarrow 0$, otherwise there should exist an interval $\left(0, \varepsilon \right)$ where $(u^{1})^{\prime } < 0.$ Thus we deduce that $u^{1}\left(0\right) e^{-\psi\left(0\right) }-C^{EQ} < 0$ and therefore $u^{1}\left(0\right) \geq C^{EQ}e^{\psi\left(0\right) }\geq C^{EQ}e^{-M}$. If $x_{\min } = 1$, after integration over $\left(\varepsilon_{k}, 1\right)$ we have

at least along a sequence $\varepsilon _{k}\rightarrow 1.$ Therefore it cannot be $u^{1}\left(1\right) e^{-\psi\left(1\right) }-C^{EQ} < 0$ so that $u^{1}\left(1\right) \geq C^{EQ}e^{\psi\left(1\right) }\geq C^{EQ}e^{-M}$. This completes the proof.

8.3.3.   Determining the carriers $u_{p}^{1}, u_{n}^{1}$

In this section we solve problems (3.16a)–(3.19d) where we denote $\psi ^{(1)}$ by $\psi$. We additionally assume that $N\geq u_{n}^{(0)}\geq m_{n} > 0$ and $N\geq u_{p}^{(0)}\geq m_{p} > 0$, where $m_{n}, m_{p}$ are not specified yet. The weak formulation for problems (3.16a)–(3.19d) reads:

To find $u_{n}, u_{p}\in H^{1}\left(\Omega _{2}\right)$ such that for all $\forall \varphi \in H^{1}\left(\Omega _{2}\right)$

and

Since

and

both bilinear forms in (8.25), (8.26) are continuous and coercive. The following result holds.

Theorem 8.8. The variational problems (8.25), (8.26) have a unique solution $u_{n}^{1}, u_{p}^{1},$ satisfying the stability estimate

Moreover, both $u_{n}, u_{p}$ belong to $H^{3}\left(\Omega _{2}\right)$ and:

a) $u_{n}^{1}, u_{p}^{1}$ are positive in $\Omega _{2};$

b) $u_{n}^{1}, u_{p}^{1}$ attain their maximum at a point in $\Omega _{2}$ with:

Proof. a) Let $\min u_{n}^{1} = u_{n}^{1}\left(x_{0}\right) \leq 0.$ If $x_{0}\in \Omega _{2}$ we find the contradiction

If $x_{0} = R_{1},$ from the Hopf principle we get $(u_{n}^{1})^{\prime }\left(R_{1}^{+}\right) > 0,$ while if $x_{0} = R_{2}$ we have $(u_{n}^{1})^{\prime }\left(R_{2}^{-}\right) < 0;$ in both cases we get a contradiction with the Robin conditions. Thus $\min u_{n}^{1} > 0.$ The argument for $u_{p}^{1}$ is similar.

b) $u_{n}^{1}$ and $u_{p}^{1}$ cannot attain their (positive) maximum at an end point $x = R_{1}$ or $x = R_{2}$, because in the former case $(u_{n, p}^{1})^{\prime }\left(R_{1}^{+}\right) \leq 0,$ while in the latter case $u_{n, p}^{\prime }\left(R_{2}^{-}\right) \geq 0;$ both are in contrast with the Robin conditions.

The inequalities (8.28) and (8.29) follow by taking $\varphi = 1$ in (8.25) and (8.26).

Remark 8.3. Inserting $\varphi = u_{n, p}^{1}$ in the weak formulations for $u_{n}^{1}$ and $u_{p}^{1}$, we also find the estimates

and

The following result gives a characterization of $m_{n}$ and $m_{p}$.

Corollary 8.9. If

then

If

then

Proof. We have

from which

Assume that, for a small $\varepsilon$,

Then

or

and finally,

Choosing $\varepsilon = 1/2$, from (8.36) we get (8.33). The argument for $u_{p}^{1}$ is similar.

8.4.   Further estimates for $u^{1}, u_{n}^{1}, u_{p}^{1}$

To proceed further we need to complete the control from below of $u^{1}$ and to verify that $u_{n}^{1}, u_{p}^{1}$ are bouded above by $N.$ We replace in all the previous estimates the quantity $M$ with the parameter $M^{\ast }$ defined as

with:

We also let:

Lemma 8.10. Assume that $u_{\alpha}^{(0)}, u^{(0)}, u_{p}^{(0)}, u_{n}^{(0)}\in {\bf X}$ (defined in (5.11)) and that $u^{1}\geq \min \left\{ u\left(R_{1}\right), u\left(R_{2}\right) \right\}$ in $\Omega _{1, 3}.$ Then, there exists $m > 0$, depending only on $U_{\ast }$, $U_{np}^{\ast }$ and $\max \left\{ u_{\alpha, N}, \bar{u}_{\alpha }\right\}$, such that

Proof. Assume that there exists a sequence $u_j = \left\{ (u_{\alpha }^{(0)}, u^{(0)}, u_{p}^{(0)}, u_{n}^{(0)})_{j}\right\} \in {\bf X}$ such that, say, $u_{j}\left(R_{1}\right) \rightarrow 0.$ Same argument if $u_{j}\left(R_{2}\right) \rightarrow 0.$ Correspondingly, there is a sequence of electric potentials $\left\{ \psi _{j}\right\}$ equibounded in $V.$

Therefore there are sequences $\psi _{j_{k}}, u_{j_{k}}^{(1)}, \left(u_{n}^{(0)}\right) _{j_{k}},$ $\left(u_{p}^{(0)}\right) _{j_{k}}$ weakly convergent in their Sobolev spaces and strongly in $C^{\ast }$ (by the compact embeddings of these spaces into $C^{\ast }$) to $\psi ^{\ast },$ $u^{\ast },$ $u_{n}^{\ast },$ $u_{p}^{\ast }.$ In particular, in $\Omega _{1}$, $u^{\ast }$ is a solution of the Robin-Neumann problem

with $(u^{\ast })^{\prime }\left(0\right) = 0$ and

However, we have also $u^{\ast }\left(R_{1}^{-}\right) = 0$ and $\left(u^{\ast }\right) ^{\prime }\left(R_{1}^{-}\right) = 0$, which imply $u^{\ast }\equiv 0$ in $\Omega _{1}.$ Contradiction.

Lemma 8.11. Let $u^{0}\geq m^{\ast } = \min \left\{ C^{EQ}e^{-M^{\ast }}, m\right\}$. If

Then, we have

where:

If we also assume that $R_{2}-R_{1}$ is small enough to have (8.39a) and $K_{n}, K_{p}\leq N$, then from (8.18) we also have

Proof. We start with the estimate for $u_{n}$. From $u^{0}\geq m^{\ast }$, since $C^{EQ}e^{-M^{\ast }} < \tilde{C} < 1$, it follows that

and from the weak formulation for $u_{n}$ with $\varphi = 1$ we get

Hence, using (8.30), we obtain

We distinguish two cases: either $u_{n}\left(x_{\max }\right) \leq 1$ or $u_{n}\left(x_{\max }\right) > 1.$ In the latter case $\sqrt{u_{n}\left(x_{\max }\right) }\leq u_{n}\left(x_{\max }\right)$ and we can write

If (8.39a) holds, we deduce

We now address the estimate for $u_{p}$. From $u^{0}\geq m^{\ast }$ and from the weak formulation for $u_{n}$ with $\varphi = 1$ we get

Hence, from (8.31), we have

From here on we can proceed as for $u_{n}.$

8.5.   Existence of a fixed point

We are now in the position to prove Theorem 5.1. The following assumptions are made:

${\bf{Hp1}}$ $\beta = \frac{C^{EQ}k_{n}}{k_{1}\tilde{C}}e^{M_{1}+M_{2}}$ is sufficiently small according to Remark 8.2;

${\bf{Hp2}}$ $R_{2}-R_{1}$ is sufficiently small to ensure that (8.32) and (8.34) are satisfied and that $K_{2}\leq N$ and $K_{p}\leq N$.

Replace in all the estimates $M$ with $M^{\ast }$, fix ($u_{\alpha }^{(0)}, u^{(0)}, u_{p}^{(0)}, u_{n}^{(0)})\in {\bf X}$ and solve for $\psi^{(1)} = \mathcal{T}(u_{\alpha }^{(0)}, u^{(0)}, u_{p}^{(0)}, u_{n}^{(0)})\in C^{\ast }$ (from Theorem 8.3). The map $\mathcal{T}:{\bf X}\rightarrow C^{\ast }$ is continuous and compact (from Theorem 8.3). Moreover, because of Hp1 and Hp2, we have

Given $\psi ^{(1)},$ solve for $(u_{\alpha }^{(1)}, u^{(1)}, u_{p}^{(1)}, u_{n}^{(1)}) = \mathcal{P}(\psi^{(1)}, u_{\alpha }^{(0)}, u^{(0)}, u_{p}^{(0)}, u_{n}^{(0)})$. The map $\mathcal{P}$ is continuous and compact from $C^{\ast }\times {\bf X}$ into ${\bf X}$ (from Theorems 8.4, 8.5, 8.6 and 8.8). The application of Schauder Theorem concludes the proof of Theorem 5.1.

9.   Conclusions and future perspectives

The continuous increase of questions regarding the coupling mechanisms in the bio-hybrid system constituted by a NP, a retinal neuron and the intermediate aqueous environment, has pushed the need for new tools to investigate the open problems in the realization of new generation retinal prostheses.

In our work we have proposed a mathematical model as a Virtual Laboratory complementing the indispensable experimental activity in the study and comprehension of the electrochemical phenomena that occur at the NP-neuron interface. In order to prove the reliability of our formulation, we have performed a theoretical study of the model, specifying the assumptions on the data that guarantee the existence of a solution to the nonlinear system of partial differential equations. Then, we have constructed a consistent and stable numerical approximation of the model based on the use of the finite element method. Finally, we have thouroughly investigated the numerical performance of the computational algorithm and the biophysical soundness of simulation predictions.

With the use of the proposed model we have been able to describe the coupled system comprising a neuron, an electrolytic solution and a NP immersed in the solution. We have taken into account the light-induced polarization of the NP as well as the interface photo-cathodic reaction of P3HT in an oxygenated environment. In particular, the choice of modeling the cleft as a fully electrolytic medium has revealed some limits of the model, wherein ions are able to totally screen the electrostatic charging of the NP. In the future, a better description of the proteinic nature of the cleft would help us provide a more faithful model picture of the electrostatic mechanisms which may occur at the bio-hybrid interface.

Regardless of the above mentioned limitations, the model has proved to be able to adequately represent the production and diffusion of O$_2^-$ at the interface of the NP, thereby providing a quantitatively accurate estimate of the ROS molecule concentration in proximity of the neuron membrane as a function of the light intensity illuminating the NP.

Acknowledgements

Greta Chiaravalli and Guglielmo Lanzani were supported by the Italian Ministry of University and Research. Grant title: "Membrane targeted light driven nanoactuators for neuro-stimulation"; grant number: PRIN 2020XBFEMS.

Conflict of interest

The authors declare no conflict of interest.