Numerical analysis of multi-dimensional time-fractional diffusion problems under the Atangana-Baleanu Caputo derivative

1.   Introduction

Aerodynamics is the study of the behavior of air as it interacts with moving objects ^[1]. This field is of utmost importance in various engineering disciplines, including aerospace, marine, and energy, among others. Understanding the principles of aerodynamics is crucial for engineers and scientists, for the optimization of the performance, safety, and overall functionality of vehicles, structures, and machinery that operate in or interact with air and other fluid media.

In the past decades, theoretical, computational, and experimental investigations have been the main research paradigms in aerodynamics. There are several challenges in this area. First, analytical models are derived based on assumptions and simplifications, making the model less generalizable. Second, the aerodynamic behaviors are intrinsically complex. For example, the flow exhibits multi-scale dynamics, where both the large-scale and small-scale components need to be properly resolved ^[2]. Furthermore, the flow is usually unsteady where the dynamics are time-dependent. Third, the resolution capability of complex aerodynamic flows in both experimental and numerical studies is limited, where the cost grows drastically as the required resolution increases.

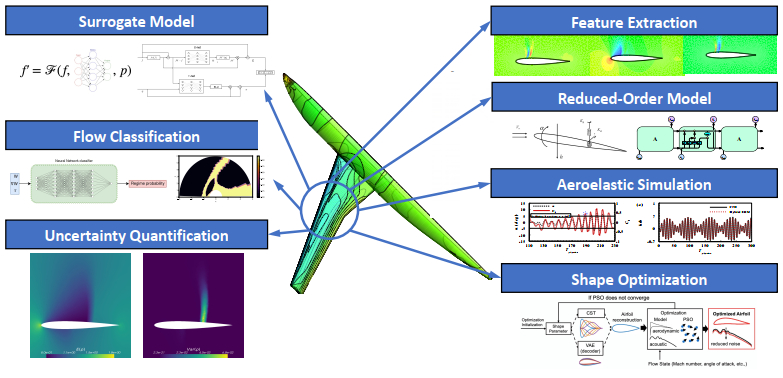
In recent years, research in aerodynamics has remained popular, making a large amount of aerodynamic data available. The vast amount of data has motivated the wide adoption of data-driven methods in aerodynamics ^[3]. Generally, aerodynamic data includes both the integrated coefficients (e.g., lift or drag) and the high-dimensional flow variables (e.g., velocity or pressure field). Additionally, these data come from multiple sources, such as experiments or simulations, making the accuracy, quality of data, and cost of data generation different. From these data, surrogate models can be built to predict the characteristic physics in outflow fields efficiently and to produce reliable aerodynamic data. Therefore, preferable data-driven methods take the advantage of efficient and effective use of aerodynamic data to obtain reasonable models. So far, researchers have conducted significant works to integrate artificial intelligence and machine learning in the investigation of aerodynamics, where different topics have been explored, as shown in Figure 1. These works will be detailed in the following sections.

Figure 1.  Active research areas in artificial intelligence and machine learning for aerodynamics from the authors. Surrogate model ^[4,5]; Flow classification ^[6]; Uncertainty Quantification ^[7,8]; Feature extraction: ^[9,10,11]; Reduced-order model: ^[12,13,14]; Aeroelastic simulation: ^[15,16]; Shape Optimization: ^[17].

DownLoad: Full-Size Img PowerPoint

The goal of data-driven methods is to derive insights, make predictions, or inform decision-making processes by analyzing and interpreting data ^[18]. These methods can be broadly categorized into several types in terms of classification, clustering, regression, etc. While data-driven methods encompass a broader range of approaches, with the rapid development of computing technology and resources, machine learning as a specialized subset has been attracting the lion's share of attention. Machine learning aims to develop algorithms and models that enable computers to learn patterns and make predictions without being explicitly programmed ^[19]. Compared to classical data-driven methods, machine learning often involves more complex models with higher degrees of freedom, e.g., neural networks, decision trees, or support vector machines. Machine learning is a core component of achieving artificial intelligence. With the advent of machine learning (ML), the analysis and utilization of data have taken on a new level of importance.

There have been several important reviews on artificial intelligence and machine learning in fluid mechanics. Brunton et al. ^[20] overviewed the potential of machine learning for fluid mechanics. Vinuesa and Brunton ^[21] reviewed three research directions to enhance computational fluid dynamics with machine learning, including simulation acceleration, reduced-order modeling, and turbulence modeling. Vinuesa et al. ^[22] gave a review on the transformative potential of machine learning for experiments in fluid mechanics. Zhang et al. gave a comprehensive review on the potential of artificial intelligence in fluid mechanics ^[23]. Thereafter, Zhang et al. ^[24] reviewed how to integrate artificial intelligence (the so-called fourth paradigm, the data-intensive scientific research paradigm) into existing research paradigms (theoretical, experimental, and computational research) in fluid mechanics, to extend and create novel research topics in this area.

The present paper overviews the applications of artificial intelligence and machine learning to aerodynamic problems. Generally, they can be classified into four groups: 1) knowledge discovery; 2) theoretical modeling; 3) numerical simulation; 4) multidisciplinary applications. The overall structure of this review paper is given in Figure 2. In what follows, detailed discussions on these areas will be provided, including the capabilities and limitations of existing methodologies.

Figure 2.  Overall structure of this paper, including different research directions of artificial intelligence and machine learning in aerodynamics.

DownLoad: Full-Size Img PowerPoint

2.   Knowledge discovery

Machine learning and artificial intelligence have created a new research paradigm that enables the discovery of new mechanisms for physical problems and new conservation laws for physical processes.

2.1.   Feature extraction

Data-driven methods enable the extraction of flow physics to reveal new mechanisms and discover unknown governing equations. On the one hand, various feature extraction methods have been developed. The basic idea of feature extraction is to obtain representative flow structures that describe the flow evolution in a compact form. These structures are so-called coherent structures that characterize the main flow structures dominating the flow dynamics ^[25]. These methods can be classified into linear and nonlinear feature extraction approaches. On the one hand, linear feature extraction methods decompose the flow into a linear superposition of flow modes, where modal analysis remains the mainstream ^[26]. Two common perspectives are to capture modes with the lowest residual (highest energy) or pure frequencies ^[27]. Proper orthogonal decomposition (POD) ^[28] is the most common strategy for high-dimensional flow data compression, which obtains spatially orthogonal modes that best capture the energy in the flow. From a mathematical point of view, POD offers the least error in the l2-norm. Another popular modal analysis method is dynamic modes decomposition (DMD) ^[29,30], which fits the time-dependent flow dynamics through a linear approximation and obtains dynamic mode with a single frequency and growth rate (thus, orthogonal in time). This approach is well-suited for unsteady flows where several dominant frequencies exist, e.g., the Kármán vortex street ^[10] or transonic buffet over airfoils ^[9]. Motivated by these perspectives, two different spectral POD methods have been proposed ^[31,32]. The first method extracts flow modes and thus bridges between lowest residual and pure frequencies ^[31]. The second method obtains flow modes that are both orthogonal in time and space ^[32]. Another popular method is the cluster-based reduced-order modeling ^[33], which obtains representative flow patterns based on cluster analysis. These methods lead to efficient and accurate reduced-order models for complex flows that are beneficial to interpreting flow mechanisms and constructing reduced-order models, where the latter will be further discussed in Section 3.2. An important application of feature extraction is urban climate modeling ^[34], where data-driven methods are used to characterize flow structures as a way to further understand the dynamics of urban flows. These methods offer to supplement the investigation of this area, where traditional models, including METRAS, COSMO, PALM, MITRAS, and MISKAM models ^[35,36], are widely used.

Due to the intrinsic nonlinearity of the Navier-Stokes equations, linear feature extraction usually suffers from generalization issues that only work well around the linearized equilibrium state. Therefore, nonlinear feature extraction methods have been developed to overcome this challenge. Koopman analysis ^[37,38] is an attractive approach that offers a theoretical background to approximate the nonlinear dynamics (of a finite-dimensional system) in an infinite-dimensional space of observables. It should be noted that DMD is an efficient approach to compute Koopman operators. The Koopman mode theory unifies and provides a rigorous background for different concepts in fluid mechanics, including global mode analysis, triple decomposition, and DMD. Manifold learning ^[39,40] is a class of methods for nonlinear feature extraction that discovers the low-dimensional manifold where the higher-dimensional data usually lies. Based on the concept of deep learning, autoencoders have been attractive as a nonlinear dimensionality reduction approach ^[41,42]. The basic idea of an Autoencoders are to construct a self-mapping of the high-dimensional flow snapshot, i.e., the input and output of the neural network remain the same while the inner layer contains a few neurons to reduce the dimension of the input layer. Autoencoder is composed of two parts, including an encoder part and a decoder part, where the first part performs dimensionality reduction and the second part recovers the flow field. It may potentially overcome the error bound given by linear POD methods ^[42]. Deep learning has also been applied to super-resolution problems where high-resolution flow is reconstructed from low-resolution and coarse-grained snapshots ^[43]. Recently, transfer learning has been applied to construct reduced-order models for flow reconstruction ^[11], through fusing aerodynamic data with different fidelities. So far, nonlinear feature extraction remains to be an active research direction in this area.

Currently, the limitations of the feature extraction methods are also clear. The linear feature extraction shows the difficulty in handling nonlinear dynamics, e.g., the description of shock waves where the pressure distribution is discontinuous on the airfoil surface. However, nonlinear feature extraction methods cannot fully solve such problems, due to the intrinsic complexity in selecting proper functions and hyperparameters. For example, Koopman analysis relies on the proper definition of the observable, which is difficult to find. Autoencoders have a neural-network-like structure, making the determination of hyperparameters, including the number of neurons, layers, and the parameter in the activation function, very challenging. Therefore, future research in nonlinear feature extraction lies in the improvement of robustness and generalization.

2.2.   Equation identification

Another direction goes into the data-driven discovery of physical models. Symbolic regression approaches are widely used to determine the most probable underlying dynamics of a complex system from data, including sparse regression with automatic relevance determination (ARD) ^[44,45] and sparse identification of nonlinear dynamical systems (SINDy) ^[46,47,48]. Given the observed data, among other things, SINDy first extracts the relevant features and employs sparse regression to determine a set of governing equations. The identification process typically involves solving an optimization problem to find the most credible coefficients or parameters of the identified equations. These coefficients represent the strength and form of the relationships between the chosen features, e.g., the transport coefficients in the Navier-Stokes equations. SINDy is especially useful when dealing with complex systems where it is challenging to derive a reliable model through traditional analytical methods. Further application of sparse identification to aerodynamic studies can be found in ^[49,50,51]. It is worth noting that the success of SINDy relies on the automatic combination of manageable forms of algebraic and differential operators. For complex nonlinear systems, e.g., integral equations like the Fokker-Planck and Boltzmann equations, the applicability is questionable.

Another important element of equation identification is to determine the parameters and coefficients that appear in the equation. Gaussian processes (GPs) can be employed in a Bayesian optimization framework to identify near-optimal parameters by sequentially evaluating the objective function based on the current understanding of the parameter space provided by the model. Relevant work has been applied to nonlinear dynamical systems ^[52,53], Navier-Stokes equations ^[54], and turbulence modeling ^[55]. Several other approaches have been explored to couple accurate prediction and equation discovery, most notably neural networks ^[56,57]. Cranmer et al. employed graph neural networks to extract symbolic representations of physical laws that hold good out-of-distribution performance ^[58]. Berg and Nyström developed deep learning algorithms to apply coordinate transformations and discover model features of partial differential equations from measurement data ^[59]. Xu et al. treated the governing equations as a parameterized constraint and recovered the missing flow dynamics from limited experimental observations and data ^[60]. These works indicate that machine learning is a powerful tool to discover useful knowledge from aerodynamic data. Note that machine learning models, e.g., GPs and neural networks, are generally better suited for interpolation within the range of observed data, while the extrapolation performance can be unreliable. The discovered models are generally not interpretable and can be sensitive to the choice of specific kernels and architectures ^[19]. Therefore, data-driven methods should be used judiciously in conjunction with physics-driven methods.

3.   Theoretical modeling

Constructing models from data that balance accuracy and efficiency well lays the foundation for various engineering applications. To this end, data-driven machine learning modeling aims to provide better closure terms for solving the governing equations or develop low-dimensional flow models that are of primary interest to the optimization and design of aerodynamic devices.

3.1.   Turbulence modeling

Even though the governing equations (e.g., Euler and Navier-Stokes) are known, solving these equations numerically can be very expensive. Furthermore, due to the limited computational capability to perform direct numerical simulation (DNS), under-resolved simulations with proper closure terms (so-called turbulence models) are usually considered. For example, large eddy simulation (LES) with subgrid models for subgrid scales enables accurate turbulence simulation using a relatively coarser grid (and thus less computational cost). Reynolds-Averaged Navier-Stokes (RANS) equations belong to another example, which handles high-Reynolds-number flows on a much coarser grid but more popular in engineering use, despite being less accurate than LES and DNS. In recent years, artificial intelligence and machine learning have been utilized to develop data-driven turbulence models, which can be more accurate but less costly than traditional ones. This has become an active research area with significant progress ^[61]. Given high-fidelity data, the data-driven models can be used for coarse-grained simulation with better turbulence closures. These works mainly include closure modeling for RANS and LES, where machine learning has been used to develop better turbulence models, to describe the discrepancy between coarse-grained simulation and DNS, or to replace the near-wall modeling techniques for wall-modeled methods.

In terms of RANS modeling, Ling et al. ^[62] first proposed to use deep neural networks to learn a model for the Reynolds stress anisotropy tensor from high-fidelity simulation data. Wang et al. ^[63] then proposed a data-driven, physics-informed machine learning approach for reconstructing discrepancies in RANS-modeled Reynolds stresses. Both efforts improved the accuracy of traditional RANS models by combining machine learning and data. Parish and Duraisamy ^[64] introduced the field inversion and machine learning approach to infer better functional forms in RANS models, which reconstructs a functional correction that is consistent with the low fidelity (RANS) model and yields accurate predictive solutions. Gene expression programming (GEP) has also been applied to identify and enhance explicit algebraic Reynolds stress models ^[65,66]. GEP allows for giving explicitly the algebraic form of the RANS turbulence model, therefore showing good performance in practical RANS calculations. Many efforts have also been applied to enhance the performance of turbulence models based on eddy viscosity ^[67]. These machine-learning augmented RANS models give reliable mapping between the flow features and eddy viscosity ^[68], which improves the prediction of separated flows ^[69].

Apart from efforts in RANS modeling, different machine-learning methods have been proposed to improve LES closures. Maulik and San ^[70] proposed to use artificial neural networks for approximate deconvolution of filtered turbulence. Maulik et al. ^[71] introduced a data-driven turbulence closure framework for the subgrid modeling of Kraichnan turbulence. Beck et al. ^[72] presented a data-based approach to turbulence modeling for LES by artificial neural networks. The model is used to predict the underlying unknown non-linear mapping from the coarse grid quantities to the closure terms without a priori assumptions. To further reduce the computational cost, wall-modeled LES has been developed, where near-wall turbulence is modeled by a wall function that allows for a much coarser near-wall grid. Neural networks have been trained to construct wall models for LES to accurately predict the wall shear stress ^[73,74]. Lozano-Durán and Bae proposed to divide the flow into several building blocks and implemented neural networks as a building-block wall model for wall-modeled LES. Moreover, reinforcement learning has been utilized for the discovery of wall models for LES, resulting in substantially lower computational cost over fully-resolved simulations while reproducing key flow quantities ^[75].

Data-driven turbulence modeling faces the challenges of generalization and interpretability. First, the model should be generalized to different types of flows, including laminar and turbulent regions, attached and separated flows, etc. Since it mainly depends on the data used to generate the model, the training data is critical to ensure model performance. Second, the interpretation of model performance remains challenging, making it difficult to identify whether the resulting model obeys the basic physical laws or shows similarity to traditional models.

3.2.   Reduced-Order modeling

Constructing low-dimensional aerodynamic models from data has been an active research topic in past decades ^[76,77]. Although many theoretical aerodynamic models exist for different applications, such as the Theodorsen model ^[78], dynamic stall models ^[79], and wake oscillators ^[80], their accuracy and extensibility are limited due to the assumption and the simplification used to derive the models. On the other hand, numerical modeling can achieve accurate prediction of nonlinear and multi-scale flows, while the computational cost hinders wide adoption in engineering applications.

In recent years, data-driven modeling ^[3] has become a new and promising research direction, thanks to the widespread use of artificial intelligence and machine learning. Data-driven modeling aims at developing reduced-order models (ROMs) that represent complex aerodynamics by simplified, low-dimensional dynamic models with reasonable accuracy while being computationally efficient. Generally, ROMs serve two main purposes: 1) to accelerate the full-order simulations for fast characterization and design purposes; 2) to obtain physical insights to help interpret complicated mechanisms. Successful applications have been achieved for both purposes, ranging from flow control ^[81] to fluid-structure interaction ^[82]. As discussed by Kou and Zhang ^[3], current ROMs include system identification, feature extraction, as well as data-fusion-based methods.

System identification ^[83] refers to the technique of constructing mathematical models from observed input-output data extracted from dynamic systems. Here the input data can be the flow states or the structural displacement, while the output data can be the aerodynamic coefficients (e.g., lift, drag, moment, etc.) of interest. There are four main ingredients in system identification: (1) the data itself, (2) the set of candidate models, (3) the criterion of fit, and (4) the validation procedure. Among them, the set of candidate models is the main factor that leads to different types of models, which can be classified into linear and nonlinear ones. It is well-known that the Navier-Stokes equations are nonlinear, while they can be locally linearized around an equilibrium state. This leads to the basic theory of global stability analysis ^[84], which is also applied to modeling unsteady aerodynamics. Therefore, linear or nonlinear ROMs can be derived based on aerodynamic data following either linear or nonlinear dynamics. Linear ROMs work well under small perturbations of the underlying aerodynamics, where state-space models can be identified through the least-squares method. The Eigensystem Realization Algorithm ^[85] and AutoRegressive with eXogeneous input (ARX) ^[86] models are two common methods that construct linear ROMs. Indicial functions identified from the response of the aerodynamic loads to a step change ^[87,88] represents another type of linear ROM. Nonlinear ROMs contain a wider range of approaches, which model unsteady aerodynamics at large amplitude or under various operation conditions. This includes volterra series ^[89], Kriging ^[90], neural networks ^[12,91], block-oriented models ^[92], and deep learning ^[13]. Applications of these models will be introduced in the following sections, and are well summarized in Kou and Zhang ^[3].

As introduced in Section 2.1, different feature extraction methods based on high-dimensional flow field data have been proposed in past decades. The extracted features not only represent the dominant flow behaviors, but also can be used to predict the evolution of flow dynamics. Depending on whether the governing equations are taken into account in reduced-order modeling of flow dynamics, two different types of ROMs are derived, including intrusive and non-intrusive ROMs. Intrusive ROMs are also called projection-based model order reduction ^[93], whose idea is to project the flow modes (e.g., POD modes that are orthogonal in space) onto the governing equations, to obtain low-dimensional models that respect the flow physics. Noack et al. ^[94] are the first to apply this method to obtain ROMs to describe the Hopf bifurcation of flow past a cylinder (from linear instability to the vortex shedding state) with only three degrees of freedom. This first-principle-based model has then been extended to more complex flows, such as cavity flows ^[95], shear layer ^[96], fluidic pinball ^[97], etc. Non-intrusive ROMs ^[98] model the evolution of flow dynamics in a model-free manner, where the underlying governing equations can be unknown. Since this method does not require the governing equations, minimal modification of the numerical solver can be achieved. Traditional techniques include combining POD with surrogate models or system identification to predict the dynamics of the mode coefficients. These models have been extensively used in different aerodynamic and flow problems ^[99,100]. DMD can be regarded as another non-intrusive method where the system dynamics of the observable is modeled linearly. Nonlinear non-intrusive ROMs can be achieved not only using the nonlinear system identification for the modal coefficient ^[101], but also using nonlinear feature extraction like with autoencoders ^[102]. Moreover, operator inference ^[103] is a recent technique that incorporates physical governing equations by defining a structured polynomial form for the reduced model, and then learns the corresponding reduced operators from simulated training data.

Apart from the two typical data-driven methods, one should also realize that aerodynamic data comes from multiple sources, resulting in widespread data fusion in modeling aerodynamics ^[3]. Aerodynamic data can come from analytical models, experimental studies, and numerical simulations, which vary in fidelity, cost, and efficiency of data generation. Data fusion serves to integrate the data from different sources, to produce refined predictions on high-fidelity aerodynamics. Broadly, data fusion includes two different research areas, including data assimilation and multi-fidelity modeling. Data assimilation aims at combining sparse space-time observations of a real physical system and a numerical solver to produce a refined simulation of the predicted states ^[104,105]. Multi-fidelity modeling integrates the data from multiple sources, to offer more accurate high-fidelity prediction while reducing the cost of generating high-fidelity data. Multi-fidelity ROMs for steady ^[106] and unsteady aerodynamics ^[14] have been developed for aerodynamic optimization and aeroelasticity. Machine learning plays an important role in modeling the discrepancy between low-fidelity theoretical models and the experimental aerodynamic data based on the wind tunnel test ^[107]. Based on flow field data with multiple fidelities, machine learning can be used to predict the distribution of flow quantities over a wing with improved fidelity and reduced cost ^[108]. Recent work also applies transfer learning to reconstruct flow fields based on multi-fidelity data ^[11]. These works indicate that data fusion is still an active research direction in data-driven modeling that potentially overcomes the current limitation of modeling aerodynamics from only one source of data.

It should be noted that the development of ROMs faces several challenges ^[3], including the model stability, generalization capability (concerning different types of motion and flow states), and consideration of both linear and nonlinear dynamics. Due to the purely data-driven nature of such models, incorporating physical knowledge into the modeling procedure will further improve the reliability and explainability of the models. For example, physics-informed ROMs have been developed to predict unsteady aerodynamics ^[109] where aerodynamic physics is introduced into the modeling process as a constraint. These topics require further in-depth exploration in future works.

4.   Numerical simulation

Machine learning and artificial intelligence offer new possibilities for solving fluid dynamic equations and generalized aerodynamic physics.

4.1.   Flow simulations

Direct numerical simulation of nonlinear governing equations can be prohibitively expensive in aerodynamic applications. The most straightforward idea for constructing a data-driven approach to solving aerodynamic problems efficiently is to build a data-to-solution mapping that approximates the aerodynamic solution, e.g. mapping the solution of laminar flows ^[110] and turbulent flows ^[111]. Provided with the interpolation performance of machine learning models, such methods are robust concerning low resolution and noises in the observation data. However, these strategies are mostly driven by data and usually have little correlation with underlying physics. The black-box nature of most machine-learning approaches restricts the physical interpretability of the proposed models and numerical methods. Thus, it is challenging to prove that the solution is well-posed and holds a certain order of convergence. Specific strategies for building machine learning models and training parameters may need to be adapted on a case-by-case basis. In addition, a large amount of high-quality data will be needed to overcome potential over-fitting. Given the high expense of conducting experiments and numerical simulations, e.g. in fluid mechanics and aerodynamics, it is challenging to establish such an all-around database ^[112].

One idea to improve the generalization performance and interpretability of data-driven numerical methods is to introduce prior knowledge of underlying physics into the machine learning process. In one direction, neural network (NN) models are used to approximate solutions of high-dimensional partial differential equations (PDEs), among which physics-informed neural networks (PINNs) ^[113,114] have attracted great attention due to the flexibility for solving forward and inverse problems. A PINN model encodes prior knowledge from differential equations into NNs. By minimizing a loss function that represents the residual of differential equations, the numerical solutions can be iterated along with the training process. While PINNs have led to a wide range of applications in fluid mechanics and aerodynamics ^{[115,116,117]}, there are a number of pitfalls. First, the commonly used fully connected neural networks sometimes fail to show stable training behavior and thus are unable to produce accurate predictions ^[118]. Such pathology can be partly attributed to multi-scale interactions between different terms in the PINN's loss function, which ultimately leads to stiffness in the gradient flow dynamics ^[119]. Since the iterative optimization of neural network parameters can be regarded as an explicit time-integration scheme for a partial differential equation ^[120], stringent stability requirements must be enforced on the learning rate. It has also been shown that conventional fully connected architectures, such as the ones typically used in PINNs, suffer from the so-called spectral bias and are incapable of learning functions with high frequencies ^[121].

Another direction for solving governing equations in aerodynamics with the help of machine learning is operator learning. Operator learning focuses on learning mathematical operators that map solutions to initial-value problems of governing equations. By learning these operators, machine learning enables surrogate models that make predictions about the behavior of aerodynamic systems without the need to explicitly solve the underlying equations. Driven by advances in neural networks and deep learning, operator learning has been successfully applied to studies in aerodynamics-related fields, including fluid dynamics, heat conduction, structural mechanics, and other fields where understanding and predicting the behavior of physical systems are essential. Representative operator learning methods include DeepONets ^{[122,123,124]} and Fourier neural operators ^{[125,126,127,128]}. Both methods construct the neural network function with the help of expansion forms. It has been demonstrated that the latter in its continuous form can be thought of as a subcase of DeepONet with a specially designed trigonometric basis ^[129]. Such methods can break the curse of dimensionality in the input space for solution operators arising from the majority of partial and integral differential equations. Related work is applied to high-speed flows ^[130,131], damage and fracture prediction ^[132,133], and broader kinetic equations ^[4,5]. In principle, operator learning is a purely data-driven methodology. High-quality datasets need to be constructed first and then used for parameter optimization. In other words, data production, training, and inference are packaged into segmented tasks and are difficult to organize into end-to-end workflows. Operators, despite being well-defined mathematical concepts, have to be represented by discrete sensor points, which inevitably introduce artificiality and uncertainty. Also, the extrapolation performance of data-driven models needs further verification and validation ^[134].

Predicting the flow field in an end-to-end manner is the most straightforward way to achieve fast flow prediction. Sekar et al. ^[135] used a combination of a deep convolutional neural network and a deep multilayer perceptron, to achieve fast flow field prediction over airfoils. Han et al. ^[136] developed a spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural networks. Bhatnagar et al. ^[137] proposed to use convolutional neural networks for flow field predictions over airfoils. Hui et al. ^[138] predicted the pressure distribution of airfoils rapidly using deep learning. Thuerey et al. ^[111] investigated the accuracy of deep learning models for the inference of RANS solutions. Wang et al. ^[139] performed flow field prediction of supercritical airfoils via a variational autoencoder-based deep learning framework. Hu and Zhang ^[140] proposed a convolution operator with mesh resolution independence for flow field modeling. Zuo et al. ^[141] proposed to predict the aerodynamics of laminar airfoils based on a deep attention network, using the idea of transformers. This topic remains an active area of research, which is a promising technique for optimization design.

4.2.   Numerical method

Machine learning and artificial intelligence can serve as an important complement to workflows in computational fluid dynamics (CFD), which is ubiquitously employed in both academic and industrial domains ^[142]. A general CFD workflow includes mesh generation, spatial discretization with proper numerical schemes, time integration, post-processing, etc. First, machine learning strategies have been developed to automate the workflow of mesh generation ^{[143,144,145]} and thereafter the evaluation of mesh quality ^[146]. Second, it has been shown that many effective neural network architectures can be interpreted as different numerical discretizations of differential equations ^[147]. Thus, neural networks and numerical discretization can be seamlessly integrated into numerical solvers. A typical example is to describe the finite difference method as a localized convolution operator (CNN), while the time marching scheme can be described using the framework of a recurrent neural network (RNN) ^[148,149]. Furthermore, high-order methods can be accelerated by neural networks to simulate turbulent flows ^[150,151]. Another example that can be analogized to classical numerical methods is the graph neural network ^{[152,153,154]}, where the simulated flow fields own a natural consistency with the computational graph topology. It is worth noting that most of the current work is focused on conceptualization, and there is still a large distance from engineering applications. Machine learning only surrogates part of the CFD workflow and does not necessarily outperform classical methods.

As the development of high-order numerical schemes becomes a highly visible direction in CFD study, machine learning is also expected to play an important role ^{[155,156,157]}. Since high-order methods, e.g., discontinuous Galerkin, spectral difference, and flux reconstruction, are often less robust due to the reduced numerical dissipation, one research direction that integrates machine learning is to help detect troubling elements. Due to the Gibbs phenomenon, these elements often appear near strong discontinuous flow solutions, e.g., shock waves. A classification task is drawn based on experimental and simulation data, and additional numerical dissipation is introduced in the targeted element ^{[158,159,160]}. A similar idea can be implemented in the detection of turbulence ^[161,162]. Note that the whole flow field can be partitioned based on prior criteria, which helps develop a dynamically adaptive hybrid solver and thus accelerates the simulation workflow ^[6]. The connection of different partitions can rely on physics-driven or data-driven modeling strategies, e.g., the reconstruction of fine-grained flow information from coarse-level simulation based on the maximum entropy principle ^[163] or machine learning ^{[164,165,166,167]}. As previously discussed, purely data-driven criteria may suffer from the lack of reliable samples, leading to insufficient interpolation performance. The solution may be to introduce as many physical structures into machine learning models, which needs further investigation.

4.3.   Uncertainty quantification

Machine learning methods can provide estimates of the uncertainty associated with models, equations, and algorithms, and thus enable informed decision-making and risk assessment. Bayesian inference provides a statistical framework for reasoning under uncertainty, which can seamlessly integrate machine learning techniques. Bayesian methods utilize probability distributions to represent uncertainty in model parameters and predictions. As a result, Markov chain Monte Carlo (MCMC) methods can efficiently approximate posterior distributions, enabling the quantification of prediction uncertainty ^{[168,169,170,171]}. The idea is extended to deep learning, resulting in the so-called Bayesian neural network. Unlike traditional neural networks, which output deterministic values, Bayesian neural networks assign probability distributions to their predictions, offering a measure of uncertainty associated with each prediction. This makes them particularly useful in scenarios where uncertainty is a critical factor ^{[172,173,174,175,176]}.

Another common strategy in the study of uncertainty quantification goes to ensemble methods, which combine multiple models to produce a more robust and accurate prediction. Averaging or blending the predictions from an ensemble can reduce overall uncertainty and provide a more reliable representation of the true underlying process. The efficiency gained from machine learning-based surrogate models and numerical methods brings the computational advantage for uncertainty quantification tasks where a large number of realizations have to be evaluated ^[177]. Combining deep learning techniques, the deep ensemble method has been developed accordingly in the context of uncertainty quantification. The main idea is to train multiple instances of the same model architecture independently, and then use the predictions from these individual models to estimate uncertainty in the predictions ^{[178,179,180]}. This approach is particularly useful for tasks where intrusive analysis is prohibitively expensive. It is worth mentioning that the study of uncertainty quantification can be integrated with operator learning discussed in a previous part ^[181,182]. As with traditional methods, conducting uncertainty quantification using machine learning techniques relies on a priori knowledge, which has to be obtained from data, pre-determined distributions, and empirical experience.

5.   Multidisciplinary applications

Recent years have witnessed the trend of multidisciplinary applications in fluid mechanics. We discuss three areas that have significant engineering applications, including fluid-structure interaction, aerodynamic shape optimization, and flow control, in this section.

5.1.   Multiphysics problems: Fluid-Structure interaction

Engineering problems always encounter multiphysics phenomena, where the fluid, structure, heat, etc. are tightly coupled together. Simulating these problems poses great challenges for traditional numerical methods, where the computational cost remains a key bottleneck. It should be noted that, in most of the problems, flow simulation dominates the overall cost. Therefore, artificial intelligence and machine learning can not only accelerate aerodynamic simulation but also speed up the simulation of multiphysics problems. As a typical multiphysics problem, fluid-structure interaction is of great interest in a variety of engineering phenomena, which is taken as an example to discuss the potential of recent trends.

Fluid-structure interaction ^[76] refers to the interaction of a flexible structure immersed in a flowing fluid, which occurs for aircraft wings, blood flows, buildings, wind turbines, etc. Particularly, aeroelasticity is a representative phenomenon coming from the interaction of unsteady aerodynamics and a flexible aircraft ^[80]. Artificial intelligence and machine learning create new paths to model and understand these phenomena. Here we focus on the applications of these methods to model unsteady aerodynamics, subsequently coupled with a structural solver to perform the aeroelastic prediction. Two main problems are of interest in the research of aeroelasticity: 1) linear stability (e.g., flutter), 2) nonlinear response (e.g., Limit-Cycle Oscillation, LCO). Different linear ROMs for flutter have been proposed using the models in Section 3.2. For example, Silva and Bartels ^[183] applied the ERA method for flutter analysis of the AGARD 445.6 wing. Amsallem and Farhat ^[184] developed ROMs for linear aeroelasticity based on POD across different flow conditions, using an interpolation scheme of the state-space model in the Grassmann manifold. Winter and Breitsamter ^[185] developed aeroelastic ROMs for flutter across multiple Mach numbers based on fuzzy neural networks. Mechanisms of fluid-structure interaction have been elaborated by using the stability of linear ROMs. For example, Zhang et al. ^[186] and Yao and Jaiman ^[187] developed ROMs to analyze frequency lock-in in vortex-induced vibrations at low Reynolds numbers. Gao et al. ^[188] applied the linear ROMs to analyze the mechanism of frequency lock-in in transonic buffeting flow.

Predicting nonlinear LCO responses across various operation conditions is another research focus in aeroelasticity. Nonlinear aeroelastic analysis focuses on the prediction of the LCO trend, i.e., the amplitude of structural oscillation versus the reduced velocity. Balajewicz and Dowell ^[189] proposed sparse Volterra models for reduced-order modeling of LCO prediction. Zhang et al. ^[190] developed nonlinear unsteady aerodynamic ROMs based on recursive radial basis function neural networks to predict the LCO trends of transonic flow over airfoils. Mannarino and Mantegazza^[191] performed nonlinear aeroelastic reduced order modeling by recurrent neural networks, to accurately predict LCO responses of transonic flow past an airfoil. Support vector machines (SVMs) have also been used to predict nonlinear aeroelastic responses such as by Chen et al. ^[192]. A representative deep-learning-based ROM was developed by Li et al. ^[13], where long short-term memory (LSTM) was used to model nonlinear unsteady aerodynamics across various Mach numbers. The resulting ROM produced accurate LCO predictions at different transonic Mach numbers. Deep learning has also been used to predict the buffet response ^[193], which is due to the instability of transonic flows. The other paradigm to model nonlinear unsteady aerodynamics is to combine both linear and nonlinear models for a better description of both linear and nonlinear aeroelastic phenomena. To this end, significant progress has been made, where both serial-structured ^[194] and parallel-structured ^{[16,195,196,197]} ROM frameworks have been proposed. It is clear that the generalization capability of ROM for predicting fluid-structure interactions remains an open challenge. For real engineering applications, complex geometries with multi-frequency responses are always encountered, indicating the need to develop robust and reliable ROMs.

5.2.   Design optimization

Aerodynamic shape optimization ^[198,199] refers to the technique of designing the geometry of a flying vehicle to reach the expected lift and drag properties. The basic workflow of aerodynamic shape optimization is composed of a well-defined objective function, constraints, and design variables. However, the computational cost of aerodynamic simulation and the high dimensionality of design variables used for shape parameterization hinder the widespread applications of this technique for real engineering problems, e.g., designing an entire aircraft. To handle this problem, on the one hand, an adjoint-enabled gradient-based optimization algorithm has been proposed ^[200] to efficiently compute the derivatives of the objective function with respect to all design variables. On the other hand, the surrogate model ^{[201,202,203]} is a popular alternative to replace the costly simulation that improves the efficiency of aerodynamic shape optimization.

Artificial intelligence and machine learning have shown great potential in aerodynamic shape optimization. A comprehensive review of machine learning for aerodynamic shape optimization was recently given by Li et al. ^[204]. For adjoint-based methods, Xu et al. ^[205,206] proposed to use machine learning for modeling and predicting adjoint vectors. For surrogate-based optimization, three key procedures have been improved. First, data-driven methods can be used to efficiently parameterize the geometry to reduce the number of design variables. POD can be used to represent the airfoil geometry as linear supervision of representative modes ^[207]. Autoencoder can also be used to map the airfoil geometry in a reduced parameter space with lower dimension than the traditional parameterization method, e.g. CST. An example is given by Kou et al. ^[17] to efficiently optimize the acoustic properties of airfoils. Second, deep learning can be used to learn the full-order CFD solver to construct the surrogate model for evaluating the objective function, which was reviewed by Sun and Wang ^[208]. Chen et al. ^[209] utilized a deep neural network to construct surrogate models for shape optimization to find a minimal drag profile. Transfer learning can be used to obtain the surrogate model more efficiently, by combining both low-fidelity and high-fidelity aerodynamic data ^[210]. Third, optimization algorithms can be learned through machine learning, where reinforcement learning becomes a promising solution ^[211]. More details can be found in Li et al. ^[204]. Finally, it should be noted that aerodynamic optimization still faces the so-called 'curse of dimensionality' problem, where the dimension of parameter space remains prohibitively high, that limiting the engineering applications for three-dimensional wings or aircraft.

5.3.   Flow control

Manipulating flows for engineering applications to reduce drag and improve energy efficiency is a classic but important research topic. To control complex flows, lots of successes have been achieved in past decades ^{[212,213,214]}. Depending on whether additional energy input is needed, passive and active control techniques are developed. A vortex generator over a wing is a typical example of a passive flow control strategy ^[215]. Active flow control ^[216,217], including open-loop and closed-loop techniques, introduces steady or unsteady excitation that manages the flow, through different actuators ^[218] such as synthetic jet ^[219], trailing edge flap ^[220], and moving surfaces ^[221]. A comprehensive review of closed-loop flow control is provided by Brunton and Noack ^[214].

Artificial intelligence and machine learning have demonstrated transformative capabilities in the development of diverse control laws, ROMs for control design, and techniques for sensor selection and state estimation. Rowley and Dawson ^[222] reviewed model order reduction approaches used for flow control. Ahuja and Rowley ^[223] presented an estimator-based control design procedure for flow control, using reduced-order models of the governing equations linearized about a possibly unstable steady state. Duriez et al. ^[224] proposed machine learning control to tame nonlinear dynamics and turbulence, based on genetic programming that explicitly discovers the parameters in the control law. Gao et al. ^[225] designed control laws for transonic buffet over airfoils with a trailing edge flap, based on the linear ROM identified by the ARX method. Ren et al. ^[226] developed adaptive control laws to suppress transonic buffet using neural networks. Nair and Goza ^[227] proposed deep learning to construct nonlinear ROMs for state estimation. Recently, Rabault et al. ^[228] introduced deep reinforcement learning to discover control law for active flow control of flow past a circular cylinder. Thereafter, Paris et al. ^[229] applied deep reinforcement learning for robust flow control and optimal sensor placement. For complete reviews on machine learning for flow control, Rabault et al. ^[230] summarized the use of deep reinforcement learning in active flow control and shape optimization. Ren et al. ^[231] briefly reviewed different works in active flow control using machine learning. Recent progress of machine learning in active flow control has been summarized by Li et al. ^[232]. Although machine learning and artificial intelligence lead to useful models for control law design, engineering application of model-based control design is not straightforward, where challenges in sensor placement, state estimation, and feedback laws still exist. In addition, the cost of reinforcement learning to find efficient control laws remains high, since repeated simulation in the parameter space is needed.

6.   Conclusions

Artificial intelligence and machine learning have forged a novel research paradigm in aerodynamics, yielding substantial benefits to theoretical, experimental, and computational investigations. This transformative influence extends to the exploration of new possibilities within the research community. As outlined in this review, considerable progress has been made in recent years, contributing to an enhanced comprehension of flow physics, the development of more accurate and efficient aerodynamic models, the advent of innovative simulation technologies, and the emergence of multidisciplinary engineering applications. Despite the inclusive nature of this review, certain topics are not covered, notably the applications of artificial intelligence and machine learning in experimental studies.

Despite the progress reviewed in this paper, challenges remain in artificial intelligence and machine learning for aerodynamics. We briefly enumerate the following. First, interpretability and explainability are key aspects of machine learning-based low-dimensional models. Comprehensive mathematical theories and systematical numerical experiments are needed to address the universality of data-driven models and quantify the generalization gap. Causal analysis can be a possible solution to discover the underlying casual relationship for new physical insights that improve the model performance. Second, due to the high overhead of flight tests, wind tunnel experiments, and numerical simulations, data-efficient learning paradigms that can efficiently build models from limited data are required to build sufficiently reliable artificial intelligence. Combining prior knowledge with data can be a natural solution to offer better models. Third, developing large (language) models for fluid mechanics ^[233] is an interesting trend, but there is still a need to find suitable usage scenarios outside of transformer-based natural language processing. Therefore, future research directions in developing low-dimensional aerodynamic models through machine learning and artificial intelligence will focus on how to introduce and incorporate flow physics, as well as how to integrate multi-source aerodynamic data, into the model. Furthermore, extending the applications of these methods to a wider research area and multidisciplinary environment will also be a research trend in the future. We look forward to seeing the studies addressing the above challenges and achieving more successful engineering applications in the near future.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Tianbai Xiao acknowledges the financial support of the National Science Foundation of China (No. 12302381) and the computing resources provided by Hefei Advanced Computing Center.

Conflict of interest

The authors declare no conflict of interest.