Dynamics and approximation of positive solution of the stochastic SIS model affected by air pollutants

1.   Introduction

Nowadays, hundreds of millions of residents have shrouded in the heavy smog especially in winter ^[1]. Numerous epidemiological studies have shown associations of particulate air pollution with risk for various adverse health outcomes, in which the most affected pathologies are chronic obstructive pulmonary disease, lung cancer, influenza and respiratory infectious diseases (e.g., measles) ^{[2,3,4,5,6,7]}. Therefore, it is of great significance to study the respiratory infectious disease affected by air pollution through mathematical means.

Actually, for the respiratory infectious disease, the susceptible-infective(SI) and SIS models are usually used to describe this epidemic dynamic. For instance, Wang et al.^[8] discussed the persistence and periodic orbits for a SIS model in a polluted environment. Liu et al.^[9] analyzed dynamics behavior of an SI epidemic model. Note that these studies did not consider the influence of random environmental factors. In fact, AQI depends on pollutants emissions, weather conditions, wind speed and air temperature, which are generated randomly. Therefore, it is more reasonable to use stochastic differential equation to establish an infectious disease model with air pollution.

Considering random air pollution, there have been many studies on epidemic models. For instance, He et al.^[10] studied the dynamics of infectious respiratory disease spread by developed a stochastic SIS model. Zhao et al.^[11] discussed the existence of a positive stochastic periodic solution of a SI epidemic model by constructing a nonnegative function. He et al.^[12] analyzed dynamics behavior of a stochastic SIS model by applying Itô formula. However, it is worth pointing out that stationary distribution of epidemic models with stochastic air pollution has not been investigated until now.

In addition, it is almost impossible to know the analytical solution of stochastic SIS epidemic model. In view of this, in order to quickly predict the number of infected people at a certain time $t$, it is important to seek an effective numerical algorithm. It is well known that classical Euler-Maruyama (EM) algorithm is widely used to approximate stochastic differential equation (SDE) because of its fast calculation speed and simple format. However, if EM method is used to approximate stochastic SIS model, it will produce negative values ^[13], which is meaningless. Hence, there is the challenging work to establish positive preserving numerical algorithm for stochastic SIS model which the transmission coefficient is a function of AQI by using EM scheme.

In this paper, we study dynamics and approximation of positive solution of the stochastic SIS model. Our main contributions of the work are as follows:

● We develop a stochastic SIS model with air pollution which the transmission coefficient is a function of AQI. It extends the work of ^[12].

● We identify the conditions that guarantee the extinction and the stationary distribution by Foguel alternative, Khasminsk$\check{\rm l}$ function and Itô formula.

● We establish the positive preserving numerical algorithm for stochastic SIS model which the transmission coefficient is a function of AQI through the logarithmic transformed EM method and prove the positive preserving algorithm has first-order convergence rate. It extends the work of ^[14,15,16] which can only achieve convergence rate of 1/2.

The rest of the paper is so organized as. In Section 2, preliminaries and introduction of a stochastic SIS model affected by air pollutants. The existence of kernel operator and the sufficient conditions that guarantee the stationary distribution and the extinction are obtained in Section 3. In Section 4, to approximate the solution a positivity-preserving numerical method is introduced. Section 5 verifies the theoretical results by numerical simulations. In Section 6, we conclude the paper.

2.   Model and preliminaries

In this section, we obtain a stochastic SIS model affected by air pollutants and some preliminary knowledge is given for future needs.

2.1.   Preliminaries

Since the proof of result is based on the theory of integral Markov semigroups, we need some auxiliary definitions and results concerning Markov semigroups (see, ^[17,18,19]). For the convenience of the reader, these definitions and results are presented. Let $\Sigma = \mathscr{B}(\mathbb{X})$ be the $\sigma$-algebra of Borel subset of $\mathbb{X}$ and $m$ the $\sigma$-finite measure on $(\mathbb{X}, \Sigma)$, then the triple $(\mathbb{X}, \Sigma, m)$ be a $\sigma$-finite measure space. Denote by $\mathbb{D}$ the subset of the space $L^{1} = L^{1}(\mathbb{X}, \Sigma, m)$ which contains all densities, i.e.,

where $\|\cdot\|$ represent the norm in $L^{1}$. A linear mapping $P : L^{1}\rightarrow L^{1}$ is called a Markov operator if $P(\mathbb{D})\in \mathbb{D}$.

Assume that $k : \mathbb{X}\times \mathbb{X}\rightarrow [0, \infty)$ is a measurable function such that

for almost all $y\in \mathbb{X}$, and

is an integral Markov operator. The function $k$ is called a kernel operator of the Markov operator $P$.

A family $\{P(t)\}_{t\geq 0}$ of Markov operator is called a Markov semigroup, if $\{P(t)\}_{t\geq 0}$ satisfies

(a) $P(0) = Id$,

(b) $P(t+s) = P(t)P(s)$ for $s, t\geq 0$,

(c) The function $t\mapsto P(t)f$ is continuous for every $f\in L^{1}$.

A Markov semigroup $\{P(t)\}_{t\geq 0}$ is called integral, if for each $t > 0$, the operator $P(t)$ ia an integral Markov operator, i.e., there exists a measurable function $k : (0, \infty)\times \mathbb{X} \times \mathbb{X}\rightarrow [0, \infty)$ such that

for every density $f$.

We need also two definitions concerning the asymptotic behavior of a Markov semigroup. A density $f_{*}$ is called invariant if $P(t)f_{*} = f_{*}$ for each $t > 0$. The Markov semigroup $\{P(t)\}_{t\geq 0}$ is called asymptotically stable if there is an invariant density $f_{*}$ such that

A Markov semigroup $\{P(t)\}_{t\geq 0}$ is called sweeping with respect to a set $A\in \Sigma$ if for every $f\in \mathbb{D}$

The following Lemma summarizes result of asymptotic stability and sweeping.

Lemma 2.1. Let $\mathbb{X}$ be a metric space and $\Sigma$ be the $\sigma$-algebra of Borel sets ^[17]. Let $\{P(t)\}_{t\geq 0}$ be an integral Markov semigroup with a continuous kernel $k(t, x, y)$ for $t > 0$, which satisfies Eq $(2.1)$ for any $y\in \mathbb{X}$. We assume that for every $f\in \mathbb{D}$ we have

then the semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable or is sweeping with respect to compact sets.

The property that a Markov semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable or sweeping from a sufficiently large family of sets(e.g. from all compact sets) is called the Foguel alternative.

Throughout this paper we use the following notation. $|\cdot|$ is Euclidean norm on $\mathbb{R}$. $\emptyset$ denote the empty set. Given $a, b\in \mathbb{R}$, $a\vee b$ and $a\wedge b$ denote the maximum of $a$ and $b$ and the minimum of $a$ and $b$, respectively. For any $\Delta\in(0, 1]$ and $T\in(0, \infty)$, $\lfloor T/\Delta \rfloor$ represents the integer part of $T/\Delta$. $C$ stands for the generic positive real constants whose value may change between occurrences and is independent of $\Delta$ and positive integer $T$.

2.2.   Model derivation

According to the mechanism of respiratory infectious diseases, He et al.^[12] proposed the following model:

with initial values $S_{0}, F_{0}$ and $I_{0}$, where $S(t)$, $I(t)$ and $F(t)$ represent the number of susceptible humans, the number of infected humans and AQI at time $t$, respectively. $c$, $\theta$ and $\gamma$ denote the inflow rate of pollutants into the air, the clearance rate of pollutants and the recovery rate for infected individuals, respectively. $\beta F(t)$ is the infection rate. $S(t)+I(t) = N$ and $N$ is the total number of people. $c$, $\theta$, $\gamma$ and $\beta$ are non-negative numbers.

Because the inflow rate of pollutants $c$ including the emission of automobile exhaust, industrial exhaust and so on is affected by random noise. Hence, we now perturb the inflow rate of pollutants $c$. In this case, $c$ changes to a random variable and then we replace $c$ by $c+\sigma B(t)$, where $B(t)$ is a white noise. In addition, the infectious disease model with birth rate and natural mortality is more realistic. Therefore, based on Eq (2.2), we can get the following model:

where $B(t)$ is a standard Brownian motion defined on a complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$ with a filtration $\{\mathcal{F}_{0}\}_{t\geq 0}$ satisfying the usual conditions(i.e., it is right continuous and $\mathcal{F}_{0}$ contains all $\mathbb{P}$-null sets). $\mu$ and $\sigma$ denote the per capita death rate and the noise intensity. $\mu$ and $\sigma$ are non-negative numbers. The meaning of other symbol is similar to that in Eq (2.2). Since the second equation of model (2.3) does not appear $S(t)$ and $I(t)$, through the same method as literature^[12] the stochastic SIS model affected by air pollutants can be represented as follow:

where $m(t) = \frac{c}{\theta}+(F_{0}-\frac{c}{\theta})e^{-\theta t}$, $n(t) = \frac{\beta}{\theta}(1-e^{-\theta t})$. Combining with $S(t)+I(t) = N$, it is immediate to get an equation about $I(t)$:

3.   Dynamic behavior

In this section, the existence and uniqueness of the positive solution of Eq (2.5) is proved. Then, we have obtained the sufficient conditions that guarantee the existence of stationary distribution and the extinction of the disease.

3.1.   Existence and uniqueness of positive solution

In order to make Eq (2.5) meaningful, we need to show not only that it has a unique global solution but also that the solution will remain within $(0, N)$ whenever it starts from $(0, N)$. To guarantee these properties, it is therefore necessary to establish the following theorem.

Theorem 3.1. For any given initial value $I_{0}\in(0, N)$, there exists a unique global positive solution $I(t)\in(0, N)$ for all$t\geq0$ with probability one, namely,

Proof. By the same method as literature^[12], we can complete the proof.

Denote

Since the existence of positive solution of Eq (2.5) has been obtained by Theorem 3.1, we let $\mathbb{X} = \mathbb{R}_{+}$. Moreover, it is easy to check that the region $\Gamma^{*} = \{(S(t), I(t))\in\mathbb{R}_{+}\times\mathbb{R}_{+}:0 < S(t)+I(t) < N\}$ is a positively invariant set of Eq (2.4). Hence, we always assume that $(S_{0}, I_{0})\in\Gamma^{*}$.

3.2.   Disease extinction

For Eq (2.5), we get the condition which lead to the extinction of the disease under the stochastic disturbance. Denote

which can be seen as a threshold of the extinction (i.e., disease-free) or persistence (i.e., endemic) of disease for Eq (2.5).

Theorem 3.2. If $R_{0}^{s} < 1$ and $\delta^{2} < \frac{c\theta}{\beta N}$, then for any initial value $I(0)\in(0, N)$ the solution $I(t)$ of Eq $(2.5)$ has the following property:

That is, the disease will die out with probability one.

Proof. By Itô formula, it is easy to get that

where

For the function $f_{1}(I(s))$, when

it is immediate to get that

From Eq (3.5), it follows that

With the help of the L'Hospital law, it is immediate to get that

Hence, it follows that

Similarly, we can get

Bring Eqs (3.8)–(3.9) into Eq (3.7), it is easy to get that

Through the large number theorem for martingales, it is easy to get

Bring Eqs (3.6), (3.10) and (3.11) into Eq (3.4), it follows that $\limsup\limits_{t\rightarrow \infty}\frac{\ln I(t)}{t} = 0$. Therefore, based on the analyses above we conclude that $I(t)$ tends to zero exponentially almost surely. This completes the proof.

3.3.   Stationary distribution

For any $A\in \Sigma$, the transition probability function is denoted by $P(t, x_{0}, A)$ for the diffusion process $I(t)$, i.e.,

with the initial value $I(0) = x$, where $I(t)$ be a solution of Eq (2.5) such that the distribution of $I(0)$ is absolutely continuous and has the density $v(x)$. Then $I(t)$ has also the density $U(t, x)$, where $U(0, x) = v(x)$, and $U(t, x)$ satisfies the following Fokker-Planck equation (see ^[19,20])

where

Now we introduce a Markov semigroup associated with Eq (3.12). Let $P(t)v(x) = U(t, x)$ for $v(x)\in \mathbb{D}$. Since the operator $P(t)$ is a contraction on $\mathbb{D}$, it can be extended to a contraction on $L^{1}$. Hence, the operator $\{P(t)\}_{t\geq 0}$ generates a Markov semigroup. Denote $\mathcal{A}$ the infinitesimal generator of semigroup $\{P(t)\}_{t\geq 0}$, i.e.,

The adjoint operator of $\mathcal{A}$ is as follows:

For the convenience of discussing the main results of this section, Some useful lemmas are given.

Lemma 3.1. For every point $x_{0}\in (0, N)$ and $t > 0$, the transition probability function $P(t, x_{0}, A)$ has a continuous density $k(t, x, x_{0})\in C^{\infty}(\mathbb{R}_{+}, \mathbb{R}_{+}, \mathbb{R}_{+})$.

Proof. Let

where $\phi\in(0, N)$. Since for any $\phi\in(0, N)$ we have $b(\phi) > 0$, $b(\phi)$ span the space $(0, N)$. Based on Hörmander theorem(See Theorem 8 in ^[19]), the transition probability function $P(t, x_{0}, A)$ has a continuous density $k(t, x, x_{0})\in C^{\infty}(\mathbb{R}_{+}, \mathbb{R}_{+}, \mathbb{R}_{+})$.

According to Lemma 3.1, it follows that for any $f\in \mathbb{D}$,

Hence, the semigroup $\{P(t)\}_{t\geq 0}$ is an integral Markov semigroup. Next, we rewrite Eq (2.5) of Itô type as Stratonovitch type:

where

Now we briefly describe the method based on support theorems ^[21,22,23] which allows us to check where the kernel $k$ is positive. Fixing a point $x_{0}\in \mathbb{R}_{+}$ and a function $\varphi\in L^{2}([0, T];\mathbb{R})$, consider the following system of integral equations:

Let $D_{x_{0}, \varphi}$ be the Frechét derivative of the function $h\mapsto x_{\varphi+h}(t)$ from $L^{2}([0, T];\mathbb{R})$ to $\mathbb{R}$. If for some $\varphi\in L^{2}([0, T];\mathbb{R})$ the Frechét derivative $D_{x_{0}, \varphi}$ has rank 1, then $k(t, x, x_{0}) > 0$ for $x = x_{\varphi}(T)$. The derivative $D_{x_{0}, \varphi}$ can be found by means of the perturbation method for ordinary differential equations. Let $\Gamma(t) = \hat{f}'(x_{\varphi}(t))+b'(x_{\varphi}(t))\varphi$. For $0\leq t_{0}\leq t\leq T$, let $Q(t, t_{0})$ is the matrix function such that $Q(t_{0}, t_{0}) = 1$, $\frac{\partial Q(t, t_{0})}{\partial t} = \Gamma(t)Q(t, t_{0})$. Then,

Lemma 3.2. For each $x_{0}\in \mathbb{R}_{+}$, and for every $x\in \mathbb{R}_{+}$, there exists $T > 0$ such that $k(t, x, x_{0}) > 0$.

Proof. We first verify that the rank of $D_{x_{0}, \varphi}$ is 1. Let $\epsilon\in(0, T)$ and $h(t) = \frac{1_{[T-\epsilon, T]}(t)}{n(t)x_{\varphi}(t)(N-x_{\varphi}(t))}$, $t\in[0, T]$, where $1_{[T-\epsilon, T]}(t)$ is the characteristic function of interval $[T-\epsilon, T]$. Since $Q(T, s) = 1-\Gamma(T)(T-s)+o(T-s)$, it is easy to get that

Since $\Gamma(T)\neq 0$, $D_{x_{0}, \varphi}$ has rank 1.

Next we show that for any two points $x_{0}\in \mathbb{R}_{+}$ and $x\in \mathbb{R}_{+}$, there exist a control function $\varphi$ and $T > 0$ such that $x_{\varphi}(0) = x_{0}, x_{\varphi}(T) = x$. The Eq (3.13) can be replaced by the following equation:

By the same discussion as in reference ^[24], it is easy to find a control function $\varphi$ and $T > 0$ such that $x_{\varphi}(0) = x_{0}, x_{\varphi}(T) = x_{1}$. This claims $k(t, x, x_{0}) > 0$.

Lemma 2.1 and Lemma 3.2 yield that the Markov semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable or is sweeping. Next, the sufficient condition that guarantee Markov semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable will be given by using Foguel alternative.

Theorem 3.3. Let $(S(t), I(t))$ be a solution of the Eq $(2.4)$ for any given initial value $(S(0), I(0))\in\Gamma^{*}$. If

hold, then the semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable, where $S^{*}(t) = \frac{\beta c}{\theta(\mu+\gamma)}$, $I^{*}(t) = N-\frac{\beta c}{\theta(\mu+\gamma)}$.

Proof. According to Lemma 3.1, it follows that $\{P(t)\}_{t\geq 0}$ is an integral Markov semigroup with a continuous kernel $k(t, x, x_{0})$. Then from Lemma 3.2 for every $f\in \mathbb{D}$, it is immediate to get that

By virtue of Lemma 2.1, it follows that the semigroup $\{P(t)\}_{t\geq 0}$ is asymptotically stable or sweeping with respect to compact sets. In order to exclude the sweeping case, we shall construct a non-negative $C^{2}$-function $V$ and a closed set $O\in\Sigma$ such that

Such function is called Khasminski$\check{\rm l}$ function. In fact, it is easy to get that Eq (2.4) has an endemic equilibrium $E^{*} = (S^{*}, I^{*}) = (\frac{\beta c}{\theta(\mu+\gamma)}, N-\frac{\beta c}{\theta(\mu+\gamma)})$. Then we know

Let

where $\lambda = \frac{2\theta\mu}{c\beta}$.Then,

Conditions Eq (3.14) implies that the ball

lies entirely in the positive zone of $\mathbb{R}_{+}^{2}$. Hence there exists a closed set $O\in\Sigma$ which contains the ellipsoid and $C > 0$ such that

The proof is hence completed.

4.   Numerical approximation of positive solution

Since it is impossible to know the explicit solution of Eq (2.5), constructing appropriate numerical methods to approximate Eq (2.5) and even preserve properties of Eq (2.5) is important and necessary. In this section, to approximate Eq (2.5) a positivity-preserving numerical method is introduced.

4.1.   The logarithmic EM method

In order to obtain a positive numerical solution, we first make a transformation

According to Eq (2.5), applying Itô formula to $y(t)$ yields

with $y_{0} = \ln(I_{0})-\ln(N-I_{0})$, where

Now, we apply the EM scheme to Eq (4.2) then obtain

for any $\Delta\in(0, 1]$ and $k\geq 0$, where $\Delta B(t_{k}) = B(t_{k+1})-B(t_{k})$ and $t_{k} = k\Delta$. Transforming back, i.e.,

gives a strictly positive approximation of Eq (2.5). The forthcoming results concern exponential property of $I(t)$ and $X(t)$, $t\in[0, T]$, which will be used in convergence analysis of the numerical scheme.

Theorem 4.1. For any $p\geq0$

where

Proof. Define a continuous function $V:(0, N)\rightarrow \mathbb{R}^{+}$ by

By the Itô formula, it is easy to get that

where $J = -p\sigma n(t)(N-I)I^{-p}$. we choose $m_{0} > 0$ sufficiently large such that $1/m_{0} < I_{0} < N-1/m_{0}$. For each integer $m\geq m_{0}$, define a stopping time

Integrating both sides of Eq (4.5) and then taking expectation, it is immediate to get that

With the help of the Gronwall inequality, it follows that

Then, letting $m\rightarrow \infty$ and using the Fatou lemma yield

According to calculations similar to those for obtaining Eqs (4.6)–(4.8), it is easy to get that

Therefore the desired conclusion holds.

Remark 4.2. As for moment boundedness, Theorem 4.1 proves the boundedness of inverse moments and we can obtain the boundedness of positive moments by using Theorem 3.2.

Now, we will concern exponential integrability property of analysis solution $y(t)$, $t\in[0, T]$ through using Theorem 4.1.

Theorem 4.3. For any $p\in \mathbb{R}$, Eq $(4.2)$ has the following exponential integrability property

where $K_{p}$ is given by Theorem 4.1.

Proof. Through Eq (4.1) and Theorem 4.1, for any $p\geq0$, it is easy to get that

For any $p < 0$, it follows that

Hence the desired conclusion holds.

The forthcoming theorem concerns exponential property of numerical solution $X(t)$, $t\in[0, T]$, which plays an important role in discussing strong convergence rate of arithmetic.

Theorem 4.4. For any $P > 0$, Eq $(4.4)$ has the property that

Proof. By Eq (4.1), it is immediate to get that

Substituting Eq (4.9) into Eq (4.4), it is immediate to get that

for any integer $k\geq1$. For any $p > 0$, using the Itô formula and the Gronwall inequality further yields

The proof is complete.

4.2.   Strong convergence rate of method

In this subsection, the first order strong convergence of positivity preserving logarithmic EM method for Eq (2.5) is proved by using Theorem 4.1, Theorem 4.3 and Theorem 4.4.

Theorem 4.5. For any $q > 0$ there exists a constant $C > 0$ such that for any $\Delta\in(0, 1]$

Proof. By integrating on both sides of Eq (4.2), it is easy to get that

Using Eqs (4.1), (4.4) and (4.10), it follows that

where

Let $u_{k} = X(t_{k})-y(t_{k})$, $J_{k} = J^{(1)}_{k}+J^{(2)}_{k}+J^{(3)}_{k}+J^{(4)}_{k}$ and $Z_{k} = Z^{(1)}_{k}+Z^{(2)}_{k}$, then

Further, it is immediate to get that

By using Lagrange mean value theorem, it follows that

where $\xi\in (X(t_{k})\wedge y(t_{k}), X(t_{k})\vee y(t_{k}))$.Then, Eq (4.15) can be estimated as

Let $\mathfrak{M}_{0} = 0$, and $\mathfrak{M}_{k} = \sum^{k-1}_{i = 0}(2+C\Delta)^{k-1-i}u_{i}Z^{(2)}_{i}$ for any $k\geq 1$, since

it is then easy to show that $\mathbb{E}[\mathfrak{M}_{k+1}|\mathcal{F}_{k}] = \mathfrak{M}_{k}+u_{k} \mathbb{E}[Z^{(2)}_{k}|\mathcal{F}_{k}] = \mathfrak{M}_{k}$. This implies immediate that $\mathfrak{M}_{k}$ is a martingale. Using Burkholder-Davis-Gundy inequality and Hölder inequality, it is easy to get that

for any $q\geq2$ and $l = 0, \cdot\cdot\cdot, \lfloor T/\Delta \rfloor$.Using Eq (4.17) and the basic inequality $(\sum_{i = 1}^{n}a_{i})^{p}\leq C\sum_{i = 1}^{n}a_{i}^{p}$ for Eq (4.16), it follows that

then, using the Hölder inequality, the triangle inequality and the basic inequality, it is easy to get that

for any $q\geq 2$ and $l = 0, 1, \cdot\cdot\cdot, \lfloor T/\Delta\rfloor$.By using Lagrange mean value theorem, it follows that

Combining Eq (4.19), Theorem 4.3, Theorem 4.4 and Young inequality, it is easy to get that

For any $q\geq2$, using triangle inequality, basic inequality, Hölder inequality, Theorem 3.1 and Theorem 4.1 for Eq (4.13), it is immediate to get that

Using Hölder inequality, Burkholder-Davis-Gundy inequality, Theorem 3.1 and Theorem 4.1 for Eq (4.14), it is immediate to get that

Thus, the Hölder inequality gives that

For any $q\geq2$, using Eqs (4.11) and (4.12) and Theorem 3.1, it follows that

using Eq (4.12), Burkholder-Davis-Gundy inequality and Lagrange mean value theorem, it follows that

For any $q\geq2$, the Canchy-Schwarz inequality gives that

Thus, substituting Eqs (4.20)–(4.30) into Eq (4.18), it is immediate to get that

for any $q\geq2$, and $l = 0, 1, \cdot\cdot\cdot, \lfloor T/\Delta \rfloor$, and applying the Gromwall inequality we obtain

for any $q\geq2$, and $l = 0, 1, \cdot\cdot\cdot, \lfloor T/\Delta \rfloor$. This completes now the proof of the assertion for $q\geq2$. The Hölder inequality yields

for any $p\in(0, 2)$, and $l = 0, 1, \cdot\cdot\cdot, \lfloor T/\Delta \rfloor$. The proof is complete.

Above, the convergence rate of the EM method of Eq (4.2) is given. Below, we will give the convergence rate of the original Eq (2.5) of Eq (4.2).

Theorem 4.6. For any $p > 0$, there exists a constant $C > 0$ such that for any $\Delta\in (0, 1]$

Where $\bar{I}(t_{k})$ and $I(t_{k})$ denote the value of the analytical solution at time $t_{k}$ and the value of the numerical solution at time $t_{k}$ respectively.

Proof. The Lamperti-type transformation yields

Thus, by applying Theorem 4.5, we infer that

for any $\Delta\in (0, 1]$. The proof is complete.

Remark 4.7. For positive preserving numerical methods of nonlinear SDE, Mao et al.^[25] have established a truncated EM method for stochastic Lotka-Volterra competition model but without any convergence rate of the algorithm. Theorem 4.6 has stated that for a stochastic SIS model which the transmission coefficient and the noise intensity are the function of AQI, the logarithmic EM method has the first-order $p$th-moment convergence rate over a finite time for all $p > 0$. This is a major innovation of this paper.

5.   Numerical simulations

In this section, we want to illustrate the correctness of our theoretical results obtained in previous section by numerical simulations.

5.1.   Numerical simulations of stationary distribution

In this subsection, in order to show theoretical result of stationary distribution, some numerical simulations are presented. By using explicit Milsteins method ^[26], the numerical scheme for Eq (2.4) is given by:

where $\xi_{k}(k = 1, 2, \cdot\cdot\cdot)$ are independent Gaussian random variables $N(0, 1)$.

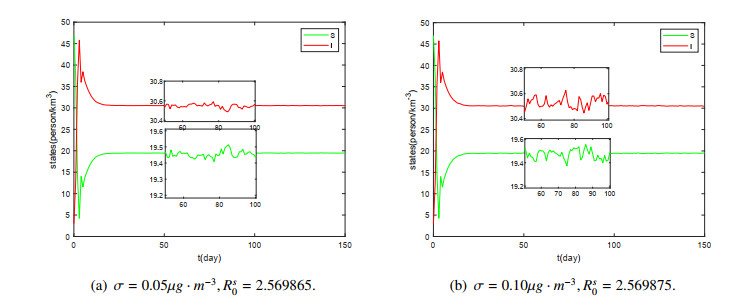
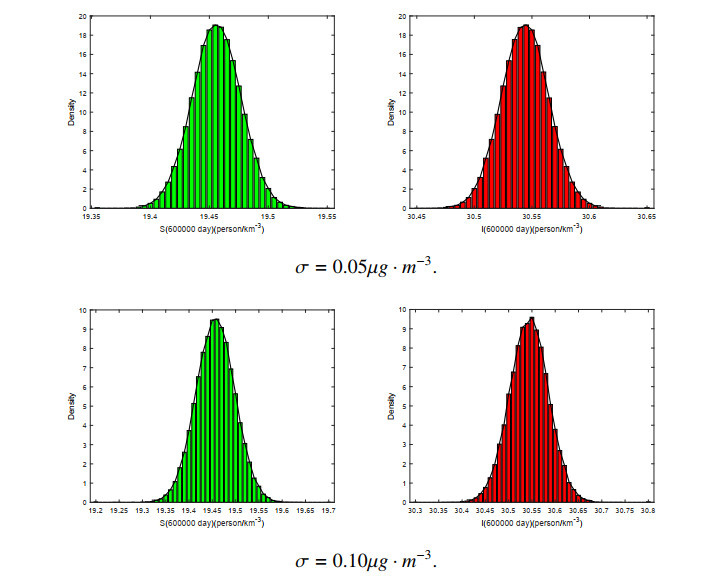
With the parameters in Table 1 and taking $T = 600, 000\; day, \Delta t = 1\; day$, $\sigma = 0.05\; \mu g \cdot m^{-3}$(resp.$\sigma = 0.10\; \mu g \cdot m^{-3}$), simple calculation further yields that $R^{s}_{0} = 2.569865 > 1, \sigma^{2} = 2.5\times 10^{-3}\; \mu g ^{2}\cdot m^{-9} < 2.47\times 10^{-3}\; \mu g ^{2}\cdot m^{-9} = \frac{2\mu\theta^{2}}{\gamma I^{*}\beta^{2}N^{2}}\min\{S^{*2}, I^{*2}\}-\frac{2\beta\max(I^{*}, S^{*})|F_{0}-\frac{c}{\mu}|\theta^{2}}{NI^{*}\beta^{2}}$(resp.$R^{s}_{0} = 2.569875 > 1, \sigma^{2} = 1\times 10^{-2}\; \mu g ^{2}\cdot m^{-9} < 2.47\times 10^{-2}\; \mu g ^{2}\cdot m^{-9} = \frac{2\mu\theta^{2}}{\gamma I^{*}\beta^{2}N^{2}}\min\{S^{*2}, I^{*2}\}-\frac{2\beta\max(I^{*}, S^{*})|F_{0}-\frac{c}{\mu}|\theta^{2}}{NI^{*}\beta^{2}}$) by Eqs (3.2) and (3.14). Thus, it is immediate to get that Eq (2.4) exists stationary distribution under noise intensity $\sigma = 0.05\; \mu g \cdot m^{-3}$ and $\sigma = 0.1\; \mu g \cdot m^{-3}$ by Theorem 4.1. Actually, as shown in from Figure 2, for Eq (2.4), the probability density functions of $S(600000\; day)$ and $I(600000\; day)$ population satisfy normal distribution under two different values of $\sigma = 0.05\; \mu g \cdot m^{-3}$ and $\sigma = 0.10\; \mu g \cdot m^{-3}$. This is the same conclusion as given by Theorem 4.1.

5.2.   Numerical simulations of approximation of positive solution

In this subsection, in order to illustrate the efficiency of the logarithmic Euler-Maruyama scheme, some numerical simulations are given.

5.2.1.   Numerical simulations of the positive-preserving property

By using logarithmic Euler-Maruyama method, Eq (2.5) can be discretized in the following form:

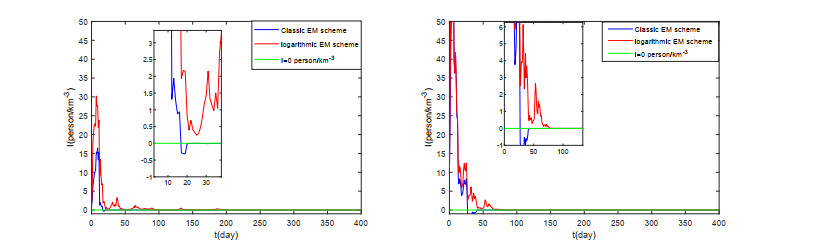
With the parameters in Table 2, Figure 3 plots the sample paths of the numerical solutions of the logarithmic EM scheme, the classic EM scheme and $I = 0\; person\cdot km^{-3}$ under different initial values ($I_{0} = 1\; person\cdot km^{-3}$ and $I_{0} = 10\; person\cdot km^{-3}$, respectively). It is clear to see from Figure 3 that the purple line will have negative values, but red line will achieve the effect of maintaining positive.

5.2.2.   Numerical simulations of convergence rate

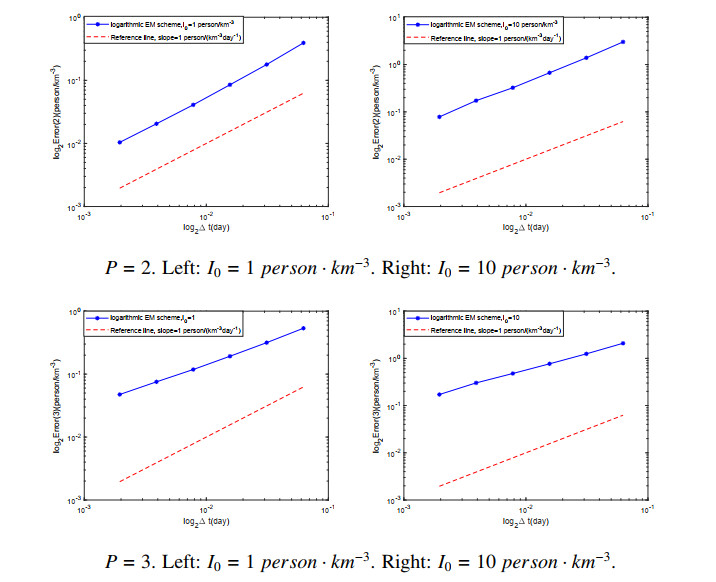
In this subsubsection, the parameters of simulations are those in Table 2. Since the exact solution of Eq (2.5) cannot be obtained, we regard the classic EM scheme with small step size $\Delta = 2^{-19}\; day$ as the replacement of the exact solution $I(t)$ of Eq (2.5). Figure 4 respectively shows that when $p = 2$ and $p = 3$ the $\log_{2}\; day-\log_{2}\; person\cdot km^{-3}$ approximation errors Error(2) and Error(3) between the exact solution $I(t)$ and the numerical solution $I(t_{k})$ with different step sizes $\Delta\in[2^{-9}\; day, 2^{-8}\; day, \cdot\cdot\cdot, 2^{-4}\; day]$ for 10, 000 simulations. According to Theorem 4.6, we can get that when $p$ is other positive values, it also has the first-order convergence rate. In Figure 4, the blue solid line depicts $\log_{2}\; day-\log_{2}\; person\cdot km^{-3}$ error while the red dashed is a reference line of slope $1\; person\cdot km^{-3}\cdot day^{-1}$, and

where $j$ stands for the $j$th sample path. It is clear to see from Figure 4 that the logarithmic Euler-Maruyama method has the first-order convergence rate. This is the same conclusion as given by Theorem 4.6.

6.   Conclusions

In this paper, we obtain an epidemic model affected by air pollution through disturbing the inflow rate of pollutants. First, we prove existence and uniqueness of positive solution of Eq (2.5) in Theorem 3.1. Then, the sufficient conditions for diseases extinction and existence of stationary distribution is given by Theorem 3.2 and Theorem 3.3. Next, to approximate Eq (2.5) a positivity-preserving numerical method logarithmic Euler-Maruyama method is introduced. Finally, for Eq (2.5), we prove that the logarithmic Euler-Maruyama method has the $p$th-moment convergence rate over a finite time interval for all $p > 0$ in Theorem 4.5.

It is well known that different places have huge divergence in the degree of air pollution. In view of this, considering the heterogeneity of each individual is an important factor in constructing more realistic models, that is, spatially heterogeneous epidemic models affected by air pollutants. The theoretical analysis of these models affected by air pollutants may be more complicated and we leave it for further investigation.

Acknowledgments

The authors thank the editor and referees for their careful reading and valuable comments. The research was supported by the Ningxia Natural Science Foundation Project (2020AAC03067) and the Natural Science Foundation of China (12161068).

Conflict of interest

The authors have no conflict of interest.