Stationary distribution and optimal control of a stochastic population model in a polluted environment

1.   Introduction

With the development of big data, cloud computing, internet of things and other technologies, the data generated by the network has reached the order of magnitude of ZB, and the number of devices on edge also reached 50 billion. Centralized processing, such as cloud computing, can no longer efficiently process the data generated by edge devices. Mainly manifested in the following aspects ^[1]:

1) The capacity of centralized cloud computing for linear growth of data cannot cope with the explosive growth of massive data on edge ^[2].

2) The transfer of massive data from the edge device to the cloud center leads to a sharp increase in the load of network transmission bandwidth, resulting in a long network delay ^[3].

3) Data on edge involves personal privacy, which makes the issue of privacy security more prominent ^[4].

In other words: There are serious challenges to the capacity and security of ICT's three pillars (computing, network, storage) in IoE application. Among the above three elements, the "computing" be mainly focused on in the paper, using the design methodology of "description-synthesis-simulation-optimization" to design TAC3 accelerator as ECN to enhance computing power. For the "network", the resource management and task scheduling algorithms be explored and optimized through behavior simulation. The processing for big data based on the edge computing model came into being ^[5,6], as well as combined with the existing centralized processing for big data with cloud computing model ^[7,8]. Then the edge intelligence will put AI into the edge computing, energizing each other. The convergence of all three (edge computing, cloud computing, AI) will provide a highly efficient and intelligent service model for the IoE.

Edge computing is located at the edge of the network near the end user and data source. And its core capabilities of network, computing, storage and application are integrated to provide edge intelligent services nearby to meet the key needs of industry digitalization in agile connection, real-time business, data optimization, application intelligence, security and privacy protection. In order to implement the above functions, the edge computing distributed open platform requires it to increase the processing capacity of performing task computing and data analysis on the network edge equipment, offload part or all of the original cloud computing tasks to the network edge equipment, reduce the computing load of the cloud computing center, the pressure of network bandwidth, and the transmission delay of the client.

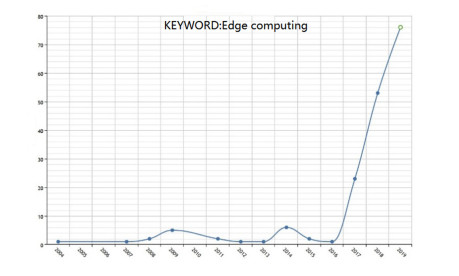
Because of its outstanding advantages, edge computing can meet the needs of the future IoE ^[9]. Since 2016, it has been developed rapidly, which has attracted close attention at home and abroad. The top-level conferences on edge computing, such as SEC (IEEE/ACM Symposium on Edge Computing), have been co-hosted by ACM and IEEE since 2016. Workshops for edge computing, such as ICDCS (IEEE International Conference on Distributed Computing Systems), MiddleWare, have also begun to host in a number of important international conferences since 2017. The research on edge computing in China also shows an explosive trend, and the number of dissertation published in recent years is shown in Figure 1.

2.   Related platform model

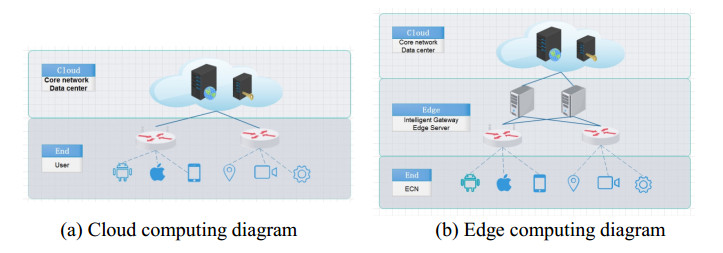
At first, edge computing is compared with the cloud computing as shown in Figure 2.

The delivery of cloud computing services through the Internet, which resources include tools, data storage, servers, databases, networking, software and applications. The core capabilities of network, computing, storage and application are integrated by edge computing to provide edge intelligent services nearby ^[10].

There are also other several models that related edge computing.

2.1.   Mobile edge computing

According to ETSI (European Telecommunication Standardization Institute) standard, MEC provides IT service environment and cloud computing capability at the edge of mobile network. Servers running at the edge of a mobile network can handle tasks that are not handled by a traditional network infrastructure, such as an M2M gateway, a control function, an intelligent video acceleration, and the like ^[11]. It can acquire network data such as base station ID, available bandwidth and the information related to the user position in real time, so as to carry out the link-aware adaptation, and provide the possibility of deployment for the location-based application to greatly improve the user-related service quality experience. With the continuous progress to the 5G stage, the mobile network will be shone in these new scenarios, such as HD video experience and smart venue service based on mobile CDN, mobile game based on AR/VR, marketing based on location service, traffic assistance system and intelligent driving system combined with vehicle network, etc. In the future 5G, a large platform that combines computing and communication technology, MEC must be an in-dispensable and important link, which will bring unlimited possibilities for the innovation of network business and services. Wireless network and IT are integrated effectively by MEC ^[12]. Through wireless API, the information interaction between wireless network and business server is opened. And at the service level, MEC can provide customized and differentiated services to the industry, thus improving the efficiency of network utilization and the added value ^[13].

2.2.   Fog computing

Fog computing ^[14] was proposed by Cisco in 2012 to cope with the upcoming era of the IoE. The name comes from that the fog is closer to the ground than clouds. Like edge computing, fog computing focuses data, data-related processing, and applications on devices at the edge of the network, rather than saving it all in the cloud ^[15]. Different from edge computing, fog computing emphasizes the cloud to things continuum between data center and data source to provide computing, storage and network services for users, so that the network becomes a "pipeline" of data processing, not just a "data pipeline". In other words, the components of both the edge and the core network are the infrastructure of fog computing. At present, Cisco-defined implementation of fog computing is its IO_X system ^[16,17]. IO_X runs on routers and switches, making it easy for developers to develop applications and deploy services on these devices. Its functions include executing complex rules of dynamic data, intelligently de-duplicating, compressing and transmitting data in the best way. Thus, the computer power is increased at the edge, and the data of multiple edge nodes are agammaegated and scattered. In the data processing process, no additional delay is added to support managers to make key decisions and appropriate actions.

2.3.   Edge intelligence

Edge intelligence combines AI and edge computing technology to push intelligent services from cloud computing center to edge devices to improve the quality of intelligent services ^[18]. Edge computing and AI, two new technologies with rapid development, have great potential to empower each other ^[19,20]. On the one hand, the mobile device running AI application (deep learning) offloads part of the model inferencing tasks to the adjacent edge computing nodes for operation, so as to coordinate the end device and the edge server, and integrate the complementary advantages of both computing locality and strong computing power. On the other hand, for the dynamic migration and placement of edge computing services, the mapping relationship can be automatically extract by AI technology between the optimal migration decision and high-dimensional input ^[21]. So that when given a new user location, the services can be quickly mapped to the optimal decision by corresponding machine learning model.

Research interests of edge intelligence include edge cloud collaboration, model segmentation, model compression, reduction of redundant data transmission and design of lightweight accelerated architecture. Among them, edge cloud collaboration, model segmentation and model compression are mainly to reduce the dependence of edge intelligence on edge devices in computing and storage requirements. Reduction of redundant data transmission is mainly used to improve the utilization efficiency of edge network resources. The lightweight acceleration architecture is designed to improve the efficiency of intelligent computing for specific edge applications. As a new paradigm of energizing each other between edge computing and AI, edge intelligence will give birth to a large number of innovative research opportunities, which will have a wide range of application prospects in many fields such as intelligent IoT, intelligent manufacturing, smart city and so on ^[22,23].

3.   Edge computing architecture

This based on MDE (Model Driven Engineering) design methodology, the edge computing architecture models the knowledge of objects, thus realizing the model driven intelligent distributed framework and platform. The elements on edge with physical autonomy and physical collaboration intelligence are as follows ^[24].

1) ECN: Through the integration of ICT resources such as network, computing and storage, the basic network, computing and storage capabilities are provided.

2) Gateway: It connect Intelligent Front-End through network connection, protocol conversion and other functions to provide lightweight connection management, real-time data analysis and application management functions.

3) System: It is composed of multiple distributed intelligent gateways or servers coordination, which provide elastic expansion of network, capabilities of computing and storage.

4) Service: Based on the model driven unified service framework, it provides development service framework and deployment operation service framework for system operation and maintenance personnel, business decision makers, system integrators, application developers and other roles.

ICT resources such as network, computing and storage can be logically abstracted as ECN. Intelligent ECN should be compatible with multiple heterogeneous connections to support real-time processing and response, and provide integrated software and hardware security. Its development framework and product realization process are as follows: ECN logical node definition (bus protocol adaptation, real-time connection, real-time streaming data analysis, sequential data access, policy implementation, device plug and play, resource management) → Development framework selection (real-time computing system, lightweight computing system, intelligent gateway system, intelligent distributed system) → Related product construction (perceptron, embedded controller, independent controller, ICT fusion gateway, distributed business gateway, edge cluster, edge cloud). The functional hierarchy of ECN is divided from bottom to top as follows.

1) Basic Resources Layer: There are three type of modules: Network, computing and storage. SDN (Software-Defined Networking) has gradually become the mainstream of the development of network technology. Its design concept is to separate the control of the network from the data forwarding, and to realize programmable control. The application of SDN to edge computing can support the access and flexible expansion of millions of massive network devices, provide efficient and low-cost automatic operation and maintenance management, and realize the coordination and integration of network and security policies. HC (Heterogeneous Computing) is the key computing hardware architecture on the edge. Therefore, a new computing architecture is proposed, which combines different types of instruction sets with different architecture computing units, that is heterogeneous computing, in order to give full play to the advantages of various computing units and achieve the balance of performance, cost, power consumption, portability and so on. At the same time, the application of the new generation of AI, represented by deep learning, also needs new technical optimization on edge.

2) Virtualization Layer: There are two typical virtualization technologies: Bare metal architecture and host architecture. The former is that the hypervisor and other functions run directly on the system hardware platform, and then the operating system and virtualization functions run, with better real-time performance. The latter is that the virtualization layer functions run on the host operating system.

3) EVF (Edge Virtualization Function) Layer: EVF makes the function as software and service, and decouples from the proprietary hardware platform. It can be flexibly combination and arrangement, migrated and extended on different hardware platforms and devices to realize dynamic resource scheduling and business agility. Based on virtualization technology, the hardware, system and specific EVF are combined according to the business on the same hardware platform, and multiple independent business segments are virtualized and separated from each other.

Edge computing also need to consider collaboration with cloud computing. That is, multiple network interfaces, protocols and topologies, real-time business processing and deterministic delay, data processing and analysis, distributed intelligence and security and privacy protection need to be supported on edge. It's difficult for cloud to meet the above requirements, which requires the collaboration between edge computing and cloud computing in network, business, application and intelligence. Cloud computing is suitable for non-real-time, long-cycle data and business decision scenarios, while edge computing plays an irreplaceable role in the opposite aspect.

A typical application scenario of edge-cloud collaboration is to deploy the training process on the cloud and the trained model on the edge device. Obviously, this service model can make up for the demand of AI for computing, storage and other capabilities on edge devices to some extent. Two products has been launched by Google to develop and deploy smart connected devices ^[21]: "Edge TPU" and "Cloud IOT Edge". "Edge TPU" is a small ASIC for running TensorFlow Lite model of machine learning on edge devices. "Cloud IoT Edge" is a software system that extends the data processing and machine learning capabilities of the Google Cloud to gateway and terminal devices.

4.   Model description for TAC³

The core elements of the ECN's underlying resources are computing, network, and storage. The key technologies based HC and SDN are adopted as EC efficient mainstream architecture. HC architecture aims to synergize and exploit the unique advantages of various computing units: CPU is good at system control, task decomposition and scheduling. GPU has strong floating-point and vector computing capabilities, and is good at parallel computing such as matrix and vector computing. FPGA has the advantages of hardware programmable and low delay. ASIC has the advantages of low power consumption, high performance and cost effective. The goal of HC is to integrate the separate processing units on the same platform to become a close collaborative whole to handle different types of computing loads. At the same time, the software can run across platforms through the open and unified programming interface. SDN implements "software definition" through open and programmable interfaces. Its architecture includes controller, South/North interface, various application and infrastructure network elements in application layer. The controller realizes the configuration and management of the forwarding strategy to support the forwarding control based on multiple flow tables in the infrastructure layer.

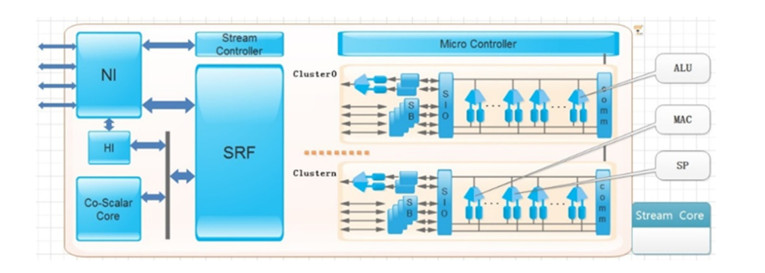
Building a lightweight acceleration architecture is the key to improving ECN computing power. Although NVIDIA's GPU chip plays a leading role in the AI training phase of data center, it is not suitable for effective inferencing as an edge device. For a variety of applications, reconfigurable hardware features are utilized to optimize and accelerate architecture programming design, improve resource utilization, and expand application scope while maintaining hardware area. The experimental results of CNN on an embedded FPGA for edge computing show that ^[23]: Compared with Xeon E5 CPU and GTX Titan GPU, the optimized network model has certain advantages in power consumption and performance, and is suitable for application in edge computing. In summary, there are two ways to enhance ECN. That is, processor mode (such as CPU, GPU) and dedicated module (such as FPGA, SoC). The former is universal and easy to realize. The latter is more efficient, but needs to be specially designed. Drawing on the advantages of both, the ECN with TAC³ model is put forward based on the design methodology as shown in Figure 3.

The designers be allowed to describe the system by the design methodology of "description-synthesis-simulation-optimization" in a purely behavioral form excluding implementation details, and ultimately integrate into system implementation. The system structure can be generated using automatic tools by the method, which applied to all levels of abstraction. Specifically, the system is divided into "behavior-structure-physics" three parts, whose functions required in the model are realized by a set of physical components provided in the architecture. The design idea of Tile-Architecture ^{[25,26,27,28]} is to organize computing, storage and interconnection resources into tile units, which are relatively simple and reusable, connected by a high-energy and scalable on-chip network, and adopt a distributed control mode. The Tile processor runs the EDGE (Explicit Data Graph Execution) ISA, which is programmed in BLOCK. The dependencies between instructions in BLOCK are represented by data flow and between BLOCKs by control flow. ISA well defines the representation of data dependencies within and between loops. The ILP and DLP capabilities of processors are improved because of the avoidance of centrally-controlled dependency detection. TLP task is processed by "Kernel-Stream" mode for "Producer-Consumer" streaming data. By using methods such as configuring the processor core as a larger logical core and explicitly providing/exposing its configuration mechanism to the application, it is possible to support polymorphous (that is, ILP, TLP, and DLP) parallelism ^[29], adapt to application specific to achieve higher efficiency and performance.

First, Tile object is define the as T = {T_p, C₁, C₂, C₃}, where T_p is the type of tile, T_p∈[G-Tile, R-Tile, I-Tile, D-Tile, E-Tile, M-Tile, N-Tile]. C₁ represents the computing power of tile, C₂ (Cache) represents the storage capacity of tile, and C₃ represents the cost of tile. Another important object OCN (On Chip Network) fabric is represented as N = {T_p, R, B, C}, where T_p is the Type of OCN，T_p∈[GDN, OPN, GSN, GCN]. R (Router) with programmable translation tables represents communication between tiles, B represents the communication bandwidth, and C still represents the cost of OCN.

The function metrics can be the time (such as us) that represents the speed of the operation and the clocks that the operation runs, which can be derived by Eq (1) and measured by simulation and experiment.

Since the tile-architecture ISA runs in block-atomic mode, the metrics for the instructions and their actions are calculated in blocks. T_Block is the time of block setup, T_M2Q is the overhead of data transfer from memory to queue through read/write and load/store, and T_OPnd is the time of operands in place, including within and between tiles. T_op is the simplest, which is a fixed operand processing time. T_Commit is the commit time at the end of the block. The block completes when all instructions in the block commit to the globe controller.

T_M2Q is the data transfer time of the entire storage system (i.e., M-Tile, D-Tile, R-Tile and various Queues), calculated as follows ^[30]:

where k is the number of levels of on-chip caches, R_i is data traffic ratio.

The execution pattern for tile-architecture is data-driven. That is, the node executes immediately once the operands are in place. As soon as there is an instruction with a long execution time, the node will wait. The processing time is the longest time value within the instruction range to obtain the result. The T_OPnd calculation formula is as follows:

For C₂, the metrics of access time performance are reflected in the T_M2Q section of M_C1, and the metrics of memory capacity are represented by ∑W_i × Cap_i in Eq (2).

C₃ is mainly composed of power consumption and area, as shown in Eq (2) :

where the power consumption in Eq (2) is governed by the Eq (2a) ^[31]:

where α is the average switching activity factor of the transistors, C is capacitance, V is the power supply voltage, f is the clock frequency, and I_off is the leakage current. IC physical power consumption be expressed by Eq (2a), and the energy expenditure of the processor at run time is also different by operation category, such as memory, Load/Store, Branch/indicator ^[32].

The area weighting coefficient W_i can be set according to the performance or cost of each type of storage.

The metrics for OCN are similar and will not be discussed in detail.

The metrics of TAC³ in Figure 3 can be regarded as two parts from the view of organization function: Inter cluster and intra cluster, which are described as follows:

1) The main function of inter cluster is to realize data parallel processing.

The computing power can be described as O = [O_i] (i∈1…n), which represents the result of a total of n clusters. In actual operation, the corresponding result set can be generated according to the instruction. Other performance metrics, such as processing time and resource area, will be reflected in behavioral synthesis and functional simulation.

2) Heterogeneous functional units in the cluster implement different operations according to instructions.

The output is O_i = Cluster (OP, Dat[a, b])_i (i∈1…n). The above expression represents the output of the ith cluster, where OP and Dat [a, b] are opcodes and operands respectively.

Different data set processing patterns can be implemented depending on the functional structure of TAC³, such as {OP, [A, B]}, {[OP₀, (A₀, B₀)], …, [OP_n, (A_n, B_n)]}. It is convenient to optimize the computing model and obtain real-time response for typical applications, such as CNN, FFT, FIR, etc., so as to adapt to edge computing.

5.   Behavior synthesis for ECN

This paper focuses on the functional metrics of TAC³ as ECN and the service behaviors of CCF (Connectivity and Computing Fabric).

5.1.   Behavior of block execution and computing power of TAC³

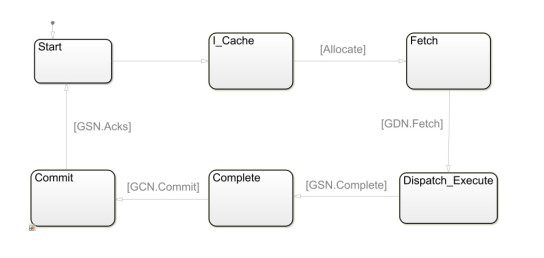
The behavior of block execution can be described by the state machine shown in Figure 4.

Tile-architecture processor instructions are executed in block atomic pipeline and parallel in the form of tile.

Tile architecture has features of polymorphous parallelism of thread, instruction and data. That is to say, efficient ILP performance can be achieved through the parallelism of intra block, inter block and super block, multi-dimensional frame space management and high bandwidth fetch. Complex TLP applications can be supported by state/logic thread frame management and block access/submit/clear operations. Fast DLP operations are provided by ALU cluster high-density computing and fast communication. Through the construction of native function tile and dynamic configuration mode, special algorithm acceleration is supported from the bottom layer (data transmission, instruction operation) to adapt to multi field applications.

According to the model described in the previous section, the behavior of TAC³ can be synthesized by the underlying functional organization and computing power. Without losing generality, the performance and resource consumption of TAC³ can be analyzed through the typical DSP module, the computing power embodied in TAC³ is realized by event server module. The physical implementation of TAC³ is based on FPGA Fabric. Because of the DSP slice built in modern FPGA to speed up the computing power, the on-chip data processing ability is greatly optimized. FPGA native DSP module was used by TAC³ to realize the ECN computing function. This not only improves the computing power, but also reduces the hardware resources and power consumption. The behavior of ECN server includes not only processing function, but also processing time and other performance metrics.

5.2.   Service behavior of CCF

CCF is a virtualized connection and computing service layer whose main functions are as follows:

1) Resource awareness: The key input for computing load balance and task scheduling on the edge is provided by awareness of the ICT resource status (such as the quality of network connection, CPU occupancy, etc.), performance specifications (real-time), location and other physical information of each ECN node.

2) Service perception for EVF (Edge Virtualization Function): The input for tasks scheduling is provided by sensing the distribution of EVF services, the computing tasks for each EVF service and the status of task execution, etc.

3) Computing task scheduling: It not only supports active task scheduling to automatically split tasks into sub-tasks and assign them to multiple ECN nodes for collaborative calculation according to resource awareness, service perception, connection bandwidth between ECN nodes, and computing task requirements. It also supports opening computing resources, service resources, etc., to the business through an open interface so that the business can control the scheduling process of computing tasks.

4) Data collaboration: It refers to the protocol (protocol adaptation to the south, unified data connection protocol for east-west connection between ECN nodes) and sharing (including simple broadcast, Pub-Sub mode, etc.). Through data collaboration, nodes can interact with each other in data, knowledge model, etc.

Similarly, the service behavior of CCF can be described by the event queuing model shown in Figure 5.

The multi-EIS (Edge Intelligent Server) in intelligent cooperative scenarios can be well simulated by multi-server M/M/C/∞/∞ model. Among them, the main operation metrics for service number of is L = L_q + λ/μ, and the system stay time is W = W_q + 1/μ.

Among the above services, the computing task scheduling service plays a key role in determining how tasks and resources are allocated and configured. That is, edge-cloud collaboration. Edge intelligence can be realized by further design of efficient algorithm and perfect system. Resource awareness not only knows the ICT resource state of ECN, but also uses it intelligently. EVF service perception further encapsulates and abstracts ECN to decouple hardware and flexibly compose services. Data collaboration not only realizes basic ECN data transmission and sharing, but also manages data intelligently. To sum up, the complete system behavior is summarized as: As a controller, scheduling service perceives (receives) basic (parameters, states) and virtual (abstract functions, services) ECN ICT information, and transmits, shares and manages data through various connections. The scheduler allocates tasks, schedules resources, and optimizes algorithms to achieve edge-cloud collaboration and edge intelligence.

6.   Simulation for EC

The EC simulation shall support the software and hardware of ECN nodes to simulate its specifications (such as core, memory, storage space, etc.) with different granularity in the target application scenario. Then based on the simulation nodes, the application-oriented networking and system building, as well as functional verification can be carried out. The architecture, function, interface, etc. can be defined by its model to support multi-language description and code generation, visual presentation of business process, edge computing domain model and vertical industry domain model library. It can be presented with multiple views according to users and business logic to shield the complexity of physical connection. For example, each user only needs to see the computing task he is running and its distribution on CCF. At the same time, the required physical information such as intelligent assets, intelligent gateways and locations of intelligent systems can be flexibly superimposed in simulation.

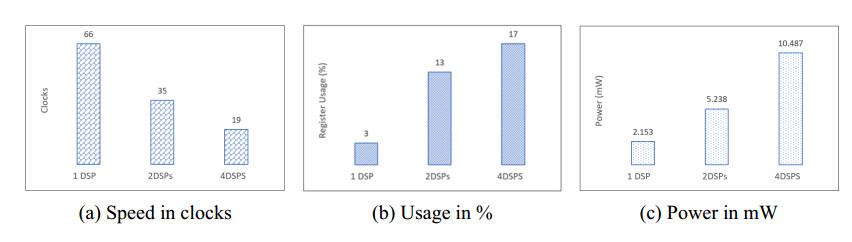
The methodologies with two-layers (behavior/function) ensures both precision of the simulation and high efficiency of DSE, whose semantics are consistent from top layer to bottom layer (vertical direction), and it is easy to coordinate the tiles (horizontal direction) interface protocol and their data flow operation. The attributes of the hardware unit are abstracted to construct a system level design pattern. Through the simulation with third party EDA and so on, tool chain methodology is established to implement the executable design specification and improve the design efficiency. Based on the executable specification of polymorphous parallel tile-architecture, the simulation system establishes the model view of ECN structure, behavior and sequential logic relationship in edge computing, and mainly simulates the functions of Tile ILP, TLP and DLP to quickly obtain the optimal path of DSE. The working state information and design scheme suitable for real-time application of ECN are obtained based on the analysis of simulation experiment. The DSP slice in FPGA fabric as underlying functional structure of ECN is simulated by ModelSim to obtain its DLP performance, resource and consumption, as shown in Figure 6.

In the above experiment, the typical formula $\sum _{i = 0}^{63}{g}_{i}\times {x}_{i}$ was calculated with single DSP, the 2 DSPs and 4 DSPs to explore its function metrics.

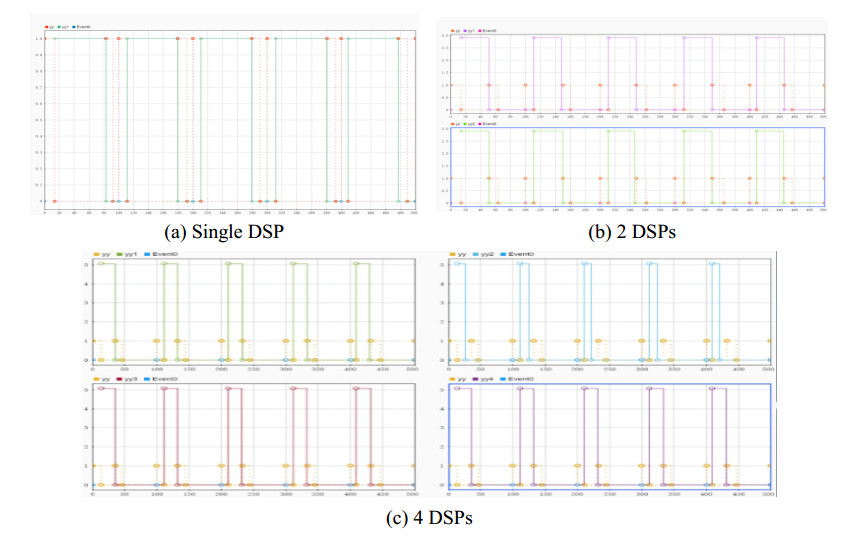
Corresponding ECN behavior is simulated by MATLAB/Simulink tool, which is mature, reliable, time-saving and efficient. Complex models are developed by componentization using event modules (Stateflow, SimEvents) and pre-built modules, as well as reusable system components and libraries. The simulation of ECN behavior is shown in Figure 7.

The behavioral simulation above refers to the metrics obtained from the functional simulation, with the horizontal axis representing speed performance (by clocks) and the vertical axis given by M_C3 metrics in Eq (2). In the case of "Single DSP", the cost is normalized to 1.

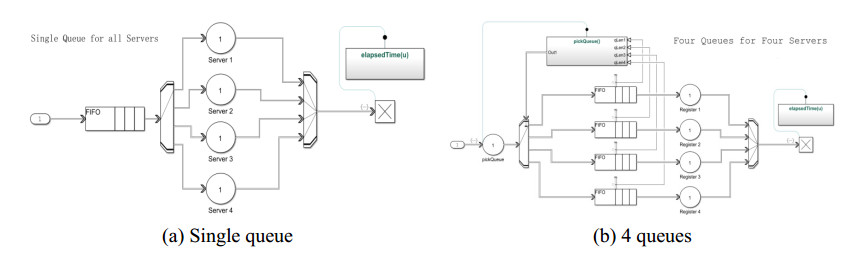
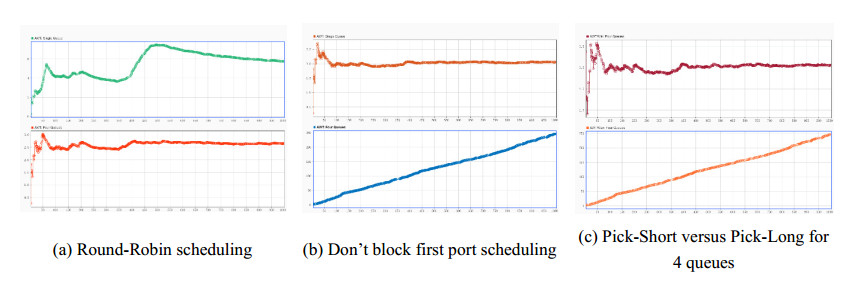
Similarly, the simulation of CCF service behavior based on the event queuing model (See Figure 5) is shown in Figure 8.

The above (a, b) in Figure 8 compare the average waiting time of two schedulings between single queue and 4 queues route modes, and (c) compares between the Pick-Short and Pick-Long algorithms in 4 queues mode.

Combining the model into a system-level simulation, system modeling can be carried out to build the Tile-Architecture ECN edge computing mode. Finally, the simulation results in EC are compared with the cloud computing model in terms of performance (response time, bandwidth occupancy, acceleration ratio) to determine the pros and cons of the scheme and its rationality.

7.   Conclusions

Edge computing has experienced rapid development from theory to practice, and the core concepts of architecture and technology have been implemented in practice. Its ecological chain includes heterogeneous computing hardware platform (x86/GPU/arm/FPGA), open distributed software platform (SDN, streaming data analysis, VM container, application life cycle management, security strategy and mechanism), experiential development and test cloud (development and test environment and tool chain, simulation environment, developer community, code libraries). The technical framework and platform are improved horizontally by edge computing according to industry scenarios and requirements, and a number of industry solutions are built vertically.

There are not an either-or relationship between edge computing model and cloud computing model, but a complementary. The organic combination of the two will provide a perfect hardware and software support platform for information processing in the era of IoE. The "edge-cloud" cooperates and complements each other; the "edge-AI" empowers each other. Technologies such as integrating CPU + GPU resources through heterogeneous computing, real-time acceleration of CPU + FPGA units, and artificial intelligence algorithm running by edge servers have been widely used in computer vision, intelligent robots and other fields.

In this paper, the typical DSP unit is used as the TAC³ ECN function structure, which can't simulate the object unit accurately and completely. Further refinement is needed in the future. Due to the complexity of EC (edge – cloud - end), the actual data of CCF service is closely related to system software and application tasks, so it is difficult to accurately describe by model. Therefore, hybrid simulation technology can be considered.

Acknowledgements

The authors acknowledge the JIT fund (Grant No. 40620025), the National Natural Science Foundation of China (No. 61142006), the Major Project of the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 19KJA510004). The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no. RGP-264.

Conflict of Interests

The author declare they have no conflict of interests.