Clustering algorithm with strength of connectedness for $m$-polar fuzzy network models

1.   Introduction

Zadeh's ^[1] fuzzy sets (FS) have captured the attention of many researchers in a wide range of scientific fields, including management sciences ^[2], decision making ^[3], medicine ^[4] or political sciences ^[5]. Atanassov ^[6] introduced the concept of intuitionistic fuzzy set (IFS), an extension of FS ^[1] that together with a membership grade $\mu$, make use of a non-membership grade $\nu$, and they are jointly subject to the condition $\mu + \nu < 1$. Although the mathematical performance of IFSs is quite good ^[7], still they fail to capture many situations where the sum of membership and non-membership degrees exceeds 1 (at some option). Yager ^[8,9] presented the less stringent concept of Pythagorean fuzzy sets (PFSs) for which the condition $\mu + \nu \leq 1$ imposed by IFSs is relaxed to $\mu^{2} + \nu^{2} \leq 1$. Nevertheless real world models often contain multi-attribute, multi-index, multi-object and multi-information data. For example, multi-polar technology, which can be used for the management of large scale applications of information technology. With this practical motivation Chen et al. ^[10] gave the concept of $m$-polar fuzzy set ($m$-PF set) model which further extended the scope of FSs. In an $m$-PF set, the membership value (MV) of an object belongs to $[0, 1]^m$. It aims to represent all the different characteristics of the object, each being a component of the MV ^[11]. This structure is better suited for a number of real-world problems, where data come from several agents hence multi-polar information arises naturally (but it cannot be properly represented by FSs).

The applied part of our paper concerns clustering. Here this is thought of as a process of classification of vertices into a collection of groups (clusters) depending on the characteristics of the graph. The goal is that the members within a cluster must be similar to each other, but members in different clusters should be different. The role of clustering processes is remarkable for example in supply chain networks ^[12], biology ^[13], data mining ^[14], etc. Traditional cluster analysis is a kind of binary division, which strictly assigns objects to specific groups. But in fact, many objects have no strict restrictions, so we cannot directly identify which group they belong to. Therefore, such collections of objects need a more flexible division.

Fuzzy logic provides an excellent analytical tool for defining and producing flexible divisions. Ruspini ^[15] firstly put forward the concept of fuzzy divisions, which marks the beginning of fuzzy cluster analysis. Based on fuzzy relations ^[1], Kaufmann ^[16] provided another basic idea, namely, fuzzy graphs (FGs). FG theory has numerous applications in several areas like cluster analysis ^[17], but also network analysis ^[3], information theory ^[4], and database theory ^[2]. Rosenfeld ^[18] studied fuzzy relations on FSs too. He investigated fuzzy analogues of certain elementary graph-theoretical concepts such as paths, cycles, trees, connectedness, or bridges, and he proved several related results. With these results, the theory of FGs is effectively established by Rosenfeld ^[18], although FGs had been independently introduced by Yeh and Bang ^[17]. These authors presented various connectivity parameters of a FG and investigated their applications by constructing $\epsilon$-clusters with the aid of the connectivity reachability matrix of a FG. Fuzzy node connectivity and fuzzy arc connectivity should be credited to Mathew and Sunitha ^[4]. They are the generalizations of Yeh and Bang's ^[17] connectivity parameters. In reference ^[4], Mathew and Sunitha also discussed a fuzzy analogue of Whitney's theorem and introduced clustering techniques based on fuzzy arc connectivity. Sebastian et al. ^[3] proposed generalized FG connectivity parameters with application to human trafficking. Mordeson and Peng ^[19] introduced different operations on FGs. Later on, some concepts of connectivity regarding fuzzy cut-vertex and fuzzy bridges appeared in Bhattacharya ^[20]. Bhattacharya and Suraweera ^[21] presented an algorithm to find the connectivity between pairs of vertices in FGs. Further, Banerjee ^[22] provided an optimal algorithm to find the strength of connectedness in FGs. Also, Tong and Zheng ^[23] obtained an algorithm to find the connectivity matrix of a FG, whereas Xu ^[2] applied the connectivity parameters of FGs to problems of chemical structures. Bhutani and Rosenfeld ^[24] introduced the concepts of strong arcs and strong paths in FGs. Mathew and Sunitha ^[25] classified different types of arcs in FGs and obtained the arc identification procedure. In addition, they established a sufficient condition for a node to become a fuzzy cut-node.

In relation with multi-polarity, Akram and Waseem ^[26] introduced the notion of $m$-PF graph to deal with network models possessing multi-attribute and multi-polar information. Later on, different authors presented various new concepts, including $m$-PF labeling graphs ^[27], $m$-PF graph structures ^[28], certain types of edge $m$-PF graphs ^[29], faces and dual of $m$-PF graphs ^[30], fuzzy coloring of $m$-PF graphs ^[31], $m$-PF tolerance graphs ^[32], products in $m$-PF graphs ^[33], regularity in product $m$-PF graphs ^[34], and double dominating energy of $m$-PF graphs ^[35]. Singh ^[36] introduced a method based on the properties of $m$-PF sets and its concept lattice diagram. Further, this author generalized the mathematical background of concept lattice with $m$-PF sets and its graphical properties ^[37]. In reference ^[38], Singh focused on drawing the object and attribute based $m$-PF concept lattice using the projection operator. The calculus of complex multi-fuzzy set and its granulation is introduced in ^[39] for handling complex multi-fuzzy context and its graphical traversal. Moreover, Singh ^[40] presented single-valued plithogenic graphs which enable us to handle multi-valued attribute data and its context. Furthermore, a framework for solving a multi-attribute group decision making problem, namely, the selection of a firm for participation in a Saudi oil refinery project in Pakistan is discussed in ^[41]. Recently, the strength of connectedness between two vertices in an $m$-PF graph has been studied in ^[42,43]. Mandal et al. ^[43] discussed certain basic concepts like strongest $m$-PF path, strong $m$-PF path, $m$-PF bridge, $m$-PF forests etc. Further, types of edges in $m$-PF graphs are known since ^[42]. References ^{[10,26,33,42,43,44]} provide further fundamental terminologies to understand our research work, which are highlighted in Section 2.

1.1.   Motivation and contribution

The $m$-PF graph theory is a natural generalization of FG theory. Even though, there are many fuzzy graph-theoretic results that have not yet been studied in the case of $m$-PF graph theory, e.g., vertex and edge connectivity parameters, clustering methods for vertices in $m$-PF graphs, etc. Particularly, the literature about $m$-PF graph theory has provided no clustering method for grouping the vertices in $m$-PF graphs, as far as we are aware of. However, there are some situations when we have to make groups of members as a function of uncertain information, and this information is multi-polar. For example, consider a social network organized as an $m$-PF graph, whose vertices represent students, and whose edges represent relationships between pairs of students. The MVs of the vertices may depend on several parameters. Suppose a case where the MVs of the vertices (students) are measured according to their level of confidence, sources of knowledge, and communication skills. The MVs of the edges are measured according to the similarity between two students with respect to their level of confidence, sources of knowledge, and communication skills. Then if we need to classify the students in different groups with respect to their similarity measure, a clustering method to classify vertices in $m$-PF graphs must be applied.

This research gap motivates us to study clustering method for vertices in $m$-PF graphs. More precisely, our proposal will be based on the strength of connectedness between pairs of vertices.

The main contributions of this research study are as follows:

$1)$ This research helps to determine the strong degree of a vertex in an $m$-PF graph. Also, we shall emphasize the distinction between degree and strong degree of vertices in $m$-PF graphs.

$2)$ In $m$-PF graphs, our research allows us to associate a sequence of real numbers with respect to each $j$-th component of membership values of vertices.

$3)$ Connectivity is the most natural parameter associated with a network. For example, when we have numerous routers for Internet access, the higher the strength of connectivity between two routers, the more stable and dynamic the network will be. The proposed research helps in the determination of a connectivity parameter in $m$-PF graphs.

$4)$ The proposed research provides a clustering method for vertices in $m$-PF graphs that is based on the strength of connectedness between pairs of vertices in $m$-PF graphs.

$5)$ As to the applied part, the proposed clustering method is used to categorize different companies with full utilization of their their multi-polar uncertain information. A comparative analysis of this work with existing techniques is included in order to demonstrate its feasibility and effectiveness.

1.2.   Framework of the paper

The structure of the paper is as follows:

$1)$ In Section 2, some basic definitions and results which are helpful to state properties in our research work are provided.

$2)$ In Section 3, we first define the strong degree of a vertex in $m$-PF graphs. We then discuss various useful properties and results for the strong degrees of vertices in complete $m$-PF graphs. Further, we introduce the concept of $m$-PF strength sequence of vertices and study this concept in complete $m$-PF graphs. We also discuss connectivity parameters in $m$-PF graphs, namely, the $m$-PF vertex connectivity parameter and $m$-PF edge connectivity parameter with fully developed examples. Then we investigate the $m$-PF analogue of Whitney's theorem. Furthermore, we define $r$-connected $m$-PF graphs and $r$-edge connected $m$-PF graphs, and we discuss some theorems related to them.

$3)$ In Section 4, depending on the strength of connectedness between pairs of vertices, we provide a clustering method for vertices in $m$-PF graphs. In order to understand this methodolgy, we first introduce some basic necessary terms and concepts. These include $\epsilon_A$-reachable vertices in $m$-PF graphs, $\epsilon_A$-connected $m$-PF graphs, and $\epsilon_A$-connected $m$-PF subgraphs (which are useful in the investigation of $m$-PF graphs that are not $\epsilon_A$-connected). Moreover, we discuss an application for clustering different companies that makes full utilization of their multi-polar uncertain information. We also provide an algorithm to clearly understand the clustering method applied in our application.

$4)$ In Section 5, a comparison between our research work and existing techniques is given.

$5)$ Section 6 highlights the merits and limitations of the proposed work.

$6)$ Section 7 contains the concluding remarks of our research study and future directions for research.

Throughout this research study, we will use the following list of abbreviations (Table 1).

2.   Preliminaries

An $m$-PF set ^[10] on a non-empty set $X$ is a mapping $\mu : X \rightarrow [0, 1]^m$. The set of all $m$-PF sets on $X$ is denoted by $m(X)$. Note that for a natural number $m$, $[0, 1]^m$ is considered as a poset with the point-wise order $\leq$, where "$\leq$'' is defined by $x \leq y$ $\leftrightarrow$ $P_j(x) \leq P_j(y)$, where $x, y \in [0, 1]^m$ and for each $1 \leq j \leq m$, $P_j : [0, 1]^m \rightarrow [0, 1]$ is defined as the $j$-th projection mapping.

Definition 2.1. Let $\mu$ be an $m$-PF set on $X$. An $m$-PF relation $\sigma$ on $\mu$ is a mapping $\sigma = (P_1 \circ \sigma, P_2 \circ \sigma, \ldots , P_{m} \circ \sigma) : \mu \longrightarrow \mu$ such that for all $x, y \in X$ ^[26],

$1 \leq j \leq m$, where $P_j \circ \mu(x)$ and $P_j \circ \sigma(xy)$ represent the $j$-th MV of vertex $x$ and edge $xy$, respectively. An $m$-PF relation $\sigma$ on $X$ is said to be a symmetric relation if for each $1 \leq j \leq m$, $P_j \circ \sigma(xy) = P_j \circ \sigma(yx)$, where $x, y \in X$.

Definition 2.2. An $m$-PF graph on $X$ is an ordered pair of functions $G = (\mu, \sigma)$, where $\mu : X \longrightarrow [0, 1]^m$ is an $m$-PFS on $X$ and $\sigma : X \times X \longrightarrow [0, 1]^m$ is an $m$-PF relation on $X$ such that for all $xy \in E$ ^[26],

$1 \leq j \leq m$. Note that for each $xy \in X \times X \setminus E$, $\sigma(xy) = {\bf 0}$, where ${\bf 0} = (0, 0, \ldots , 0)$ is the smallest element in $[0, 1]^m$ and ${\bf 1} = (1, 1, \ldots , 1)$ is the largest element in $[0, 1]^m$.

Definition 2.3. An $m$-PF path $P$ in an $m$-PF graph $G = (\mu, \sigma)$ is a sequence of distinct vertices $x = x_1, x_2, x_3, \ldots , x_n = y$ such that there exists at least one $1 \leq j \leq m$ for each $1 \leq i \leq n - 1$ satisfying $P_j \circ (x_ix_{i + 1}) > 0$. An $m$-PF path $P$ between two vertices $x_i$ and $x_k$ is denoted by $[x_i, x_k]$-$m$-PF path, where $1 \leq i, k \leq n$. An $[x_i, x_k]$-$m$-PF path is said to be an $m$-PF cycle $C$ if $x_i = x_k$ and $n \geq 3$. The strength of an $m$-PF path $P$ is defined as $S(P) = (\inf \limits_{1 \leq i < k \leq n} P_1 \circ \sigma(x_ix_{k}), \inf \limits_{1 \leq i < k \leq n} P_2 \circ \sigma(x_ix_{k}), \ldots , \inf \limits_{1 \leq i < k \leq n} P_m \circ \sigma(x_ix_{k}))$. The strength of connectedness between two vertices $x_i$ and $x_k$ ($CONN_{G}(x_i, x_k)$) is the maximum of the strengths of all $m$-PF paths between $x_i$ and $x_k$. Mathematically, it is defined as $CONN_{G}(x_i, x_k) = ((P_1 \circ \sigma(x_ix_{k}))^{\infty},$ $(P_2 \circ \sigma(x_ix_{k}))^{\infty}, \ldots , (P_m \circ \sigma(x_ix_{k}))^{\infty})$, where $(P_j \circ \sigma(x_ix_{k}))^{\infty}$$= \max \{\inf \limits_{1 \leq i < k \leq n} P_j \circ \sigma(x_ix_{k})\}$. An $m$-PF path is said to be a strongest $m$-PF path if $S(P) = CONN_{G}(x_i, x_k)$. An $m$-PF graph $G = (\mu, \sigma)$ is defined to be connected if there is an edge between each pair of vertices, i.e., $(P_j \circ \sigma(x_ix_{k}))^{\infty} > 0$ for at least one $j$ ^[33].

Throughout this study, we assume that $G$ is a connected $m$-PF graph.

Definition 2.4. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $P^1$, $P^2$ be two $[x, y]$-$m$-PF paths of $G$, where $x, y \in X$ ($x \neq y$). Then $P^1$ and $P^2$ are called edge-disjoint $[x, y]$-$m$-PF paths if $E(P^1) \cap E(P^2) = \emptyset$, i.e., $P^1$ and $P^2$ have no common edges. Two edge-disjoint $[x, y]$-$m$-PF paths are called internally disjoint $[x, y]$-$m$-PF paths if $V(P^1) \cap V(P^2) = \{x, y\}$, i.e., $P^1$ and $P^2$ have no common vertices except $x$ and $y$ ^[42].

Definition 2.5. Let $G = (\mu, \sigma)$ be an $m$-PF graph. The sum of MVs of all $m$-PF edges incident at vertex $x \in X$ is called degree of $x$. It is denoted by $D(x) = (P_1 \circ d(x), P_2 \circ d(x), \ldots , P_m \circ d(x))$ such that for each $1 \leq j \leq m$, $P_j \circ d(x) = \sum_{y \in X} P_j \circ \sigma(xy)$ ^[44].

Definition 2.6. An $m$-PF graph $G = (\mu, \sigma)$ is said to be strong $m$-PF graph if for each $xy \in E$, $P_j \circ \sigma(xy) = \inf \{P_j \circ \mu(x), P_j \circ \mu(y)\}$, $1 \leq j \leq m$. An $m$-PF graph $G = (\mu, \sigma)$ is said to be complete $m$-polar fuzzy graph if for each $x, y \in X$, $P_j \circ \sigma(xy) = \inf \{P_j \circ \mu(x), P_j \circ \mu(y)\}$, $1 \leq j \leq m$ ^[33].

Definition 2.7. An $m$-PF graph $\widetilde{G} = (\widetilde{\mu}, \widetilde{\sigma})$ is said to be a partial $m$-PF subgraph of $m$-PF graph $G = (\mu, \sigma)$ if for every $1 \leq j \leq m$, $P_j \circ \widetilde{\mu}(x) \leq P_j \circ \mu(x)$ for each $x \in \widetilde{X}$ and $P_j \circ \widetilde{\sigma}(xy) \leq P_j \circ \sigma(xy)$ for each $xy \in \widetilde{E}$. In particular, a partial $m$-PF subgraph $\widetilde{G} = (\widetilde{\mu}, \widetilde{\sigma})$ is said to be an $m$-PF subgraph of $G = (\mu, \sigma)$ if for every $1 \leq j \leq m$, $P_j \circ \widetilde{\mu}(x) = P_j \circ \mu(x)$ for each $x \in \widetilde{X}$ and $P_j \circ \widetilde{\sigma}(xy) = P_j \circ \sigma(xy)$ for each $xy \in \widetilde{E}$ ^[43].

Definition 2.8. Let $G = (\mu, \sigma)$ be an $m$-PF graph. An edge $xy \in E$ is defined to be a strong $m$-PF edge of $G$ if for each $1 \leq j \leq m$, $P_j \circ \sigma(xy) \geq P_j \circ CONN_{G \setminus \{xy\}}(x, y)$, i.e., if the MV of edge $xy \in E$ is at least as great as the connectedness of its incident vertices $x$ and $y$ when edge $xy$ is deleted then edge $xy$ is said to be a strong $m$-PF edge of $G$. The vertices $x$ and $y$ incident to a strong $m$-PF edge are called strong $m$-PF neighbors if for each $1 \leq j \leq m$, $P_j \circ \sigma(xy) > 0$. An $[x, y]$-$m$-PF path $P$ is defined to be a strong path if each edge contributing to that path is strong $m$-PF edge. An edge $xy \in E$ is defined to be a weak $m$-PF edge of $G$ if it is not strong $m$-PF edge of $G$, i.e., if it does not satisfy the condition $P_j \circ \sigma(xy) \geq P_j \circ CONN_{G \setminus \{xy\}}(x, y)$ for some $1 \leq j \leq m$. Otherwise, it is said to be a mixed $m$-PF edge of $G$ ^[43].

Throughout this study, we assume that $G$ has no mixed $m$-PF edges.

Definition 2.9. Let $G = (\mu, \sigma)$ be an $m$-PF graph. An edge $ab \in E$ is defined to be a weakest $m$-PF edge of $G$ if for each $1 \leq j \leq m$, $P_j \circ \sigma(ab) < P_j \circ \sigma(xy)$ for any edge $xy \in E$ different from edge $ab \in E$. An edge $cd \in E$ is defined to be a strongest $m$-PF edge of $G$ if for each $1 \leq j \leq m$, $P_j \circ \sigma(cd) > P_j \circ \sigma(xy)$ for any edge $xy \in E$ different from edge $cd$ ^[42].

Definition 2.10. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $E_S$ be the set of all strong $m$-PF edges of $G$. Then strong size of $m$-PF graph $G$ is denoted by $S_S(G) = (P_1 \circ S_S(G), P_2 \circ S_S(G), \ldots , P_m \circ S_S(G))$, where $P_j \circ S_S(G) = \sum_{xy \in E_S}P_j \circ \sigma(xy)$ for each $1 \leq j \leq m$ ^[42].

Definition 2.11. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $xy$ be an edge of $G$ such that it is not a strong $m$-PF edge. A set $X'$ of vertices is defined to be an $x-y$ strength reducing set of vertices (SRSVs) if for each $1 \leq j \leq m$, $P_j \circ \sigma_{G \setminus X'}(xy) < P_j \circ \sigma_{G}(xy)$ for some pair of vertices $x$ and $y$ of $G \setminus X'$. An $x-y$ SRSVs with $n$ members is defined to be a minimum $x-y$ SRSVs if there does not exist any $x-y$ SRSVs having less than $n$ members ^[42].

Definition 2.12. Let $G = (\mu, \sigma)$ be an $m$-PF graph. A set $E'$ of edges is defined to be an $x-y$ strength reducing set of edges (SRSEs) if for each $1 \leq j \leq m$, $P_j \circ \sigma_{G \setminus E'}(xy) < P_j \circ \sigma_{G}(xy)$ for some pair of vertices $x$ and $y$ of $G \setminus E'$. An $x-y$ SRSEs with $n$ members is defined to be a minimum $x-y$ SRSEs if there does not exist any $x-y$ SRSEs having less than $n$ members ^[42].

3.   Strong degree of a vertex in an $m$-PF graph

In this section, we introduce new concepts related to $m$-PF graphs and discuss some of their basic properties.

Definition 3.1. Let $G = (\mu, \sigma)$ be an $m$-PF graph. The sum of MVs of all strong $m$-PF edges incident at vertex $x \in X$ is called strong degree (SD) of $x$. It is denoted by $D_S(x) = (P_1 \circ d_S(x), P_2 \circ d_S(x), \ldots , P_m \circ d_S(x))$. Mathematically, it is defined as $D_S(x) = (\sum_{y \in N_S(x)} P_1 \circ \sigma(xy),$$\sum_{y \in N_S(x)} P_2 \circ \sigma(xy), \ldots , \sum_{y \in N_S(x)} P_m \circ \sigma(xy))$. Here, $N_S(x) = \{y(P_1 \circ \sigma(xy), P_2 \circ \sigma(xy), \ldots , P_m \circ \sigma(xy)) :$$P_j \circ CONN_G(x, y) \geq P_j \circ CONN_{G \setminus \{xy\}}(x, y), 1 \leq j \leq m\}$ is the collection of all strong $m$-PF neighbors of $x$.

Definition 3.2. Let $G = (\mu, \sigma)$ be an $m$-PF graph. The minimum strong degree (SD$_{min}$) is $\delta_S(G) = (P_1 \circ \delta_S(G), P_2 \circ \delta_S(G), \ldots , P_m \circ \delta_S(G))$, where $P_j \circ \delta_S(G) = \min \{P_j \circ d_S(x) : x \in X\}$ for each $1 \leq j \leq m$. The maximum strong degree (SD$_{max}$) is $\Delta_S(G) = (P_1 \circ \Delta_S(G), P_2 \circ \Delta_S(G), \ldots , P_m \circ \Delta_S(G))$, where $P_j \circ \Delta_S(G) = \max \{P_j \circ d_S(x) : x \in X\}$ for each $1 \leq j \leq m$.

Remark 3.1 Let $G = (\mu, \sigma)$ be an $m$-PF graph. Then for each $1 \leq j \leq m$, $P_j \circ \delta_S(G) \leq P_j \circ d_S(G) \leq P_j \circ \Delta_S(G)$ for all vertices $x \in X$.

Definition 3.3. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $x \in X$ be any vertex of $G$. Then $x$ is called a strong $m$-PF vertex of $G$ if all edges incident at vertex $x$ are strong $m$-PF edges. The collection of all strong $m$-PF vertices of $G$ is denoted by $V_S(G)$.

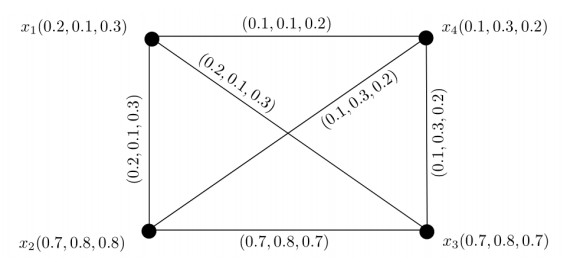
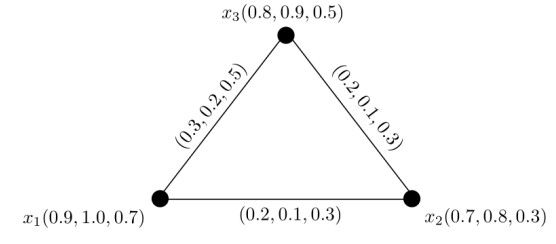
Example 3.1. Let $X = \{x_1, x_2, x_3, x_4\}$ be the set of vertices and $E = \{x_1x_2, x_2x_3, x_2x_4, x_3x_4\}$ be the set of edges. Let $\mu$ be a $3$-PF set on $X$ (Table 1) and $\sigma$ be a $3$-PF relation on $X$ (Table 3). The related $3$-PF graph $G = (\mu, \sigma)$ is given in Figure 1. The degrees of vertices are $D(x_1) = (0.2, 0.1, 0.2)$, $D(x_2) = (1.1, 1.1, 1.3)$, $D(x_3) = (1.0, 1.1, 1.2)$, and $D(x_4) = (1.3, 1.7, 1.5)$. Here, $N_S(x_1) = \{x_2(0.2, 0.1, 0.2)\}$, $N_S(x_2) = \{x_1(0.2, 0.1, 0.2), x_3(0.6, 0.8, 0.7)\}$, $N_S(x_3) = \{x_2(0.6, 0.8, 0.7), x_4(0.7, 0.9, 0.7)\}$, and $N_S(x_4) = \{x_2(0.3, 0.2, 0.4), x_3(0.7, 0.9, 0.8)\}$. The SDs of vertices are $D_S(x_1) = (0.2, 0.1, 0.2)$, $D_S(x_2) = (0.8, 0.9, 0.9)$, $D_S(x_3) = (1.3, 1.7, 1.5)$, and $D_S(x_4) = (0.7, 0.9, 0.8)$. Here, $x_1$ and $x_3$ both are strong $m$-PF vertices of $G$. Thus, $V_S(G) = \{x_1, x_3\}$. The SD$_{min}$ and SD$_{max}$ of $G$ are $\delta_S(G) = (0.2, 0.1, 0.2)$ and $\Delta_S(G) = (1.3, 1.7, 1.5)$, respectively.

It is always possible to find a strong $m$-PF path between any two vertices of a connected $m$-PF graph $G$ according to Theorem 4.8 ^[43]. This means that we are always able to find at least one strong $m$-PF neighbor of any vertex of a connected $m$-PF graph $G$. Thus, we have the following proposition.

Proposition 3.1. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph. Then for each $1 \leq j \leq m$, $0 < P_j \circ d_S(x) \leq P_j \circ d(x)$ for all vertices $x \in X$.

We now have Handshaking lemma for $m$-PF graphs.

Lemma 3.2. The sum of SDs of each vertex in an $m$-PF graph $G$ is equal to twice the sum of MVs of each strong $m$-PF edges in $G$, that is, for each $1 \leq j \leq m$, $2 P_j \circ S_S(G) = \sum_{x \in X} P_j \circ d_S(x)$.

It is interesting to note that all edges in an complete $m$-PF graph $G$ are strong $m$-PF edges. This means that for each $1 \leq j \leq m$, $P_j \circ d_S(x) = P_j \circ d(x)$ for each $x \in X$ and hence $P_j \circ S_S(G) = \sum _{xy \in E} P_j \circ \sigma(xy)$ for each $1 \leq j \leq m$ and for every edge $xy \in E$ in complete $m$-PF graph $G$. Also, all vertices in an complete $m$-PF graph $G = (\mu, \sigma)$ are strong $m$-PF vertices and hence their SDs can be calculated for each $1 \leq j \leq m$ as $P_j \circ d_S(x) = \sum _{x \neq y} \inf \{P_j \circ \mu(x), P_j \circ \mu(y)\}$ for each vertex $x \in X$.

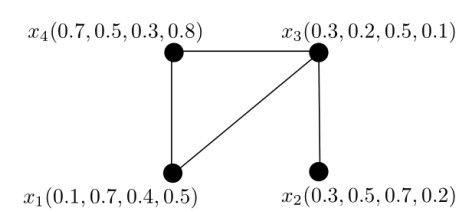
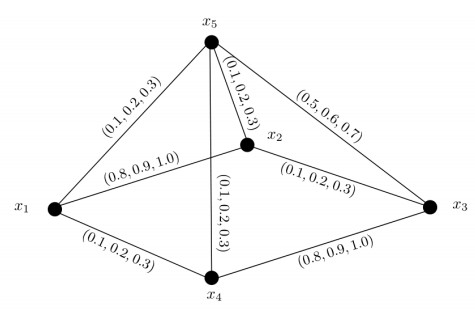
Example 3.2. Let $X = \{x_1, x_2, x_3, x_4\}$ be the set of vertices and $E = \{x_1x_2, x_1x_3, x_1x_4, x_2x_3, x_2x_4, x_3x_4\}$ be the set of edges. Let $\mu$ be a $3$-PF set on $X$ (Table 4) and $\sigma$ be a $3$-PF relation on $X$ (Table 5). The related $3$-PF graph $G = (\mu, \sigma)$ is given in Figure 2. It is easy to see that $G$ is an complete $m$-PF graph. Thus, all of its edges are strong $m$-PF edges. Also, all of its vertices are strong $m$-PF vertices. The SDs of vertices are $D_S(x_1) = (0.4, 0.5, 0.7)$, $D_S(x_2) = (1.1, 1.0, 1.3)$, $D_S(x_3) = (1.0, 1.2, 1.2)$, $D_S(x_4) = (0.3, 0.7, 0.6)$ and $S_S(G) = (1.4, 1.7, 1.9)$.

Proposition 3.3. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph with $|X| = n$ such that for each $1 \leq j \leq m$, $P_j \circ \mu(x_i) \leq P_j \circ \mu(x_i + 1)$ $(i = 1, 2, \ldots , n - 1)$. Then for each $1 \leq j \leq m$, $P_j \circ d_S(x_i) = P_j \circ d_S(x_k)$ for at least one pair of vertices $x_i$ and $x_k$ ($1 \leq i, k \leq n$ and $i \neq k$) of $G$.

Theorem 3.4. Let $x_1, x_2, \ldots , x_n$ be the vertices of an complete $m$-PF graph $G = (\mu, \sigma)$ such that for each $1 \leq j \leq m$,

Then for each $1 \leq j \leq m$,

1) There exists at least one weakest $m$-PF edge $x_1x_k$ $(k = 2, 3, \ldots , n)$ in $G$.

2) There exists at least one strongest $m$-PF edge $x_kx_n$ $(k = 1, 2, \ldots , n - 1)$ in $G$.

3) The SD$_{min}$ $\delta_S(G)$ is equal to SD of first vertex $x_1$, i.e., $P_j \circ d(x_1) = P_j \circ \delta_S(G) = (n - 1) P_j \circ \mu(x_1)$.

4) The SD$_{max}$ $\Delta_S(G)$ is equal to SD of last vertex $x_n$, i.e., $P_j \circ d(x_n) = P_j \circ \Delta_S(G) = \sum_{i = 1}^{n - 1} P_j \circ \mu(x_i)$.

Proof. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph with $|X| = n$. Suppose that $x_1$ be a vertex having unique minimum MV, i.e., for each $1 \leq j \leq m$, $P_j \circ \mu(x_1) < P_j \circ \mu(x_k)$ $(k = 2, 3, \ldots , n)$ and $x_n$ be a vertex having unique maximum MV, i.e., for each $1 \leq j \leq m$, $P_j \circ \mu(x_k) < P_j \circ \mu(x_n)$ $(k = 1, 2, \ldots , n - 1)$. Throughout this proof, we assume that for each $1 \leq j \leq m$,

1) We have to show that edge $x_1x_k$ $(k = 2, 3, \ldots , n)$ is a weakest $m$-PF edge in $G$. Suppose on contrary that $x_1x_b$ $(b = 2, 3, \ldots , n)$ is not weakest $m$-PF edge. Also, let $x_ax_b$ $(2 \leq a < b \leq n, a \neq b)$ be a weakest $m$-PF edge in $G$. Thus, we have for each $1 \leq j \leq m$,

Since, $a \neq 1$, this contradicts to the assumption that $x_1$ is the unique vertex with minimum MV. Hence, we have shown that edge $x_1x_k$ $(k = 2, 3, \ldots , n)$ is a weakest $m$-PF edge in $G$.

2) We have to show that edge $x_kx_n$ $(k = 1, 2, \ldots , n - 1)$ is a strongest $m$-PF edge in $G$. Suppose on contrary that $x_ax_n$ $(a = 1, 2, \ldots , n - 1)$ is not strongest $m$-PF edge. Also, let $x_ax_b$ $(1 \leq a < b \leq n - 1, a \neq b)$ be a strongest $m$-PF edge in $G$. Thus, we have for each $1 \leq j \leq m$,

which is a contradiction. Hence, we have shown that edge $x_kx_n$ $(k = 1, 2, \ldots , n - 1)$ is a strongest $m$-PF edge in $G$.

3) We have to show that for each $1 \leq j \leq m$, $P_j \circ d(x_1) = P_j \circ \delta_S(G) = (n - 1) P_j \circ \mu(x_1)$. For this, consider

Now, to show that SD$_{min}$ is exactly equal to SD of first vertex. Suppose on contrary that it is not equal, i.e., $P_j \circ \delta_S(G) \neq P_j \circ d_S(x_1)$ for at least one $1 \leq j \leq m$. Also, let $x_k$ $(k = 2, 3, \ldots , n, k \neq 1)$ be a vertex of $G$ with SD$_{min}$, i.e., for each $1 \leq j \leq m$, $P_j \circ d_S(x_k) = P_j \circ \delta_S(G)$. Then

As $\inf \{P_j \circ \mu(x_1), P_j \circ \mu(x_i)\} = P_j \circ \mu(x_1)$, $\inf \{P_j \circ \mu(x_k), P_j \circ \mu(x_1)\} = P_j \circ \mu(x_1)$ for $l = 1$, and $\inf \{P_j \circ \mu(x_k), P_j \circ \mu(x_l)\} > P_j \circ \mu(x_1)$ for all other $l = 2, 3, \ldots , n$. Thus,

This is a contradiction. Hence, for each $1 \leq j \leq m$, $P_j \circ d_S(x_1) = P_j \circ \delta_S(G) = (n - 1) P_j \circ \mu(x_1)$.

4) Finally, we have to show that for each $1 \leq j \leq m$, $P_j \circ \mu(x_n) = \sum_{k = 1}^{n - 1} P_j \circ \mu(x_k) = P_j \circ \Delta_S(G)$. We know that $x_n$ is the vertex of $G$ with maximum MV, i.e., for each $1 \leq j \leq m$, $P_j \circ \mu(x_n) > P_j \circ \mu(x_k)$ $(k = 1, 2, \ldots , n - 1)$. Also, $G$ is an complete $m$-PF graph. Therefore,

Thus,

Now, to show that SD$_{max}$ is exactly equal to SD of last vertex. Suppose on contrary that it is not equal, i.e., $P_j \circ \Delta_S(G) \neq P_j \circ d_S(x_n)$ for at least one $1 \leq j \leq m$. Also, let $x_l$ $(l = 1, 2, \ldots , n - 1, l \neq n)$ be a vertex of $G$ with SD$_{max}$, i.e., for each $1 \leq j \leq m$, $P_j \circ d_S(x_l) = P_j \circ \Delta_S(G)$. Then

Since, $G$ is an complete $m$-PF graph. So, SD of vertex $x_l$ can be written as

This shows that $P_j \circ d_S(x_l) \leq P_j \circ d_S(x_n)$ which is a contradiction. Hence, for each $1 \leq j \leq m$, $P_j \circ d_S(x_n) = P_j \circ \Delta_S(G) = \sum_{k = 1}^{n - 1} P_j \circ \mu(x_k)$. This completes the proof.

Note 3.1. We have assumed that there is only one vertex with minimum MV and only one vertex with maximum MV throughout the proof of Theorem 3.4. However, if there are more than one vertices having minimum MVs and more than one vertices having maximum MVs, the proof of the Theorem 3.4 will remain same.

3.1.   $m$-PF strength sequence of vertices in an $m$-PF graph

In $m$-PF graphs, the MVs of vertices as well as edges are $m$-tuples of real numbers in $[0, 1]$. Therefore, we can associate a sequence of real numbers with respect to each $j$-th component of MVs of vertices.

Definition 3.4. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $|X| = n$. Then $m$-PF strength sequence of vertices $x_1, x_2, x_3, \ldots , x_n$ with respect to each $j$-th component $(1 \leq j \leq m)$ of MVs of vertices ($m$-PF$^{(j)}$ strength sequence) is defined to be $\{a_i^{(j)} = P_j \circ \mu(x_i)\}_{i = 1}^{n}$, where $a_i^{(j)} \in [0, 1]$ represents the MV of vertex $x_i$ with respect to $j$-th component $(1 \leq j \leq m)$ when vertices are arranged such that their MVs with respect to each $j$-th component $(1 \leq j \leq m)$ are non-decreasing, that is, $a_1^{(j)} \leq a_2^{(j)} \leq \ldots \leq a_n^{(j)}$. In particular, $a_1^{(j)}$ represent the smallest MVs of vertices with respect to $j$-th component $(1 \leq j \leq m)$ and $a_n^{(j)}$ represent the largest MVs of vertices with respect to $j$-th component $(1 \leq j \leq m)$.

Definition 3.5. Let $G = (\mu, \sigma)$ be an $m$-PF graph and $|X| = n$. Then $m$-PF strength sequence of vertices $x_1, x_2, x_3, \ldots , x_n$ is defined to be $\{[a_i^{(1)}, a_i^{(2)}, \ldots , a_i^{(m)}]\}_{i = 1}^{n}$ such that $\{a_i^{(j)}\}_{i = 1}^n$ is the $m$-PF$^{(j)}$ strength sequence ($1 \leq j \leq m$).

Example 3.3. Let $X = \{x_1, x_2, x_3, x_4\}$ be the set of vertices and $E = \{x_1x_3, x_1x_4, x_2x_3, x_3x_4\}$ be the set of edges. Let $\mu$ be a $4$-PF set on $X$ (Table 6) (Here, we consider MVs of vertices only. Since we are talking about $m$-PF strength sequence of vertices, therefore, we can eliminate the discussion of MVs of edges). The related $4$-PF graph $G = (\mu, \sigma)$ is given in Figure 3. The $m$-PF$^{(1)}$ strength sequence is $\{0.1, 0.3, 0.3, 0.7\}$ or $\{0.1, 0.3^2, 0.7\}$ ($0.3^2$ means that term $0.3$ is repeated two times in this sequence). The $m$-PF$^{(2)}$ strength sequence is $\{0.2, 0.5, 0.5, 0.7\}$ or $\{0.2, 0.5^2, 0.7\}$, $m$-PF$^{(3)}$ strength sequence is $\{0.3, 0.4, 0.5, 0.7\}$ and the $m$-PF$^{(4)}$ strength sequence is $\{0.1, 0.2, 0.5, 0.8\}$. Now, the $m$-PF strength sequence of vertices is $\{[0.1, 0.1, 0.2, 0.3], [0.2, 0.3, 0.4, 0.5], [0.3, 0.5, 0.5, 0.5],$$[0.7, 0.7, 0.7, 0.8]\} = \{[0.1^2, 0.2, 0.3],$$[0.2, 0.3, 0.4, 0.5], [0.3, 0.5^3], [0.7^3, 0.8]\}$.

Considering $m$-PF$^{(j)}$ strength sequence $(1 \leq j \leq m)$ of vertices in an complete $m$-PF graph $G$, we can obtain the number of vertices having SD$_{min}$ $\delta_S(G)$ and the number of vertices having SD$_{max}$ $\Delta_S(G)$ with the help of the following theorem.

Theorem 3.5. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph and $|X| = n$. Then for each $1 \leq j \leq m$,

1) If $m$-PF$^{(j)}$ strength sequence of vertices is of the form $\{(a_1^{(j)})^{n - 1}, a_2^{(j)}\}$, then $P_j \circ \delta_S(G) = (n - 1) a_1^{(j)} = P_j \circ \Delta_S(G) = P_j \circ d_S(x_k)$ $(k = 1, 2, \ldots , n)$.

2) If $m$-PF$^{(j)}$ strength sequence of vertices is of the form $\{(a_1^{(j)})^{l_1}, (a_2^{(j)})^{n - l_1}\}$ with $0 < l_1 \leq n - 2$, then there exists exactly $l_1$ vertices having $P_j \circ \delta_S(G)$ and exactly $n - l_1$ vertices having $P_j \circ \Delta_S(G)$.

3) If $m$-PF$^{(j)}$ strength sequence of vertices is of the form $\{(a_1^{(j)})^{l_1}, (a_2^{(j)})^{l_2}, \ldots , (a_k^{(j)})^{l_k}\}$ with $l_k \geq 2$ and $k \geq 3$, then there exists exactly $l_1$ vertices having $P_j \circ \delta_S(G)$ and exactly $l_k$ vertices having $P_j \circ \Delta_S(G)$.

4) If $m$-PF$^{(j)}$ strength sequence of vertices is of the form $\{(a_1^{(j)})^{l_1}, (a_2^{(j)})^{l_2}, \ldots , (a_{k - 1}^{(j)})^{l_{k - 1}}, a_k\}$ with $k \geq 3$, then there exists exactly $1 + l_k$ vertices having $P_j \circ \Delta_S(G)$.

Proof. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph and $|X| = n$. The proof of $(1)$ and $(2)$ are obvious. We now prove $(3)$ and $(4)$.

3) Let $(x_i)^q$ be the set of vertices in $G$ with $P_j \circ d_S((x_i)^q) = a_i^{(j)}$ ($q = 1, 2, \ldots , l_i$ and $i = 1, 2, \ldots , k$) for each $1 \leq j \leq m$. According to Theorem 3.4, we have $P_j \circ d_S((x_1)^q) = P_j \circ \delta_S(G) = (n - 1)a_1^{(j)}$ ($q = 1, 2, \ldots , l_1$). Any vertex having $j$-th component MV greater than $a_1^{(j)}$ can not have $P_j \circ \delta_S(G)$ since, $P_j \circ \sigma((x_i)^q(x_{i + 1})^r) = P_j \circ \mu((x_i)^q) > a_1^{(j)}$ ($q = 1, 2, \ldots , l_i$, $r = 1, 2, \ldots , l_{i + 1}$, $q = 2, 3, \ldots , k$). Thus, there exists exactly $l_1$ vertices having $P_j \circ \delta_S(G)$. We now prove that $P_j \circ \mu((x_k)^t) = P_j \circ \Delta_S(G)$ ($t = 1, 2, \ldots , l_k$). Since, $P_j \circ \mu((x_k)^t)$ is maximum vertex MV, we have $P_j \circ \sigma((x_k)^t(x_k)^q) = a_k^{(j)}$ ($t, q = 1, 2, \ldots , l_k, t \neq q$) and $P_j \circ \sigma((x_k)^t(x_i)^q) = \inf \{P_j \circ \mu((x_k)^t), P_j \circ \mu((x_i)^q)\} = P_j \circ \mu((x_i)^q)$ ($i = 1, 2, \ldots , k - 1, q = 1, 2, \ldots , l_i, t = 1, 2, \ldots , l_k$). Thus, for $t = 1, 2, \ldots , l_k$,

Using Theorem 3.4. Further, if $y$ is a vertex such that $P_j \circ \mu(y) = a_{k - 1}^{(j)}$, we have

Thus, there exists exactly $l_k$ vertices having $P_j \circ \Delta_S(G)$.

4) Let $(x_k)^1 = x_k$ be the vertex in $G$ such that $P_j \circ d_S(x_k) = a_k^{(j)}$. Then, by using Theorem 3.1, $P_j \circ d_S(x_k) = P_j \circ \Delta_S(G) = \sum_{i = 1}^{n - 1} P_j \circ \mu(y_i)$. Now, let $y_{k - 1}{t}$, $t = 1, 2, \ldots , l_{k - 1}$. Then, for $t = 1, 2, \ldots , l_{k - 1}$,

But, $P_j \circ \sigma((x_i)^qx_{k - 1}^t) = P_j \circ \mu((x_i)^q)$ ($i = 1, 2, \ldots , k - 2$ and $q = 1, 2, \ldots , l_i$). Also, $P_j \circ \sigma(x_{k - 1}^qx_{k - 1}^m) = a_{k - 1}^{(j)}$ and $P_j \circ \sigma(x_{k - 1}^rx_k) = a_{k - 1}^{(j)}$. Thus,

Thus, there exists $l_{k - 1} + 1$ vertices having $P_j \circ \Delta_S(G)$. Now, if $y$ is a vertex with $P_j \circ \mu(y) < a_{k - 1}^{(j)}$ as in proof of $(3)$, we can show that $P_j \circ d_S(y) < P_j \circ \Delta_S(G)$. Thus, there exists exactly $l_{k - 1} + 1$ vertices having $P_j \circ \Delta_S(G)$. Hence, the theorem is proved.

3.2.   Connectivity parameters in $m$-PF graphs

In this section, we introduce vertex cut and edge cut in an $m$-PF graph $G$ by using the concept of strong $m$-PF edges ^[4,42].

Definition 3.6. Let $G$ be a non-trivial connected $m$-PF graph. A subset $\widetilde{X} = \{x_1, x_2, \ldots , x_k\} \subseteq X$ is defined to be an $m$-PF vertex cut if either the removal of $\widetilde{X}$ results a trivial $m$-PF graph or its removal reduces the strength of connectedness between some pairs of vertices in $G$, i.e., $P_j \circ CONN_{G \setminus \widetilde{X}}(x, y) < P_j \circ CONN_{G}(x, y)$ ($1 \leq j \leq m$) for $x, y \in X$ such that $x, y \neq x_i$ ($i = 1, 2, \ldots , k$).

There exists a strong $m$-PF path between any two vertices of a connected $m$-PF graph $G$ according to Theorem 4.8 of ^[43]. This means that we are able to find at least one strong $m$-PF edge incident on any vertex $x$ of a connected $m$-PF graph $G$. Thus, we have the following definition.

Definition 3.7. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph and $\widetilde{X}$ be an $m$-PF vertex cut of $G$. Then the strong weight of $\widetilde{X}$ is denoted by $S_W(\widetilde{X}) = (P_1 \circ S_W(\widetilde{X}), P_2 \circ S_W(\widetilde{X}), \ldots , P_m \circ S_W(\widetilde{X}))$ and it is defined as $S_W(\widetilde{X}) = (\sum_{x \in \widetilde{X}} P_1 \circ \sigma(xy), \sum_{x \in \widetilde{X}} P_2 \circ \sigma(xy), \ldots , \sum_{x \in \widetilde{X}} P_m \circ \sigma(xy))$ where for each $1 \leq j \leq m$, $\sum_{x \in \widetilde{X}} P_j \circ \sigma(xy)$ represents the sum of minimum MVs of strong $m$-PF edges incident on $x \in \widetilde{X}$.

Definition 3.8. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph. The $m$-polar fuzzy vertex connectivity of $G$ is denoted by $\kappa(G) = (P_1 \circ \kappa(G), P_2 \circ \kappa(G), \ldots , P_m \circ \kappa(G))$ in which each $j$-th component ($1 \leq j \leq m$) is defined as $P_j \circ \kappa(G) = \min \{P_j \circ S_W(\widetilde{X}_i); i \in \omega \}$, i.e., it is the minimum of strong weights of $m$-PF vertex cuts of $G$.

Example 3.4. Let $G = (\mu, \sigma)$ be a connected $3$-PF graph as shown in Figure 4. It is easy to see that strength of connectedness between $x_2$ and $x_4$ is (0.2, 0.5, 0.6). Then $m$-PF vertex cut containing one vertex is $\widetilde{X} = \{x_3\}$ as $CONN_{G \setminus \{x_3\}}(x_2, x_4) = (0.2, 0.3, 0.5) < (0.2, 0.5, 0.6) = CONN_{G}(x_2, x_4)$. Here, $m$-PF vertex cut containing two vertices is $\widetilde{X} = \{x_1, x_3\}$ as $CONN_{G \setminus \{x_1, x_3\}}(x_2x_4) = (0.1, 0.3, 0.4) < (0.2, 0.5, 0.6) = CONN_{G}(x_2x_4)$. Also, the removal of vertices $x_2$ and $x_4$ results a trivial $m$-PF graph so $m$-PF vertex cut $= \{x_2, x_4\}$. The strength of connectedness between vertices of $G$ are: $CONN_G(x_1, x_2) = (0.2, 0.3, 0.5)$, $CONN_G(x_1, x_4) = (0.2, 0.4, 0.5)$, $CONN_G(x_3, x_4) = (0.2, 0.3, 0.5)$, $CONN_G(x_2, x_3) = (0.1, 0.3, 0.4)$ and $CONN_G(x_2, x_4) = (0.2, 0.5, 0.6)$. It is easy to verify that $x_1x_2$, $x_3x_4$, $x_2x_3$ are strong $m$-PF edges. The $m$-PF vertex cuts containing one or two vertices with their strong weights are $\widetilde{X}_1 = \{x_3\}$ $S_W(\widetilde{X}_1) = (0.2, 0.5, 0.6)$, $\widetilde{X}_2 = \{x_1, x_3\}$ $S_W(\widetilde{X}_2) = (0.5, 0.9, 1.1)$ and $\widetilde{X}_3 = \{x_2, x_4\}$ $S_W(\widetilde{X}_3) = (0.8, 1.4, 1.8)$. Also, any set with three vertices of $G$ will be considered as $m$-PF vertex cut with strong weight greater than $S_W(\widetilde{X}_i)$ (i = 1, 2, 3). Therefore, $\kappa(G) = (0.2, 0.5, 0.6)$.

Definition 3.9. Let $G$ be a non-trivial connected $m$-PF graph. A subset $m$-PF edges $\widetilde{E} = \{e_1, e_2, \ldots , e_k\}$ $\subseteq E$ is defined to be an $m$-PF edge cut if either the removal of $\widetilde{E}$ results a trivial $m$-PF graph or its removal reduces the strength of connectedness between some pairs of vertices in $G$, i.e., $P_j \circ CONN_{G \setminus \widetilde{E}}(x, y) < P_j \circ CONN_{G}(x, y)$ ($1 \leq j \leq m$) for $x, y \in X$ such that at least one of $x$ or $y$ is different from end nodes of edges $e_i$ ($i = 1, 2, \ldots , k$). Here, we consider only strong $m$-PF edges in $\widetilde{E}$ as weak $m$-PF edges do not effect the strength of connectedness between any two vertices.

Definition 3.10. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph and $\widetilde{E}$ be an $m$-PF edge cut of $G$. Then the strong weight of $\widetilde{E}$ is denoted by $S'_W(\widetilde{E}) = (P_1 \circ S'_W(\widetilde{E}), P_2 \circ S'_W(\widetilde{E}), \ldots , P_m \circ S'_W(\widetilde{E}))$ and it is defined as $S'_W(\widetilde{E}) = (\sum_{e_i \in \widetilde{E}} P_1 \circ \sigma(e_i), \sum_{e_i \in \widetilde{E}} P_2 \circ \sigma(e_i), \ldots , \sum_{e_i \in \widetilde{E}} P_m \circ \sigma(e_i))$ where for each $1 \leq j \leq m$, $\sum_{e_i \in \widetilde{E}} P_j \circ \sigma(e_i)$ represents the sum of the MVs of strong $m$-PF edges in $\widetilde{E}$.

Definition 3.11. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph. The $m$-polar fuzzy edge connectivity of $G$ is denoted by $\kappa'(G) = (P_1 \circ \kappa'(G), P_2 \circ \kappa'(G), \ldots , P_m \circ \kappa'(G))$ in which each $j$-th component ($1 \leq j \leq m$) is defined as $P_j \circ \kappa'(G) = \min \{P_j \circ S'_W(\widetilde{E}_i); i \in \omega \}$, i.e., it is the minimum of strong weights of $m$-PF edge cuts of $G$.

Example 3.5. Consider $3$-PF graph $G$ as given in Figure 4. It is already observed that $x_1x_2$, $x_2x_3$ and $x_3x_4$ are strong $m$-PF edges. Consider two vertices $x_2$ and $x_4$. Here, $CONN_G(x_2, x_4) = (0.2, 0.5, 0.6)$. Then $m$-PF edge cuts containing one edge with their strong weights are $\widetilde{E}_1 = \{x_2x_3\}$ $S'_W(\widetilde{E}_1) = (0.2, 0.5, 0.6)$ and $\widetilde{E}_2 = \{x_3x_4\}$ $S'_W(\widetilde{E}_2) = (0.3, 0.5, 0.7)$. Also, any two or three strong $m$-PF edges of $G$ can be considered as $m$-PF edge cut with strong weight greater than $\widetilde{E}_i$ (i = 1, 2). Therefore, $\kappa'(G) = (0.2, 0.5, 0.6)$.

We now present the $m$-PF analogue of Whitney's renowned result on vertex connectivity, edge connectivity and minimum degree of a graph.

Theorem 3.6. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph. Then for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \leq P_j \circ \kappa'(G) \leq P_j \circ \delta_S(G)$.

Proof. Let $G = (\mu, \sigma)$ be a non-trivial connected $m$-PF graph. To show that $P_j \circ \kappa'(G) \leq P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$. Suppose that $x$ be a vertex of $G$ with $P_j \circ d_S(x) = P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$. Also, let $F$ be the collection of strong $m$-PF edges which are incident at vertex $x$. Then

Case ⅰ. If the strong $m$-PF edges in $F$ are the only edges incident at $x$, then the removal of $F$ from $G$ results a disconnected $m$-PF graph.

Case ⅱ. If not, let $xy$ be an $m$-PF edge incident at vertex $x$ such that it is weak. Then $y$ is a vertex different from end vertices of strong $m$-PF edges in $F$. Since, $xy$ is not strong. This implies that for each $1 \leq j \leq m$, $P_j \circ \sigma(xy) < P_j \circ CONN_G(x, y)$. This implies that there exists at least one strongest $m$-PF path (say $P$) between $x$ and $y$ in $G$ such that it passes through one of the strong $m$-PF edge at $x$. Therefore, the removal of $F$ from $G$ must reduces the strength of connectedness between $x$ and $y$. Hence, in both cases, $F$ is an $m$-PF edge cut with strong weight $\delta_S(G)$, i.e., $P_j \circ S'_W(F) = P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$. This shows that $P_j \circ \kappa'(G) \leq P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$.

Now, to show first inequality $P_j \circ \kappa(G) \leq P_j \circ \kappa'(G)$ for each $1 \leq j \leq m$. Assume that $F$ be an $m$-PF edge cut with strong weight $S'_W(F) = \kappa'$. Then following are the two cases:

Case ⅰ. One end vertex of all strong $m$-PF edges in $F$ is same (say $x$). Then $F = \{xx_k; k = 1, 2, \ldots , n\}$. Let $\widetilde{X} = \{x_1, x_2, \ldots , x_n\}$. Obviously, $\widetilde{X}$ is an $m$-PF vertex cut. Now, $\inf \limits_{y \in X}\{P_j \circ \sigma(x_ky)\} \leq P_j \circ \sigma(xx_k)$ for each $1 \leq j \leq m$. Therefore, $\sum \limits_{k = 1}^n[\inf \limits_{y \in X}\{P_j \circ \sigma(x_ky)\}] \leq \sum \limits_{k = 1}^n P_j \circ \sigma(xx_k)$ for each $1 \leq j \leq m$. Thus, $P_j \circ \kappa(G) \leq P_j \circ \kappa'(G)$ for each $1 \leq j \leq m$.

Case ⅱ. There is no common end vertex of strong $m$-PF edges in $F$. Let $F = \{x_ky_k; k = 1, 2, \ldots , n\}$. Let $\widetilde{X}_1 = \{x_1, x_2, \ldots , x_n\}$ and $\widetilde{X}_2 = \{y_1, y_2, \ldots , y_k\}$. By assumption, we have for each $1 \leq j \leq m$, $P_j \circ CONN_{G \setminus F}(u, v) < P_j \circ CONN_G(u, v)$ for some pair of vertices $u, v \in X$ such that at least one of them is different from both $x_k$ and $y_k$ ($k = 1, 2, \ldots , n$). Then either $u$ and $v$ does not belong to $\widetilde{X}_1 \bigcup \widetilde{X}_2$ or one of them belongs to $\widetilde{X}_1 \bigcup \widetilde{X}_2$.

(a) When $u, v \notin \widetilde{X}_1 \bigcup \widetilde{X}_2$. Let $\widetilde{X} = \widetilde{X}_1$ or $\widetilde{X} = \widetilde{X}_2$. Then obviously $\widetilde{X}$ is an $m$-PF vertex cut as its removal from $G$ reduce the strength of connectedness between $u$ and $v$. Thus, for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \leq P_j \circ S_W(\widetilde{X}) \leq P_j \circ S'_W(F) = P_j \circ \kappa'(G)$.

(b) When $u$ or $v$ $\in \widetilde{X}_1 \bigcup \widetilde{X}_2$. Suppose that $u \in \widetilde{X}_1 \bigcup \widetilde{X}_2$ with out the loss of generality. Also, let $u \in \widetilde{X}_1$ and let $\widetilde{X} = \widetilde{X}_2$. Obviously, $\widetilde{X}$ is an $m$-PF vertex cut as its removal from $G$ reduce the strength of connectedness between $u$ and $v$. Thus, for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \leq P_j \circ S_W(\widetilde{X}) \leq P_j \circ S'_W(F) = P_j \circ \kappa'(G)$.

Hence, for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \leq P_j \circ \kappa'(G) \leq P_j \circ \delta_S(G)$ in all cases. This completes the proof.

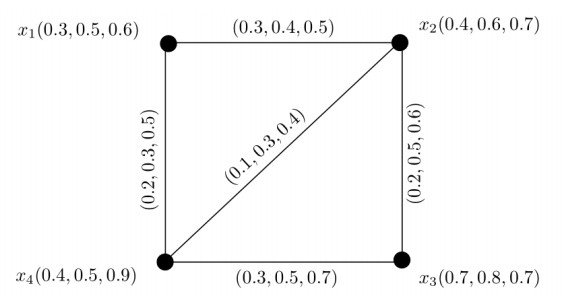
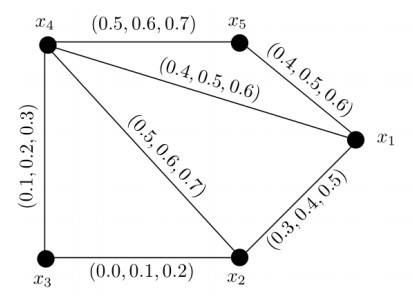
Example 3.6. Let $X = \{x_1, x_2, x_3, x_4\}$ be the set of vertices and $E = \{x_1x_2, x_1x_3, x_1x_4, x_2x_3, x_3x_4\}$ be the set of edges. Let $\mu$ be a $3$-PF set on $X$ (Table 7) and $\sigma$ be a $3$-PF relation on $X$ (Table 8). The related $3$-PF graph $G = (\mu, \sigma)$ is given in Figure 5. The SDs of vertices are $D_S(x_1) = (1.0, 0.7, 1.1)$, $D_S(x_2) = (1.5, 0.9, 1.3)$, $D_S(x_3) = (2.1, 1.8, 2.4)$, $D_S(x_4) = (1.2, 1.0, 1.4)$. The SD$_{min}$ of $G$ is $\delta_S(G) = (1.0, 0.7, 1.1)$. Here, $\kappa(G) = (0.4, 0.3, 0.5)$ and $\kappa'(G) = (1.2, 1.0, 1.4)$. It is easy to verify for each $1 \leq j \leq m$ that $P_j \circ \kappa(G) \leq P_j \circ \kappa'(G) \leq P_j \circ \delta_S(G)$.

Theorem 3.7. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph. Then for each $1 \leq j \leq m$, $P_j \circ \kappa(G) = P_j \circ \delta_S(G) = P_j \circ \kappa'(G)$.

Proof. Let $G = (\mu, \sigma)$ be an complete $m$-PF graph with $|X| = n$. Then the removal of any set (say $F$) containing $n - 2$ edges from $G$ will reduce the strength of connectedness between the pairs of end vertices of edges in $F$ only. (Note: Since $G$ is an complete $m$-PF graph, all of its edges are strong $m$-PF edges. Therefore, the removal of any edge will not reduce the strength of connectedness of vertices other than its end vertices.) Now, any set containing $n - 1$ edges incident at a vertex $x$ in $G$ is an $m$-PF edge cut with $P_j \circ S'_W(G) = P_j \circ d_S(x)$ for each $1 \leq j \leq m$. Let $y$ be a vertex in $G$ such that for each $1 \leq j \leq m$, $P_j \circ d_S(y) = P_j \circ \delta_S(G)$. Obviously the set of edges incident at vertex $y$ is an $m$-PF edge cut with minimum strong weight. Therefore, for each $1 \leq j \leq m$, $P_j \circ \kappa'(G) = P_j \circ d_S(y) = P_j \circ \delta_S(G)$.

Next, we will show that for each $1 \leq j \leq m$, $P_j \circ \kappa(G) = P_j \circ \delta_S(G)$. Suppose on contrary that equality does not hold, i.e., $P_j \circ \kappa(G) \neq P_j \circ \delta_S(G)$ for some $j$. According to Theorem 3.3, for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \leq P_j \circ \delta_S(G) \leq P_j \circ \kappa'(G)$. This implies that $P_j \circ \kappa(G) \leq P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$. However, the removal of $i$ vertices $1 \leq i \leq n - 2$ again results in a non-trivial complete $m$-PF graph, any $m$-PF vertex cut should contain at least $n - 1$ vertices. Let $A_1$ be an $m$-PF vertex cut among such $m$-PF vertex cuts such that $A_1$ does not contain a vertex $y$ having $P_j \circ d_S(y) = P_j \circ \delta_S(G)$. As the edges incident at vertices of $A_1$ with one of its end at $y$ are the set of edges with minimum weights at vertices of $A_1$, i.e., $A_1$ will have the minimum strong weight. Therefore, $P_j \circ \kappa(G) = P_j \circ S(A_1) < P_j \circ \delta_S(G)$ for each $1 \leq j \leq m$. Suppose that $F_1$ contains all edges incident at vertex $y$, then $F_1$ is an $m$-PF edge cut such that for each $1 \leq j \leq m$, $P_j \circ S'(F_1) = P_j \circ S(A_1) < P_j \circ \delta_S(G)$. This contradicts the fact that for each $1 \leq j \leq m$, $P_j \circ \kappa'(G) = P_j \circ \delta_S(G)$. Thus, for each $1 \leq j \leq m$, $P_j \circ \kappa(G) = P_j \circ \delta_S(G) = P_j \circ \kappa'(G)$. Hence, the theorem is completed.

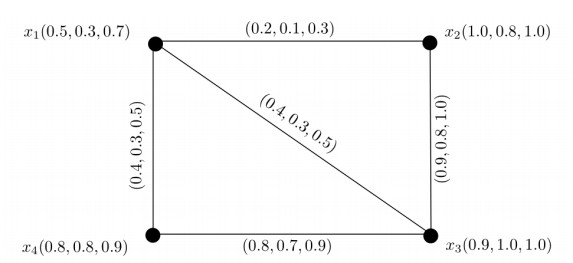
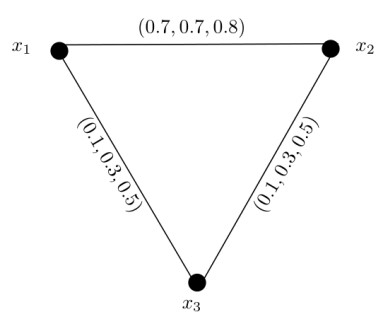
The converse of Theorem 3.7 does not hold in general, that is, if for each $1 \leq j \leq m$, $P_j \circ \kappa(G) = P_j \circ \kappa'(G) = P_j \circ \delta_S(G)$ then it is not necessary that the considered $G$ is an complete $m$-PF graph. For illustration, consider the following $3$-PF graph $G$ (Figure 6). The SDs of vertices are $D_S(x_1) = (0.2, 0.1, 0.3)$, $D_S(x_2) = (0.4, 0.2, 0.6)$, $D_S(x_3) = (0.2, 0.1, 0.3)$. The SD$_{min}$ of $G$ is $\delta_S(G) = (0.2, 0.1, 0.3)$. Here, $\kappa(G) = (0.2, 0.1, 0.3)$ = $\kappa'(G) = \delta_S(G)$. However, it is clear that $G$ is not complete $m$-PF graph.

Note 3.2. Note that Theorem 3.6 does not hold in general. It is valid in case of particular $m$-PF graphs having same relationship between all components of MVs of edges or the MVs of edges are comparable with each other.

Definition 3.12. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph. Also, let $r = (r_1, r_2, \ldots , r_m)$ such that $r_j \in (0, \infty)$ ($j = 1, 2, \ldots , m$). Then $G$ is said to be $r$-connected if $P_j \circ \kappa(G) \geq r_j$ for each $1 \leq j \leq m$. It is said to be $r$-edge connected if $P_j \circ \kappa'(G) \geq r_j$ for each $1 \leq j \leq m$.

Example 3.7. Let $X = \{x_1, x_2, x_3, x_4, x_5\}$ be the set of vertices and $E = \{x_1x_2, x_1x_4, x_1x_5, x_2x_3, x_3x_5, x_3x_4, x_3x_5, x_4x_5\}$ be the set of edges. Let $\mu(x_i) = (1, 1, 1)$ for $i = 1, 2, \ldots , 5$. Let $\sigma$ be a $3$-PF relation on $X$ (Table 9). The related $3$-PF graph $G = (\mu, \sigma)$ is given in Figure 7. The $m$-PF vertex cuts with their strong weights are: $\widetilde{X}_1 = \{x_3\}$ $S_W(\widetilde{X}_1) = (0.1, 0.2, 0.3)$, $\widetilde{X}_2 = \{x_3, x_4\}$ $S_W(\widetilde{X}_2) = (0.2, 0.4, 0.6)$, $\widetilde{X}_3 = \{x_2, x_3\}$ $S_W(\widetilde{X}_3) = (0.2, 0.4, 0.6)$, $\widetilde{X}_4 = \{x_1, x_2, x_3\}$ $S_W(\widetilde{X}_4) = (0.3, 0.6, 0.9)$ and $\widetilde{X}_5 = \{x_1, x_2, x_3, x_5\}$ $S_W(\widetilde{X}_5) = (0.4, 0.8, 1.2)$. Here, $\kappa(G) = (0.1, 0.2, 0.3)$. Thus, $G$ is $r$-connected such that $r_1 \in (0, 0.1]$, $r_2 \in (0, 0.2]$ and $r_3 \in (0, 0.3]$. The $m$-PF edge cuts with their strong weights are: $\widetilde{E}_1 = \{x_3x_4\}$ $S'_W(\widetilde{E}_1) = (0.8, 0.9, 1.0)$, $\widetilde{E}_2 = \{x_4x_5\}$ $S'_W(\widetilde{E}_2) = (0.5, 0.6, 0.7)$, $\widetilde{E}_3 = \{x_1x_2\}$ $S'_W(\widetilde{E}_3) = (0.8, 0.9, 1.0)$. The $m$-PF edge cuts other than $\widetilde{E}_1$, $\widetilde{E}_2$ and $\widetilde{E}_3$ will have strong weights greater than $(0.8, 0.9, 1.0)$. Therefore, the minimum strong weight among all $m$-PF edge cuts is $\kappa'(G) = (0.5, 0.6, 0.7)$. Hence, $G$ is $r$-edge connected such that $r_1 \in (0, 0.5]$, $r_2 \in (0, 0.6]$ and $r_3 \in (0, 0.7]$.

We now discuss some results related to $r$-connected $m$-PF graphs and $r$-edge connected $m$-PF graphs as follows:

Theorem 3.8. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph and $x, y \in X$. Also, let $t$ be the number of internally disjoint strongest $m$-PF paths between $x$ and $y$ in $G$. Then $G$ is $r$-connected $m$-PF graph if and only if for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$.

Proof. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph and $x, y \in X$. Also, let $t$ be the number of internally disjoint strongest $m$-PF paths between $x$ and $y$ in $G$. Suppose that $G$ is $r$-connected $m$-PF graph. By definition, $P_j \circ \kappa(G) \geq r_j$ for each $1 \leq j \leq m$. We have to show that for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$. Suppose on contrary that this relation does not exist for some pair of vertices $x$ and $y$ then for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] < r_j$. Let $\widetilde{X}$ be a minimal $x-y$ SRSVs in $G$ with minimum strong weight $S_W(\widetilde{X})$. Since there are $t$ internally disjoint $[x, y]$-$m$-PF paths in $G$. By Theorem 4.5 ^[42], $|\widetilde{X}| = t$. Let $P^1$, $P^2$, $\ldots$, $P^t$ be the internally disjoint $[x, y]$-$m$-PF paths in $G$. Then by Theorem 4.3 ^[42], $P^i$ ($i = 1, 2, \ldots , t$) must contain at least one vertex from $\widetilde{X}$. Also, $P^i$ ($i = 1, 2, \ldots , t$) are internally disjoint so there is no common vertex in them except $x$ and $y$. This implies that each $P^i$ ($i = 1, 2, \ldots , t$) contains exactly one vertex (say $y_i$) from $\widetilde{X}$. Also, if $P$ is a strongest is a strongest $m$-PF path different from $P^i$ ($i = 1, 2, \ldots , t$) then $P$ must have common vertex with some $P^i$ ($i = 1, 2, \ldots , t$) from $\widetilde{X}$. This implies that $\widetilde{X}$ is $m$-PF vertex cut in $G$. Since $\widetilde{X}$ is of minimum strong weight. Therefore, at least one of the edges incident at $y_i$ in $P^i$ ($i = 1, 2, \ldots , t$) $P_j \circ \sigma(x_iy_i) = P_j \circ CONN_G(x, y)$ for each $1 \leq j \leq m$. This implies that $S_W(\widetilde{X}) = |\widetilde{X}| [P_j \circ CONN_G(x, y)] = t [P_j \circ CONN_G(x, y)] < r_j$. This means that $P_j \circ \kappa(G) < r_j$ for each $1 \leq j \leq m$. This is contradiction to our supposition that for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \geq r_j$. Hence, for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$.

Next, for converse of the theorem, suppose that $t[P_j \circ CONN_G(x, y)] \geq r_j$ for each $1 \leq j \leq m$. We have to show that $G$ is $r$-connected $m$-PF graph. For this we have to show that for each $1 \leq j \leq m$, $P_j \circ \kappa(G) \geq r_j$. Suppose on contrary that for each $1 \leq j \leq m$, $P_j \circ \kappa(G) < r_j$. Then there exists an $m$-PF vertex cut $\widetilde{X}$ such that $P_j \circ S_W(\widetilde{X}) < r_j$ for each $1 \leq j \leq m$. Also, $P_j \circ CONN_{G \setminus \widetilde{X}}(x, y) < P_j \circ CONN_G(x, y)$ for each $1 \leq j \leq m$ and for some $x, y \in X$. This implies that $\widetilde{X}$ is $x-y$ SRSVs in $G$. Then by Theorem 4.5 ^[42], $t =$ number of vertices in minimal $x-y$ SRSVs $\leq |\widetilde{X}|$. Therefore, $t[P_j \circ CONN_G(x, y)] \leq |\widetilde{X}| [P_j \circ CONN_G(x, y)] \leq P_j \circ S_W(\widetilde{X}) < r_j$ for each $1 \leq j \leq m$. This completes the prove.

For illustration of Theorem 3.8, consider the following $3$-PF graph $G$ as shown in Figure 8. Here, the $m$-PF vertex cuts with their strong weights are: $\widetilde{X}_1 = \{x_1, x_2\}$ $S_W(\widetilde{X}_1) = (0.2, 0.6, 1.0)$, $\widetilde{X}_2 = \{x_1, x_3\}$ $S_W(\widetilde{X}_2) = (0.2, 0.6, 1.0)$ and $\widetilde{X}_3 = \{x_2, x_3\}$ $S_W(\widetilde{X}_3) = (0.2, 0.6, 1.0)$. Hence, $\kappa(G) = (0.2, 0.6, 1.0)$. Therefore, $G$ is $r$-connected $m$-PF graph such that $r_1 \in (0, 0.2]$, $r_2 \in (0, 0.6]$ and $r_3 \in (0, 1.0]$. Now, consider two vertices $x_1$ and $x_3$ in $G$. There are two internally disjoint $m$-PF paths between them (thus $t = 2$), namely $P^1 : x_1 - x_3$ and $P^2 : x_1 - x_2 - x_3$. Both these paths are strongest $m$-PF paths with equal strengths $(0.1, 0.3, 0.5) = CONN_G(x_1, x_3)$. It is easy to verify for each $j$-th component ($1 \leq j \leq m$) that $t[P_j \circ CONN_G(x_1, x_3)] = P_j \circ \kappa(G) \geq r_j$ where $r_1 \in (0, 0.2]$, $r_1 \in (0, 0.6]$ and $r_1 \in (0, 1.0]$. It can also be verified for remaining pairs of vertices in $G$. Hence, the result holds.

Theorem 3.9. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph and $x, y \in X$. Also, let $t$ be the number of edge-disjoint strongest $m$-PF paths between $x$ and $y$ in $G$. Then $G$ is $r$-edge connected $m$-PF graph if and only if for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$.

Proof. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph and $x, y \in X$. Also, let $t$ be the number of edge-disjoint strongest $m$-PF paths between $x$ and $y$ in $G$. Suppose that $G$ is $r$-connected $m$-PF graph. By definition, $P_j \circ \kappa'(G) \geq r_j$ for each $1 \leq j \leq m$. We have to show that for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$. Suppose on contrary that this relation does not exist for some pair of vertices $x$ and $y$ then for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] < r_j$. Let $\widetilde{E}$ be a minimal $x-y$ SRSEs in $G$ with minimum strong weight $S'_W(\widetilde{E})$. Since there are $t$ edge-disjoint $[x, y]$-$m$-PF paths in $G$. By Theorem 4.5 ^[42], $|\widetilde{E}| = t$. Let $P^1$, $P^2$, $\ldots$, $P^t$ be the edge-disjoint $[x, y]$-$m$-PF paths in $G$. Then by Theorem 4.4 ^[42], $P^i$ ($i = 1, 2, \ldots , t$) must contain at least one vertex from $\widetilde{E}$. Also, $P^i$ ($i = 1, 2, \ldots , t$) are edge-disjoint so there is no common edge in them. This implies that each $P^i$ ($i = 1, 2, \ldots , t$) contains exactly one edge from $\widetilde{E}$. Also, if $P$ is a strongest $m$-PF path different from $P^i$ ($i = 1, 2, \ldots , t$) then $P$ must have common edge with some $P^i$ ($i = 1, 2, \ldots , t$) from $\widetilde{E}$. This implies that $\widetilde{E}$ is $m$-PF edge cut in $G$. Since $\widetilde{E}$ is of minimum strong weight. This implies that $S_W(\widetilde{E}) = |\widetilde{E}| [P_j \circ CONN_G(x, y)] = t [P_j \circ CONN_G(x, y)] < r_j$. This means that $P_j \circ \kappa'(G) < r_j$ for each $1 \leq j \leq m$. This is contradiction to our supposition that for each $1 \leq j \leq m$, $P_j \circ \kappa'(G) \geq r_j$. Hence, for each $1 \leq j \leq m$, $t[P_j \circ CONN_G(x, y)] \geq r_j$.

Next, for converse of the theorem, suppose that $t[P_j \circ CONN_G(x, y)] \geq r_j$ for each $1 \leq j \leq m$. We have to show that $G$ is $r$-edge connected $m$-PF graph. For this we have to show that for each $1 \leq j \leq m$, $P_j \circ \kappa'(G) \geq r_j$. Suppose on contrary that for each $1 \leq j \leq m$, $P_j \circ \kappa'(G) < r_j$. Then there exists an $m$-PF edge cut $\widetilde{E}$ such that $P_j \circ S'_W(\widetilde{E}) < r_j$ for each $1 \leq j \leq m$. Also, $P_j \circ CONN_{G \setminus \widetilde{E}}(x, y) < P_j \circ CONN_G(x, y)$ for each $1 \leq j \leq m$ and for some $x, y \in X$. This implies that $\widetilde{E}$ is $x-y$ SRSEs in $G$. Then by Theorem 4.5 ^[42], $t =$ number of edges in minimal $x-y$ SRSEs $\leq |\widetilde{E}|$. Therefore, $t[P_j \circ CONN_G(x, y)] \leq |\widetilde{E}| P_j \circ CONN_G(x, y) \leq P_j \circ S'_W(\widetilde{E}) < r_j$ for each $1 \leq j \leq m$. This completes the prove.

4.   Application of $m$-PF graph clustering

In this section we will analyze $m$-PF graphs from connectedness point of view. The related results will be applied to clustering analysis.

Definition 4.1. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph. A vertex $x \in X$ is said to be $\epsilon_A$-reachable from another vertex $y$ if $\frac{\sum_{j = 1}^m P_j \circ CONN_G(x, y)}{m} \geq \epsilon_A$ for some $\epsilon_A \in (0, 1]$.

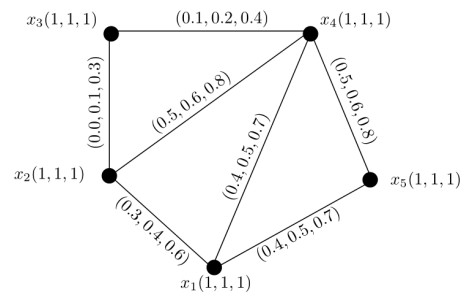
Example 4.1. Let $X = \{x_1, x_2, x_3, x_4\}$ be the set of vertices and $E = \{x_1x_2, x_1x_3, x_1x_4, x_2x_3, x_2x_4, x_3x_4\}$ be the set of edges. Let $\mu(x_1) = (1, 1, 1) = \mu(x_2) = \mu(x_3) = \mu(x_4) = \mu(x_5)$ be a $3$-PF set on $X$ and $\sigma$ be a $3$-PF relation on $X$ (Table 10). The related $3$-PF graph $G = (\mu, \sigma)$ is given in Figure 9. Consider two vertices $x_1$ and $x_3$. The $m$-PF paths from $x_1$ to $x_3$ with their strengths are $P^1 : x_1 - x_2 - x_3$ $S(P^1) = (0.0, 0.1, 0.2)$, $P^2 : x_1 - x_4 - x_3$ $S(P^2) = (0.1, 0.2, 0.3)$, $P^3 : x_1 - x_4 - x_2 - x_3$ $S(P^3) = (0.0, 0.1, 0.2)$, $P^4 : x_1 - x_5 - x_4 - x_3$ $S(P^4) = (0.1, 0.2, 0.3)$ and $P^5 : x_1 - x_5 - x_4 - x_2 - x_3$ $S(P^5) = (0.0, 0.1, 0.2)$. The strength of connectedness between $x_1$ and $x_3$ is $CONN_G(x_1, x_3) = (0.1, 0.2, 0.3)$. Here, $\frac{\sum_{j = 1}^3 P_j \circ CONN_G(x_1, x_3)}{3} = \frac{0.1 + 0.2 + 0.3}{3} = \frac{0.6}{3} = 0.2$. Thus, $x_1$ is $\epsilon_A$-reachable from $x_3$ for $\epsilon_A = 0.2$. This means that similarity between $x_1$ and $x_3$ is at most $20 \%$. Similarly, we can check $\epsilon_A$-reachability between other pairs of vertices of $G$.

Definition 4.2. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph. It is said to be $\epsilon_A$-connected $m$-PF graph if and only if all pairs of vertices are mutually $\epsilon_A$-reachable from each other in $G$.

Remark 4.1. If any two vertices in $G$ are mutually $\epsilon_A$-reachable then it is not necessary that $G$ is itself $\epsilon_A$-connected $m$-PF graph.

Remark 4.2. If $G$ is $\epsilon_A$-connected $m$-PF graph then any two vertices in $G$ are necessarily mutually $\epsilon_A$-reachable.

Remark 4.3. If $G$ is not $\epsilon_A$-connected $m$-PF graph but some pairs of vertices in $G$ are mutually $\epsilon_A$-reachable then an $m$-PF subgraph $\widetilde{G}$ containing all mutually $\epsilon_A$-reachable pairs of vertices is said to be $\epsilon_A$-connected $m$-PF subgraph of $G$.

Definition 4.3. Let $G = (\mu, \sigma)$ be a connected $m$-PF graph such that it is not $\epsilon_A$-connected $m$-PF graph. Then a maximal $\epsilon_A$-connected $m$-PF subgraph $\widetilde{G}$ of $G$ is defined to be $\epsilon_A$-connected $m$-PF component such that it is not properly contained in any other maximal $\epsilon_A$-connected $m$-PF subgraph of $G$.

We now use Definition 4.3 of $\epsilon_A$-connected $m$-PF components to define $\epsilon_A$-clusters of vertices of $G$ in Definition 4.4.

Definition 4.4 Let $G = (\mu, \sigma)$ be a connected $m$-PF graph. A collection $C_{\epsilon_A}$ of subsets of $X$ is said to be $\epsilon_A$-cluster if $m$-PF subgraphs of $G$ induced by members of $C_{\epsilon_A}$ are $\epsilon_A$-connected $m$-PF components of $G$.

4.1.   Algorithm for $m$-PF graph clustering

To construct $\epsilon_A$-clusters of vertices of $G$, we will use the following algorithm:

Step 1. Consider a connected $m$-PF graph $G = (\mu, \sigma)$ with $|X| = n$ and $E$ be the set of edges of $G$.

Step 2. Compute matrix $R(G) = [r_{ik}]_{n \times n}$ such that its main diagonal entries $x_ix_k$ for which $i = k$ are $(1, 1, \ldots , 1)$, its $ik$-th entries for which $i \neq k$ and $x_ix_k \in E$ are MVs of edges $x_ix_k$, its $ik$-th entries for which $i \neq k$ and $x_ix_k \not\in E$ are $(0, 0, \ldots , 0)$. Mathematically, entries of $R(G)$ are given as below:

We call $R(G)$ as a direct reachable matrix of $G$.

Step 3. Compute matrix $C(G) = [c_{ik}]_{n \times n}$ such that its main diagonal entries $x_ix_k$ for which $i = k$ are $(1, 1, \ldots , 1)$, its $ik$-th entries for which $i \neq k$ represent the strength of connectedness between each pair of distinct vertices in $G$. Mathematically, entries of $C(G)$ are given as below:

We call $C(G)$ as matrix of strength of connectedness between pairs of vertices of $G$.

Step 4. Compute matrix $C_A(G) = [c_A{_{ik}}]_{n \times n}$ such that its main diagonal entries $x_ix_k$ for which $i = k$ are $1$, its $ik$-th entries for which $i \neq k$ represent the average of all $j$ components of strength of connectedness between each pair of distinct vertices in $G$. Mathematically, entries of $C_A(G)$ are given as below:

We call $C_A(G)$ as matrix of average strength of connectedness between pairs of vertices of $G$.

Step 5. Construct the collection $C_{\epsilon_A}$ containing the subsets $C_i \subseteq X$ such that all vertices in $C_i$ are mutually $\epsilon_A$-reachable from each other, i.e.,

Then each subset $C_i$ of $X$ in $C_{\epsilon_A}$ is $\epsilon_A$-cluster of vertices of $G$.

Let us consider the following example to obtain $\epsilon_A$-clusters of vertices of $G$ by applying the previous algorithm.

Example 4.2. Consider an $3$-PF graph $G = (\mu, \sigma)$ as shown in Figure 10.

The direct reachable matrix $R(G)$ of $G$ is given below:

The matrix $C(G)$ of strength of connectedness between pairs of vertices of $G$ is calculated as below:

The matrix $C_A(G)$ of average strength of connectedness between pairs of vertices of $G$ is calculated as below:

The different $\epsilon_A$-clusters of vertices of $G$ are as follows:

4.2.   Application

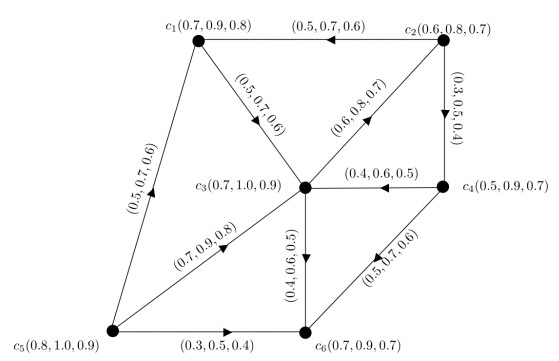
In daily life, we are using different products of different companies. We conducted a survey on consumer decision making process and how consumers are interested in evaluation of alternatives before buying a product. The survey data collection contains the information of 6 companies. Each company aim to facilitate their consumers with best quality of products and services. They have to make sure that prices and policies should be change at right time. This task is possible by planning efficient advertisements for the sale of products. The consumers will take the decision to purchase product from a particular company after considering following parameters, including price of the product, quality of the product and services of the company. All these parameters related to each company according to the consumers are uncertain in nature with respect to time period. Therefore, fuzziness can be added for representing each parameter related to each company. Let $X = \{c_1, c_2, c_3, c_4, c_5, c_6\}$ be the set of six companies (vertices) who offered different prices, qualities and services to the consumers. For each company from set $X$, the consumers can assign a MV in $(0, 1]$ corresponding to their parameters, including price of product, quality of the product and services of the company. The MVs corresponding to the parameters of each company are given in Table 11. The directed edges between two companies represent their common policies related to price, quality and services offering to the consumers. The MVs of directed edges are given in Table 12. The corresponding directed $3$-PF graph $G = (\mu, \overrightarrow{\sigma})$ is shown in Figure 11, where $\mu$ is $3$-PF set of companies with respect to their price, quality and services and $\overrightarrow{\sigma}$ is a $3$-PF relation of common policies of companies.

The direct reachable matrix $R(\overrightarrow{G})$ of $\overrightarrow{G}$ is given below:

The matrix $C(G)$ of strength of connectedness between pairs of vertices of $G$ is calculated as below:

The matrix $C_A(G)$ of average strength of connectedness between pairs of vertices of $G$ is calculated as below:

The different $\epsilon_A$-clusters of vertices of $\overrightarrow{G}$ are as follows:

From the above clusters, it is observed that the policies of companies $c_1, c_2, c_3, c_5$ are almost same while policies of company $c_4$ and $c_6$ are totally different.

We now present the general procedure of our method which is used in our application from the algorithm given below.

5.   Comparative analysis and discussion

In this section, we discuss the already existing models to check the validity and superiority of our proposed model. The aim of clustering is to divide the observations into groups with a high degree of "association'' among members of the same group and a low degree of "association'' among members of the different groups. Clustering is nothing more than partitioning a graph based on qualitative aspects of the data in graph-theoretical aspects. The first two articles on FG theory by Rosenfeld ^[18] and Yeh and Bang ^[17] were intended to present FG clustering techniques. Rosenfeld ^[18] proposed FG clustering based on distance, while Yeh and Bang ^[17] introduced connectivity parameters in FGs and proposed FG clustering based on connectivity. To extract FG clusters, Yeh and Bang ^[17] introduced a series of processes such as single linkage, $k$-linkage, $k$-edge connectivity, $k$-vertex connectivity, and complete linkage.

a. Arc connectivity based clustering

In reference ^[4], Mathew and Sunitha proposed fuzzy arc connectivity based clustering techniques. This approach is demonstrated with a cancer detection problem, in which cell clusters in a tissue are classified into different stages of cancer based on their distribution, density, and fuzzy connectivity within the tissue. This method aids in qualitatively analyzing the cancer's complex progression. This approach is based on three steps:

${\bf{1)}}$ Obtain the cohesive matrix ^[17] $M$ of the FG $G = (\mu, \sigma)$.

${\bf{2)}}$ Obtain the $t$-threshold graph $G^t$ of $M$.

${\bf{ 3)}}$ The maximal complete subgraphs of $G^t$ are the $t$-fuzzy edge components or fuzzy clusters of level $t$.

But, the computation of the cohesive matrix $M$ of FG $G$, $t$-threshold graph $G^t$ and maximal complete subgraphs of $G^t$ is difficult and it increases the time as well as calculation complexity in case of the large data.

${\bf{b.}}$ Connectivity reachability matrix based clustering

The idea of cohesion is simply connectedness between pairs of vertices. Yeh and Bang ^[17] built $\epsilon$-clusters using the connectivity reachability matrix of a FG. This approach is based on two simple steps:

${\bf{1)}}$ Compute the direct reachable matrix $R(G)$ and matrix of strength of connectedness between pairs of vertices of the FG $G = (\mu, \sigma)$.

${\bf{2)}}$ Compute $\epsilon$-clusters of vertices of $G$ by constructing the collection $C_{\epsilon}$, $C_{\epsilon} = \{C_i \subseteq X : CONN_G(x, y) \geq \epsilon, \epsilon \in (0, \infty), x, y \in C_i\}$.

This approach is quite simple and easy to compute. However, it is only applicable for single uncertain information, it cannot be utilized for multi-polar uncertain information. Multi-polar uncertain information can not be properly handled by FGs. This is our main motivation to introduced $\epsilon_A$-clusters using the connectivity reachability matrix of an $m$-PF graph which is a generalization of a FG.

Let us take an example of 5 students, namely Alexander, Elsa, Robert, Anthony, and Korey for numerical comparison of all these approaches. All the students are different according to their level of confidence, sources of knowledge, and communication skills. Also, the similarity of relationships among the students may be different according to their level of confidence, sources of knowledge, and communication skills. All the mentioned terms are uncertain in nature. Suppose, we want to classify the students with respect to the similarity of each relationship, including their level of confidence, sources of knowledge, and communication skills at a time.

${\bf{c.}}$ Comparison with arc connectivity based clustering

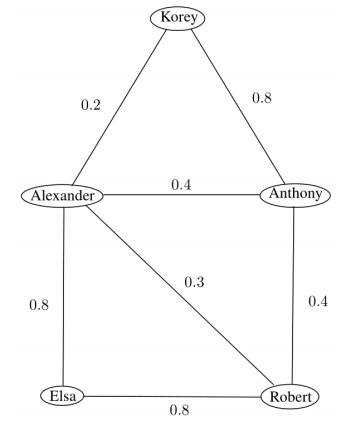
To classify the students with respect to each relationship, we have to make a separate FG representing that particular relationship. In Figure 12, a FG representing relationship among students with respect to their level of confidence is given. For the sake of simplicity, let us take $\mu_1(x_i) = 1$ for all $i = 1, 2, \ldots , 5$.

The cohesive matrix $M$ of FG $G_1 = (\mu_1, \sigma_1)$ and the matrix representing threshold graph $G_1^{0.8}$ for $t = 0.8$ of $M$ are given below:

The clusters of students under the relation of level of confidence obtained from $G_1^{0.8}$ are $\{$Alexander, Elsa, Robert, Anthony, Korey$\}$. Similarly, the clusters of students under the relations of sources of knowledge and communications skills can be analyzed. But, it is difficult and time consuming to find out clusters with respect to each relationship separately.

${\bf{d.}}$ Comparison with connectivity reachability matrix based clustering

We now classify the students using connectivity reachability matrix base clustering technique. For this, consider the FG $G_1 = (\mu_1, \sigma_1)$ as shown in Figure 12. The direct reachable matrix $R(G_1)$ and matrix of strength of connectedness between pairs of vertices $C(G_1)$ of $G_1$ are given below:

The clusters of students under the relation of level of confidence are $\{$Alexander, Elsa, Robert$\}$ and $\{$Anthony, Korey$\}$. Similarly, the clusters of students under the relations of sources of knowledge and communications skills can be analyzed. Although, we are able to find out more clusters of students based on this method as compared to the previous one. But, it is still difficult and time consuming to find out clusters with respect to each relationship separately.

${\bf{e. }}$ Proposed method clustering approach

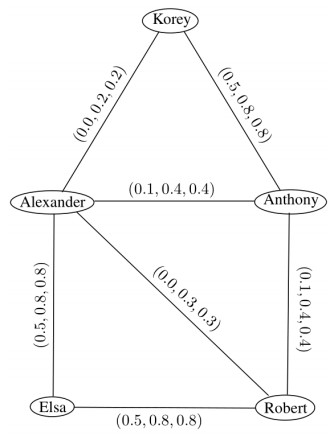
An $m$-PF graph is an extended approach of a FG. In an $m$-PF graph, all vertices and edges are multi-polar uncertain in nature and their MVs have multi-components according to the multi-polar uncertain statements. In which each component of MV can be any real number in $[0, 1]$. All these components are independent from each other. An $m$-PF graph is an efficient approach to discuss several relationships among students at a time. For example, consider a 3-PF graph $G = (\mu, \sigma)$ as shown in Figure 12. For the sake of simplicity, let us take $P_j \circ \mu(x_i) = 1$ for all $i = 1, 2, \ldots , 5$ and $1 \leq j \leq 3$.

Here, the MVs of vertices (students) are measured according to their level of confidence, sources of knowledge, and communication skills. The relationship among the students are represented by $3$-PF edges. Thus, the MV of each edge is measured according to the similarity between two students with respect to their level of confidence, sources of knowledge, and communication skills. Suppose, we want to classify the students with respect to their similarity corresponding to their level of confidence, sources of knowledge, and communication skills. The direct reachable matrix $R(G)$ and matrix of strength of connectedness between pairs of vertices $C(G)$ of $G$ are given below:

The matrix of average strength of connectedness between pairs of vertices $C_A(G)$ of $G$ is given below:

The clusters of students under the relations of level of confidence, sources of knowledge, and communication skills are $\{$Alexander$\}$, $\{$Elsa$\}$, $\{$Robert$\}$, $\{$Anthony$\}$, $\{$Korey$\}$. Here, we have obtained more clusters as compared to the previous two techniques. Therefore, an $m$-PF graph model provide an accurate information about clusters of students with respect to each relationship at a time. Thus, an $m$-PF graph is shown to be useful model in adapting problems if it is necessary to make decisions with a group of agreements.

6.   Merits and limitations of the proposed method

The following are some of the advantages of the proposed research work:

$1)$ The proposed research work discuss multi-polarity of the uncertain information and provides more flexible results.

$2)$ The provided method computes the $\epsilon_A$-clusters using the strength of connectedness between the pairs of vertices of an $m$-PF graph which increases the efficiency and feasibility of the proposed method.

Besides these advantages, the proposed method has certain drawbacks, which are given below:

$1)$ The proposed method of computing $\epsilon_A$-clusters of vertices of an $m$-PF graph $G = (\mu, \sigma)$ based on the matrix of average strength of connectedness between the pairs of vertices which is very convenient to apply, but on the other hand, it cannot provide accurate results if there are a few extreme MV corresponding to some component in the data.

$2)$ The proposed model is appropriate to deal with multi-polarity of the uncertain information which provides flexible results, but on the other hand it is difficult to handle multi-components of the MVs in case of large data and it increases the time as well as computation complexity.

7.   Conclusions

As a natural extension of fuzzy graphs, $m$-PF graphs have numerous applications in various fields, including decision-making, networking, or management sciences. In this study we have put forward novel tools for the investigation of these structures. These include the notions of strong degree and $m$-PF strength sequence of vertices, whose properties in complete $m$-PF graphs have been thoroughly examined. We have discussed connectivity parameters for $m$-PF graphs and presented the $m$-PF analogue of Whitney's theorem. We have characterized $r$-connected $m$-PF graphs and $r$-edge connected $m$-PF graphs, and we have discussed some of theorems related to them. Depending on the strength of connectedness between pairs of vertices, we have provided a clustering method for vertices in $m$-PF graphs. Moreover, we have discussed an application for clustering different companies in consideration of their multi-polar uncertain information. Finally, we have provided an algorithm to clearly express the various steps of the clustering method that we have used in our application.

The investigation of $m$-PF graphs can still produce many additional concepts and novel results. In particular, our research work can be further extended to incorporate $(1)$ Connectivity indices of $m$-PF graphs; $(2)$ cyclic connectivity index of $m$-PF graphs; and $(3)$ average cyclic connectivity index of $m$-PF graphs.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Acknowledgments

This project is partially funded by NRPU project no. 9073, HEC Islamabad.

Conflict of interest

The authors declare there is no conflict of interest.